Как найти остаточную сумму квадратов отклонений - Исправление недочетов и поиск решений вместе с Examum.ru

Пусть на количественный
нормально распределенный признак X
воздействует фактор F,
который имеет p
постоянных уровней. Будем предполагать,
что число
наблюдений
(испытаний) на каждом уровне одинаково
и равно q.

Таблица 1

Номер испытания	Уровни фактора
		…
1 2 … q	…	…	… … … …	…
Групповая средняя			…

Пусть наблюдалось
значений

признака X,
где i
– номер испытания (j
– номер уровня фактора (
Результаты наблюдений приведены в
таблице 1.

Введем,
по определению,

(общая
сумма
квадратов отклонений наблюдаемых
значений от общей средней ),

(факторная
сумма квадратов
отклонений групповых средних от общей
средней, которая характеризует рассеяние
«между группами»),

(остаточная
сумма
квадратов отклонений наблюдаемых
значений группы от своей групповой
средней, которая характеризует рассеяние
«внутри групп»).

Практически
остаточную сумму находят по равенству:

Элементарными
преобразованиями можно получить формулы,
более удобные для расчетов:

где
– сумма квадратов значений
признака на уровне

сумма
значений признака на уровне .

Замечание.
Для упрощения
вычислений вычитают из каждого
наблюдаемого значения одно и то же число
C,
примерно равное общей средней. Если
уменьшенные значения ,
то

где
– сумма квадратов
уменьшенных значений признака на

уровне

– сумма уменьшенных значений
признака на уровне

Для вывода формул

и
достаточно подставить

в
соотношение
и
в

соотношение

Пояснения.
1. Убедимся,
что
характеризует воздействие фактора F.
Допустим, что фактор оказывает
существенное влияние на X.
Тогда группа наблюдаемых значений при
одном определенном уровне, вообще
говоря, отличается от групп наблюдений
на других уровнях. Следовательно,
различаются и групповые средние, причем
они тем больше рассеяны вокруг общей
средней, чем большим окажется воздействие
фактора. Отсюда следует, что для оценки
воздействия фактора целесообразно
составить сумму квадратов отклонений
групповых средних об общей средней
(отклонение возводят в квадрат, чтобы
исключить погашение положительных и
отрицательных отклонений). Умножив эту
сумму на q,
получим .
Итак,
характеризует воздействие фактора.

2. Убедимся, что

отражает влияние случайных причин.
Казалось бы, наблюдения одной группы
не должны различаться. Однако, поскольку
на X,
кроме фактора F,
воздействуют и случайные причины
наблюдения одной и той же группы, вообще
говоря, различны и, значит, рассеяны
вокруг своей групповой средней. Отсюда
следует, что для оценки влияния случайных
причин целесообразно составить сумму
квадратов отклонений наблюдаемых
значений каждой группы от своей групповой
средней, т.е. .
Итак,
характеризует воздействие случайных
причин.

3. Убедимся, что

отражает влияние и фактора и случайных
причин. Будем рассматривать все наблюдения
как единую совокупность. Наблюдаемые
значения признака различны вследствие
воздействия фактора и случайных причин.
Для оценки этого воздействия целесообразно
составить сумму квадратов отклонений
наблюдаемых значений от общей средней,
т.е. .

Итак,
характеризует влияние фактора и случайных
причин.

Приведем пример,
который наглядно показывает, что
факторная сумма отражает влияние
фактора, а остаточная – влияние случайных
причин.

Пример.
Двумя приборами произведены по два
измерения физической величины, истинный
размер которой равен x.
Рассматривая в качестве фактора
систематическую ошибку C,
а в качестве его уровней – систематические
ошибки
и
соответственно первого и второго
прибора, показать, что
определяется систематическими, а
– случайными ошибками измерений.

Решение.
Введем обозначения:
– случайные ошибки первого и второго
измерений первым прибором;
– случайные ошибки первого и второго
измерений вторым прибором.

Тогда наблюдения
значения результатов измерений
соответственно равны (первый индекс
при x
указывает номер измерения, а второй –
номер прибора):

Средние значения
измерений первым и вторым приборами
соответственно равны:

Общая
средняя

факторная
сумма

Подставив величины,
заключенные в скобках, после элементарных
преобразований получим

Мы видим, что
определяется главным образом, первым
слагаемым (поскольку случайные ошибки
измерений малы) и, следовательно,
действительно отражает влияние фактора
C.

Остаточная сумма

Подставив
величины, заключенные в скобках, получим

Мы видим, что
определяются случайными ошибками
измерений и, следовательно, действительно
отражает влияние случайных причин.

Замечание.
То, что
порождается случайными причинами,
следует также из равенства:

Действительно,

является результатом воздействия
фактора и случайных причин; вычитая
мы исключаем влияние фактора. Следовательно,
«оставшаяся часть» отражает влияние
случайных причин.

Источник

Что такое остаточная сумма квадратов?

Остаточная сумма квадратов (RSS) — это статистический метод, который помогает определить уровень несоответствия в наборе данных, не предсказанный регрессионной моделью. Таким образом, он измеряет дисперсию значения наблюдаемых данных по сравнению с его прогнозируемым значением в соответствии с моделью регрессии. Следовательно, RSS указывает, хорошо ли модель регрессии соответствует фактическому набору данных или нет.

Также называемая суммой квадратов ошибок (SSE), RSS получается путем сложения квадрата остатков. Остатки представляют собой предполагаемые отклонения от фактических значений данных и представляют ошибки в регрессии Регрессия Регрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать дальшеоценка модели. Более низкий RSS указывает на то, что модель регрессии хорошо соответствует данным и имеет минимальную вариацию данных. В финансах Финансы — это широкий термин, который по существу относится к управлению капиталом или направлению денег для различных целей. Более того, инвесторы используют RSS для отслеживания изменений цен на акции, чтобы предсказать их будущие движения цен.

Оглавление

Что такое остаточная сумма квадратов?
- Объяснение остаточной суммы квадратов
- Остаточная сумма квадратов в финансах
- Формула
- Пример расчета
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Остаточная сумма квадратов (RSS) — это статистический метод, используемый для измерения отклонения в наборе данных, не объясненного регрессионной моделью.
Остаток или ошибка — это разница между фактическим и прогнозируемым значением наблюдения.
Если значение RSS низкое, это означает, что данные хорошо соответствуют модели оценки, что указывает на наименьшую дисперсию. Если он равен нулю, модель идеально соответствует данным, не имея вообще никакой дисперсии.
Это помогает игрокам фондового рынка оценивать будущие движения цен на акции, отслеживая колебания цен на акции.

Объяснение остаточной суммы квадратов

RSS — это один из типов суммы квадратов (SS), остальные два — это общая сумма квадратов (TSS) и сумма квадратов из-за регрессии (SSR) или объясненная сумма квадратов (ESS). Сумма квадратов — это статистическая мера, посредством которой дисперсия данных. Дисперсия В статистике дисперсия (или разброс) — это средство описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных. Читать далее оценивается, чтобы определить, насколько хорошо данные будут соответствовать модели в регрессионном анализе.

В то время как TSS измеряет изменение значений наблюдаемой переменной по отношению к ее выборочному среднему, SSR или ESS вычисляют отклонение между оценочным значением и средним значением наблюдаемой переменной. Если TSS равен SSR, это означает, что модель регрессии идеально подходит для данных, поскольку она отражает всю изменчивость фактических данных.

С другой стороны, RSS измеряет степень изменчивости наблюдаемых данных, не отображаемых регрессионной моделью. Чтобы вычислить RSS, сначала найдите уровень ошибки или остатка модели, вычитая фактические наблюдаемые значения из оценочных значений. Затем возведите в квадрат и сложите все значения ошибок, чтобы получить RSS.

Чем ниже ошибка модели, тем лучше прогноз регрессии. Другими словами, более низкий RSS означает, что регрессионная модель лучше объясняет данные, указывая на наименьшую дисперсию. Это означает, что модель хорошо соответствует данным. Аналогичным образом, если значение достигает нуля, оно считается наиболее подходящим без отклонений.

Обратите внимание, что RSS не похож на R-SquaredR-SquaredR-squared (R2 или коэффициент детерминации) — это статистическая мера, которая показывает степень вариации зависимой переменной из-за независимой переменной. Подробнее. В то время как первый определяет точную величину вариации, R-квадрат — это величина вариации, определяемая относительно доли общей вариации.

Остаточная сумма квадратов в финансах

Несоответствие, обнаруженное в наборе данных через RSS, указывает, соответствуют ли данные регрессионной модели или нет. Таким образом, это помогает фондовому рынкуФондовый рынокФондовый рынок работает по основному принципу согласования спроса и предложения посредством аукционного процесса, когда инвесторы готовы заплатить определенную сумму за актив и они готовы продать то, что у них есть, по определенной цене. узнайте больше игроков, чтобы понять колебания цен на активы, что позволит им оценить свои будущие движения цен.

Функции регрессии формируются для прогнозирования движения цен акций. Но польза от этих регрессионных моделей зависит от того, хорошо ли они объясняют колебания цен на акции. Однако если в модели есть ошибки или остатки, не объясняемые регрессией, то модель может оказаться бесполезной для прогнозирования движения запасов в будущем.

В результате инвесторы и инвестиционные менеджеры получают возможность принимать оптимальные и наиболее взвешенные решения с помощью RSS. Кроме того, RSS также позволяет политикам анализировать различные переменные, влияющие на экономическую стабильность страны, и соответствующим образом формировать экономические модели.

Формула

Вот формула для вычисления остаточной суммы квадратов:

Где,

Пример расчета

Рассмотрим следующее остаточная сумма квадратов пример на основе набора данных ниже:

Абсолютную дисперсию можно легко узнать, применив приведенную выше формулу RSS:

= {1 – [1+(2*0)]}2 + {2 – [1+(2*1)]}2 + {6 – [1+(2*2)]}2 + {8 – [1+(2*3)]}2

= 0+1+1+1 = 3

Часто задаваемые вопросы (FAQ)

Что такое остаточная сумма квадратов (RSS)?

RSS — это статистический метод, используемый для определения уровня несоответствия в наборе данных, не выявленного с помощью регрессии. Если остаточная сумма квадратов приводит к меньшему значению, это означает, что модель регрессии объясняет данные лучше, чем когда результат выше. На самом деле, если его значение равно нулю, оно считается наилучшим соответствием без каких-либо ошибок.

В чем разница между ESS и RSS?

ESS расшифровывается как «Объясненная сумма квадратов», что означает изменение данных, объясненное регрессионной моделью. С другой стороны, остаточная сумма квадратов (RSS) определяет вариации, отмеченные несоответствиями в наборе данных, не объясняемыми моделью оценки.

Чем отличаются TSS и RSS?

Общая сумма квадратов (TSS) определяет отклонения наблюдаемых значений или наборов данных от среднего значения. Напротив, остаточная сумма квадратов (RSS) оценивает ошибки или расхождения в наблюдаемых данных и смоделированных данных.

Пример 1: Остаточная сумма квадратов для простой линейной регрессии

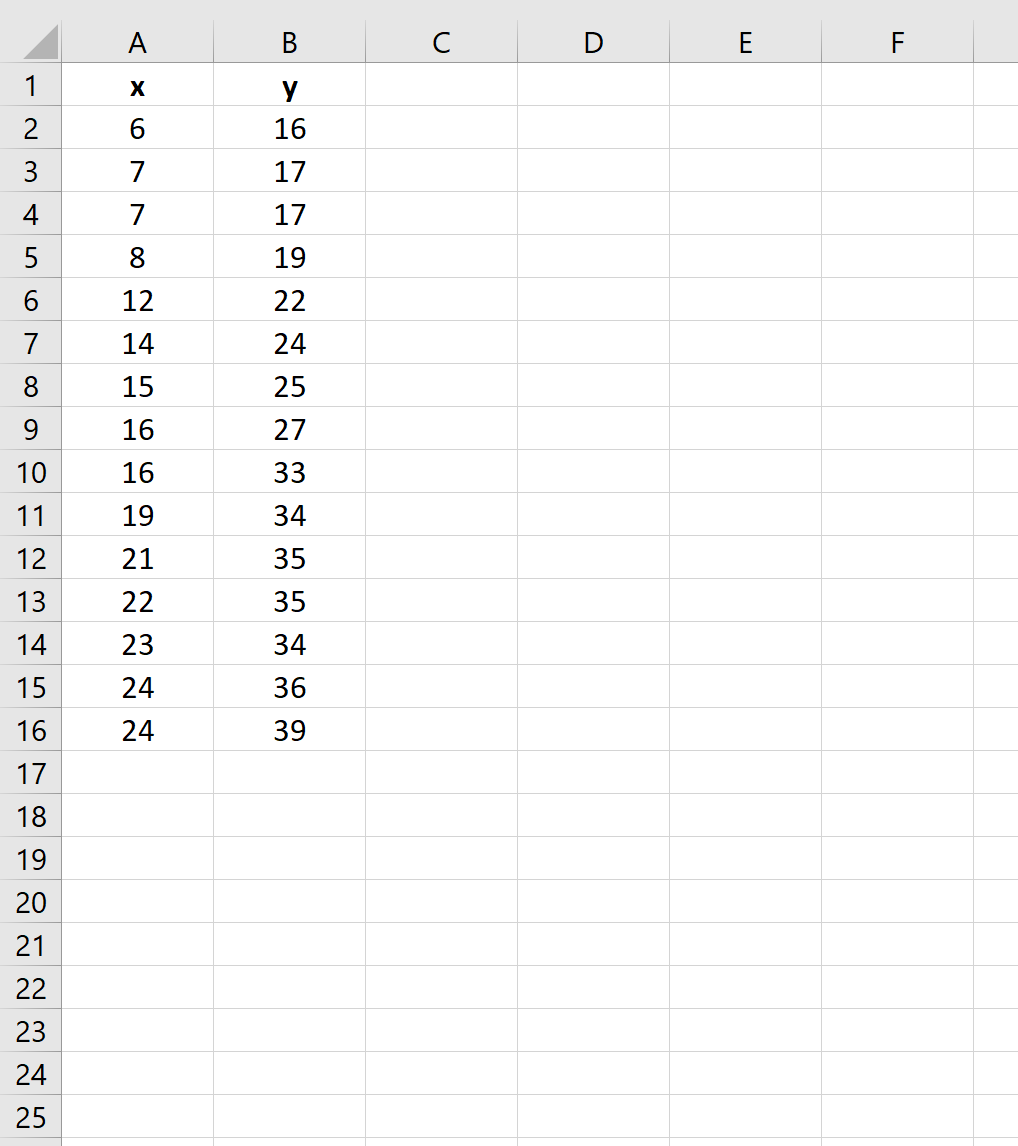
Предположим, у нас есть следующий набор данных в Excel:

Чтобы вычислить остаточную сумму квадратов для простой модели линейной регрессии, используя x в качестве переменной предиктора и y в качестве переменной ответа, мы можем использовать функцию ЛИНЕЙН() , которая использует следующий синтаксис:

ЛИНЕЙН(известные_ys, [известные_xs], [const], [статистика])

куда:

known_ys: диапазон значений y
known_sx: диапазон значений x.
const: принуждать ли константу b к нулю. Мы оставим это поле пустым.
stats: список статистики регрессии. Мы укажем, что это TRUE.

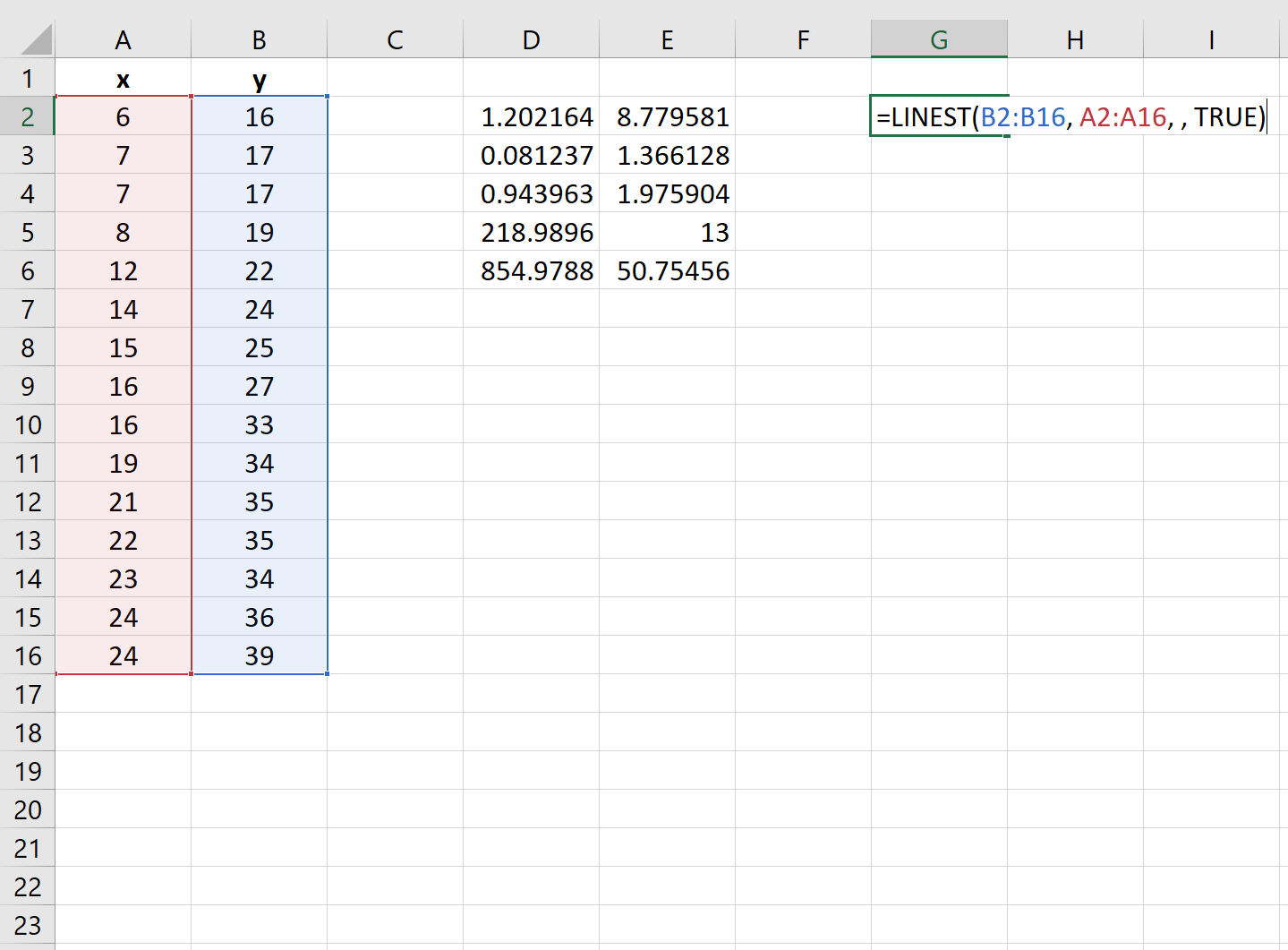
На следующем снимке экрана показано, как использовать эту функцию на практике:

Остаточная сумма квадратов для регрессионной модели отображается в последней ячейке второго столбца выходных данных. В этом примере остаточная сумма квадратов оказывается равной 50,75 .

Пример 2: Остаточная сумма квадратов для множественной линейной регрессии

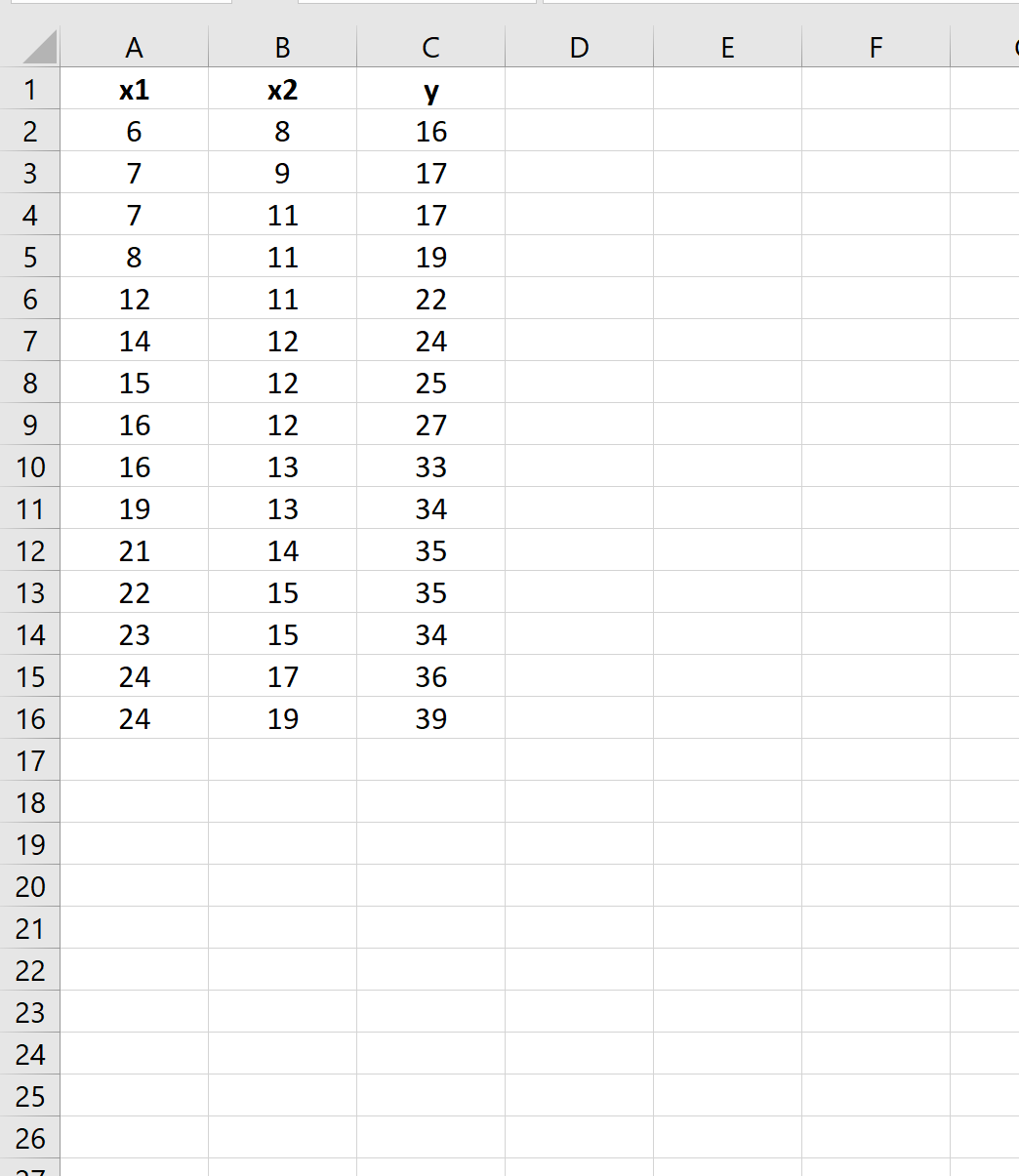
Предположим, у нас есть следующий набор данных в Excel:

Мы снова можем использовать функцию ЛИНЕЙН() для вычисления остаточной суммы квадратов для модели.

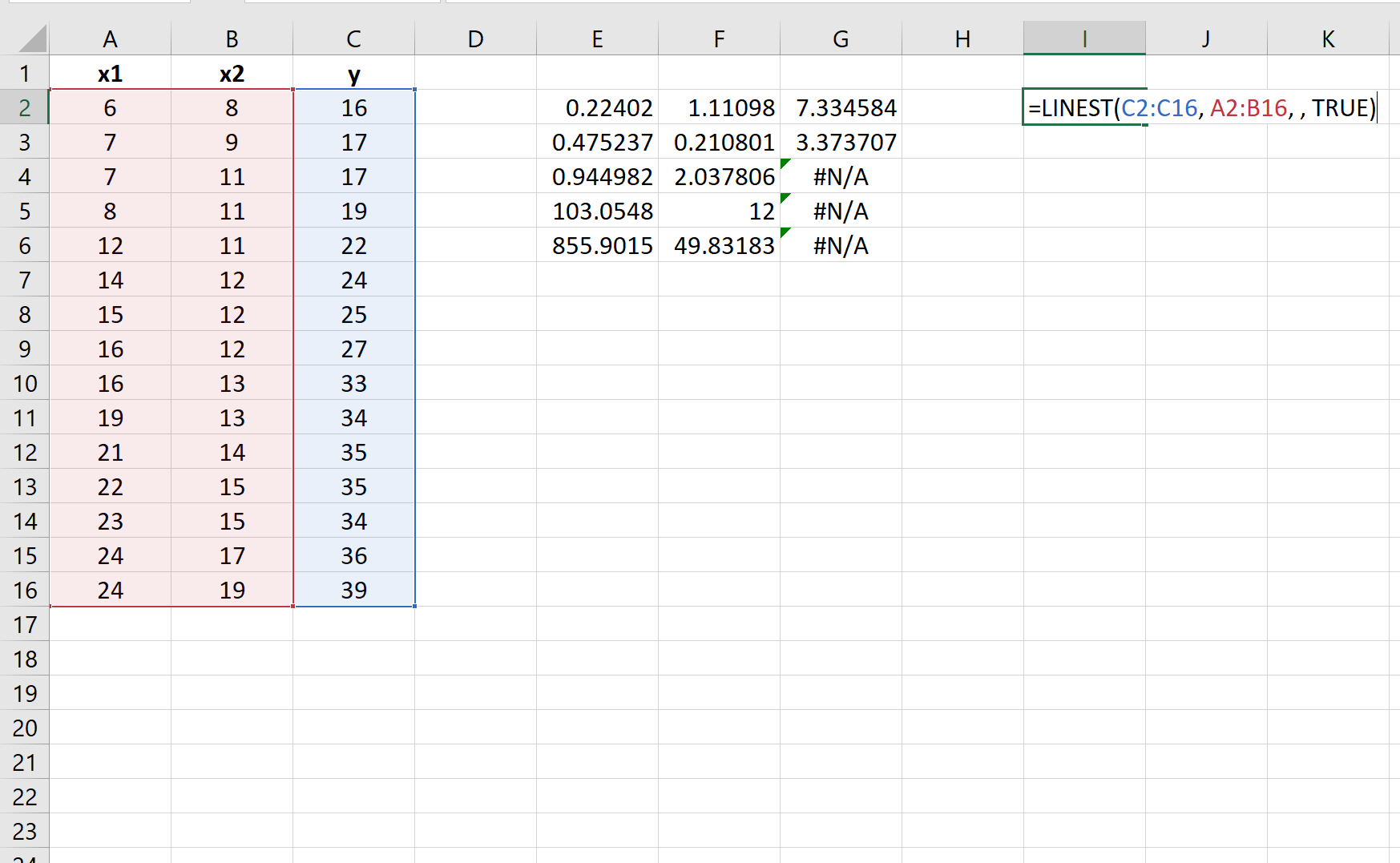
Единственное отличие состоит в том, что мы укажем два столбца значений для аргумента known_xs :

Остаточная сумма квадратов для этой модели множественной линейной регрессии оказывается равной 49,83 .

Дополнительные ресурсы

Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Калькулятор остаточной суммы квадратов

Источник

From Wikipedia, the free encyclopedia

In statistics, the residual sum of squares (RSS), also known as the sum of squared residuals (SSR) or the sum of squared estimate of errors (SSE), is the sum of the squares of residuals (deviations predicted from actual empirical values of data). It is a measure of the discrepancy between the data and an estimation model, such as a linear regression. A small RSS indicates a tight fit of the model to the data. It is used as an optimality criterion in parameter selection and model selection.

In general, total sum of squares = explained sum of squares + residual sum of squares. For a proof of this in the multivariate ordinary least squares (OLS) case, see partitioning in the general OLS model.

One explanatory variable[edit]

In a model with a single explanatory variable, RSS is given by:^[1]

${displaystyle operatorname {RSS} =sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}}$

where y_i is the i^th value of the variable to be predicted, x_i is the i^th value of the explanatory variable, and $f(x_{i})$ is the predicted value of y_i (also termed ${hat {y_{i}}}$ ).
In a standard linear simple regression model, ${displaystyle y_{i}=alpha +beta x_{i}+varepsilon _{i},}$ , where alpha and beta are coefficients, y and x are the regressand and the regressor, respectively, and ε is the error term. The sum of squares of residuals is the sum of squares of ${displaystyle {widehat {varepsilon ,}}_{i}}$ ; that is

${displaystyle operatorname {RSS} =sum _{i=1}^{n}({widehat {varepsilon ,}}_{i})^{2}=sum _{i=1}^{n}(y_{i}-({widehat {alpha ,}}+{widehat {beta ,}}x_{i}))^{2}}$

where is the estimated value of the constant term alpha and is the estimated value of the slope coefficient beta .

Matrix expression for the OLS residual sum of squares[edit]

The general regression model with n observations and k explanators, the first of which is a constant unit vector whose coefficient is the regression intercept, is

where y is an n × 1 vector of dependent variable observations, each column of the n × k matrix X is a vector of observations on one of the k explanators, beta is a k × 1 vector of true coefficients, and e is an n× 1 vector of the true underlying errors. The ordinary least squares estimator for beta is

${displaystyle X^{operatorname {T} }X{hat {beta }}=X^{operatorname {T} }yiff }$

${displaystyle {hat {beta }}=(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y.}$

The residual vector ${displaystyle {hat {e}}=y-X{hat {beta }}=y-X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y}$ ; so the residual sum of squares is:

${displaystyle operatorname {RSS} ={hat {e}}^{operatorname {T} }{hat {e}}=|{hat {e}}|^{2}}$

(equivalent to the square of the norm of residuals). In full:

${displaystyle operatorname {RSS} =y^{operatorname {T} }y-y^{operatorname {T} }X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y=y^{operatorname {T} }[I-X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }]y=y^{operatorname {T} }[I-H]y}$

where H is the hat matrix, or the projection matrix in linear regression.

Relation with Pearson’s product-moment correlation[edit]

The least-squares regression line is given by

where and ${displaystyle a={frac {S_{xy}}{S_{xx}}}}$ , where ${displaystyle S_{xy}=sum _{i=1}^{n}({bar {x}}-x_{i})({bar {y}}-y_{i})}$ and ${displaystyle S_{xx}=sum _{i=1}^{n}({bar {x}}-x_{i})^{2}.}$

Therefore,

${displaystyle {begin{aligned}operatorname {RSS} &=sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}=sum _{i=1}^{n}(y_{i}-(ax_{i}+b))^{2}=sum _{i=1}^{n}(y_{i}-ax_{i}-{bar {y}}+a{bar {x}})^{2}\[5pt]&=sum _{i=1}^{n}(a({bar {x}}-x_{i})-({bar {y}}-y_{i}))^{2}=a^{2}S_{xx}-2aS_{xy}+S_{yy}=S_{yy}-aS_{xy}=S_{yy}left(1-{frac {S_{xy}^{2}}{S_{xx}S_{yy}}}right)end{aligned}}}$

where ${displaystyle S_{yy}=sum _{i=1}^{n}({bar {y}}-y_{i})^{2}.}$

The Pearson product-moment correlation is given by ${displaystyle r={frac {S_{xy}}{sqrt {S_{xx}S_{yy}}}};}$ therefore, ${displaystyle operatorname {RSS} =S_{yy}(1-r^{2}).}$

References[edit]

^ Archdeacon, Thomas J. (1994). Correlation and regression analysis : a historian’s guide. University of Wisconsin Press. pp. 161–162. ISBN 0-299-13650-7. OCLC 27266095.

Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley. ISBN 0-471-17082-8.

Источник

Связь между
общей, факторной и остаточной суммами

Покажем, что

Для упрощения
вывода ограничимся двумя уровнями
и двумя испытаниями на каждом уровне
и двумя испытаниями на каждом уровне
и двумя испытаниями на каждом уровне

Результаты испытаний представим в виде
таблицы
2.

Таблица
2

Номер испытания	Уровни фактора
l
1 2

Тогда

Вычтем и прибавим
к каждому наблюдаемому значению на
первом уровне групповую среднюю
а на втором – .
Выполнив возведение в квадрат и учитывая,
что сумма всех удвоенных произведений
равна нулю (рекомендуем читателю
убедиться в этом самостоятельно), получим

Итак,

Следствие.
Из полученного равенства вытекает
важное следствие:

Отсюда видно, что
нет надобности непосредственно вычислять
остаточную сумму: достаточно найти
общую и факторную суммы, а затем их
разность.

2.4.Общая,
факторная и остаточная дисперсии

Разделив суммы
квадратов отклонений на соответствующее
число степеней свободы, получим общую,
факторную и остаточную дисперсии:

где
— число уровней фактора;
— число наблюдений на каждом уровне;
– число степеней свободы факторной
дисперсии;
– число степеней свободы остаточной
дисперсии.

Если нулевая
гипотеза о равенстве средних справедлива,
то все эти дисперсии являются несмещенными
оценками генеральной дисперсии. Например,
учитывая, что объем выборки ,
заключаем, что

– исправленная
выборочная дисперсия, которая, как
известно, является несмещенной оценкой
генеральной дисперсии.

Замечание.
Число степеней свободы
остаточной дисперсии равно разности
между числами степеней свободы общей
и факторной дисперсий. Действительно,

2.5.Сравнение
нескольких средних методом дисперсионного
анализа

Вернемся к задаче,
поставленной в п. 2.1: проверить при
заданном уровне значимости нулевую
гипотезу: о равенстве нескольких
средних нормальных совокупностей с
неизвестными, но одинаковыми диспериями.
Покажем, что решение этой задачи сводится
к сравнению факторной и остаточной
дисперсий по критерию Фишера – Снедекора.

1. Пусть нулевая
гипотеза о равенстве нескольких средних
(далее будем называть их групповыми)
правильна. В этом случае факторная и
остаточная дисперсии являются несмещенными
оценками неизвестной генеральной
дисперсии (см. п. 2.4) и, следовательно,
различаются незначимо. Если сравнить
эти оценки по критерию ,
то очевидно, критерий укажет, что нулевую
гипотезу о равенстве факторной и
остаточной дисперсий следует принять.

Таким образом,
если гипотеза о равенстве групповых
средних правильна, то верна и гипотеза
о равенстве факторной и остаточной
дисперсий.

2. Пусть нулевая
гипотеза о равенстве групповых средних
ложна. В этом случае с возрастанием
расхождения между групповыми средними
увеличивается факторная дисперсия, а
вместе с ней и отношение
В итоге
окажется больше
и, следовательно, гипотеза о равенстве
дисперсий будет отвергнута.

Таким образом,
если гипотеза о равенстве групповых
средних ложна, то ложна и гипотеза о
равенстве факторной и остаточной
дисперсий.

Легко доказать от
противного справедливость обратных
утверждений: из правильности (ложности)
гипотезы о дисперсиях следует правильность
(ложность) гипотезы о средних.

Итак, для
того чтобы проверить нулевую гипотезу
о равенстве групповых средних нормальных
совокупностей с одинаковыми дисперсиями,
достаточно проверить по критерию
нулевую гипотезу о равенстве факторной
и остаточной дисперсий. В
этом и состоит метод дисперсионного
анализа.

Замечание
1. Если
факторная дисперсия окажется меньше
остаточной, то уже отсюда следует
справедливость гипотезы о равенстве
групповых средних и, значит, нет надобности
прибегать к критерию .

Замечание
2.
Если нет уверенности в справедливости
предположения о равенстве дисперсий
рассматриваемых p
совокупностей, то это предположение
следует проверить предварительно,
например по критерию Кочрена.

Пример.
Произведено по 4 испытания на каждом из
трех уровней. Результаты испытаний
приведены в таблице 3.
Методом
дисперсионного анализа при уровне
значимости 0,05 проверить нулевую гипотезу
о равенстве групповых средних.

Таблица 3

Номер испытания	Уровни фактора
i
1 2 3 4	51 52 56 57	52 54 56 58	42 44 50 52
	54	55	47

Предполагается,
что выборки извлечены из нормальных
совокупностей с одинаковыми дисперсиями.

Решение.
Для упрощения
расчета вычтем
из каждого наблюдаемого значения:
Составим расчетную таблицу 4.

Таблица 4

Номер испытания	Уровни фактора	Итоговый столбец
i

1 2 3 4	–1 0 4 5	1 0 16 25	0 2 4 6	0 4 16 36	– 10 – 8 – 2 0	100 64 4 0
		42		56		168
	8		12		– 20
	64		144		400

Пользуясь таблицей
и учитывая, что число уровней фактора
,
число испытаний на каждом уровне ,
найдем общую и факторную суммы квадратов
отклонений (см. п. 2.2, формулы
и ):

Найдем остаточную
сумму квадратов отклонений:

Найдем факторную
и остаточную дисперсии:

Сравним, факторную
и остаточную дисперсии по критерию F,
для чего найдем наблюдаемое значение
критерия:

Учитывая, что число
степеней свободы числителя
а знаменателя
и уровень значимости
по таблице приложения 1 находим критическую
точку:

Так как —
нулевую гипотезу о равенстве групповых
средних отвергаем. Другими словами,
групповые средние «в целом» различаются
значимо. Если требуется сравнить средние
попарно, то следует воспользоваться
критерием Стьюдента.

Замечание
3. Если
наблюдаемые значения —
десятичные дроби с одним знаком после
запятой, то целесообразно перейти к
числам ,
где C
– примерно среднее значение чисел
В итоге получим сравнительно небольшие
целые
числа. Хотя при этом факторная и остаточная
дисперсия увеличиваются в
раз, их отношение не изменится. Например,
если

то, приняв
получим:

Аналогично
поступают, если после запятой имеется
знаков:

Источник

Что такое остаточная сумма квадратов?

Объяснение остаточной суммы квадратов

Остаточная сумма квадратов в финансах

Формула

Пример расчета

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи

Пример 1: Остаточная сумма квадратов для простой линейной регрессии

Пример 2: Остаточная сумма квадратов для множественной линейной регрессии

Дополнительные ресурсы

One explanatory variable[edit]

Matrix expression for the OLS residual sum of squares[edit]

Relation with Pearson’s product-moment correlation[edit]

See also[edit]

References[edit]