Найти число по остатку от деления
| Модуль (пробел) остаток (запятая) Модуль (пробел) остаток и т.д. |
Одна древняя китайская задача гласила:
«Найти число, которое при делении на 3 дает остаток 2, при делении на 5 дает остаток 3, а при делении на 7 дает остаток 2»
Что бы решать подобные задачи, сделаем следущее
Исходное число по исходным данным можно выразить вот так
Где k — целые числа
Выпишем ряды меняя k от 0 по возрастающей
Несложно заметить что 23, встречается во всех трех рядах.
Это и есть наш ответ, следущее число (128) встретится только через 105=3*5*7 отсчетов. Так как эти числа взаимно простые, то и берем просто их произведение.
И таким образом общий ответ нашей задачи имеет вид
Легкий алгоритм для понимания, не правда ли?
Но он не совсем неудобен, когда встречаются большие числа, и опять же, при составлении элементов ряда можно банально ошибиться.
Есть другой способ
Пусть нам дана система сравнений
где 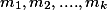
Пусть 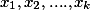
Такие уравнения мы уже можем решать Сравнения 1 степени. Теория чисел.
Узнав эти корни, мы можем вычислить наше исходное число по формуле
Для нашего примера исходные данные выглядят так
Тогда система сравнений будет иметь вид
Решая их получим
И наше решение имеет вид
Или то же самое что и
Как видите, ответ совпадает.
Наш бот решает подобные задачи используя библиотеку PHP GMP. Поэтому к точности расчетов и ограничений на длину значений, это к ним 
Хотя есть и свои материалы в частности: Расчет значения функции Эйлера, Остаток числа в степени по модулю и Диофантовое уравнение с тремя неизвестными
Важно: Логично и это надо учитывать при ввводе чисел, в паре чисел (модуль- остаток), модуль (всегда!) больше чем остаток.
Второе важное замечание. Модуль всегда(!) положительное число, остаток, может быть отрицательным, но лучше все таки привести его к положительному числу.
Как это сделать? Все ссылки на сопутствующие материалы уже приведены.
Пример
Узнать какое загадано число, если остаток при делении его на 37 равно 11, при делении на 9 равно 4, при делении на 7 равно 1, а при делении на 100 остаток равен 25.
Заметим, что модули, то есть числа (37, 9, 7, 100) на которые мы делим неизвестное число, попарно взаимно простые. То есть у нас нет ни одной пары из этих чисел, так что бы они имели общий делитель.
Раз так, то мы можем решать подобную задачу тем, методом который описан выше.Вводим в поле ввода
37 11, 9 4, 7 1, 100 25
За мгновение получим ответ
| Полученное число |
mod(233100)) |
Удачных расчетов!
Остаток от деления отрицательных чисел
Пятница, 28 октября, 2016
В этой статье я расскажу о том, как правильно находить остаток от деления отрицательных чисел. Этой теме, к сожалению, уделяется очень мало внимания в школе, хотя для понимания учеником базовых основ математики она чрезвычайно важна. Именно поэтому, как репетитор по математике, на своих занятиях я разбираю это материал с учениками во всех подробностях. Это значительно упрощает дальнейшую подготовку к ЕГЭ, ОГЭ, вступительным экзаменам и олимпиадам по математике.
Итак, приступим. Чтобы разделить друг на друга два целых числа с остатком, нужно воспользоваться следующей теоремой:
Здесь — делимое,
— делитель,
— неполное частное,
— остаток. Сразу обращаем внимание, что остаток
— это неотрицательное число. Понятно, что условие
возникает потому, что деление на нуль невозможно.
Звучит довольно сложно, но на самом деле в этой теореме нет ничего сложного. Чтобы во всём разобраться, перейдём к примерам.
Примеры нахождения остатка от деления отрицательных чисел
Пример 1. Деление с остатком положительного целого числа на положительное целое число.
Допустим, что требуется разделить с остатком 27 на 4. Вопрос состоит в том, сколько раз число 4 содержится в числе 27? Но мы знаем, что нет такого целого числа, на которое можно умножить 4, чтобы получить 27. Поэтому вопрос нужно переформулировать. На какое число нужно умножить 4, чтобы получить число, максимально близкое к 27, но не превзойти его? Очевидно, что это число 6. Если 4 умножить на 6, то получится 24. До исходного делимого 27 не хватает 3. Следовательно, остаток от деления 27 на 4 составляет 3:
ост.
.
Пример 2. Деление с остатком отрицательного целого числа на положительное целое число.
Что если требуется найти остаток от деления отрицательного целого числа -15 на положительное целое число 4? Начнём с того, что неполное частное должно получиться отрицательным, поскольку при делении отрицательного числа на положительное, результат получается отрицательным. Кто-нибудь может предположить, что неполное частное в данном случае должно быть равно -3. Но в этом случае, умножив -3 на 4, мы получим -12. И чтобы получить исходное делимое -15, нужно к результату -12 прибавить число -3, которое не может быть остатком, потому что остаток не может быть отрицательным!
Поэтому в данном случае неполное частное равно -4. В этом случае, умножая -4 на делитель 4, мы получаем -16. И теперь, чтобы получить исходное делимое -15, нужно к этому результату прибавить число 1. Оно неотрицательно и меньше модуля делителя (то есть 4). То есть оно и является остатком:
ост.
.
Пример 3. Деление положительного целого числа на отрицательное целое число.
Рассмотрим теперь пример деления с остатком положительного целого числа 113 на отрицательное целое число -3. Неполное частное, как и в предыдущем примере, должно быть отрицательным, потому что при делении положительного числа на отрицательное, результат отрицателен. Давайте думать, чему конкретно равно неполное частное. Очевидно, что оно равно -37. Действительно, при умножении -37 на -3 получается 111. Теперь, чтобы получить исходное делимое, нужно прибавить к этому результату число 2, которое неотрицательно и меньше модуля делителя (то есть модуля -3, что равно 3). Итак, наш ответ:
ост.
.
Пример 4. Деление с остатком отрицательного целого числа на отрицательное целое число.
Ну и последний пример. Отрицательное целое число -15 требуется поделить с остатком на отрицательное целое число -7. Неполное частное должно быть положительно по знаку, потому что при делении отрицательных чисел результат получается положительным. И оно равно 3. Действительно, умножая 3 на -7, получаем -21. Теперь к этому числу нужно прибавить положительное и меньшее модуля -7 (то есть 7) число 6, чтобы получить наше исходное делимое -15. Следовательно, остаток от деления отрицательных чисел -15 на -7 равен:
ост.
.
Проверьте, насколько хорошо вы поняли этот урок. Найдите самостоятельно остаток от деления отрицательных чисел:
а) -16 на 7;
б) 8 на -9;
в) -114 на -4.
Свои ответы пишите в комментариях, я их проверю.
Материал подготовил репетитор по математике и физике по скайпу, Сергей Валерьевич
Деление c остатком (деление по модулю) — арифметическая операция, играющая большую роль в арифметике, теории чисел и алгебре. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть 






Таким образом, результатами деления с остатком являются два целых числа: 



Примеры.
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.
Содержание
- 1 Определение
- 1.1 Натуральные и целые числа
- 1.2 Обобщения
- 1.2.1 Вещественные числа
- 1.2.2 Гауссовы целые числа
- 1.2.3 Многочлены
- 2 В программировании
- 2.1 Знак остатка
- 2.2 Как запрограммировать, если такой операции нет?
- 3 См. также
- 4 Примечания
- 5 Ссылки
Определение[править | править вики-текст]
Натуральные и целые числа[править | править вики-текст]
Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше.
Для практического выполнения целочисленного деления 




Здесь скобки 
Обобщения[править | править вики-текст]
Вещественные числа[править | править вики-текст]
Если два числа 



Формально:
- если
, то
, где
Пример:
(остаток 1,6)
Гауссовы целые числа[править | править вики-текст]
Гауссово число — это комплексное число вида 



где частное 




Многочлены[править | править вики-текст]
При делении с остатком двух многочленов 

, причём
Пример:
(остаток 3), так как 2x² + 4x + 5 = (x + 1)(2x + 2) + 3
В программировании[править | править вики-текст]
| Язык | Неполное частное |
Остаток | Знак остатка |
|---|---|---|---|
| ActionScript | % |
Делимое | |
| Ada | mod | Делитель | |
| rem | Делимое | ||
| ASP | Mod |
Не определено | |
| Бейсик | |
MOD |
Не определено |
| Си (ISO 1990) | / |
% |
Не определено |
| Си (ISO 1999) | / |
% |
Делимое[3] |
| C++ (ISO 2003) | / |
% |
Не определено[4] |
| C++ (ISO 2011) | / |
% |
Делимое[5] |
| C# | / |
% |
Делимое |
| ColdFusion | MOD |
Делимое | |
| Common Lisp | mod |
Делитель | |
rem |
Делимое | ||
| Delphi | div |
mod |
Делимое |
| Eiffel | // |
\ |
Делимое |
| Erlang | div |
rem |
Делимое |
| Euphoria | remainder |
Делимое | |
| Microsoft Excel (англ.) | QUOTIENT() |
MOD() |
Делитель |
| Microsoft Excel (рус.) | ЧАСТНОЕ() |
ОСТАТ() |
|
| FileMaker | Div() |
Mod() |
Делитель |
| Fortran | mod |
Делимое | |
modulo |
Делитель | ||
| GML (Game Maker) | div |
mod |
Делимое |
| Go | / |
% |
Делимое |
| Haskell | div |
mod |
Делитель |
quot |
rem |
Делимое | |
| J | |~ |
Делитель | |
| Java | / |
% |
Делимое[6] |
Math.floorDiv |
Math.floorMod |
Делитель (1.8+) | |
| JavaScript | % |
Делимое | |
| Lua | % |
Делитель | |
| Mathematica | Mod |
Делитель | |
| MATLAB | idivide(?, ?, 'floor') |
mod |
Делитель |
idivide |
rem |
Делимое | |
| MySQL | DIV |
MOD% |
Делимое |
| Objective Caml | mod |
Не определено | |
| Pascal | div |
mod |
Делимое[7] |
| Perl | Нет | % |
Делитель |
| PHP | Нет[8] | % |
Делимое |
| PL/I | mod |
Делитель (ANSI PL/I) | |
| Prolog (ISO 1995) | mod | Делитель | |
| PureBasic | / |
Mod% |
Делимое |
| Python | // |
% |
Делитель |
| QBasic | |
MOD | Делимое |
| R | %% | Делитель | |
| RPG | %REM | Делимое | |
| Ruby | % | Делитель | |
| Scheme | modulo | Делитель | |
| SenseTalk | modulo | Делитель | |
| rem | Делимое | ||
| Tcl | % | Делитель | |
| Verilog (2001) | % | Делимое | |
| VHDL | mod | Делитель | |
| rem | Делимое | ||
| Visual Basic | |
Mod |
Делимое |
Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получении случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа. Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
78 mod 33 = 12 78 div 33 = 2
Знак остатка[править | править вики-текст]
Важно отметить, что операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:
- Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
- Знак остатка совпадает со знаком делителя: неполное частное округляет к −∞.
Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.
- Есть сумма n копеек, положительная или отрицательная. Перевести её в рубли и копейки. —
n div 100иn mod 100. Знак остатка совпадает со знаком делимого. - Есть бесконечное клеточное поле, каждая клетка — 16×16 пикселей. В какую клетку попадает точка (x, y), и каковы координаты относительно верхнего левого угла клетки? —
(x div 16, y div 16)и(x mod 16, y mod 16)соответственно. Знак остатка совпадает со знаком делителя.
Как запрограммировать, если такой операции нет?[править | править вики-текст]
Неполное частное можно запрограммировать как ![q = left[frac{a}{b}right]](https://web.archive.org/web/20160430141554im_/https://upload.wikimedia.org/math/f/7/1/f714da379d07864de682eaaf2754b14a.png)
При отсутствии команды mod остаток программируется как 
Если b положительно, а знак r совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой 
См. также[править | править вики-текст]
- Алгоритм Евклида
- Делимость
- Наибольший общий делитель
- Непрерывная дробь
- Сравнение по модулю
Примечания[править | править вики-текст]
- ↑ Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
- ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
- ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the
/operator is the algebraic quotient with any fractional part discarded. [This is often called “truncation toward zero”.]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится. - ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
- ↑ N3242=11-0012 (Working draft), текст совпадает с C99
- ↑ К. Арнолд, Дж. Гослинг, Д. Холмс. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
- ↑ Стандарт 1973 года: div — division with truncation.
- ↑ PHP: Arithmetic Operators — Manual
Ссылки[править | править вики-текст]
- Деление с остатком: онлайн-калькулятор
Математические термины
Во всём последующем материале никак не фигурирует понятие “модуль числа”
в привычном смысле ((lvert x rvert)). Речь идёт о “сравнении по модулю”.
Если вы не знакомы с этим понятием, вкратце сравнение по модулю выглядит
следующим образом:
[a equiv b pmod{m}.]
Это читается “(a) сравнимо с (b) по модулю (m)”, и в привычных для
информатики терминах обозначает следующее:
[(a — b) bmod m = 0]
или
[a bmod m = b bmod m,]
где (bmod) — операция взятия остатка от деления.
Поле по модулю
В некоторых задачах фигурирует условие следующего вида: “выведите остаток от
деления ответа на 1000000007” или “выведите ответ по модулю 1000000007”. Это
вовсе не значит, что вам нужно посчитать ответ обычным способом и вывести
ans % 1000000007. Ответ в таких задачах
часто настолько огромен, что его сложно представить даже с помощью длинной
арифметики. Для их решения нужно вносить изменения во все
промежуточные вычисления, чтобы не выйти за границы целочисленного типа.
Можно сказать, что в таких задачах мы оперируем не числами, а
их остатками от деления на 1000000007. Это возможно благодаря
следующим свойствам вычислений с остатком:
[(a + b) bmod m = ((a bmod m) + (b bmod m)) bmod m \
(a — b) bmod m = ((a bmod m) — (b bmod m)) bmod m \
(ab) bmod m = ((a bmod m) * (b bmod m)) bmod m]
Таким образом, мы можем выполнять три важнейшие математические операции,
даже не зная точных значений чисел, только их остатки от деления на заданное
число (модуль). Деление — отдельная тема,
которую мы обсудим позже.
Не углубляясь в определения терминов из высшей математики, операции с остатками
от деления на модуль называются операциями в поле по модулю, а сами
остатки — числами по модулю.
Примечание: термин “поле” применим только в том случае, когда модуль —
простое число. В противном случае это называется “кольцо”. Отличие
заключается в том, что для поля определена операция деления, а для кольца —
нет.
Доказательство возможности сложения, вычитания и умножения по модулю
Для начала докажем достаточно очевидное утверждение:
[forall n in mathbb{Z}: x bmod m = (x + nm) bmod m.]
Доказательство:
[((x + nm) — x) bmod m = nm bmod m = 0]
Значит, по определению сравнимости, (forall n in mathbb{Z}: x equiv x + nm pmod{m}),
что и требовалось доказать.
Докажем возможность сложения ((x) и (y) — целые части от
деления (a) и (b) на (m) соответственно):
[(a + b) bmod m = \
= (xm + a bmod m + ym + b bmod m) bmod m = \
= (a bmod m + b bmod m + m(x + y)) bmod m, = \
= (a bmod m + b bmod m) bmod m,]
что и требовалось доказать.
Вычитание и умножение доказываются похожим образом:
[(a — b) bmod m = \
= (xm + a bmod m — ym — b bmod m) bmod m = \
= (a bmod m — b bmod m + m(x — y)) bmod m, = \
= (a bmod m — b bmod m) bmod m,]
[(a * b) bmod m = \
= ((xm + a bmod m) * (ym + b bmod m)) bmod m = \
= (a bmod m * b bmod m + a bmod m * ym + b bmod m * xm + xym^2) bmod m = \
= (a bmod m * b bmod m + m(a bmod m * y + b bmod m * x + xym)) bmod m = \
= (a bmod m * b bmod m) bmod m]
Пример: вычисление факториала по модулю
В качестве примера, вычислим значение (10^8!) по модулю (10^9 + 7):
Как видите, на практике вычисления в поле по модулю отличаются от обычных
лишь наличием взятия всех промежуточных результатов по модулю (строка 8).
Однако существует два момента, которые нужно всегда учитывать для избежания
ошибок:
-
Взятие отрицательных чисел по модулю.
Согласно математическому определению, (-1 bmod 5 = 4), так как (-1 = -1 * 5 + 4).
К сожалению, оператор%в С++ реализован иначе, и по его версии (-1 bmod 5 = -1).
Это может привести к ошибкам в вычислениях, поэтому нужно вручную обрабатывать такие
случаи следующим образом:long long result; //... result -= x; result %= MOD; if (result < 0) result += MOD; //Теперь всё должно работать. -
Переполнение типа
intпри умножении.
Не рекомендуется использовать типintдля хранения чисел по модулю
1000000007, так как при умножении двух таких чисел результат может достигать (10^{18}),
что вызывет переполнение. При умножении чисел по модулю всегда используйте тип
long long!
Возведение в степень по модулю. Бинарное возведение в степень
Возможность умножения по модулю позволяет нам естественным образом возводить
числа в различные степени по модулю. При операциях в поле по модулю степени часто
сильно превышают привычные значения, и тривиальный алгоритм с линейным временем
работы оказывается неприменимым. В таких ситуациях чаще всего используется
алгоритм бинарного возведения в степень.
Алгоритм бинарного возведения в степень достаточно лаконичен. Его идея
заключается в том, чтобы использовать возведение в квадрат промежуточных
результатов, когда это возможно. Используется следующее очевидное свойство:
[x^{2n} = x^n * x^n]
Таким образом засчёт одной операции умножения можно уменьшить степень вдвое.
Если же текущая степень нечётная, то можно просто уменьшить её на единицу простым
умножением, и получить чётную.
Простой рекурсивный вариант на C++:
Можно заметить, что в худшем случае на каждом втором вызове функции
степень будет уменьшаться вдвое. Значит, время работы алгоритма можно оценить
как (O(log p)).Разумеется, бинарное возведение в степень можно использовать и без модуля,
но степени в таких случаях слишком малы, чтобы заметить разницу в скорости.Деление в поле по модулю
К сожалению, деление не так легко адаптируется к полю по модулю, как другие
арифметические операции. В этом разделе описывается один из способов деления
по модулю, но не приводится его доказательство, так как оно значительно
усложнило бы эту лекцию.С делением по модулю связана одна особенность. Чтобы операция (a/b bmod m)
имела смысл, необходимо, чтобы числа (b) и (m) были взаимнопростыми. Если модуль
(m) — простое число, он является взаимнопростым со всеми числами по модулю
(m), то есть, делить можно на все числа. Но если модуль составной, то операция
деления имеет смысл лишь для некоторых чисел, и определяется значительно сложнее.
На практике считается, что делить можно только в поле по простому модулю.Деление по модулю определяется через умножение следующим образом:
[{a over b} bmod b = (a * {1 over b}) bmod m = ab^{-1} bmod m.]
Ключевую роль играет значение (b^{-1}), называющееся обратный элемент в
поле по модулю. Оно никак не связано с классическим понятием обратного
числа, хотя бы тем, что всегда является целым (так как в поле по модулю
существуют только целые числа). Для обратного элемента должно выполняться
следующее условие:[(x * x^{-1}) bmod m = 1.]
Например, обратным элементов в поле по модулю (1000000007) для числа (2) является
число (500000004), так как ((2 * 500000004) bmod 1000000007 = 1). Следовательно, в
поле по модулю (1000000007) делению на (2) соответствует умножение на (500000004)Алгоритм нахождения обратного элемента в поле по простому модулю
достаточно прост (в реализации) и выражается следующей формулой:[x^{-1} bmod m = x^{m — 2} bmod m]
Как можно заметить, число (x) возводится в достаточно большую степень, и
линейный алгоритм в этой ситуации не подойдёт. Вот и пример необходимости
использования бинарного возведения в степень по модулю.Реализация на C++:
Стоит заметить что из-за использования бинарного возведения в степень,
деление по модулю имеет сложность (O(log m)), тогда как все остальные
арифметические операции по модулю работают за (O(1)).
Модулярная арифметика
Калькулятор выполняет арифметические операции по заданному модулю.
Калькулятор решает заданное математическое выражение по модулю с отображением пошагового решения. Можно просто ввести целое число — калькулятор вычислит его остаток от деления по модулю. Также можно использовать следующие операции:
- + сложение по модулю
- — вычитание по модулю
- * умножение по модулю
- / деление по модулю ( операция доступна для всех чисел только тогда, когда модуль — простое число )
- ^ возведение в степень
- () группировка выражений
Вычисления по модулю
Симметричное представление
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Решение сравнений по модулю
- • Простая дробь по модулю
- • Обратный элемент в кольце по модулю
- • Обратная матрица по модулю
- • Быстрое возведение в степень по модулю
- • Раздел: Алгебра ( 46 калькуляторов )
PLANETCALC, Модулярная арифметика



mod(105))
mod(m_1),%20&%20x=(c_2)mod(m_2),....,x=(c_k)mod(m_k))
mod(m_1)\\m_1m_3...m_kx_2=(1)mod(m_2)\\.........\\m_1m_2...m_{k-1}x_k=(1)mod(m_k))
mod%20(m_1m_2...m_k))
mod(3),%20&%20x=(3)mod(5),x=(2)mod(7))
mod(3)=1\\%20&%20(21x_2)mod(5)=1\\(15x_3)mod(7)=1)
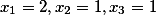
mod(3*5*7)=(233)mod(105))
mod(105)=(233-105-105)mod(105)=23mod(105))






 , то
, то  , где
, где 
 (остаток 1,6)
(остаток 1,6)

 , причём
, причём 
 (остаток 3), так как
(остаток 3), так как