Виды углов
- Прилежащие углы
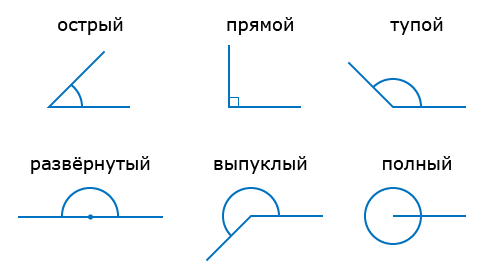
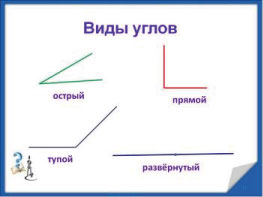
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.
Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.
- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB — ∠COB,
∠COB = ∠AOB — ∠AOC.
Угол, который полностью помещается внутри прямого угла, называется острым.
— острый угол.
Угол, внутри которого полностью помещается прямой угол, называется тупым углом.
— тупой угол.
Обрати внимание!
В ромбе, если он не является квадратом, два угла острых и два угла тупых.
Углы (ABC) и (ADC) — острые.
Углы (BAD) и (BCD) — тупые.
Источники:
Рис. 1. Углы, угольник, ромб. © ЯКласс
|
Какой угол в геометрии называется острым, прямым, тупым? Сколько градусов в остом угле, тупом угле, прямом угле? Как определить острый угол, прямой угол, тупой угол? Угол образованный пересечением двух перпендикулярных прямых называется прямым. Также прямой угол может возникнуть при делении окружности на ровные четыре части (1/4 окружности). Прямой угол равен 90 градусам. Когда стороны угла совпадают, такой угол называется нулевым Нулевой угол равен 0 градусам. Все углы, значения в градусах которых больше нулевого и меньше прямого называется острыми. Острый угол — больше 0 градусов и меньше 90 градусов. Если стороны угла лежат в противоположных направлениях и образуют прямую, такой угол называется развернутым и равен он 180 градусам. Углы, значения в градусах которых больше прямого и меньше развернутого называются тупыми. Тупой угол — больше 90 градусов и меньше 180 градусов. Всех их объединяет одно: острый, прямой и тупой углы — все они выпуклые. автор вопроса выбрал этот ответ лучшим Всё достаточно просто. Проведём аналогию с обычными часами. Если одну из стрелок установить так, чтобы она указывала на двенадцать часов, а другою, чтоб указывала на три — то они образуют прямой угол в девяносто градусов. Если же начать двигать стрелку указывающую на три часа в обратном направлении( в двухчасовой отметки на циферблате) — то она будет образовывать, вместе со второй стрелкой, острые углы(менее 90 градусов). Когда же стрелки будут указывать в одну точку — они образуют нулевой угол в ноль градусов.А если вернуть вторую стрелку к исходной( трехчасовой отметке) и начать передвигать её вперед по циферблату — то вплоть до шестичасовой отметки она вместе с первой будут образовывать тупые углы( более 90 градусов). Когда стрелки будут указывать, одна на 12, а другая на 6 — это будет, так называемый, развёрнутый угол в 180 градусов. Острый угол — это угол меньше 90°. Тупой угол — это угол больше 90°, но меньше 180°. Прямой угол — это угол 90°. Есть ещё развёрнутый угол, то есть угол, находящийся в диапазоне между 180° и 360°. Если угол больше 360°, то чтобы узнать, какой угол, следует отнять от значения этого угла 360 и посмотреть, что останется. Если всё равно больше, то повторить эту операцию нужное число раз. Угол 0°, также как и 180° с одной стороны используются в расчётах как угол, но фактически являются началом отрезка или линии, а не углом. Если брать треугольники, то их углы должны находиться в диапазоне между 0° и 180°, так как при таких углах треугольника (0° и 180°) это будет уже не треугольник, а отрезок, а при бóльших углах треугольника не получится. chipmunk 9 лет назад В этом вопросе нужно отталкиваться от прямого угла: 1.Прямой угол равен 90 градусов 2.Все углы которые меньше прямого угла, то есть меньше 90 градусов, считаются острыми. К примеру, углы 89 градусов, 60 градусов, 30 градусов. 3.Все углы, которые больше прямого угла, то есть больше 90 градусов, считаются тупыми. К примеру, 91 градус, 120 градусов, 179 градусов -тупые углы Еще нужно учесть, что угол равный 180 градусов называется развернутым. Mstitel007 9 лет назад Острый угол- это тот угол, градусная мера которого меньше 90 градусов. Прямой угол- это тот угол, градусная мера которого 90 градусов. Тупой угол- это тот угол, градусная мера которого больше 90 градусов. Определить каждый угол можно с помощью транспортира или линейки. Асюшка 9 лет назад Это достаточно просто определить. Для этого даже транспортир не понадобится. ПРЯМОЙ УГОЛ — всегда равен 90 градусам. Можно представить себе перпендикуляр. ТУПОЙ УГОЛ — всегда больше 90 градусов, он словно развёрнут, как книга. ОСТРЫЙ УГОЛ — всегда меньше 90 градусов. А вот для того, чтобы узнать сколько всё-таки точно градусов в том или ином угле, понадобится транспортир. Skiyers 8 лет назад Острый угол — от нуля до 90 градусов (не включительно). Выглядят они вот так Прямой угол равен 90 градусам, его стороны перпендикулярны друг другу. Есть ещё тупые углы — от 90 градусов до 180, вот так они выглядят: Какой перед вами угол, в общем-то, можно определить «на глаз», но если нужны точные градусы, нужно пользоваться транспортиром. Элементарно просто, берем уголок, или линейку или транспортир, можно и все вместе. С транспортиром все просто, уведите соответствующие отметки, то есть 90%- прямой угол; то что больше 90%-91,99,120,170 называется тупым углом; в свою очередь, то что меньше 90%-89, 75, 40,15 называется острым углом. Ошибиться практически невозможно. я Таня 8 лет назад Прямой угол — это угол 90 градусов, встречается в таких четырехугольниках, как квадрат и прямоугольник. Тупой угол — это угол, градусная мера которого больше 90 градусов, но меньше 180, встречается в ромбе, многоугольгике, произвольных параллелограммах. Острый угол — это угол до 90 градусов, его, например, нет в квадрате. stepanoff 8 лет назад Это геометрия 7-го класса. Возможно даже и раньше в школе проходят, точно не помню. Для измерения величины угла используют транспортир. Так вот, прямой угол равен 90 градусов, острый угол всегда меньше 90 градусов (даже на 1 градус), а тупой угол всегда больше 90 градусов. Наталья Соколова 8 лет назад Острым называется угол, величина которого меньше 90 градусов. Прямой угол с раствором 90 градусов. Тупым называется угол, величина которого больше 90 градусов, но меньше 180 градусов. Прямой угол сразу видно на глаз. Знаете ответ? |
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Угол. Виды углов
Мы узнаем, что углы бывают, острыми, прямыми и тупыми.
Вспомни, чтобы начертить угол, нужно поставить точку и из неё провести два луча в разные стороны.
Луч — это сторона угла.
Вершина — это точка, из которой выходят лучи.
Прямой угол
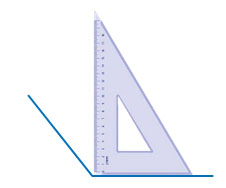
Прямой угол — это угол в 90о (90 градусов). Его легко определять по треугольнику, например, такому:
Острый угол
Острый угол — это угол, который МЕНЬШЕ прямого угла, меньше 90о.
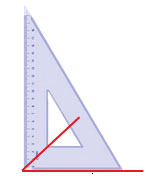
Тупой угол
Острый угол — это угол, который БОЛЬШЕ прямого угла, больше 90о.
Советуем посмотреть:
Круг. Шар. Овал
Треугольники
Многоугольники
Обозначение геометрических фигур буквами
Периметр многоугольника
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 44. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 36,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 18. Урок 6,
Петерсон, Учебник, часть 2
Страница 24. Урок 8,
Петерсон, Учебник, часть 2
Страница 25. Урок 9,
Петерсон, Учебник, часть 2
Страница 89. Урок 37,
Петерсон, Учебник, часть 2
Страница 16. Урок 5,
Петерсон, Учебник, часть 3
3 класс
Страница 16,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 43,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 102,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 50. Урок 20,
Петерсон, Учебник, часть 2
Страница 75. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 24,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 56. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 50,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 15. Урок 5,
Петерсон, Учебник, часть 1
Страница 30. Урок 10,
Петерсон, Учебник, часть 1
Математика, 2 класс
Урок № 33. Угол. Виды углов: прямой, острый, тупой
Перечень вопросов, рассматриваемых в теме:
— Какие бывают углы?
— Как распознавать углы?
Глоссарий по теме:
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.8-9.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.3.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.16.
Теоретический материал для самостоятельного изучения
Рассмотрите фигуры и выберите лишнюю.
Лишняя фигура под номером 2. Она образована незамкнутой линией.
Она называется угол.
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Посмотрите на рисунки: по-разному открытый веер, образует разные углы.
У каждого угла есть две стороны и вершина. Углы бывают прямые, острые и тупые. Углы определить можно помощью чертежного угольника.
Прямой угол определяем с помощью чертежного угольника.
Угол, который меньше прямого угла называется острым углом.
Угол, который больше прямого угла называется тупым углом.
Посмотрите, как из обычного листа бумаги можно сделать модель прямого угла. Моделью можно воспользоваться, если у вас нет чертежного угольника. Возьмите лист бумаги и перегните его 2 раза, как показано на рисунках 1 и 2. И получите модель прямого угла.
Разверните лист. Линии сгиба образовали 4 прямых угла.
Чтобы определить, какой угол начерчен, на него накладывают угольник или модель прямого угла.
Вывод: Углы могут быть прямыми и непрямыми. Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник. Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол – прямой. Не совпадут – непрямой. Непрямые углы делятся на: тупые и острые. Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.
Тренировочные задания.
1.Посмотрите на крыши домов и домиков. Какие углы ты видишь на рисунке? Соотнесите вид угла с изображением домика.
Правильные ответы:
2. Выберите цифры, в записи которых присутствуют только прямые углы.
Правильные ответы: