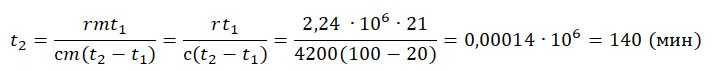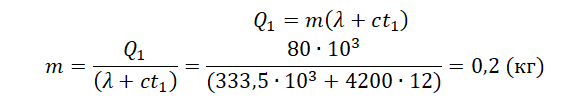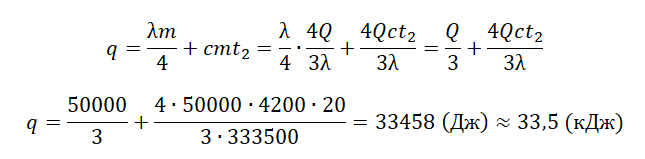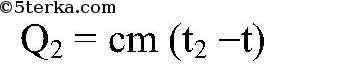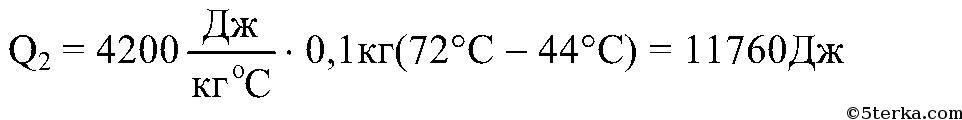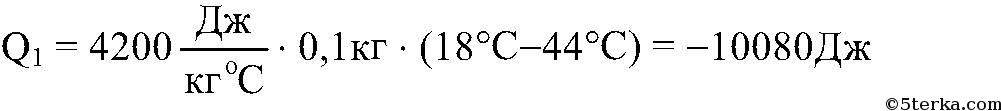Привет, если у нас одни и теже учебники , то тогда тебе повезло:)
Лабораторная работа 1
Сравнение количеств теплоты при смешивании воды разной температуры
Цель работы: определить количество теплоты, отданное горячей водой и полученное холодной при теплообмене, и объяснить полученный результат.
Приборы и материалы: калориметр, измерительный цилиндр (мензурка), термометр, стакан.
Ход работы:
1. Нальем в калориметр горячей воды массой 100 г. Возьмем столько же холодной воды и нальем ее в стакан. Измерим с помощью термометра температуру холодной и горячей воды. Результаты измерений занесем в таблицу.
2. Вольем холодную воду в калориметр, в сосуд с горячей водой, помешаем термометром и измерим температуру полученной смеси (72°С). Результат измерений занесем в таблицу.
3. Рассчитаем количество теплоты отданное горячей и полученное холодной водой по следующим формулам:
rде: Q — количество теплоты отданное горячей водой; Q1 — количество теплоты полученное холодной водой; m — масса холодной или горячей воды; с = 4200 — теплоемкость воды; t – температура горячей воды; t1 – температура холодной воды; t2 – температура смеси.
Выводы: В результате измерений было установлено, что количество теплоты отданное горячей водой равно количеству теплоты полученное холодной водой. Таким образом, подтверждается закон сохранения энергии.
Количество теплоты – это физическая величина, которая обозначается буквой Q; скалярная величина; может быть положительной или отрицательной.
Энергия, которую получает или теряет тело при теплопередаче, называется количеством теплоты. В СИ измеряется в джоулях [Дж].
Для нагревания и охлаждения рассчитать количество теплоты можно по формуле Q = cm (t2 – t1).
c – удельная теплоёмкость вещества, у каждого вещества своя, берётся в таблице
m – масса, кг
t2 – конечная температура, °C
t1 – начальная температура, °С
Физическая величина, численно равная количеству теплоты, которое необходимо передать телу массой 1 кг для того, чтобы его температура изменилась на 1°С, называется удельной теплоёмкостью вещества.
Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
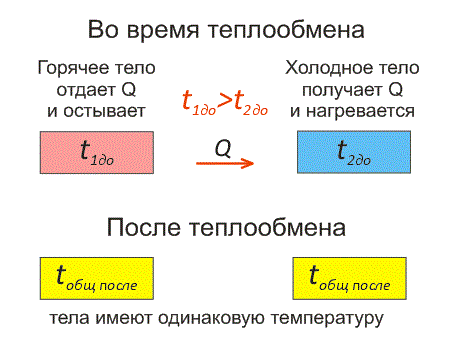
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.
Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Плавление и отвердевание
ОпределениеПлавление — переход вещества из твердого состояния в жидкое.
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
Q=λm
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
ОпределениеОтвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Q=−λm
Парообразование и конденсация
ОпределениеПарообразование, или кипение — переход вещества из жидкого состояния в газообразное.
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
Q=rm
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
ОпределениеКонденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Q=−rm
Тепловые процессы при нагревании и охлаждении
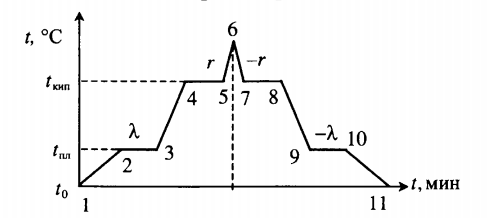
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
| Процесс | Что происходит | Количество выделенной теплоты |
| 1–2 | Нагревание твердого тела |
Q=cтm(tпл−t0) ст — удельная теплоемкость вещества в твердом состоянии. |
| 2–3 | Плавление при температуре плавления (tпл) |
Q=λm |
| 3–4 | Нагревание жидкости |
Q=cжm(tкип−tпл) сж — удельная теплоемкость вещества в жидком состоянии. |
| 4–5 | Кипение при температуре кипения (tкип) |
Q=rm |
| 5–6 | Нагревание пара |
Q=cпm(t−tкип) сп — удельная теплоемкость вещества в газообразном состоянии. |
| 6–7 | Охлаждение пара |
Q=cпm(tкип−t) |
| 7–8 | Кипение при температуре кипения (tкип) |
Q=−rm |
| 8–9 | Охлаждение жидкости |
Q=cжm(tпд−tкип) |
| 9–10 | Отвердевание при температуре плавления (tпл) |
Q=−λm |
| 10–11 | Охлаждение твердого тела |
Q=cтm(t0−tпл) |
Внимание! На участках 2–3 и 9–10 вещество частично находится в жидком и твердом состояниях, а на 4–5 и 7–8 — в жидком и газообразном.
Частные случаи тепловых процессов
| Что происходит | График | Формула количества теплоты |
| Полностью растопили лед, имеющий отрицательную температуру. | 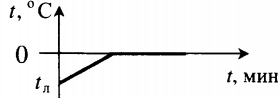 |
Q=cлm(tпл−tл)+λm cл — удельная теплоемкость льда, tл — начальная температура льда. |
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 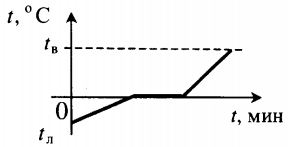 |
Q=cлm(tпл−tл)+λm+cвm(tв−tпл) cв — удельная теплоемкость воды. |
| Взяли лед при температуре 0 оС и полностью испарили. | 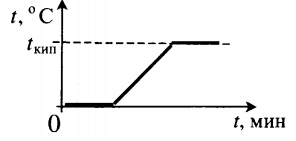 |
Q=λm+cвm(tкип−tпл)+rm |
| Взяли воду при комнатной температуре и половину превратили в пар. | 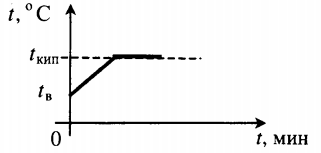 |
Q=cвm(tкип−tв)+rm2 |
Подсказки к задачам
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 оС. |
| Объем воды 5 л | m = 5 кг, так как:
m=ρV=103· Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 оС, чтобы превратить его в воду и нагреть ее до температуры +30 оС?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q=Q1+Q2+Q3
Q=cлm(0−t1)+λm+cвm(t2−0)
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙103 Дж/кг.
Отсюда:
Q=2050·2(0−(−10))+333,5·103·2+4220·2·30=961200 (дж)=961,2 (кДж)
Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Qотд=−Qпол
Отданное количество теплоты меньше нуля (Qотд < 0), а полученное количество теплоты положительно (Qполуч > 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 оС. Учтите, что лед плавится, если он находится при температуре 0 оС и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 оС, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 оС, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 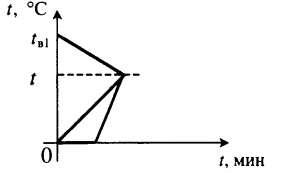
Уравнение теплового баланса: Q1+Q2+Q3=0 cвmв1(t−tв1)+cвmв2(t−0)+λmл+cвmл(t−0)=0 |
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 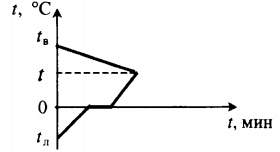
Уравнение теплового баланса: Q1+Q2=0 cвmв(t−tв)+cлmл(0−tл)+λmл+cвmл(t−0)=0 |
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 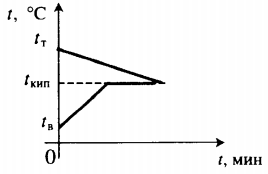
Уравнение теплового баланса: Q1+Q2=0 cтmт(100−tт)+cвmв(100−tв)+rmп=0 |
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 оС. | 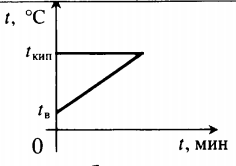
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmв(100−tв)=0 |
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 оС. | 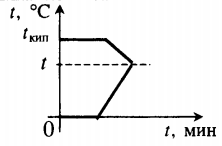
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmп(t−tкип)+λmл+cвmл(t−tпл)=0 |
Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 оС, долили 3 л кипятка. Какая температура воды установилась?
2 л = 2 кг
3 л = 3 кг
Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:
cm1(t−t0)=−cm2(t−tкип)
Или:
m1(t−t0)=−m2(t−tкип)
m1t+m2t=m1t0+m2tкип
(m1+m2)t=m1t0+m2tкип
t=m1t0+m2tкипm1+m2
t=2·25+3·1002+3=3505=70 (°C)
Взаимные превращения механической и внутренней энергии
Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.
Частные случаи закона сохранения энергии
| При неупругом ударе о стенку пуля нагрелась |
mv22=cmΔt |
| Тело падает с некоторой высоты и в момент падения нагревается |
mgh=cmΔt |
| В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули |
0,5(mv202−mv22)=cmΔt |
| Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления |
mv22=cmΔt+λm |
| Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии |
0,6mgh=cmΔt+rm |
| Вследствие сгорания топлива ракета поднялась на некоторую высоту |
qmтоп=mрgh |
| Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии |
0,25qmтопmсv22 |
Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).
Запишем закон сохранения энергии для этого случая:
0,52mv22=cmΔt
Δt=0,52v22c=0,52·10022·130=20 (К)
Примеры КПД
| Устройство | Полезная энергия (работа), затраченная энергия (полная работа) | КПД |
| Электронагреватель, электроплитка, электрочайник, кипятильник. |
Qполезн=cmΔT Иногда: Qполезн=cmΔT+rm Wзатр=Pt (произведение мощности на время) |
η=cmΔTPt100% |
| Газовая горелка, паровая турбина, спиртовка, плавильная печь. |
Qполезн=cmΔT Qзатр=qmтоп |
η=cmΔTqmтоп100% |
| Двигатель автомобиля, самолета. |
Aполезн=Nt=Nsv Qзатр=qmтоп |
η=cmΔTvqmтоп100 |
| Ружье с пороховым зарядом, пушка |
Eполезн=mv22 Qзатр=qmпор |
η=mv22qmпор100 |
Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:
Q1t1=Q2t2
Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 оС потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.
Будем считать, что мощность электроплитки постоянна. Поэтому:
Q1t1=Q2t2
Количество теплоты, сообщенное воде при нагревании:
Q1=сm(t2−t1)
Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:
Q1=rm
Отсюда:
сm(t2−t1)t1=rmt2
Задание EF17544
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Ответ:
а) 0°С
б) 4°С
в) 6°С
г) 9°С
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать уравнение теплового баланса для первого случая.
Решение
Запишем исходные данные:
• Начальная температура льда: t0 = 0 oC.
• Конечная температура воды в первом случае: t1 = 12 oC.
• Количество теплоты, выделенное электронагревателем в первом случае: Q1 = 80 кДж.
• Количество теплоты, выделенное электронагревателем во втором случае: Q2 = 60 кДж.
Составим уравнение теплового баланса для первого случая:
Q1=λm+cmt1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
Отсюда:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 оС.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18791
Внимательно прочитайте текст задания и выберите верный ответ из списка
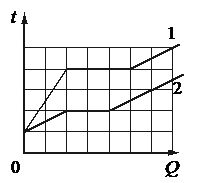
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера.
Ответ:
а) Температура плавления первого тела в 1,5 раза больше, чем второго.
б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии
в 3 раза больше, чем первого.
г) Оба тела имеют одинаковую удельную теплоту плавления.
д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
Ответ: вд
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22685
В сосуде лежит кусок льда. Температура льда t1 = 0 °C. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать уравнение теплового баланса.
3.Выполнить решение в общем виде.
4.Определить и вычислить искомую величину.
Решение
Запишем исходные данные:
• Начальная температура льда: t1 = 0 oC.
• Конечная температура воды: t2 = 20 oC.
• Количество теплоты, переданное льду изначально: Q = 50 кДж.
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
50 кДж = 50000 Дж
333,5 кДж = 333500 Дж
Составим уравнение теплового баланса:
Qобщ=Q+q
где q — количество теплоты, необходимое для того, чтобы окончательно растопить лед и нагреть воду:
q=Q2+Q3
Мы знаем, что изначально было растоплено 3/4 льда. Поэтому:
Q=3λm4
Отсюда масса льда равна:
m=4Q3λ
На растопку оставшегося льда уйдет следующее количество теплоты:
Q2=λm4
На нагревание воды уйдет следующее количество теплоты:
Q3=cmt2
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Отсюда:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.3k
Цель работы: Определить количество теплоты, отданное горячей водой и полученное холодной при теплообмене. Сравнить результаты.
Мы знаем, что внутреннюю энергию тела можно изменить не только за счет работы, но и за счет нагревания тела. При этом процесс передачи энергии от одного тела к другому без совершения работы называют теплообменом. Изменение внутренней энергии при теплообмене называют полученной или
отданной теплотой. Мы знаем также, что количество теплоты, необходимое для нагревания тела (или выделяемое им при охлаждении), зависит от рода вещества, из которого оно состоит, от массы этого тела и от изменения его температуры:
Измерить количество переданной теплоты можно в калориметрах. Это устройство мы будем использовать в этой работе.
Калориметр состоит из двух сосудов: внутреннего и внешнего. Внешний сосуд должен предохранять внутренний от потери тепла за счет теплообмена с окружающей средой. Сверху оба сосуда закрываются крышкой с установленным на ней термометром.
Если в калориметр налить воды массой m1 при температуре а затем еще добавить воды массой m2 при температуре t2 , то в сосуде начнется теплообмен, а спустя некоторое время установится состояние теплового равновесия. При этом обе части воды будут иметь одну и ту же температуру t, и количество теплоты, отданное горячей водой, равно количеству теплоты, полученной холодной водой. Последнее утверждение составляет смысл уравнения теплового баланса:
Пример выполнения работы:
Вычисления:
Количество теплоты, отданное горячей водой:
Количество теплоты, полученное холодной водой:
Вывод:
Количество теплоты, полученное холодной водой, приблизительно равно количеству теплоты, отданному горячей водой.
Точность приближения зависит от потерь теплоты в окружающую среду.