Количество
теплоты ,
Дж,
отданное (воспринятое) телом за
время τ
в
процессе охлаждения (нагревания), равно
,
(4.11) где
-количество
теплоты, переданное за время полного
охлаждения (нагревания), Дж;
— средняя по объему безразмерная
температура тела в момент времени τ
.
Для
пластины
толщиной
2δ и площадью поверхности F
теплота,
переданная за время полного охлаждения,
равна
(4.12)
где m
—
масса пластины, кг; с
—
теплоемкость материала пластины,
Дж/(кг∙К); — его
плотность, кг/м3.
Средняя
по объему безразмерная температура
пластины в момент времени τ:
при
Fо≥0,3

Для
цилиндра
радиусом
и
длиной l
теплота,
отданная за время полного охлаждения,
равна
.(4.14)
Средняя
по объему безразмерная температура
цилиндра в момент времени τ
при Fо≥0,3
равна

Средняя безразмерная
температура цилиндра конечной длины
,(4.16)
где
функция
определяется
по формуле (4.13), а
— по (4.15).
Для
параллелепипеда
со
сторонами ,
,
(рис. 7) теплота, отданная за время
полного охлаждения, равна
.(4.17)
Средняя безразмерная
температура параллелепипеда
,(4.18)
где функции ,
,
определяются по формуле (4.14).
Если
Fо<0,3,
то для вычисления
используется ряд, члены которого
определяются формулами типа (4.14), (4.16),
причем величины ,
,
…,
определяются по таблицам, приведенным,
например, в [12].
Лекция
№12
Тема: Нестационарный
процесс теплопроводности.
План лекции
4.4. Регулярный
режим охлаждения (нагревания) тел
4.4. Регулярный режим охлаждения (нагревания) тел
Теорию
регулярного режима разработал Г. М.
Кондратьев. Процесс охлаждения тела в
среде с постоянной температурой tж
и постоянным коэффициентом теплоотдачи
α можно разделить на три режима:
1)
неупорядоченный
—
на процесс влияет начальное распределение
температуры в теле;
2)
регулярный
—
в любой точке тела относительная скорость
изменения температуры, называемая
темпом охлаждения (нагревания)
остается постоянной и не зависит от
времени;
3)
стационарный
—
температура во всех точках тела равна
температуре среды (тепловое равновесие).
В
регулярном режиме темп охлаждения
(нагревания), m,
,
определенный по двум моментам времени
и ,
равен
,(4.19)
где
и
—избыточные
температуры в любой точке тела в моменты
времени
и
.
Темп
охлаждения т
зависит
от физических свойств тела, его размеров
и формы, коэффициента теплоотдачи и не
зависит от времени и координат.
Первая
теорема Г. М. Кондратьева для регулярного
режима выражается формулой
,(4.20)
где
F
и V
—
площадь поверхности и объем тела; ψ —
коэффициент неравномерности распределения
температуры в теле, определяемый
следующим образом:
,(4.21)
где
—
модифицированная форма числа Bi
; K
— коэффициент
формы
тела, м2.
Коэффициент
ψ зависит от условий процесса на
поверхности тела при Вi<0,1
ψ = 1 (температуры, усредненные по
поверхности и объему тела, одинаковы),
при Вi>100
ψ = 0 (температура поверхности тела
равна температуре среды).
Вторая
теорема Г. М. Кондратьева: при высокой
интенсивности
теплоотдачи
темп охлаждения пропорционален
коэффициенту температуропроводности
материала тела а,
м2/с:
.(4.22)
Коэффициент
формы К.
различных
тел:
для
шара радиусом
;
(4.23)
для
цилиндра
длиной l
и радиусом r0

для
параллелепипеда со сторонами a,
b,
c
.
(4.25)
Лекция
№ 13
Тема:
ТЕОРИЯ ПОДОБИЯ ПРИМЕНИТЕЛЬНО К ТЕПЛОВЫМ
ПРОЦЕССАМ
План лекции
5.1
Числа теплового и гидромеханического
подобия
процессов
При
экспериментальном изучении тепловых
процессов принято выражать математическое
описание процесса и расчетные уравнения
в виде зависимостей между числами
(критериями) подобия, представляющими
собой безразмерные комплексы.
Уравнения
подобия, выражая обобщенную зависимость
между величинами, характеризующими
процесс, справедливы для всех подобных
между собой процессов. Первая теорема
подобия: для подобных между собой
процессов все одноименные числа подобия
численно одинаковы, например Re
= idem,
Pr
= idem.
Согласно второй теореме подобия связь
между числами подобия выражается в
форме однозначной функциональной
зависимости, например Nu=f
(Rе,
Рr,
Gг,
…).
Третья
теорема подобия утверждает, что условия
подобия физических явлений, заключаются
в подобии условий однозначности и
равенстве одноименных чисел подобия,
составленных из величин, входящих в
эти условия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Количество теплоты – это физическая величина, которая обозначается буквой Q; скалярная величина; может быть положительной или отрицательной.
Энергия, которую получает или теряет тело при теплопередаче, называется количеством теплоты. В СИ измеряется в джоулях [Дж].
Для нагревания и охлаждения рассчитать количество теплоты можно по формуле Q = cm (t2 – t1).
c – удельная теплоёмкость вещества, у каждого вещества своя, берётся в таблице
m – масса, кг
t2 – конечная температура, °C
t1 – начальная температура, °С
Физическая величина, численно равная количеству теплоты, которое необходимо передать телу массой 1 кг для того, чтобы его температура изменилась на 1°С, называется удельной теплоёмкостью вещества.
Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
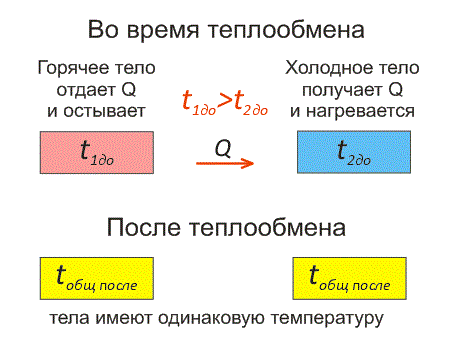
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.
Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
Привет, если у нас одни и теже учебники , то тогда тебе повезло:)
Лабораторная работа 1
Сравнение количеств теплоты при смешивании воды разной температуры
Цель работы: определить количество теплоты, отданное горячей водой и полученное холодной при теплообмене, и объяснить полученный результат.
Приборы и материалы: калориметр, измерительный цилиндр (мензурка), термометр, стакан.
Ход работы:
1. Нальем в калориметр горячей воды массой 100 г. Возьмем столько же холодной воды и нальем ее в стакан. Измерим с помощью термометра температуру холодной и горячей воды. Результаты измерений занесем в таблицу.
2. Вольем холодную воду в калориметр, в сосуд с горячей водой, помешаем термометром и измерим температуру полученной смеси (72°С). Результат измерений занесем в таблицу.
3. Рассчитаем количество теплоты отданное горячей и полученное холодной водой по следующим формулам:
rде: Q — количество теплоты отданное горячей водой; Q1 — количество теплоты полученное холодной водой; m — масса холодной или горячей воды; с = 4200 — теплоемкость воды; t – температура горячей воды; t1 – температура холодной воды; t2 – температура смеси.
Выводы: В результате измерений было установлено, что количество теплоты отданное горячей водой равно количеству теплоты полученное холодной водой. Таким образом, подтверждается закон сохранения энергии.
Содержание:
- Определение и формула количества теплоты
- Формула расчета теплоты при изменении температуры
- Формула количества теплоты при фазовых переходах
- Единицы измерения количества теплоты
- Примеры решения задач
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.
Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем,
что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом
случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система
микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии,
которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Определение
Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой).
Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики.
Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $delta Q$. Обратим внимание,
что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом.
Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
$$delta Q=C d T(1)$$
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
$$delta Q=c m d T=nu c_{mu} d T(2)$$
где $c=frac{C}{m}$ – удельная теплоемкость тела, m – масса тела,
$c_{mu}=c cdot mu$ — молярная теплоемкость,
$mu$ – молярная масса вещества,
$nu=frac{m}{mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты
($Delta Q$), которое получает тело при увеличении его температуры на величину
$Delta t = t_2 — t_1$ можно вычислить как:
$$Delta Q=c m Delta t(3)$$
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности
($Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Формула количества теплоты при фазовых переходах
Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты,
которая носит название теплоты фазового перехода.
Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты
($delta Q$) равное:
$$delta Q=lambda d m$$
где $lambda$ – удельная теплота плавления, dm – элемент массы тела.
При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества.
При кристаллизации происходит выделение тепла равного (4).
Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:
$$delta Q=r d m$$
где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Пример
Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура
одной массы воды t1=10С, второй массы воды t2=60С?
Решение. Запишем уравнение теплового баланса в виде:
$$Q=Q_{1}+Q_{2}(1.1)$$
где Q=cmt – количество теплоты приготовленной после смешивания воды; Q1=cm1t1 —
количество теплоты части воды температурой t1 и массой m1;
Q2=cm2t2— количество теплоты части воды температурой t2 и массой m2.
Из уравнения (1.1) следует:
$$
begin{array}{l}
mathrm{cmt}=mathrm{cm}_{1} t_{1}+mathrm{~cm}_{2} t_{2} rightarrow mathrm{mt}=mathrm{m}_{1} t_{1}+mathrm{~m}_{2} t_{2} rightarrow \
rightarrow rho mathrm{Vt}=rho V_{1} t_{1}+rho mathrm{V}_{2} t_{2} rightarrow mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2)
end{array}
$$
При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:
$$$
V=V_{1}+V_{2}(1.3)
$$$
Так, мы получаем систему уравнений:
$$
left{begin{array}{c}
V t=V_{1} t_{1}+V_{2} t_{2} \
V=V_{1}+V_{2}
end{array}right.
$$
Решив ее получим:
$$
begin{array}{l}
V_{1}=frac{left(t_{2}-tright)}{t_{2}-t_{1}} V \
V_{2}=frac{left(t-t_{1}right)}{t_{2}-t_{1}} V
end{array}
$$
Проведем вычисления (это можно сделать, не переходя в систему СИ):
$$
begin{array}{l}
V_{1}=frac{(60-40)}{60-10} 200=80 text { (л) } \
V_{2}=frac{(40-10)}{60-10} 200=120 text { (л) }
end{array}
$$
Ответ. V1=80 л, V2=120 л.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
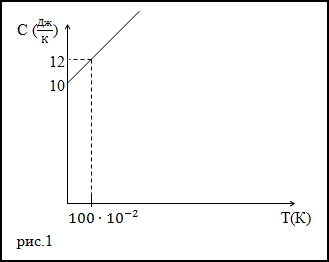
Задание. Теплоемкость тела изменяется по линейному закону (рис.1) в зависимости от абсолютной температуры в
рассматриваемом интервале $T_{1} leq T leq T_{2}$ .
Какое количество теплоты получает тело, если T1=300 К, T2=400 К.
Решение. Исследуя график функции теплоемкости (C(T)) (рис.1) запишем его аналитическое выражение, оно получится:
$C(T)=10+2 cdot 10^{-2} T$ (Дж/К)
Основой для решения задачи послужит формула для количества теплоты в виде:
$$delta Q=C d T(2.2)$$
Подставим полученное выражение для теплоемкости (2.1) в формулу (2.2) поведем интегрирование в заданном интервале температур:
$$
begin{array}{c}
Delta Q=int_{300}^{400}left(10+2 cdot 10^{-2} Tright) d T=left.left(10 cdot T+10^{-2} T^{2}right)right|_{300} ^{400}= \
=left(10 cdot 400+10^{-2} cdot(400)^{2}right)-left(10 cdot 300+10^{-2} cdot(300)^{2}right)=1700left(mathrm{~A}^{*}right)
end{array}
$$
Ответ. $Delta Q$=1700 Дж
Читать дальше: Формула напряженности магнитного поля.