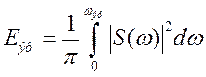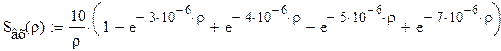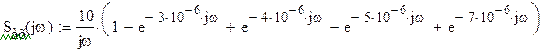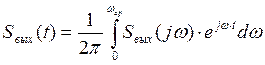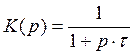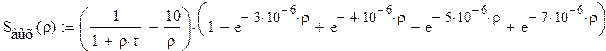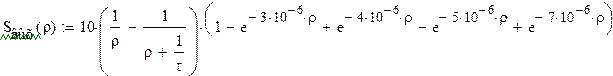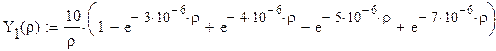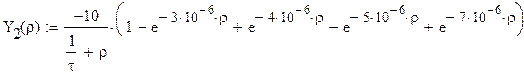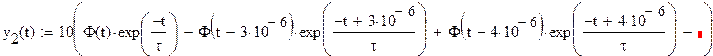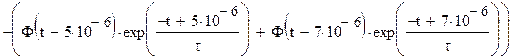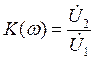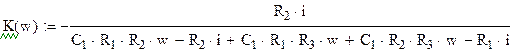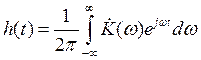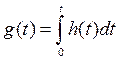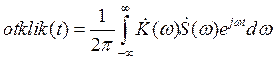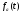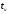Как найти отклик цепи

 

Тогда эффективную ширину спектра можно определить по
формуле:

Подставляя в данный интеграл ,
находим, что эффективная ширина спектра:

В данном случае мы предполагали лишь положительную
область спектра, но в силу симметричности для всей области спектра эффективная ширина
его умножается на 2.

·  Найти сигнал,
который получается из заданного при воздействии фильтра с прямоугольной АЧХ и
линейной ФЧХ (частота среза  фильтра в МГц и
крутизна  ФЧХ в рад/МГц приведены в табл. 2),
построить временной график полученного сигнала

Таблица
2

Вариант	9
fср, МГц	2,8
Подвариант	2
S, рад/МГц	0,8

Передаточная функция цепи имеет вид:

где— функция включения
Хевисайда.

Исходный сигнал, записанный как линейная комбинация
функций включения:

Представим исходный сигнал в операторном виде,
применив прямое преобразование Лапласа:

Заменив  на , получаем выражение для входного сигнала в
частотной области:

Выражение
для выходного сигнала в частотной области можно получить путем перемножения
комплексной частотной характеристики цепи и входного сигнала.

    

Тогда
выходной сигнал во временной области может быть получен как обратное
преобразование Фурье от выходного сигнала в частотной области:

    

График
выходного сигнала имеет вид:

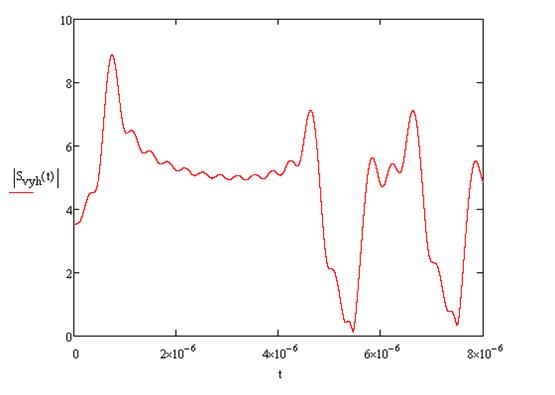График
выходного сигнала

·  Найти сигнал,
который получается из заданного при воздействии RC-фильтра НЧ с
параметрами, указанными в табл. 3 ( в кОм,  в мФ), построить временной график
полученного сигнала

                                    
Таблица 3

Вариант	9
R, кОм	2,8
Подвариант	9
C, мФ	0,8

Представим исходный сигнал в операторном виде,
применив прямое преобразование Лапласа:

Передаточная функция фильтра в операторном виде:

    

где — постоянная времени,
которая определяется следующим образом:

Выражение для выходного сигнала можно получить путем
перемножения передаточной функции фильтра и входного сигнала  в операторном
виде:

Преобразуем выражение для :

Т.о. сигнал на выходе можно представить как разность
двух составляющих, одна из которых есть входной сигнал. Найдем обратное
преобразование Лапласа от обоих составляющих:

Откуда:

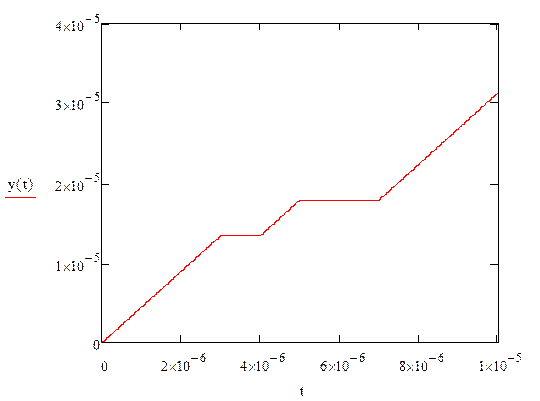
График выходного сигнала, построенный с помощью
математического пакета MathCAD,
имеет вид:

График
выходного сигнала

2.
Линейные инвариантные к сдвигу цепи

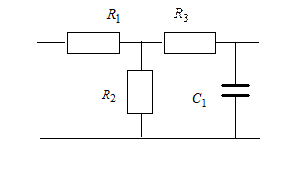
2.1ЛИС-цепь
определяется схемой согласно варианту (табл. 4), ее параметры ( в кОм,  в пФ,  в мГн ) – согласно подварианту
(табл. 5).

9

            Таблица 4Таблица
5

Подвариант	8
R1,кОм	2,2
R2,кОм	1,2
R3,кОм	1,7
С1,пФ	80

·             2.2    
Требуется:
 Найти комплексную частотную характеристику цепи, построить графики АЧХ и ФЧХ

КЧХ
можно найти как отношение выходного напряжения к входному:

Для нахождения входного напряжения
свернем схему относительно входных зажимов:

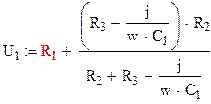Для нахождения выходного напряжения,
воспользуемся методом делителя токов:

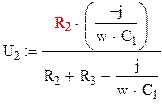Тогда КЧХ:

Построим графики АЧХ и ФЧХ комплексно
частотной характеристики:

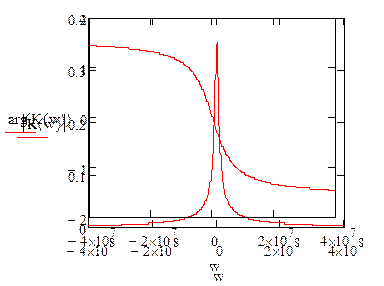·  Найти импульсную
и переходную характеристики, построить графики

Импульсная характеристика – отклик цепи
на дельта функцию. В теории сигналов, КЧХ связана с импульсной характеристикой
парой преобразований Фурье.

Импульсная характеристика цепи:

Построим график импульсной
характеристики:

Переходная характеристика – интеграл от импульсной
характеристики с переменным верхним пределом интегрирования:

Построим график переходной характеристики:

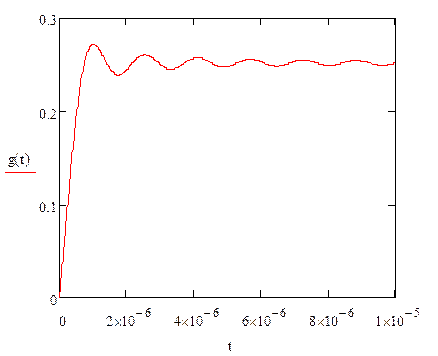·  Найти отклик
цепи на заданный сигнал, построить график

В теории сигналов, отклик цепи может быть найден как
обратное преобразование Фурье от произведения КЧХ на спектральную плотность
сигнала:

Построим график отклика цепи:

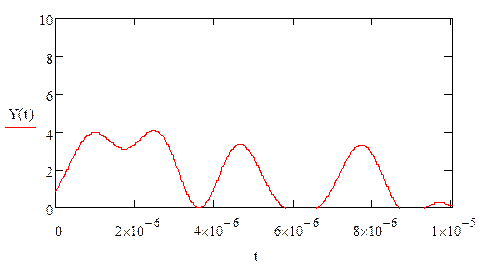5.4.1. Классический метод

5.4.2. Временной метод

5.4.3. Спектральный метод

5.4.4. Операторный метод

Основной задачей анализа является определение реакции (выходного) сигнала цепи при действии на её входе сигнала известной формы. При этом, входной сигнал может быть описан как во временной, так и в частотной области. В связи с этим различают следующие методы анализа: классический, временной (или метод интеграла наложения), спектральный и операторный. Выбор того или иного метода зависит от структуры цепи, вида воздействующего на неё сигнала, формы представления (временная или частотная) входного сигнала.

5.4.1. Классический метод

Классический метод основывается на решении дифференциального уравнения вида (5.16), описывающего линейную цепь. Решение этого уравнения представляет собой сумму двух слагаемых

, (5.19)

где первое слагаемое представляет собой общее решение однородного дифференциального уравнения

, (5.20)

а второе слагаемое – частотное решение (5.16) при , где – правая часть уравнения (5.16). Физически – свободная составляющая полного отклика (выходного сигнала), представляет собой реакцию цепи на отключение(или включение) входного сигнала и характеризует переходные процессы в цепи. Второе слагаемое – вынужденная составляющая, является реакцией цепи после окончания переходных процессов и характеризует установившейся(стационарный) режим преобразования цепью входного сигнала. Обычно, классический метод используется для изучения переходных процессов, что приводит к необходимости решения уравнения (5.20). Общее решение однородного уравнения (5.20) имеет вид

, (5.21)

где , ,…, – постоянные коэффициенты, определяемые начальными условиями,

, ,…, – корни характеристического уравнения:

. (5.22)

Это уравнение имеет ровно n корней, при этом корни могут быть либо вещественными, либо комплексными, что определяет характер переходных процессов. Что же касается , то если входной сигнал является постоянным или периодическим, то после окончания переходных процессов выходной сигнал принимает форму входного сигнала. Так, если представляет собой гармонический сигнал, то также будет гармоническим, отличаясь от входного сигнала амплитудой и начальной фазой.

В качестве примера рассмотрим, что собой представляет отклик RC-цепи (рис. 5.3,8) на входной сигнал вида .

Дифференциальное уравнение цепи (5.15) перепишем в виде

,

где – постоянная времени.

Поскольку дифференциальное уравнение имеет порядок n=1, решение однородного уравнения

согласно (5.21), запишется в виде

,

где – корень характеристического уравнения

,

откуда следует . Тогда

.

До поступления входного сигнала ёмкость С разряжена. В момент поступления входного сигнала (скачка) ёмкость не может мгновенно зарядиться до , это произойдёт по мере перехода к установившемуся режиму. Очевидно в установившемся режиме

.

Таким образом, суммарный выходной сигнал

.

Коэффициент найдём из начальных условий. Начальными условиями при исследовании линейных цепей называют значения токов в индуктивностях и напряжений на емкостях в момент времени . Так как в этот момент времени , то можно записать

,

Откуда следует . Тогда окончательно суммарный выходной сигнал

.

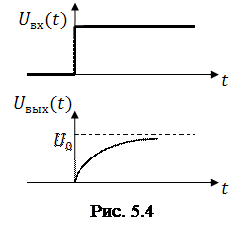
На рис. 5.4. изображены эпюры напряжений на входе и выходе исследуемой RC-цепи.

5.4.2. Временной метод

Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( – функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы.

Выберем в качестве элементарного сигнала – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом

.

Очевидно, выходной сигнал

.

Так как оператор не зависит от времени, его можно внести под знак интеграла. Тогда, с учётом (5.5)

. (5.23)

Если момент появления входного сигнала , то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид

. (5.24)

Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента и заканчивая текущим моментом времени . Роль весовой функции выполняет импульсная характеристика цепи.

Выражение (5.24) носит название интеграла Дюамеля. Это выражение было получено в предположении, что входной сигнал представлен в виде суммы элементарных сигналов вида – функций. Если входной сигнал представить в виде (1.15) комбинаций сигналов вида единичного скачка, то можно получить другие формы интеграла Дюамеля, в частности

. (5.25)

Здесь – переходная характеристика цепи.

Итак, для использования метода интеграла наложения необходимо знать импульсную характеристику или переходную характеристику . Эти характеристики можно определить несколькими способами. Прямой (непосредственный способ состоит в решении дифференциального уравнения (5.20) в предположении, что входной сигнал является очень коротким импульсом(для определения импульсной характеристики) или сигналом вида единичного скачка( для определения переходной характеристики).

В выше приведённом примере было решено дифференциальное уравнение и найден отклик RC-цепи на воздействие сигнала

.

Очевидно, форма отклика не изменится, если входной сигнал будет единичным скачком, при этом масштаб отклика изменится в раз. Тогда выходной сигнал

, (5.26)

поскольку реакция цепи на единичный скачок является переходной характеристикой. В соответствии с (5.7) определяется импульсная характеристика

(5.27)

Второй способ определения импульсной или переходной характеристики, назовём его косвенным, состоит в использовании однозначного соответствия между импульсной характеристикой и комплексным коэффициентом передачи.

5.4.3. Спектральный метод

При рассмотрении характеристик линейной цепи было получено соотношение (5.10), связывающее спектральные характеристики входного и выходного сигнала с комплексным коэффициентом передачи цепи. Это соотношение лежит в основе спектрального анализа. Если задачей анализа является определение частотных характеристик выходного сигнала, то при известных и использование (5.10) полностью решает эту задачу. В ряде случаев сигнал представлен во временной области и требует найти отклик цепи как функцию времени. При этом использование метода интеграла наложения может быть затруднено сложностью нахождения импульсной характеристики цепи. В то же время комплексный коэффициент передачи найти достаточно просто. Тогда спектральный метод анализа сводится к следующим операциям:

— для входного сигнала прямым преобразованием Фурье находится комплексный спектр ;

— определяется комплексный коэффициент передачи цепи ;

— в соответствии с (5.10) определяется комплексный спектр выходного сигнала ;

— обратным преобразованием Фурье вычисляется форма сигнала на выходе цепи.

Итак, важнейшим условием использования спектрального метода является знание комплексного коэффициента передачи исследуемой цепи. Найти комплексный коэффициент передачи можно, используя методы теории цепей (метод узловых потенциалов или метод контурных токов). Если известно аналитическое описание цепи дифференциальным уравнением (5.16), то комплексный коэффициент передачи находится в соответствии с (5.18). Наконец, цепь можно представить в виде делителя напряжения, элементами которого являются комплексные сопротивления

; ; .

Проиллюстрируем последний подход на примере уже рассматривавшейся выше RC-цепи. Если представить цепь как делитель напряжения, то выходной сигнал представляет собой напряжение на ёмкости С. Тогда, если комплексный ток, протекающий в цепи, то

,

и комплексный коэффициент передачи

,

что совпадает с результатом, полученным в подразделе 5.3.

5.4.4. Операторный метод

Операторный метод является обобщением спектрального метода. В основе метода лежит преобразование Лапласа. Рассмотрим некоторый сигнал , определённый на интервале времени (0, ). Умножим этот сигнал на и полученный новый сигнал подвергнем преобразованию Фурье

.

Обозначая через , получим

. (5.28)

Выражение (5.28) называется односторонним преобразованием Лапласа функции . При этом, называют оригиналом, а изображением.

Нетрудно убедиться, что при выражение (5.28) преобразуется к виду

,

что соответствует преобразованию Фурье. Таким образом если преобразование Фурье представляет собой спектральное разложение сигнала по гармоническим составляющим , то преобразование Лапласа – разложение сигнала по экспоненциально – косинусным составляющим . Действительно, представим

.

Здесь использована формула Эйлера

.

С другой стороны

,

где .

Тогда окончательно

представляет собой экспоненциально – косинусную функцию.

Переход от изображения к оригиналу осуществляется при помощи обратного преобразования Лапласа

. (5.29)

Для значительной части функций широко используемых при описании оригиналов были рассчитаны изображения по Лапласу. Некоторая часть оригиналов и изображений приведена в таблице 5.1.

Поскольку преобразование Лапласа является обобщением преобразования Фурье, то оно обладает теми же свойствами, что и преобразование Фурье. Остановимся на некоторых из них, которые будем использовать в дальнейшем. Пару преобразований (прямое и обратное) будем обозначать следующим образом

.

1. Линейность преобразований Лапласа

(5.30)

2. Свойство временного сдвига

(5.31)

3. Операция дифференцирования

; (5.32)

4. Операция интегрирования

. (5.33)

Применим к обеим частям уравнения (5.16) прямое преобразования Лапласа. Тогда с учётом (5.32), получим

(5.34)

откуда следует

. (5.35)

Это отношение называется передаточной функцией цепи или её операторным коэффициентом. Таким образом, передаточная функция является оператором преобразования линейной цепью в базисе экспоненциально – косинусных сигналов.

Сравним выражение комплексного коэффициента передачи (5.18) с выражением (5.35). Из этого сравнения следует, что комплексный коэффициент передачи является частным случаем при , т.е.

(5.36)

Таким образом, если известна передаточная функция цепи, то операторный метод поиска отклика цепи состоит в следующем:

— находится изображение по Лапласу входного сигнала

; (5.37)

— находится изображение выходного сигнала как произведение

; (5.38)

— определяется оригинал выходного сигнала

. (5.39)

Установим связь между временными характеристиками и передаточной функцией. Произведя в (5.12) замену на , получим

.

Таким образом, передаточная функция и импульсная характеристика связаны между собой преобразованием Лапласа

.

Что касается переходной характеристики, то применяя к (5.8) преобразование Лапласа и учитывая (5.33), получим

.

В заключение отметим, что операторный метод позволяет сводить линейные дифференциальные уравнения вида (5.16) к алгебраическим уравнениям (5.34), что позволяет в ряде случаев упростить анализ цепей. Помимо этого, учитывая широкое распространение таблиц преобразований Лапласа для большого числа функций, можно исключить громоздкие вычисления, непосредственно обращаясь к этим таблицам.

Рассмотрим применение операторного метода на примере анализа определения отклика RC-цепи на входной сигнал вида . Эта задача была решена классическими временными методами. Спектральным методом был найден комплексным коэффициент передачи. Заменив в выражении для цепи на , получим передаточную функцию цепи

.

Следуя операторному методу найдём изображение по Лапласу входного сигнала, воспользовавшись при этом таблицей 5.1

.

Далее, в соответствии с (5.38), определим изображение выходного сигнала

.

И наконец, по таблице 5.1 (позиция 5) находим оригинал

,

что совпадает с полученными ранее результатами.

1. Импульсная характеристика цепи

Расчет
отклика цепи во многих случаях может
быть упрощен, если входной сигнал
представить суммой элементарных
воздействий в виде прямоугольных
импульсов малой длительности. Для этого
сначала рассмотрим связь между функциями
и,
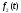
изображенными на рис.5.8а,6, которые можно
записать в виде:

Вторая
функция является единичным импульсом,
который рассмотрен нами в п.2.4. Как видно,
функция

является производной от функции
,
т.е..
Осуществим в этих функциях предельный
переход при.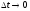
При этом функцияперейдет в единичную функцию,
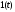
а функция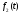в
функцию.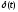
Тогда в силу равенстваследует, что единичный импульс, или— функция является производной единичной
функции.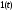

Для
линейной цепи отсюда заключаем, что
ее отклик на единичный импульс
,
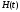
называемый импульсной характеристикой
цепи, является производной переходной
характеристики цепи, т.е.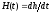или

(5.12)

Размерность
импульсной характеристики равна
размерности переходной характеристики,
деленной на время.

Нахождение
импульсной характеристики в большинстве
случаев проще, чем нахождение переходной
характеристики. Действительно, как
показано в п. 2.4, спектральная функция
единичного импульса
,
а поэтому для импульсной характеристики
с помощью интеграла Фурье получаем
выражение

(5.13)

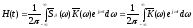
Из
этого выражения следует, что спектральная
функция характеристики равна комплексному
коэффициенту передачи цепи, т.е.
или, пользуясь прямым преобразованием
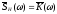
Фурье, запишем:

(5.14)

To
есть импульсная характеристика цепи
так же, как и переходная характеристика,
определяется через коэффициент передачи,
но для импульсной характеристики в
большинстве случаев подынтегральное
выражение в интеграле Фурье оказывается
проще.

В
качестве примера применим соотношение
(5.14) для опреде­ления спектра импульсной
характеристики интегрирующей
цепи,
переходная характеристика которой.
Для импульсной характеристики получаем

при
.

Пользуясь
здесь выражением (5.14), необходимо учесть,
что переходная характеристика при

тождественно
равна нулю, и поэтому нижний предел в
интеграле выражения (5.14) будет нуль.
Тогда спектральная функция импульсной
характеристики
равна

,

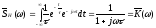
т.е.
получили коэффициент передачи
интегрирующей цепи, соответствующий
ранее полученному выражению (3.16).

Зная
импульсную характеристику, можно найти
отклик цепи на воздействие сигнала
любой формы, либо предварительно найдя
по соотношению (5.12) переходную
характеристику, а затем воспользовавшись
одним из выражений интеграла Дюамеля,
либо непосредственно через функцию
.
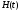
В
последнем случае входную функцию, т.е.
воздействующий сигнал

необходимо
представить в виде суммы импульсов, как
показано на рис. 5.9.

Такое
представление функции

будет
точнее, если
,
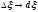
т.е.
если она представлена суммой бесконечно
большого числа бесконечно малых по
длительности импульсов, являющихся
здесь элементарными воздействиями.
Если бы элементарным воздействием был
единичный импульс,
площадь
которого равна единице, то откликом
цепи на такой импульс, появляющийся в
момент времени
,
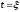
была бы импульсная характеристика.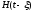
В рассматриваемом случае элементарный
импульс имеет величину, равную мгновенному
значению функции в момент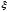и длительность,
равную
,
т.е. его площадь равна.
Тогда откликом на элементарное воздействие
будет величина.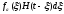
Отклик цепи на воздействие, заданное
функцией,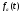
будет суммой откликов на все элементарные
воздействия, временное положение которых
соответствует интервалу от 0 до
,
т.е.

. (5.15)

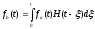
Это
выражение, являющееся еще одним видом
записи интеграла Дюамеля, называется
также сверткой функций. Оно по виду
совпадает с оригиналом свертки изображений
двух функций в формуле (4.21).

Импульсную
характеристику цепи можно получить с
помощью эксперимента, наблюдая отклик
цепи (выходное напряжение) на электронном
осциллографе. На вход цепи необходимо
подать импульс весьма малой длительности.
Для примера рассмотрим импульсную
характеристику последовательного
колебательного контура, считая, что
выходное напряжение снимается с емкости
С.
Выше
в п.1.6 мы рассмотрели переходный процесс
при включении постоянного напряжения
на такой контур. Если величина поданного
напряжения равна единице, то напряжение
на емкости, являющееся переходной
характеристикой цепи равно, согласно
(1.33),

при
.

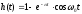
Эта
переходная характеристика представлена
на рис.5.10а. Тогда импульсная характеристика
контура

при
.

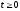
Считая
добротность контура большой, полагаем

и
тогда
первым
членом можно пренебречь:

при
.

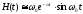
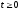
Эта
характеристика представлена на рис.5.10б.
Она соответствует осциллограмме
свободных колебаний в контуре,
рассмотренных нами в п.1.5.

Таким
образом, для того чтобы экспериментально
наблюдать импульсную характеристику
контура, необходимо на вход контура
подать импульс малой длительности, т.е.
(как было пояснено в п.2.4) чтобы его
длительность

удовлетворяла
условию
.

Соседние файлы в папке Лекц рожко

• #
• #
• #
• #
• #
• #

Записи по теме

Если выход электрической цепи для входа изменяется во времени, то это называется временной реакцией . Время отклика состоит из следующих двух частей.

• Переходный ответ
• Устойчивый государственный ответ

В этой главе сначала давайте обсудим эти два отклика, а затем рассмотрим эти два отклика в последовательной цепи RL, когда она возбуждается источником постоянного напряжения.

Переходный ответ

После применения входа к электрической цепи, выходу требуется определенное время для достижения устойчивого состояния. Таким образом, выходной сигнал будет в переходном состоянии, пока он не перейдет в устойчивое состояние. Следовательно, отклик электрической цепи во время переходного состояния известен как переходный отклик .

Переходный отклик будет нулевым для больших значений «t». В идеале это значение t должно быть бесконечностью. Но практически пяти постоянных времени достаточно.

Присутствие или отсутствие переходных процессов

Переходные процессы происходят в ответе из-за внезапного изменения в источниках, которые применяются к электрической цепи и / или из-за действия переключения. Есть два возможных переключения. Это выключатель размыкания и замыкания.

• Переходная часть не будет присутствовать в ответе электрической цепи или сети, если она содержит только сопротивления. Потому что резистор имеет возможность регулировать любое количество напряжения и тока.

• Переходная часть возникает в ответе электрической цепи или сети из-за присутствия элементов накопления энергии, таких как индуктор и конденсатор . Потому что они не могут мгновенно изменить энергию, хранящуюся в этих элементах.

Переходная часть не будет присутствовать в ответе электрической цепи или сети, если она содержит только сопротивления. Потому что резистор имеет возможность регулировать любое количество напряжения и тока.

Переходная часть возникает в ответе электрической цепи или сети из-за присутствия элементов накопления энергии, таких как индуктор и конденсатор . Потому что они не могут мгновенно изменить энергию, хранящуюся в этих элементах.

Поведение индуктора

Предположим, что действие переключения происходит при t = 0. Ток индуктора не изменяется мгновенно, когда происходит действие переключения. Это означает, что значение тока индуктора сразу после действия переключения будет таким же, как и перед действием переключения.

Математически это можно представить как

iL(0+)=iL(0−)

Конденсаторное поведение

Напряжение на конденсаторе не изменяется мгновенно, подобно току индуктора, когда происходит переключающее действие. Это означает, что значение напряжения на конденсаторе сразу после переключения будет таким же, как и перед переключением.

Математически это можно представить как

vc(0+)=vc(0−)

Устойчивый государственный ответ

Часть временного отклика, которая остается даже после того, как переходный отклик стал нулевым значением для больших значений «t», называется устойчивым откликом . Это означает, что не будет никакой переходной части в ответе в устойчивом состоянии.

Поведение индуктора

Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько катушек индуктивности и резисторов (дополнительно) в течение длительного времени, то эта электрическая цепь или сеть, как говорят, находятся в устойчивом состоянии. Следовательно, энергия, запасенная в катушке индуктивности этой электрической цепи, максимальна и постоянна.

Математически это можно представить как

WL= fracLiL22= Максимум и константа

 RightarrowiL= Максимум и константа

Следовательно, индуктор действует как источник постоянного тока в устойчивом состоянии.

Напряжение на индуктивности будет

VL=L fracdiLdt=0V

Таким образом, индуктор действует как короткое замыкание в устойчивом состоянии.

Конденсаторное поведение

Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько конденсаторов и резисторов (необязательно), в течение длительного времени, то говорят, что эта электрическая цепь или сеть находятся в устойчивом состоянии. Следовательно, энергия, запасенная в конденсаторе (-ах) этой электрической цепи, является максимальной и постоянной.

Математически это можно представить как

Wc= fracCvc22= Максимум и константа

 Rightarrowvc= Максимум и константа

Следовательно, конденсатор действует как источник постоянного напряжения в устойчивом состоянии.

Ток, протекающий через конденсатор, будет

ic=C fracdvcdt=0A

Таким образом, конденсатор действует как разомкнутая цепь в устойчивом состоянии.

Нахождение ответа серии RL Circuit

Рассмотрим следующую схему RL серии .

В вышеупомянутой схеме переключатель оставался открытым до t = 0, и он был закрыт при t = 0. Таким образом, источник постоянного напряжения, имеющий V вольт, не подключен к последовательной цепи RL до этого момента. Следовательно, через индуктор не протекает начальный ток .

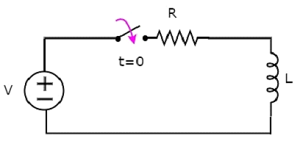
Принципиальная электрическая схема, когда переключатель находится в закрытом положении, показана на следующем рисунке.

Теперь ток i течет во всей схеме, поскольку источник постоянного напряжения, имеющий V вольт, подключен к последовательной цепи RL.

Теперь примените KVL вокруг петли.

V=Ri+L fracdidt

 fracdidt+ lgroup fracRL rgroupi= fracVL Уравнение 1

Вышеупомянутое уравнение является дифференциальным уравнением первого порядка, и оно имеет вид

 fracdydt+Py=Q Уравнение 2

Сравнивая Уравнение 1 и Уравнение 2, мы получим следующие соотношения.

x=t

y=i

P= fracRL

Q= fracVL

Решение уравнения 2 будет

ye intpdx= intQe intpdxdx+k Уравнение 3

Где k постоянная

Подставим значения x, y, P & Q в уравнение 3.

ie int lgroup fracRL rgroupdt= int( fracVL) lgroupe int lgroup fracRL rgroupdt rgroupdt+k

 Rightarrowie lgroup fracRL rgroupt= fracVL inte lgroup fracRL rgrouptdt+к

 Rightarrowie lgroup fracRL rgroupt= fracVL lbrace frace lgroup fracRL rgroupt fracRL rbrace+k

 Rightarrowi= fracVR+ke− lgroup fracRL rgroupt Уравнение 4

Мы знаем, что в цепи нет начального тока. Следовательно, замените t = 0 и ? = 0 в уравнении 4, чтобы найти значение константы k .

0= fracVR+ke− lgroup fracRL rgroup(0)

0= fracVR+k(1)

k=− fracVR

Подставим значение k в уравнение 4.

i= fracVR+ lgroup− fracVR rgroupe− lgroup fracRL rgroupt

i= fracVR− fracVRe− lgroup fracRL rgroupt

Следовательно, ток, протекающий по цепи

i=− fracVRe− lgroup fracRL rgroupt+ fracVR Уравнение 5

Итак, отклик цепи последовательного RL, когда она возбуждается источником постоянного напряжения, имеет следующие два члена.

• Первый член − fracVRe− lgroup fracRL rgroupt соответствует переходному ответу .

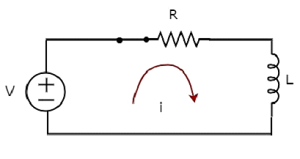
• Второе слагаемое  fracVR соответствует отклику установившегося состояния . Эти два ответа показаны на следующем рисунке.

Первый член − fracVRe− lgroup fracRL rgroupt соответствует переходному ответу .

Второе слагаемое  fracVR соответствует отклику установившегося состояния . Эти два ответа показаны на следующем рисунке.

Мы можем переписать уравнение 5 следующим образом:

i= fracVR lgroup1−e− lgroup fracRL rgroupt rgroup

 Rightarrowi= fracVR lgroup1−e− lgroup fract tau rgroup rgroup Уравнение 6

Где τ – постоянная времени, и ее значение равно  fracLR.

И Уравнение 5, и Уравнение 6 одинаковы. Но мы можем легко понять вышеуказанную форму волны тока, протекающего по цепи из уравнения 6, подставив несколько значений t, таких как 0, τ, 2τ, 5τ и т. Д.

В приведенной выше форме волны тока, протекающего по цепи, переходный отклик будет представлять до пяти постоянных времени от нуля, тогда как отклик в установившемся режиме будет присутствовать с пяти постоянных времени.