|
0 / 0 / 0 Регистрация: 14.05.2012 Сообщений: 15 |
|
|
1 |
|
Составить таблицу отклонений от среднего значения19.05.2012, 16:40. Показов 13742. Ответов 2
Задача: Даны результаты ежедневного измерения температуры воздуха первой декады марта: Нужно найти среднюю температуру. Я нашла, у меня получилось 0,9. Далее надо составить таблицу отклонений от средней температуры воздуха в каждый день из декады. Помогите, пожалуйста, как составить такую таблицу? Буду очень признательна.
0 |
|
призрак 3261 / 889 / 119 Регистрация: 11.05.2012 Сообщений: 1,702 Записей в блоге: 2 |
|
|
19.05.2012, 17:11 |
2 |
|
если в каждый день — то это просто таблица разностей между температурой данного дня и средней температурой.
1 |
|
0 / 0 / 0 Регистрация: 14.05.2012 Сообщений: 15 |
|
|
19.05.2012, 17:52 [ТС] |
3 |
|
Спасибо Вам большое
0 |
Как найти среднее квадратическое отклонение
Среднее квадратичное отклонение является важной количественной характеристикой в статистике, теории вероятностей и оценке точности измерений. Согласно определению средним квадратичным отклонением называется корень квадратный из дисперсии. Однако из этого определения не совсем понятно – что характеризует эта величина и как посчитать значение дисперсии.
Вам понадобится
- Калькулятор, компьютер
Инструкция
Пусть имеется несколько чисел, характеризующих какие-либо однородные величины. Например, результаты измереений, взвешиваний, статистических наблюдений и т.п. Все представленные величины должны измеряться одной и той же единицей измерения. Чтобы найти среднее квадратичное отклонение, проделайте следующие действия.
Определите среднее арифметическое всех чисел: сложите все числа и разделите сумму на общее количество чисел.
Найдите отклонение каждого числа от его среднего значения: вычтите от каждого числа среднее арифметическое значение, посчитанное в предыдущем пункте.
Определите дисперсию (разброс) чисел: сложите квадраты найденных ранее отклонений и разделите полученную сумму на количество чисел.
Извлеките из дисперсии квадратный корень. Полученное число и будет средним квадратическим отклонением данного множества чисел.
Пример.
В палате лежат семь больных с температурой 34, 35, 36, 37, 38, 39 и 40 градусов Цельсия.
Требуется определить среднее квадратическое отклонение от средней температуры.
Решение:
• «средняя температура по палате»: (34+35+36+37+38+39+40)/7=37 ºС;
• отклонения температур от среднего (в данном случае нормального значения): 34-37, 35-37, 36-37, 37-37, 38-37, 39-37, 40-37, получается: -3, -2, -1, 0, 1, 2, 3 (ºС);
• дисперсия: ((-3)²+(-2)²+(-1)²+0²+1²+2²+3²)/7=(9+4+1+0+1+4+9)/7=4 (ºС²);
• среднее квадратическое отклонение: √4=2 (ºС);
Ответ: В среднем по палате температура – нормальная: 37 ºС, но среднее квадратическое отклонение температуры равняется 2 ºС, что указывает на серьезные проблемы у пациентов.
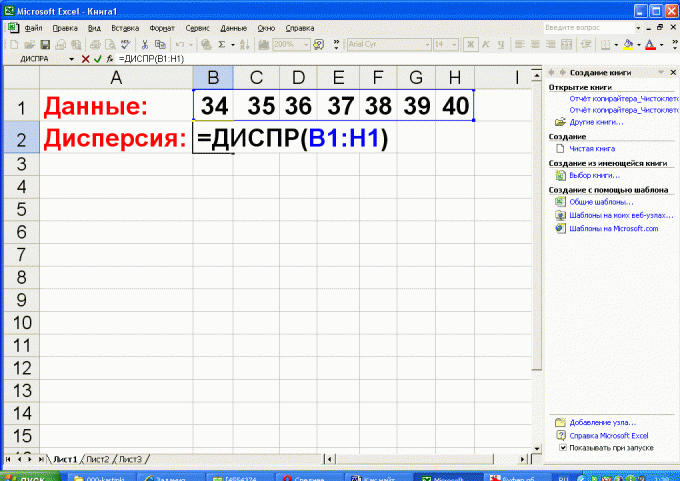
Если имеется возможность воспользоваться программой Excel, то вычисление дисперсии, а соответственно и среднего квадратического отклонения можно существенно упростить.
Для этого разместите данные измерений в один ряд (одну колонку) и воспользуйтесь статистической функцией ДИСПР. В качестве аргументов функции укажите диапазон ячеек таблицы, где размещены введенные числа.
Источники:
- как вычислить среднее квадратическое
Calculating average temperatures gives you a more accurate picture of the temperature in a specific location than a single measurement ever could. Temperatures fluctuate throughout the day, over the course of a week, month to month and year to year, as well as varying substantially depending on where exactly you are. Making sense of this and coming up with one figure for your purposes requires calculating the mean temperature, which is a specific type of average. You do this by adding up all of your individual measurements and dividing by the number of measurements.
TL;DR (Too Long; Didn’t Read)
Calculate the average temperature from several temperature measurements using the formula:
Average temperature = sum of measured temperatures ÷ number of measurements
Where the sum of measured temperatures is found by adding up every measurement. Ensure that all of the measurements are in the same temperature unit before applying this formula. Convert from Celsius to Fahrenheit or vice-versa using the following expressions:
Temperature in Fahrenheit = (Temperature in Celsius × 1.8) + 32
Temperature in Celsius = (Temperature in Fahrenheit – 32) ÷ 1.8
Decide What You Want the Average Of
Plan your calculations based on what exactly you want to work out. Do you want the average temperature for the week in one location, for the day over multiple locations or something else? The calculations are essentially the same in most cases, but this determines what data you need to collect for the calculation.
Take Your Measurements or Obtain Your Data
Take your measurements or find the data you need from an online source. (For example, the National Centers for Environmental Information has data for the U.S. See Resources for a link.) If you’re looking for data to determine the average temperature for the week, you can collect data each day (preferably at the same time in the day in the same location), but if you’re looking for data covering a longer period or over a larger area, it will probably be easier to use existing data.
Convert the Data Into the Same Unit
Celsius, Kelvin and Fahrenheit all express temperature, but all of your data has to be in the same unit if you want to calculate the average. To convert from Celsius to Kelvin, simply add 273 to the temperature in Celsius:
text{temperature in Kelvin}=text{temperature in Celsius}+273
Use the following formulas to convert from Celsius to Fahrenheit or vice-versa:
text{temperature in Fahrenheit}=1.8(text{temperature in Celsius})+32
text{temperature in Celsius}=frac{(text{temperature in fahrenheit}-32)}{1.8}
Add Up Your Individual Measurements
Start calculating your average by taking the sum of your individual measurements, all in the same unit of temperature. Imagine you have the following data for measurements taken over a week, all in degrees Fahrenheit: 70, 68, 79, 78, 73, 69 and 72. Take the sum as follows:
text{sum} = 70 + 68 + 79 + 78 + 73 + 69 + 72=509
Divide by the Number of Measurements
Divide the total from the previous step by the number of measurement to find the average temperature. In the example, there were seven measurements taken, so you divide by 7 to find the average:
text{average temperature}=frac{text{sum of measured temperatures}}{text{number of measurements}}
The result from the previous step gives:
text{average temperature}=frac{509}{7}=72.7text{ degrees Fahrenheit}
Expand this approach as needed for other situations. For example, you can take an average of measurements taken at different times in the day or at different locations to find the average temperature for each day. Then you can find the mean of these results to come up with an average temperature for the whole week.
Я работаю над набором данных, который будет универсальным для нескольких климатических станций для анализа температуры и осадков. Я наткнулся на кирпичную стену, проектируя «климатические нормы», успешно рассчитал среднесуточную температуру.TAVG, среднемесячная темп. AVG_TAVG, и подвел итоги PRCP а также SNOW для ежемесячных итогов.
Там, где я зашла в тупик, подсчитываю отклонение от нормы, в настоящее время данные с 1981 по 2010 год считаются климатическими нормами.
Вот как сейчас выглядит мой набор данных:
mso_light
year month day date PRCP SNOW SNWD TMAX TMIN TAVG
1 1948 1 1 1948-01-01 0 0 102 44 -122 -39.0
2 1948 1 2 1948-01-02 3 0 51 44 6 25.0
3 1948 1 3 1948-01-03 0 0 25 44 -39 2.5
4 1948 1 4 1948-01-04 38 64 76 33 -56 -11.5
5 1948 1 5 1948-01-05 0 0 76 -6 -83 -44.5
6 1948 1 6 1948-01-06 107 0 51 22 -61 -19.5
7 1948 1 7 1948-01-07 147 0 25 28 -17 5.5
8 1948 1 8 1948-01-08 8 13 25 39 -83 -22.0
9 1948 1 9 1948-01-09 0 0 25 -6 -117 -61.5
10 1948 1 10 1948-01-10 8 10 25 -11 -156 -83.5
Поэтому я изначально чувствовал, что мне нужен date для сортировки я удалю его, если он не понадобится в будущем.
Далее я хотел бы добавить столбец для DepNormT, который рассчитывается путем взятия 1 января — 31 декабря с 1981 по 2010 гг. и усреднения TAVGчтобы найти нормальную среднюю температуру. затемDepNormT будет разница между собой и TAVG для всего набора данных.
Я пробовал несколько способов добиться этого, вот две версии:
mso_DeptT <- mso_light %>%
group_by(month, day) %>%
mean(mso_light$TAVG[1981:2010], na.rm = T) %>%
ungroup()
Это дает мне следующую ошибку:
no applicable method for 'ungroup' applied to an object of class "c('double', 'numeric')"
In addition: Warning message:
In mean.default(., mso_light$TAVG[1981:2010], na.rm = T) :
argument is not numeric or logical: returning NA
Это еще одна версия:
##mso_DeptT <- filter(mso_light, year >= "1981", year <= "2010") %>%
## group_by(day, month) %>%
## mutate(daily_DeptT = mean(TAVG, na.rm = T)) %>%
## ungroup()
mso_sum <- mso_light %>%
group_by(month, year) %>%
summarize(AVG_TAVG=mean(TAVG, na.rm = TRUE),
T_PRCP=sum(PRCP, na.rm=TRUE),
T_SNOW=sum(SNOW, na.rm=TRUE)) %>%
ungroup()
## To find monthly normal precipitation and snowfall - using dataset mso_sum
cli_Avg <- filter(mso_sum, year >= "1981", year <= "2010") %>%
group_by(month) %>%
summarize(Mon_Precip = mean(T_PRCP, na.rm = T),
Mon_Snow = mean(T_SNOW, na.rm = T))
Это дало мне среднее значение за 30 лет, которое было равно среднему значению за каждый день. TAVG. Например:
year month day date PRCP SNOW SNWD TMAX TMIN TAVG DepNormT
1 1948 1 1 1948-01-01 0 0 102 44 -122 -39.0 -39.0
2 1948 1 2 1948-01-02 3 0 51 44 6 25.0 25.0
3 1948 1 3 1948-01-03 0 0 25 44 -39 2.5 2.5
4 1948 1 4 1948-01-04 38 64 76 33 -56 -11.5 ect
5 1948 1 5 1948-01-05 0 0 76 -6 -83 -44.5 .
6 1948 1 6 1948-01-06 107 0 51 22 -61 -19.5 .
7 1948 1 7 1948-01-07 147 0 25 28 -17 5.5 .
8 1948 1 8 1948-01-08 8 13 25 39 -83 -22.0
9 1948 1 9 1948-01-09 0 0 25 -6 -117 -61.5
10 1948 1 10 1948-01-10 8 10 25 -11 -156 -83.5
Спасибо за предложения.



