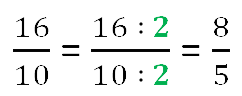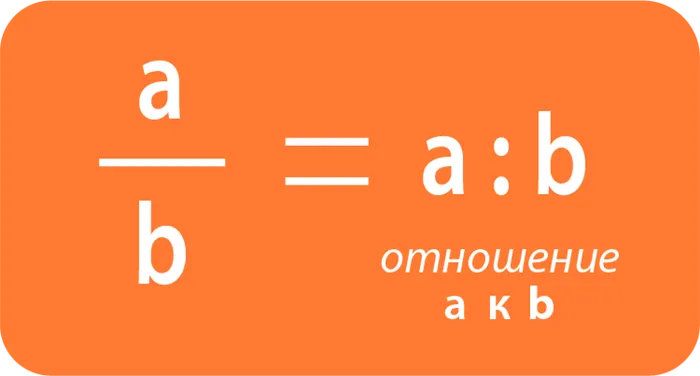Определение и понятие
История возникновения десятичных дробей тесно связана с учением о мерах. В Древнем Китае десятичную систему использовали для обозначения порядка. Полную теорию дробей в XV веке предложил узбекский астроном Джемшид Гиясэддин ал-Каши. Позже Стевин в своей книге «Десятая» начал записывать такие выражения в одну строку. Таким же образом их обозначал и Иоганн Кеплер. Используемая им запись осталась актуальной и сегодня.
Под дробью в математике понимают число, в состав которого входит одна или несколько равных долей единицы. Если стоит задача определить дробь конкретной величины, то её считают соответствующей единице. Например, пусть имеется круг, разделённый на шесть равных частей. Эти части называют долями. Всего их шесть, то есть каждая доля составляет шестую часть круга, исходную величину которого принимают как равную единице.
В математике это отношение обозначают в виде записи 1/6 и называют дробью. Читают его как «одна шестая». Любая дробь состоит из трёх элементов:
- Числителя — цифры или числа, стоящей в верхней части. Он показывает, сколько частей отобрано у целого, и является делимым.
- Знаменателя — числа, показывающего, на какое количество долей разделяют числитель.
- Дробной черты — разделяет числитель со знаменателем и фактически заменяет собой знак деления.
В школьных классах для того, чтобы ученики запомнили, где находится числитель, а где — знаменатель, предлагают ассоциации. Например, человек стоит на земле, она снизу, знаменатель — внизу. Таким образом, запись 3/6 будет обозначать, что круг разделили на шесть частей и три из них убрали.
Форма записи
При записи десятичной дроби используют следующую форму: сначала пишут целую часть, затем ставят разделитель целой и дробной доли (запятую), а после уже указывают дробную составляющую. Количество цифр, идущих после запятой, зависит от размерности. Различают десятые доли, их записывают одной цифрой, сотые — двумя, тысячные — тремя и так далее.
Записанные десятичные отношения выглядят так: 6,7; 3,26; 0, 234. Их принято указывать без знаменателя. Например, 7/10 = 0,7; 32/100 = 0,32. Удобнее всего пояснить на реальном примере. Пусть есть дробь 69/10. В знаменателе стоит число десять, имеющее один ноль. Отсчитав справа налево в числителе количество знаков, соответствующих числу нулей, в этом случае один, ставят запятую. В рассматриваемом примере запись будет выглядеть как 6,9. Тут 6 — целая часть, а 9 — дробная.
С отношениями можно выполнять любые действия. Их можно складывать, вычитать, делить и умножать. Десятичные дроби — это один из видов отношений. Они соответствуют выражениям, где знаменатель определяется как 10 в степени n, а n — натуральное число, то есть возникающее при счёте естественным образом.
Виды дробей
Дробные числа используют не только в математике, но и повседневной жизни. Наиболее типичное применение — это кулинария, где приготовление еды происходит с помощью смешивания определённых частей ингредиентов между собой. В качестве примера можно привести и спортивные состязания, пошив одежды, нумерацию.
Кроме десятичных отношений, существуют ещё и другие виды дроби:
- обыкновенная (простая) — записывают как отношение двух рациональных чисел;
- правильная — это выражение, у которого значение числителя меньше знаменателя;
- неправильная — в этом случае числитель больше или совпадает по величине со знаменателем;
- смешанная — образуется из неправильных как сумма натурального числа и правильной дроби.
Любую дробь можно преобразовать в другую. Самая простая операция, которую можно сделать — это перевод обыкновенного отношения в десятичное. Для этого вначале конвертируют числитель, а затем знаменатель. Но не с каждой дробью это возможно сделать.
Есть правило, по которому легко определить, существует ли возможность преобразования. Согласно ему, обыкновенную дробь можно преобразовать в конечную десятичную лишь в том случае, если её знаменатель можно разложить на множители два и пять, которые имеют свойство повторяться. Например, 11/40, знаменатель можно представить в виде произведения 2*2*2*5, поэтому привести к десятичной её возможно. А вот 13/60 преобразовать нельзя, так как в знаменателе при разложении есть число три: 5 * 2 * 2 * 3 = 60.
Для переведения простого отношения в десятичное нужно верхнюю и нижнюю часть выражения умножить на одно и то же число, но таким образом, чтобы внизу записи появилось число, кратное десяти. Например, 7/20 = 7*5/20*5 = 35/100 = 0,35. Или такой пример: 13/40 = 13/2*2*2*5 = 13*25/40*25 = 325/1000 = 0,325.
Есть и более сложный способ приведения, но при этом используют его чаще. В основе метода лежит деление уголком. То есть выполняют просто деление числителя на знаменатель. Например, 69/200. На первом этапе следует убедиться, что дробь может быть конечной десятичной, для этого раскладывают знаменатель: 200 = 5*5*2*2*2. На втором шаге выполняют деление в столбик и получают ответ: 0,345.
Популярность второго способа связана с тем, что всё же некоторые отношения проще разделить, чем подбирать, как правильно преобразовать знаменатель. Наиболее часто встречаются следующие дроби, которые поддаются преобразованию: ½ = 0,5; ¼ = 0,25; ¾ = 0,75; 1/5 = 0,2; 1/8 = 0,125; 1/10 = 0,1. А вот такие выражения, как 1/3, 1/7, 5/6, преобразовать в десятичные числа невозможно.
Преобразование отношения
Любое число можно преобразовать в дробь. Десятичные числа как слышатся, так и пишутся. Ноль целых три сотых — дробь 3/100. Выражение одна целая десять сотых можно записать как 1 (10/100).
Преобразуя десятичное число в дроби, можно сокращать. Например, 1,06 = 1 (5/100) = 1 (1/20). Часто приходится выполнять и обратное преобразование: 4/100 = 0,04. Смешанное отношение вида 3 (4/5) может быть преобразовано в неправильное. Для этого нужно целую часть умножить на нижнюю часть дроби и сложить с верхней. Знаменатель оставляют без изменений. То есть (3*5+4)/5 = 19/5.
При превращении смешанной дроби в неправильную используют правило сложения дробей. Например, выражение 3 (2/13) можно записать как 3 + 2/13 = 3/1 + 2/13 = (3*13+2)/13 = (39+2)/13 = 41/13. Для того чтобы перевести смешанную дробь в десятичную, необходимо выделить целую долю.
Выделяя часть, нужно определить, сколько целых знаменателей вмещается в числитель. Пусть нужно преобразовать 27/6. Вначале следует определить, сколько шестёрок помещается в числе 27. Для этого нужно 27 разделить на шесть, число, стоящее перед запятой, будет искомым. Это четыре. Далее найти числитель по правилу 4*6 = 24 и вычесть полученное значение из знаменателя 27 − 24 = 3. Теперь находят лишнее, что осталось от числителя 27, если убрать максимально помещающее число шестёрок. В результате получится ответ: 27/6 = 4 (2/3).
По похожему алгоритму выполняется преобразование периодической дроби в обыкновенную. Для решения задания нужно из числа, занимающего позицию до второго периода, отнять число, стоящее до первого периода, а полученную разницу перенести в числитель. В знаменатель записать девятку столько раз, сколько цифр в периоде. После девяток пишут нули, количество которых определяется числом цифр стоящих между запятой и первым периодом. Например, 0,23 (7) = (237 — 23)/900 = 214/900 = 107/450.
Действия с десятичными числами
С дробями можно также выполнять и сравнения. Для этого используют алгебраические правила. Сложение дробей между собой осуществляют по правилу столбика. Это удобный метод, практически не позволяющий допускать ошибок. Согласно объяснению способа в математике, для сложения нужно записать два числа друг под другом так, чтобы их правые цифры были в одном столбике. Затем сложить цифры в нём, используя способ переноса десятков.
При сложении десятичных дробей происходит всё то же самое, но при этом нужно обязательно расположить выражения так, чтобы их запятые стояли чётко друг под другом. Сложение выполняют так, как и с натуральными числами, не учитывая запятые. После подсчёта запятую просто сносят вертикально вниз, отделяя целую часть от дольной.
При вычитании происходит всё аналогичным образом. При сложении и вычитании выполняют четыре пункта:
- Уравнивают количество знаков после запятой.
- Записывают дроби друг под другом так, чтобы запятые совпадали по вертикали.
- Складывают или вычитают по правилам арифметики.
- В полученном числе ставят запятую соответственно другим записям.
Для умножения дробей их записывают в столбик, а далее находят произведение, как и с обычными числами. Затем считают количество знаков после запятой первого умножаемого и умножителя и складывают их количество. Для получения ответа справа налево отсчитывают такое же количество знаков и после последнего ставят запятую. Умножаться могут любые дроби, исключений нет.
Чтобы разделить десятичную дробь, следует знать правило: если целая часть делимого меньше делителя, то в частном целых не будет. Деление выполняют по правилу того же столбика. Две части записывают через уголок и определяют неполное частное, сравнивая делимое с делителем. Далее выполняют действие, записывая цифру в частное. При записи под неполным частным правая его величина должна располагаться над правой цифрой произведения. После того как закончится деление целой части делимого, ставят запятую.
Если число после запятой бесконечно повторяется, то оно будет называться периодом. В этом случае используют сокращение записи. Например, если в ответе получают 4, 67644444, то его можно заменить на запись 4,67 (4). Такое выражение называют бесконечной десятичной дробью.
Сравнение выражений
Чтобы сравнить две дроби, нужно составить уравнение из их целых частей. Если их части равные, то сравниваются десятые доли. Стоит отметить, что в этом случае учитывают разряд числа. Меньшей будет та дробь, у которой значение числа в разряде меньше.
Для того чтобы провести сравнение дробей, применяют следующую последовательность действий:
- Пробуют сократить выражения.
- Приводят дроби к одинаковому числу знаков путём дописывания в случае необходимости нулей.
- Выполняют сравнение по старшинству разрядов, начиная с целой части, а в случае равенства — с десятой, сотой и так далее.
- Если при сравнении разрядов один из них будет больше или меньше, задача считается выполненной.
Например, нужно сравнить дроби 237,4 и 238,2 и результат выразить через процентное отношение. Так как 237 меньше 238, то дробные части сравнивать уже будет не нужно. Для того чтобы определить процентное отношение, большую часть принимают за 100%, а меньшую — за X. Составляют пропорцию и делают вычисление: 237,4 * 100 = 238,2 * Х.
Это обыкновенное уравнение с одним неизвестным: Х = 237,4 * 100 / 238,2 = 99,66%. То есть первое выражение меньше второго на 100 — 99,66 = 0,34%. Десятичные выражения, как и натуральные, можно записывать в ряд, а значит, откладывать на координатной прямой. На ней правее будет стоять отношение, которое больше.
Небольшие задания решать несложно. Но существуют задачи, для решения которых нужно не только проявить максимальное внимание, но и затратить много времени. Например, как при вычислении совместных дробей. В таких случаях есть резон использовать калькулятор десятичных дробей с запятыми онлайн. Чтобы им воспользоваться, особых знаний не нужно. Загрузив сайт и введя в таблицу исходные данные, пользователю нужно всего лишь нажать кнопку «Рассчитать» и получить точный результат.
Рассмотрим на примерах, как заменить отношение дробных чисел отношением натуральных чисел.
Чтобы преобразовать отношение дробных чисел, можно либо разделить эти числа, либо воспользоваться основным свойством отношений:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, отличное от нуля.
Примеры.
Заменить отношение дробных чисел отношением натуральных чисел:
Решение:
Делим числа. (Чтобы разделить число на дробь, данное число умножаем на число, обратное дроби).
В частном получили отношение натуральных чисел. Его можно также записать в виде 9:5, но переходить к такой форме записи необязательно.
63 и 45 сокращаем на 9, 64 и 56 — на 8. В частном — отношение натуральных чисел.
Чтобы разделить смешанные числа, переводим их в неправильные дроби и делимое умножаем на число, обратное делителю.
14 и 35 сокращаем на 7, 9 и 27 — на 9. Частное — отношение натуральных чисел.
В этом примере удобно и числитель, и знаменатель умножить на 10. Полученное отношение натуральных чисел сокращаем сначала на 7, затем — на 2 (или сразу на 14).
Здесь и числитель, и знаменатель умножаем на 100, затем последовательно сокращаем дробь на 64 и на 2.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Отношение чисел
Поддержать сайт
Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.
Если вам знакомо понятие отношение чисел, можете смело переходить к теме
пропорции.
Что называют отношением двух чисел
Запомните!
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Покажем на примере, где используется понятие отношение двух чисел.
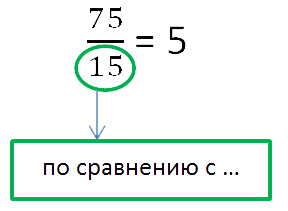
В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15.
В этом году — 75. Во сколько раз увеличилось количество участников в этом году по
сравнению с предыдущим годом?
Прежде чем решать задачу, подчёркиваем важные данные.
Запишем отношение количества участников в этом году к количеству участников в предыдущем.
Запомните!
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».
Запомните!
Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.
При внимательном изучении правила выше, можно подметить, что правило записанное выше,
есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.
Отношение 16 к 10:
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 апреля 2023 в 20:44
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
Просмотров 1.4к. Опубликовано 30.09.2022
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Отношения
Мы знаем это, чтобы ответить на вопрос, насколько часто одно число больше (или меньше) другого, или насколько одно число является дробью другого. найти частное данных чисел.
Частное двух чисел не равный нулю, называется отношением чисел , или отношением числа .
Где — члены отношения число перед термином отношенияследующий срок отношения.
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
количество
1,15 : 0,36 — отношение от числа 1,15 до числа 0,36.
Отношение двух чисел Показывает, как часто одно число больше другого или как сильно одно число зависит от другого. Это отношение чисел указывает, сколько раз число или сколько частей числа .
Помните, что деление можно заменить дробью, поэтому, отношение чисел можно записать двумя способами: и
Основное свойство отношения:
Отношение не меняется, когда его члены умножаются или делятся на одно и то же число, которое не равно нулю.
Запишем отношение от 3 до 10 и найти его значение:
То есть отношение двух чисел Он может быть выражен в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, какой процент число составляет от другого числа.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и добавить знак процента к результату.
Пример:
В каком проценте число 5 равно числу 10?
5 10 2 1 — 100 % = 1 2 — 100 % = 100 2 % = 50 % .
Ответ: 50% равно 5 умножить на 10.
Если значение двух величин выражено в одних и тех же единицах, то. их отношение называют также отношением. Если две величины выражены в разных единицах, то отношения эти величины должны быть сначала переведены в одну и ту же единицу измерения.
Например:
Дан прямоугольник длиной 12 см и шириной 1 м. Найти отношение длины сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 12 : 100 = 100.
Отношение ширины прямоугольника к его длине равно 100 : 12 =
Дробь взаимно обратная, поэтому и отношения 12 к 100 и 100 к 12 называются взаимно обратными.
На практике отношение Обратные дроби используются, например, при составлении чертежей и географических карт. В этом случае земельные участки рисуются на бумаге в уменьшенном виде, а на карте или картографии изображаются отношение, указывает, как часто длина отрезка на чертеже меньше длины соответствующего отрезка на местности.
Соотношение между длиной отрезка на карте и длиной соответствующего отрезка на местности называется масштабом карты (чертежа).
Предположим, что карта имеет масштаб
Давайте выясним, какова длина отрезка в 5 см на карте на земле.
Для решения обозначим длину отрезка на земле (в сантиметрах). Затем отношение длина отрезка на карте к длине отрезка на местности составляет: 5 :, данная отношение равна масштабу карты, что дает уравнение:
5 :
Решите это уравнение:
10 000;
50 000 см = 500 м = 0,5 км.
Ответ: Отрезок в 5 см на карте равен 0,5 км на местности.
Давайте выясним, какая длина на карте соответствует отрезку 9,5 км на карте.
Для решения обозначьте длину участка на карте (в километрах). Затем отношение длина отрезка на карте с длиной отрезка на местности: : 9,5, данная отношение равна масштабу карты, что дает уравнение:
Решите это уравнение:
0,00095 км = 0,95 м = 95 см.
Ответ: Отрезок 9,5 км на карте равен 95 см на карте.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Отношение чисел
Отношение чисел — это коэффициент от деления одного числа на другое.
Отношение чисел A и b можно записать двумя способами: со знаком деления или через косую черту (как дробь):
Эти признаки следующие: отношение a к b или отношение числа a к числу b.
Числа a и b, составляющие отношение a : b становятся терминами отношения. Делителем является предыдущий член отношения, а делитель — предпоследний член. отношения. Таким образом, a — предыдущий член, b — следующий.
Соотношение используется для сравнения двух чисел. Так, отношение a : b показывает, во сколько раз a больше b (если делитель больше делимого) или сколько процентов от числа b составляет a (если делитель меньше делимого).
Отношение 35 к 7 показывает, что число 35 в пять раз больше числа 7.
2)
Отношение 12 к 15 показывает, что число 12 в 0,8 раза больше числа 15.
Из основного свойства квоты следует, что. отношения :
Отношение не меняется, когда его члены умножаются или делятся на одно и то же ненулевое число.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Помните.
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Давайте на примере покажем, в чем суть концепции. отношение двух чисел.
В городе Липецке проходят соревнования по велоспорту. В прошлом году было 15 участников, в этом году — 75. На сколько больше участников в этом году, чем в прошлом?
Прежде чем решить проблему, давайте остановимся на самых важных фактах. Запишите отношение количество участников в этом году с количеством участников в прошлом году.
Помните.
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Помните.
Если вы умножите или разделите оба термина отношения на одно и то же число, которое не равно нулю, вы получите отношение, равное данному.
Если вы внимательно изучите приведенное выше правило, то обнаружите, что написанное выше правило — это не что иное, как основное свойство дробей, с помощью которого мы можем легко их сокращать.
Основное свойство коэффициента заключается в том, что он остается неизменным при умножении или делении делителя и делимого на одно и то же число.
Задания для самостоятельной работы
На пост президента претендовали два кандидата. Явка составила 120 человек. Распределение голосов соответствует соотношению 3:5. Необходимо определить количество голосов, полученных победителем.
Соотношение между количеством хвойных и лиственных деревьев в лесу можно представить как 1:4. Необходимо рассчитать долю лиственных деревьев.
На площади 24 га выращиваются сельскохозяйственные культуры. Зерновые и овощи распределяются в соответствии с с отношением 5:3. Необходимо рассчитать площадь возделывания овощных культур в гектарах.
Основное свойство отношения: Путем умножения или деления членов отношения на одно и то же число, отличное от нуля, данный отношение останется неизменным.
Отношения в задачах
Теперь давайте узнаем, как отношения в задачах.
Давайте сразу перейдем к примерам, чтобы увидеть, какой может быть формулировка отношения.
Проблема 1
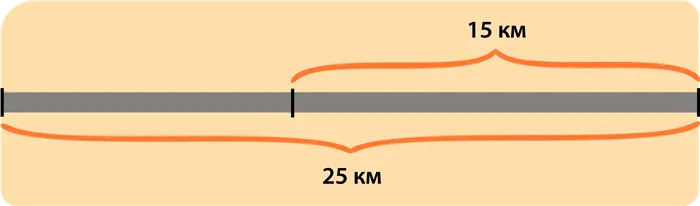
Протяженность дороги составляет 25 километров. Он освещен на протяжении 15 километров.
(α) Найдите, какая часть дороги освещена.
(b) Во сколько раз вся проезжая часть длиннее освещенной части?
Решение:
В начале урока мы обнаружили отношение меньшего числа в большее, определяя тем самым, какая часть первого числа содержится во втором.
Это первый вопрос.
Для нахождения отношения Отношение длины освещенного участка к длине всей дороги делится на единицу:
Значит, длина освещенного участка составляет (mathbf>) по всей длине дороги.
Второй вопрос: «Во сколько раз больше?». — соответствует отношению от большего числа к меньшему.
Чтобы найти это отношения это разделить длину всей дороги на длину освещенной части дороги:
Это отвечает на вопрос второго пункта.
Важно также всегда следить за тем, чтобы количество было одинаковым.
Так, если что-то дано нам в тоннах и килограммах, и мы хотим найти отношения Чтобы узнать эти количества, мы должны либо перевести тонны в килограммы, либо наоборот.
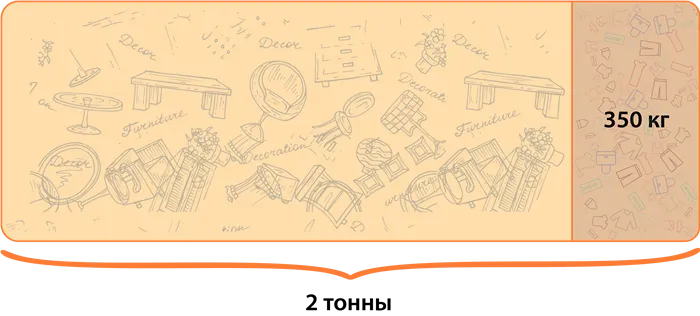
Проблема 2
Масса груза составляет 2 тонны. Известно, что часть груза — это одежда, масса которой составляет 350 кг.
Определите, сколько процентов от массы груза составляет масса одежды.
Решение:
Давайте сначала переведем тонны в килограммы. Оказывается, что масса груза составляет 2000 кг.
Теперь давайте найдем неизвестное. отношение:
Теперь попробуйте решить задачу самостоятельно и воспользуйтесь подсказками, если у вас возникнут трудности.
Вы можете пройти тест и получить результат после того, как войдете в систему или зарегистрируетесь.
Интересная информация
Сегодня вы научитесь математическим фокусам!
Их идея заключается в том, что можно запутать людей с помощью математических преобразований, которые дают нам то, что нам нужно.
Уловка 1.
Попросите зрителя придумать число и никому его не называть.
Теперь попросите их умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть число в уме.
Теперь вы можете с уверенностью сказать, что зритель получил число 4.
Это происходит потому, что при преобразовании исходное число удаляется из арифметической цепочки, оставляя только четверку.
Попробуйте доказать это с помощью формул, вычитая исходное число X
Уловка 2
В этой игре вы можете угадать день рождения человека.
Попросите зрителя умножить количество дней рождения на 2. Затем попросите его прибавить к результату 5 и умножить целое число на 50. Затем попросите зрителя добавить номер месяца, в котором он родился (1 января, 2 февраля и т.д.).
Чтобы узнать день рождения человека по полученному числу, вычтите 250 из числа, указанного зрителем — вы получите трех- или четырехзначное число, где первые одна или две цифры обозначают день рождения, а последние две цифры — месяц.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.








![Rendered by QuickLaTeX.com [2)frac{{63}}{{64}}:frac{{45}}{{56}} = frac{{63}}{{64}} cdot frac{{56}}{{45}} = frac{{mathop {63}limits^7 cdot mathop {56}limits^7 }}{{mathop {64}limits_8 cdot mathop {45}limits_5 }} = frac{{49}}{{40}}.]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-59d3fc861c39b1f320efc78c352608f9_l3.png)
![Rendered by QuickLaTeX.com [ = frac{{mathop {14}limits^2 cdot mathop {27}limits^3 }}{{mathop 9limits_1 cdot mathop {35}limits_5 }} = frac{{2 cdot 3}}{{1 cdot 5}} = frac{6}{5}.]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-308e20734d55f519ba83c3a7b26e95d3_l3.png)