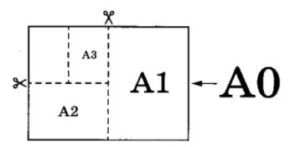
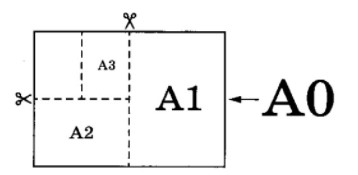
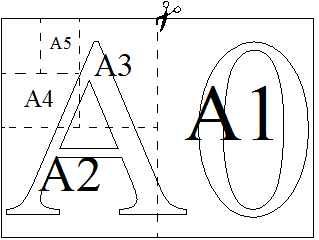
1) Начнем с того, что А0 самый большой по площади лист, поэтому его размеры самые большие 1189х841 (при умножении получится 999949 кв.мм или почти 1 кв.м). А0 — лист номер 3. Далее все проще, у листа А1 длина должна быть равна 841 мм, это лист номер 4. У листа А2 длина должна быть равна 594 мм, такого листа нет. Далее смотрим самый маленький по размерам лист из перечисленных, это А4, значит его размеры 297х21 (номер 1), тогда у листа А3 ширина должна быть равна 297, это лист под номером 2. Ответ на 1-ое задание: 3421.
2) Сколько листов формата А6 получится из одного листа формата А3? Из А3 получим 2 листа А4, далее 4 листа А5 и 8 листов А6. Ответ: 8.
3) Найдите площадь листа формата А5. Так как А0 имеет площадь 1 кв.м или 10000 кв см, то А1 — 5000 кв.см, А2 — 2500 кв см, А3 — 1250, А4 — 625, А5 — 312,5 кв см. Ответ: 312,5.
4) Найдите отношение длины диагонали листа формата А7 к его меньшей стороне. По условию отношение большей стороны к меньшей стороне листа каждого формата одно и то же (листы всех форматов подобны), поэтому и отношение отношение длины диагонали листа к его меньшей стороне для всех листов тоже одинаково. Найдем это отношение для А4. Длина диагонали этого листа равна 363,74… (по теореме Пифагора). 363,7/210=1,7. Ответ: 1,7.
5) Бумагу формата А5 упаковали в пачки по 1000 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м. равна 144 г. Площадь одного листа А5 мы нашли, она равна 312,5 кв см, значит общая площадь всех листов в пачке равна: 312,5*1000=312500 кв.см или 31,25 кв.м. Теперь найдем массу пачки. 31,25*144=4500 г. Ответ: 4500.
Во всем мире принят единый формат листов бумаги, он обозначается буквой $A$ и цифрой, идущей на ней: $А0$, $А1$, $А2$ и так далее. Площадь листа формата $А0$ равна $1$ квадратному метру, если его разрезать пополам, получим два листа формата $А1$ и так далее.
В листах каждого формата отношение большей стороны к меньшей одинаковое, поэтому все листы подобны. Делается это для того, чтобы пропорции текста сохранялись при изменении шрифта или формата листа.
Чтобы решать данные задания необходимо:
- уметь переводить одни единицы измерения длины в другие;
- знать и уметь применять на практике теорему Пифагора;
- уметь выполнять действия с десятичными дробями;
- уметь определять кратность числа;
- знать правила математического округления числа;
- уметь извлекать корень из числа.
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: $$c^2=a^2+b^2$$
Примеры на нахождение отношения сторон
Найдите отношение меньшей стороны листа формата $textcolor{coral}{А3}$ к большей. Ответ округлите до десятых.
Решаем вместе
Скрыть
Воспользуемся таблицами, заполненными при решении первого задания:
| Номер листа | Длина (мм) | Ширина (мм) |
| $А4$ | $297$ | $210$ |
| $textcolor{coral}{А3}$ | $textcolor{coral}{420}$ | $textcolor{coral}{297}$ |
| $А0$ | $1189$ | $841$ |
| $А1$ | $841$ | $594$ |
Меньшая сторона листа формата $textcolor{coral}{А3}$ равна $297$ $мм$, большая сторона равна $420$ $мм$.
Найдем отношение сторон: $$frac{textcolor{coral}{297}}{textcolor{coral}{420}}=0,70…$$
Так как в задании сказано, что нужно округлить до десятых, достаточно посчитать до следующего за десятыми разряда (сотых).
Произведем округление. Так как разряд, следующий за тем, до которого необходимо округлить, меньше $5$, округляем в меньшую сторону, получим: $0,7$
Ответ: $0,7$.
Пример №2
Найдите отношение большей стороны листа формата $А1$ к меньшей. Ответ округлите до десятых.
Решаем вместе
Скрыть
Воспользуемся таблицами, заполненными при решении первого задания:
| Номер листа | Длина (мм) | Ширина (мм) |
| $А4$ | $297$ | $210$ |
| $А3$ | $420$ | $297$ |
| $А0$ | $1189$ | $841$ |
| $А1$ | $841$ | $594$ |
Пример №3
Найдите отношение большей стороны листа формата $А5$ к меньшей. Ответ округлите до десятых.
Решаем вместе
Скрыть
Воспользуемся таблицами, заполненными при решении первого задания:
| Номер листа | Длина (мм) | Ширина (мм) |
| $А4$ | $297$ | $210$ |
| $А3$ | $420$ | $297$ |
| $А0$ | $1189$ | $841$ |
| $А1$ | $841$ | $594$ |
Примеры на нахождение отношения диагоналей и сторон
Найдите отношение длины диагонали листа формата $А2$ к его меньшей стороне. Ответ округлите до десятых.
Решаем вместе
Скрыть
Воспользуемся таблицами, заполненными при решении первого задания:
| Номер листа | Длина (мм) | Ширина (мм) |
| $А4$ | $297$ | $210$ |
| $А3$ | $420$ | $297$ |
| $А0$ | $1189$ | $841$ |
| $А1$ | $841$ | $594$ |
В таблице нет листа формата $А2$, но по рисунку видно, что длина листа формата $А2$ равна ширине листа формата $А1$: $594$ $мм$. Ширина листа формата $А2$ равна длине листа формата $А3$: $420$ $мм$.
Чтобы найти диагональ листа формата $А2$, воспользуемся теоремой Пифагора, так как диагональ и стороны листа образуют прямоугольный треугольник.
Квадрат гипотенузы равен сумме квадратов катетов. В данном случае диагональ листа будет являться гипотенузой, а его стороны — катетами. Для упрощения возведения в квадрат и извлечения корня переведем миллиметры в сантиметры и округлим до целых:
$420$ $мм$ $=$ $42$ $см$
$594$ $мм$ $=$ $59,4$ $см$
Так как за последним целым разрядом идет число, которое меньше $5$, округляем в меньшую сторону: $59$ $см$.
Применим теорему Пифагора: $$sqrt{42^2+59^2}=sqrt{1764+3481}=sqrt{5245}$$
По таблице квадратов найдем, к квадрату какого числа ближе число $5245$.
$5245$ ближе к $5184$. $5184$ это квадрат $72$. Диагональ примерно равна $72$ $см$.
Найдем отношение длины диагонали листа к его меньшей стороне:$$frac{72}{42}=1,71..$$
Округлим полученный ответ до десятых: $1,7$.
Ответ: $1, 7$.
Найдите отношение длины диагонали листа формата $А1$ к его меньшей стороне. Ответ округлите до десятых.
Решаем вместе
Скрыть
Воспользуемся таблицами, заполненными при решении первого задания:
| Номер листа | Длина (мм) | Ширина (мм) |
| $А4$ | $297$ | $210$ |
| $А3$ | $420$ | $297$ |
| $А0$ | $1189$ | $841$ |
| $А1$ | $841$ | $594$ |
Ответ:
1,7
Пошаговое объяснение:
Размер листа формата А0: a x b = 1189 x 841 мм.
Школьное решение:
Длина его диагонали:
мм
Отношение длины диагонали к его меньшей стороне:
Инженерное решение:
Чертёжный лист любого формата имеет отношение сторон 1 : √2.
Это сделано специально, если лист разделить пополам, то у двух новых листов опять будет такое же отношение сторон 1 : √2.
И это получатся листы следующего формата: А1, А2, и т.д. до А7.
Если меньшая сторона b = 1, а большая a = √2, то диагональ:
Отношение диагонали к меньшей стороне:
У нас примерно так и получилось: 1,7317.
Задание № 1
— ОГЭ — математика
— задачи о листах бумаги —
Правила
Правила
- Самый большой лист имеет формат А0. Это прямоугольник шириной 841 мм и длиной 1189 мм. (не надо запоминать). Если его разрезать пополам, как показано на рисунке, то получится два листа формата А1. Это также прямоугольники, чтобы узнать их ширину и длину, нужно размеры листа А0 разделить на 2: ширина = 420 мм и длина = 595 мм.
- Если продолжить разрезание листов, то буду получаться листы формата А2, А3, А4 и так далее, их размеры будут уменьшаться каждый раз в два раза). (см рисунок)
- Возможные форматы листов: А0; А1; А2; А3; А4 и так далее. Чем больше цифра в формате, тем размеры листа меньше.
- Чтобы понять какое количество листов получится, изобразите на чертеже лист А0 и начните его делить.
- Чтобы узнать ширину или длину листа нужного формата, подпишите на рисунке известные размеры какого-нибудь листа (обязательно какие-нибудь размеры будут известны), разделите их пополам, если нужно найти меньший лист или умножьте на два, если нужно найти бОльший лист Подпишите эти размеры на рисунке. Эту процедуру можно (и нужно) повторить до тех пор, пока Вы не дойдете до листа, о котором Вас спрашивают в задании.
- Площадь любого из этих листов можно найти, если умножить ширину на длину, то есть нужно воспользоваться формулой площади прямоугольника: S=a•b.
- Правила округления:
- подчеркните цифру в разряде, который должен остаться одной чертой;
- если соседняя справа цифра больше 4, то увеличьте подчеркнутую цифру на единицу, а «хвост» отбросьте;
- если соседняя цифра меньше 5, то просто отбросьте «хвост».
- подчеркните цифру в разряде, который должен остаться одной чертой;
- Чтобы округлить до ближайшего целого числа, кратного 10
- подчеркните цифру в разряде сотен одной чертой;
- определите какая цифра стоит в разряде десятков (НЕ десятых);
- если эта цифра больше 4, то увеличьте подчеркнутую цифру на единицу, на месте десятков напишите 0, а «хвост» отбросьте;
- если эта цифра меньше 5, то на месте десятков напишите ноль, а «хвост» отбросьте..
- Чтобы найти отношение ширины листа к его длине:
- найдите ширину;
- найдите длину;
- разделите первый результат на второй.
- Чтобы найти отношение диагонали листа к его меньшей или большей стороне:
- найти значение диагонали по теореме Пифагора (диагональ является гипотенузой, длина и ширина листа — катеты);.
- Задачи про шрифты. Так как листы подобны, то
- неизвестную величину обозначаем за х;
- делим ширину первого листа на ширину второго;
- делим высоту шрифта первого листа на высоту шрифта второго листа;
- приравниваем получившиеся выражения;
- используя свойство пропорции, находим х.
[свернуть]
Общая информация для всех заданий:
- Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Каждый из этих листов представляет собой прямоугольник определенной ширины и определенной длины. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 м². Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2 и так далее.
- Отношение длины листа к его ширине у всех листов равно одному и тому же числу, то все листы подобны друг другу. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
- На практике размеры листа округляется до целого числа миллиметров.
-
Порядковый номер листа
Ширина листа (мм)
Длина листа (мм)
1
148
210
2
210
297
3
105
148
4
297
420
— Образцы решения —
Определить формат листа
Для листов бумаги форматов А3, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр.
-
-
Форматы бумаги А3 А4 А5 А6 Порядковые номера - Решение:
- необходимое правило: чем МЕНЬШЕ цифра в формате листа, тем БОЛЬШЕ размеры листа;
- выбираем из таблицы в разделе «Общая информация» для анализа один (ОДИН!) столбик: или с данными по ширине, или с данными о длине (ИЛИ!);
- к НАИБОЛЬШЕМУ числу из выбранного столбца вписываем формат с НАИМЕНЬШЕЙ цифрой из таблицы ответов (в нашей таблице ответов указаны форматы: А3; А4; А5; А6);
-
Порядковый номер листа Ширина листа (мм) Длина листа (мм) 1 148 (А5) 210 2 210 (А4) 297 3 105 (А6) 148 4 297 (А3) 420 - выписываем в таблицу ответов к каждому формату соответствующий порядковый номер:
-
Формат бумаги А3 А4 А5 А6 Порядковые номера 4 2 1 3
- в ответ выписываем: 4213
- необходимое правило: чем МЕНЬШЕ цифра в формате листа, тем БОЛЬШЕ размеры листа;
-
[свернуть]
Найти количество листов
Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата А2?
- Решение:
- необходимое правило: все последующие листы получаются в результате разрезания бОльшего листа пополам (на две равные части); помогаем себе дополнительными построениями;
- рисуем для себя лист и принимаем, что его формат А2;
- разделим его пополам, так мы получим два листа формата А3;
- разделим ОБА листа А3 пополам, получим четыре листа формата А4;
- разделим все четыре листа А4 пополам, получим 8 листов формата А5;
- разделим ВСЕ восемь листов пополам, получим 16 листов формата А6;
- в ответ выписываем: 16
- необходимое правило: все последующие листы получаются в результате разрезания бОльшего листа пополам (на две равные части); помогаем себе дополнительными построениями;
[свернуть]
Найти длину стороны листа
1. Найдите длину бОльшей стороны листа бумаги формата А1. Ответ дайте в миллиметрах.
-
- Решение:
- необходимое правило: пользуемся данными из предыдущих заданий; помогаем себе дополнительными построениями;
- из задания 1 найдем тот формат, что ближе всего к формату А1; в нашем случае это формат А3;
- выполним чертеж, на котором покажем (СЕБЕ) как из листа А0 получаются форматы А1 и А3; подпишем на чертеже размеры листа А3 (берем их из таблицы в задании 1);
- по чертежу видим, что бОльшая сторона листа А1 состоит из двух сторон листа А3, равных 420;
- 420+420=840;
- в ответ выписываем 840
- необходимое правило: пользуемся данными из предыдущих заданий; помогаем себе дополнительными построениями;
- Решение:
2. Найдите длину меньшей стороны листа бумаги формата А1. Ответ дайте в миллиметрах.
-
-
-
- Решение:
- необходимое правило: пользуемся данными из предыдущих заданий; помогаем себе дополнительными построениями;
- из задания 1 найдем тот формат, что ближе всего к формату А1; в нашем случае это формат А3;
- выполним чертеж, на котором покажем (СЕБЕ) как из листа А0 получаются форматы А1 и А3; подпишем на чертеже размеры листа А3 (берем их из таблицы в задании 1);
- по чертежу видим, что меньшая сторона листа А1 состоит из двух сторон листа А3, равных 297;
- 297+297=594;
- в ответ выписываем 594
- необходимое правило: пользуемся данными из предыдущих заданий; помогаем себе дополнительными построениями;
- Решение:
-
-
[свернуть]
Найти отношение сторон листа
1. Найдите отношение длины бОльшей стороны листа к меньшей у бумаги формата А5. Ответ дайте с точностью до десятых.
-
- Решение:
- необходимые правила: используем данные из предыдущих заданий или учим наизусть, что отношение бОльшей стороны к меньшей ВСЕГДА 1,4;
- из задания 1 (из таблицы) выписываем значение длины и ширины А5, при этом значение длины в числитель, а значение ширины в знаменатель, получим 210/148=1,4
- в ответе пишем: 1,4
- Решение:
2. Найдите отношение длины диагонали листа формата А6 к его большей стороне. Ответ округлите до десятых.
-
- Решение:
- необходимые правила:
-
- используем данные из предыдущих заданий;
- диагональ листа является гипотенузой;
- длина и ширина листа являются катетами;
- т. Пифагора: квадрат гипотенузы равен сумму квадратов катетов; правила округления;
-
- из задания 1 выписываем значение длины и ширины: 105 мм и 148 мм;
- по теореме Пифагора найдем гипотенузу: 105²+148²=11025+21904=32929; не забываем извлечь квадратный корень: 181,46
- запишем соотношение и округлим до десятых: 181,46/148= 1,2;
- необходимые правила:
- в ответе пишем: 1,2
- Решение:
[свернуть]
Найти площадь листа
Найдите площадь листа бумаги формата А4. Ответ дайте в квадратных сантиметрах.
- Решение:
- необходимое правило: пользуемся данными из предыдущих заданий; лист имеет форму прямоугольника; площадь прямоугольника = ширина × длина;
- из задания 1 выписываем ширину и длину листа А4; в нашем случае это 210мм и 297мм;
- переводим эти значения в см:
- 210:10=21 и 297:10=29,7;
- площадь = 21×29,7=623,7 см²;
- в ответ выписываем: 623,7
- необходимое правило: пользуемся данными из предыдущих заданий; лист имеет форму прямоугольника; площадь прямоугольника = ширина × длина;
[свернуть]
Размер типографского шрифта
1. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 12 пунктов на листе формата А5? Размер шрифта округлите до целого.
Решение:
-
- необходимое правило:
-
-
- отношение бОльшего листа к меньшему = отношение шрифта с бОльшего листа к шрифту с меньшего листа;
- отношение бОльшего листа к меньшему ВСЕГДА равно 1,4;
- чем больше цифра в формате листа, тем размеры листа меньше;
- правила округления;
-
-
- что известно?
-
-
- отношение бОльшего листа к меньшему = 1,4;
- шрифт на меньшем листе 12;
- шрифт на бОльшем листе х;
-
-
- подставляем все известное и неизвестное в формулу и округляем: 1,4=х/12, отсюда х=17;
- необходимое правило:
- в ответ выписываем: 17
2. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 16 пунктов на листе формата А4? Размер шрифта округлите до целого.
Решение:
-
-
- необходимое правило:
-
- отношение бОльшего листа к меньшему = отношение шрифта с бОльшего листа к шрифту с меньшего листа;
- отношение бОльшего листа к меньшему ВСЕГДА равно 1,4;
- чем больше цифра в формате листа, тем размеры листа меньше;
- правила округления;
-
- что известно?
-
- отношение бОльшего листа к меньшему = 1,4;
- шрифт на меньшем листе х;
- шрифт на бОльшем листе 16;
-
- подставляем все известное и неизвестное в формулу и округляем: 1,4=16/х, отсюда х=11;
- необходимое правило:
-
- в ответ выписываем: 11
[свернуть]
Найти массу упаковки
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Решение:
-
-
- необходимые правила:
-
- используем данные из предыдущих заданий;
- площадь прямоугольника равна произведению длины на ширину;
- масса некоторого количества листов = площадь одного листа × на количество листов × массу 1 м²;
-
- из задания 1 выписываем значения длины и ширины листа А5: 210мм и 148мм; сразу переведем эти значения в метры, 210:1000=0,21 м и 148:1000=0,148 м;
- найдем площадь листа А5: 0,21×0,148=0,03108 м²;
- по формуле найдем массу 500 листов: 0,03108×500×80=1243,2 грамма;
- необходимые правила:
-
в ответе пишем: 1243,2
[свернуть]
— Тренировочные задания-
Общая информация для всех заданий:
- Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Каждый из этих листов представляет собой прямоугольник определенной ширины и определенной длины. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 м². Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2 и так далее.
- Отношение длины листа к его ширине у всех листов равно одному и тому же числу, то есть все листы подобны друг другу. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
- На практике размеры листа округляются до целого числа миллиметров.
Вариант 1
Вариант 1
1.В таблице даны размеры листов неизвестных форматы. Установите соответствия между форматами и номерами листов бумаги из таблицы. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр.
| Номер листа | Длина (мм) | Ширина (мм) |
| 1 | 841 | 594 |
| 2 | 1189 | 841 |
| 3 | 297 | 210 |
| 4 | 594 | 420 |
Ответ: 2143.
2. Сколько листов формата А5 получится из одного листа формата А1?
Ответ: 16.
3. Найдите длину меньшей стороны листа бумаги формата А3. Ответ дайте в миллиметрах.
Ответ: 297.
4. Найдите площадь листа формата А1. Ответ дайте в см².
Ответ: 4995,54.
5. Бумагу формата А1 упаковали в пачки по 80 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 120 г. Ответ дайте в граммах.
Ответ: 4795,7184.
6. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4? Размер шрифта округляется до целого.
Ответ: 21.
7. Найдите отношение длины большей стороны листа формата А3 к меньшей. Ответ округлите до десятых.
Ответ: 1,4.
8. Найдите отношение длины диагонали листа формата А4 к его большей стороне. Ответ округлите до десятых.
Ответ: 1,2.
[свернуть]
Вариант 2
Вариант 2
1.В таблице даны размеры листов, имеющих некоторые форматы. Установите соответствия между форматами и номерами листов бумаги из таблицы. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр.
| Номер листа | Длина (мм) | Ширина (мм) |
| 1 | 210 | 148 |
| 2 | 594 | 420 |
| 3 | 420 | 297 |
| 4 | 841 | 594 |
Ответ: 4231.
2. Сколько листов формата А3 получится из одного листа формата А0?
Ответ: 8.
3. Найдите длину большей стороны листа бумаги формата А0. Ответ дайте в миллиметрах.
Ответ: 1188.
4. Найдите площадь листа формата А3. Ответ дайте в квадратных сантиметрах.
Ответ: 1247,4.
5. Бумагу формата А3 упаковали в пачки по 100 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 90 г. Ответ дайте в граммах.
Ответ: 1122,66.
6. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 12 пунктов на листе формата А5? Размер шрифта округляется до целого.
Ответ: 24.
7. Найдите отношение длины большей стороны листа формата А6 к меньшей. Ответ округлите до десятых.
Ответ: 1,4.
8. Найдите отношение длины диагонали листа формата А5 к его большей стороне. Ответ округлите до десятых.
Ответ: 1,2.
[свернуть]
Вариант 3
Вариант 3
1.В таблице даны размеры листов, имеющих некоторые форматы. Установите соответствия между форматами и номерами листов бумаги из таблицы. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр.
| Номер листа | Длина (мм) | Ширина (мм) |
| 1 | 297 | 210 |
| 2 | 148 | 105 |
| 3 | 594 | 420 |
| 4 | 210 | 148 |
Ответ: 3142.
2. Сколько листов формата А6 получится из одного листа формата А0?
Ответ: 64.
3. Найдите длину меньшей стороны листа бумаги формата А3. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Ответ: 300.
4. Найдите площадь листа формата А5. Ответ дайте в квадратных сантиметрах.
Ответ: 150.
5. Бумагу формата А3 упаковали в пачки по 150 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 100 г. Ответ дайте в граммах.
Ответ: 1871,1.
6. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 14 пунктов на листе формата А2? Размер шрифта округляется до целого.
Ответ: 5 .
7. Найдите отношение длины меньшей стороны листа формата А2 к большей. Ответ округлите до десятых.
Ответ: 0,7.
8. Найдите отношение длины диагонали листа формата А1 к его меньшей стороне. Ответ округлите до десятых.
Ответ: 1,7.
[свернуть]
Вариант 4
Вариант 4
1.В таблице даны размеры листов, имеющих некоторые форматы. Установите соответствия между форматами и номерами листов бумаги из таблицы. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр.
| Номер листа | Длина (мм) | Ширина (мм) |
| 1 | 594 | 420 |
| 2 | 148 | 105 |
| 3 | 210 | 148 |
| 4 | 841 | 594 |
Ответ: 4132.
2. Сколько листов формата А6 получится из одного листа формата А2?
Ответ: 16.
3. Найдите длину большей стороны листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Ответ: 300.
4. Найдите площадь листа формата А6. Ответ дайте в см².
Ответ: 155,4.
5. Бумагу формата А4 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 95 г? Ответ дайте в граммах.
Ответ: 2962,575.
6. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А2 так же, как этот же текст, напечатанный шрифтом высотой 18 пунктов на листе формата А4? Размер шрифта округляется до целого.
Ответ: 36.
7. Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.
Ответ: 0,7.
8. Найдите отношение длины диагонали листа формата А2 к его меньшей стороне. Ответ округлите до десятых.
Ответ: 1,7.
[свернуть]
Страница 3 из 7
Практические задачи №1-5 к ОГЭ по математике
Прочитайте внимательно текст и выполните задания 1–5.
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
297 |
210 |
|
2 |
420 |
297 |
|
3 |
1189 |
841 |
|
4 |
841 |
594 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 3421
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А5 и А6.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
210 |
148 |
|
2 |
594 |
420 |
|
3 |
148 |
105 |
|
4 |
420 |
297 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 2413
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А3 и А4.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
841 |
594 |
|
2 |
420 |
297 |
|
3 |
594 |
420 |
|
4 |
297 |
210 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 1324
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А3, А4, А5 и А6.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
148 |
105 |
|
2 |
210 |
148 |
|
3 |
420 |
297 |
|
4 |
297 |
210 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3421
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А5 и А6.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
594 |
420 |
|
2 |
148 |
105 |
|
3 |
210 |
148 |
|
4 |
841 |
594 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4132
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А4 и А6.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
594 |
420 |
|
2 |
420 |
297 |
|
3 |
148 |
105 |
|
4 |
297 |
210 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 1243
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А2 и А4.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
841 |
594 |
|
2 |
1189 |
841 |
|
3 |
297 |
210 |
|
4 |
594 |
420 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 2143
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А4 и А5.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
420 |
297 |
|
2 |
297 |
210 |
|
3 |
841 |
594 |
|
4 |
210 |
148 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3124
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А4, А5 и А6.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
297 |
210 |
|
2 |
148 |
105 |
|
3 |
594 |
420 |
|
4 |
210 |
148 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3142
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А4 и А6.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
148 |
105 |
|
2 |
420 |
297 |
|
3 |
297 |
210 |
|
4 |
841 |
594 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4231
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А2, А3 и А5.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
594 |
420 |
|
2 |
420 |
297 |
|
3 |
1189 |
841 |
|
4 |
210 |
148 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3124
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А5 и А6.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
210 |
148 |
|
2 |
841 |
594 |
|
3 |
420 |
297 |
|
4 |
148 |
105 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 2314
Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А3 и А5.
|
Номер листа |
Длина (мм) |
Ширина (мм) |
|
1 |
210 |
148 |
|
2 |
594 |
420 |
|
3 |
420 |
297 |
|
4 |
841 |
594 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение:
А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4231
Задание 2.
Сколько листов формата А3 получится из одного листа формата А2?
Решение:
А2 594*420
А3 420*297Ответ: 2
Задание 2.
Сколько листов формата А3 получится из одного листа формата А1?
Решение:
А1 841*594
А2 594*420 — 2 шт
А3 420*297 — 4 шт.Ответ: 4
Задание 2.
Сколько листов формата А3 получится из одного листа формата А0?
Решение:
А0 1189*841
А1 841*594 — 2 шт.
А2 594*420 — 2*2= 4 шт
А3 420*297 — 4*2 = 8 шт.Ответ: 8
Задание 2.
Сколько листов формата А5 получится из одного листа формата А0?
Решение:
А0 1189*841
А1 841*594 — 2 шт
А2 594*420 — 4 шт.
А3 420*297 — 8 шт.
А4 297*210 — 16 шт.
А5 210*148 — 32 шт.
Ответ: 32
Задание 2.
Сколько листов формата А5 получится из одного листа формата А1?
Решение:
А1 841*594
А2 594*420 — 2 шт.
А3 420*297 — 4 шт.
А4 297*210 — 8 шт.
А5 210*148 — 16 шт.
Ответ: 16
Задание 2.
Сколько листов формата А5 получится из одного листа формата А3?
Решение:
А3 420*297
А4 297*210 — 2 шт.
А5 210*148 — 4 шт.
Ответ: 4
Задание 2.
Сколько листов формата А6 получится из одного листа формата А2?
Решение:
А2 594*420
А3 420*297 — 2 шт.
А4 297*210 — 4 шт.
А5 210*148 — 8 шт.
А6 148*105 — 16 шт.
Ответ: 16
Задание 2.
Сколько листов формата А6 получится из одного листа формата А0?
Решение:
А0 1189*841
А1 841*594 — 2
А2 594*420 — 4
А3 420*297 — 8
А4 297*210 — 16
А5 210*148 — 32
А6 148*105 — 64
Ответ: 64
Задание 2.
Сколько листов формата А6 получится из одного листа формата А3?
Решение:
А3 420*297
А4 297*210 — 2
А5 210*148 — 4
А6 148*105 — 8
Ответ: 8
Задание 2.
Сколько листов формата А6 получится из одного листа формата А1?
Решение:
А1 841*594
А2 594*420 — 2
А3 420*297 — 4
А4 297*210 — 8
А5 210*148 — 16
А6 148*105 — 32
Ответ: 32
Задание 2.
Сколько листов формата А4 получится из одного листа формата А2?
Решение:
А2 594*420
А3 420*297 — 2
А4 297*210 — 4
Ответ: 4
Задание 2.
Сколько листов формата А4 получится из одного листа формата А1?
Решение:
А1 841*594
А2 594*420 — 2
А3 420*297 — 4
А4 297*210 — 8
Ответ: 8
Задание 2.
Сколько листов формата А4 получится из одного листа формата А0?
Решение:
А0 1189*841
А1 841*594 — 2
А2 594*420 — 4
А3 420*297 — 8
А4 297*210 — 16
Ответ: 16
Задание 3.
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
Решение:
Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5000 см2Ответ: 5000
Задание 3.
Найдите площадь листа формата А2. Ответ дайте в квадратных сантиметрах.
Решение:
Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2500 см2
Ответ: 2500
Задание 3.
Найдите площадь листа формата А3. Ответ дайте в квадратных сантиметрах.
Решение:
Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Ответ: 1250
Задание 3.
Найдите площадь листа формата А6. Ответ дайте в квадратных сантиметрах.
Решение:
Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см2/2=625 см2
Лист формата А5 имеет форму прямоугольника, площадь которого равна 625 см2/2=312,5 см2
Лист формата А6 имеет форму прямоугольника, площадь которого равна 312,5 см2/2=156,25 см2Ответ: 156,25
Задание 3.
Найдите площадь листа формата А5. Ответ дайте в квадратных сантиметрах.
Решение:
Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см2/2=625 см2
Лист формата А5 имеет форму прямоугольника, площадь которого равна 625 см2/2=312,5 см2Ответ: 312,5
Задание 3.
Найдите площадь листа формата А4. Ответ дайте в квадратных сантиметрах.
Решение:
Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см2/2=625 см2Ответ: 625
Задание 3.
Найдите ширину листа бумаги формата А0. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А0 1189*841, то есть ширина кратная 10 будет 840
Ответ: 840
Задание 3.
Найдите ширину листа бумаги формата А1. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А1 841*594 , то есть ширина кратная 10 будет 590
Ответ: 590
Задание 3.
Найдите ширину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А2 594*420 , то есть ширина кратная 10 будет 420
Ответ: 420
Задание 3.
Найдите ширину листа бумаги формата А3. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А3 420*297 , то есть ширина кратная 10 будет 300
Ответ: 300
Задание 3.
Найдите ширину листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А4 297*210 , то есть ширина кратная 10 будет 210
Ответ: 210
Задание 3.
Найдите ширину листа бумаги формата А5. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А5 210*148, то есть ширина кратная 10 будет 150
Ответ: 150
Задание 3.
Найдите ширину листа бумаги формата А6. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 5.
Решение:
А6 148*105, то есть ширина кратная 10 будет 110
Ответ: 110
Задание 4.
Найдите длину листа бумаги формата А1. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А1 841*594, то есть длина кратная 10 будет 840
Ответ: 840
Задание 4.
Найдите длину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А2 594*420, то есть длина кратная 10 будет 600
Ответ: 600
Задание 4.
Найдите длину листа бумаги формата А3. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А3 420*297, то есть длина кратная 10 будет 420
Ответ: 420
Задание 4.
Найдите длину листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А4 297*210, то есть длина кратная 10 будет 300
Ответ: 300
Задание 4.
Найдите длину листа бумаги формата А5. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А5 210*148, то есть длина кратная 10 будет 210
Ответ: 210
Задание 4.
Найдите длину листа бумаги формата А6. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение:
А6 148*105, то есть длина кратная 10 будет 150
Ответ: 150
Задание 4.
Найдите длину листа бумаги формата А7. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 5.
Решение:
А7 105*74, то есть длина кратная 10 будет 110
Ответ: 110
Задание 4.
Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.
Решение:
А3 420*297
420/297=1,41Ответ: 1,4
Задание 4.
Найдите отношение длины меньшей стороны листа формата А4 к большей. Ответ округлите до десятых.
Решение:
А4 297*210
297/210=1,41
Ответ: 1,4
Задание 4.
Найдите отношение длины меньшей стороны листа формата А5 к большей. Ответ округлите до десятых.
Решение:
А5 210*148
210/148=1,41
Ответ: 1,4
Задание 4.
Найдите отношение длины большей стороны листа формата А2 к меньшей. Ответ округлите до десятых.
Решение:
А2 594*420
594/420=1,41
Ответ: 1,4
Задание 4.
Найдите отношение длины большей стороны листа формата А6 к меньшей. Ответ округлите до десятых.
Решение:
А6 148*105
148/105=1,409
Ответ: 1,4
Задание 4.
Найдите отношение длины большей стороны листа формата А1 к меньшей. Ответ округлите до десятых.
Решение:
А1 841*594
841/594=1,41
Ответ: 1,4
Задание 4.
Найдите отношение длины диагонали листа формата А2 к его меньшей стороне. Ответ округлите до десятых.
Решение:
А2 594*420
Меньшая сторона формата А2 равна 420 мм, большая сторона формата А2 594 мм. Диагональ является гипотенузой треугольника с катетами 420 мм и 594 мм, по теореме Пифагора имеем:
$sqrt{594*594+420*420}≈727$ мм
Найдем отношения длины диагонали к меньшей стороне:
727/420 ≈ 1,7.Можно решить иначе.
Зная отношение меньшей стороны к большей (420/594=0,7), можно найти гипотенузу подобного треугольника с таким же отношением — со сторонами 7 и 10. Получится квадратный корень из 149, это ≈ 12.
Тогда отношение гипотенузы к меньшей стороне 12:7=1,7Ответ: 1,7.
Задание 4.
Найдите отношение длины диагонали листа формата А0 к его меньшей стороне. Ответ округлите до десятых.
Решение:
А0 1189*841
Меньшая сторона формата А0 равна 841 мм, большую сторона формата А0 1189 мм. Диагональ является гипотенузой треугольника с катетами 841 мм и 1189 мм, по теореме Пифагора имеем:
$sqrt{841*841+1189*1189}≈1456$ мм
Найдем отношения длины диагонали к меньшей стороне:
1456/841 ≈ 1,7.Ответ: 1,7
Задание 4.
Найдите отношение длины диагонали листа формата А7 к его меньшей стороне. Ответ округлите до десятых.
Решение:
А7 105*74
Меньшая сторона формата А7 равна 74 мм, большую сторона формата А7 105 мм. Диагональ является гипотенузой треугольника с катетами 74 мм и 105 мм, по теореме Пифагора имеем:
$sqrt{74*74+105*105}≈129$ мм
Найдем отношения длины диагонали к меньшей стороне:
129/74 ≈ 1,7.
Ответ: 1,7
Задание 5.
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 32 листа формата А5, поэтому площадь листа формата А5 в 32 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
80/32, а вес пачки равен 80/32 * 500=1250 граммов.
Ответ: 1250
Задание 5.
Бумагу формата А4 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г? Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 16 листа формата А4, поэтому площадь листа формата А4 в 16 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
80/16, а вес пачки равен 80/16 * 500=2500 граммов.
Ответ: 2500
Задание 5.
Бумагу формата А3 упаковали в пачки по 200 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
80/8, а вес пачки равен 80/8 * 500=5000 граммов.
Ответ: 5000
Задание 5.
Бумагу формата А3 упаковали в пачки по 250 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 120 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
120/8, а вес пачки равен 120/8 * 250=3750 граммов.
Ответ: 3750
Задание 5.
Бумагу формата А2 упаковали в пачки по 100 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 96 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 4 листа формата А2, поэтому площадь листа формата 2 в 4 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А2 равен дробь:
96/4, а вес пачки равен 96/4 * 100=2400 граммов.
Ответ: 2400
Задание 5.
Бумагу формата А1 упаковали в пачки по 80 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 120 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 2 листов формата А1, поэтому площадь листа формата А1 в 2 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А1 равен дробь:
120/2, а вес пачки равен 120/2 * 80=4800 граммов.
Ответ: 4800
Задание 5.
Бумагу формата А3 упаковали в пачки по 120 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 96 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
96/8, а вес пачки равен 96/8 * 120=1440 граммов.
Ответ: 1440
Задание 5.
Бумагу формата А4 упаковали в пачки по 800 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 16 листов формата А4, поэтому площадь листа формата А4 в 16 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
80/16, а вес пачки равен 80/16 * 800=4000 граммов.
Ответ: 4000
Задание 5.
Бумагу формата А5 упаковали в пачки по 1000 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 144 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 32 листов формата А5, поэтому площадь листа формата А5 в 32 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
144/32, а вес пачки равен 144/32 * 1000=4500 граммов.
Ответ: 4500
Задание 5.
Бумагу формата А6 упаковали в пачки по 320 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 108 г. Ответ дайте в граммах.
Решение:
На листе формата А0 помещается 64 листа формата А6, поэтому площадь листа формата А6 в 64 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А6 равен дробь:
108/64, а вес пачки равен 108/64 * 320=540 граммов.
Ответ: 540
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
15*1,41=21,15 мм ≈21
Ответ: 21
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 16 пунктов на листе формата А4? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
16/1,41=11,34 мм ≈11
Ответ: 11
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
8 пунктов на листе формата А5. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 таким же образом? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
8*1,41=11,28 мм ≈11
Ответ: 11
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
12 пунктов на листе формата А4. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 таким же образом? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
13*1,41=16,92 мм ≈17
Ответ: 17
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 12 пунктов на листе формата А5? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
12*1,41=16,92 мм ≈17
Ответ: 17
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
22 пункта на листе формата А3. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А2 таким же образом? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
22*1,41=31,02 мм ≈31
Ответ: 31
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
20 пунктов на листе формата А4. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 таким же образом? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
20*1,41=28,2 мм ≈28
Ответ: 28
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 17 пунктов на листе формата А3? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
17/1,41=12,06 мм ≈12
Ответ: 12
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 21 пункт на листе формата А3? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
21/1,41=14,89 мм ≈15
Ответ: 15
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 20 пунктов на листе формата А4? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
20/1,41=14,84 мм ≈15 мм
Ответ: 15
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.
Решение:
Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.
10*1,41=14,1 мм ≈14 мм
Ответ: 14
B9A7F7