Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Отношение чисел
Поддержать сайт
Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.
Если вам знакомо понятие отношение чисел, можете смело переходить к теме
пропорции.
Что называют отношением двух чисел
Запомните!
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Покажем на примере, где используется понятие отношение двух чисел.
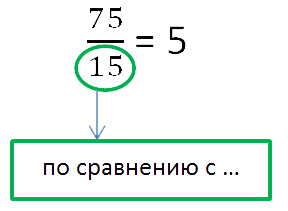
В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15.
В этом году — 75. Во сколько раз увеличилось количество участников в этом году по
сравнению с предыдущим годом?
Прежде чем решать задачу, подчёркиваем важные данные.
Запишем отношение количества участников в этом году к количеству участников в предыдущем.
Запомните!
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».
Запомните!
Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.
При внимательном изучении правила выше, можно подметить, что правило записанное выше,
есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.
Отношение 16 к 10:
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 апреля 2023 в 20:44
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
Что такое отношение 2 к 3?
Понимание «Отношение чисел» используется для сравнения двух величин и показывает во сколько раз первое число больше второго, либо какую часть первое число составляет от второго. В нашем примере отношение показывает, что число 2 составляет 2/3 от числа 3. Отношение показывает, что число 5 составляет 1/2 от числа 10.
Что значит три к одному?
Ответ: Пошаговое объяснение: 1:3 это когда первое число в 3 раза меньше второго. 3:1 это когда первое число в 3 раза больше второго.
Что такое соотношение чисел?
, а иногда выражаемое арифметически как безразмерное отношение (результат деления) двух чисел, непосредственно отображающее, сколько раз первое число содержит второе (не обязательно целое). … Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого.
Как найти соотношение между числами?
Правило. Чтобы найти процентное отношение двух чисел , нужно одно число разделить на другое, а результат умножить на 100. Например, вычислить, сколько процентов составляет число 52 от числа 400.
Как найти сколько процентов составляет число от другого числа?
Сколько процентов составляет одно число от другого Чтобы вычислить процентное отношение чисел, нужно одно число разделить на другое и умножить на 100%. Число 12 составляет 40% от числа 30. Например, книга содержит 340 страниц.
Как посчитать процент одного числа от другого на калькуляторе?
Процент одного числа от другого Как посчитать сколько процентов составляет одно числа от другого? Задачка решается при помощи бесплатного онлайн калькулятора, который использует для вычисления формулу: Первое число / Второе число * 100%.
Как легко посчитать проценты?
Чтобы найти проценты от какого-либо числа надо это число разделить на 100 и результат деления умножить на количество процентов. Например, чтобы найти 30% от 250, надо 250 поделить на сто (получим 2,5) и потом 2,5 умножить на 30. В результате получится 75. Таким образом, 30% от 250 = 75.
Как рассчитать проценты от суммы?
Чтобы найти процент от суммы, необходимо разделить это число на 100 и умножить на число процентов.
Как найти процент от числа формула?
Математическая формула расчета процентов выглядит следующим образом: (искомая часть / целое число) * 100. Чтобы найти процент от числа, применяется такой вариант формулы: (число * процент) / 100.
Как рассчитать 5 процентов от суммы?
Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на 100 и вычесть 100. Число 20 больше числа 5 на 300%.
Как посчитать проценты в обратную сторону?
Обратный процент или процент от суммы Для этого от 100% нужно отнять заданный процент, затем разделить заданное число на полученный процент и найти значение 1%.
Как посчитать общий процент от всех процентов?
В=А*Р/100%. Есть специальная формула для вычисления по проценту. При этом нужно узнать от какого значения %. Если известно В, которое составляет Р процентов от числа А, то количество А находится так.
Как считается процент от выручки?
Если от выручки, то это все полученные доходы умножить на величину процента и разделить на 100. А если от прибыли, то из доходов нужно вычесть расходы, а полученную цифру умножить на величину процента и разделить на 100.
Как посчитать общий процент выполнения плана?
Для того, чтобы рассчитать процент выполнения плана, нужно воспользоваться формулой: %плана = (факт / план) * 100%. Эти показатели могут быть выражены как в количественных, так и в стоимостных единицах, а также складываться из нескольких компонентов.
Как найти процент выполнения задания?
Таким образом, чтобы определить процент выполнения плана, необходимо найти частное достигнутых результатов на данный момент и запланированных к определенному сроку, а затем умножить получившееся число на 100. ПВП — процент выполнения плана; ТР — текущие результаты; ЗР — запланированные результаты.
Как посчитать средний процент от суммы процентов?
Прежде всего, давайте выясним, как рассчитать величину доли в процентах одного числа от другого. Общая формула вычисления выглядит следующим образом: «=(число)/(общая_сумма)*100%. Итак, для того, чтобы показать вычисления на практике, узнаем, сколько процентов составляет число 9 от 17.
Как правильно посчитать процент с продаж?
Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.
Как рассчитать средний процент выполнения задания?
Средний процент выполнения работы. Как посчитать процент выполнения плана
- Процента выполнения плана на текущую дату = план / кол-во рабочих дней * на кол-во отработанных дней
- Процент выполнения плана = фактически выполненный план на текущую дату / план на текущую дату
- Практика №1.
- Средние величины.
- МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Как посчитать процент выполнения плана на текущую дату?
Подсчитываем ежедневно выполнение плана продаж
- Первое, что должен сделать владелец бизнеса для увеличения выручки, — это установить цели на несколько месяцев вперед и ежедневно следить за их выполнением. …
- Процента выполнения плана на текущую дату = план / кол-во рабочих дней * на кол-во отработанных дней
Как рассчитать индекс выполнения плана?
Этот индекс рассчитывается как отношение фактических затрат на фактически произведенную продукцию к плановым затратам на эту же продукцию.
Как рассчитать прогноз выполнения плана?
Рассчитывается Run-rate просто: Любой выполненный показатель делится на количество прошедших рабочих дней с начала года и умножается на общее количество рабочих дней в году. Чтобы составить прогноз до конца года, к получившемуся значению прибавляем выполненный показатель.
Как сделать прогноз по продажам?
Для того, чтобы рассчитать прогноз продаж по методу скользящей средней, необходимо:
- Рассчитать коэффициенты сезонности;
- Выбрать период для расчета среднего значения;
- Рассчитать прогноз, т. е. среднее значение умножить на коэффициент сезонности;
- Учесть дополнительные факторы, которые значительно влияют на продажи;
Как рассчитать план продаж формула?
Чтобы его рассчитать, нужно:
- Взять общую сумму продаж за прошлый год и разделить ее на 12. Таким образом, вы получите среднемесячное значение.
- Сумму продаж за каждый месяц расчетного года разделить на среднее значение.
Что такое Runrate?
Ключевой показатель эффективности отдела продаж – выполнение плана. Ранрейт (дословно: скорость выполнения) позволяет вам контролировать успешность достижения плана в любой день месяца. … Если говорить простыми словами, это показатель на текущий день, который указывает на необходимый уровень продаж.
Как рассчитать прогноз выполнения плана магазина?
- Отчет «Прогноз выполнения плана продаж» отображает информацию о динамике выполнения плана продаж с учетом изменения данных по оборотам продаж.
- (Продажи на момент измерения/количество прошедших рабочих дней) Х количество рабочих дней за весь период.
- Прогноз выполнения ( RR сумма/количество) / План продаж *100%
Кто составляет план продаж?
Обычно план продаж спускается от собственника бизнеса к коммерческому директору, от коммерческого директора к начальнику отдела продаж, от начальника отдела старшему менеджеру (или супервайзеру) к менеджерам по продажам.
Как рассчитать прирост плана?
Для этого находят разницу конечного и начального показателей, затем ее нужно разделить на количество периодов. Прирост может получиться отрицательным. Например, если стоимость акций к концу года составила 210 тыс. рублей, то прирост будет равен: (0)/-19%.
Просмотров 1.4к. Опубликовано 30.09.2022
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Отношения
Мы знаем это, чтобы ответить на вопрос, насколько часто одно число больше (или меньше) другого, или насколько одно число является дробью другого. найти частное данных чисел.
Частное двух чисел не равный нулю, называется отношением чисел , или отношением числа .
Где — члены отношения число перед термином отношенияследующий срок отношения.
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
количество
1,15 : 0,36 — отношение от числа 1,15 до числа 0,36.
Отношение двух чисел Показывает, как часто одно число больше другого или как сильно одно число зависит от другого. Это отношение чисел указывает, сколько раз число или сколько частей числа .
Помните, что деление можно заменить дробью, поэтому, отношение чисел можно записать двумя способами: и
Основное свойство отношения:
Отношение не меняется, когда его члены умножаются или делятся на одно и то же число, которое не равно нулю.
Запишем отношение от 3 до 10 и найти его значение:
То есть отношение двух чисел Он может быть выражен в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, какой процент число составляет от другого числа.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и добавить знак процента к результату.
Пример:
В каком проценте число 5 равно числу 10?
5 10 2 1 — 100 % = 1 2 — 100 % = 100 2 % = 50 % .
Ответ: 50% равно 5 умножить на 10.
Если значение двух величин выражено в одних и тех же единицах, то. их отношение называют также отношением. Если две величины выражены в разных единицах, то отношения эти величины должны быть сначала переведены в одну и ту же единицу измерения.
Например:
Дан прямоугольник длиной 12 см и шириной 1 м. Найти отношение длины сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 12 : 100 = 100.
Отношение ширины прямоугольника к его длине равно 100 : 12 =
Дробь взаимно обратная, поэтому и отношения 12 к 100 и 100 к 12 называются взаимно обратными.
На практике отношение Обратные дроби используются, например, при составлении чертежей и географических карт. В этом случае земельные участки рисуются на бумаге в уменьшенном виде, а на карте или картографии изображаются отношение, указывает, как часто длина отрезка на чертеже меньше длины соответствующего отрезка на местности.
Соотношение между длиной отрезка на карте и длиной соответствующего отрезка на местности называется масштабом карты (чертежа).
Предположим, что карта имеет масштаб
Давайте выясним, какова длина отрезка в 5 см на карте на земле.
Для решения обозначим длину отрезка на земле (в сантиметрах). Затем отношение длина отрезка на карте к длине отрезка на местности составляет: 5 :, данная отношение равна масштабу карты, что дает уравнение:
5 :
Решите это уравнение:
10 000;
50 000 см = 500 м = 0,5 км.
Ответ: Отрезок в 5 см на карте равен 0,5 км на местности.
Давайте выясним, какая длина на карте соответствует отрезку 9,5 км на карте.
Для решения обозначьте длину участка на карте (в километрах). Затем отношение длина отрезка на карте с длиной отрезка на местности: : 9,5, данная отношение равна масштабу карты, что дает уравнение:
Решите это уравнение:
0,00095 км = 0,95 м = 95 см.
Ответ: Отрезок 9,5 км на карте равен 95 см на карте.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Отношение чисел
Отношение чисел — это коэффициент от деления одного числа на другое.
Отношение чисел A и b можно записать двумя способами: со знаком деления или через косую черту (как дробь):
Эти признаки следующие: отношение a к b или отношение числа a к числу b.
Числа a и b, составляющие отношение a : b становятся терминами отношения. Делителем является предыдущий член отношения, а делитель — предпоследний член. отношения. Таким образом, a — предыдущий член, b — следующий.
Соотношение используется для сравнения двух чисел. Так, отношение a : b показывает, во сколько раз a больше b (если делитель больше делимого) или сколько процентов от числа b составляет a (если делитель меньше делимого).
Отношение 35 к 7 показывает, что число 35 в пять раз больше числа 7.
2)
Отношение 12 к 15 показывает, что число 12 в 0,8 раза больше числа 15.
Из основного свойства квоты следует, что. отношения :
Отношение не меняется, когда его члены умножаются или делятся на одно и то же ненулевое число.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Помните.
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Давайте на примере покажем, в чем суть концепции. отношение двух чисел.
В городе Липецке проходят соревнования по велоспорту. В прошлом году было 15 участников, в этом году — 75. На сколько больше участников в этом году, чем в прошлом?
Прежде чем решить проблему, давайте остановимся на самых важных фактах. Запишите отношение количество участников в этом году с количеством участников в прошлом году.
Помните.
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Помните.
Если вы умножите или разделите оба термина отношения на одно и то же число, которое не равно нулю, вы получите отношение, равное данному.
Если вы внимательно изучите приведенное выше правило, то обнаружите, что написанное выше правило — это не что иное, как основное свойство дробей, с помощью которого мы можем легко их сокращать.
Основное свойство коэффициента заключается в том, что он остается неизменным при умножении или делении делителя и делимого на одно и то же число.
Задания для самостоятельной работы
На пост президента претендовали два кандидата. Явка составила 120 человек. Распределение голосов соответствует соотношению 3:5. Необходимо определить количество голосов, полученных победителем.
Соотношение между количеством хвойных и лиственных деревьев в лесу можно представить как 1:4. Необходимо рассчитать долю лиственных деревьев.
На площади 24 га выращиваются сельскохозяйственные культуры. Зерновые и овощи распределяются в соответствии с с отношением 5:3. Необходимо рассчитать площадь возделывания овощных культур в гектарах.
Основное свойство отношения: Путем умножения или деления членов отношения на одно и то же число, отличное от нуля, данный отношение останется неизменным.
Отношения в задачах
Теперь давайте узнаем, как отношения в задачах.
Давайте сразу перейдем к примерам, чтобы увидеть, какой может быть формулировка отношения.
Проблема 1
Протяженность дороги составляет 25 километров. Он освещен на протяжении 15 километров.
(α) Найдите, какая часть дороги освещена.
(b) Во сколько раз вся проезжая часть длиннее освещенной части?
Решение:
В начале урока мы обнаружили отношение меньшего числа в большее, определяя тем самым, какая часть первого числа содержится во втором.
Это первый вопрос.
Для нахождения отношения Отношение длины освещенного участка к длине всей дороги делится на единицу:
Значит, длина освещенного участка составляет (mathbf>) по всей длине дороги.
Второй вопрос: «Во сколько раз больше?». — соответствует отношению от большего числа к меньшему.
Чтобы найти это отношения это разделить длину всей дороги на длину освещенной части дороги:
Это отвечает на вопрос второго пункта.
Важно также всегда следить за тем, чтобы количество было одинаковым.
Так, если что-то дано нам в тоннах и килограммах, и мы хотим найти отношения Чтобы узнать эти количества, мы должны либо перевести тонны в килограммы, либо наоборот.
Проблема 2
Масса груза составляет 2 тонны. Известно, что часть груза — это одежда, масса которой составляет 350 кг.
Определите, сколько процентов от массы груза составляет масса одежды.
Решение:
Давайте сначала переведем тонны в килограммы. Оказывается, что масса груза составляет 2000 кг.
Теперь давайте найдем неизвестное. отношение:
Теперь попробуйте решить задачу самостоятельно и воспользуйтесь подсказками, если у вас возникнут трудности.
Вы можете пройти тест и получить результат после того, как войдете в систему или зарегистрируетесь.
Интересная информация
Сегодня вы научитесь математическим фокусам!
Их идея заключается в том, что можно запутать людей с помощью математических преобразований, которые дают нам то, что нам нужно.
Уловка 1.
Попросите зрителя придумать число и никому его не называть.
Теперь попросите их умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть число в уме.
Теперь вы можете с уверенностью сказать, что зритель получил число 4.
Это происходит потому, что при преобразовании исходное число удаляется из арифметической цепочки, оставляя только четверку.
Попробуйте доказать это с помощью формул, вычитая исходное число X
Уловка 2
В этой игре вы можете угадать день рождения человека.
Попросите зрителя умножить количество дней рождения на 2. Затем попросите его прибавить к результату 5 и умножить целое число на 50. Затем попросите зрителя добавить номер месяца, в котором он родился (1 января, 2 февраля и т.д.).
Чтобы узнать день рождения человека по полученному числу, вычтите 250 из числа, указанного зрителем — вы получите трех- или четырехзначное число, где первые одна или две цифры обозначают день рождения, а последние две цифры — месяц.
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Эта информация доступна зарегистрированным пользователям
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как (mathbf{a div b}) или же через дробную черту: (mathbf{frac{a}{b}})
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
- может получиться натуральное число
- обыкновенная дробь
- смешанное число
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
(mathbf{256div8=32})
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
- если отношение получилось больше 1, значит, первое число больше второго
- если меньше 1, то второе число больше первого
- если отношение оказалось равно 1, значит, числа равны
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
(mathbf{15div12=frac{15}{12}=frac{5cdot3}{4cdot3}=frac{5}{4}=1frac{1}{4}})
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в (mathbf{1frac{1}{4}}) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
(mathbf{16div24=frac{16}{24}=frac{8cdot2}{8cdot3}=frac{2}{3}})
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в (mathbf{frac{2}{3}}) раза.
Мы можем сформулировать вывод и так: 16 составляет (mathbf{frac{2}{3}}) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
(mathbf{14div28=frac{14}{28}=frac{14cdot1}{14cdot2}=frac{1}{2}})
И посчитаем отношение 28 к 14
(mathbf{28div14=2})
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно (mathbf{frac{2}{5}}), найдем отношение b к a
Для этого надо найти обратное число к (mathbf{frac{2}{5}})
(mathbf{1divfrac{2}{5}=frac{5}{2}=2frac{1}{2}})
Значит, отношение b к a равняется (mathbf{2frac{1}{2}})
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно (mathbf{frac{1}{3}})
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно (mathbf{frac{1}{3}})
Эта информация доступна зарегистрированным пользователям
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него (mathbf{frac{3}{8}})
Перемножив, мы получим:
(mathbf{4cdotfrac{3}{8}=frac{4cdot3}{8}=frac{4cdot3}{4cdot2}=frac{3}{2}=1frac{1}{2}})
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
(mathbf{1frac{1}{2}div4=frac{3}{2}div4=frac{3}{2cdot4}=frac{3}{8}})
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна (mathbf{2frac{1}{2}})
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
(mathbf{2frac{1}{2}div10=frac{2cdot2+1}{2}div10=frac{5}{2}div10=frac{5}{2cdot10}=frac{1}{2cdot2}=frac{1}{4}})
Ответ: дробь, взяв которую от 10 получили (mathbf{2frac{1}{2}}), равняется (mathbf{frac{1}{4}})
Пример 2
Отношение первого числа ко второму равно (mathbf{1frac{1}{5}}), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к (mathbf{1frac{1}{5}})
(mathbf{1div1frac{1}{5}=1divfrac{6}{5}=1cdotfrac{5}{6}=frac{5}{6}})
Теперь можно найти второе число, домножим первое на эту дробь:
(mathbf{6cdotfrac{5}{6}=frac{6cdot5}{6}=5})
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
(mathbf{6div5=frac{6}{5}=1frac{1}{5}})
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно (mathbf{1frac{1}{2}})
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
(mathbf{1div1frac{1}{2}=1divfrac{3}{2}=frac{2}{3}})
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
(mathbf{8divfrac{2}{3}=8cdotfrac{3}{2}=frac{8cdot3}{2}=4cdot3=12})
Ответ: число a равняется 12
Эта информация доступна зарегистрированным пользователям
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
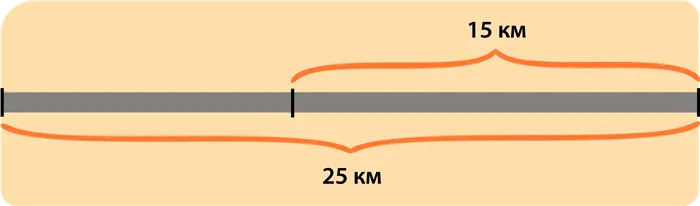
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Эта информация доступна зарегистрированным пользователям
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
(mathbf{15div25=frac{15}{25}=frac{3cdot5}{5cdot5}=frac{3}{5}})
Значит, длина освещенного участка составляет (mathbf{frac{3}{5}}) от длины всей улицы.
Во втором вопросе нас спрашивают: «Во сколько раз больше?» — это соответствует отношению большего числа к меньшему.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
(mathbf{25div15=frac{25}{15}=frac{5cdot5}{3cdot5}=frac{5}{3}=1frac{2}{3}})
Что отвечает на вопрос второго пункта.
Ответ: a) (mathbf{frac{3}{5}}), б) (mathbf{1frac{2}{3}})
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
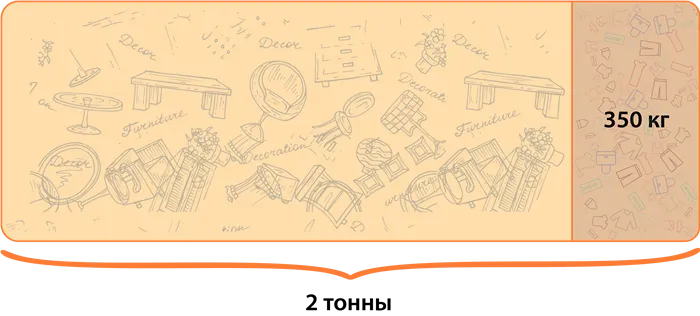
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Эта информация доступна зарегистрированным пользователям
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
(mathbf{frac{350}{2000}=frac{35}{200}=frac{7cdot5}{5cdot40}=frac{7}{40}})
Ответ: (mathbf{frac{7}{40}}).
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Эта информация доступна зарегистрированным пользователям
Эта информация доступна зарегистрированным пользователям
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц.
Что такое формула соотношения? – Обзоры Вики
Формула отношения
Общая форма представления отношения между двумя величинами, скажем, «а» и «b», представляет собой отношение : b, которое читается как «а к b». Дробная форма, которая представляет это соотношение, — a/b. Чтобы еще больше упростить отношение, мы следуем той же процедуре, которую используем для упрощения дроби. а:б = а/б.
Отсюда, каково соотношение 3 к 5? 3:5=? : 40. (3 из 5 — это сколько из 40?) «5 входит в число 40 восемь раз. Восемь раз по 3 равно 24».
Как найти отношение двух чисел онлайн? Пример: упростить соотношение 8: 36
- Множители 8: 1, 2, 4, 8.
- Делителями числа 36 являются: 1, 2, 3, 4, 6, 9, 12, 18, 36.
- Наибольший общий делитель 8 и 36 равен 4.
- Разделите оба члена на 4.
- 8 ÷ 4 = 2.
- 36 ÷ 4 = 9.
- Перепишите соотношение, используя результаты. Упрощенное соотношение — 2: 9.
- 8: 36 = 2: 9 в простейшей форме.
Дополнительно Как рассчитать коэффициент 2 1? Соотношение 2 к 1 это простейшая форма соотношения 4 к 2. И соотношения эквивалентны, потому что отношения между каждой парой чисел одинаковы. Например, если у нас есть отношение 250 к 150, мы можем упростить его, разделив оба числа на 10, а затем на 5, чтобы получить 5 до 3: 250: 150 25: 15 5: 3.
Как рассчитать коэффициенты на калькуляторе? Нажмите кнопка деления, введите наибольший общий делитель и нажмите кнопку равенства. Запишите это число. В этом примере вы вычисляете 84 ÷ 12 = 7. Выразите соотношение, используя число из шага 3 и число из шага 5.
Какой процент составляет соотношение 2 к 1?
Простое преобразование процентов и соотношений.
| Соотношение | Процент -% |
|---|---|
| 2.5 — 1 | 29% |
| 2 — 1 | 33% |
| 1.5 — 1 | 40% |
| 1 — 1 | 50% |
Как вы работаете соотношение в простейшей форме? Соотношения можно полностью упростить, как и дроби.
Что такое отношение числа?
В математике соотношение указывает, сколько раз одно число содержит другое. Например, если в миске с фруктами находится восемь апельсинов и шесть лимонов, то соотношение апельсинов и лимонов будет восемь к шести (то есть 8∶6, что эквивалентно соотношению 4∶3). … В большинстве случаев оба числа должны быть положительными.
Также каково соотношение 4 к 3? Соотношение сторон 4:3 широко известно как полноэкранное соотношение сторон. Формат 4 × 3 (1.33: 1) стал первым стандартным соотношением сторон для телевизоров и компьютерных мониторов, поскольку его было легко использовать из-за форматов камеры.
Какое соотношение 1 к 10?
Таким образом, как часть 3/30 можно упростить до 1/10, соотношение 3:30 (или 4:40, 5:50, 6:60 и т.
Как в процентах написать 2 2? Чтобы дать процент, обычно должно быть два значения, поэтому мы можем знать, с чем сравнивается 2.
- В этом случае давайте работать с 2, что означает 2.00.
- 2.00 = 200100 = 200%
- = 20%
- Чтобы выразить число или дробь в процентах →×100%
- 2 × 100% = 200%
Как рассчитать коэффициент в процентах?
В заключение, шаги для преобразования отношения в проценты приведены ниже:
- Шаг 1: Определите соотношение.
- Шаг 2: Выразите отношение a:b в виде дроби a/b.
- Шаг 3: Умножьте дробь на 100.
- Шаг 4: Упростите и напишите ответ с символом процента (%).
Что такое соотношение 50%?
2: 4 можно записать как 2/4 = 0.5; Умножаем 0.5 на 100, получаем 0.5 × 100 = 50, поэтому соотношение 2: 4 составляет 50%.
Как решить задачу на соотношение? Как решить задачу на соотношение
- Сложите доли коэффициента, чтобы найти общее количество долей.
- Разделите общую сумму на общее количество акций.
- Умножьте на необходимое количество акций.
Каково соотношение 3 к 12? Обратите внимание, что отношение 12 к 3 считается эквивалентным отношению 4 — 1, то есть 12:3 = 4:1.
Какое соотношение 2 и 3?
2 + 3 = 5. Наше соотношение 2:3 содержит всего 5 частей.
Соотношения — это то же самое, что и дроби? Соотношение. Соотношение – это сравнение чисел или величин. Отношение двух чисел может быть записано в виде дроби (или упрощенно в виде десятичной дроби), но не может представлять собой отношение. То же самое дробь делает. Знаменатель дроби ВСЕГДА представляет собой количество равных частей, на которые делится целое.
Какое соотношение сторон у 1024 × 768?
XGA (1024×768 пикселей, 4:3 соотношение сторон): XGA широко используется. Большинство компьютеров используют XGA в качестве исходного разрешения, поэтому сопряжение компьютеров с проекторами XGA является обычным явлением.
Каково соотношение 10 к 15? Разделив 15 и 10 на 5, вы получите упрощенную дробь 3/2. 15:10 становится 3:2, а 15:10 становится 3:2.
Какое соотношение 1 7?
So 2: 14 и 3: 21 два соотношения, равные 1:7. Студентов также просят определить, равны ли два заданных отношения, сначала записав каждое отношение в виде дроби, а затем записав каждую дробь в наименьшем выражении. Если две дроби одинаковы при записи в наименьших терминах, то отношения равны.
Каково соотношение 2 к 3? 2 + 3 = 5. Наше соотношение 2:3 содержит всего 5 частей.
Какое соотношение 1 100?
Масштаб 1: 100 — это представление объекта и / или предмета, который В 100 раз меньше, чем реальный размер 1. Таким образом, при чтении этой шкалы 1 единица эквивалентна 100 единицам.
Что такое 02 в процентах? Таблица преобразования десятичных чисел в проценты
| Десятичная дробь | Процент |
|---|---|
| 0.01 | 1% |
0. 02 02 |
2% |
| 0.03 | 3% |
| 0.04 | 4% |
Что такое 2% в виде десятичной дроби?
Таблица преобразования процентов в десятичные числа
| Процент | Десятичная дробь |
|---|---|
| 2% | 0.02 |
| 3% | 0.03 |
| 4% | 0.04 |
| 5% | 0.05 |
Что такое 1.0 в процентах?
Процент — особый вид дроби
| 100% | = 100 / 100 | = 1.0 (десятичный) |
|---|---|---|
| 25% | = 25 / 100 | = 0.25 (десятичный) |
| 40% | = 40 / 100 | = 0.4 (десятичный) |
| 5% | = 5 / 100 | = 0.05 (десятичный) |
| 0.5% | = 5 / 1000 | = 0. 005 (десятичный) 005 (десятичный) |
Расчеты
Рассчитываем различные величины, которые встречаются в повседневной жизни.
Пропорция 1 к 8 – это сколько?
Разбираемся, что собой представляет соотношение 1 к 8.
2021-05-12 13:10:11
Пропорция 1 к 7 – это сколько?
Разбираемся, что представляет собой пропорция 1 к 7.
2021-05-12 12:58:05
Пропорция 1 к 8 – это сколько?
Разбираемся как получить соотношение 1 к 8.
2021-05-12 12:09:00
Пропорция 1 к 40 – это сколько?
Разбираемся, что собой представляет соотношение 1 к 40.
2021-05-12 11:55:48
1, 2, 3, 4, 5, 6, 7, 8, 9, 10 дм в квадрате – это сколько см квадратных?
Разбираемся, как квадратные дециметры перевести в квадратные сантиметры.
2021-02-14 18:51:43
0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7, 0,8, 0,9 г – это сколько мг, мкг?
Разбираемся, как перевести 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7, 0,8, 0,9 грамм в мг, мкг.
2021-02-12 17:24:12
1, 2, 3, 4, 5, 6, 7, 8, 9, 10 дм – это сколько мм, см, метров?
Разбираемся, как перевести 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 дециметр в мм, см, метров.
2021-02-12 16:04:28
1, 2, 3, 4, 6, 7 процентов от суммы – это сколько?
Разбираемся, как посчитать 1, 2, 3, 4, 6, 7 процента от суммы.
2021-02-11 14:55:13
5, 10, 15, 20, 25 процентов от суммы – это сколько?
Разбираемся, как посчитать 5, 10, 15, 20, 25 процентов от суммы.
2021-02-11 14:39:31
Пропорция 1 к 30 – это сколько?
Разбираемся, как рассчитать соотношение 1 к 30.
2021-02-11 11:00:58
Пропорция 1 к 20 – это сколько?
Разбираемся, как посчитать соотношение 1 к 20.
2021-02-10 18:45:59
Пропорция 3 к 4 – это сколько?
Разбираемся, как получить соотношение 3 к 4.
2021-01-25 13:03:34
Шланг 3/4 дюйма это сколько см, мм?
Разберемся, сколько сантиметров или миллиметров шланг диаметром 3/4 дюйма.
2019-09-06 10:15:36
Сколько будет 4 в минус 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 степени?
Узнаем, как число в четвертой степени переводит в десятичную дробь
2019-09-06 09:09:58
Сколько будет 5 в минус 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 степени?
Разберемся, как число пять возводить в отрицательную степень.
2019-09-06 00:12:47
Соотношение 1 к 10 – это сколько?
Разберемся, как посчитать соотношение 1 к 10. Приведем примеры.
2019-09-05 23:51:09
Пропорция 1 к 25 – это сколько?
Разберемся, что обозначает соотношение 1 к 25. Узнаем, как рассчитать данную пропорцию на примерах.
2019-09-04 17:53:27
Пропорция 1 к 50 – это сколько?
Разберемся, что обозначает пропорция 1 к 50. Узнаем, как это соотношение применять на конкретных примерах.
2019-09-04 14:54:28
Пропорция 1 к 2 – это сколько?
Разберемся, что обозначает пропорция 1 к 2. Рассмотрим, примеры как построить соотношение 1 к 2.
2019-09-04 14:37:29
Пропорция 1 к 3 – это сколько?
Разберемся, что обозначает пропорция 1 к 3. Рассмотрим, как рассчитать пропорцию 1 к 3.
2019-09-04 13:56:00
Калькулятор соотношения
| iCalculator™
Соотношение — это математический термин, показывающий отношение между двумя числами одного типа.
Используйте этот калькулятор, чтобы упростить отношение и выразить его в виде 1:n, или нажмите на опции ниже, чтобы выполнить альтернативные математические вычисления для отношений:
Сложить отношения Вычесть отношения Умножить отношения Разделить отношения Упростить отношения Эквивалентные отношения Преобразовать отношения Объяснение коэффициентов
Пожалуйста, оставьте оценку этому калькулятору коэффициентов, это поможет нам сохранить этот калькулятор и другие наши калькуляторы бесплатными для всех по всему миру.
★ ★ ★ ★ ★ [1476 голосов]
Соотношения объясняются
Коэффициенты могут быть выражены несколькими способами.
Как складывать, вычитать, умножать и делить отношения
Теперь, когда мы рассмотрели основы выражения отношений, вы можете просмотреть дополнительную информацию о выражении отношений или сразу перейти к учебникам по отношениям, описывающим основные математические функции с отношениями. :
- Как сложить два отношения с помощью калькулятора сложения отношений
- Как вычесть два отношения с помощью калькулятора вычитания отношений
- Как умножить два отношения с помощью калькулятора умножения отношений
- Как разделить два коэффициента с помощью вспомогательного калькулятора деления коэффициентов
Как можно выразить коэффициенты?
Соотношения могут быть выражены различными способами, в виде десятичной дроби, дроби в виде связанного сравнения или, что чаще встречается в процентах.
- 1-2 — это отношение, выраженное с помощью дефиса, хотя это довольно часто используется, его следует избегать, поскольку дефис также представляет знак минус в математике и может быть запутанным в длинных алгоритмах или при использовании компьютерного кода или компьютеров для обработки математических вычислений
- 1:2 — отношение, выраженное в типичном математическом формате с использованием двоеточия
- 1 к 2 — отношение, выраженное в письменной форме
- 1 на 2 — соотношение, выраженное в письменной форме
- 0,5 — отношение, выраженное в десятичной дроби число
- 50% — отношение, выраженное в процентах.
- ½ — отношение, выраженное в виде дроби.
Калькулятор соотношения сторон — 4:3, 16:9, 21:9 (Калькулятор соотношения)
Используйте этот калькулятор соотношения для проверки размеров при изменении размера изображений.
Общие пресеты
CustomHD Video 16:9Стандартный монитор 4:3Классический фильм 3:2Cinemascope 21:9Ширина соотношения
Соотношение высоты
Ширина
пикселей
Высота в пикселях
Возможно, вы не знаете об этом факте, но каждый кадр, цифровое видео, холст, адаптивный дизайн и изображение часто имеют прямоугольную форму, которая исключительно точно в пропорции (или соотношении).
Соотношение должно быть четко определенным, чтобы формы соответствовали различным средам, таким как компьютер, кино, телевидение и экраны камер.
Соотношение сторон изображения
Подгонка соотношений к различным средам часто является проблемой для дизайнеров, особенно если им приходится обрезать и конвертировать контент.
К счастью, наличие калькулятора соотношения сторон
упрощает задачу.Если вы работаете с цифровым видео, важно сначала сжать файлы цифрового видео, чтобы получить точные размеры (или соотношения сторон) видео.
Это требует много вычислений. И вот здесь на помощь приходит калькулятор соотношения сторон, который поможет сделать эти расчеты точными.
Чтобы получить точные форматы для вашего видео, просто введите одно измерение, и калькулятор рассчитает другое измерение.
Что такое соотношение сторон?
Вы должны понимать, что такое соотношение сторон, чтобы легко перемещать проекты, изображения и сжимать цифровые видеофайлы/контент с одного носителя на другой без ошибок в расчетах.
Для справки, пропорциональная связь между высотой и шириной прямоугольника — это то, что метко называют соотношением сторон.
Расчет соотношения сторон имеет большое значение в зависимости от того, с чем вы работаете: с изображением, дизайнерским проектом или цифровым видео.
Прочтите отзыв о нас от Fixthephoto.com.
Соотношения сторон в значительной степени определяются числами, как в математическом соотношении , которое четко определяет, сколько дюймов в высоту и сколько дюймов в ширину должны иметь ваши видео, изображения и дизайн-проекты.
Несмотря на то, что соотношения сторон являются измерениями высоты и ширины, они часто уменьшаются до наименьшего применимого соотношения, чтобы идеально вписаться в любую среду.
Для достижения идеального соотношения сторон необходимо использовать калькулятор соотношения сторон . Это уменьшает любую погрешность. Проверьте пост о соотношении сторон.
Посетите ProjectorScreen.
com, чтобы узнать обо всех ваших потребностях в проекторах и экранах для всех соотношений сторон.
Таблицы размеров обуви
Рассчитайте международные размеры обуви с помощью конвертера размеров обуви. При покупке обуви в Европе вы могли заметить другую систему размеров обуви.
Справочник по размеру обуви поможет вам понять и правильно измерить размер стопы. Вы также можете скачать и использовать распечатанную таблицу размеров обуви, чтобы точно определить свой размер обуви.
Безвизовые страны
В зависимости от того, какой у вас паспорт, вы можете свободно посещать безвизовые страны без каких-либо дополнительных документов.
Посетить безвизовую страну проще , так что вам не нужно запрашивать разрешение перед поездкой.
Немецкий паспорт в настоящее время является наиболее приемлемым паспортом, а афганский паспорт — наименее принятым.
Расчет стоимости такси
Мы предпочитаем прозрачность, но индустрия такси всегда находит новые способы взимать более высокую плату со своих пассажиров.



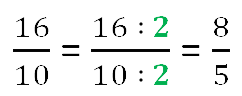



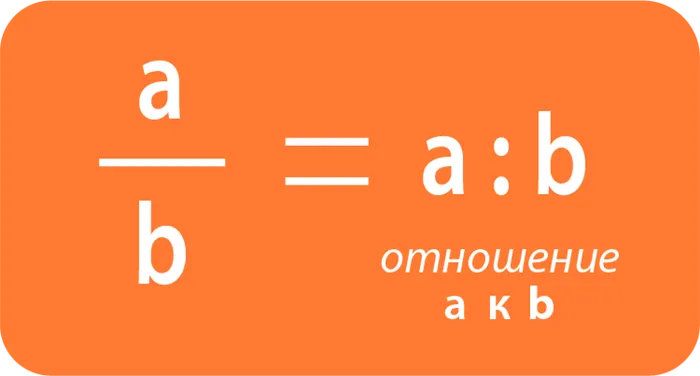




 com, чтобы узнать обо всех ваших потребностях в проекторах и экранах для всех соотношений сторон.
com, чтобы узнать обо всех ваших потребностях в проекторах и экранах для всех соотношений сторон.