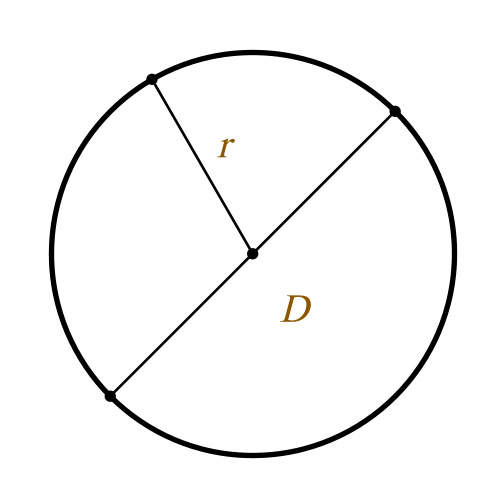
Как найти отношение длины окружности к длине диаметра
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности. В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для расчетов используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.

Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две точки, находящиеся на линии окружности. Линейкой измерьте длину получившегося отрезка. Допустим, диаметр окружности в данном случае будет равен 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности. Измерьте получившуюся длину нитки. Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см : 7 см = 3,1428…. Округлите полученное число до сотых (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись тем самым в этом свойстве окружности, открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или радиуса по формулам:С = 2*п*R или С = D*п, где С — длина окружности, D — длина ее диаметра, R — длина ее радиуса.Для нахождения площади круга (плоскости, ограниченной линиями окружности) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом. Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как относятся длины двух окружностей
Скачать
презентацию
Что обозначает греческая буква >>
Вопрос 4. Как относятся длины двух окружностей? Ответ. Отношение длин двух окружностей равно отношению их радиусов.
Слайд 9 из презентации «Как найти длину окружности» к урокам геометрии на тему «Окружность»
Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке геометрии, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Как найти длину окружности.ppt» можно в zip-архиве размером 133 КБ.
Окружность
«Длина окружности» — Древний Египет. С – длина окружности. Древний Рим. С=?d, C=2?r. Практическая работа «Измерение кофейных банок». D – диаметр окружности. Обозначения. R – радиус окружности. ?? 3,14. Эйлер. В Древнем Риме считали, что ?? 3,12. Великий ученый Древней Греции Архимед. Чем больше я знаю, Тем больше умею. В Древнем Египте считали, что ??3,16.
«Как найти длину окружности» — Теорема. Приближенное вычисление числа. Найдите длину окружности, описанной около квадрата. Три равные окружности. Найдите нижнюю и верхнюю оценки для числа. Как выражается периметр правильного n-угольника. Чему равна длина дуги окружности. Как изменится длина окружности. Как относятся периметры двух правильных n-угольников.
«Числовая окружность» — Макет 2: третьи части дуг четвертей. 3. Аналитическая запись дуги числовой окружности. Отметьте заданные точки на числовой окружности: Макет 1: середины дуг четвертей. 2. Движение по числовой окружности. 1. Числовая прямая. 4. Аналитическая запись дуги числовой окружности. ЛЕКЦИЯ с примерами. Числовая окружность.
«Окружность и круг» — Часть окружности называется дугой. Категория — высшая. Точку называют центром окружности. Круг. Тренировочные упражнения. МАТЕМАТИКА-5 Тематическое планирование Ход урока Автор Ресурсы. Любимое занятие-чтение. Дуга.
«Урок Касательная к окружности» — Актуализация опорных знаний. Т е м а: « окружность». Задача 1. Дано: окр.(О;ОМ), МР – касательная, угол КМР=45?. Решение задач. Обобщающий урок. Докажите, что прямая АС является касательной к данной окружности. Провести касательную к данной окружности. Сделать обозначения и записи. Вычислите длину ВС, если ОD=3см.
«Эллипс» — Касательная. Точки F1, F2 называются фокусами эллипса. Постройка эллипса. Оказывается, что все планеты движутся вокруг Солнца не по кругу, а по эллипсу. Кратеры на Луне также имеют форму эллипса. Общая точка называется точкой касания. Эллипс. Интересные факты. Пусть A – произвольная точка эллипса с фокусами F1, F2.
Две окружности на плоскости.
Общие касательные к двум окружностям
| Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Взаимное расположение двух окружностей
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости | ||
| Каждая из окружностей лежит вне другой | ||
| Внешнее касание двух окружностей | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
| Каждая из окружностей лежит вне другой | ||
| Внешнее касание двух окружностей | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
| Каждая из окружностей лежит вне другой | ||
|
Расстояние между центрами окружностей больше суммы их радиусов |
||
| Внешнее касание двух окружностей | ||
|
Расстояние между центрами окружностей равно сумме их радиусов |
||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
|
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой |
||
| Внутренняя касательная к двум окружностям | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
| Внешнее касание двух окружностей | ||
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
Формулы для длин общих касательных и общей хорды двух окружностей
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Длина общей хорды двух окружностей вычисляется по формуле
| Фигура | Рисунок | Формула |
| Внешняя касательная к двум окружностям | ||
| Внутренняя касательная к двум окружностям | ||
| Общая хорда двух пересекающихся окружностей |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
|
Длина общей хорды двух окружностей вычисляется по формуле Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Найдите отношение длин окружностей и площадей двух кругов, если диаметр одного из них составляет 1 / 3 радиуса второго?Математика | 5 — 9 классы Найдите отношение длин окружностей и площадей двух кругов, если диаметр одного из них составляет 1 / 3 радиуса второго. Помогите с объянениями и с понятными решениями дам 30 баллов. К. радиус равен 1 / 2 диаметра, то : Длина окружности равна C = 2πr. C1 = 2πR2•1 / 6 = πR2 / 3 C1 / C2 = (πR2 / 3) / 2πR2 = 1 / 6 Площадь круга равна S = πr². S1 = πR1² = π(1 / 6R2)² = πR2² / 36 S1 / S2 = (πR2² / 36) / πR² = 1 / 36. Ответ : 1 : 6 ; 1 : 36. Радиус окружности составляет одну вторую диаметра сколько радиусов содержится диаметр окружности?Радиус окружности составляет одну вторую диаметра сколько радиусов содержится диаметр окружности. Диаметр одного круга в два раза больше диаметра другого круга?Диаметр одного круга в два раза больше диаметра другого круга. Длина окружности ограничивающая второй круг 1. 2 м. Найди площадь первого круга. 40 баллов?Радиус окружности равен 2. Найдите ее диаметр, длину окружности и площадь круга ограниченного этой окружностью. 1. Площадь круга через радиус?1. Площадь круга через радиус. 2. Площадь круга через диаметр. 3. Длина окружности через радиус. 4. Длина окружности через диаметр. 5. Площадь прямоугольника. 1. Площадь круга через радиус?1. Площадь круга через радиус. 2. Площадь круга через диаметр. 3. Длина окружности через радиус. 4. Длина окружности через диаметр. 5. Площадь прямоугольника. Найдите Отношение длины окружности если радиус одного из них составляет одну третью диаметра второй?Найдите Отношение длины окружности если радиус одного из них составляет одну третью диаметра второй. Найдите отношение длинн окружностей и площадей 2 кругов если радиус 1 из них составляет 1 / 3 диаметра другого?Найдите отношение длинн окружностей и площадей 2 кругов если радиус 1 из них составляет 1 / 3 диаметра другого. Радиус одного круга равен 8см, а другого 6см?Радиус одного круга равен 8см, а другого 6см. Найдите отношение а) диаметров ; б) длин окружностей ; в) площадей малого и большого кругов. Найти отношение длин окружностей, если радиус одной из них составляет 1 / 5 диаметра второй?Найти отношение длин окружностей, если радиус одной из них составляет 1 / 5 диаметра второй. Помогите пожалуйста, надо решение с об’ яснением. Формула нахождения длины окружности и площади круга (через радиус и через диаметр)?Формула нахождения длины окружности и площади круга (через радиус и через диаметр). Вы перешли к вопросу Найдите отношение длин окружностей и площадей двух кругов, если диаметр одного из них составляет 1 / 3 радиуса второго?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей. Задание № 3 : Два пешехода должны выйти навстречу друг другу из двух пунктов, расстояние между которыми 20 км. Если первый выйдет на полчаса раньше второго, то он встретит второго пешехода через 2, 5 ч после своего выхода. Если второй выйдет на 1 ч.. 48 — 2, 2, 2, 2, 3 8 — 2, 2, 2 Нок 2 * 2 * 2 * 2 * 3 = 48. 48 = 2 * 2 * 2 * 2 * 3 48 = 2 * 2 * 2 * 2 * 3 8 = 2 * 2 * 2 НОК(48, 8, 48) = 2 * 2 * 2 * 2 * 3 = 48. 4000 * 8 : 100 = 320 грн — 8% 4000 + 320 = 4320 грн. Будет на счету Ответ : 4320 гривен будет на счету через год. Прости, но могу решить на русском 8% годовых, то есть через год будет 100 + 8 = 108% годовых 4000 грн = 100% х грн = 108% х = (108 * 4000) / 100 = 108 * 40 = 4320 грн. Нам нужно узнать расстояние между деревнями. Для этого мы умножаем скорость на время, то есть 40×330. Получаем 13200 метров расстояние между деревнями. А теперь чтобы вычислить скорость на обратном пути нужно 13200 : 30 = 440метров в минуту скорос.. 1) x — y + 3 = 0 y — = — x — 3 y = x + 3 2) x + y — 1 = 0 y = — x + 1 Точка пересечения графиков : x + 3 = — x + 1 2x = — 2 x = — 1 y = 1 + 1 = 2 ( — 1 ; 2) . 1) 0, 075 км / ч 2) 0, 00125 км / м 3) 125 м / м. Возьмем вес третьего куска железа за x тогда первый будет x + 2 2 / 3 , а второй x + 1. 5 получаем : x + x + 2 2 / 3 + x + 1. 5 = 4 2 / 3 x = 3. 5. источники: http://www.resolventa.ru/demo/him/demohim.htm http://matematika.my-dict.ru/q/7118072_najdite-otnosenie-dlin-okruznostej-i-plosadej/ |
Наружный диаметр полого вала с учетом основного напряжения
Идти
Внешний диаметр полого вала = ((16*(Изгибающий момент в полом валу+sqrt(Изгибающий момент в полом валу^2+Крутящий момент в полом валу^2))/(pi*Максимальное основное напряжение в полом валу*(1-Отношение внутреннего к внешнему диаметру полого вала^4))))^(1/3)
Соотношение диаметров с учетом главного напряжения
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(16*(Изгибающий момент в полом валу+sqrt(Изгибающий момент в полом валу^2+Крутящий момент в полом валу^2))/(pi*Внешний диаметр полого вала^3*Максимальное основное напряжение в полом валу)))^(1/4)
Главное напряжение — теория максимума главного напряжения
Идти
Максимальное основное напряжение в полом валу = 16*(Изгибающий момент в полом валу+sqrt(Изгибающий момент в полом валу^2+Крутящий момент в полом валу^2))/(pi*Внешний диаметр полого вала^3*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Соотношение диаметров с учетом угла поворота полого вала и жесткости на кручение
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(584*Крутящий момент в полом валу*Длина полого вала/(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*Угол поворота полого вала)))^(1/4)
Наружный диаметр полого вала с учетом угла крутильной жесткости
Идти
Внешний диаметр полого вала = (584*Крутящий момент в полом валу*Длина полого вала/(Модуль жесткости полого вала*Угол поворота полого вала*(1-Отношение внутреннего к внешнему диаметру полого вала^4)))^(1/4)
Длина вала при заданном угле закручивания полого вала на основе жесткости на кручение
Идти
Длина полого вала = Угол поворота полого вала*(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))/(584*Крутящий момент в полом валу)
Момент кручения при заданном угле кручения на основе жесткости на кручение
Идти
Крутящий момент в полом валу = Угол поворота полого вала*(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))/(584*Длина полого вала)
Модуль жесткости при заданном угле закручивания полого вала на основе жесткости на кручение
Идти
Модуль жесткости полого вала = 584*Крутящий момент в полом валу*Длина полого вала/(Угол поворота полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Угол поворота полого вала на основе жесткости на кручение
Идти
Угол поворота полого вала = 584*Крутящий момент в полом валу*Длина полого вала/(Модуль жесткости полого вала*(Внешний диаметр полого вала^4)*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Соотношение диаметров с учетом растягивающего напряжения в полом валу
Идти
Отношение внутреннего к внешнему диаметру полого вала = sqrt((1-(Осевая сила на полом валу/((pi/4)*Растягивающее напряжение в полом валу*Внешний диаметр полого вала^2))))
Отношение диаметра к заданному напряжению сдвига при кручении в полом валу
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(16*Крутящий момент в полом валу/(pi*(Внешний диаметр полого вала^3)*Напряжение сдвига при кручении в полом валу)))^(1/4)
Наружный диаметр вала с учетом напряжения сдвига при кручении
Идти
Внешний диаметр полого вала = (16*Крутящий момент в полом валу/(pi*Напряжение сдвига при кручении в полом валу*(1-Отношение внутреннего к внешнему диаметру полого вала^4)))^(1/3)
Напряжение сдвига при кручении, когда вал подвергается воздействию чистого крутящего момента
Идти
Напряжение сдвига при кручении в полом валу = 16*Крутящий момент в полом валу/(pi*(Внешний диаметр полого вала^3)*(1-(Отношение внутреннего к внешнему диаметру полого вала^4)))
Крутящий момент при напряжении сдвига в полом валу
Идти
Крутящий момент в полом валу = Напряжение сдвига при кручении в полом валу*(pi*Внешний диаметр полого вала^3*(1-Отношение внутреннего к внешнему диаметру полого вала^4))/16
Наружный диаметр полого вала с учетом напряжения изгиба полого вала
Идти
Внешний диаметр полого вала = (32*Изгибающий момент в полом валу/(pi*Напряжение изгиба в полом валу*(1-Отношение внутреннего к внешнему диаметру полого вала^4)))^(1/3)
Соотношение диаметров с учетом напряжения изгиба полого вала
Идти
Отношение внутреннего к внешнему диаметру полого вала = (1-(32*Изгибающий момент в полом валу/(pi*Внешний диаметр полого вала^3*Напряжение изгиба в полом валу)))^(1/4)
Изгибающий момент при изгибающем напряжении полого вала
Идти
Изгибающий момент в полом валу = Напряжение изгиба в полом валу*(pi*(Внешний диаметр полого вала^3)*(1-(Отношение внутреннего к внешнему диаметру полого вала^4)))/32
Напряжение изгиба полого вала
Идти
Напряжение изгиба в полом валу = 32*Изгибающий момент в полом валу/(pi*Внешний диаметр полого вала^3*(1-Отношение внутреннего к внешнему диаметру полого вала^4))
Осевая сила растяжения при заданном растягивающем напряжении в полом валу
Идти
Осевая сила на полом валу = Растягивающее напряжение в полом валу*((pi/4)*(Внешний диаметр полого вала^2-Внутренний диаметр полого вала^2))
Растягивающее напряжение в полом валу под действием осевой силы
Идти
Растягивающее напряжение в полом валу = Осевая сила на полом валу/((pi/4)*(Внешний диаметр полого вала^2-Внутренний диаметр полого вала^2))
Внутренний диаметр полого вала при заданном соотношении диаметров
Идти
Внутренний диаметр полого вала = Отношение внутреннего к внешнему диаметру полого вала*Внешний диаметр полого вала
Наружный диаметр при заданном соотношении диаметров
Идти
Внешний диаметр полого вала = Внутренний диаметр полого вала/Отношение внутреннего к внешнему диаметру полого вала
Отношение внутреннего диаметра к внешнему диаметру
Идти
Отношение внутреннего к внешнему диаметру полого вала = Внутренний диаметр полого вала/Внешний диаметр полого вала
Длина окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
L = πD = 2πr
r – радиус окружности
D – диаметр окружности
L – длина окружности
π – 3.14
Пример нахождения длинны окружности
Задача:
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = πD = 2πr
где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Как найти отношение длины окружности к длине диаметра
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности. В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для расчетов используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две точки, находящиеся на линии окружности. Линейкой измерьте длину получившегося отрезка. Допустим, диаметр окружности в данном случае будет равен 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности. Измерьте получившуюся длину нитки. Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см : 7 см = 3,1428…. Округлите полученное число до сотых (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись тем самым в этом свойстве окружности, открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или радиуса по формулам:С = 2*п*R или С = D*п, где С — длина окружности, D — длина ее диаметра, R — длина ее радиуса.Для нахождения площади круга (плоскости, ограниченной линиями окружности) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.