Евгений Смирнов
«Квантик» №1, 2017
Возьмём обычный лист белой бумаги — того формата, который подходит для большинства принтеров и называется А4. На пачке бумаги (или в Википедии, или в настройках принтера) написано, что этот лист имеет длину 297 миллиметров, а ширину — 210. Откуда взялись такие странные числа? И откуда в названии формата четвёрка?
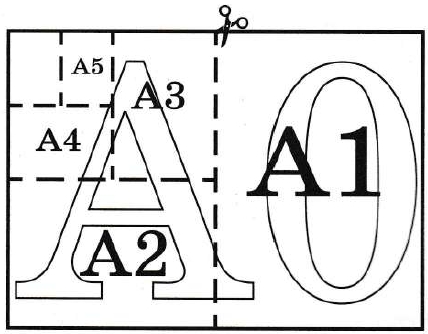
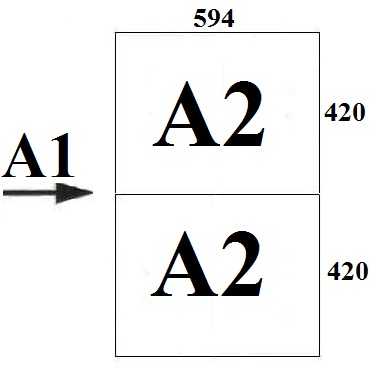
Давайте разберёмся во всём этом по порядку. Оказывается, бывают и другие форматы бумаги, в названии которых есть буква А, — от А0 до А6. Лист каждого следующего формата получается как половина листа предыдущего формата. Например, лист А5 получается, если сложить лист А4 пополам. И наоборот, если склеить два листа А4 вдоль длинной стороны, получится лист А3 (некоторые большие принтеры умеют печатать на таких листах). Если приложить друг к другу два листа А3, мы получим лист А2 — на бумаге такого формата обычно печатаются газеты. Из двух листов А2 получается лист А1, а из двух листов А1 — лист А0. Может быть, вам доводилось видеть плотную чертёжную бумагу — так называемые ватманские листы; они как раз имеют формат А0, и тем самым каждый такой лист можно разрезать на 16 листов формата А4, разделив его по вертикали и горизонтали на 4 равные части.
У всех этих листов есть одно замечательное свойство: они представляют собой подобные прямоугольники. Иными словами, отношение длины к ширине у каждого из этих листов одно и то же. За счёт этого две страницы формата А4 можно уместить на одну, уменьшив длину и ширину в одно и то же число раз и переведя исходные страницы в формат А5 (в настройках большинства принтеров можно указать опцию «печатать две страницы на одной». Это бывает очень удобно, если вам нужно распечатать большой текст и хочется сэкономить бумагу или чернила). Отсюда можно найти отношение сторон, если написать простую пропорцию:
длина А4
ширина А4
=
длина А5
ширина А5
и при этом помнить, что длина листа А5 такая же, как ширина у А4, а ширина А5 равна половине длины А4.
Отсюда получается, что
длина А4
2
ширина А4
2
=
2
,
то есть отношение сторон листа А4 (а значит, и листов всех остальных форматов от А0 до А6) должно равняться корню из двух — примерно 1,414213562…
Корень из двух — число иррациональное, то есть не равное отношению никаких двух целых чисел. А для технологических целей длины сторон у листов бумаги хочется всё-таки выражать целым числом миллиметров. Поэтому в качестве формата принято отношение 297/210, что равно 99/70 = 1,4142857… Как мы видим, эта дробь очень близка к
2
— эти числа расходятся только в пятом знаке после запятой и различаются лишь на пять тысячных процента!
Итак, с отношением сторон мы разобрались. Но почему же ширина листа равна именно 210 миллиметрам, а, скажем, не 200 и не 220? Оказывается, что длины сторон были выбраны именно такими для того, чтобы лист формата А0 (самый большой в этой серии форматов) имел площадь, равную одному квадратному метру. Согласно международному стандарту ISO 216, длина и ширина листа А0 равна 1189 мм и 841 мм соответственно. В квадратном метре миллион квадратных миллиметров, а произведение 841 и 1189 даёт 999 949, что очень близко к миллиону.
Соотношение длины и ширины бумажного листа, равное корню из двух, было предложено ещё в 1786 году немецким учёным Георгом Кристофом Лихтенбергом и стало впервые применяться во Франции в конце XVIII века. Сейчас оно распространено по всему миру, кроме США и Канады, где принято использовать бумагу так называемого формата Letter, с соотношением сторон 8,5×11 дюймов — примерно 216×279 мм. Такой лист немножко шире и короче привычного нам листа А4. Но откуда взялось именно такое соотношение, автору неизвестно…
Художник Артём Костюкевич
Приложения: мир вокруг нас
Математика: подобие, квадратный корень, иррациональные числа
Каким должно быть отношение сторон прямоугольного листа бумаги, чтобы у половины этого листа было такое же отношение сторон?
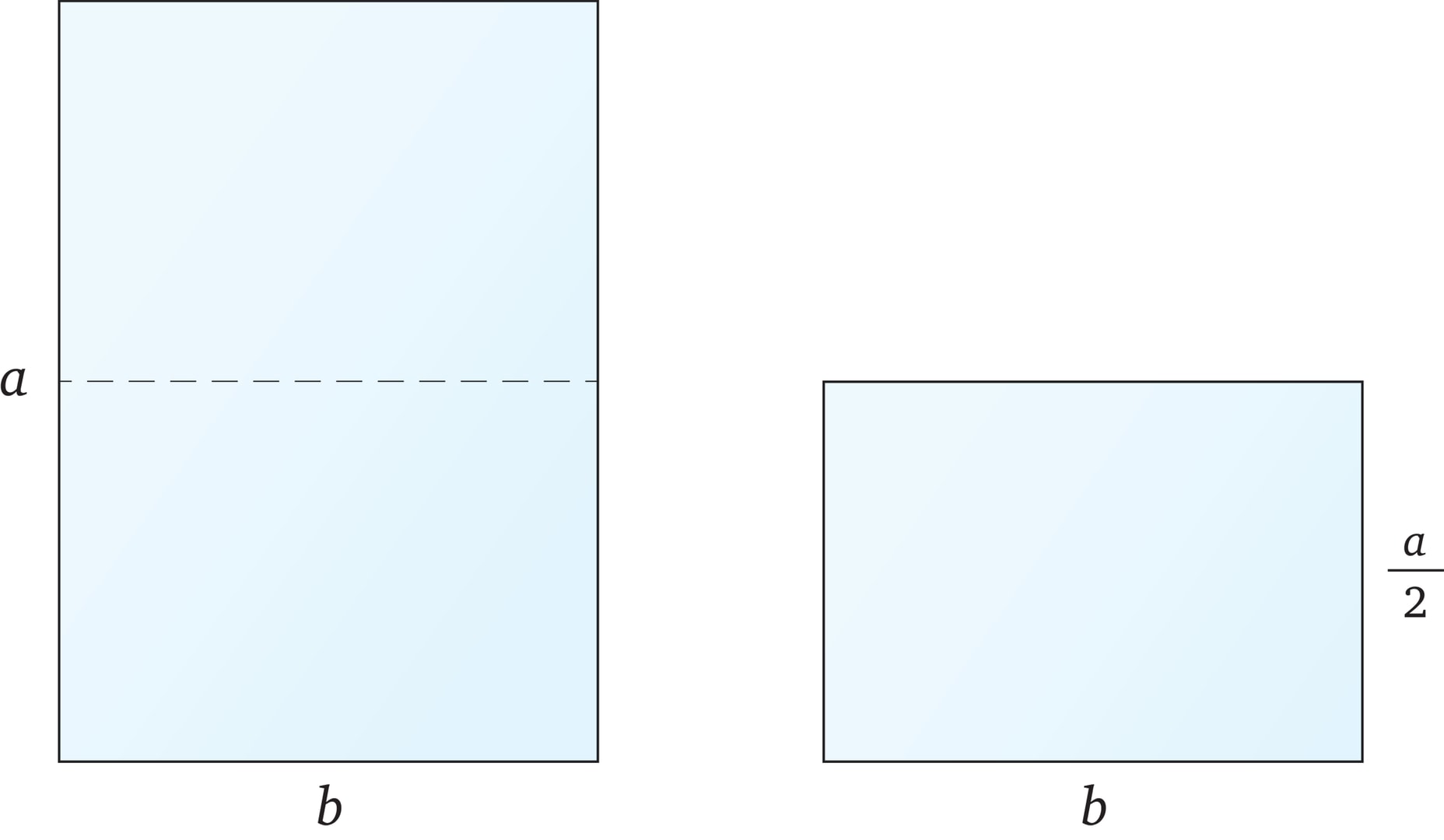
Представим сформулированное условие в виде формулы:
$$ frac{a}{b}=frac{b}{a/2}. $$
Отсюда находим отношение сторон:
$$ frac{a}{b}=sqrt{2}.$$
У листа с таким отношением сторон имеется свойство, ценное и в делопроизводстве, и в полиграфии: сложив его пополам, мы получим лист с теми же пропорциями и, значит, также удовлетворяющий сформулированному требованию. С точки зрения геометрии, всё дело в том, что исходный прямоугольник и его половина подобны. А если листы подобны, то макет страницы, разработанный для одного из них, можно перенести на второй простым масштабированием.
Стандарты на бумажные форматы, удовлетворяющие сформулированному требованию, были введены в 20‐х годах XX века. Применяются серии «А», «B», «С», каждая состоит из последовательности уменьшающихся листов. Выбор самого большого листа в серии («базового», получающего нулевой индекс), связан с той или иной нормировкой. В каждой серии лист с номером $n+1$ выглядит как сложенный вдвое лист с номером $n$.
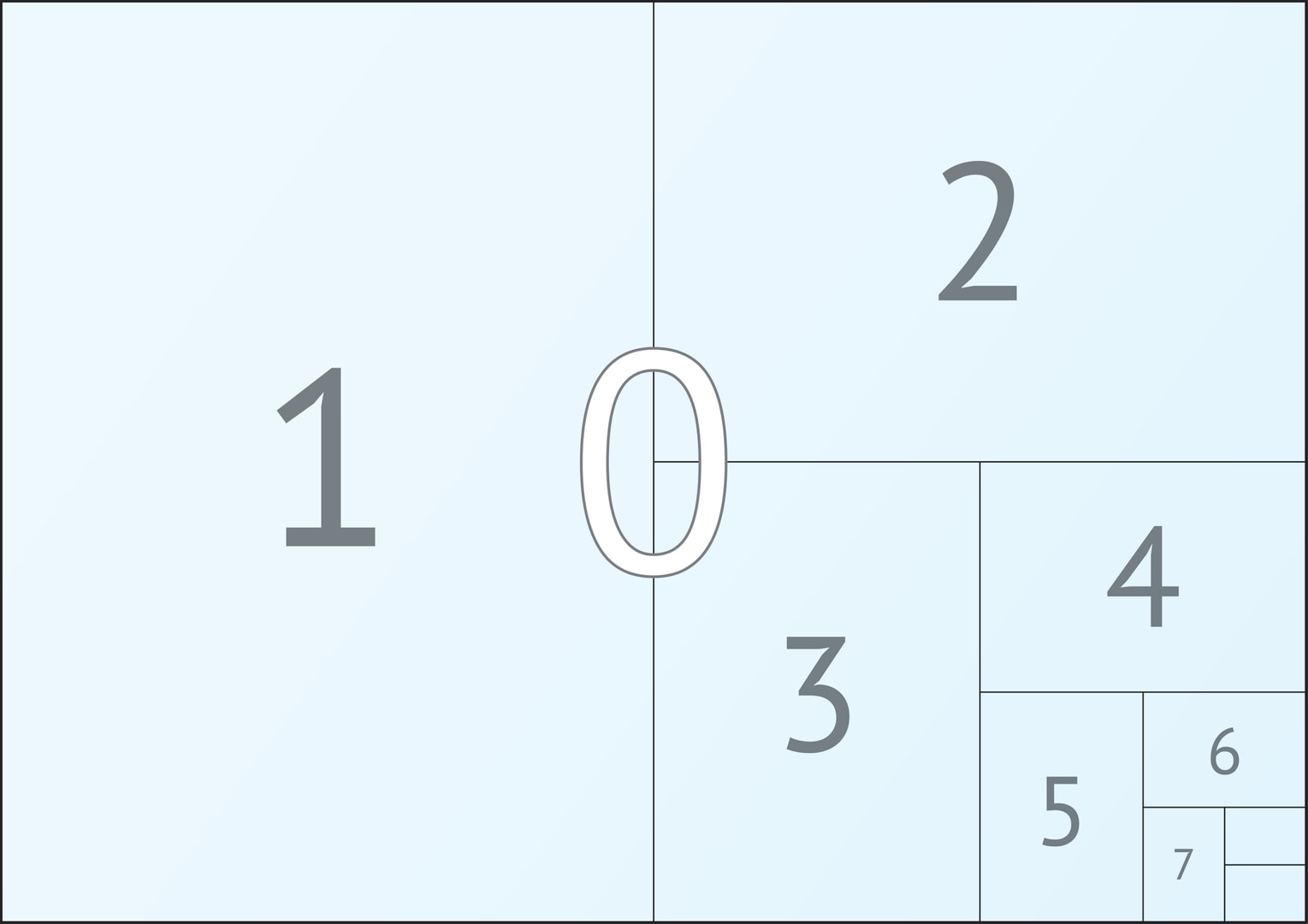
Число $sqrt{2}$, которое теоретически определяет отношение сторон прямоугольных листов всех номеров во всех сериях, является иррациональным. Это означает, что число $sqrt{2}$ нельзя представить в виде отношения двух целых чисел, соответствующая ему десятичная дробь — бесконечная непериодическая
$$ sqrt{2}=1,414213562373…$$
На практике приходится использовать рациональные числа. В выборе форматов серий «А», «B», «С» длины сторон листов выражаются целыми числами (в миллиметрах), эти числа подобраны так, чтобы их отношение было близким к $sqrt{2}$.
В серии «А» в качестве листа А0 взят лист, имеющий размеры $1189times 841$ мм. Размеры листа выбраны так, что его площадь (с большой точностью) равна одному квадратному метру. В повседневной жизни наиболее часто встречается формат бумаги A4. Длины сторон листа равны 297 и 210 мм, это примерно одна четвёртая часть длин сторон листа A0, площадь листа A4 — примерно 1/16 квадратного метра. При плотности стандартной офисной бумаги 80 грамм на квадратный метр, один лист весит около 5 грамм, а пачка из 500 листов — $2,5$ килограмма.
В серии «B» лист B0 выбран так, что длина его меньшей стороны равна 1 метру. Чтобы отношение сторон было близко к $sqrt{2}$, в качестве большей стороны листа принято значение $1,414$ м. Область применения серии «B» — специальные разделы делопроизводства. Например, паспорт гражданина Российской Федерации имеет формат B7 — $125times 88$ мм, что соответствует рекомендациям, содержащимся в международном стандарте.
Разворот книги
Дополнения, комментарии
Знание отношения сторон в формате А и десятичной записи числа $sqrt{2}$ облегчает выполнение стандартных офисных операций. Например, как на копировальном аппарате перевести лист А4 в лист А3? Коэффициент подобия этих листов равен $sqrt{2}$, для решения задачи копирования можно взять приближённое значение $sqrt{2}≈ 1{,}4$ и выставить на ксероксе коэффициент увеличения, равный 140%. А если надо «превратить» лист А4 в лист A5, то коэффициент уменьшения будет равен $frac{1}{sqrt{2}}$. Замечательно, что его «рабочее» значение легко найти и без технических средств: $frac{1}{sqrt{2}}=frac{sqrt{2}}{2}≈ 0{,}7$. Значит, на ксероксе нужно выставить показатель 70%.
Среди форматов серий «A», «B» и «C» первый — самый «правильный» с точки зрения приближения ключевого числа $sqrt{2}$ рациональными дробями.
Цепная дробь (см. статью «Високосное летосчисление», и список литературы к сюжету) числа $sqrt{2}$ бесконечна, её элементы — двойки:
$$ sqrt{2}=1+ frac1{2+frac1{2+frac1{2+frac1{2+frac1{2+vphantom{frac12} dotsm }}}}}. $$
Приведём первые подходящие дроби разложения:
$$ displaylines{ 1,quad 1+frac{1}{2}=frac{3}{2},quad 1+frac1{2+frac1{2}}=frac{7}{5},quad 1+frac1{2+frac1{2+frac1{2}}}=frac{17}{12},cr 1+frac1{2+frac1{2+frac1{2+frac1{2}}}}=frac{41}{29},quad 1+frac1{2+frac1{2+frac1{2+frac1{2+frac1{2}}}}}=frac{99}{70}.cr} $$
Значение $frac{41}{29}=1{,}41379…$ — неплохое рациональное приближение числа $sqrt{2}=1{,}41421…$, оно фактически определяет базовый лист А0: его размеры $1189times 841$ мм соответствуют пропорции $frac{41}{29}=frac{1189}{841}$.
Производные размеры листов серии «A» получаются последовательно делением большей стороны пополам: $841times 594$ мм (А1), $594times 420$ мм (А2), $420times 297$ мм (А3), $297times 210$ мм (А4). Видно, что «основой» форматов А2 и А4 является лучшее приближение числа $sqrt{2}$, чем у А0: $frac{99}{70}=frac{594}{420}=frac{297}{210}$, дробь $frac{99}{70}=1{,}41428…$ отличается от $sqrt{2}$ только в пятом знаке после запятой в десятичном разложении.
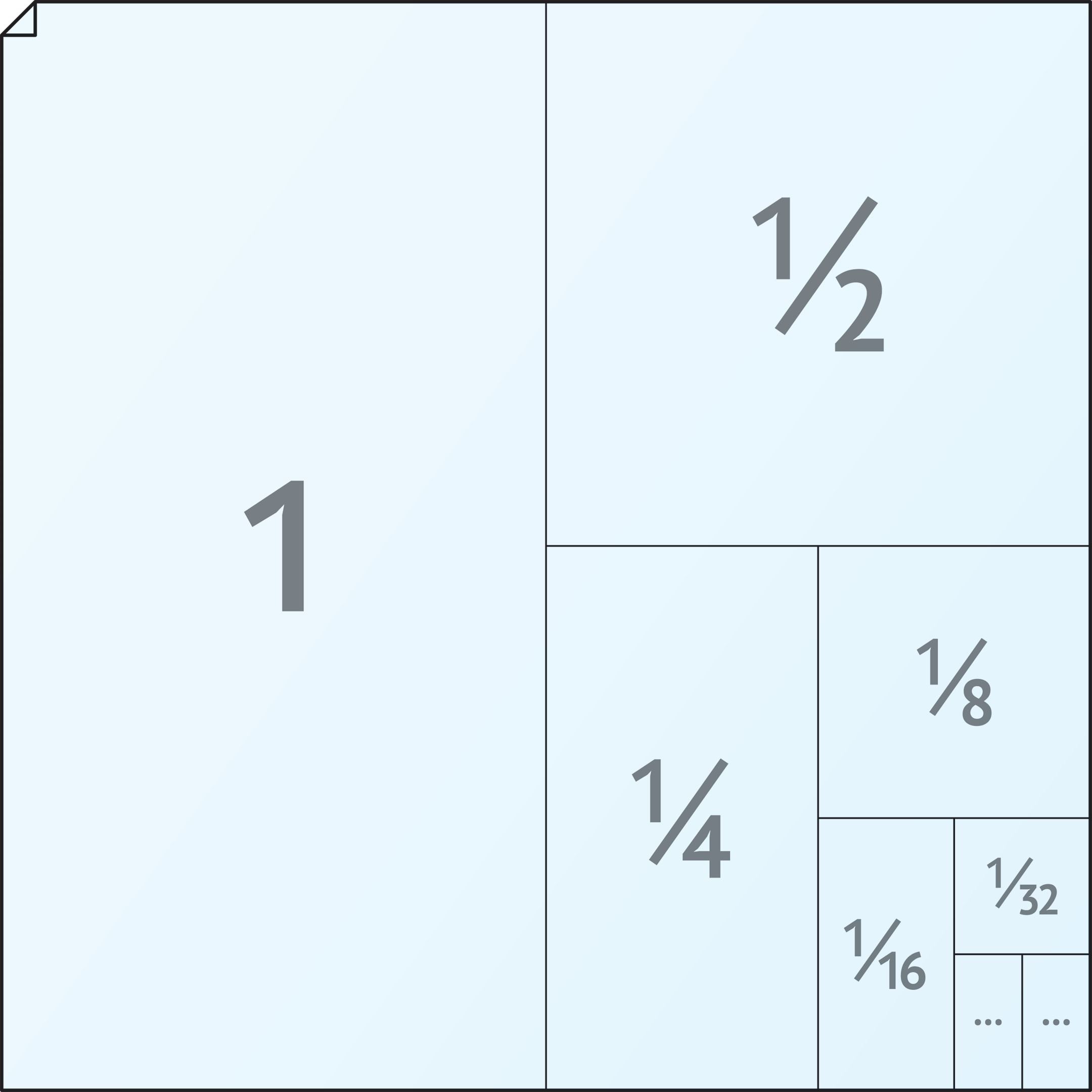
Рисунок, на котором были представлены форматы, можно использовать и для геометрической иллюстрации того, почему сумма бесконечной геометрической прогрессии (см. «Практическая бесконечность»)
$$ 1+frac{1}{2}+frac{1}{2^2}+frac{1}{2^3}+frac{1}{2^4}+frac{1}{2^5}+… $$
равна 2. Пропорции листа в этом случае роли не играют.
Чтобы вопрос опубликовался, войди или зарегистрируйся
Восстановление пароля
Мы отправили письмо со ссылкой на смену пароля на username@mail.ru.
Если письма нет, проверь папку «Спам».
Чтобы вопрос опубликовался, войди или зарегистрируйся
Нужна регистрация на Учи.ру
«Ваш урок» теперь называется Учи.Ответы. Чтобы зайти на сайт, используй логин и пароль от Учи.ру. Если у тебя их нет, зарегистрируйся на платформе.
Версия для печати и копирования в MS Word
Найдите отношение длины диагонали листа формата А2 к его меньшей стороне. Ответ округлите до десятых.
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
Спрятать решение
Решение.
Меньшая сторона формата А2 совпадает с большей стороной формата А3 — они равны 420 мм, большую сторону формата А2 можно найти, умножив меньшую сторону формата А3 на 2: Диагональ является гипотенузой треугольника с катетами 420 мм и 594 мм, по теореме Пифагора имеем:
мм.
Найдем отношения длины диагонали к меньшей стороне:
Ответ: 1,7.
Приведем другое решение.
Заметим, что для всех форматов отношение большей стороны к меньшей составляет (см. примечание к задаче 408294). Пусть меньшая сторона равна 1, тогда большая сторона равна
а диагональ равна
Отношение диагонали к меньшей стороне составит
1
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.
| Номер листа | Длина (мм) | Ширина (мм) |
|---|---|---|
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
2
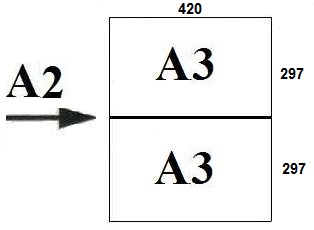
Сколько листов формата А3 получится из одного листа формата А2?
3
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
4
Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.
5
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Площадь листа формата А0 равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата А1. Если лист А1 разрезать пополам, получаются два листа формата А2 и так далее.
Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится). На практике размеры листа округляются до целого числа миллиметров.
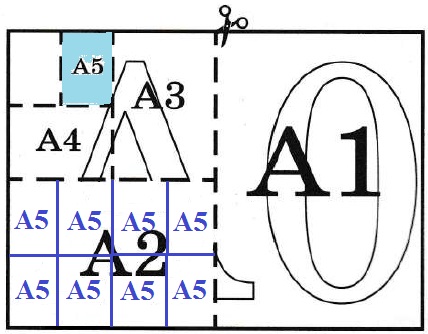
В таблице 1 даны размеры листов бумаги четырёх форматов: от А3 до А6.
Источник: ОГЭ Ященко 2022 (36 вар)
Задание 1
Для листов бумаги форматов А6, А5, А4 и А3 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
Решение
Чем больше число стоит у буквы А, тем формат бумаги меньше по размеру, т.к. его больше раз разрезали.
Формат А6 – самый маленький, А3 – самый большой. Выбираем из Таблицы 1, размеры по возрастанию:
Ответ: 3142.
Задание 2
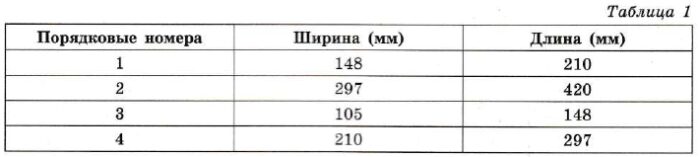
Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А2?
Решение
Порежем лист формата А2 на листы формата А5:
Получаем 8 лисов А5.
Ответ: 8.
Задание 3
Найдите длину меньшей стороны листа бумаги формата А1. Ответ дайте в миллиметрах.
Решение
Из таблицы 1, знаем размер А3, а лист А2 это два листа А3, соединённых большей стороной:
Тогда у А2 стороны 420 и 297 + 297 = 594.
Лист А1 это два листа А2, соединённых большей стороной:
Тогда у А1 стороны 594 и 420 + 420 = 840.
Меньшая из них равна 594.
Ответ: 594.
Задание 4
Найдите площадь листа бумаги формата А6. Ответ дайте в квадратных сантиметрах.
Решение
Из таблицы 1, знаем размеры листа А6:
Ширина = 105 мм
Длина = 148 мм
Площадь листа равна:
105·148 = 15540 мм2
Переведём в см2:
1 см = 10 мм
1см2 = 10·10 = 100 мм2
15540/100 = 155,4 см2
Ответ: 155,4.
Задание 5
Найдите отношение длины меньшей стороны листа к большей у бумаги формата А2. Ответ дайте с точностью до десятых.
Решение:
Из задания №3 знаем размеры листа А2:
Ширина = 420 мм
Длина = 594 мм
Найдём отношение меньшей стороны к большей, округлив до десятых:
frac{420}{594}=frac{70}{99}≈0,70…≈0,7
Ответ: 0,7.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 80
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.