Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Отношение чисел
Поддержать сайт
Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.
Если вам знакомо понятие отношение чисел, можете смело переходить к теме
пропорции.
Что называют отношением двух чисел
Запомните!
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Покажем на примере, где используется понятие отношение двух чисел.
В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15.
В этом году — 75. Во сколько раз увеличилось количество участников в этом году по
сравнению с предыдущим годом?
Прежде чем решать задачу, подчёркиваем важные данные.
Запишем отношение количества участников в этом году к количеству участников в предыдущем.
Запомните!
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».
Запомните!
Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.
При внимательном изучении правила выше, можно подметить, что правило записанное выше,
есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.
Отношение 16 к 10:
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 апреля 2023 в 20:44
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
Просмотров 1.4к. Опубликовано 30.09.2022
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Отношения
Мы знаем это, чтобы ответить на вопрос, насколько часто одно число больше (или меньше) другого, или насколько одно число является дробью другого. найти частное данных чисел.
Частное двух чисел не равный нулю, называется отношением чисел , или отношением числа .
Где — члены отношения число перед термином отношенияследующий срок отношения.
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
количество
1,15 : 0,36 — отношение от числа 1,15 до числа 0,36.
Отношение двух чисел Показывает, как часто одно число больше другого или как сильно одно число зависит от другого. Это отношение чисел указывает, сколько раз число или сколько частей числа .
Помните, что деление можно заменить дробью, поэтому, отношение чисел можно записать двумя способами: и
Основное свойство отношения:
Отношение не меняется, когда его члены умножаются или делятся на одно и то же число, которое не равно нулю.
Запишем отношение от 3 до 10 и найти его значение:
То есть отношение двух чисел Он может быть выражен в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, какой процент число составляет от другого числа.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и добавить знак процента к результату.
Пример:
В каком проценте число 5 равно числу 10?
5 10 2 1 — 100 % = 1 2 — 100 % = 100 2 % = 50 % .
Ответ: 50% равно 5 умножить на 10.
Если значение двух величин выражено в одних и тех же единицах, то. их отношение называют также отношением. Если две величины выражены в разных единицах, то отношения эти величины должны быть сначала переведены в одну и ту же единицу измерения.
Например:
Дан прямоугольник длиной 12 см и шириной 1 м. Найти отношение длины сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 12 : 100 = 100.
Отношение ширины прямоугольника к его длине равно 100 : 12 =
Дробь взаимно обратная, поэтому и отношения 12 к 100 и 100 к 12 называются взаимно обратными.
На практике отношение Обратные дроби используются, например, при составлении чертежей и географических карт. В этом случае земельные участки рисуются на бумаге в уменьшенном виде, а на карте или картографии изображаются отношение, указывает, как часто длина отрезка на чертеже меньше длины соответствующего отрезка на местности.
Соотношение между длиной отрезка на карте и длиной соответствующего отрезка на местности называется масштабом карты (чертежа).
Предположим, что карта имеет масштаб
Давайте выясним, какова длина отрезка в 5 см на карте на земле.
Для решения обозначим длину отрезка на земле (в сантиметрах). Затем отношение длина отрезка на карте к длине отрезка на местности составляет: 5 :, данная отношение равна масштабу карты, что дает уравнение:
5 :
Решите это уравнение:
10 000;
50 000 см = 500 м = 0,5 км.
Ответ: Отрезок в 5 см на карте равен 0,5 км на местности.
Давайте выясним, какая длина на карте соответствует отрезку 9,5 км на карте.
Для решения обозначьте длину участка на карте (в километрах). Затем отношение длина отрезка на карте с длиной отрезка на местности: : 9,5, данная отношение равна масштабу карты, что дает уравнение:
Решите это уравнение:
0,00095 км = 0,95 м = 95 см.
Ответ: Отрезок 9,5 км на карте равен 95 см на карте.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Отношение чисел
Отношение чисел — это коэффициент от деления одного числа на другое.
Отношение чисел A и b можно записать двумя способами: со знаком деления или через косую черту (как дробь):
Эти признаки следующие: отношение a к b или отношение числа a к числу b.
Числа a и b, составляющие отношение a : b становятся терминами отношения. Делителем является предыдущий член отношения, а делитель — предпоследний член. отношения. Таким образом, a — предыдущий член, b — следующий.
Соотношение используется для сравнения двух чисел. Так, отношение a : b показывает, во сколько раз a больше b (если делитель больше делимого) или сколько процентов от числа b составляет a (если делитель меньше делимого).
Отношение 35 к 7 показывает, что число 35 в пять раз больше числа 7.
2)
Отношение 12 к 15 показывает, что число 12 в 0,8 раза больше числа 15.
Из основного свойства квоты следует, что. отношения :
Отношение не меняется, когда его члены умножаются или делятся на одно и то же ненулевое число.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Помните.
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Давайте на примере покажем, в чем суть концепции. отношение двух чисел.
В городе Липецке проходят соревнования по велоспорту. В прошлом году было 15 участников, в этом году — 75. На сколько больше участников в этом году, чем в прошлом?
Прежде чем решить проблему, давайте остановимся на самых важных фактах. Запишите отношение количество участников в этом году с количеством участников в прошлом году.
Помните.
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Помните.
Если вы умножите или разделите оба термина отношения на одно и то же число, которое не равно нулю, вы получите отношение, равное данному.
Если вы внимательно изучите приведенное выше правило, то обнаружите, что написанное выше правило — это не что иное, как основное свойство дробей, с помощью которого мы можем легко их сокращать.
Основное свойство коэффициента заключается в том, что он остается неизменным при умножении или делении делителя и делимого на одно и то же число.
Задания для самостоятельной работы
На пост президента претендовали два кандидата. Явка составила 120 человек. Распределение голосов соответствует соотношению 3:5. Необходимо определить количество голосов, полученных победителем.
Соотношение между количеством хвойных и лиственных деревьев в лесу можно представить как 1:4. Необходимо рассчитать долю лиственных деревьев.
На площади 24 га выращиваются сельскохозяйственные культуры. Зерновые и овощи распределяются в соответствии с с отношением 5:3. Необходимо рассчитать площадь возделывания овощных культур в гектарах.
Основное свойство отношения: Путем умножения или деления членов отношения на одно и то же число, отличное от нуля, данный отношение останется неизменным.
Отношения в задачах
Теперь давайте узнаем, как отношения в задачах.
Давайте сразу перейдем к примерам, чтобы увидеть, какой может быть формулировка отношения.
Проблема 1
Протяженность дороги составляет 25 километров. Он освещен на протяжении 15 километров.
(α) Найдите, какая часть дороги освещена.
(b) Во сколько раз вся проезжая часть длиннее освещенной части?
Решение:
В начале урока мы обнаружили отношение меньшего числа в большее, определяя тем самым, какая часть первого числа содержится во втором.
Это первый вопрос.
Для нахождения отношения Отношение длины освещенного участка к длине всей дороги делится на единицу:
Значит, длина освещенного участка составляет (mathbf>) по всей длине дороги.
Второй вопрос: «Во сколько раз больше?». — соответствует отношению от большего числа к меньшему.
Чтобы найти это отношения это разделить длину всей дороги на длину освещенной части дороги:
Это отвечает на вопрос второго пункта.
Важно также всегда следить за тем, чтобы количество было одинаковым.
Так, если что-то дано нам в тоннах и килограммах, и мы хотим найти отношения Чтобы узнать эти количества, мы должны либо перевести тонны в килограммы, либо наоборот.
Проблема 2
Масса груза составляет 2 тонны. Известно, что часть груза — это одежда, масса которой составляет 350 кг.
Определите, сколько процентов от массы груза составляет масса одежды.
Решение:
Давайте сначала переведем тонны в килограммы. Оказывается, что масса груза составляет 2000 кг.
Теперь давайте найдем неизвестное. отношение:
Теперь попробуйте решить задачу самостоятельно и воспользуйтесь подсказками, если у вас возникнут трудности.
Вы можете пройти тест и получить результат после того, как войдете в систему или зарегистрируетесь.
Интересная информация
Сегодня вы научитесь математическим фокусам!
Их идея заключается в том, что можно запутать людей с помощью математических преобразований, которые дают нам то, что нам нужно.
Уловка 1.
Попросите зрителя придумать число и никому его не называть.
Теперь попросите их умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть число в уме.
Теперь вы можете с уверенностью сказать, что зритель получил число 4.
Это происходит потому, что при преобразовании исходное число удаляется из арифметической цепочки, оставляя только четверку.
Попробуйте доказать это с помощью формул, вычитая исходное число X
Уловка 2
В этой игре вы можете угадать день рождения человека.
Попросите зрителя умножить количество дней рождения на 2. Затем попросите его прибавить к результату 5 и умножить целое число на 50. Затем попросите зрителя добавить номер месяца, в котором он родился (1 января, 2 февраля и т.д.).
Чтобы узнать день рождения человека по полученному числу, вычтите 250 из числа, указанного зрителем — вы получите трех- или четырехзначное число, где первые одна или две цифры обозначают день рождения, а последние две цифры — месяц.
Основные правила математики с примерами. 6 класс. Часть 2.
Содержание
Начало: Основные правила математики с примерами. 6 класс. Часть 1.
- Умножение. Свойства умножения
- Умножение обыкновенных дробей
- Умножение рациональных чисел
- Деление обыкновенных дробей
- Деление рациональных чисел
- Нахождение дроби от числа
- Нахождение числа по его дроби
- Степень числа
- Числовые и буквенные выражения
- Приведение подобных слагаемых
- Раскрытие скобок
- Свойства уравнений
- Отношения
- Пропорции
- Основное свойство пропорции
- Процентное отношение двух чисел
- Прямая и обратная пропорциональная зависимость
Умножение. Свойства умножения
Произведением числа на натуральное число
не равное 1, называют сумму, состоящую из
слагаемых, каждое из которых равно а:
a · b = a +a +a+…+a⏟b
4· 5 =4 + 4 + 4 + 4 + 4⏟5
Если один из двух множителей равен 1, то произведение равно второму множителю:
m · 1 = 1 · m = m
5 · 1 = 5;1 · 5 = 5.
Если один из множителей равен нулю, то произведение равно нулю:
5 · 0 = 0;0 · 5 = 0.
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
!Важное правило. Помогает решать уравнения
(x — a)(x — b) = 0;Или x — a = 0 ,или x—b = 0;2 корня x=a и x = b.(x — 5)(x + 2) = 0;Или x — 5 = 0 ,или x+ 2 = 0;2 корня x=5 и x = —2.
Умножение обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:
ab·n=a·nb
27 · 3= 2 · 37 = 67
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
ab · cd = a · cb · d
27 · 45 = 2 · 47 · 5 = 835
Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
113 · 235 = 43 · 135 = 5215 = 3715
Умножение рациональных чисел
Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».
—5⏞—5=5 · 15 ⏞15=15= —(5 · 15) = —75.
Чтобы умножить два отрицательных числа, надо умножить их модули.
—8⏞—8=8 · (—5) ⏞—5=5= 8 · 5 = 40.
Для любого рационального числа :
a · (—1) = —a
12 · (—1) = —12;
Если произведение •
— положительное, то числа
и
имеют одинаковые знаки;
a = 3 и b = 2;a · b = 3 · 2 = 6 >0.а =—3 и b = —2;a · b = —3 · (—2) = 6 >0
Если произведение •
— отрицательное, то числа
и
имеют разные знаки.
a = 3 и b = —2;a · b = 3 · (—2) =—6 < 0.а =—3 и b = 2;a · b = —3 · 2 = 6 < 0
Деление обыкновенных дробей
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
ab : cd = ab · dc
23 : 57 = 23 · 75 = 1415
Деление рациональных чисел
Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
—15⏞—15=15 · 5 ⏞5=5= —(15 : 5) = —3
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.
—18⏞—18=18 : (—3) ⏞—3=3= 18 : 3 = 6
Нахождение дроби от числа
Чтобы найти дробь от числа, можно число умножить на эту дробь.
Найти 0,7 от числа 20:0,7 · 20 = 14.Найти 37 от числа 70:37 · 70 = 30
Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.
Найти 15% от числа 200:15% = 15100;15100 · 200 = 30
Нахождение числа по его дроби
Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.
Найти число, если известно, что
его дробь 57 составляет число 15:15 : 57 = 15 · 75 = 153 · 751 = 21
Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
Найти число, если известно, что
24% этого числа равны 48.24% = 24100;48 : 24100 = 48 · 10024 = 482 · 100241 = 200
Степень числа
Степенью числа с натуральным показателем
, большим
, называют произведение
множителей, каждый из которых равен
:
an=a · a · a ·…·a⏟n
Число при этом называют основанием степени.
54 = 5 · 5 · 5 · 5;5 — основание; 4 — показатель степени
Степенью числа с показателем
называют само число
a1=a
71 = 7
Вторую степень числа называют также квадратом числа. Например, запись читают: «
в квадрате».
Третью степень называют кубом числа, а запись читают: «
в кубе».
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.
Найти значение выражения
5 · 23 +15
5 ·2 231 +315 = 5 · 8 + 15 = 40 + 15 =55
Числовые и буквенные выражения
Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.
2 + 3 · 5 — 7;15 : 5
Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.
2x — 3y + 6;6x
Приведение подобных слагаемых
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
2x + 3x — 11x = (2 + 3 — 11)x =—6x
Раскрытие скобок
Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
16 — (3x + 6 —15y —21) = 16 —3x — 6 + 15y + 21
Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.
22 + (3x — 10 —25y) = 22 + 3x — 10 —25y
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
2x + 5 = 17 | —52x + 5 —5 = 17 —52x = 12x = 12 : 2x = 6
- Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
0·x = 20 —не имеет корней.0·x = 20 | +50 ·x +5 = 20 +50·x∥0 +5 =255 = 25 — неверно, корней нет.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
—2x — 5 = 9x←—9x→+5 +50—2x —9x = 50 +5—11x = 55x = 55 : (—11)x =—5.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
x2 + 34 = 6 | ×44 · (x2 + 34) = 4 · 64 · x2 + 4 · 34 = 242x + 3 = 242x = 24 — 32x = 21x = 21 : 2x =10,5
Отношения
a : b = ab частное или отношение чисел а и b.a = 5 и b =7:57 частное (отношение) чисел 5 и7
показывает, что число 10 в 5 раз больше числа 2 или число 2 в 5 раз меньше числа 10.
- Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
2436 — отношение.24 : 1236 : 12 = 23
Пропорции
Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:
a : b =c : d или ab = cd
Числа и
называют крайними членами пропорции, а числа
и
— средними членами пропорции.
Пропорци x : 5 = 8 : 17 или другая записьx5 = 817;x и 17 — крайние члены пропорции;5 и 8 — средние члены пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов:
ab = cd ⇒ ad = bc
Если ,
,
и
числа, не равные нулю, и
•
=
•
, то отношения
ab и cd
могут образовывать пропорцию
ab = cd
Пропорция 23 = 69 Перемножим крест накрест по основному свойству пропорции 23 = 69Получим 2 · 9 = 3 · 6. Также можно составить еще 3 верные пропорции:26 = 39;96 = 32;93 = 62
Процентное отношение двух чисел
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Числа 5 и 20.Найдем отношение 5 к 20 и умножим на 100 %:51204 · 100% = 1 · 1002541% = 25%.Значит, число 5 — это 25 % от числа 20.
Прямая и обратная пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Формула пути S = V · t.S —путь, V —скорость, t —время.Величины S и V, а также S и t —прямо пропорциональны.Пусть V = 5 км/ч, t = 2ч.Тогда S = 5 * 2 = 10(км).Если мы увеличим, например, скорость в 5 раз V = 5 · 5 =25(км/ч)Тогда S = 25 · 2 = 50(км).Путь был 10 км, стал 50км, увеличился в 5 раз.
Если величины и
обратно пропорциональны, то их соответствующие значения удовлетворяют равенству
y = kx
, где -число, постоянное для данных величин.
V = S tV— скорость и t —время обратно пропорцилональны.Чем выше скорость, тем меньше времени требуется на путь. Пусть объект проехал S = 100 км за t =2ч.Тогда V = 1002 =( 50 км/ч).Если же время потребуется 5 ч, то скорость объекта V = 1005 = (20 км/ч)
Начало: Основные правила математики с примерами. 6 класс. Часть 1.
Правила и определения опираются на УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир. Примеры составлены мной (Косыхина Н.В.)
Отношение чисел | СПАДИЛО
теория по математике 🎲 числа и вычисления
Определение
Отношением пары чисел называют результат их деления одно на другое. То есть понятия частного и отношения являются синонимами, обозначая одно и то же понятие. При этом число, которое делят, называют предыдущим членом, а число, на которое осуществляется деление, – последующим.
Для обозначения отношения чисел используется знак деления «:» либо черта дроби.
Общая форма записи отношения чисел: a : b или, соответственно
В таких записях a – предыдущий член отношения, b – последующий. Обязательное условие для всякого отношения: b≠0.
Свойства отношений
Свойство №1
Членами всякого отношения могут быть как целые, так и дробные, рациональные или другие числа.
Свойство №2
Если члены отношения умножить (либо разделить) на одно и то же число, то его значение не изменится. Это свойство называют основным для отношений чисел. Деление членов отношения на одно и то же число называют сокращением отношения.
Это свойство нередко используется для перехода от нецелых членов отношения к целым, что более удобно для расчетов.
Свойство №3
В отношении могут участвовать и более 2-х членов. Так, в прикладных задачах нередко используются пропорциональные величины, значения которых выражаются как раз через их отношения. Количество членов при этом может быть произвольным и равняться трем, четырем и так далее. В общем виде такие отношения записываются как a:b:c:d:…n и читаются так: «величины относятся между собой как a, b, c…»
Пример №4. Имеется треугольник, длины сторон которого относятся как 3:4:5.
Пример №5. Даны 4 пропорциональных числа, которые относятся между собой как 1:2:4:5.
В задачах, в которых приведены такого рода отношения, обычно вводится коэффициент пропорциональности и, используя свойства объекта, для которого они приведены, и (или) данные из условия, по заданному отношению находят абсолютные значения величин для этого объекта.
При этом под абсолютными величинами понимают величины, выраженные в конкретных единицах измерения – кг, км и так далее.
Процентное отношение
Определение
Процентное отношение – это характерное и одно из наиболее распространенных направлений прикладного использования отношения чисел. Обозначение процентного отношения – % (процент). 1 % – это сотая часть от целого.
Процентное отношение основывается на обычном отношении, которое множат на 100. Процентное отношение показывает часть объекта (величины) в сравнении с его 100 частями, которые принимаются за целое.
Математическая запись:
Где a – часть целого, выраженная в единицах измерения, b – значение целого, выраженное в тех же единицах, z – количество процентов, которое составляет данная часть от целого.
Пример. На книжной полке 80 книг. Сколько процентов от этого количества составляют 36 книг?
Обозначим искомую величину через х. Тогда получаем:
Пример.
Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?
Обозначим искомую величину через х. Составим процентное отношение на основании данных задачи:
Нередко вместо понятия процентного отношения используют понятие долей. В этом случае целое абстрактно принимается за 1, а понятие процента не используется. Доля (часть) от данного целого в такой ситуации – это всегда будет величина, меньшая 1. Для определения доли (части) от целого используется обычное отношение:
Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.
Специальной единицы измерения доля не имеет и измеряется просто в единицах.
Пример. Какую долю тиража изданной книги удалось продать писателю, если тираж составляет 10 тысяч экземпляров, а приобретено было 6830 книг?
Обозначим искомую величину через х. Составим отношение и найдем х:
Переход от долей к процентам предельно прост: достаточно умножить долю на 100.
Пример. С 1 га планировалось собрать 40 тонн картофеля. Реальная урожайность составила 0,7 от планируемой. Сколько тонн картофеля собрали?
Обозначим искомую величину через х. Составим выражение для расчета реальной урожайности и найдем х:
Пропорция
Определение
Пропорцией называют равенство двух числовых отношений. В общем виде такое равенство записывают как:
где a и d называют крайними членами пропорции, b и c – средними. Прочтение пропорции: отношение a к b равно отношению c к d, или a относится к b как c к d, или a во столько раз больше b во сколько больше d.
Примеры конкретных пропорций:
При решении практических задач с использованием отношений в виде пропорции чаще всего от деления переходят к умножению ее членов. Для этого используют основное ее свойство.
Основное свойство пропорции
Произведение ее крайних членов равно произведению средних.
Пример:
Если провести дальнейшие вычисления, то в итоге мы должны прийти к равенству чисел слева и справа. А именно:
Отсюда следует важная особенность: основное свойство применяют для проверки истинности составленной пропорции. Если в результате числовых преобразований получено верное равенство, то это означает, что исходные 4 числа действительно могут составить пропорцию.
Как найти неизвестный член пропорции?
Когда один из членов пропорции неизвестен и требуется найти его, то применяют правило: для вычисления неизвестного крайнего (среднего) члена перемножают средние (крайние) и делят полученное произведение на известный крайний (средний) член.
Математически это выражается так:
То есть для определения неизвестного члена перемножают пару соответствующих известных и делят их на тот известный член, который не имеет известной пары.
Пример. Дана пропорция:
Требуется найти х.
Пример. Дана пропорция:
Необходимо найти х.
Даниил Романович | Просмотров: 4k | Оценить:
Отношения / Отношения и пропорции / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Частное двух чисел и , отличных от нуля, называют отношением чисел и , или отношением числа к числу .
Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.
Например:
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
— отношение числа к числу ;
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .
Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = .
Отношение ширины прямоугольника к его длине равно 100 : 12 = .
Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.
На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Например:
Пусть на карте задан масштаб , то есть карта сделана в масштабе одна десятитысячная.
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через длину отрезка на местности (в сантиметрах).
5 : = 1 : 10 000;
Решаем данное уравнение:
= 510 000;
= 50 000;
50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:
: 9,5 = 1 : 10 000;
Решаем данное уравнение:
= 9,5 : 10 000;
= 0,00095;
0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 582,
Мерзляк, Полонский, Якир, Учебник
Номер 673,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 681,
Мерзляк, Полонский, Якир, Учебник
Номер 686,
Мерзляк, Полонский, Якир, Учебник
Задание 800,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 828,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 993,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1312,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1498,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 146,
Мерзляк, Полонский, Якир, Учебник
Номер 149,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 405,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 846,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
Основные правила математики 6 класс(кратко).
Содержание
- Делимость натуральных чисел
- Простые и составные числа
- Признаки делимости натуральных чисел
- Основное свойство дроби
- Сокращение дробей
- Приведение дробей к наименьшему общему знаменателю
- Целые числа. Рациональные числа
- Модуль числа
- Сложение и вычитание дробей
- Сложение и вычитание рациональных чисел
- Умножение. Свойства умножения
- Умножение обыкновенных дробей
- Умножение рациональных чисел
- Деление обыкновенных дробей
- Деление рациональных чисел
- Нахождение дроби от числа
- Нахождение числа по его дроби
- Степень числа
- Числовые и буквенные выражения
- Приведение подобных слагаемых
- Раскрытие скобок
- Свойства уравнений
- Отношения
- Пропорции
- Основное свойство пропорции
- Процентное отношение двух чисел
- Прямая и обратная пропорциональная зависимость
Делимость натуральных чисел
Если натуральное число делится нацело на натуральное число , то число называют кратным числа , число — делителем числа
.
a · 1, a · 2, a · 3,…
является кратным числа .
Наименьшим делителем любого натурального числа является число , а наибольшим — само число .
Среди чисел, кратных , наибольшего нет, а наименьшее есть — это само число .
Если каждое из чисел и делится нацело на число ,то и сумма также делится нацело на число .
Если число делится нацело на число , а число не делится нацело на число , то сумма также не делится нацело на число .
Простые и составные числа
Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число. Натуральное число, имеющее более двух делителей, называют составным.
Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.
Если наибольший общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми.
Признаки делимости натуральных чисел
Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.
Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.
Если натуральное число разделить на 10, то остаток равен числу, записанному последней цифрой этого числа.
Если запись натурального числа оканчивается четной цифрой, то это число делится нацело на 2.
Если запись натурального числа оканчивается нечетной цифрой, то это число не делится нацело на 2.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.
Если запись натурального числа оканчивается любой цифрой, отличной от цифр 0 и 5, то это число не делится нацело на 5.
Если сумма цифр натурального числа делится нацело на 9, то и само число делится нацело на 9.
Если сумма цифр натурального числа не делится нацело на 9, то и само число не делится нацело на 9.
Если сумма цифр натурального числа делится нацело на 3, то и само число делится нацело на 3.
Если сумма цифр натурального числа не делится нацело на 3, то и само число не делится нацело на 3.
Основное свойство дроби
Если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получим дробь, равную данной:
ab = a · nb · n
Если числитель и знаменатель данной дроби разделить на их общий делитель (или на одно и то же натуральное число), то получим дробь, равную данной:
a : nb : n = ab
Сокращение дробей
Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют сокращением дроби.
Дробь, числитель и знаменатель которой — взаимно простые числа, называют несократимой.
Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получим несократимую дробь.
Приведение дробей к наименьшему общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю, надо:
- найти наименьший общий знаменатель данных дробей;
- найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Целые числа. Рациональные числа
Все натуральные числа, противоположные им числа и число 0 называют целыми числами.
Натуральные числа называют целыми положительными числами. Числа -1, -2, -3, … называют целыми отрицательными числами.
Объединив натуральные числа с целыми отрицательными и нулем, получим целые числа.
Объединив целые числа с дробными, получим рациональные числа.
Модуль числа
Модулем числа называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.
Модуль числа обозначают так:
a
(читают: «модуль a»).
Модуль положительного числа равен этому числу; модуль отрицательного числа равен числу, противоположному данному;
a = a, a≥0—a, a<0
Модуль числа принимает только неотрицательные значения. Модули противоположных чисел равны:
a = —a
Сложение и вычитание дробей
Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а потом применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
Сложение и вычитание рациональных чисел
Чтобы сложить два числа с разными знаками, надо:
- найти модули слагаемых;
- из большего модуля вычесть меньший модуль;
- перед полученным числом поставить знак слагаемого с большим модулем.
Чтобы сложить два отрицательных числа, надо:
- найти модули слагаемых;
- сложить модули слагаемых;
- перед полученным числом поставить знак «-».
Сумма двух противоположных чисел равна нулю:
—a+a=0 или a—a=0
Для любого рационального числа
a+0 = 0+a = a
Чтобы найти разность двух чисел можно
к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение. Свойства умножения
Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:
a · b = a +a +a+…+a⏟b
Если один из двух множителей равен 1, то произведение равно второму множителю:
m · 1 = 1 · m = m
Если один из множителей равен нулю, то произведение равно нулю:
m · 0 = 0 · m = 0
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Умножение обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:
ab·n=a·nb
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
ab · cd = a · cb · d
Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Умножение рациональных чисел
Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».
Чтобы умножить два отрицательных числа, надо умножить их модули.
Для любого рационального числа :
a · (—1) = —a
Если произведение • — положительное, то числа и имеют одинаковые знаки;
Если произведение • — отрицательное, то числа и имеют разные знаки.
Деление обыкновенных дробей
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
ab : cd = ab · dc
Деление рациональных чисел
Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.
Нахождение дроби от числа
Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.
Нахождение числа по его дроби
Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
[ads2]
Степень числа
Степенью числа с натуральным показателем , большим , называют произведение множителей, каждый из которых равен :
an=a · a · a ·…·a⏟n
Число при этом называют основанием степени.
Степенью числа с показателем называют само число
a1=a
Вторую степень числа называют также квадратом числа. Например, запись читают: « в квадрате». Третью степень называют кубом числа, а запись читают: « в кубе».
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.
Числовые и буквенные выражения
Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением. Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.
Приведение подобных слагаемых
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
Раскрытие скобок
Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
- Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
Отношения
- Частное двух чисел и , не равных нулю, еще называют отношением чисел и , или отношением числа к числу .
- Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .
- Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Пропорции
Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:
a : b =c : d или ab = cd
Числа и называют крайними членами пропорции, а числа и — средними членами пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов:
ab = cd ⇒ ad = bc
Если , , и числа, не равные нулю, и • = • , то отношения
ab и cd
могут образовывать пропорцию
ab = cd
Процентное отношение двух чисел
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Прямая и обратная пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если величины и обратно пропорциональны, то их соответствующие значения удовлетворяют равенству
y = kx
, где — число, постоянное для данных величин.
Данная информация составлена на базе УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
1. Отношение двух чисел — Стоматология в Химках
Соотношение математика
При делении одного числа на другое мы находим, во сколько раз одно число больше другого или, наоборот, какую часть одно число составляет от другого. В этом и есть смысл отношения двух чисел.
Поскольку 5 2 = 10 4 = 50 20 = 2,5 1 , то отношение (5 : 2) можно заменить и отношением (10 : 4), и отношением (50 : 20), и отношением (2,5 : 1).
Отношение не изменится, если члены его умножить или разделить на одно и то же отличное от нуля число.
Например, найдём отношение (30) см к (2) м. Сначала выразим обе эти величины в сантиметрах, а потом разделим одну на другую:
При делении одного числа на другое мы находим, во сколько раз одно число больше другого или, наоборот, какую часть одно число составляет от другого. В этом и есть смысл отношения двух чисел.
Поскольку 5 2 = 10 4 = 50 20 = 2,5 1 , то отношение (5 : 2) можно заменить и отношением (10 : 4), и отношением (50 : 20), и отношением (2,5 : 1).
Отношение не изменится, если члены его умножить или разделить на одно и то же отличное от нуля число.
Например, найдём отношение (30) см к (2) м. Сначала выразим обе эти величины в сантиметрах, а потом разделим одну на другую:
В этом и есть смысл отношения двух чисел.
Www. yaklass. ru
18.07.2018 0:27:02
2018-07-18 00:27:02
Источники:
Https://www. yaklass. ru/p/matematika/6-klass/otnosheniia-proportcii-protcenty-13922/otnoshenie-dvukh-chisel-13923/re-865b0783-d38a-488d-bcbd-2d02677303c9
Соотношение и Пропорция » /> » /> .keyword { color: red; }
Соотношение математика
Основой математических исследований является возможность получить знание об определённых величинах, сравнивая их с другими величинами, которые либо Равны, либо Больше или Меньше, чем те которые являются предметом исследования. Это обычно производится с помощью ряда Уравнений и Пропорций. Когда мы используем уравнения, то мы определяем искомую величину, находя её Равенство с какой-то другой уже знакомой величиной или величинами.
Однако, часто бывает, что мы сравниваем неизвестную величину с другими, которые Не равны ей, а больше или меньше её.
Являясь компонентом обширного и важного предмета, пропорция зависит от соотношений, поэтому необходимо чёткое и полное понимание этих понятий.
338. Арифметическое соотношение Это Разница Между двумя величинами или рядом величин. Сами по себе величины называются Членами соотношения, то есть члены, между которыми есть соотношение. Таким образом 2 это арифметическое соотношение 5 и 3. Это выражается помещая знак минус между двумя величинами, то есть 5 — 3.
339. Если оба члена арифметического соотношения Умножить или Разделить на одну и ту же величину, то Соотношение, в конечном итоге, будет умножено или разделено на эту величину.
Таким образом, если имеем a — b = r
Тогда перемножим обе стороны на h, (Акс. 3.) ha — hb = hr
И разделив на h, (Акс. 4.) $frac-frac=frac$
340. Если члены арифметического соотношения добавляют или отнимают от соответствующих членов другого, то соотношение суммы или разности будет равно сумме или разности двух соотношений.
Если a — b
И d — h,
Являются двумя соотношениями,
Тогда (a + d) — (b + h) = (a — b) + (d — h). Что в каждом случае = a + d — b — h.
И (a — d) — (b — h) = (a — b) — (d — h). Что в каждом случае = a — d — b + h.
Таким образом арифметическое отношение 11 — 4 равно 7
И арифметическое отношение 5 — 2 равно 3
Отношение суммы членов 16 — 6 это 10, — сумма соотношений.
Отношение разности членов 6 — 2 это 4, — разность соотношений.
341. Геометрическое соотношение — это отношение между величинами, которое выражается ЧАСТНЫМ, если одну величину делят на другую.
Таким образом соотношение 8 к 4, можно записать как 8/4 или 2. То есть частное деления 8 на 4. Другими словами, оно показывает сколько раз 4 содержится в 8.
Тем же самым способом, соотношение любой величины к другой может быть определено, разделив первую на вторую или, что, в принципе, одно и то же, сделав первую числителем дроби, а вторую — знаменателем.
Так соотношение a к b это $frac$
Соотношение d + h к b + c это $frac$.
342. Геометрическое соотношение также записывается, размещая две точки одну над другой между сравниваемыми величинами.
Таким образом a:b это запись соотношения a к b, а 12:4 — соотношения 12 к 4. Две величины вместе формируют Пару, в которой первый член называется Антецедентом, а последний — Консеквентом.
343. Эта запись с помощью точек и другая, в форме дроби, являются взаимозаменяемыми по мере необходимости, при этом антецедент становится числителем дроби, а консеквент — знаменателем.
Таким образом 10:5 это то же, что и $frac$ а b:d, то же, что и $frac$.
344. Если из этих трёх значений: антецедента, консеквента и соотношения даны любые Два, то третье можно найти.
Соотв. 1. Если у двух пар антецеденты и консеквенты равны, то их соотношения тоже равны.
Соотв. 2. Если у двух пар соотношения и антеценденты равны, то и консеквенты равны и если соотношения и консеквенты равны, то и антецеденты равны.
345. Если две сравниваемые величины Равны, то их соотношение равно единице или соотношению равенства. Соотношение 3*6:18 равно единице, так как частное любой величины разделённой на саму себя равно 1.
Если антецедент пары Больше, чем консеквент, то соотношение больше единицы. Так как делимое больше, чем делитель, то частное больше единицы.
С другой стороны, если антецедент Меньше, чем консеквент, то соотношение меньше единциы и это называется соотношением Меньшего неравенства. Так соотношение 2:3 меньше единицы, потому что делимое меньше делителя.
Отсюда обратное соотношение выражается Путём инвертирования дроби, которая отображает прямое соотношение, либо, когда запись ведётся с помощью точек, Инвертируя порядок записи членов.
Таким образом a относится к b обратно тому, как b к a.
347. Сложное соотношение это соотношение Произведений соответствующих членов с двумя и более простыми соотношениями.
Так соотношение 6:3, равно 2
И соотношение 12:4, равно 3
Составленное из них соотношение 72:12 = 6.
Здесь сложное соотношение получается, умножая между собой два антецедента и также два консеквента простых соотношений.
Так соотношение составленное
Из соотношения a:b
И соотношения c:d
И соотношения h:y
Это соотношение $ach:bdy=frac$.
Сложное соотношение не отличается по своей Природе от любого другого соотношения. Этот термин используется, чтобы в определённых случаях показать происхождение соотношения.
Соотв. Сложное соотношение равно произведению простых соотношений.
Соотношение a:b, равно $frac$
Соотношение c:d, равно $frac$
Соотношение h:y, равно $frac$
И соотношение сложенное из этих трёх будет ach/bdy, что является произведением дробей, которые выражают простые соотношения.
348. Если в последовательности соотношений в каждой предыдущей паре консеквент является антецедентом в последующей, то Соотношение первого антецедента и последнего консеквента равны тому, которое получено из промежуточных соотношений.
Так в ряде соотношений
A:b
B:c
C:d
D:h
Соотношение a:h равно соотношению, сложенному из соотношений a:b, и b:c, и c:d, и d:h. Так сложное соотношение в последней статье равно $frac=frac$, или a:h.
Таким же образом все величины, которые являются и антецедентами и консеквентами Исчезнут, когда произведение дробей будет упрощено до своих младших членов и в остатке сложное соотношение будет выражаться первым антецедентом и последним консеквентом.
349. Особый класс сложных соотношений получается при умножении простого соотношения на Самого себя или на другое Равное соотношение. Эти соотношения называются Двойными, Тройными, Четверными, и так далее, в соответствии с количеством операций умножения.
Соотношение, составленное из Двух равных соотношений, то есть, Квадрата простого соотношения, называют Двойным соотношением.
Составленное из Трёх, то есть, Куб простого соотношения, называют Тройным, и так далее.
Аналогично соотношение Квадратных корней двух величин, называется соотношением Квадратного корня, а соотношение Кубических корней — соотношением Кубического корня, и так далее.
Таким образом простое соотношение a к b, равно a:b
Двойное соотношение a к b, равно a 2 :b 2
Тройное соотношение a к b, равно a 3 :b 3
Соотношение квадратного корня a к b, равно √ a :√ b
Соотношение кубического корня a к b, равно 3 √ a : 3 √ b, и так далее.
Термины Двойной, Тройной, и так далее не нужно смешивать с Удвоенным, Утроенным, и так далее.
Соотношение 6 к 2 равно 6:2 = 3
Удвоим это соотношение, то есть, соотношение дважды, то получим 12:2 = 6
Утроим это соотношение, то есть это соотношение трижды, то получим 18:2 = 9
А Двойное соотношение, то есть Квадрат соотношения, равен 6 2 :2 2 = 9
И Тройное соотношение, то есть куб соотношения, равен 6 3 :2 3 = 27
350. Для того, чтобы величины можно соотнести друг с другом, они должны быть одинакового рода, так, чтобы можно было с уверенностью утверждать равны ли они между собой, или одна из них больше или меньше. Фут относится к дюйму, как 12 к 1: он в 12 раз больше, чем дюйм. Но нельзя, например, сказать, что час длиннее или короче, чем палка, или акр больше или меньше, чем градус. Однако, если эти величины выражены в Числах, то может существовать соотношение между этими числами. То есть может существовать соотношение между количеством минут в часе и количеством шагов в миле.
351. Обратившись к Природе соотношений, следующим шагом нам нужно учесть способ, каким образом скажется на самом соотношении изменение одного или двух членов, которые сравнивают между собой. Вспомним, что прямое соотношение выражается в виде дроби, где Антецедет пары всегда это Числитель, а Консеквент — Знаменатель. Тогда будет легко из свойства дробей получить, что изменения в соотношении происходят путём варьирования сравниваемых величин. Соотношение двух величин такое же как и Значение дробей, каждая из которых представляет Частное: числитель делённый на знаменатель. (Статья. 341.) Теперь было показано, что умножать числитель дроби на любую величину, это то же, что и умножать Значение на эту же величину и что деленить числитель, это то же, что и деленить значения дроби. Поэтому,
352. Умножать антецедент пары на любую величину, значит умножать соотношения на эту величину, а делить антецедент — деленить это соотношение.
Таким образом соотношение 6:2 равное 3
И соотношение 24:2 равное 12.
Здесь антецедент и соотношение в последней паре в 4 раза больше, чем в первой.
Отношение a:b равно $frac$
И отношение na:b равно $frac$.
Соотв. При известном консеквенте, чем больше Антецедент, тем больше Соотношение, и, наоборот, чем больше соотношение, тем больше антецедент.
353. Умножая консеквент пары на любую величину, в результате получаем деление соотношения на эту величину, а деля консеквент — умножаем соотношение. Умножая знаменатель дроби, делим значение, а деля знаменатель — значение умножается..
Так соотношение 12:2 равно 6
И соотношение 12:4 равно 3.
Здесь консеквент второй пары в Два раза больше, а соотношение В два раза меньше, чем первое.
Соотношение a:b равно $frac$
И соотношение a:nb равно $frac$.
Соотв. При данном антецеденте, чем больше консеквент, тем меньше соотношение. И наоборот, чем больше соотношение, тем меньше консеквент.
354. Из двух последних статей следует, что Умножение антецедента пары на любую величину окажет такой же эффект на соотношение, как Деление консеквента на эту величину, а Деление антецедента, окажет такой же эффект, как Умножение консеквента.
Поэтому соотношение 8:4, равно 2
Умножая антецедент на 2, соотношение 16:4 равно 4
Разделив антецедент на 2, соотношение 8:2 равно 4.
Соотв. Любой Множитель или Делитель может быть перенесён от антецедента пары к консеквенту или от консеквента к антецеденту без изменения соотношения.
Стоит заметить, что когда множитель таким образом переносится от одного члена к другому, то он становится делителем, а переносимый делитель становится множителем.
Так соотношение 3.6:9 = 2
Перенеся множитель 3, $6:frac=2$
То же самое соотношение.
355. Как очевидно из Статей. 352 и 353, Если антецедент и консеквент оба умножить или разделить на одну и ту же величину, то соотношение не меняется.
Соотв. 1. Соотношение двух Дробей, у которых есть общий знаменатель, такое же как отношение их Числителей.
Таким образом соотношение a/n:b/n, то же самое, что и a:b.
Соотв. 2. Прямое соотношение двух дробей, у которых есть общий числитель, равно обратному соотношению их Знаменателей.
356. Из статьи легко определить соотношение любых двух дробей. Если каждый член умножить на два знаменателя, то соотношение будет задано интегральными выражениями. Таким образом умножая члены пары a/b:c/d на bd, получаем $frac$:$frac$, что становится ad:bc, путём сокращения общих величин из числителей и знаменателей.
356. b. Соотношение Большего неравенства, сложенное с другим соотношением, Увеличивает его
Пусть соотношение большего неравенства будет задано как 1+n:1
И любое соотношение как A:b
Сложное соотношение будет (Статья. 347,) a + na:b
Что больше, чем соотношение a:b (Статья. 351. соотв.)
Но соотношение Меньшего неравенства, сложенное с другим соотношением, Уменьшает его.
Пусть соотношение меньшей разности 1-n:1
Любой заданное соотношение A:b
Сложное соотношение a — na:b
Что меньше, чем a:b.
357. Если к или от членов любой пары Прибавить Или отнять две другие величины, которые находятся в таком же соотношении, то суммы или остатки будут иметь такое же соотношение.
Пусть соотношение a:b
Будет такое же, как и c:d
Тогда соотношение Суммы антецедентов к сумме консеквентов, а именно, a + c to b + d, тоже одинаковое.
То есть $frac$ = $frac$ = $frac$.
Доказательство.
Соотношение Разницы антецедентов к разнице консеквентов также одинаковое.
358. Если в нескольких парах соотношения равны, то Сумма всех антецедентоа относится к сумме всех консеквентов, как любой антецедент к своему консеквенту.
Таким образом соотношение
|12:6 = 2
|10:5 = 2
|8:4 = 2
|6:3 = 2
Таким образом соотношение (12 + 10 + 8 + 6):(6 + 5 + 4 + 3) = 2.
Так как последний числитель больше, чем другой, то Соотношение больше.
Если вместо добавления ту же самую величину Отнять от двух членов, то очевидно, что эффект на соотношение будет обратным.
Примеры.
1. Что больше: соотношение 11:9, или соотношение 44:35?
3. Если антецедент пары равен 65, а соотношение равно 13, то какой консеквент?
4. Если консеквент пары равен 7, и соотношение равно 18, то какой антецедент?
5. Как выглядит сложное соотношение составленное из 8:7, и 2a:5b, а также (7x+1):(3y-2)?
6. Как выглядит сложное соотношение составленное из (x+y):b, и (x-y):(a + b), а также (a+b):h? Отв. (x 2 — y 2 ):bh.
7. Если соотношения (5x+7):(2x-3), и $(x+2):left(frac+3right)$ образуют сложное соотношение, то какое соотношение получится: большее или меньшее неравенство? Отв. Соотношение большего неравенства.
8. Каково соотношение составленное из (x + y):a и (x — y):b, и $b:frac$? Отв. Соотношение равенства.
9. Каково соотношение сложенное из 7:5, и удвоенного соотношения 4:9, и утроенного соотношения 3:2?
Отв. 14:15.
10. Каково соотношение составленное из 3:7, и утроенного соотношения x:y, и извлечения корня из соотношения 49:9?
Отв. x 3 :y 3 .
© 2005 — 2022
Копирование запрещено! В случае копирования администрация сайта обратится в компетентные органы.
Каково соотношение составленное из x y a и x — y b, и b frac.
Www. math20.com
21.07.2017 7:52:55
2017-07-21 07:52:55
Источники:
Https://www. math20.com/ru/algebra/proporcia/sootnoshenie-proporcia. html
Пропорции математика. Пропорция – это равенство двух отношений. Соотношение. » /> » /> .keyword { color: red; }
Соотношение математика
Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Четыре величины (4, 2, 8 ) и (4) находятся в отношении, если (frac=frac) .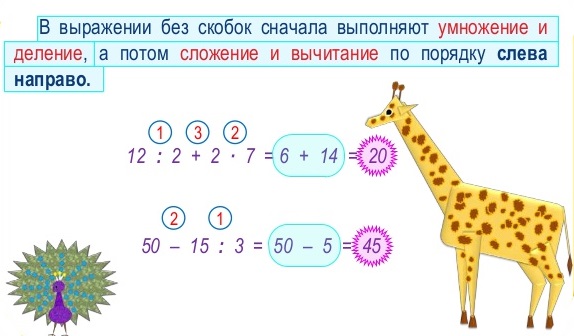
Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.
- (AB=CD) (AD=BC)
Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.
(12) человек → (5) дней (6) человек → (x) дней (frac= frac) умножаем крест на крест члены пропорции и сокращаем на (6) : (2*15=5x) (30 =5x) Делим на 5 обе части равенства: (frac=x) , откуда находим
Задача 3. Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?
((10+x)(18+x)=(22+x)(38+x)) (380+48x+2x=396+40x+2x) (8x=16) (x=2)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Репетитор по русскому языку 5-11 классы. Подготовка к ОГЭ, ЕГЭ, ВПР по русскому языку.
Репетитор 1-11 классов. Считаю математику своим призванием. Имею большой опыт работы в школе, а также индивидуально с учениками разных возрастов, лично и онлайн, в России и за рубежом. Работаю по классической методике преподавания, с применением новых форм обучения.
Репетитор по математике 8-11 классы. Веду подготовку к ОГЭ/ЕГЭ/ВПР Математика-царица точных наук, следовательно, она помогает в жизни выстраивать точные последовательности действий, организует, а также всегда может пригодится в быту. Работаю по принципу «пирамиды»: от простого к сложному. Всегда ищу индивидуальный подход к каждому ученику, разрабатываю индивидуальные планы осваивания материала. Люблю работать как с сильными, так и слабыми учениками. Нравится разбираться в задачах вместе с учеником, наводящими вопросами выстраивать логическую цепочку решений.
Когда соотношение остается постоянным, это соотношение называется пропорциональным.
Myalfaschool. ru
02.05.2017 2:16:00
2017-05-02 02:16:00
Источники:
Https://myalfaschool. ru/articles/proporciya-v-matematike
Презентация по математике на тему Отношение чисел доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по математике на тему Отношение чисел, предмет презентации: Математика.
Слайд 1Текст слайда:
Тема урока:
Отношение двух чисел
Урок математики в 6 классе
Ипатова Ирина Викторовна – учитель математики
высшей квалификационной категории
МАОУ СОШ № 6 с УИОП г. Калининград
Слайд 2Текст слайда:
УРОК 1
Слайд 3Текст слайда:
1) Латунь – это сплав меди и цинка, взятых в отношении 3 : 2.
2) Готовя варенье, смешивают сливы и сахар в отношении два к трем.
3) От куска материи длиной 5м отрезали 2м.
4) Масса станка 9,6 ц, а масса электромотора 36 кг. Найдите отношение массы электромотора к массе станка.
5) В автопарке стоят 36 легковых машин и 12 грузовых. Во сколько раз легковых машин больше, чем грузовых?
Слайд 4Текст слайда:
Тема урока:
Отношение двух чисел
Слайд 5Текст слайда:
Задачи урока:
познакомиться с понятием «отношение», узнать, что оно показывает;
научиться составлять и читать
отношения;
решать задачи на определение отношений.
Слайд 6Текст слайда:
«Отношение — взаимная связь разных величин, предметов, действий.»
Дружеские отношения
Семейные отношения
Ожегов С.И.
Учитель строг в отношении к ученикам.
Слайд 7Текст слайда:
В математике
Отношение двух чисел — это частное от деления одного из них на другое.
a : b
Слайд 8Текст слайда:
Что показывает отношение
двух чисел?
a : b
Отношение показывает, во сколько раз
первое число больше второго
Или
какую часть первое число
составляет от второго числа.
Слайд 9
Слайд 10Текст слайда:
ЗАДАЧА 1. В классе 36 учащихся
15
?
Какую часть учащихся составляют мальчики, а какую девочки?
Слайд 11Текст слайда:
ЗАДАЧА 2.
Масса станка 9,6 ц, а масса электромотора
36 кг. Найдите отношение массы
электромотора к массе станка.
Запомни!
Единицы измерения величин в отношении должны быть одинаковыми.
Слайд 12Текст слайда:
Найдите отношение:
1) 56 к 7
2) 8 к 10
3) 9,6 к 0,32
4) 0,25 к 0,55
Слайд 13Текст слайда:
Домашнее задание:
У: стр.
«Что называют отношением
двух чисел»,
№322, 327, 328.
Слайд 14Текст слайда:
УРОК 2
Слайд 15Текст слайда:
Устные упражнения:
Что называют отношением
двух чисел?
Отношение двух чисел — это частное от деления одного из них на другое.
Слайд 16Текст слайда:
Записать возможные отношения:
а) зеленые к желтым
б) зеленые к розовым
в) розовые к желтым
Ответ
Слайд 17Текст слайда:
На столе стоят кружки.
Что означают отношения:
а) 6 к 10
б) 4 к 10
в) 4 к 6
г) 6 к 4
Слайд 18Текст слайда:
Заполни пропуски
«Отношение 64:16 (или _____) показывает,__________________________
«Отношение 9:__ (или 9/11) показывает, _________________________________________
Слайд 19Текст слайда:
Молоко разлили в три бидона.
В первый налили 0,1 всего молока.
0,1
Во второй налили 0,3 всего молока.
0,3
А в третий – 0,6 всего молока.
0,6
Что показывает отношение?
Слайд 20Текст слайда:
Подсказка
Ответ
Слайд 21Текст слайда:
Ответ
Отношение a к b равно 1,25
Найдите обратное отношение.
Слайд 22Текст слайда:
Общее количество спортсменов на Зимней Олимпиаде в Сочи — 2800 человек из 88 стран мира, Россию представят 223 спортсмена. Какую часть спортсмены из России составляет от общего количества участников олимпиады?
Слайд 23Текст слайда:
1
2
3
9
6
12
11
10
8
7
4
5
Какую часть урока заняла самостоятельная работа,
которая длилась 10 минут, если продолжительность
урока 45 мин?
Ответ
Слайд 24Текст слайда:
1) Латунь – это сплав меди и цинка, взятых в отношении 3 : 2.
2) Готовя варенье, смешивают малину и сахар в отношении два к трем.
3) Сплав содержит золото и серебро в отношении 57: 41
4) Число 120 разделить в отношении 4 : 11
Слайд 25Текст слайда:
МЕДЬ
ЦИНК
3 ЧАСТИ
ЛАТУНЬ
5 ЧАСТЕЙ
2 ЧАСТИ
ЛАТУНЬ – ЭТО СПЛАВ МЕДИ И ЦИНКА, ВЗЯТЫХ В ОТНОШЕНИИ 3 : 2
Слайд 26Текст слайда:
Готовя варенье, смешивают малину и сахар в отношении два к трем.
Для приготовления ягодного варенья берутся объемы ягод и сахара в отношении 1 : 1. Сколько литров сахара нужно досыпать к 5 литрам ягод, чтобы получить качественное варение?
2 части
3 части
Слайд 27Текст слайда:
57 частей
41 часть
Сплав содержит золото и серебро
в отношении 57: 41
ЗОЛОТО
СЕРЕБРО
Слайд 28Текст слайда:
Задача 1.
Слайд 29Текст слайда:
Задача 2.
Мама купила сливы и груши в отношении 3 : 4. Сколько фруктов каждого вида купила мама, если всего она купила 2 кг 800г фруктов.
Решение
1) 2800 : (3 + 4) = 400 (г) – 1 часть фруктов.
2) 400 * 3 = 1200 (г) – слив.
3) 400 * 4 = 1600(г) – груш.
Ответ: 1 кг 200 г и 1 кг 600 г
Слайд 30
Слайд 31Текст слайда:
Описать ситуацию:
Отношение числа учащихся, не выполнивших домашнее задание к общему числу учащихся равно 1 : 25
а) ___ часть учащихся выполнили домашнее задание
б) каждый _______ учащийся не выполнил домашнее задание
в) ____ ученика из ____ выполнили домашнее задание
Слайд 32Текст слайда:
Домашнее задание:
№324, 329, 330 (а, б).
Скачать презентацию
Что такое shareslide.ru?
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Конспект урока по математике «Отношения» 6 класс
Тема урока «Отношения» математика 6 класс
Цели:
-
Создать условия для осознания и осмысления нового математического понятия «отношение»; показать правила записи и прочтения отношений;
-
Развивающие: развивать познавательный интерес, умение сравнивать, обобщать; развивать внимание, воображение учащихся, их кругозор, культуру математической речи, прививать интерес к изучению математики.
-
Воспитательные: воспитание аккуратности, чувство коллективизма, самоконтроля.
Оборудование: Видеопроектор, презентация к уроку в среде PowerPoint, карточки для актуализации знаний и тест, сопроводительный материал к уроку,калькулятор.
План урока
I. Организационный момент.
Теоретический опрос
II. Устная работа
III. Подготовительная работа
IV. Объяснение
V. Закрепление
VI. Исследовательская работа
VII. Проверочная работа
VIII. Домашнее задание
IX. Подведение итогов урока.
Ход урока
I.Организационный момент.
Проверить готовность учащихся к уроку. Проверьте, пожалуйста, все ли имеется на ваших столах для успешной работы на уроке.
Ребята, мы завершили изучение большого раздела «Умножение и деление обыкновенных дробей». Мы умеем выполнять все арифметические действия с натуральными числами, десятичными и обыкновенными дробями.
Цель сегодняшнего урока это изучение нового материала.
Девиз нашего урока: Основа хорошего понимания математики –
умение считать, думать, рассуждать,
находить удачные решения задачи.
Прежде чем приступить к изучению нового материала, повторим некоторые понятия из пройденного ранее, чтобы создать базу для восприятия нового.
II. Повторение – мать учения.( теоретический опрос)
-
Что значит сократить дробь?
-
Сформулируйте правило умножения десятичной дроби на 100
-
Как заменить обыкновенную дробь десятичной?
-
Как обратить дробь в проценты?
-
Правило округления чисел.
-
Какая дробь называется правильной, неправильной.
III. Устный счет
А теперь займемся устным счетом.
Вам нужно отгадать ключевое слово.
Вы расшифровали слово ОТНОШЕНИЕ.
Значение этого термина широкое. Это отношение между учениками, дружеские отношения, деловые и международные отношения. А что же означает термин «отношение» в математике?
Но прежде чем ответить на этот вопрос, мы решим задачу, составленную по результатам контрольной работы , которую вы решали на прошлом уроке по теме «Деление обыкновенных дробей».
IV.Подготовительная работа.
Задача №1.
За контрольную работу по математике отметку «4» и «5» получили 8 учеников, отметку «3» — 7 учеников и отметку «2» — 1 ученик. Сколько процентов учащихся класса получили отметку «4» и «5»?
Подумайте, как бы вы решили эту задачу? ( ход решения обсуждается устно).
Попробуем решить эту задачу другим способом.
Контрольную работу выполняли 16 человек. Какую часть класса составляет 1 ученик? ( 1/16) А 8 учеников? ( 8/16).
Решение. 8/16 = ½ = 0,5 = 0,5 * 100% = 50 %
(Ответ к задаче записать в обыкновенных дробях, десятичных дробях и в процентах)
Ответ: 50 % учащихся получили отметку «4» и «5».
Ребята, полученное частное чисел 8 и 16 в математике называют отношением этих чисел.
Откроем тетради, запишем число , классная работа, тему урока «Отношение».
Запишем решение задачи №1.
V. Объяснение.
а : b = а / b. ( читается — отношение числа а к числу b; отношение чисел а и b? Отношение а к b)
— Что же показывает отношение двух чисел?
-
Если отношение — дробь неправильная, то оно показывает: 1) во сколько раз первое число больше второго.
-
Если же отношение — дробь правильная, то оно показывает какую часть первое число составляет от второго.
-
Отношение, выраженное в процентах, называют процентным отношением .
А о практическом применении отношения вы узнаете по окончании изучения темы «отношение»
VI. Закрепление
Решите задачу на составление отношений.
Задача №2
Перед вами лежат рабочие тетради. Подсчитайте количество чистых и исписанных листов.
Всего листов: …; чистых: …; исписанных: ….
Составьте отношение:
-
чистых к исписанным;
-
исписанных к чистым;
-
чистых к общему количеству листов.
Ответ: 1) … 2) … 3) …
Что показывают полученные отношения?
-
Какую часть составляют чистые от исписанных?
-
Во сколько раз исписанных больше чем чистые?
-
Какую часть всех листов составляют чистые?
Как по записи понять, что показывают данные отношения?
— отношение , больше единицы, показывает, во сколько раз одно число больше ( или меньше) другого;
— отношение, меньше единицы, показывает, какую часть одно число составляет от другого .
А теперь ребята решим следующую задачу.
Задача №3
В нашем районе дружно проживают люди разных национальностей. Все население нашего района составляет 20226 человек. Из них 12155 русские, 3385 мордва и 4386 татары. Какую часть населения района составляют мордва. Во сколько раз русских больше чем татар?
1) 3385/20226 = 0,1673…=0,17, 0,17*100%= 17%
2) 12155/4386 = 2,7713…=2,77 раза
Ответ: 0,17 населения района составляют мордва или 17 %; русских больше чем татар в 2,77 раза.
Давайте сделаем один из главных выводов нашего урока . Прочтите высказывание ,подумайте , какими словами нужно его дополнить?
Запомните!
Отвечая на вопросы задачи, будьте внимательны.
При составлении отношения двух чисел, важно
понимать, какое число из двух данных будет ДЕЛИМЫМ, какое ДЕЛИТЕЛЕМ.
VII. Исследовательская работа.
А сейчас ребята продолжим нашу исследовательскую работу.
Я предоставляю слово …
Ученик: Тема нашей исследовательской работы «Подписка населения поселка Ромоданово на издания периодической печати»
Цель работы: выяснить отношение населения поселка к подписке на периодические издания и определить наиболее популярное издание .
Метод исследования: опрос.
Были опрошены 150 человек.
Данные опроса отражены в следующей таблице
Название газеты
Для завершения исследовательской работы нам необходимо ответить на вопросы: Какая часть опрошенных жителей поселка выписали газету «Победа» и «Республика Молодая»
1)107/150=0,7133…=0,77=77% населения поселка выписали газету «Победа».
2)9/150=0,06=6% населения поселка выписали газету «Республика Молодая»
3) 24/150=0,16=16% населения выписали журнал «1000 советов»
Ответ: 77%, 6%.
Ребята, мы только для двух изданий представили частное в процентном отношении .Поэтому, какой предварительный вывод вы можете сделать из проделанной работы?
Вывод: (ученик) По предварительным результатам можно сделать следующий вывод: большая часть населения поселка отдают предпочтение районной газете «Победа» и только 6% населения поселка выписали газету «Республика Молодая»
VIII. Тест.
В завершении нашего урока проведем проверочный тест. После выполнения теста вы получите слово , которое охарактерезует вашу работу на уроке.
Тест – Проверь себя!
1.Какое из выражений является отношением двух чисел?
А) 7 + 5
Б) 7 : 5
В) 7 – 5
Г) 7 * 5
2. Какую часть от 11 составляет число 3?
Р) 3/11
Г) 14
В) 8
М) 11/3
3.
Р) в 0,5 раза
Н) в 1/2 раза
А) 2 раза
Г) нельзя определить
И) 0,2 %
В) 25 %
З) 20 %
Р) 4 %
О) 60 %
Т) 0,6 %
К) 1 %
А) 166
Вы получили слово «БРАВО» ,значит молодцы.
Сегодня на уроке отличились:
Неплохо поработали…………………….. и те, ребята, которые участвовали в исследовательской работе.
IX. Домашнее задание:
п. 20, заполнить таблицу «Подписка …..», т.е. составить отношения для всех изданий и полученное отношение выразить в процентах, 1 вариант заполняет первую колонку,а 2 вариант вторую колонку.
X. Итог урока:
1.С каким ключевым словом познакомились?
2.Что называют отношением двух чисел?
3. Что показывает отношение?
4.Как узнать, какую часть число а составляет от числа b?( составить отношение а к b)
|
Кол-во подписок |
% |
Название журнала |
Кол-во подписок |
% |
|
|
«Победа» |
107 |
77 |
«1000 советов» |
24 |
16 |
|
«Республика молодая» |
9 |
6 |
«Чилисема» |
1 |
|
|
«Известия Мордовии» |
22 |
«Моя семья» |
2 |
||
|
«Столица «С» |
21 |
«Сядко» |
1 |
||
|
«Жизнь» |
7 |
«Айболит» |
1 |
||
|
«Сельская газета» |
2 |
«Непоседа « |
2 |
||
|
«Вечерний Саранск» |
7 |
«Диагональ» |
2 |
||
|
«Эрзянь правда» |
1 |
«Пенсионер» |
7 |
Соотношение — значение, упрощение, таблица, примеры
Соотношение в математике — это термин, который используется для сравнения двух или более чисел.
| 1. | Что такое отношение? |
| 2. | Расчет коэффициентов |
| 3. | Как упростить пропорции? |
| 4. | Эквивалентные соотношения |
| 5. | Часто задаваемые вопросы о Ratio |
Что такое соотношение?
Отношение определяется как сравнение двух количеств одних и тех же единиц , который указывает, сколько одного количества присутствует в другом количестве.
Формула отношения
Мы используем формулу отношения при сравнении отношений между двумя числами или количествами. Общая форма представления отношения между двумя величинами, скажем, «а» и «b», представляет собой а: b, , что читается как «а к b».
Форма дроби, которая представляет это соотношение, — a/b. Чтобы еще больше упростить отношение, мы следуем той же процедуре, которую используем для упрощения дроби.
Пример: В классе из 50 учеников 23 девочки, остальные мальчики. Найдите отношение количества мальчиков к количеству девочек.
Общее количество студентов = 50; Количество девочек = 23.
Общее количество мальчиков = Общее количество учащихся — Общее количество девочек
= 50 — 23
= 27
Таким образом, искомое соотношение равно (Количество мальчиков: Количество девочек), то есть 27:23.
Расчет коэффициентов
Чтобы рассчитать отношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления пышных оладий необходимо 15 стаканов муки и 20 стаканов сахара, рассчитаем соотношение муки и сахара в рецепте.
- Шаг 1: Найдите количества для обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
- Шаг 2: Запишите в виде дроби a/b.
Итак, мы пишем это как 15/20.
- Шаг 3: Если возможно, еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 можно упростить до 3/4.
- Шаг 4: Следовательно, отношение муки к сахару можно выразить как 3:4.
Используйте бесплатный онлайн-калькулятор коэффициентов Cuemath, чтобы проверить свои ответы при расчете коэффициентов.
Как упростить пропорции?
Отношение показывает, сколько одного количества требуется по сравнению с другим количеством. Два члена отношения можно упростить и выразить в самой низкой форме. Соотношения, выраженные в самых низких терминах, легко понять, и их можно упростить так же, как мы упрощаем дроби. Чтобы упростить отношение, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, упростим соотношение 18:10.
- Шаг 1: Запишите данное отношение a:b в виде дроби a/b. Записав отношение в виде дроби, мы получим 18/10.
- Шаг 2: Найдите наибольший общий делитель чисел ‘a’ и ‘b’. В этом случае GCF 10 и 18 равен 2,
- Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, получим (18÷2)/(10÷2) = 9/5.
- Шаг 4: Представьте эту дробь в форме отношения, чтобы получить результат. Следовательно, упрощенное соотношение равно 9:5.
.
Используйте бесплатный онлайн-калькулятор коэффициентов упрощения Cuemath, чтобы проверить свои ответы.
Советы и рекомендации по соотношению:
- В случае, если оба числа ‘a’ и ‘b’ равны в соотношении a:b, то a:b = 1.
- Если a > b в отношении a : b, то a : b > 1.
- Если a < b в отношении a : b, то a : b < 1,
- Перед их сравнением необходимо убедиться, что единицы измерения двух величин одинаковы.
Эквивалентные отношения
Эквивалентные соотношения аналогичны эквивалентным дробям.
Таблица соотношений
Таблица соотношений представляет собой список, содержащий эквивалентные соотношения любого заданного соотношения в структурированном виде. В следующей таблице соотношений показано соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные отношения связаны друг с другом путем умножения числа. Эквивалентные соотношения получаются путем умножения или деления двух членов отношения на одно и то же число.
Воспользуйтесь бесплатным онлайн-калькулятором эквивалентных соотношений Cuemath, чтобы проверить свои ответы.
☛ Похожие темы
- Процентная доля
- Определение скорости
- Калькулятор нормы прибыли
Примеры соотношений
-
Пример 1: В школьной аудитории 49 мальчиков и 28 девочек. Выразите отношение количества мальчиков к количеству девочек.
Решение:
Дано, количество мальчиков = 49; а количество девочек = 28. НОД 49 и 28 равен 7. Теперь, чтобы упростить, разделите два слагаемых на их НОД, который равен 7. Это означает, что (49 ÷ 7)/(28 ÷ 7) = 7/ 4. Следовательно, соотношение числа мальчиков и девочек = 7:4.
-
Пример 2: В музыкальном классе 30 учеников.
Из них 10 взрослых, остальные дети. Каково отношение количества детей к общему количеству учащихся в музыкальном классе?
Решение:
Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно к 20. Отношение общего количества детей к общему количеству учащихся в музыкальном классе = 20:30, что при упрощении дает 2:3.
-
Пример 3: Упростите данное соотношение, 87:75.
Решение:
Чтобы упростить данное отношение, мы сначала найдем НОД 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, что (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшем виде равно 29:25.
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что».
Записаться на бесплатный пробный урок
Практические вопросы по соотношению
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Ratio
Что такое соотношение в математике?
Соотношение можно определить как соотношение или сравнение между двумя числами одной и той же единицы для проверки того, насколько одно число больше другого. Например, если количество баллов, набранных за тест, равно 7 из 10, то отношение полученных баллов к общему количеству баллов записывается как 7:10.
Какие существуют способы записи отношения?
Соотношение можно записать, разделив две величины двоеточием (:), или его можно записать в дробной форме. Например, если есть 4 яблока и 8 дынь, то отношение яблок к дыням можно записать как 4:8 или 4/8, что можно еще упростить как 1:2.
Как рассчитать соотношение между двумя числами?
Чтобы рассчитать отношение двух величин, мы можем использовать следующие шаги.
- Шаг 1: Обратите внимание на количество обоих ингредиентов, для которых мы определяем соотношение. В данном случае это 14 и 28.
- Шаг 2: Запишите в виде дроби a/b. Итак, мы пишем это как 14/28.
- Шаг 3: Если возможно, еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 14/28 можно упростить до 1/2.
- Этап 4: Следовательно, отношение масла к сахару можно выразить как 1:2.
Как найти эквивалентные соотношения?
Два отношения называются эквивалентными, если они представляют одно и то же значение в упрощенном виде. Это понятие похоже на эквивалентные дроби. Например, когда отношение 1: 4 умножается на 2, это означает умножение обоих членов отношения на 2. Таким образом, мы получаем, (1 × 2) / (4 × 2) = 2/8 или 2: 8 , Здесь 1:4 и 2:8 являются эквивалентными соотношениями.
Что такое таблица соотношений?
Таблица соотношений показывает список эквивалентных соотношений, которые получаются путем умножения или деления обеих величин на одно и то же значение. Например, если таблица соотношений начинается с соотношения 1 : 3, то в последующих строках будет соотношение 2 : 6, 3 : 9, 4 : 12 и т. д. Когда эти соотношения упрощены, они представляют одно и то же значение, то есть 1:3.
Что такое золотое сечение?
Золотое сечение — это число, значение которого примерно равно 1,618. Символом для этого является греческая буква «фи», представленная как ϕ. Это особый атрибут, который используется в искусстве, геометрии и архитектуре, потому что считается, что золотое сечение создает наиболее приятную и красивую форму.
Почему коэффициенты важны?
Соотношения важны, потому что они позволяют нам выражать количества таким образом, чтобы их было легче интерпретировать. Это инструмент, который используется для сравнения размера двух или более величин по отношению друг к другу. Например, если в классе 30 девочек и 20 мальчиков. Мы можем представить количество девочек к количеству мальчиков с помощью соотношения, которое в данном случае равно 3:2.
Что такое формула соотношения?
Формула отношения используется для сравнения отношений между двумя числами или количествами. Общая форма представления отношения между двумя величинами, скажем, «а» и «b», представляет собой а: b, , что читается как «а к b».
Что такое соотношение и пропорция?
Соотношение — это отношение или сравнение между двумя величинами одной и той же единицы измерения для проверки того, насколько одно число больше другого.
Как сравнить коэффициенты?
Существуют различные методы сравнения коэффициентов. Например, сравним 1:2 и 2:3 методом НОК.
- Шаг 1: Запишите коэффициенты в виде дроби. Здесь это означает 1/2 и 2/3.
- Шаг 2: Сократите дроби по отдельности. Здесь обе дроби 1/2 и 2/3 уже находятся в сокращенной форме.
- Шаг 3: Теперь сравните 1/2 и 2/3, найдя НОК (наименьшее общее кратное) знаменателей. LCM 2 и 3 равен 6,9.0084
- Шаг 4: Приравняйте знаменатели, умножив числитель и знаменатель первой дроби на 3, то есть (1 × 3)/(2 × 3) = 3/6. Затем умножьте числитель и знаменатель второй дроби на 2, то есть (2 × 2)/(3 × 2) = 4/6.
- Шаг 5: Теперь можно легко сравнить 3/6 и 4/6. Это показывает, что 4/6 больше, чем 3/6.
Следовательно, 2:3 > 1:2.
Как преобразовать пропорции в дроби?
Соотношения можно записать в виде дробей очень простым способом. Предшественник записывается как числитель, а консеквент — как знаменатель. Например, если мы возьмем соотношение 3: 5. Здесь 3 — это антецедент, а 5 — консеквент. Таким образом, мы можем записать это как 3/5.
Как преобразовать дроби в отношения?
Дроби могут быть записаны в виде отношений после упрощения. Это означает, что мы сначала приводим данную дробь к ее наименьшему члену, а затем записываем числитель как антецедент, а знаменатель как следствие. Например, дробь 16/48 сначала уменьшится до 1/3, а затем ее можно будет выразить в виде отношения 1:3.
Как преобразовать отношения в десятичные дроби?
Соотношения можно легко преобразовать в десятичные, записав отношение в виде дроби, а затем дробь преобразуется в десятичную путем деления числителя на знаменатель. Например, 3:7 можно записать как 3/7.
Как преобразовать соотношения в проценты?
Соотношения можно преобразовать в проценты, выполнив следующие действия. Например, переведем 5:6 в виде процентов.
- Шаг 1: Запишите коэффициент в виде дроби. Здесь 5:6 можно записать как 5/6.
- Шаг 2: Умножьте эту дробь на 100 и добавьте символ процента. В этом случае 5/6 × 100 = 83,33%.
Прочтите эту статью о «отношении к процентам», чтобы узнать больше.
Скачать БЕСПЛАТНЫЕ учебные материалы
Скачать бесплатно рабочие листы для 6 класса
Рабочие листы по отношениям
Отношения в математике
Отношение — это отношение между сущностями в нашем мире. Это могут быть числа, физические величины, предметы, продукты или даже люди.
В математике отношение чаще используется как «сколько раз одно число содержит другое».
Например, если есть четыре яблока и две груши, то отношение «четыре к двум» (то есть 4∶2, что эквивалентно отношению 2∶1), или если мы поменяем местами яблоки и груши , «от двух до четырех».
Отношение выражается как a к b (где вместо a и b любые числа), но чаще можно увидеть так a : b . Существуют различные способы прочтения этого обозначения:
- от a до b
- отношение a к b
Запишем соотношение четырех яблок и двух груш, используя символ отношения ( двоеточие ):
4 : 2
Это соотношение можно прочитать как «четыре к двум» или « отношение четырех». яблоки к двум грушам » или « четыре яблока к двум грушам ».
Если мы поменяем местами яблоки и груши, то получим соотношение 2 : 4. Это соотношение можно прочитать как «два к четырем» или «две груши к четырем яблокам». «.
Что такое соотношение?
Соотношение, как упоминалось ранее, записывается в виде a:b. Его также можно записать в виде дроби. А мы знаем, что такое обозначение в математике означает деление. Тогда результатом отношения является частное чисел a и b.
Отношение в математике — это частное двух чисел. Равные частные соответствуют равным отношениям.
Отношение позволяет узнать, сколько раз одно число содержит другое
Вернемся к соотношению четырех яблок к двум грушам (4 : 2). Это соотношение позволяет нам узнать, сколько яблок приходится на единицу груши. Под одной мы подразумеваем одну грушу. Сначала запишем отношение 4 : 2 в виде дроби:
Это отношение есть деление числа 4 на число 2. Если мы произведем это деление, то получим ответ на вопрос « Каково соотношение яблок и груш?»
Получили 2. Итак, четыре яблока на две груши (4 : 2)
На диаграмме показано, как четыре яблока и две груши связаны друг с другом Вы видите, что на каждую грушу приходится два яблока.
Отношение можно изменить, написав его как . Тогда мы получим отношение двух груш к четырем яблокам, или » отношение двух груш к четырем яблокам «.
Чтобы найти значение дроби нужно вспомнить как делить меньшее число на большее
Получили 0,5. Преобразуем эту десятичную дробь в обыкновенную:
Уменьшим полученную дробь на 5
Ответ: (половина груши). Таким образом, две груши и четыре яблока (2 : 4) относятся друг к другу так, что одно яблоко составляет половину груши
На рисунке показано, каково отношение между двумя грушами и четырьмя яблоками. Вы видите, что на каждое яблоко приходится половинка груши.
Числа, составляющие отношение, называются членами отношения .
. другие примеры соотношений. Рецепт предназначен для приготовления чего-либо. Рецепт основан на соотношении продуктов. Например, для овсянки обычно требуется чашка хлопьев на две чашки молока или воды. Соотношение 1:2 (« один к двум » или « одна чашка хлопьев к двум чашкам молока «).
Преобразуем соотношение 1 : 2 в дробь, получим . Подсчитав эту дробь, получим 0,5. Итак, один стакан хлопьев а два стакана молока связаны друг с другом таким образом, что один стакан молока равен половине стакана хлопьев
Если мы инвертируем соотношение 1 : 2, то получим соотношение 2 : 1 («два к одному»). » или «два стакана молока на один стакан каши»). Преобразуем соотношение 2 : 1 в дробь, получим . Подсчитав эту дробь, получим 2. Значит, два стакана молока и один стакан каши связаны друг к другу таким образом, что на один стакан хлопьев приходится два стакана молока.
Пример 2. В классе 15 учеников. Из них 5 мальчиков и 10 девочек. Мы можем записать соотношение девочек и мальчиков 10:5 и преобразовать это соотношение в дробь. Если мы посчитаем эту дробь, то получим 2. Вот и все, девочки и мальчики связаны друг с другом таким образом, что на каждого мальчика приходится две девочки
На рисунке показано, как связаны между собой десять девочек и пять мальчиков Другой.
Не всегда возможно перевести отношение в дробь и найти частное. В некоторых случаях это будет нелогично.
Итак, если вы перевернете соотношение, вы получите , то есть соотношение мальчиков и девочек. Если вы вычислите эту дробь, вы получите 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что каждая девочка наполовину мальчик. Математически, конечно, это правильно, но с точки зрения реальности не совсем разумно, потому что мальчик — живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.
Умение построить правильное соотношение является важным навыком при решении задач. Итак, в физике отношение пройденного расстояния ко времени есть скорость движения.
Расстояние обозначается переменной S , время переменной t , а скорость символом v . Тогда фраза «отношение пройденного пути ко времени есть скорость движения» будет описываться следующим выражением:
Предположим, автомобиль проехал 100 километров за два часа.
Скоростью принято называть расстояние, пройденное телом за единицу времени. Единицей времени является 1 час, 1 минута или 1 секунда. А соотношение, как упоминалось ранее, позволяет узнать, сколько одного объекта приходится на единицу другого объекта. В нашем примере отношение ста километров к двум часам показывает, сколько километров приходится на один час движения. Мы видим, что на каждый час движения приходится 50 километров
Следовательно, скорость измеряется в км/ч, м/мин, м/с . Символ дроби (/) указывает на отношение расстояния ко времени: километров в час, метров в минуту и метров в секунду соответственно.
Пример 2. Отношение стоимости товаров к их количеству равно цене одной единицы товара
Если мы взяли в магазине пять шоколадных пирожных и их общая стоимость составила 100 долларов, то мы можем определить цена одного торта.
Сравнение величин
Ранее мы узнали, что соотношение между величинами различных форм природы является новой величиной. Например, отношение пройденного пути ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.
Но соотношение также можно использовать для сравнения значений. Результатом соотношения является число, показывающее, во сколько раз первое значение больше второго.
Чтобы узнать, во сколько раз первое значение больше второго, запишите большее значение в числитель, а меньшее — в знаменатель.
Чтобы узнать, какая часть первого значения является второй, запишите в числитель меньшее значение, а в знаменатель большее значение.
Рассмотрим числа 20 и 2. Выясним, во сколько раз число 20 больше числа 2.
Значение этого отношения равно десяти
Отношение числа 20 к числу 2 составляет число 10. Это число показывает, во сколько раз число 20 больше числа 2. Таким образом, число 20 в десять раз число 2.
Пример 2. В классе 15 учеников. Из них 5 мальчиков и 10 девочек. Определите, во сколько раз девочек больше, чем мальчиков.
Запишите соотношение девочек и мальчиков. Запишите количество девочек в числителе и количество мальчиков в знаменателе:
Значение этого отношения равно 2. Таким образом, в классе из 15 учащихся вдвое больше девочек, чем мальчиков.
Вопрос о том, сколько девочек приходится на одного мальчика, больше не стоит. В этом случае соотношение используется для сравнения числа девочек и числа мальчиков.
Пример 3. Какая часть числа 20 равна числу 2.
Найдите отношение 2 к 20.
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее
Значение отношения числа 2 к числу 20 равно числу 0,1
В этом случае десятичную 0,1 можно преобразовать в правильную дробь. Этот ответ будет легче понять:
Таким образом, число 2 из 20 составляет одну десятую.
Вы можете сделать тест. Для этого нужно найти число 20. Если мы все сделали правильно, то должно получиться число 2
20 : 10 = 2
2 × 1 = 2
Мы получили число 2. Значит одна десятая от 20 это число 2. Отсюда делаем вывод, что задача решена правильно.
Пример 4. В классе 15 человек. Из них 5 мальчиков и 10 девочек. Определить, какую часть от общего числа учащихся составляют мальчики.
Запишите долю мальчиков к общему количеству учащихся. Запишите пять мальчиков в числителе и общее количество учеников в знаменателе.
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае число 5 делится на число 15.
Разделив 5 на 15, мы получим периодическую дробь. Преобразуем эту дробь в обыкновенную
Уменьшим полученную дробь на 3
Окончательный ответ . Итак, мальчики составляют треть класса.
Из рисунка видно, что в классе из 15 учеников треть класса составляют 5 мальчиков.
Если мы найдем из 15 учеников, которых нужно проверить, мы получим 5 мальчиков
15 : 3 = 5
5 × 1 = 5
Пример 5. Во сколько раз 35 больше числа
?
Напишите отношение числа 35 к числу 5. Запишите число 35 в числителе и число 5 в знаменателе, но не наоборот.
Значение этого отношения равно 7. Таким образом, число 35 в семь раз больше , чем число 5.
Пример 6. В классе 15 человек. Из них 5 мальчиков и 10 девочек. Определите, какую часть от общего числа составляют девочки.
Запишите соотношение девушек к общему количеству учащихся. Запишите в числителе коэффициента десять девочек, а в знаменателе — общее количество студентов. Общее количество учеников 5 мальчиков плюс 10 девочек, поэтому запишем 15 в знаменателе отношения
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае число 10 нужно разделить на число 15
Деление 10 на 15 дает периодическую дробь. Преобразуем эту дробь в обыкновенную
Уменьшим полученную дробь на 3
Окончательный ответ . Итак, девочки составляют две трети класса.
Из рисунка видно, что в классе из 15 учеников две трети класса составляют 10 девочек.
Если мы найдем 15 школьников для проверки, мы получим 10 девочек
15 : 3 = 5
5 × 2 = 10
Пример 7.
Запишите отношение десяти сантиметров к двадцати пяти сантиметрам. Запишите в числителе 10 см, а в знаменателе 25 см
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае нам нужно число 10 разделить на число 25
Преобразовать полученную десятичную дробь в обыкновенную дробь
Уменьшим полученную дробь на 2
Получили окончательный ответ . Значит 10 см это 25 см.
Пример 8. Во сколько раз 25 см больше 10 см
Запишите отношение двадцати пяти сантиметров к десяти сантиметрам. Запишем 25 см в числителе и 10 см в знаменателе
Найдем значение этого отношения
Ответ 2,5. Итак, 25 см в 2,5 раза больше 10 см (в два с половиной раза).
Важное примечание. При нахождении соотношения одноименных физических величин эти величины должны быть выражены в одной и той же единице измерения , иначе ответ будет неверным.
Например, если мы имеем дело с двумя длинами и хотим узнать, во сколько раз первая длина больше второй, то сначала обе длины должны быть выражены в одной единице (км, м, мили).
Пример 9. Во сколько раз 150 см больше 1 метра?
Во-первых, давайте выразим обе длины в одной единице. Для этого переведем 1 метр в сантиметры. Один метр — это сто сантиметров.
1 м = 100 см
Теперь найдем отношение ста пятидесяти сантиметров к ста сантиметрам. Запишем в числителе 150 сантиметров, а в знаменателе 100 сантиметров
Найдем значение этого отношения
Ответ: 1,5. Значит 150 см в 1,5 раза больше 100 см (в полтора раза).
А если бы мы не переводили метры в сантиметры, а сразу попытались найти отношение 150 см к одному метру, то мы бы имели следующее:
Получилось бы, что 150 см в сто пятьдесят раз больше более одного метра, и это неправильно. Поэтому необходимо обратить внимание на единицы физических величин, которые участвуют в соотношении.
Пример 10. В прошлом месяце зарплата директора банка составляла 25 000 долларов, а в этом месяце зарплата увеличилась до 27 000 долларов. Определите, во сколько раз новая заработная плата больше старой.
Запишите соотношение двадцать семь тысяч к двадцати пяти тысячам. Запишем 27000 в числителе и 25000 в знаменателе
Найдем значение этого отношения
Ответ был 1,08. Это означает, что заработная плата увеличилась на 1,08. В дальнейшем, когда мы познакомимся с процентами, такие показатели, как заработная плата, будем выражать в процентах.
Пример 11. Жилой дом имеет ширину 80 метров и высоту 16 метров. Каково соотношение между шириной дома и его высотой?
Запишите отношение ширины дома к его высоте:
Значение этого отношения равно 5.
Свойства из Отношение
-
- Отношение остается неизменным, если его члены умножаются или делятся на одно и то же ненулевое число ,
- a/b = pa/pb = qa/qb , p, q ≠0
- a/b = (a/p) / (b/p) = (a/q) / (b/q) , p, q ≠0
- Два отношения в представлении дробей можно сравнивать так же, как мы сравниваем действительные числа .
- a/b = p/q ⟺ aq = bp
- a/b > p/q ⟺ aq > bp
- a/b < p/q ⟺ aq < bp
- Если два отношения a/b и c/d равны
- a/b = c/d ⟹ b/a = d/c (Invertendo)
- a/b = c/d ⟹ a/c = b/d (Альтернэндо)
- a/b = c/d ⟹ (a+b)/b = (c+d)/d (Componendo)
- a/b = c/d ⟹ (a-b)/b = (c-d)/d (дивидендо)
- Отношение остается неизменным, если его члены умножаются или делятся на одно и то же ненулевое число ,
Отношение не изменится, если его члены умножить или разделить на одно и то же число.
Это одно из наиболее важных свойств следующего соотношения. Мы знаем, что если частное и делитель умножить или разделить на одно и то же число, то частное не изменится. А так как отношение есть не что иное, как деление, то свойство частного работает и на него.
Вернемся к соотношению девочек и мальчиков (10 : 5). Это соотношение показывает, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.
В нашем примере удобнее делить члены отношения на их наибольший общий делитель (НОД).
НОД членов 10 и 5 равен числу 5. Следовательно, можно разделить члены отношения на число 5
У нас есть новый коэффициент . Это соотношение два к одному (2:1). Это соотношение, как и предыдущее соотношение 10:5, показывает, что на каждого мальчика приходится две девочки.
На рисунке показано соотношение 2 : 1 (два к одному).
Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз девочек в первом классе больше, чем мальчиков? Во сколько раз девочек во втором классе больше, чем мальчиков?
В обоих классах девочек в два раза больше, чем мальчиков, потому что отношения и равны .
Свойство ratio позволяет создавать разные модели, имеющие параметры, схожие с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 м и высоту 10 м.
Чтобы нарисовать подобный дом на бумаге, нужно нарисовать его в том же соотношении 30 : 10.
Разделим оба члена этого соотношения на число 10. Тогда получим соотношение 3 : 1. Это отношение равно 3, как и предыдущее отношение равно 3
Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров.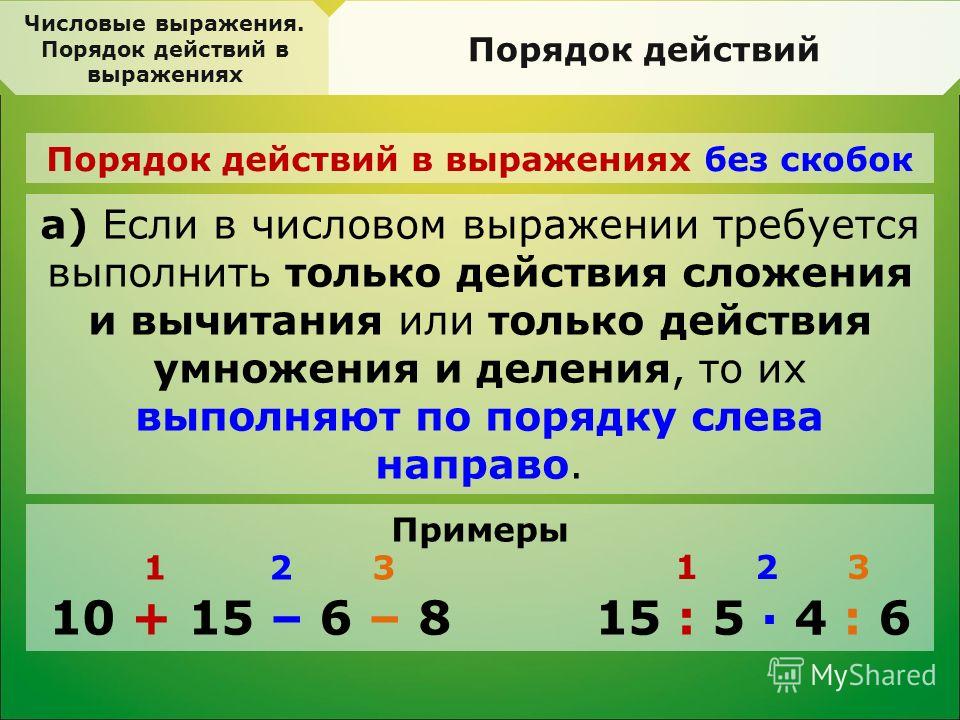
3 м = 300 см
1 м = 100 см
Соотношение 300 см : 100 см. Разделим слагаемое этого соотношения на 100. Получится соотношение 3 см : 1 см. Теперь мы можем нарисовать дом шириной 3 см и высотой 1 см.
Конечно, нарисованный дом намного меньше реального дома, но соотношение ширины и высоты остается прежним. Это позволило нам нарисовать дом максимально похожим на настоящий дом
Отношение можно понимать и по-другому. Изначально было сказано, что настоящий дом имеет ширину 30 метров и высоту 10 метров. Итого 30+10, то есть 40 метров.
Эти 40 метров можно представить как 40 частей. Соотношение 30 : 10 означает, что 30 частей относятся к ширине и 10 частей к высоте.
Затем члены соотношения 30 : 10 поделили на 10. Получилось соотношение 3 : 1. Это соотношение можно понимать как 4 части, три из которых — ширина, а одна — высота. В этом случае обычно требуется знать, сколько конкретных метров приходится на ширину и высоту.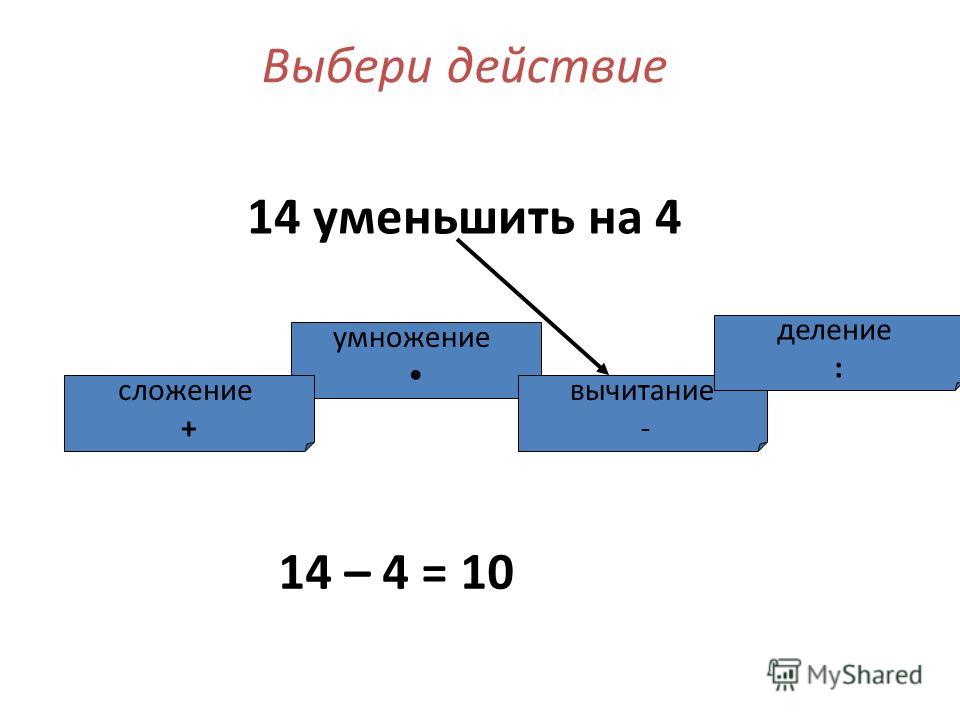
Другими словами, нужно узнать, сколько метров в 3 частях и сколько метров в 1 части. Для начала нужно узнать, сколько метров приходится на одну деталь. Для этого разделите сумму 40 метров на 4, так как в соотношении 3 : 1 всего четыре части
40 м : 4 = 10 м
Затем с помощью умножения определите, сколько метров приходится на ширину и высоту . В качестве коэффициента используются условия, которые приведены в соотношении.
Определить, сколько метров приходится на ширину:
10 м × 3 = 30 м
Определим, сколько метров приходится на высоту:
10 м × 1 = 10 м
Несколько членов в соотношении
Если в соотношении дано более одного члена , их можно понимать как части чего-то.
Пример 1. Купили 18 яблок. Яблоки раздали маме, папе и дочке в соотношении 2 : 1 : 3. Сколько яблок получил каждый?
Соотношение 2 : 1 : 3 означает, что мама получила 2 части, папа – 1 часть, а дочь – 3 части.
Если сложить члены отношения 2 : 1 : 3, то можно узнать, сколько всего частей:
2 + 1 + 3 = 6 (частей)
Давайте узнаем, сколько яблок на одну часть. Для этого 18 яблок разделим на 6
18 : 6 = 3 (яблоки на одну часть)
Теперь определим, сколько яблок получил каждый человек. Умножив три яблока на каждого члена соотношения 2 : 1 : 3, можно определить, сколько яблок досталось маме, сколько яблок досталось папе и сколько яблок досталось дочери.
Посмотрим, сколько яблок получила мама:
3 × 2 = 6 (яблок)
Посмотрим, сколько яблок получил папа:
3 × 1 = 3 (яблок)
Посмотрим, сколько яблок Дочь получила:
3 × 3 = 9 (яблоки)
Пример 2. Новое серебро (альпака) — сплав никеля, цинка и меди в соотношении 3 : 4 : 13. Сколько килограммов каждый металл должен быть взят, чтобы сделать 4 кг нового серебра?
4 килограмма нового серебра будут содержать 3 части никеля, 4 части цинка и 13 частей меди.
3 + 4 + 13 = 20 (деталей)
Определим, сколько килограммов будет в одной части:
4 кг : 20 = 0,2 кг
Определим, сколько килограммов никеля будет содержаться в 4 кг новой Серебряный. Соотношение 3 : 4 : 13 указывает на то, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:
0,2 кг × 3 = 0,6 кг никеля
Теперь определим, сколько килограммов цинка будет содержаться в 4 кг нового серебра. Соотношение 3 : 4 : 13 указывает на то, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:
0,2 кг × 4 = 0,8 кг цинка
Теперь определим, сколько килограммов меди будет содержаться в 4 килограммах нового серебра. Соотношение 3 : 4 : 13 говорит о том, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:
0,2 кг × 13 = 2,6 кг меди
Итак, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.
Пример 3. Латунь представляет собой сплав меди и цинка, масса которого составляет 3 : 2. Для изготовления куска латуни требуется 120 г меди. Сколько цинка требуется для изготовления этого куска латуни?
Определить, сколько граммов сплава содержится в изделии. В условии сказано, что для изготовления куска латуни требуется 120 граммов меди. Там же сказано, что три части сплава содержат медь. Если 120 разделить на 3, то узнаем, сколько граммов сплава в одной детали:
120 : 3 = 40 грамм на деталь
Теперь определим, сколько цинка нужно для изготовления куска латуни. Для этого умножьте 40 граммов на 2, так как соотношение 3 : 2 указывает на то, что две части содержат цинк:
40 г × 2 = 80 г цинка
Пример 4. Берут два сплава золота и серебра. В одном из них соотношение этих металлов 1:9, а в другом 2:3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, содержащего золото и серебро в соотношении 1:4?
Раствор
15 кг нового сплава должны состоять из соотношения 1 : 4.
Определим массу одной детали. Для этого сначала сложите все части (1 и 4), затем разделите массу сплава на количество этих частей
1 + 4 = 5
15 кг : 5 = 3 кг
Одна часть сплав будет иметь массу 3 кг. Тогда 15 кг нового сплава будут содержать 3 × 1 = 3 кг золота и 3 × 4 = 12 кг серебра.
Следовательно, нам потребуется 3 кг золота и 12 кг серебра для получения сплава массой 15 кг.
Теперь ответим на вопрос задачи — « Сколько нужно взять каждого сплава? »
Возьмем 10 кг первого сплава, так как золото и серебро в нем находятся в соотношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.
Для второго сплава возьмем 5 кг, так как золото и серебро находятся в соотношении 2 : 3. Таким образом, этот второй сплав даст нам 2 кг золота и 3 кг серебра
Видео урок
Содержание
- Отношение чисел
- Урок 21 Бесплатно Отношения
- Отношение
- Отношение и часть от числа
- Отношения в задачах
- Интересная информация
- Заключительный тест
- Относительное целое число
- Резюме
- Мотивация
- Фрагменты истории
- Правила эксплуатации
- Добавление
- Умножение
- Набор целых чисел
- Строительство
- Состав
- Расширения
- Общее использование
Отношение чисел
Отношение чисел — это частное от деления одного числа на другое.
Отношение чисел a и b можно записать двумя способами: с помощью знака деления, либо с помощью дробной черты (в виде дроби):
Эти записи читаются так: отношение a к b или отношение числа a к числу b .
Числа a и b, составляющие отношение a : b, называются членами отношения. Делимое называется предыдущим членом отношения, а делитель — последующим членом отношения. Так, a — предыдущий член, b — последующий.
Отношение используют для сравнения двух чисел. Так, отношение a : b показывает, во сколько раз a больше b (если делимое больше делителя) или какую часть числа b составляет a (если делимое меньше делителя).
Отношение 35 к 7 показывает, что число 35 в 5 раз больше, чем число 7.
2)
Отношение 12 к 15 показывает, что число 12 составляет 0,8 от числа 15.
Из основного свойства частного следует основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, отличное от нуля.
Источник
Урок 21 Бесплатно Отношения
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Отношение
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как (mathbf) или же через дробную черту: (mathbf<frac>)
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
- может получиться натуральное число
- обыкновенная дробь
- смешанное число
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
- если отношение получилось больше 1, значит, первое число больше второго
- если меньше 1, то второе число больше первого
- если отношение оказалось равно 1, значит, числа равны
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в (mathbf<1frac<1><4>>) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в (mathbf<frac<2><3>>) раза.
Мы можем сформулировать вывод и так: 16 составляет (mathbf<frac<2><3>>) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
И посчитаем отношение 28 к 14
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно (mathbf<frac<2><5>>), найдем отношение b к a
Для этого надо найти обратное число к (mathbf<frac<2><5>>)
Значит, отношение b к a равняется (mathbf<2frac<1><2>>)
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно (mathbf<frac<1><3>>)
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно (mathbf<frac<1><3>>)
Пройти тест и получить оценку можно после входа или регистрации
Отношение и часть от числа
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него (mathbf<frac<3><8>>)
Перемножив, мы получим:
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна (mathbf<2frac<1><2>>)
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
Ответ: дробь, взяв которую от 10 получили (mathbf<2frac<1><2>>), равняется (mathbf<frac<1><4>>)
Пример 2
Отношение первого числа ко второму равно (mathbf<1frac<1><5>>), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к (mathbf<1frac<1><5>>)
Теперь можно найти второе число, домножим первое на эту дробь:
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно (mathbf<1frac<1><2>>)
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
Ответ: число a равняется 12
Пройти тест и получить оценку можно после входа или регистрации
Отношения в задачах
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
Значит, длина освещенного участка составляет (mathbf<frac<3><5>>) от длины всей улицы.
Во втором вопросе нас спрашивают: «Во сколько раз больше?» — это соответствует отношению большего числа к меньшему.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
Что отвечает на вопрос второго пункта.
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Источник
Относительное целое число
В математике , А относительное число является числом , которое появляется в качестве натурального числа к которым мы добавили положительный или отрицательный знак , указывающий его положение относительно 0 на ориентированную оси. Положительные целые числа (больше нуля) отождествляются с натуральными целыми числами : 0, 1, 2, 3… в то время как отрицательные целые числа являются их противоположностями : 0, −1, −2, −3… Таким образом, целое число 0 является единственным числом, которое как положительные, так и отрицательные.
Вещественное число является целым числом , если он не имеет дробную части , то есть , если его десятичные письма не включают цифру (кроме нуля ) «после десятичной точки».
Относительные целые числа используются для выражения разницы между любыми двумя натуральными числами. Среди других значений различия мы можем указать положение на оси, ориентированной относительно опорной точки (ось с дискретными положениями , то есть прерывистая); перемещение из исходного положения в любом направлении; или вариация целочисленного значения, поэтому подсчитывается в единицах (положительное изменение для выигрыша, отрицательное для проигрыша).
Множество целых чисел обозначаются « Z », заглавная буква жир текста набранного постепенно вытесняется рукописным сценарием с слэшем перфорированным «ℤ». Наличие звездочки в верхнем индексе (« Z *») обычно обозначает набор ненулевых относительных целых чисел, даже если это обозначение иногда используется для набора обратимых элементов Z [ ref. желаемый] , то есть пара целых чисел <−1, 1>. Обозначение « Z — » обозначает набор отрицательных целых чисел. Реже можно встретить обозначение « Z + », замененное обозначением « N » натуральных чисел при идентификации.
Этот набор ( полностью ) упорядочен для обычного отношения сравнения, унаследованного от натуральных чисел. Он также снабжен операциями сложения и умножения, которые составляют основу понятия кольца в алгебре .
Относительные целые числа также иногда называют рациональными целыми числами , это имя не следует путать с рациональными числами или дробями. Это название происходит от английского рационального целого числа , и обозначает конкретный случай алгебраических чисел , построенных на номер поле из рациональных чисел . Мы находим это имя у Николя Бурбаки и некоторых математиков, которые являются частью движения современной математики , включая Жоржа Папи .
Резюме
Мотивация
Основная причина введения отрицательных чисел — возможность решить все уравнения вида:
a + x = b , где x — неизвестное, а a и b — параметры.
В наборе натуральных чисел только некоторые из этих уравнений имеют решение.
5 + x = 8 тогда и только тогда, когда x = 3 9 + x = 4 не имеет решения в множестве натуральных чисел. У него есть решение в наборе относительных целых чисел, равном −5.
Фрагменты истории
Первый намек на отрицательные числа появляется в индийских текстах, таких как Арибхатия индийского математика Арьябхата (476–550), где определены правила сложения и вычитания. Затем отрицательные числа отображаются как долги, а положительные числа — как поступления. Несколько веков спустя в трудах персидского математика Абу л-Вафы (940–998) появляются произведения отрицательных чисел на положительные числа. Однако число по-прежнему связано с физическими величинами, а отрицательное число не имеет юридического статуса . Аль Хуваризми (783-850), например, в своей работе « Транспонирование и редукция» предпочитает иметь дело с шестью типами квадратных уравнений вместо того, чтобы рассматривать вычитания.
В Европе относительные числа появляются поздно, мы обычно приписываем Саймону Стевину (1548–1620) знаменитое правило знаков для произведения двух относительных целых чисел. Сам Даламбер (1717-1783) в Энциклопедии считает относительное число опасной идеей.
«Мы должны признать, что нелегко закрепить идею отрицательных величин, и что несколько умных людей даже поспособствовали тому, чтобы запутать ее своими неточными представлениями о ней. Сказать, что отрицательная величина меньше ничто, означает выдвинуть вперед нечто, чего нельзя вообразить. Те, кто утверждает, что 1 не сравнимо с -1 и что соотношение между 1 и -1 отличается от отношения между -1 и 1, совершают двойную ошибку […] Следовательно, на самом деле нет абсолютно изолированной отрицательной величины. : −3 взято абстрактно, не представляет для ума никакой идеи. «
— Д’Аламбер, Разумный словарь наук, искусств и ремесел, т. 11
Нам нужно подождать еще два столетия и появление формализма, чтобы увидеть появление формального построения множества относительных целых чисел из классов эквивалентности пар натуральных чисел.
Именно к Дедекинду (1831-1916) , что мы должны эта конструкция. Сам он использовал букву K для обозначения набора относительных целых чисел. Было использовано несколько других условных обозначений, пока Николя Бурбаки не популяризировал использование буквы , инициала немецкого Zahlen (чисел). Z < Displaystyle mathbb >
Правила эксплуатации
В относительном числе мы различаем знак (+ или -) и абсолютное значение : −3 имеет абсолютное значение 3.
Добавление
Сумма двух целых чисел с одинаковым знаком получается сложением двух абсолютных значений и сохранением общего знака:
(−3) + (−5) = −8, запись сокращенно −3-5 = −8, удаление рабочего знака +.
Сумма двух относительных целых чисел с противоположными знаками получается путем вычисления разницы между двумя абсолютными значениями и присвоения ей знака целого числа с наибольшим абсолютным значением:
(+3) + (−5) = −2, записывая, что мы сокращаемся до 3-5 = −2.
Умножение
Результат умножения называется произведением. Произведение двух относительных чисел с одинаковым знаком всегда положительно (+) и получается как произведение абсолютных значений:
(+3) × (+4) = +12, которое мы сокращаем до 3 × 4 = 12 (−3) × (−7) = + 21 = 21
(+ не является обязательным, если продукт не отрицательный)
Произведение двух относительных чисел с разными знаками всегда отрицательно (-) и получается путем произведения абсолютных значений.
больше, умноженное на большее , дает больше продукта . меньше умножается на меньшее , дает больше продукта меньше, умноженное на большее или большее, умноженное на меньшее, дает меньше продукта
Набор целых чисел
Строительство
Множество Z относительных целых чисел можно рассматривать как симметризацию полукольца N натуральных чисел.
Состав
Набор относительных целых чисел, снабженный законами сложения и умножения, является прототипом понятия кольца . Это даже евклидово кольцо в отношении евклидова деления . Следовательно, он также является главным и факториальным .
Ему может быть предоставлена дискретная топология, связанная с обычным расстоянием, индуцированным абсолютным значением разности, что делает его полным метрическим пространством . Единственные другие расстояния, совместимые с кольцевой структурой, — это p -адические расстояния , где p — простое число .
Аддитивная групповая структура ( Z , +) представляет собой моногенную группу без кручения , т.е. свободную абелеву группу ранга 1.
Множество Z является вполне упорядоченным для обычного отношения порядка.
Относительные целые числа образуют бесконечное счетное множество .
Расширения
Множество Z целых чисел погружается всех десятичных чисел , обозначаемый D , который сам по себе является частью множества рациональных чисел отмечено Q .
Понятие целого числа расширяется определением алгебраических целых чисел , которые относятся к различным полям чисел так же, как относительные целые числа относятся к полям рациональных чисел . Целые рациональные числа, то есть алгебраические целые числа поля рациональных чисел, поэтому являются в точности относительными целыми числами.
Для каждого из расстояний р -адическая, заполненного Z является кольцом целых р -адического отмеченным Z р , доля тела является телом из чисел р -адического, обозначается Q р и который содержит Q .
Общее использование
Относительные числа — это числа, которые стали относительно привычными. Их обнаруживают:
Источник



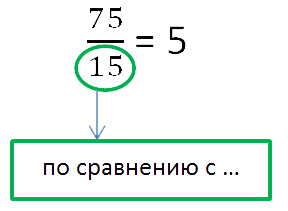
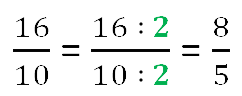



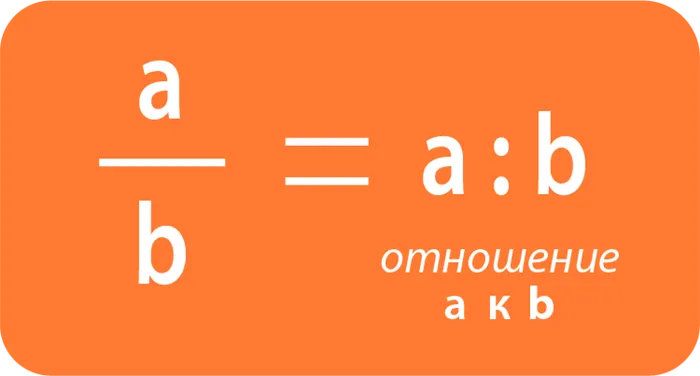
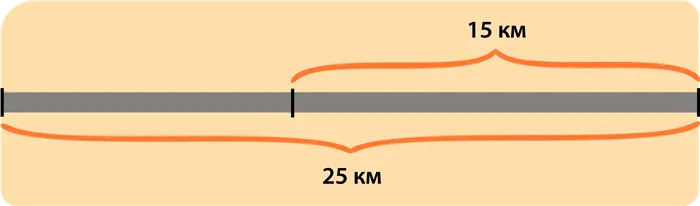
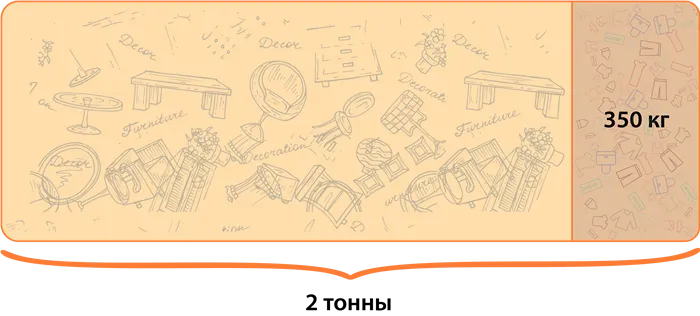


 Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?
Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?



 Итак, мы пишем это как 15/20.
Итак, мы пишем это как 15/20. 
 Из них 10 взрослых, остальные дети. Каково отношение количества детей к общему количеству учащихся в музыкальном классе?
Из них 10 взрослых, остальные дети. Каково отношение количества детей к общему количеству учащихся в музыкальном классе?  Следовательно, 2:3 > 1:2.
Следовательно, 2:3 > 1:2.