Как найти отношение энтропии

Понятие энтропии ввел Р. Клаузиус в 1865 г.

Энтропия – функция состояния

Для того чтобы выяснить в чем состоит физический смысл энтропии, рассмотрим изотермический процесс и приведенное количество теплоты в этом процессе на очень малом участке этого процесса -$frac{delta Q}{T}$, где $delta Q$ – количество теплоты, которое получает тело, $T$ – температура тела.

Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе:

$oint {frac{delta Q}{T}=0left( 1 right).}$

Равенство нулю левой части выражения (1), который берут по замкнутому контуру, означает, что отношение δQ/T – это полный дифференциал некоторой функции состояния системы, которая не зависит от формы пути перехода системы из начального состояния в конечное.

Введем следующее обозначение:

$frac{delta Q}{T}=dSleft( 2 right)$.

Для обратимых процессов изменение энтропии равно нулю:

$Delta S=0left( 3 right)$.

Если выполняется необратимый процесс, то энтропия системы увеличивается:

$Delta S$>$0, left( 4 right)$.

Все реальные процессы являются необратимыми, поэтому в реальности энтропия изолированной системы способна только расти. Она становится максимальной в состоянии термодинамического равновесия.

«Энтропия простыми словами с формулами» 👇

Неравенство Клаузиуса

Выражения (3) и (4) объединяются в неравенство, которое называется неравенством Клаузиуса:

$Delta Sge left( 5 right)$.

Неравенство Клаузиуса означает, что для замкнутой системы энтропия способна увеличиваться (если процесс необратим), или не изменяется (процесс обратим).

Неравенство Клаузиуса является математической записью второго начала термодинамики.

Знак изменения энтропии указывает направление течения процесса в обратимом процессе.

Во всех ординарных термодинамических системах при стремлении температуры к бесконечности, внутренняя энергия системы безгранично растет. Абсолютная температура при равновесных процессах может только большей нуля, следовательно, если система подвергается нагреву, то:

$dS$>$0.$

При уменьшении температуры системы имеем:

$dS$

Изменение энтропии в равновесном процессе

Допустим, что термодинамическая система совершает равновесный переход из состояния 1 в состояние 2, тогда изменение энтропии найдем как:

$Delta S=S_{2}-S_{1}=intlimits_1^2 {frac{delta Q}{T}=intlimits_1^2{frac{dU+delta A}{T}left( 6 right),} }$

где $dU$ – изменение внутренней энергии в рассматриваемом процессе; $delta A$ – работа, выполняемая в этом процессе.

Выражение (6) способно определить энтропию с точностью до аддитивной константы. Это означает то, что физическим смыслом обладает не энтропия, а ее разность.

$S=intlimits_{обр} {frac{delta Q}{T}+const, left( 7 right).}$

Свойства энтропии

Свойство аддитивности имеют:

• масса;
• внутренняя энергия;
• количество теплоты.

Аддитивными не являются:

• объем,
• температура,
• давление.

Так, при обратимом адиабатном процессе мы имеем:

$delta Q=0to S=const.$

Энтропия однородной термодинамической системы – это функция пары независимых параметров, характеризующих ее состояние, например, $ p,V$ или $ T,V$ при $ m=const$.

В этой связи можно записать, что:

$left( V,T right)=intlimits_0^T {C_{V}frac{dT}{T}+S_{01, }left( 8right).}$

или

$Sleft( p,T right)=intlimits_0^T {C_{p}frac{dT}{T}+S_{02, }left( 9right),}$

где $intlimits_0^T {C_{V}frac{dT}{T},}$ – находят для обратимого изобарного процесса; $intlimits_0^T {C_{p}frac{dT}{T}}$ – вычисляют для обратимого изохорного процесса, при изменении температуры от 0К до $T$; $C_V$ – теплоемкость изохорного процесса; $C_p$ – теплоемкость при изобарном процессе; $S_{01 }=S(V,0)$ ; $S_{02 }=S(p,0).$

Статистический смысл энтропии

Допустим, что энтропия в обратимом процессе претерпевает изменения под воздействием внешних условий, которые оказывают влияние на систему. Механизм действия этих условий на энтропию можно сформулировать так:

1. Внешние условия определяют микросостояния, которые доступны системе, а также их количество.
2. В рамках доступных для системы микросостояний, она приходит в состояние равновесия.
3. Энтропия получает соответствующее значение. Получается, что величина энтропии идет за изменением внешних условий, принимая наибольшую величину, совместимую с внешними условиями.

Глубокий смысл энтропии раскрывается в статистической физике. Энтропия связана с термодинамической вероятностью состояния системы.

Термодинамическая вероятность всегда больше или равна единице.

Энтропия системы и термодинамическая вероятность связаны между собой формулой Больцмана:

$S=k ln⁡(W) (10),$

где $k$ – постоянная Больцмана.

1. Формула (10) означает, что энтропия определена натуральным логарифмом количества микросостояний, которые реализуют рассматриваемое макросостояние.
2. Согласно формуле Больцмана, энтропия – это мера вероятности состояния термодинамической системы.
3. Говорят, что энтропия – мера беспорядка системы. Это статистическая интерпретация энтропии. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
4. Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
5. Поскольку при необратимых процессах энтропия увеличивается, при статистическом толковании это значит, процессы в замкнутой системе проходят в направлении роста количества микросостояний. Это означает, что процессы идут от менее вероятных к более вероятным, до достижения вероятностью максимальной величины.

Энтропия? Это просто!

Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora

Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.

Так что же такое энтропия?

Если в двух словах, то

Энтропия — это то, как много информации вам не известно о системе

Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.

Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём).

Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).

А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.

Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.

Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:

S = log Ω

Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B.

Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.

Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.

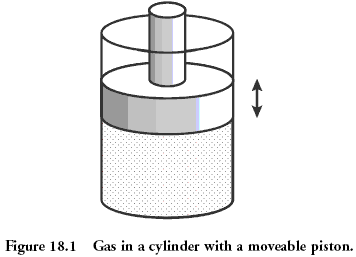
Физический пример: газ под поршнем

Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.

Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:

p = ρT

хотя вы, скорее всего, лучше знакомы с уравнением Клапейрона — Менделеева pV = νRT — это то же самое уравнение, только с добавлением пары констант, чтобы вас запутать. Чем больше микросостояний отвечают данному макросостоянию, то есть чем больше частиц входят в состав нашей системы, тем лучше уравнение состояния её описывают. Для газа характерные значения числа частиц равны числу Авогадро, то есть составляют порядка 10²³.

Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.

Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.

Твёрдые тела и потенциальная энергия

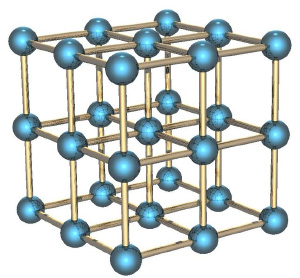
Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия.

Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.

Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.

Понимаем второй закон термодинамики

Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад.

Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.

Перемешивание газов

И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.

Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).

Разбираемся с демоном Максвелла

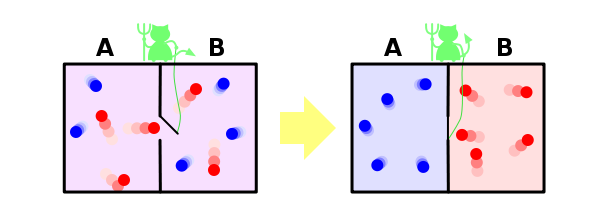
Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.

Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?

Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.

Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.

Энтропия. Примеры вычисления энтропии

Энтропия
– это такая функция состояния, дифференциал
которой определяется отношением:

.

В СИ энтропия

измеряется в Дж/К.

Приведём
формулы для подсчёта изменения энтропии
в случае изопроцессов для идеального
газа:

а) Изохорический
процесс:

,
.

б) Изобарический
процесс:

,
.

в) Изотермический
процесс:

,
.

г) Адиабатический
процесс:

,
,
.

Энтропия и второе начало термодинамики

— адиабатический процесс,

— изохорический процесс,

— изобарический процесс,

— изотермический процесс.

Понятие энтропии имеет статистическое
толкование. Состояние макроскопического
тела (т.е. тела, образованного огромным
количеством молекул) может быть задано
с помощью объёма, давления, температуры,
внутренней энергии и других макроскопических
величин. Охарактеризованное таким
способом состояние называетсямакросостоянием. Состояние
макроскопического тела, охарактеризованное
настолько подробно, что оказываются
заданными состояния всех образующих
тело молекул, называетсямикросостоянием.
Всякое макросостояние может быть
осуществлено различными способами,
каждому из которых соответствует
некоторое микросостояние тела. Число
различных микросостояний, соответствующих
данному макросостоянию, называетсястатистическим весом
илитермодинамической вероятностью
макросостояния. В статистической
физике существует теорема, которая
утверждает о равновероятности всех
микросостояний данной системы. В качестве
характеристики вероятности состояния
можно было бы выбрать статистический
вес
,
однако такая характеристика не обладала
бы свойствами аддитивности. Поэтому в
качестве характеристики состояния
принимается величинаS,
пропорциональная логарифму статистического
веса
.

,
(4)

где
— постоянная Больцмана. Такую величину
называютэнтропией.

Определённая
таким образом энтропия обладает
следующими свойствами:

1. Энтропия
   изолированной системы при протекании
   необратимого процесса возрастает.
   Действительно, изолированная, т.е.
   предоставленная самой себе, система
   переходит из менее вероятных в более
   вероятные состояния, что сопровождается
   ростом величины (4).

2. Энтропия
   системы, находящейся в равновесном
   состоянии, максимальна.

Эти
утверждения и составляют содержаниевторого начала термодинамики:

Энтропия
изолированной системы может только
возрастать, (либо по достижении
максимального значения оставаться
неизменной), т.е.
.

Итак, при протекании
в изолированной системе необратимого
процесса энтропия возрастает, т.е.

.
(5)

В статистической
физике доказывается, что в ходе обратимого
процесса, сопровождающегося сообщением
системе количества теплоты
,
энтропия системы получает приращение

,
(6)

что совпадает
с принятым ранее определением энтропии

.

В определении
(6) весьма существенна обратимость
процесса, в ходе которого системе
сообщается теплота
.
Если количество теплоты
сообщается системе в ходе необратимого
процесса, энтропия возрастает как
вследствие сообщения тепла, так и
вследствие необратимости процесса.
Поэтому имеет место неравенство

.
(7)

Под
в (7) подразумевается температура
резервуара, от которого данная система
получает теплоту
.

Формулы (6) и
(7) можно объединить вместе, написав

.
(8)

Знак равенства относится
к обратимым, знак неравенства к необратимым
процессам.

Соотношение
(8), записанное в виде

,

или

,

называется
основным термодинамическим неравенством
Клаузиуса.

При абсолютном нуле температуры всякое
тело, как правило, находится в основном
состоянии, статистический вес которого
равен единице ().
Формула (4) даёт в этом случае для энтропии
значение равное нулю. Отсюда вытекает,
что энтропия всякого тела стремится к
нулю при стремлении к нулю температуры:

.

Это утверждение
представляет собой содержание третьего
начала термодинамики.

Соседние файлы в папке Физика. Лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. Энтропия
2. Принцип существования энтропии
3. Принцип возрастания энтропии
4. Принцип действия тепловой машины
5. Цикл Карно. Максимальный КПД
6. Второе начало термодинамики

Энтропия — это физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Энтропия

Энтропия это, в широком смысле, мера хаоса в какой-либо системе. В переводе «энтропия» означает «преобразование».

Энтропия простыми словами — это то, как много информации вам не известно о системе.

В статистической физике энтропия характеризует вероятность осуществления какого-либо макроскопического состояния. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике. В этих областях знания энтропия определяется статистически и называется статистической или информационной энтропией.

В широком смысле, в каком слово часто употребляется в быту, энтропия означает меру сложности, хаотичности или неопределённости системы: чем меньше элементы системы подчинены какому-либо порядку, тем выше энтропия. Величина, противоположная энтропии, именуется негэнтропией или, реже, экстропией.

Принцип существования энтропии

В середине прошлого века было сделано существенное открытие» касающееся обратимых термодинамических процессов. Оказалось, что наряду с внутренней энергией у тела имеется еще одна замечательная функция состояния — энтропия. Также, как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. Опыт дает значение разности приращения энтропии. Если тело или система при бесконечно малом переходе из одного состояния в другое при температуре  получает тепло  то отношение  является полным дифференциалом некоторой функции  Эта функция и есть энтропия
 определяющаяся, таким образом, одним из двух эквивалентных равенств:

Утверждение о существовании функции, дифференциал которой есть носит название принципа существования энтропии и  является одним из важнейших законоз природы. Оно является существенной частью второго начала термодинамики, о чем у нас речь пойдет ниже. Открытие этого принципа, как и всего второго начала термодинамики, связано, прежде всего, с именами Карно и Клаузиу-са. Сущность принципа, несмотря на некоторую его абстрактность, легко понять: переход тела из одного состояния во второе может произойти бесчисленным количеством способов (разные кривые на графике, начинающиеся и заканчивающиеся в тех же точках); при этих переходах тело может получать самые различные количества тепла, однако во всех случаях интеграл будет иметь одинаковые значения. Отношение количества теплоты к той температуре, при которой это тепло было получено, называют иногда приведенной теплотой. Так как интеграл всегда можно представить приближенно суммой то изменение  энтропии при переходе из одного, состояния в другое равно сумме приведенных теплот. Предположим, что тело, равномерно нагреваясь от 20 до 25 °С, получает при подъеме температуры по одному джоулю тепла на каждый градус. Тогда прирост энтропии будет примерно равен

Наиболее просто выражаются изменения энтропии при изотермических процессах:
где — полученное при процессе тепло. Так, например, при таянии 1 кг льда энтропия вещества возрастает на

За нуль энтропии может быть принято значение энтропии любого состояния (кипящей воды, плавящегося льда). Однако в некоторых случаях принимают за нуль значение энтропии вещества при абсолютном нуле температуры. Для этого, впрочем, имеются некоторые теоретические основания (теорема Нернста), на которых мы останавливаться не будем.

Приняв энтропию вещества при температуре можно найти по формуле

если нагрев происходит при постоянном давлении. Как видим, чтобы знать энтропию, надо изучить ход теплоемкости с температурой.

Если известно уравнение состояния вещества, то энтропия (с точностью до произвольной постоянной) может быть вычислена  весьма просто. По определениюПодставляя значение для таким, как его дает первое начало термодинамики, получим

При помощи уравнения газового состояния исключим отсюда давление. Получим:   Если взять неопределенный интеграл, то получим выражение энтропии с точностью до произвольной постоянной

Можно также взять от определенный интеграл, пределами которого являются два состояния. Тогда получится выражение для разности энтропий двух состояний

Это — выражения для энтропии идеальных газов. Из формул видно, что энтропия возрастает при повышении температуры, а также при увеличении объема газа. Это, разумеется, полностью совпадает с общим утверждением о повышении энтропии при подводе к телу тепла.

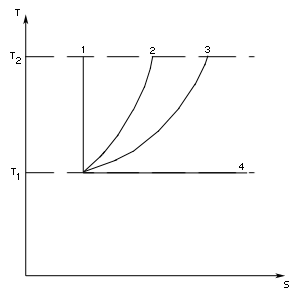
Пример. Покажем, что энтропия действительно есть функция состояния системы. Обратимся к примеру на стр. 151 (рис. 79). Путь 1—2—3. Изменение энтропии

Изменение энтропии

Полное изменение энтропии на пути 1—2—3

Видно, что действительно, каким бы путем ни совершался переход газа из состояния 1 в состояние 3, изменение энтропии одно и то же.

Принцип возрастания энтропии

Как уже говорилось, обратимых процессов, строго говоря, не существует, хотя с точностью, доступной опыту, можно осуществить множество процессов, практически неотличимых от обратимых. Имеются, однако, примеры процессов, которые всегда односторонни и уже поэтому никоим образом не могут быть обращены. Так, например, газ может расшириться сам по себе, но не может сжиматься без приложения внешних сил. Тепло может самопроизвольно переходить от горячего тела к холодному и только при затрате работы (например, электроэнергии) может переходить от холодного тела к более нагретому. При трении кинетическая энергия макроскопического движения всегда превращается во внутреннюю энергию, но никогда не происходит самопроизвольный обратный процесс. Необратимость всех остальных процессов в конечном счете связана с тем, что в каждом из них в той или иной степени присутствует один из перечисленных односторонних процессов. В реальных процессах невозможно избежать ни самопроизвольных расширений, ни трения, ни теплового рассеяния.

Нет ли какого-нибудь общего признака у всех перечисленных односторонних процессов? Оказывается, есть: этот признак состоит в том, что во всех односторонних процессах возрастает энтропия.

В случае теплообмена между двумя телами общее (всей системы) изменение энтропии равно

где — тепло, полученное более холодным телом,— тепло, потерянное более горячим телом.

Если больше так как мы считаем положительным тепло, сообщенное телу. Значит,

т. е. при теплообмене общая энтропия системы, в которой произошел теплообмен, возрастает.

Другой случай. Внутри сосуда с газом происходит интенсивное механическое движение (скажем, вертится колесо). Объем не меняется, температура растет, поэтому энтропия изменится на

Наконец, при расширении в пустоту при неизменной температуре прирост энтропииопять-таки положительный.

Итак, во всех односторонних процессах энтропия системы возрастает.

Нетрудно понять, какое значение имеет этот вывод для всех необратимых процессов. Так как каждый необратимый процесс сопровождается односторонними явлениями, идущими с повышением энтропии,.то прирост, энтропии у необратимого процесса будет завышен против того прироста, который имел бы место при обратимом переходе. Пусть — тепло, полученное телом при температуре в интересующем нас необратимом процессе. Если бы процесс был обратимым, то прирост энтропии равнялся бы в реальном процессе прирост энтропии будет больше этой величины:

Если система теплоизолирована, то и предыдущее утверждение приобретает вид

в теплоизолированной системе возможны лишь процессы, идущие с возрастанием энтропии.

Вполне понятно, что энтропия вместе с внутренней энергией являются важнейшими функциями, определяющими термодинамический процесс. Можно сказать, что энтропия является директором-распорядителем процесса, а внутренняя энергия является его бухгалтером: энтропия (определяет направление протекания процесса, энергия «оплачивает расходы» на его проведение.

Если в предыдущие формулы ввести вместо знака  краткой формулой запишется закон энтропии как для обратимых, так и для необратимых процессов:

Эта формула передает содержание второго начала термодинамики. Для замкнутых систем второе начало говорит: энтропия теплоизолированной системы возрастает или остается неизменной.

Целесообразно объединить оба начала термодинамики одной формулой

удобной для рассмотрения всех практических задач термодинамики.

Принцип возрастания энтропии относится к закрытым системам. Если же система общается со средой, другими словами, если речь идет об открытой системе, то ее энтропия может, разумеется, и убывать.

Ниже будет показано, что процессы молекулярного упорядочения связаны с уменьшением энтропии. Живой организм из неупорядоченной системы малых молекул, получаемых в процессах питания и дыхания, конструирует высокоорганизованные постройки — биологические макромолекулы (стр. 595). При этом энтропия организма падает.

Если представить себе замкнутую систему организм+среда, энтропия которой обязана расти, то ясно, что энтропия среды должна возрастать, перекрывая уменьшение энтропии организма.

Возрастание энтропии среды происходит за счет выделений организма.

Если процесс стационарной, то

Можно сказать, что жизнедеятельность организма состоит в пропускании через себя потока энтропии вещества. При этом энтропия вещества, входящего в организм, меньше энтропии, отдаваемой среде,— организм деградирует продукты питания.

Примеры. 1. В примере на стр. 57 мы рассмотрели неупругое столкновение пули с баллистическим маятником и выяснили, что при ударе в системе пуля — маятник исчезает 3920 Дж механической энергии. Это значит, что было необратимым образом передано маятнику от пули посредством теплопроводности. Если предположить, что процесс был изотермическим (т. е. теплопроводность маятника чрезвычайно велика) и температура системы, скажем, то в этом необратимом процессе энтропия системы возросла на

2.    Детский резиновый мяч массой 0,3 кг после падения с высоты 2 м подпрыгивает на I м от пола. В этом изотермическом процессе (пустьнеобратимо передается т. е. энтропия системы мяч — пол возросла на

Если бы мяч и пол были абсолютно упругими, то энтропия не менялась бы  движение мяча продолжалось бы вечно.

3.    Рассмотрим необратимый процесс передачи тепла от парового котла к конденсатору. Пусть паровой котел находится при температуре а конденсатор — при При тепловой мощности котла 10 000 кВт и к. п. д. 25% ежесекундно от котла к конденсатору будет переноситься Для котла, теряющего теплоту, это будет отрицательным, т. е. его энтропия убывает; у конденсатора энтропия растет. Но так как то энтропия системы котел — конденсатор за каждую секунду возрастает на

Принцип действия тепловой машины

Тепловая машина превращает тепло в работу, иначе говоря, забирает тепло от одних тел и передает его другим телам в форме механической работы. Для того чтобы осуществить это превращение, надо располагать двумя различно нагретыми телами, между которыми возможен теплообмен. Для краткости будем называть более горячее тело нагревателем, а более холодное — холодильником. При наличии таких двух тел процесс превращения тепла в работу рисуется следующим образом: способное расшириться тело (рабочее тело) приводится в контакт с нагревателем. Тепло ( отбирается от нагревателя и затрачивается на работу расширения которая отдается окружающим телам. Далее, рабочее тело приводится в контакт с холодильником, которому оно отдает тепло   за счет работы совершаемой внешними силами над рабочим телом.

Чтобы получить непрерывно действующую тепловую машину, необходимо закончить такт сжатия в той точке, в которой начался такт расширения; короче, процесс должен быть циклическим. Рабочее тело по проведении каждого цикла возвращается в исходное состояние. Закон сохранения энергии требует поэтому, чтобы энергия, полученная от окружающих тел, равнялась энергии, переданной окружающим телам. От среды получено: тепло при расширении и работа при сжатии рабочего тела. Среде отдано: работа при расширении тела и тепло при сжатии. Следовательно, При проведении цикла по часовой стрелке работа сжатия меньше работы расширения. Поэтому последнее равенство выражает тот простой факт, что чистая работа, переданная рабочим телом внешней среде, равна разности теплот, полученной от нагревателя и отданной холодильнику. Соответственно коэффициент полезного действия цикла, а значит, и всей машины, будет равен

Описанный процесс действия тепловой машины является, разумеется, абстрактной схемой. Однако наиболее существенные черты каждого теплового двигателя передаются этой схемой. Рабочим телом является расширяющийся и сжимающийся газ или пар, роль холодильника играет окружающая среда. Нагревателем служит паровой котел или, в двигателях внутреннего сгорания, горючая смесь.

Те же три системы являются необходимыми и для холодильной машины, в которой цикл протекает в обратную сторону. Принцип работы этой машины заключается в следующем: расширение рабочего тела производится тогда, когда оно находится в контакте с холодильником. Этим холодное тело охлаждается еще больше, что и является задачей холодильной машины. Далее, чтобы цикл стал возможным, нужно произвести сжатие рабочего тела и передать тепло, полученное от холодильника. Это выполняется при контакте рабочего тела с нагревателем. Таким образом, более горячее тело нагревается еще больше. «Противоестественный» переход тепла от тела менее нагретого к телу более нагретому «оплачивается» работой. Действительно, при совершении цикла против часовой стрелки равенство энергии, переданной среде, и энергии, отнятой от среды где мы по-прежнему

индекс 1 относим к части процесса, протекающей при контакте с более горячим телом), имеет следующий смысл: количество тепла, отнятое от системы, должно быть скомпенсировано равным количеством механической работы.

Второе начало термодинамики накладывает некоторое условие на действие тепловой машины. Если предполагать процесс обратимым, то изменение энтропии рабочего тела после прохождения цикла должно равняться нулю. Можно сказать и иначе: изменение энтропии в процессе расширения должно равняться (с обратным знаком) изменению энтропии при сжатии, т. е.

В случае же необратимого процесса энтропия замкнутой системы, состоящей из нагревателя, холодильника и рабочего тела, возрастет и поэтому

(Напоминаем, что есть алгебраическая величина. Тепло, поступившее в систему, считается положительным.) Подсчитывая значения этих интегралов для конкретных процессов, можно в ряде случаев довольно просто найти значение максимального коэффициента полезного действия того или иного цикла тепловой машины.

Цикл Карно. Максимальный КПД

Сейчас мы задаемся целью найти выражение предельно большого коэффициента полезного действия тепловой машины, достижимого для идеальной машины, работающей без потерь на обратимом цикле.

Прежде всего рассмотрим теоретический четырехтактный цикл Карно, изображенный на рис. 81. Цикл Карно состоит из двух изотерм (для температур и и двух адиабат. Первый  такт процесса пусть будет изотермическое расширение от состояния 1 к состоянию 2 — рабочее тело находится в контакте с нагревателем, имеющим температуру и процесс проводится весьма медленно. По достижении состояния 2 контакт с нагревателем нарушается, тело теплоизолируется и ему предоставляется возможность дополнительно расшириться. 

Работа происходит за счет внутренней энергии и температура тела пусть падает до Начиная с этой точки (состояние 3) начинается двухтактное сжатие. Тело сообщается с холодильником при температуре  и изотермически сжимается до состояния 4. Здесь опять тело теплоизолируется и сжатие продолжается уже адиабатическим путем с нагреванием рабочего тела за счет совершаемой работы до начальной температуры

Адиабатические процессы в цикле Карно носят вспомогательный характер: они помогают перейти с одной изотермы на другую. В энергетическом балансе эти процессы не участвуют, так как работа адиабатического расширения и работа сжатия компенсируют друг друга.

В адиабатическом процессе энтропия системы не меняется. При изотермическом расширении энтропия нагревателя уменьшается на величину энтропия холодильника возрастает на Энтропия  рабочего тела, вернувшегося в исходное состояние, остается неизменной. Если процесс обратим, то  В необратимых процессах энтропия всей системы, состоящей из холодильника, нагревателя и рабочего тела, возрастает и прирост энтропии больше убыли

откуда и  следовательно, максимальный коэффициент полезного действия цикла Карно равен 

К- п. д. цикла определяется температурами холодильника и нагревателя. Чем больше перепад температуры, тем выше к. п. д. машины. Нетрудно видеть, что коэффициент полезного действия цикла Карно дает оптимальное значение к. п. д. Нет лучшего цикла, чем цикл Карно, и в этом смысле он должен являться образцом для конструкторов тепловых машин, они должны стремиться как можно более приблизить реальные циклы к циклу этой идеальной машины.

Доказательство не составит труда. На рис. 82  показан произвольный цикл, вписанный в цикл

Карно. Уменьшение энтропии нагревателя может быть представлено интегралом
для которого несомненно справедливо неравенстве

так как — самое большое число из тех значений, которые пробегает при интегрировании. Увеличение энтропии холодильника выразится интегралом для которого справедливо неравенство так как — самое маленькое число из тех значений, которые пробегает при интегрировании. При обратимом процессе

следовательно,что и дает условие

Итак, из всех возможных циклических процессов максимальным к. п. д. обладает цикл Карно.
Формула максимального к. п. д. показывает причину низкого к. п. д. паровых машин. При к. п. д. равен 25%. Однако ведь это — максимальный коэффициент полезного действия, он достижим для идеальной машины, работающей обратимо без каких бы то ни было потерь энергии. Не приходится удивляться, что в реальных паровых машинах к. п. д. ниже 10%. В курсе теплотехники рассказывается о путях, которыми идет техника для увеличения коэффициента полезного действия. Ясно, что наиболее существенным является повышение температуры нагревателя, т. е. пара или горючей смеси.

Второе начало термодинамики

Как было указано выше, второе начало термодинамики состоит в утверждении, что энтропия в теплоизолированной системе возрастает. Это утверждение может показаться несколько абстрактным. Кроме того, приведенная формулировка не соответствует историческому развитию идей. Имея в виду огромную, значимость этого закона природы, надо кратко остановиться на других существующих формулировках второго начала термодинамики и показать их эквивалентность приведенной выше.

Исторически второе начало термодинамики вошло в науку в виде постулата Томсона о невозможности создания вечного двигателя второго рода. Вечным двигателем первого рода называют машину, создающую работу «из ничего», т. е. машину, работа которой нарушает первое начало термодинамики. Вечным двигателем второго  рода называют такой двигатель, который производит работу при помощи периодически действующей машины за счет одного лишь отнятия теплоты от окружающей среды. Такой двигатель, будь он возможен, был бы практически вечным, так как запас энергии в окружающей среде почти безграничен и охлаждение, скажем, воды океанов на один градус дало бы непредставимо огромную энергию. Масса воды в мировом океане по порядку величины составляет При охлаждении всей этой массы воды лишь на выделилось бы тепла, что эквивалентно полному сжиганию угля. Железнодорожный состав, нагруженный этим количеством угля, растянулся бы на расстояние что по порядку величины совпадает с размерами солнечной системы!

Вечный двигатель второго рода — это тепловая машина, работающая с нагревателем, но без холодильника. Такая машина могла бы поработать один такт — газ, находящийся в сосуде с поршнем, мог бы расшириться, но на этом работа двигателя и закончилась бы, так как для продолжения действия машины тепло, полученное газом, необходимо передать холодильнику. Формально невозможность вечного двигателя второго рода видна из формулы максимального к. п. д. При отсутствии теплового перепада максимальное значение к. п. д. равно нулю.

Невозможно осуществить периодически действующий вечный двигатель, комбинируя изотермическое расширение с адиабатическим процессом сжатия. Такой процесс невозможен, даже если бы удалось его сделать обратимым. При изотермическом расширении рабочего тела энтропия падает. Значит, процесс сжатия должен приводить к возрастанию энтропии. Этого, однако, не может сделать адиабатический процесс, так как он проходит при постоянной энтропии.

Вполне соответствует принятой здесь формулировке второго начала термодинамики также постулат Клаузиуса, который состоит в утверждении о невозможности перехода тепла от менее нагретого тела к более нагретому без компенсации. Процесс, противоречащий постулату Клаузиуса, протекает с уменьшением энтропии; это свойство энтропии было показано с самого начала.

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Масса
7. Взаимодействия тел
8. Механическая энергия
9. Импульс
10. Вращение твердого тела
11. Криволинейное движение тел
12. Колебания
13. Колебания и волны
14. Механические колебания и волны
15. Бегущая волна
16. Стоячие волны
17. Акустика
18. Звук
19. Звук и ультразвук
20. Движение жидкости и газа
21. Молекулярно-кинетическая теория
22. Молекулярно-кинетическая теория строения вещества
23. Молекулярно — кинетическая теория газообразного состояния вещества
24. Теплота и работа
25. Температура и теплота
26. Термодинамические процессы
27. Идеальный газ
28. Уравнение состояния идеального газа
29. Изменение внутренней энергии
30. Переход вещества из жидкого состояния в газообразное и обратно
31. Кипение, свойства паров, критическое состояние вещества
32. Водяной пар в атмосфере
33. Плавление и кристаллизация
34. Тепловое расширение тел
35. Процессы перехода из одного агрегатного состояния в другое
36. Тепловое расширение твердых и жидких тел
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома

Entropy
Common symbols	S
SI unit	joules per kelvin (J⋅K−1)
In SI base units	kg⋅m2⋅s−2⋅K−1

Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication.^[1]

The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names thermodynamic function and heat-potential.^[2] In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount of heat to the instantaneous temperature. He initially described it as transformation-content, in German Verwandlungsinhalt, and later coined the term entropy from a Greek word for transformation. Referring to microscopic constitution and structure, in 1862, Clausius interpreted the concept as meaning disgregation.^[3]

A consequence of entropy is that certain processes are irreversible or impossible, aside from the requirement of not violating the conservation of energy, the latter being expressed in the first law of thermodynamics. Entropy is central to the second law of thermodynamics, which states that the entropy of isolated systems left to spontaneous evolution cannot decrease with time, as they always arrive at a state of thermodynamic equilibrium, where the entropy is highest.

Austrian physicist Ludwig Boltzmann explained entropy as the measure of the number of possible microscopic arrangements or states of individual atoms and molecules of a system that comply with the macroscopic condition of the system. He thereby introduced the concept of statistical disorder and probability distributions into a new field of thermodynamics, called statistical mechanics, and found the link between the microscopic interactions, which fluctuate about an average configuration, to the macroscopically observable behavior, in form of a simple logarithmic law, with a proportionality constant, the Boltzmann constant, that has become one of the defining universal constants for the modern International System of Units (SI).

In 1948, Bell Labs scientist Claude Shannon developed similar statistical concepts of measuring microscopic uncertainty and multiplicity to the problem of random losses of information in telecommunication signals. Upon John von Neumann’s suggestion, Shannon named this entity of missing information in analogous manner to its use in statistical mechanics as entropy, and gave birth to the field of information theory. This description has been identified as a universal definition of the concept of entropy.^[4]

History[edit]

In his 1803 paper Fundamental Principles of Equilibrium and Movement, the French mathematician Lazare Carnot proposed that in any machine, the accelerations and shocks of the moving parts represent losses of moment of activity; in any natural process there exists an inherent tendency towards the dissipation of useful energy. In 1824, building on that work, Lazare’s son, Sadi Carnot, published Reflections on the Motive Power of Fire, which posited that in all heat-engines, whenever «caloric» (what is now known as heat) falls through a temperature difference, work or motive power can be produced from the actions of its fall from a hot to cold body. He used an analogy with how water falls in a water wheel. That was an early insight into the second law of thermodynamics.^[5] Carnot based his views of heat partially on the early 18th-century «Newtonian hypothesis» that both heat and light were types of indestructible forms of matter, which are attracted and repelled by other matter, and partially on the contemporary views of Count Rumford, who showed in 1789 that heat could be created by friction, as when cannon bores are machined.^[6] Carnot reasoned that if the body of the working substance, such as a body of steam, is returned to its original state at the end of a complete engine cycle, «no change occurs in the condition of the working body».

The first law of thermodynamics, deduced from the heat-friction experiments of James Joule in 1843, expresses the concept of energy and its conservation in all processes; the first law, however, is unsuitable to separately quantify the effects of friction and dissipation.^{[citation needed]}

In the 1850s and 1860s, German physicist Rudolf Clausius objected to the supposition that no change occurs in the working body, and gave that change a mathematical interpretation, by questioning the nature of the inherent loss of usable heat when work is done, e.g., heat produced by friction.^[7] He described his observations as a dissipative use of energy, resulting in a transformation-content (Verwandlungsinhalt in German), of a thermodynamic system or working body of chemical species during a change of state.^[7] That was in contrast to earlier views, based on the theories of Isaac Newton, that heat was an indestructible particle that had mass. Clausius discovered that the non-usable energy increases as steam proceeds from inlet to exhaust in a steam engine. From the prefix en-, as in ‘energy’, and from the Greek word τροπή [tropē], which is translated in an established lexicon as turning or change^[8] and that he rendered in German as Verwandlung, a word often translated into English as transformation, in 1865 Clausius coined the name of that property as entropy.^[9] The word was adopted into the English language in 1868.

Later, scientists such as Ludwig Boltzmann, Josiah Willard Gibbs, and James Clerk Maxwell gave entropy a statistical basis. In 1877, Boltzmann visualized a probabilistic way to measure the entropy of an ensemble of ideal gas particles, in which he defined entropy as proportional to the natural logarithm of the number of microstates such a gas could occupy. The proportionality constant in this definition, called the Boltzmann constant, has become one of the defining universal constants for the modern International System of Units (SI). Henceforth, the essential problem in statistical thermodynamics has been to determine the distribution of a given amount of energy E over N identical systems. Constantin Carathéodory, a Greek mathematician, linked entropy with a mathematical definition of irreversibility, in terms of trajectories and integrability.

Etymology[edit]

In 1865, Clausius named the concept of «the differential of a quantity which depends on the configuration of the system», entropy (Entropie) after the Greek word for ‘transformation’.^[10] He gave «transformational content» (Verwandlungsinhalt) as a synonym, paralleling his «thermal and ergonal content» (Wärme- und Werkinhalt) as the name of , but preferring the term entropy as a close parallel of the word energy, as he found the concepts nearly «analogous in their physical significance».^[10] This term was formed by replacing the root of ἔργον (‘ergon’, ‘work’) by that of τροπή (‘tropy’, ‘transformation’).^[9]

In more detail, Clausius explained his choice of «entropy» as a name as follows:^[11]

I prefer going to the ancient languages for the names of important scientific quantities, so that they may mean the same thing in all living tongues. I propose, therefore, to call S the entropy of a body, after the Greek word «transformation». I have designedly coined the word entropy to be similar to energy, for these two quantities are so analogous in their physical significance, that an analogy of denominations seems to me helpful.

Leon Cooper added that in this way «he succeeded in coining a word that meant the same thing to everybody: nothing».^[11]

Definitions and descriptions[edit]

The concept of entropy is described by two principal approaches, the macroscopic perspective of classical thermodynamics, and the microscopic description central to statistical mechanics. The classical approach defines entropy in terms of macroscopically measurable physical properties, such as bulk mass, volume, pressure, and temperature. The statistical definition of entropy defines it in terms of the statistics of the motions of the microscopic constituents of a system – modeled at first classically, e.g. Newtonian particles constituting a gas, and later quantum-mechanically (photons, phonons, spins, etc.). The two approaches form a consistent, unified view of the same phenomenon as expressed in the second law of thermodynamics, which has found universal applicability to physical processes.

State variables and functions of state[edit]

Many thermodynamic properties are defined by physical variables that define a state of thermodynamic equilibrium; these are state variables. State variables depend only on the equilibrium condition, not on the path evolution to that state. State variables can be functions of state, also called state functions, in a sense that one state variable is a mathematical function of other state variables. Often, if some properties of a system are determined, they are sufficient to determine the state of the system and thus other properties’ values. For example, temperature and pressure of a given quantity of gas determine its state, and thus also its volume via the ideal gas law. A system composed of a pure substance of a single phase at a particular uniform temperature and pressure is determined, and is thus a particular state, and has not only a particular volume but also a specific entropy.^[13] The fact that entropy is a function of state makes it useful. In the Carnot cycle, the working fluid returns to the same state that it had at the start of the cycle, hence the change or line integral of any state function, such as entropy, over this reversible cycle is zero.

Reversible process[edit]

Total entropy may be conserved during a reversible process. The entropy change of the system (not including the surroundings) is well-defined as heat transferred to the system divided by the system temperature , . A reversible process is a quasistatic one that deviates only infinitesimally from thermodynamic equilibrium and avoids friction or other dissipation. Any process that happens quickly enough to deviate from thermal equilibrium cannot be reversible, total entropy increases, and the potential for maximum work to be done in the process is also lost.^[14] For example, in the Carnot cycle, while the heat flow from the hot reservoir to the cold reservoir represents an increase in entropy in the cold reservoir, the work output, if reversibly and perfectly stored in some energy storage mechanism, represents a decrease in entropy that could be used to operate the heat engine in reverse and return to the previous state; thus the total entropy change may still be zero at all times if the entire process is reversible. An irreversible process increases the total entropy of the system and surroundings.^[15]

Carnot cycle[edit]

The concept of entropy arose from Rudolf Clausius’s study of the Carnot cycle that is a thermodynamic cycle performed by a Carnot heat engine as a reversible heat engine.^[16] In a Carnot cycle, heat Q_H is absorbed isothermally at temperature T_H from a ‘hot’ reservoir (in the isothermal expansion stage) and given up isothermally as heat Q_C to a ‘cold’ reservoir at T_C (in the isothermal compression stage). According to Carnot’s principle or theorem, work from a heat engine with two thermal reservoirs can be produced only when there is a temperature difference between these reservoirs, and for reversible engines which are mostly and equally efficient among all heat engines for a given thermal reservoir pair, the work is a function of the reservoir temperatures and the heat absorbed to the engine Q_H (heat engine work output = heat engine efficiency × heat to the engine, where the efficiency is a function of the reservoir temperatures for reversible heat engines). Carnot did not distinguish between Q_H and Q_C, since he was using the incorrect hypothesis that caloric theory was valid, and hence heat was conserved (the incorrect assumption that Q_H and Q_C were equal in magnitude) when, in fact, Q_H is greater than the magnitude of Q_C in magnitude.^[17][18] Through the efforts of Clausius and Kelvin, it is now known that the work done by a reversible heat engine is the product of the Carnot efficiency (it is the efficiency of all reversible heat engines with the same thermal reservoir pairs according to the Carnot’s theorem) and the heat absorbed from the hot reservoir:

(1)

Here is work done by the Carnot heat engine, is heat to the engine from the hot reservoir, and is heat to the cold reservoir from the engine. To derive the Carnot efficiency, which is 1 − T_C/T_H (a number less than one), Kelvin had to evaluate the ratio of the work output to the heat absorbed during the isothermal expansion with the help of the Carnot–Clapeyron equation, which contained an unknown function called the Carnot function. The possibility that the Carnot function could be the temperature as measured from a zero point of temperature was suggested by Joule in a letter to Kelvin. This allowed Kelvin to establish his absolute temperature scale.^[19] It is also known that the net work W produced by the system in one cycle is the net heat absorbed, which is the sum (or difference of the magnitudes) of the heat Q_H > 0 absorbed from the hot reservoir and the waste heat Q_C < 0 given off to the cold reservoir:^[20]

(2)

Since the latter is valid over the entire cycle, this gave Clausius the hint that at each stage of the cycle, work and heat would not be equal, but rather their difference would be the change of a state function that would vanish upon completion of the cycle. The state function was called the internal energy, that is central to the first law of thermodynamics.^[21]

Now equating (1) and (2) gives, for the engine per Carnot cycle,^[22][20]

(3)

This implies that there is a function of state whose change is Q/T and this state function is conserved over a complete Carnot cycle, like other state function such as the internal energy. Clausius called this state function entropy. One can see that entropy was discovered through mathematics rather than through laboratory experimental results.^{[citation needed]} It is a mathematical construct and has no easy physical analogy.^{[citation needed]} This makes the concept somewhat obscure or abstract, akin to how the concept of energy arose.

This equation shows an entropy change per Carnot cycle is zero. In fact, an entropy change in the both thermal reservoirs per Carnot cycle is also zero since that change is simply expressed by reverting the sign of each term in the equation (3) according to the fact that, for example, for heat transfer from the hot reservoir to the engine, the engine receives the heat while the hot reservoir loses the same amount of the heat;

(4)

where we denote an entropy change for a thermal reservoir by ΔS_r,i = — Q_i/T_i, for i as either H (Hot reservoir) or C (Cold reservoir), by considering the above-mentioned signal convention of heat for the engine.

Clausius then asked what would happen if less work is produced by the system than that predicted by Carnot’s principle for the same thermal reservoir pair and the same heat transfer from the hot reservoir to the engine Q_H. In this case, the right-hand side of the equation (1) would be the upper bound of the work output by the system, and the equation would now be converted into an inequality

When the equation (2) is used to express the work as a net or total heat exchanged in a cycle, we get

or

by considering the sign convention of heat where Q_H > 0 is heat that is from the hot reservoir and is absorbed by the engine and Q_C < 0 is the waste heat given off to the cold reservoir from the engine. So, more heat is given up to the cold reservoir than in the Carnot cycle. The above inequality can be written as

If we, again, denote an entropy change for a thermal reservoir by ΔS_r,i = — Q_i/T_i, for i as either H (Hot reservoir) or C (Cold reservoir), by considering the abovementioned signal convention of heat for the engine, then

or

(5)

telling that the magnitude of the entropy earned by the cold reservoir is greater than the entropy lost by the hot reservoir. The net entropy change in the engine per its thermodynamic cycle is zero, so the net entropy change in the engine and both the thermal reservoirs per cycle increases if work produced by the engine is less than the work achieved by a Carnot engine in the equation (1).

The Carnot cycle and Carnot efficiency as shown in the equation (1) are useful because they define the upper bound of the possible work output and the efficiency of any classical thermodynamic heat engine. Other cycles, such as the Otto cycle, Diesel cycle and Brayton cycle, can be analyzed from the standpoint of the Carnot cycle. Any machine or cyclic process that converts heat to work and is claimed to produce an efficiency greater than the Carnot efficiency is not viable because it violates the second law of thermodynamics.

For very small numbers of particles in the system, statistical thermodynamics must be used. The efficiency of devices such as photovoltaic cells requires an analysis from the standpoint of quantum mechanics.

Classical thermodynamics[edit]

The thermodynamic definition of entropy was developed in the early 1850s by Rudolf Clausius and essentially describes how to measure the entropy of an isolated system in thermodynamic equilibrium with its parts. Clausius created the term entropy as an extensive thermodynamic variable that was shown to be useful in characterizing the Carnot cycle. Heat transfer in the isotherm steps (isothermal expansion and isothermal compression) of the Carnot cycle was found to be proportional to the temperature of a system (known as its absolute temperature). This relationship was expressed in an increment of entropy that is equal to incremental heat transfer divided by temperature. Entropy was found to vary in the thermodynamic cycle but eventually returned to the same value at the end of every cycle. Thus it was found to be a function of state, specifically a thermodynamic state of the system.

While Clausius based his definition on a reversible process, there are also irreversible processes that change entropy. Following the second law of thermodynamics, entropy of an isolated system always increases for irreversible processes. The difference between an isolated system and closed system is that energy may not flow to and from an isolated system, but energy flow to and from a closed system is possible. Nevertheless, for both closed and isolated systems, and indeed, also in open systems, irreversible thermodynamics processes may occur.

According to the Clausius equality, for a reversible cyclic process: . This means the line integral is path-independent.

So we can define a state function S called entropy, which satisfies .

To find the entropy difference between any two states of a system, the integral must be evaluated for some reversible path between the initial and final states.^[23] Since entropy is a state function, the entropy change of the system for an irreversible path is the same as for a reversible path between the same two states.^[24] However, the heat transferred to or from, and the entropy change of, the surroundings is different.

We can only obtain the change of entropy by integrating the above formula. To obtain the absolute value of the entropy, we need the third law of thermodynamics, which states that S = 0 at absolute zero for perfect crystals.

From a macroscopic perspective, in classical thermodynamics the entropy is interpreted as a state function of a thermodynamic system: that is, a property depending only on the current state of the system, independent of how that state came to be achieved. In any process where the system gives up energy ΔE, and its entropy falls by ΔS, a quantity at least T_R ΔS of that energy must be given up to the system’s surroundings as heat (T_R is the temperature of the system’s external surroundings). Otherwise the process cannot go forward. In classical thermodynamics, the entropy of a system is defined only if it is in physical thermodynamic equilibrium. (But chemical equilibrium is not required: the entropy of a mixture of two moles of hydrogen and one mole of oxygen at 1 bar pressure and 298 K is well-defined.)

Statistical mechanics[edit]

The statistical definition was developed by Ludwig Boltzmann in the 1870s by analyzing the statistical behavior of the microscopic components of the system. Boltzmann showed that this definition of entropy was equivalent to the thermodynamic entropy to within a constant factor—known as the Boltzmann constant. In short, the thermodynamic definition of entropy provides the experimental verification of entropy, while the statistical definition of entropy extends the concept, providing an explanation and a deeper understanding of its nature.

The interpretation of entropy in statistical mechanics is the measure of uncertainty, disorder, or mixedupness in the phrase of Gibbs, which remains about a system after its observable macroscopic properties, such as temperature, pressure and volume, have been taken into account. For a given set of macroscopic variables, the entropy measures the degree to which the probability of the system is spread out over different possible microstates. In contrast to the macrostate, which characterizes plainly observable average quantities, a microstate specifies all molecular details about the system including the position and velocity of every molecule. The more such states are available to the system with appreciable probability, the greater the entropy. In statistical mechanics, entropy is a measure of the number of ways a system can be arranged, often taken to be a measure of «disorder» (the higher the entropy, the higher the disorder).^[25][26][27] This definition describes the entropy as being proportional to the natural logarithm of the number of possible microscopic configurations of the individual atoms and molecules of the system (microstates) that could cause the observed macroscopic state (macrostate) of the system. The constant of proportionality is the Boltzmann constant.

The Boltzmann constant, and therefore entropy, have dimensions of energy divided by temperature, which has a unit of joules per kelvin (J⋅K⁻¹) in the International System of Units (or kg⋅m²⋅s⁻²⋅K⁻¹ in terms of base units). The entropy of a substance is usually given as an intensive property – either entropy per unit mass (SI unit: J⋅K⁻¹⋅kg⁻¹) or entropy per unit amount of substance (SI unit: J⋅K⁻¹⋅mol⁻¹).

Specifically, entropy is a logarithmic measure of the number of system states with significant probability of being occupied:

( is the probability that the system is in th state, usually given by the Boltzmann distribution; if states are defined in a continuous manner, the summation is replaced by an integral over all possible states) or, equivalently, the expected value of the logarithm of the probability that a microstate is occupied

where k_B is the Boltzmann constant, equal to 1.38065×10⁻²³ J/K.
The summation is over all the possible microstates of the system, and p_i is the probability that the system is in the i-th microstate.^[28] This definition assumes that the basis set of states has been picked so that there is no information on their relative phases. In a different basis set, the more general expression is

where is the density matrix, is trace, and is the matrix logarithm. This density matrix formulation is not needed in cases of thermal equilibrium so long as the basis states are chosen to be energy eigenstates. For most practical purposes, this can be taken as the fundamental definition of entropy since all other formulas for S can be mathematically derived from it, but not vice versa.

In what has been called the fundamental assumption of statistical thermodynamics or the fundamental postulate in statistical mechanics, among system microstates of the same energy (degenerate microstates) each microstate is assumed to be populated with equal probability; this assumption is usually justified for an isolated system in equilibrium.^[29] Then for an isolated system p_i = 1/Ω, where Ω is the number of microstates whose energy equals the system’s energy, and the previous equation reduces to

In thermodynamics, such a system is one in which the volume, number of molecules, and internal energy are fixed (the microcanonical ensemble).

For a given thermodynamic system, the excess entropy is defined as the entropy minus that of an ideal gas at the same density and temperature, a quantity that is always negative because an ideal gas is maximally disordered.^[30] This concept plays an important role in liquid-state theory. For instance, Rosenfeld’s excess-entropy scaling principle^[31][32] states that reduced transport coefficients throughout the two-dimensional phase diagram are functions uniquely determined by the excess entropy.^[33][34]

The most general interpretation of entropy is as a measure of the extent of uncertainty about a system. The equilibrium state of a system maximizes the entropy because it does not reflect all information about the initial conditions, except for the conserved variables. This uncertainty is not of the everyday subjective kind, but rather the uncertainty inherent to the experimental method and interpretative model.^[35]

The interpretative model has a central role in determining entropy. The qualifier «for a given set of macroscopic variables» above has deep implications: if two observers use different sets of macroscopic variables, they see different entropies. For example, if observer A uses the variables U, V and W, and observer B uses U, V, W, X, then, by changing X, observer B can cause an effect that looks like a violation of the second law of thermodynamics to observer A. In other words: the set of macroscopic variables one chooses must include everything that may change in the experiment, otherwise one might see decreasing entropy.^[36]

Entropy can be defined for any Markov processes with reversible dynamics and the detailed balance property.

In Boltzmann’s 1896 Lectures on Gas Theory, he showed that this expression gives a measure of entropy for systems of atoms and molecules in the gas phase, thus providing a measure for the entropy of classical thermodynamics.

Entropy of a system[edit]

Entropy arises directly from the Carnot cycle. It can also be described as the reversible heat divided by temperature. Entropy is a fundamental function of state.

In a thermodynamic system, pressure and temperature tend to become uniform over time because the equilibrium state has higher probability (more possible combinations of microstates) than any other state.

As an example, for a glass of ice water in air at room temperature, the difference in temperature between the warm room (the surroundings) and the cold glass of ice and water (the system and not part of the room) decreases as portions of the thermal energy from the warm surroundings spread to the cooler system of ice and water. Over time the temperature of the glass and its contents and the temperature of the room become equal. In other words, the entropy of the room has decreased as some of its energy has been dispersed to the ice and water, of which the entropy has increased.

However, as calculated in the example, the entropy of the system of ice and water has increased more than the entropy of the surrounding room has decreased. In an isolated system such as the room and ice water taken together, the dispersal of energy from warmer to cooler always results in a net increase in entropy. Thus, when the «universe» of the room and ice water system has reached a temperature equilibrium, the entropy change from the initial state is at a maximum. The entropy of the thermodynamic system is a measure of how far the equalization has progressed.

Thermodynamic entropy is a non-conserved state function that is of great importance in the sciences of physics and chemistry.^[25][37] Historically, the concept of entropy evolved to explain why some processes (permitted by conservation laws) occur spontaneously while their time reversals (also permitted by conservation laws) do not; systems tend to progress in the direction of increasing entropy.^[38][39] For isolated systems, entropy never decreases.^[37] This fact has several important consequences in science: first, it prohibits «perpetual motion» machines; and second, it implies the arrow of entropy has the same direction as the arrow of time. Increases in the total entropy of system and surroundings correspond to irreversible changes, because some energy is expended as waste heat, limiting the amount of work a system can do.^{[25][26][40][41]}

Unlike many other functions of state, entropy cannot be directly observed but must be calculated. Absolute standard molar entropy of a substance can be calculated from the measured temperature dependence of its heat capacity. The molar entropy of ions is obtained as a difference in entropy from a reference state defined as zero entropy. The second law of thermodynamics states that the entropy of an isolated system must increase or remain constant. Therefore, entropy is not a conserved quantity: for example, in an isolated system with non-uniform temperature, heat might irreversibly flow and the temperature become more uniform such that entropy increases.^[42] Chemical reactions cause changes in entropy and system entropy, in conjunction with enthalpy, plays an important role in determining in which direction a chemical reaction spontaneously proceeds.

One dictionary definition of entropy is that it is «a measure of thermal energy per unit temperature that is not available for useful work» in a cyclic process. For instance, a substance at uniform temperature is at maximum entropy and cannot drive a heat engine. A substance at non-uniform temperature is at a lower entropy (than if the heat distribution is allowed to even out) and some of the thermal energy can drive a heat engine.

A special case of entropy increase, the entropy of mixing, occurs when two or more different substances are mixed. If the substances are at the same temperature and pressure, there is no net exchange of heat or work – the entropy change is entirely due to the mixing of the different substances. At a statistical mechanical level, this results due to the change in available volume per particle with mixing.^[43]

Equivalence of definitions[edit]

Proofs of equivalence between the definition of entropy in statistical mechanics (the Gibbs entropy formula ) and in classical thermodynamics ( together with the fundamental thermodynamic relation) are known for the microcanonical ensemble, the canonical ensemble, the grand canonical ensemble, and the isothermal–isobaric ensemble. These proofs are based on the probability density of microstates of the generalized Boltzmann distribution and the identification of the thermodynamic internal energy as the ensemble average .^[44] Thermodynamic relations are then employed to derive the well-known Gibbs entropy formula. However, the equivalence between the Gibbs entropy formula and the thermodynamic definition of entropy is not a fundamental thermodynamic relation but rather a consequence of the form of the generalized Boltzmann distribution.^[45]

Furthermore, it has been shown that the definitions of entropy in statistical mechanics is the only entropy that is equivalent to the classical thermodynamics entropy under the following postulates:^[46]

Second law of thermodynamics[edit]

The second law of thermodynamics requires that, in general, the total entropy of any system does not decrease other than by increasing the entropy of some other system. Hence, in a system isolated from its environment, the entropy of that system tends not to decrease. It follows that heat cannot flow from a colder body to a hotter body without the application of work to the colder body. Secondly, it is impossible for any device operating on a cycle to produce net work from a single temperature reservoir; the production of net work requires flow of heat from a hotter reservoir to a colder reservoir, or a single expanding reservoir undergoing adiabatic cooling, which performs adiabatic work. As a result, there is no possibility of a perpetual motion machine. It follows that a reduction in the increase of entropy in a specified process, such as a chemical reaction, means that it is energetically more efficient.

It follows from the second law of thermodynamics that the entropy of a system that is not isolated may decrease. An air conditioner, for example, may cool the air in a room, thus reducing the entropy of the air of that system. The heat expelled from the room (the system), which the air conditioner transports and discharges to the outside air, always makes a bigger contribution to the entropy of the environment than the decrease of the entropy of the air of that system. Thus, the total of entropy of the room plus the entropy of the environment increases, in agreement with the second law of thermodynamics.

In mechanics, the second law in conjunction with the fundamental thermodynamic relation places limits on a system’s ability to do useful work.^[47] The entropy change of a system at temperature absorbing an infinitesimal amount of heat in a reversible way, is given by . More explicitly, an energy is not available to do useful work, where is the temperature of the coldest accessible reservoir or heat sink external to the system. For further discussion, see Exergy.

Statistical mechanics demonstrates that entropy is governed by probability, thus allowing for a decrease in disorder even in an isolated system. Although this is possible, such an event has a small probability of occurring, making it unlikely.^[48]

The applicability of a second law of thermodynamics is limited to systems in or sufficiently near equilibrium state, so that they have defined entropy.^[49] Some inhomogeneous systems out of thermodynamic equilibrium still satisfy the hypothesis of local thermodynamic equilibrium, so that entropy density is locally defined as an intensive quantity. For such systems, there may apply a principle of maximum time rate of entropy production.^[50][51] It states that such a system may evolve to a steady state that maximizes its time rate of entropy production. This does not mean that such a system is necessarily always in a condition of maximum time rate of entropy production; it means that it may evolve to such a steady state.^[52][53]

Applications[edit]

The fundamental thermodynamic relation[edit]

The entropy of a system depends on its internal energy and its external parameters, such as its volume. In the thermodynamic limit, this fact leads to an equation relating the change in the internal energy to changes in the entropy and the external parameters. This relation is known as the fundamental thermodynamic relation. If external pressure bears on the volume as the only external parameter, this relation is:

Since both internal energy and entropy are monotonic functions of temperature , implying that the internal energy is fixed when one specifies the entropy and the volume, this relation is valid even if the change from one state of thermal equilibrium to another with infinitesimally larger entropy and volume happens in a non-quasistatic way (so during this change the system may be very far out of thermal equilibrium and then the whole-system entropy, pressure, and temperature may not exist).

The fundamental thermodynamic relation implies many thermodynamic identities that are valid in general, independent of the microscopic details of the system. Important examples are the Maxwell relations and the relations between heat capacities.

Entropy in chemical thermodynamics[edit]

Thermodynamic entropy is central in chemical thermodynamics, enabling changes to be quantified and the outcome of reactions predicted. The second law of thermodynamics states that entropy in an isolated system – the combination of a subsystem under study and its surroundings – increases during all spontaneous chemical and physical processes. The Clausius equation of introduces the measurement of entropy change, . Entropy change describes the direction and quantifies the magnitude of simple changes such as heat transfer between systems – always from hotter to cooler spontaneously.

The thermodynamic entropy therefore has the dimension of energy divided by temperature, and the unit joule per kelvin (J/K) in the International System of Units (SI).

Thermodynamic entropy is an extensive property, meaning that it scales with the size or extent of a system. In many processes it is useful to specify the entropy as an intensive property independent of the size, as a specific entropy characteristic of the type of system studied. Specific entropy may be expressed relative to a unit of mass, typically the kilogram (unit: J⋅kg⁻¹⋅K⁻¹). Alternatively, in chemistry, it is also referred to one mole of substance, in which case it is called the molar entropy with a unit of J⋅mol⁻¹⋅K⁻¹.

Thus, when one mole of substance at about 0 K is warmed by its surroundings to 298 K, the sum of the incremental values of constitute each element’s or compound’s standard molar entropy, an indicator of the amount of energy stored by a substance at 298 K.^[54][55] Entropy change also measures the mixing of substances as a summation of their relative quantities in the final mixture.^[56]

Entropy is equally essential in predicting the extent and direction of complex chemical reactions. For such applications, must be incorporated in an expression that includes both the system and its surroundings, . This expression becomes, via some steps, the Gibbs free energy equation for reactants and products in the system: [the Gibbs free energy change of the system] [the enthalpy change] [the entropy change].^[54]

World’s technological capacity to store and communicate entropic information[edit]

A 2011 study in Science (journal) estimated the world’s technological capacity to store and communicate optimally compressed information normalized on the most effective compression algorithms available in the year 2007, therefore estimating the entropy of the technologically available sources.^[57] The author’s estimate that human kind’s technological capacity to store information grew from 2.6 (entropically compressed) exabytes in 1986 to 295 (entropically compressed) exabytes in 2007. The world’s technological capacity to receive information through one-way broadcast networks was 432 exabytes of (entropically compressed) information in 1986, to 1.9 zettabytes in 2007. The world’s effective capacity to exchange information through two-way telecommunication networks was 281 petabytes of (entropically compressed) information in 1986, to 65 (entropically compressed) exabytes in 2007.^[57]

Entropy balance equation for open systems[edit]

In chemical engineering, the principles of thermodynamics are commonly applied to «open systems», i.e. those in which heat, work, and mass flow across the system boundary. Flows of both heat () and work, i.e. (shaft work) and (pressure-volume work), across the system boundaries, in general cause changes in the entropy of the system. Transfer as heat entails entropy transfer , where is the absolute thermodynamic temperature of the system at the point of the heat flow. If there are mass flows across the system boundaries, they also influence the total entropy of the system. This account, in terms of heat and work, is valid only for cases in which the work and heat transfers are by paths physically distinct from the paths of entry and exit of matter from the system.^[58][59]

To derive a generalized entropy balanced equation, we start with the general balance equation for the change in any extensive quantity in a thermodynamic system, a quantity that may be either conserved, such as energy, or non-conserved, such as entropy. The basic generic balance expression states that , i.e. the rate of change of in the system, equals the rate at which enters the system at the boundaries, minus the rate at which leaves the system across the system boundaries, plus the rate at which is generated within the system. For an open thermodynamic system in which heat and work are transferred by paths separate from the paths for transfer of matter, using this generic balance equation, with respect to the rate of change with time of the extensive quantity entropy , the entropy balance equation is:^{[60][61][note 1]}

where

If there are multiple heat flows, the term is replaced by where is the heat flow and is the temperature at the th heat flow port into the system.

Note that the nomenclature «entropy balance» is misleading and often deemed inappropriate because entropy is not a conserved quantity. In other words, the term is never a known quantity but always a derived one based on the expression above. Therefore, the open system version of the second law is more appropriately described as the «entropy generation equation» since it specifies that , with zero for reversible processes or greater than zero for irreversible ones.

Entropy change formulas for simple processes[edit]

For certain simple transformations in systems of constant composition, the entropy changes are given by simple formulas.^[62]

Isothermal expansion or compression of an ideal gas[edit]

For the expansion (or compression) of an ideal gas from an initial volume and pressure to a final volume and pressure at any constant temperature, the change in entropy is given by:

Here is the amount of gas (in moles) and is the ideal gas constant. These equations also apply for expansion into a finite vacuum or a throttling process, where the temperature, internal energy and enthalpy for an ideal gas remain constant.

Cooling and heating[edit]

For pure heating or cooling of any system (gas, liquid or solid) at constant pressure from an initial temperature to a final temperature , the entropy change is

provided that the constant-pressure molar heat capacity (or specific heat) C_P is constant and that no phase transition occurs in this temperature interval.

Similarly at constant volume, the entropy change is

where the constant-volume molar heat capacity C_v is constant and there is no phase change.

At low temperatures near absolute zero, heat capacities of solids quickly drop off to near zero, so the assumption of constant heat capacity does not apply.^[63]

Since entropy is a state function, the entropy change of any process in which temperature and volume both vary is the same as for a path divided into two steps – heating at constant volume and expansion at constant temperature. For an ideal gas, the total entropy change is^[64]

Similarly if the temperature and pressure of an ideal gas both vary,

Phase transitions[edit]

Reversible phase transitions occur at constant temperature and pressure. The reversible heat is the enthalpy change for the transition, and the entropy change is the enthalpy change divided by the thermodynamic temperature.^[65] For fusion (melting) of a solid to a liquid at the melting point T_m, the entropy of fusion is

Similarly, for vaporization of a liquid to a gas at the boiling point T_b, the entropy of vaporization is

Approaches to understanding entropy[edit]

As a fundamental aspect of thermodynamics and physics, several different approaches to entropy beyond that of Clausius and Boltzmann are valid.

Standard textbook definitions[edit]

The following is a list of additional definitions of entropy from a collection of textbooks:

• a measure of energy dispersal at a specific temperature.
• a measure of disorder in the universe or of the availability of the energy in a system to do work.^[66]
• a measure of a system’s thermal energy per unit temperature that is unavailable for doing useful work.^[67]

In Boltzmann’s analysis in terms of constituent particles, entropy is a measure of the number of possible microscopic states (or microstates) of a system in thermodynamic equilibrium.

Order and disorder[edit]

Entropy is often loosely associated with the amount of order or disorder, or of chaos, in a thermodynamic system. The traditional qualitative description of entropy is that it refers to changes in the status quo of the system and is a measure of «molecular disorder» and the amount of wasted energy in a dynamical energy transformation from one state or form to another. In this direction, several recent authors have derived exact entropy formulas to account for and measure disorder and order in atomic and molecular assemblies.^[68][69][70] One of the simpler entropy order/disorder formulas is that derived in 1984 by thermodynamic physicist Peter Landsberg, based on a combination of thermodynamics and information theory arguments. He argues that when constraints operate on a system, such that it is prevented from entering one or more of its possible or permitted states, as contrasted with its forbidden states, the measure of the total amount of «disorder» in the system is given by:^[69][70]

Similarly, the total amount of «order» in the system is given by:

In which C_D is the «disorder» capacity of the system, which is the entropy of the parts contained in the permitted ensemble, C_I is the «information» capacity of the system, an expression similar to Shannon’s channel capacity, and C_O is the «order» capacity of the system.^[68]

Energy dispersal[edit]

The concept of entropy can be described qualitatively as a measure of energy dispersal at a specific temperature.^[71] Similar terms have been in use from early in the history of classical thermodynamics, and with the development of statistical thermodynamics and quantum theory, entropy changes have been described in terms of the mixing or «spreading» of the total energy of each constituent of a system over its particular quantized energy levels.

Ambiguities in the terms disorder and chaos, which usually have meanings directly opposed to equilibrium, contribute to widespread confusion and hamper comprehension of entropy for most students.^[72] As the second law of thermodynamics shows, in an isolated system internal portions at different temperatures tend to adjust to a single uniform temperature and thus produce equilibrium. A recently developed educational approach avoids ambiguous terms and describes such spreading out of energy as dispersal, which leads to loss of the differentials required for work even though the total energy remains constant in accordance with the first law of thermodynamics^[73] (compare discussion in next section). Physical chemist Peter Atkins, in his textbook Physical Chemistry, introduces entropy with the statement that «spontaneous changes are always accompanied by a dispersal of energy or matter and often both».^[74]

Relating entropy to energy usefulness[edit]

It is possible (in a thermal context) to regard lower entropy as a measure of the effectiveness or usefulness of a particular quantity of energy.^[75] Energy supplied at a higher temperature (i.e. with low entropy) tends to be more useful than the same amount of energy available at a lower temperature. Mixing a hot parcel of a fluid with a cold one produces a parcel of intermediate temperature, in which the overall increase in entropy represents a «loss» that can never be replaced.

As the entropy of the universe is steadily increasing, its total energy is becoming less useful. Eventually, this leads to the heat death of the universe.^[76]

Entropy and adiabatic accessibility[edit]

A definition of entropy based entirely on the relation of adiabatic accessibility between equilibrium states was given by E. H. Lieb and J. Yngvason in 1999.^[77] This approach has several predecessors, including the pioneering work of Constantin Carathéodory from 1909^[78] and the monograph by R. Giles.^[79] In the setting of Lieb and Yngvason, one starts by picking, for a unit amount of the substance under consideration, two reference states and such that the latter is adiabatically accessible from the former but not conversely. Defining the entropies of the reference states to be 0 and 1 respectively, the entropy of a state is defined as the largest number such that is adiabatically accessible from a composite state consisting of an amount in the state and a complementary amount, , in the state . A simple but important result within this setting is that entropy is uniquely determined, apart from a choice of unit and an additive constant for each chemical element, by the following properties: It is monotonic with respect to the relation of adiabatic accessibility, additive on composite systems, and extensive under scaling.

Entropy in quantum mechanics[edit]

In quantum statistical mechanics, the concept of entropy was developed by John von Neumann and is generally referred to as «von Neumann entropy»,

where ρ is the density matrix, and Tr is the trace operator.

This upholds the correspondence principle, because in the classical limit, when the phases between the basis states used for the classical probabilities are purely random, this expression is equivalent to the familiar classical definition of entropy,

i.e. in such a basis the density matrix is diagonal.

Von Neumann established a rigorous mathematical framework for quantum mechanics with his work Mathematische Grundlagen der Quantenmechanik. He provided in this work a theory of measurement, where the usual notion of wave function collapse is described as an irreversible process (the so-called von Neumann or projective measurement). Using this concept, in conjunction with the density matrix he extended the classical concept of entropy into the quantum domain.

Information theory[edit]

When viewed in terms of information theory, the entropy state function is the amount of information in the system that is needed to fully specify the microstate of the system. Entropy is the measure of the amount of missing information before reception.^[81] Often called Shannon entropy, it was originally devised by Claude Shannon in 1948 to study the size of information of a transmitted message. The definition of information entropy is expressed in terms of a discrete set of probabilities so that

where the base of the logarithm determines the units (for example, the binary logarithm corresponds to bits).

In the case of transmitted messages, these probabilities were the probabilities that a particular message was actually transmitted, and the entropy of the message system was a measure of the average size of information of a message. For the case of equal probabilities (i.e. each message is equally probable), the Shannon entropy (in bits) is just the number of binary questions needed to determine the content of the message.^[28]

Most researchers consider information entropy and thermodynamic entropy directly linked to the same concept,^{[82][83][84][85][86]} while others argue that they are distinct.^[87] Both expressions are mathematically similar. If is the number of microstates that can yield a given macrostate, and each microstate has the same a priori probability, then that probability is . The Shannon entropy (in nats) is

and if entropy is measured in units of per nat, then the entropy is given by

which is the Boltzmann entropy formula, where is the Boltzmann constant, which may be interpreted as the thermodynamic entropy per nat. Some authors argue for dropping the word entropy for the function of information theory and using Shannon’s other term, «uncertainty», instead.^[88]

Measurement[edit]

The entropy of a substance can be measured, although in an indirect way. The measurement, known as entropymetry,^[89] is done on a closed system (with particle number N and volume V being constants) and uses the definition of temperature^[90] in terms of entropy, while limiting energy exchange to heat ().

The resulting relation describes how entropy changes when a small amount of energy is introduced into the system at a certain temperature .

The process of measurement goes as follows. First, a sample of the substance is cooled as close to absolute zero as possible. At such temperatures, the entropy approaches zero – due to the definition of temperature. Then, small amounts of heat are introduced into the sample and the change in temperature is recorded, until the temperature reaches a desired value (usually 25 °C). The obtained data allows the user to integrate the equation above, yielding the absolute value of entropy of the substance at the final temperature. This value of entropy is called calorimetric entropy.^[91]

Interdisciplinary applications[edit]

Although the concept of entropy was originally a thermodynamic concept, it has been adapted in other fields of study,^[60] including information theory, psychodynamics, thermoeconomics/ecological economics, and evolution.^{[68][92][93][94][95]}

Philosophy and theoretical physics[edit]

Entropy is the only quantity in the physical sciences that seems to imply a particular direction of progress, sometimes called an arrow of time. As time progresses, the second law of thermodynamics states that the entropy of an isolated system never decreases in large systems over significant periods of time. Hence, from this perspective, entropy measurement is thought of as a clock in these conditions.^{[citation needed]}

Biology[edit]

Chiavazzo et al. proposed that where cave spiders choose to lay their eggs can be explained through entropy minimization.^[96]

Entropy has been proven useful in the analysis of base pair sequences in DNA. Many entropy-based measures have been shown to distinguish between different structural regions of the genome, differentiate between coding and non-coding regions of DNA, and can also be applied for the recreation of evolutionary trees by determining the evolutionary distance between different species.^[97]

Cosmology[edit]

Assuming that a finite universe is an isolated system, the second law of thermodynamics states that its total entropy is continually increasing. It has been speculated, since the 19th century, that the universe is fated to a heat death in which all the energy ends up as a homogeneous distribution of thermal energy so that no more work can be extracted from any source.

If the universe can be considered to have generally increasing entropy, then – as Roger Penrose has pointed out – gravity plays an important role in the increase because gravity causes dispersed matter to accumulate into stars, which collapse eventually into black holes. The entropy of a black hole is proportional to the surface area of the black hole’s event horizon.^{[98][99][100]} Jacob Bekenstein and Stephen Hawking have shown that black holes have the maximum possible entropy of any object of equal size. This makes them likely end points of all entropy-increasing processes, if they are totally effective matter and energy traps.^[101] However, the escape of energy from black holes might be possible due to quantum activity (see Hawking radiation).

The role of entropy in cosmology remains a controversial subject since the time of Ludwig Boltzmann. Recent work has cast some doubt on the heat death hypothesis and the applicability of any simple thermodynamic model to the universe in general. Although entropy does increase in the model of an expanding universe, the maximum possible entropy rises much more rapidly, moving the universe further from the heat death with time, not closer.^{[102][103][104]} This results in an «entropy gap» pushing the system further away from the posited heat death equilibrium.^[105] Other complicating factors, such as the energy density of the vacuum and macroscopic quantum effects, are difficult to reconcile with thermodynamical models, making any predictions of large-scale thermodynamics extremely difficult.^[106]

Current theories suggest the entropy gap to have been originally opened up by the early rapid exponential expansion of the universe.^[107]

Economics[edit]

Romanian American economist Nicholas Georgescu-Roegen, a progenitor in economics and a paradigm founder of ecological economics, made extensive use of the entropy concept in his magnum opus on The Entropy Law and the Economic Process.^[83] Due to Georgescu-Roegen’s work, the laws of thermodynamics form an integral part of the ecological economics school.^{[108]: 204f [109]: 29–35} Although his work was blemished somewhat by mistakes, a full chapter on the economics of Georgescu-Roegen has approvingly been included in one elementary physics textbook on the historical development of thermodynamics.^{[110]: 95–112}

In economics, Georgescu-Roegen’s work has generated the term ‘entropy pessimism’.^[111]: 116 Since the 1990s, leading ecological economist and steady-state theorist Herman Daly – a student of Georgescu-Roegen – has been the economics profession’s most influential proponent of the entropy pessimism position.^{[112]: 545f [113]}

See also[edit]

Notes[edit]

References[edit]

• David, Kover. «Entropia – fyzikálna veličina vesmíru a nášho života». stejfree.sk. Retrieved 13 April 2022.

Further reading[edit]

• Adam, Gerhard; Otto Hittmair (1992). Wärmetheorie. Vieweg, Braunschweig. ISBN 978-3-528-33311-9.
• Atkins, Peter; Julio De Paula (2006). Physical Chemistry (8th ed.). Oxford University Press. ISBN 978-0-19-870072-2.
• Baierlein, Ralph (2003). Thermal Physics. Cambridge University Press. ISBN 978-0-521-65838-6.
• Ben-Naim, Arieh (2007). Entropy Demystified. World Scientific. ISBN 978-981-270-055-1.
• Callen, Herbert, B (2001). Thermodynamics and an Introduction to Thermostatistics (2nd ed.). John Wiley and Sons. ISBN 978-0-471-86256-7.
• Chang, Raymond (1998). Chemistry (6th ed.). New York: McGraw Hill. ISBN 978-0-07-115221-1.
• Cutnell, John, D.; Johnson, Kenneth, J. (1998). Physics (4th ed.). John Wiley and Sons, Inc. ISBN 978-0-471-19113-1.
• Dugdale, J. S. (1996). Entropy and its Physical Meaning (2nd ed.). Taylor and Francis (UK); CRC (US). ISBN 978-0-7484-0569-5.
• Fermi, Enrico (1937). Thermodynamics. Prentice Hall. ISBN 978-0-486-60361-2.
• Goldstein, Martin; Inge, F (1993). The Refrigerator and the Universe. Harvard University Press. ISBN 978-0-674-75325-9.
• Gyftopoulos, E.P.; G.P. Beretta (2010). Thermodynamics. Foundations and Applications. Dover. ISBN 978-0-486-43932-7.
• Haddad, Wassim M.; Chellaboina, VijaySekhar; Nersesov, Sergey G. (2005). Thermodynamics – A Dynamical Systems Approach. Princeton University Press. ISBN 978-0-691-12327-1.
• Johnson, Eric (2018). Anxiety and the Equation: Understanding Boltzmann’s Entropy. The MIT Press. ISBN 978-0-262-03861-4.
• Kroemer, Herbert; Charles Kittel (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 978-0-7167-1088-2.
• Lambert, Frank L.; entropysite.oxy.edu
• Müller-Kirsten, Harald J. W. (2013). Basics of Statistical Physics (2nd ed.). Singapore: World Scientific. ISBN 978-981-4449-53-3.
• Penrose, Roger (2005). The Road to Reality: A Complete Guide to the Laws of the Universe. New York: A. A. Knopf. ISBN 978-0-679-45443-4.
• Reif, F. (1965). Fundamentals of statistical and thermal physics. McGraw-Hill. ISBN 978-0-07-051800-1.
• Schroeder, Daniel V. (2000). Introduction to Thermal Physics. New York: Addison Wesley Longman. ISBN 978-0-201-38027-9.
• Serway, Raymond, A. (1992). Physics for Scientists and Engineers. Saunders Golden Subburst Series. ISBN 978-0-03-096026-0.
• Sharp, Kim (2019). Entropy and the Tao of Counting: A Brief Introduction to Statistical Mechanics and the Second Law of Thermodynamics (SpringerBriefs in Physics). Springer Nature. ISBN 978-3030354596.
• Spirax-Sarco Limited, Entropy – A Basic Understanding A primer on entropy tables for steam engineering
• vonBaeyer; Hans Christian (1998). Maxwell’s Demon: Why Warmth Disperses and Time Passes. Random House. ISBN 978-0-679-43342-2.

External links[edit]

• «Entropy» at Scholarpedia
• Entropy and the Clausius inequality MIT OCW lecture, part of 5.60 Thermodynamics & Kinetics, Spring 2008
• Entropy and the Second Law of Thermodynamics – an A-level physics lecture with ‘derivation’ of entropy based on Carnot cycle
• Khan Academy: entropy lectures, part of Chemistry playlist
  • Entropy Intuition
  • More on Entropy
  • Proof: S (or Entropy) is a valid state variable
  • Reconciling Thermodynamic and State Definitions of Entropy
  • Thermodynamic Entropy Definition Clarification
• Moriarty, Philip; Merrifield, Michael (2009). «S Entropy». Sixty Symbols. Brady Haran for the University of Nottingham.
• The Discovery of Entropy by Adam Shulman. Hour-long video, January 2013.
• The Second Law of Thermodynamics and Entropy – Yale OYC lecture, part of Fundamentals of Physics I (PHYS 200)