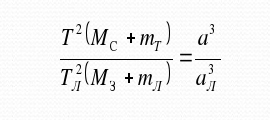Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.
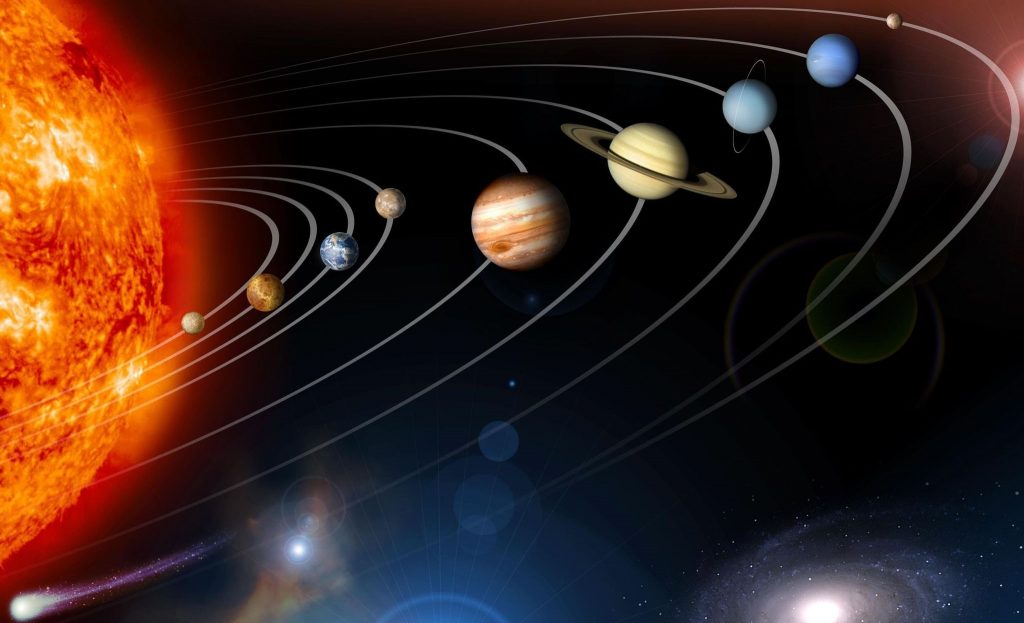
Планеты солнечной системы
Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).
Содержание:
- 1 Рассчитываем массу Земли и Луны
- 2 Общие методики определения масс планет
- 3 Значения масс планет Солнечной системы
- 4 Определение масс звезд и галактик
Рассчитываем массу Земли и Луны
Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.
Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:
Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.
Земля и луна
Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.
Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.
Общие методики определения масс планет
Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.
Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.
Значения масс планет Солнечной системы
Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.
Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.
Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.
Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.
Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Определение масс звезд и галактик
Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.
Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.
Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:
Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.
Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.
Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.
МА́ССЫ НЕБЕ́СНЫХ ТЕЛ (методы определения). Определение М. н. т. стало возможным в 17 в., после открытия всемирного тяготения закона.
Массы Земли и других планет
Одна из первых оценок массы Земли получена Г. Кавендишем после проведения опыта по эксперим. определению универсальной гравитац. постоянной. Измеряя с помощью крутильных весов силу притяжения между массивным свинцовым шаром и подвешенным вблизи него небольшим металлич. шариком, Кавендиш сравнил величину этой силы с силой притяжения шарика Землёй и сумел вычислить, во сколько раз масса Земли превышает массу свинцового шара. Таким образом была получена оценка массы Земли (6·1024 кг) и её ср. плотности (5,5 кг/м3).
Массы др. планет определяют по параметрам их орбит с помощью третьего закона Кеплера (см. Кеплера законы). В обобщённой форме этот закон имеет вид: $T_1^2(M_☉+m_1)/T_2^2(M_☉+m_2)=a_1^3/a_2^3$, где $M☉$ – масса Солнца, $m_1$ и $m_2$ – массы двух планет, $a_1$ и $a_2$ – большие полуоси их орбит, $T_1$ и $T_2$ – периоды обращения этих планет вокруг Солнца. Для планеты, имеющей спутник массой $m_с$, движущийся по планетоцентрической орбите с большой полуосью $a_с$ и периодом обращения $T_с$, этот закон приобретает вид: $T^2(M_☉+m)/T_с^2(m+m_с)=a^3/a_с^3,$ где $m$ – масса планеты, $a$ и $T$– её большая полуось и период обращения соответственно. Если в этой формуле пренебречь массой планеты по сравнению с $M_☉$ и массой спутника по сравнению с массой планеты, то можно получить соотношение, позволяющее определить отношение массы планеты к $M_☉:: m/M_☉=T^2a_с^3/T_с^2a^3$. По параметрам орбит Земли и Луны была проведена оценка массы Солнца – примерно в 333 000 раз больше массы Земли.
Массы Меркурия и Венеры, у которых отсутствуют естеств. спутники, этим способом определить невозможно. Единственный и гораздо более трудный путь состоит в использовании возмущений (всегда являющихся функциями возмущающей массы), которые планета вызывает в движении др. тел Солнечной системы. Значительно более трудную задачу представляет определение массы Луны. Являясь ближайшим к Земле небесным телом, Луна не может, строго говоря, считаться спутником нашей планеты, т. к. Солнце притягивает её в 2,5 раза сильнее, чем Земля. Вокруг Солнца обращается т. н. барицентр (центр масс) двойной планеты Земля–Луна, в то время как обе они описывают относительно барицентра эллиптич. орбиты с периодом в 1 месяц. Поэтому массу Луны можно вычислить по величине месячного смещения Земли относительно барицентра. В точных астрономич. наблюдениях долготы Солнца проявляется т. н. лунное неравенство, свидетельствующее о том, что центр Земли в течение месяца описывает эллипс с большой полуосью, равной примерно 3/4 радиуса Земли. Последнее означает, что барицентр системы Земля–Луна всегда располагается внутри Земли и никогда не выходит за пределы её поверхности. Определённая по этим данным масса Луны составляет ок. 1/81 массы Земли.
Массы всех планет Солнечной системы входят в число фундам. астрономич. постоянных, значения которых регулярно уточняются на основе всей совокупности астрономич. наблюдений и утверждаются Междунар. астрономич. союзом.
Массы звёзд
Третий закон Кеплера в его обобщённой форме позволяет также определить суммарную массу двойной звезды по известному значению её годичного параллакса. Если $m_1$ и $m_2$ – массы компонентов звёздной пары, $A$ – большая полуось орбиты звезды-спутника относительно гл. звезды, $P$ – её период обращения, $a$ – ср. расстояние от Земли до Солнца (равное 1 а. е.), $T$ – период обращения Земли вокруг Солнца (1 год), $m$ – масса Земли, то, согласно третьему закону Кеплера, $a^3/T^2(M_☉+m) =A^3/P^2(m_1+m_2)$. Пренебрегая массой Земли по сравнению с массой Солнца и выбрав в качестве единицы измерения времени год, а расстояния – а. е., получим формулу $(m_1+m_2)/M_☉=A^3/P^2$, позволяющую определить отношения суммы масс двойной звезды к $M_☉$. Значение $A$ можно вычислить, если известны годичный параллакс π двойной звезды и значение большой полуоси $a″$ относительной орбиты звезды-спутника, выраженное в угловых секундах. Тогда $A=a″/π$ и для определения отношения суммарной массы двойной звёздной системы к $M_☉$ можно воспользоваться формулой $(m_1+m_2)/M_☉= (a″ )^3/π^3P^2$. Напр., для двойной звёздной системы Сириус А и Сириус B соответствующие значения составляют $a″$=7,57″, $π$=0,37″ и $P$ = 50 лет, соответственно суммарная масса этой двойной звёздной системы оценивается в 3,4$M_☉$.
В том случае, когда удаётся измерить положения визуально-двойных звёзд относительно их барицентра, возникает возможность определить отношение масс обоих компонентов. Такие измерения требуют знания точных положений компонентов системы относительно далёких звёзд (т. н. звёзд фона) на достаточно длительных интервалах времени. Продолжит. наблюдения одиночной звезды в течение мн. лет показывают, что если она имеет собственное движение относительно звёздного фона, то её перемещение происходит по дуге большого круга небесной сферы. Но если звезда – визуально-двойная, то по дуге большого круга смещается её барицентр, а оба компонента системы движутся по криволинейным барицентрич. траекториям. Точные астрометрич. измерения положений компонентов двойной системы позволяют проследить траекторию центра масс, а затем и индивидуальные орбиты отд. компонентов. Если $α_1$ и $α_2$ – выраженные в секундах дуги угловые расстояния от гл. звезды с массой $M_1$ и звезды-спутника с массой $M_2$ до видимого положения центра масс двойной системы, то тогда, по определению центра масс, $M_1α_1=M_2α_2$, откуда следует формула для отношения масс компонентов визуально-двойной звезды: $M_1/M_2=α_2/α_1$.
Знание суммарной массы двойной звезды и отношения масс её компонентов позволяет без труда вычислить массы обеих звёзд. Типичные значения масс звёзд, полученные по наблюдениям визуально-двойных звёзд, лежат в пределах (0,1–20)$M_☉$. Более половины звёзд нашей Галактики входят в состав двойных, тройных звёзд или звёздных систем большей кратности. Именно исследования двойных звёзд позволили получить данные о звёздных массах и послужили основой для установления соотношения масса – светимость (см. Масса – светимость зависимость). Это соотношение широко используется в звёздной астрономии и астрофизике в качестве незаменимого средства оценки масс звёзд по их светимостям.
Согласно совр. представлениям, массы звёзд заключены в пределах (0,08–100)$M_☉$. Масса отд. звезды в среднем близка к $M_☉$, в то время как звёзды с массами, в десятки раз бóльшими массы Солнца, встречаются достаточно редко: это гл. обр. звёзды ранних спектральных классов O и B.
Массы звёздных скоплений и галактик
Массу $M$ шарового звёздного скопления радиуса $R$ можно оценить по величине круговой скорости $V$ звезды, движущейся на границе скопления, считая, что центростремит. ускорение звезды вызвано притяжением всех звёзд шарового скопления. Тогда масса скопления оценивается по формуле $M=V^2R/G$, где $G$ – гравитац. постоянная. Более точная оценка массы звёздного скопления получается при использовании некоторых усреднённых значений скоростей звёзд и их ср. удалённости от центра скопления.
Наличие у галактики одного спутника (играющего роль пробного тела) позволяет оценить массу галактики с помощью аналогичной формулы, но точность такой оценки очень невысока. В качестве пробного тела может рассматриваться др. галактика, шаровое скопление, расположенное на периферии галактики, и даже облако межзвёздного газа. Если у галактики имеется неск. спутников (или др. пробных тел), то можно предположить, что распределение положений и скоростей спутников имеет случайный характер. Это предположение реализуется тем точнее, чем больше имеется пробных тел (напр., в галактике М31 в созвездии Андромеды ок. 400 шаровых скоплений). Тогда в приведённой формуле можно использовать видимые расстояния и скорости пробных тел, усреднённые за промежуток времени, значительно превышающий их орбитальные периоды. Массы спиральных галактик можно оценивать с помощью облаков межзвёздного газа на круговых орбитах в галактич. плоскости. Изложенный метод измерения масс галактик (метод Ньютона) базируется на законе всемирного тяготения. Более перспективным считается метод Эйнштейна, в котором массивные галактики рассматриваются в качестве гравитац. линзы (см. Гравитационная фокусировка).
В оценке суммарной массы галактики с учётом всех её составляющих (звёзд, газа, пыли и др.) существенную роль играет круговая скорость пробного тела. Эта скорость при удалении от центра галактики должна уменьшаться по определённому закону. Однако по результатам наблюдений удалось установить, что этот закон выполняется только во внутр. области галактики. На периферии любой галактики круговая скорость почти всегда выше значения, полученного в предположении, что вся масса галактики заключена в её звёздах и газе. Чаще всего скорость вращения звёзд не уменьшается с расстоянием от центра галактики, а остаётся постоянной или даже растёт при приближении к видимому краю галактики. Для объяснения такого феномена было выдвинуто предположение о существовании в галактиках скрытой массы, повышающей величину напряжённости гравитац. поля галактики вдали от её центра. Вопрос о границах галактик и их полных массах на нач. 21 в. не решён: несветящиеся части галактик могут простираться на порядок дальше видимой границы их звёздных дисков.
В основе определения масс небесных тел лежит закон всемирного тяготения, выражаемый
ф-лой:
(1)
где F
— сила взаимного притяжения масс и , пропорциональная их произведению и обратно пропорциональная квадрату
расстояния r
между их центрами. В астрономии часто (но не всегда) можно пренебречь
размерами самих небесных тел по сравнению с разделяющими их расстояниями, отличием
их формы от точной сферы и уподоблять небесные тела материальным точкам, в к-рых
сосредоточена вся их масса.
Коэффициент пропорциональности G = наз. или постоянной тяготения. Её находят из физического эксперимента с
крутильными весами, позволяющими определить силу гравитац. взаимодействия тел известной
массы.
В случае свободного падения тел сила F
, действующая на тело, равна произведению
массы тела на ускорение свободного падения g
. Ускорение
g
может быть определено, напр., по периоду T
колебаний вертикального
маятника: , где l
— длина маятника. На широте
45 o
и на уровне моря g
= 9,806 м/с 2 .
Подстановка выражения для сил земного притяжения
в ф-лу (1) приводит к зависимости ,
где
— масса Земли, а — радиус
земного шара. Таким путём была определена масса Земли г. Определение массы Земли явл. первым звеном в цепи определений масс
др. небесных тел (Солнца, Луны, планет, а затем и звёзд). Массы этих тел находят,
опираясь
либо на 3-й закон Кеплера (см. ),
либо на правило: расстояния к.-л. масс от общего центра масс обратно пропорциональны
самим массам. Это правило позволяет определить массу Луны. Из измерений точных координат
планет и Солнца найдено, что Земля и Луна с периодом в один месяц движутся вокруг
барицентра — центра масс системы Земля — Луна. Расстояние центра Земли от барицентра
равно 0,730 (он расположен внутри земного шара). Ср. расстояние
цeнтpa Луны от центра Земли составляет 60,08 . Отсюда отношение
расстояний центров Луны и Земли от барицентра равно 1/81,3. Поскольку это отношение
обратно
отношению масс Земли и Луны, масса Луны
г.
Массу Солнца можно определить, применив 3-й закон Кеплера к движению Земли (вместе
с Луной) вокруг Солнца и движению Луны вокруг Земли:
, (2)
где а
— большие полуоси орбит, T
— периоды (звёздные или сидерические)
обращения. Пренебрегая по сравнению с , получим отношение , равное 329390. Отсюда г, или ок. .
Аналогичным путём определяют массы планет, имеющих спутников. Массы планет, не имеющих
спутников, определяют по возмущениям, к-рые они оказывают на движение соседних с
ними
планет. Теория возмущённого движения планет позволила заподозрить существование тогда
неизвестных планет Нептуна и Плутона, найти их массы, предсказать их положение на
небе.
Массу звезды (помимо Солнца) можно определить со сравнительно высокой надёжностью
только в том случае, если она явл. физ. компонентом визуально-двойной звезды (см.
), расстояние до к-рой известно. Третий закон Кеплера в
этом случае даёт сумму масс компонентов (в ед. ):
,
где а
«» -большая полуось (в секундах дуги) истинной орбиты спутника вокруг
главной (обычно более яркой) звезды, к-рую в этом случае считают неподвижной, Р
—
период обращения в годах, —
системы (в секундах дуги). Величина даёт большую полуось
орбиты в а. е. Если можно измерить угловые расстояния компонентов
от общего центра масс, то их отношение даст величину, обратную отношению масс: . Найденная сумма масс и их отношение позволяют получить
массу каждой звезды в отдельности. Если компоненты двойной имеют примерно одинаковый
блеск
и сходные спектры, то полусумма масс
даёт верную оценку массы каждого компонента и без дополнит. определения их отношения.
Для др. типов двойных звезд (затменно-двойных и спектрально-двойных) имеется ряд
возможностей приблизительно определить массы звёзд или оценить их нижний предел (т.е.
величины,
меньше которых не могут быть их массы).
Совокупность данных о массах компонентов примерно ста двойных звёзд разных типов
позволила обнаружить важную статистич. зависимость между их массами и светимостями
(см. ).
Она даёт возможность оценивать массы одиночных звёзд по их
(иначе говоря, по их абс. ).
Абс. звёздные величины М
определяются по ф-ле:
M = m
+ 5 + 5 lg — A(r)
, (3)
где m
— видимая звёздная величина в выбранном оптич. диапазоне (в определённой
фотометрич. системе, напр. U, В
или V
; см. ),
— параллакс и A(r)
— величина света в том же оптич. диапазоне в данном
направлении
до расстояния .
Если параллакс звезды не измерен, то приближённое значение абс. звёздной величины
можно определить по её спектру. Для этого необходимо, чтобы спектрограмма позволяла
не только
узнать звезды, но
и оценить относительные интенсивности нек-рых пар спектр. линий, чувствительных к
«эффекту
абс. величины». Иначе говоря, сначала необходимо определить класс светимости звезды
— принадлежность к одной из последовательностей на диаграмме спектр-светимость (см.
),
а по классу светимости — её абс. величину. По полученной таким образом абс. величине
можно найти массу звезды, воспользовавшись зависимостью масса-светимость (этой зависимости
не подчиняются лишь и ).
Ещё один метод оценки массы звезды связан с измерением гравитац. красного смещения
спектр. линий в её поле тяготения. В сферически-симметричном поле тяготения оно эквивалентно
доплеровскому красному смещению , где
— масса звезды в ед. массы Солнца, R
— радиус звезды
в
ед. радиуса Солнца, а выражено в км/с. Это соотношение было
проверено по тем белым карликам, к-рые входят в состав двойных систем. Для них были
известны
радиусы, массы и истинные
v r
, являющиеся проекциями орбитальной скорости.
Невидимые (тёмные) спутники, обнаруженные около нек-рых звёзд по наблюдённым колебаниям
положения звезды, связанным с её движением около общего центра масс (см. ), имеют массы меньше 0,02 . Они, вероятно, не явл. самосветящимися телами и больше похожи на
планеты.
Из определений масс звёзд выяснилось, что они заключены примерно в пределах от 0,03
до 60 . Наибольшее
количество
звёзд имеют массы от 0,3 до 3 .
Ср. масса звезд в ближайших окрестностях Солнца , т.е. 10 33 г. Различие
в массах звёзд оказывается много меньшим, чем их различие в светимостях (последнее
может
достигать десятков млн.). Сильно отличаются и радиусы звёзд. Это приводит к разительному
различию их ср. плотностей: от до
г/см 3 (ср. плотность Солнца 1,4 г/см 3).
Массу Солнца можно найти из условия, что тяготение Земли к Солнцу проявляется в качестве центростремительной силы, удерживающей Землю на ее орбите (орбиту Земли для упрощения мы будем считать окружностью)
Здесь масса Земли, среднее расстояние Земли от Солнца. Обозначая продолжительность года в секундах через имеем. Таким образом
откуда, подставляя числовые значения , находим массу Солнца:
Ту же формулу можно применить для вычисления массы какой-либо планеты, имеющей спутника. В этом случае среднее расстояние спутника от планеты, время его обращения вокруг планеты, масса планеты. В частности, по расстоянию Луны от Земли и числу секунд в месяце указанным способом можно определить массу Земли.
Массу Земли можно определить также, приравнивая вес какого-либо тела к тяготению этого тела к Земле, за вычетом той составляющей тяготения, которая проявляется динамически, сообщая данному телу, участвующему в суточном вращении Земли, соответствующее центростремительное ускорение (§ 30). Необходимость указанной поправки отпадает, если для такого вычисления массы Земли мы воспользуемся тем ускорением тяжести, которое наблюдается на полюсах Земли Тогда, обозначив через средний радиус Земли и через массу Земли, имеем:
откуда масса Земли
Если среднюю плотность земного шара обозначить через то, очевидно, Отсюда средняя плотность земного шара получается равной
Средняя плотность минеральных пород верхних слоев Земли равна примерно Стало быть, ядро земного шара должно иметь плотность, значительно превышающую
Исследование вопроса о плотности Земли на различных глубинах было предпринято Лежандром и продолжено многими учеными. По выводам Гутенберга и Гаалька (1924 г.) на различных глубинах имеют место примерно следующие значения плотности Земли:
Давление внутри земного шара, на большой глубине, по-видимому громадно. Многие геофизики считают, что уже на глубине давление должно достигать атмосфер, на квадратный сантиметр В ядре Земли, на глубине около 3000 и более километров давление, возможно, достигает 1-2 млн. атмосфер.
Что касается температуры а глубине земного шара, то достоверно, что она выше (температура лавы). В шахтах и буровых скважинах температура повышается в среднем на один градус на каждые Предполагают, что на глубине около температура доходит до 1500-2000° и далее остается постоянной.
Рис. 50. Относительные размеры Солнца и планет.
Полная теория движения планет, излагаемая в небесной механике, позволяет вычислить массу планеты по наблюдениям того влияния, которое данная планета оказывает на движение какой-либо другой планеты. В начале прошлого столетия были известны планеты Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран. Было замечено, что движение Урана обнаруживает некоторые «неправильности», которые указывали на то, что за Ураном находится ненаблюденная планета, влияющая на движение Урана. В 1845 г. французский ученый Леверье и независимо от него англичанин Адаме, исследовав движение Урана, вычислили массу и местоположение планеты, которую еще никто не наблюдал. Только после этого планета была найдена на небе как раз в том месте, которое было указано вычислениями; эта планета была названа Нептуном.
В 1914 г. астроном Ловелл аналогичным путем предсказал существование еще одной планеты, находящейся еще дальше от Солнца, чем Нептун. Только в 1930 г. эта планета была найдена и названа Плутоном.
Основные сведения о больших планетах
(см. скан)
В приведенной таблице содержатся основные сведения о девяти больших планетах солнечной системы. Рис. 50 иллюстрирует относительные размеры Солнца и планет.
Кроме перечисленных больших планет, известно около 1300 весьма малых планет, так называемых астероидов (или планетоидов) Их орбиты в основном находятся между орбитами Марса и Юпитера.
Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу.
Массу можно определить:
а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),
б) по третьему уточнённому закону Кеплера,
в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.
1. Первый способ применяется на Земле.
На основании закона тяготения ускорение g на поверхности Земли:
где m — масса Земли, а R — её радиус.
g и R измеряются на поверхности Земли. G = const.
С принятыми сейчас значениями g, R, G получается масса Земли:
m = 5,976 .1027г = 6 .1024кг.
Зная массу и объём, можно найти среднюю плотность. Она равна 5,5 г/см3.
2. По третьему закону Кеплера можно определить соотношение между массой планеты и массой Солнца, если у планеты есть хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг неё.
где M, m, mc- массы Солнца, планеты и её спутника, T и tc- периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а
и ас
— расстояния планеты от Солнца и спутника от планеты соответственно.
Из уравнения следует
Отношение М/m для всех планет очень велико; отношение же m/mc, очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь.
Соотношение М/m можно легко найти из уравнения.
Для случая Земли и Луны нужно сначала определить массу Луны. Это сделать очень сложно. Решается задача путём анализа возмущений в движении Земли, которые вызывает Луна.
3. По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые «лунным неравенством». Наличие этого факта в видимом движении Солнца указывает на то, что центр Земли описывает небольшой эллипс в течение месяца вокруг общего центра масс «Земля — Луна», расположенного внутри Земли, на расстоянии 4650 км. от центра Земли.
Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 — 1931 гг.
По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81,30.
В 1964 году Международный астрономический союз принял его как const.
Из уравнения Кеплера получаем для Солнца массу = 2.1033г., что в 333000 раза превосходит земную.
Массы планет, не имеющих спутников, определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, по возмущениям, производимым ими друг на друга.
Земля — уникальная планета солнечной системы. Она не самая маленькая, но и не самая крупная: занимает пятое место по габаритам. Среди планет земной группы она является крупнейшей по массе, диаметру, плотности. Планета располагается в космическом пространстве, и узнать, сколько весит Земля, сложно. Ее же нельзя положить на весы и взвесить, поэтому об ее весе говорят, суммируя массу всех веществ, из которых она состоит. Приблизительно этот показатель равен 5,9 секстиллиона тонн. Чтобы понимать, какая это цифра, можно ее просто математически записать: 5 900 000 000 000 000 000 000. От этого количества нулей как-то рябит в глазах.
История попыток определения размера планеты
Ученых всех веков и народов пытались найти ответ на вопрос о том, сколько весит Земля. В древние времена люди предполагали, что планета — это плоская тарелка, которую держат киты и черепаха. В некоторых нациях вместо китов были слоны. В любом случае разные народы мира представляли планету плоской и имеющей свой край.
Во времена Средневековья представления о форме и весе изменились. Первым, кто заговорил о сферическом виде, был Дж. Бруно, однако, за свои убеждения его казнила инквизиция. Другой вклад в науку, который показывает радиус и массу Земли, внес путешественник Магеллан. Именно он предположил, что планета круглая.
Первые открытия
Земля — физическое тело, имеющее определенные свойства, среди которых есть и вес. Это открытие позволило начать самые разные исследования. По физической теории вес — это сила действия тела на опору. Учитывая, что Земля не имеет никакой опоры, можно сделать вывод, что у нее нет веса, а вот масса имеется, и большая.
Вес Земли
Впервые определить размер планеты пытался Эратосфен — древнегреческий ученый. В разных городах Греции он проводил замеры тени, а после сравнивал полученные данные. Таким образом он пытался рассчитать объем планеты. После него провести вычисления пытался итальянец Г. Галилей. Именно он открыл закон свободного тяготения. Эстафета по определению того, сколько весит Земля, была принята И. Ньютоном. Благодаря попыткам сделать замеры, он открыл закон гравитации.
Впервые определить, сколько весит Земля, удалось шотландскому ученому Н. Мэкелин. По его вычислениям масса планеты составляет 5,9 секстиллионов тонн. Сейчас этот показатель увеличился. Различия в весе связано с оседанием на поверхности планеты космической пыли. Примерно тридцать тонн пыли ежегодно остаются на планете, делая ее тяжелее.
Масса Земли
Чтобы точно узнать, сколько весит Земля, необходимо знать состав и вес веществ, из которых состоит планета.
- Мантия. Масса этой оболочки составляет примерно 4,05 Х 10 24 кг.
- Ядро. Эта оболочка весит меньше мантии — всего 1.94 Х 10 24 кг.
- Кора земная. Данная часть очень тонкая и весит всего 0,027 Х 10 24 кг.
- Гидросфера и атмосфера. Эти оболочки весят 0,0015 Х 10 24 и 0,0000051 Х 10 24 кг, соответственно.
Сложив все эти данные, получаем вес Земли. Однако по разным источникам масса планеты различна. Так сколько весит планета Земля в тоннах, и сколько весят другие планеты? Вес планеты составляет 5,972 Х 10 21 т. Радиус — 6370 километров.
На основе принципа гравитации можно с легкостью определить вес Земли. Для этого берется нить, и на нее подвешивается маленький груз. Его местоположение определяется точно. Рядом размещают тонну свинца. Между двумя телами возникает притяжение, из-за которого груз отклоняется в сторону на незначительное расстояние. Однако даже отклонение в 0,00003 мм дает возможность вычислить массу планеты. Для этого достаточно измерить силу притяжения по отношению к весу и силу притяжения малого груза к большому. Полученные данные позволяют провести расчеты массы Земли.
Масса Земли и других планет
Земля является самой большой планетой земной группы. По отношению к ней масса Марса составляет около 0,1 земного веса, а Венера — 0,8. составляет около 0,05 от земного. Газовые гиганты во много раз крупнее Земли. Если сравнить Юпитер и нашу планету, то гигант больше в 317 раз, а Сатурн тяжелее в 95 раз, Уран — в 14. Есть планеты, которые весят больше Земли в 500 раз и более. Это огромные газовые тела, расположенные за пределами нашей солнечной системы.