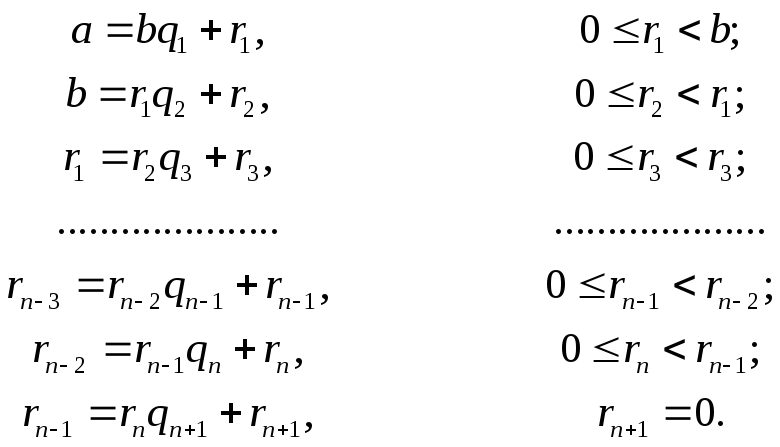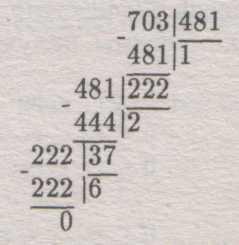Как найти отношение нок к нод

Нахождение НОД с помощью разложения на простые множители

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел. Обозначают НОД(a, b).

Рассмотрим нахождения НОД на примере двух натуральных чисел 18 и 60:

• 1 Разложим числа на простые множители:
  18 = 2 × 3 × 3
  
  60 = 2 × 2 × 3 × 5
• 2 Вычеркнуть из разложения первого числа все множители которые не входят в разложения второго числа, получим 2 × 3 × 3.
• 3 Перемножаем оставшиеся простые множители после вычеркивания и получаем наибольший общий делитель чисел: НОД(18, 60)=2 × 3= 6.
• 4 Заметим что не важно из первого или второго числа вычеркиваем множители, результат будет одинаков:
  
  18 = 2 × 3 × 3
  
  60 = 2 × 2 × 3 × 5

Нахождение НОД с помощью алгоритма Евклида

Второй способ нахождения наибольшего общего делителя с помощью алгоритма Евклида.
Алгоритм Евклида является наиболее эффективным способом нахождения НОД, используя его нужно постоянно находить остаток от деления чисел и применять рекуррентную формулу.

Рекуррентная формула для НОД, НОД(a, b)=НОД(b, a mod b), где a mod b — остаток от деления a на b.

Алгоритм Евклида

Тема: Решение примеров на нахождение наибольшего общего делителя и наименьшего общего кратного.Связь между НОК и НОД

Тип урока: комбинированный.

Цели:

Образовательные:

• отработка навыков нахождения НОД и НОК;
• применение полученных знаний для решения задач;
• повторение и закрепление признаков делимости, простых и составных чисел.

Развивающие:

• наблюдательность, внимание, речь, память, логическое мышление, самостоятельность, интерес к математике через региональный компонент, практическое применение приобретенных знаний, установление межпредметных связей.

Воспитательные:

• воспитывать у учащихся культуру труда, взаимоуважение, стремление хорошо учиться; воспитывать стремление достигать поставленную цель; уверенности в себе, умение работать в коллективе.

Ход урока

1. Организационный момент  Здравствуйте, ребята! Садитесь.

Давайте вспомним, чем мы занимались на предыдущих уроках?

(Мы находили НОД и НОК чисел разными способами и решали задачи)

2. Постановка задачи Сегодня мы с вами обобщим все полученные знания по данной теме. Откройте тетради, запишите число, классная работа, тема: «Нахождение НОД и НОК чисел».

3. Проверка домашнего задания

4. Актуализация знаний  Прежде чем приступим к решению заданий, предлагаю вспомнить некоторые правила.

Стратегия «Собери правило» Учащиеся выходят к доске и ставят соответствие нахождения алгоритма НОД и НОК

5. Обобщение и систематизация знаний и умений

Работа в парах Выполнение задания

1. НОД (4,12)=                              Ответ:
2. НОД (16,24)=                            Ответ:
3. НОД (30,120)=                          Ответ:
4. НОК (4,12)=                              Ответ:
5. НОК (15,4)=                              Ответ:
6. НОК (22,33)=                            Ответ:
7. НОД (4,16,12)=                        Ответ:

Связь между НОК и НОД

Наименьшее общее кратное двух чисел непосредственно связано с наибольшим общим делителем этих чисел. Эта связь между НОД и НОК определяется следующей теоремой.

Теорема.

Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b, деленному на наибольший общий делитель чисел a и b, то есть, НОК(a, b)=a·b:НОД(a, b).

Доказательство.

Пусть М – какое-нибудь кратное чисел a и b. То есть, М делится на a, и по определению делимости существует некоторое целое число k такое, что справедливо равенствоM=a·k. Но М делится и на b, тогда a·k делится на b.

Обозначим НОД(a, b) как d. Тогда можно записать равенства a=a1·d и b=b1·d, причемa1=a:d и b1=b:d будут взаимно простыми числами. Следовательно, полученное в предыдущем абзаце условие, что a·k делится на b, можно переформулировать так:a1·d·k делится на b1·d, а это в силу свойств делимости эквивалентно условию, что a1·kделится на b1.

В этом случае по свойству взаимно простых чисел, так как a1·k делится на b1, и a1 не делится на b1 (a1 и b1 – взаимно простые числа), то на b1 должно делиться k. Тогда должно существовать некоторое целое число t, для которого k=b1·t, а так как b1=b:d, то k=b:d·t. Подставив в равенство M=a·k вместо k его выражение вида b:d·t, приходим к равенству M=a·b:d·t.

Так мы получили равенство M=a·b:d·t, которое дает вид всех общих кратных чисел a иb. Из того, что a и b числа положительные по условию следует, что при t=1 мы получим их наименьшее положительное общее кратное, которое равно a·b:d. Этим доказано, что НОК(a, b)=a·b:НОД(a, b).

Доказанная связь между наименьшим общим кратным и наибольшим общим делителем двух данных чисел позволяет найти НОК через НОД.

Также нужно записать два важных следствия из рассмотренной теоремы.

1. Общие кратные двух чисел совпадают с кратными их наименьшего общего кратного.

Это действительно так, так как любое общее кратное M чисел a и b определяется равенством M=НОК(a, b)·t при некотором целом значении t.

1. Наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.

Обоснование этого факта достаточно очевидно. Так как a и b взаимно простые, то НОД(a, b)=1, следовательно, НОК(a, b)=a·b:НОД(a, b)=a·b:1=a·b.

6. Физкультминутка

7. Решение простейших задач на нахождение НОК и НОД с использованием

Оценивание

8.Домашнее задание

9. Итог урока

Сегодня на уроке мы повторили с вами разложение числа на простые множители, повторили нахождение НОК и НОД чисел.

 Рефлексия

1. Наибольший общий
   делитель и алгоритм Евклида.

2. Свойства наибольшего
   общего делителя.

3. Взаимно простые
   числа.

4. Наименьшее общее
   кратное.

Содержание

1.
Если каждое из целых неотрицательных
чисел а
и
b
делится
на число с,
то число с
называют
общим
делителем чисел.
Чтобы найти общие делители чисел а
и b,
достаточно
найти пересечение двух множеств:
множества делителей числа а
и
множества делителей числа b.
Это пересечение состоит из натуральных
чисел, которые не могут превосходить
меньшего из чисел а
и
b,
а
значит, в нем имеется наибольшее число.
Это число называют наибольшим общим
делителем чисел а
и b.

Определение
3.
Наибольшим
общим делителем (НОД)
чисел а
и
b
называется
самое большое натуральное число d,
являющееся
делителем для каждого из чисел а
и
b.

Наибольший
общий
делитель чисел а
и
b
будем обозначать одним из символов –
НОД(а;b)
или
(а;
b).

Непосредственно
из определения следует, что если хотя
бы одно из чисел а
и
b
отлично
от нуля, то НОД(а;b)
существует и является единственным.
Возникает вопрос: как практически
находить НОД?

Один
из способов нахождения НОД вытекает
непосредственно из определения 3.
Действительно, можно было бы сначала
найти все делители числа а,
затем – числа b.
После
этого отобрать общие делители и выбрать
из них наибольший. Такой путь, однако,
был бы весьма нерациональным, особенно
для больших чисел.

Другой,
наиболее рациональный, способ нахождения
НОД был предложен Евклидом (III
в. до н.э.).

Теорема
6.
Алгоритм
Евклида. Если
а
разделить с остатком на b
≠ 0,
затем разделить с остатком b
на
полученный остаток, затем разделить с
остатком первый остаток на второй и
т.д., то последний, отличный от нуля,
остаток равен (а;b).

Доказательство.
Проводя
последовательно деления с остатком,
указанные в формулировке теоремы,
получим:

(3)

Поскольку
последовательность остатков является
убывающей последовательностью целых
неотрицательных чисел, то через конечное
число шагов очередной остаток (например,
r_п+1)
окажется равным нулю. Пусть r_п
– последний,
отличный от нуля, остаток. Покажем, что
r_п
= (а;b).

Прежде
всего, докажем, что если а
= bq
+ r,
то
(а;b)
= (b;r).

Действительно,
если

и
,
то
по
теореме 2 о делимости разности. С другой
стороны, если
и,
то
по
теореме 1 о делимости суммы.

Таким
образом, множества общих делителей
чисел а
и
b
равны,
а значит, равны и их наибольшие общие
делители, то есть (а;b)
= (b;r).

Применяя
доказанный факт к первому из равенств
3, получим

(а;b)
= (b;r₁).
(4)

Аналогично,
из второго равенства последовательности
(3)

(b;r₁)
= (r₁;r₂).
(5)

Продолжая
аналогичные
рассуждения,
получим равенства:

;
(6)

.
(7)

Исходя
из равенств (4) – (7), можем записать: (а;b)
= (b;r₁)
= (r₁;r₂)
= … = (r_n—2;r_n—1)
= (r_n—1;r_n)
= (r_n;0)
= r_n.
Итак, (а;b)
= r_n.
Теорема
доказана.

Пример.
Найти
НОД(481; 703).

Мы
определили и показали способ нахождения
НОД двух чисел. Аналогично определяется
НОД любого конечного множества целых
неотрицательных чисел.

НОД
чисел
обозначается одним из символов – НОД()
или ().
Если,
то ()
=d_n.

Пример.
Найти
НОД чисел 840, 720, 640 и 160.

1) НОД(840; 720) = 120;

2) НОД(120; 640) = 40;

3) НОД (40; 160) = 40.

Следовательно,
НОД(840; 720; 640; 160) = 40.

2.
Рассмотрим
основные свойства НОД, выраженные
следующими теоремами.

Теорема
7.
НОД двух данных чисел делится на любой
другой общий делитель этих чисел:

.

Доказательство
теоремы вытекает из алгоритма Евклида.
Действительно, из первого равенства
последовательности (3) следует, что если
и,
то.
Во втором равенствеи,
а значит, и.
Рассуждая аналогично, мы можем установить,
что в правой части каждого из следующих
равенств алгоритма вторые слагаемые
должны делиться нас,
то есть
.
Ноr_n
= (а;b).
Следовательно,
и теорема доказана.

Теорема
8. Любой
делитель НОД двух данных чисел является
общим делителем этих чисел:

.

Доказательство.
Очевидно, что теорема 8 является обратной
для теоремы 7. Пусть
.
Докажем, чтои.

По
определениям делимости и НОД можем
записать равенства:

,
где
.
(8)

Кроме
того, по условию теоремы,
,
где
.
Заменив
в равенствах (8) НОД(а;b)
произведением

,
получим равенства
и,
которые
можно записать в виде
,.
Это означает, чтои.
Таким
образом, теорема доказана.

Теорема
9. Если
каждое из двух данных чисел умножить
на натуральное число, то НОД этих чисел
умножится на то же число:

.

Доказательство.
Пользуясь свойством монотонности
умножения, умножим обе части каждого
из равенств (3) на одно и то же число k.
В
полученных равенствах вместо натуральных
чисел

будут,
соответственно, стоять новые числа:

.

Значит,
(ak;
bk)
= r_nk,
или
(ak;
bk)
=
dk,
что
и требовалось доказать.

Теорема
10. Если
каждое из двух данных чисел разделить
на натуральное число, то НОД этих чисел
разделится на то же число:

.

Доказательство.
Поскольку
данная теорема является обратной теореме
9, то для ее доказательства достаточно
к последовательности равенств (3)
алгоритма Евклида применить преобразования
обратные тем, что были проведены в
теореме 9.

3.
Во многих вопросах теории делимости
используются числа, не имеющие общих
делителей, кроме единицы. Рассмотрим
такие числа более подробно.

Определение
4.
Если НОД чисел равен единице, то числа
называются взаимно
простыми.

–взаимно
просты
.

Если
– совокупность взаимно простых чисел,
то отсюда не следует, что любые подмножества
этой совокупности взаимно просты.

Пример.
Так,
(35; 55; 77) = 1, но (35; 55) = 5, (55; 77) = 11, (35; 77) = 7.

Теорема
11.
Если данные числа разделить на их НОД,
то полученные частные будут числами
взаимно простыми:

.

Следует
заметить, что символы
издесь представляют натуральные числа.

Справедливость
теоремы 11 вытекает из теоремы 10.
Действительно, если каждое из чисел а
и b
разделить на натуральное число d,
то и НОД этих чисел разделится на d,
а
значит, будет равен 1.

Теорема
12.
Если произведение двух чисел делится
на число, взаимно простое с одним из
множителей, то другой множитель делится
на это число:

Доказательство.
По
условию теоремы, (а;
с)
= 1.
Пользуясь
теоремой 9, умножим каждое из чисел а
и с
на число b.
Тогда
НОД этих чисел также умножится на b,
то есть (аb;
сb)
= b.
По
условию теоремы,
.
Кроме
того, очевидно, что
.
Следовательно,
с
является общим делителем чисел ab
и
сb
. Но
тогда, по теореме 7, НОД этих чисел также
делится на с,
то есть
.

Теорема
13.
(Признак
делимости на составное число.) Если
числа а
и
b
взаимно
просты, то число с
делится
на их произведение ab
тогда
и только тогда, когда с
делится
на а
и на b:

.

Доказательство.
Необходимость вытекает
из транзитивности отношения делимости.
Так как
,
то.
Аналогично,
из условия
b
следует,
что
.

Достаточность.
Пусть
и,
причем (а;b)
= 1. Докажем, что
.
Так как,
то
с
= aq₁,
где
.
Зная,
что
,
имеем,
где (а;b)
= 1.
По
теореме 12 это означает, что
,
то естьq_l
= bq₂,
где
.
Итак,
с
= aq₁
= a(bq₂)
= (ab)q₂,
то
есть
.
Теорема
полностью доказана.

Из
этой теоремы вытекает ряд признаков
делимости на числа, каждое из которых
является произведением двух взаимно
простых чисел. Например:

1.
Число х
делится
на 6 тогда и только тогда, когда оно
делится на 2 и 3.

2.
Число х
делится
на 36 тогда и только тогда, когда оно
делится на 4 и 9.

Аналогично
формулируются признаки делимости на
числа 12, 15, 18, 24, 45 и др.

4.
Пусть
а
и
b
– произвольные натуральные числа.
Натуральное число m
называется общим
кратным этих
чисел, если m
делится на каждое из чисел а
и
b.
Если
m
– общее кратное чисел а
и
b,
то,
по транзитивности отношения делимости,
каждое из чисел 2m,
3m,
4m,
… также является общим кратным чисел
а
и
b.
Среди
натуральных общих кратных, по принципу
наименьшего числа, существует наименьшее
общее кратное.

Определение
5.
Наименьшим
общим кратным (НОК)
чисел а
и
b
называется
наименьшее натуральное число т,
являющееся
общим кратным этих чисел.

Наименьшее
общее кратное
чисел а
и
b
будем
обозначать
одним
из
символов – НОК(а;b)
или
[а;
b].

Примечание.
Нуль,
как известно, является общим кратным
для любых натуральных чисел, но, по
определению, НОК(а;b)
> 0.

Теорема
14.
Любое общее кратное двух чисел делится
на их наименьшее общее кратное.

Доказательство
теоремы
проведем методом от противного. Пусть
с
– произвольное
общее кратное чисел а
и
b,
т = [а;
b].
Предположим, что с
не
делится нацело на m.
Тогда, разделив
с
на
m
с
остатком, получим с
= mq
+ r,
0 ≤ r
< m.
Поскольку
с
кратно а
и
b,
mq
кратно
а
и
b,
то, по теореме 2 о делимости разности, r
кратно
а
и
b.
Но
это противоречит тому, что m
является НОК, ибо r
< m.
Полученное противоречие доказывает
теорему.

Докажем
теперь теорему, устанавливающую связь
НОД и HОК
двух чисел. Эта теорема дает практический
способ нахождения НОК двух чисел.

Теорема
15.
НОК и НОД двух натуральных чисел а
и
b
связаны
соотношением

аb
= (а;b)
· [а;
b].

Доказательство.
По
определению НОД можем записать равенства
а
= (а;
b)
а₁,
b
=
(а;
b)b₁.
Тогда

и
.

Из
последних равенств следует, что число


является общим кратным чисел а
и
b,
а значит, по теореме 14, оно делится на
[а;
b].

Следовательно,
можем записать:

.
(9)

Докажем
теперь, что последнее равенство возможно
только при q
= 1.

По
определению НОК можем записать: [а;
b]
= aq₁
и
[а;
b]
= bq₂.
Подставляя
новые
выражения НОК в равенство (9), получим

и

.

Из последних
равенств, в свою очередь, имеем

и

.

Отсюда
и.Таким
образом, выражение (а;b)q
является
общим делителем чисел а
и
b.
Но это возможно только
при q
= 1.

Итак, равенство
(9) можем переписать в виде

,
или
ab
= (а;b)
[а;
b]

Теорема доказана.

Следствие.
НОК двух взаимно простых чисел равно
их произведению.

Пример.
Найти НОК чисел 315 и 126.

НОК(315;
126) =
.

Мы
рассмотрели определение и способ
нахождения НОК двух чисел. Аналогично
определяется НОК любого конечного
множества чисел. НОК чисел
обозначают[]
и находят по следующему правилу: сначала
находят
[а₁;а₂]
= m₂,
затем – [m₂;a₃]
= m₃,
[m₃;a₄]
= m₄,
…, [m_n—1;a_n]
= m_n.
Тогда [a₁;a₂;
…;a_n]
=m_n.

Пример.
Найти
НОК чисел 30, 120, 72 и 64.

1) НОК(30; 120) = 120;

2)
НОК(120; 72) =
;

3)
НОК(360;64) =
.

Следовательно,
НОК(30; 120; 72; 64) = 2880.

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.