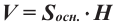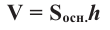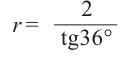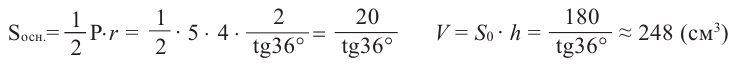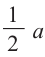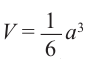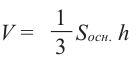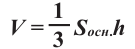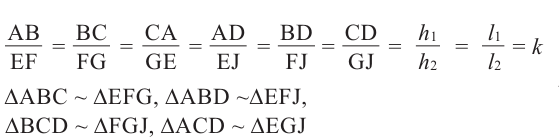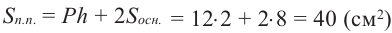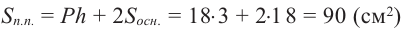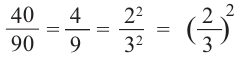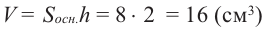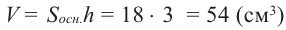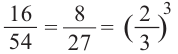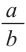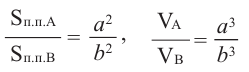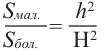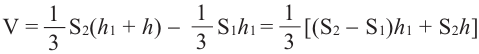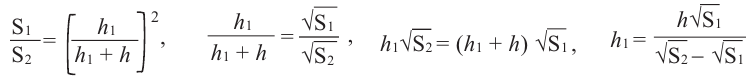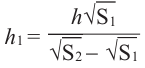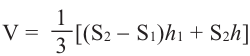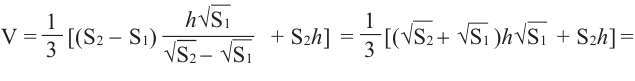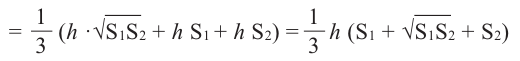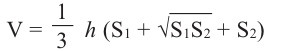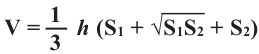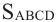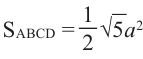Слайд 1
Задачи на сравнение объемов многогранников. Выполнил: Раздобарин Дмитрий, 11ИМ, лицей «Дубна». Учитель: Рычкова Татьяна Викторовна. 2009г. Дубна
Слайд 2
Оглавление. Введение. Теоретический материал. Ключевые задачи на сравнение объемов многогранников. Задачи из ЕГЭ части C4. Литература.
Слайд 3
Теоретический материал.
Слайд 4
2 . Объемы пирамид с общим основанием пропорциональны проведенным к нему высотам . 1 . Объемы пирамид с общей высотой пропорциональны площадям их оснований : B C D A K S H L A B C D S S 1 H 2 H 1
Слайд 5
3 . Если вершины S и T пирамид SA 1 …A n и TA 1 …A n лежат по одну сторону от плоскости A 1 …A n , то эти пирамиды равновелики тогда и только тогда, когда прямая ST параллельна плоскости A 1 …A n . S T T T A 1 A 4 A 3 A 2
Слайд 6
4 . Если тетраэдры SABC и SA 1 B 1 C 1 имеют общий трехгранный угол при вершине S, то 5 . Отношение объемов подобных многогранников равно кубу коэффициента подобия. S A B C C 1 B 1 A 1 A A 1 D C B D 1 C 1 B 1 A 2 C 2 B 2 B 3 C 3 D 3 A 3 D 2
Слайд 7
Ключевые задачи на сравнение объемов.
Слайд 8
Задача 1 . Дана правильная четырехугольная пирамида SABCD. Точка F – середина ребра BC. Найдите, в каком отношении делит объем пирамиды плоскость DSF. Решение . Поскольку пирамида и части, на которые она разбивается плоскостью сечения, имеют одинаковую высоту, то отношение объемов частей равно отношению площадей оснований: Диагональ квадрата ABCD делит его на два равных треугольника ABD и BDC, а прямая DF делит треугольник BDC на две равновеликие части (высоты треугольников равны CD, основания тоже равны). Следовательно, квадрат ABCD прямой DF делится на части, отношение которых равно 3:1. A B D C S F
Слайд 9
∆ COS подобен ∆ CMF Проведем FM ┴ AC. FM = h. Задача 2 . В правильной четырехугольной пирамиде SABCD через середину бокового ребра SC – точку F – и диагональ основания BD проведено сечение. Найдите отношение объемов фигур, на которые плоскость сечения делит пирамиду. Решение. Пусть AB = a, OS = H. B C D A F S O a H M
Слайд 10
В каком отношении делит объем пирамиды плоскость, параллельная основанию и пересекающая боковые ребра пирамиды? Решение. Исходная и отсекаемая пирамиды подобны с коэффициентом подобия Следовательно, отношение их объемов равно кубу коэффициента подобия. Две плоскости, параллельные основанию пирамиды, делят ее на три равновеликие части. В каком отношении эти плоскости делят высоту пирамиды? Два сечения делят фигуру на три подобных фигуры с объемами V, 2V, 3V.
Слайд 11
Олимпиадные задачи на сравнение объемов многогранников.
Слайд 12
C B A S L K M N Решение. Многогранники, на которые делит тетраэдр плоскость KMN, не поддаются стандартной классификации, поэтому хотя бы один из них, например, M KC NLB , разрежем на части: проведем L C и LM , тогда он окажется составленным из двух пирамид — LMNBC и LMKC . Будем сравнивать их объемы с объемом тетраэдра SABC . В треугольно пирамиде SABC проведена плоскость, параллельная ребрам SA и BC. Эта плоскость пересекает ребро AC в точке M так, что AM : MC = 1 : 2. В каком отношении эта плоскость делит объем пирамиды? 1 . LMNBC LABC (имеют общую высоту , ∆ANM подобен ∆АВС ) . 2 . LABC SАВС (имеют общий трехгранный угол при вершине В, основание АВС, высоту, проведенную из вершины С). 3 . LMKC LA SC SABC. Итак, Ответ: 20 /7 .
Слайд 13
P B L A C M N E T K В пирамиде TABC AB : BC = 3 : 5, точка K – середина ребра TA, точка M расположена на ребре AC, AM : MC = 3 : 1. Плоскость проходит через точки K и M параллельно биссектрисе BE треугольника ABC и делит пирамиду на две части. Вычислите отношение их объемов. A E C N B P 3b 5b 3a 2a 3a P B A T K L 1. Многогранник B LNAKM удобно рассматривать как часть тетраэдра PAKM с «отколотым куском» — тетраэдром PBLN. (Тетраэдры имеют общий трехгранный угол при вершине P, значит, надо найти отношения отрезков PL : PK, P B : PA и PN : PM ). 2 . Тетраэдры PAKM и TABC имеют общий трехгранный угол при вершине Р, поэтому нужно знать отношение АК:АТ, АМ:АС и АВ:АР. AE = 3a EC = 5a, AC = 8a. MC = 2a, EM = 3a. следовательно, Далее: тогда В итоге Ответ: 11 /9.
Слайд 14
S C B Y X A M L J D N K C X D B M A Y В основании четырехугольной пирамиды SABCD лежит параллелограмм ABCD. Через середину ребер AB, AD и SC проведена плоскость. Найдите отношение объемов частей, на которые эта плоскость делит пирамиду. 1 . Многогранник MNJKLBCD представляет собой часть тетраэдра с отколотыми кусками XJDN и YMBL в форме тетраэдров (Тетраэдры имеют с ним по общему трехгранному углу, нужно вычислить XJ : XK, XD : XC, XN : XY, YL : YK, YB : YC, YM, YX). 2 . Тетраэдр CXKY имеет общий трехгранный угол с тетраэдром CSBD, объем которого равен половину объема пирамиды SABCD ( Нужно вычислить CX : CD, CY : CB, CK : CS). XD : XC = 1:3, CX : CD = 3 : 2, YB : YC = 1 : 3, CY : CB = 3 : 2 Y B T K S L C a 2a YB = a, YC = 3a, BC = 2a, YL : YK = 1 : 2. Аналогично , XJ: XK = 1 : 2. BT = TC = a. Ответ: 1.
Слайд 15
Задачи из ЕГЭ части C4.
Слайд 16
В основании пирамиды DABC лежит треугольник ABC, в котором угол C = 60°, AC = 14, BC = 8. Боковые грани DAC и DAB перпендикулярны плоскости основания, а ребро AD = 4 √ 3 . Сечение пирамиды плоскостью, проходящей через середину ребра BD параллельно прямым BC и AD, является основанием второй пирамиды, вершина которой в точке C. Найдите объем второй пирамиды. В основании пирамиды DABC лежит треугольник ABC, в котором угол C = 30°, AC = 20, BC = 8/√ 3 . Боковое ребро AD равно 6 √ 3 и перпендикулярно плоскости ABC. Сечение пирамиды плоскостью, проходящей через середину ребра BD параллельно прямым BC и AD, является основанием второй пирамиды. Ее вершина T – основание высоты BT треугольника ABC. Найдите объем второй пирамиды. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 . На его боковых ребрах AA 1 и BB 1 лежат точки M и N соответственно так, что AM : MA 1 = 8 : 11, B 1 P : PB = 2 : 1. Во сколько раз объем данного параллелепипеда больше объема пирамиды с вершиной в точке P, основанием которой является сечение данного параллелепипеда плоскостью BMD 1
Слайд 17
Основанием пирамиды является треугольник АВС , в котором АВ = 4, АС =6 и угол АВС =90 ° Ребро AF перпендикулярно АВС и равно 12. Отрезок АL является биссектрисой треугольника FАВ, а отрезок АN является высотой треугольника FАС. Найдите объем пирамиды АLNC. A C B N L F 1 . Заметим, что пирамиды ALNC и ALNF имеют общую высоту из вершины L, поэтому отношение объемов этих пирамид равно отношению их граней ANC и ANF: Отношение площадей треугольников ANC и ANF равно отношению отрезков NC и NF ( высота треугольников из вершины A является общей): Таким образом: Аналогично: Перемножая (1) и (2) получаем: 2. Найдем отношения Так как AL – биссектриса треугольника AFB, то По условию AF = 12, AB = 4 FL = 3BL Так как AN – высота к гипотенузе прямоугольного треугольника AFC, то Воспользовавшись (3) получим: Ответ: 2 ,4√5.
Слайд 18
Литература. Туманов С. И. «Поиски решения задач». Зеленский А. С. «Сборник конкурсных задач по математике». Куланин Е. Д., Федин С. Н., Федяев О. И. «Геометрия 10-11 класс». Шарыгин И. Ф., Голубев В. И., «Решение задач. 11 класс». Готман Э. Г., Скопец З. А. «Задача одна – решения разные: Геометрические задачи. Книга для учащихся». Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев «Геометрия: Учебник для 10-11 классов общеобразовательных учреждений». Погорелов А. В. «Геометрия: учебник для 7-11 классов общеобразовательных учреждений». Потоскуев Е. В. Звавич Л. И. «Геометрия 11 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики». В. И. Мусатов «Сборник задач по геометрии. Стереометрия. Для 10 — 11-х классов ФМШ». Судаков Д. А. «Методическое пособие». Шарыгин И.Ф., Гордин Р. К. «Сборник задач по геометрии. 5000 задач с ответами. Учебное пособие для общеобразовательных учреждений.
Объем пространственных фигур — определение и вычисление с примерами решения
Содержание:
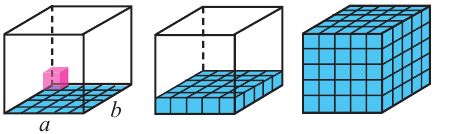
Исследование. Соберите не менее 4 призм различных размеров из кубиков и изобразите полученные призмы.
- Предположим, что ребро каждого кубика, из которых состоит призма, равна 1 единице, площадь грани равна 1 квадратной единице, а объём равен 1 кубической единице.
- Данные для каждой призмы запишите в таблицу.
- Какая связь существует между площадью основания призмы и высотой?
- Вытащите один кубик из угла конструкции и изобразите вид впереди, сверху и сбоку каждого кубоида.
Если тело можно разделить на конченое число треугольных пирамид, то оно называется простым телом. Для простых тел объём — положительная величина, численное значение которой удовлетворяет следующим свойствам.
- Объёмы конгруэнтных тел равны.
- Объём куба, ребро которого равно единице, равен кубической единице.
- Если тело можно разделить на простые части, то его объём равен сумме объёмов полученных частей.
Тела, имеющие одинаковые объёмы называются равновеликими. Объём прямоугольного параллелепипеда, размеры которого являются натуральными числами, равен
количеству кубических единиц, из которых он состоит. Можно также показать, что объём прямоугольного параллелепипеда, размеры которого заданы любыми действительными числами равен произведению трёх измерений: 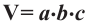
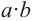
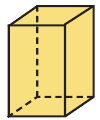
Следствие: Объём куба с ребром а равен:
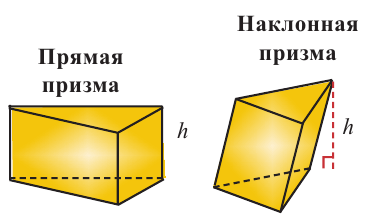
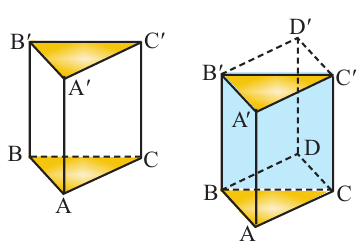
Объём любой прямой призмы равен произведению площади основания и высоты. Справедливость данного утверждения проверим на прямой призме, в основании которой лежит прямоугольный треугольник.
Достроим основание призмы до прямоугольника, получим призму, достроенную до прямоугольного параллелепипеда. Объём полученной призмы равен 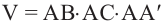
Плоскость 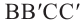
В треугольнике ABC, являющимся основанием прямой призмы, проведём высоту так, чтобы она пересекала противоположную сторону во внутренней области: 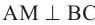
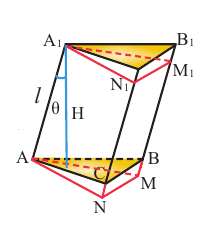
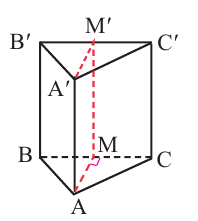
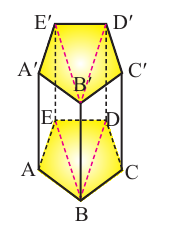
Если основанием прямой призмы является произвольный многоугольник, то её также можно разделить на треугольные призмы и найти её объём как сумму объёмов данных призм. Наклонную призму АВСА’В’С’ преобразуем в прямую призму равного объёма. Для этого:
- проведём плоскость перпендикулярную боковым рёбрам;
- отделим оставшуюся при сечении верхнюю часть призмы;
- переместим и соединим её с оставшейся внизу частью;
- высота полученной прямой призмы является боковым ребром наклонной призмы, т.е.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
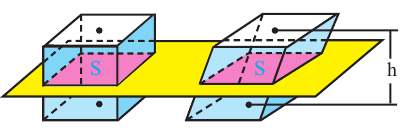
Следствие. Объём наклонной призмы равен произведению перпендикулярного сечения и ребра призмы: 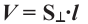
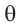
Поэтому, 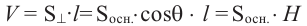
Таким образом объём призмы равен произведению площади основания и высоты.
Принцип Кавальери для нахождении объёмов
Если площади сечений параллельных основаниям двух тел равны, то равны и их объёмы, при условии, что основания лежат в одной плоскости, а высоты равны. Этот принцип открыл итальянский математик Бонавентура Кавальери (1598 — 1647).
Объем призмы
Объем призмы равен произведению площади основания и высоты.
Пример №1
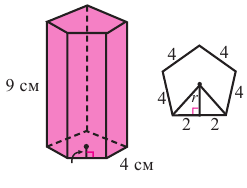
Найдём объём правильной пятиугольной призмы, стороны основания которой равны 4 см, а длина бокового ребра 9 см. Центральный угол правильного пятиугольника равен 360 : 5 = 72° значит апофема равна:
Площадь правильного многоугольника равна полупроизведению периметра и апофемы.
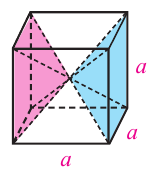
Исследование. 1. Диагонали куба деляг его на 6 конгруэнтных пирамид. Основание каждой пирамиды — грань куба, а высота
каждой пирамиды равна
а)Докажите, что объём каждой пирамиды равен
б)Докажите, что объём каждой пирамиды равен
Объём пирамиды
Объем пирамиды равен одной третьей произведения площади основанию на высоту.
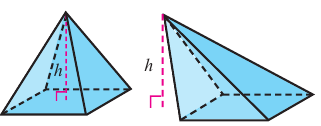
1)заданной пирамиды ТАВС;
Основания 2-ой и 3-ей пирамид конгруэнтны: 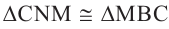
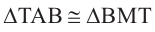
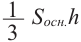
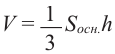
Подобие фигур в пространстве
Подобные фигуры имеют одинаковую форму и пропорциональные размеры.
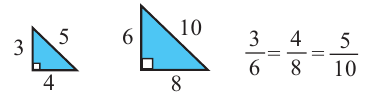
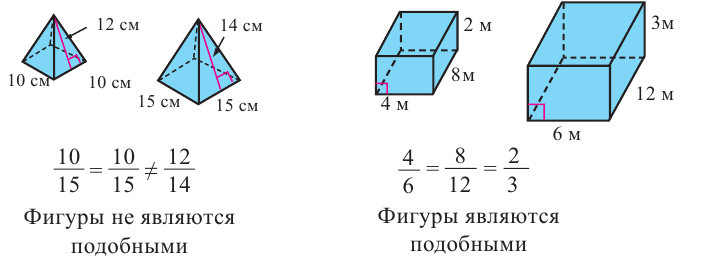
Например, прямоугольные треугольники на рисунке подобны, так как отношения соответствующих сторон равны.
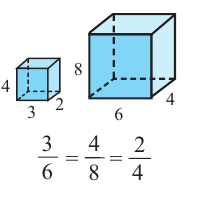
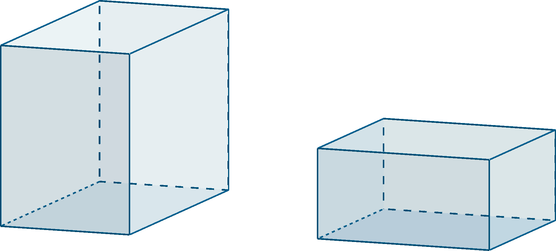
Прямоугольные параллелепипеды на рисунке подобны, так как отношения соответствующих линейных размеров равны и соответствующие грани являются подобными четырёхугольниками. Правильные многогранники подобны. В частном случае подобными являются все кубы, правильные тетраэдры и т.д.
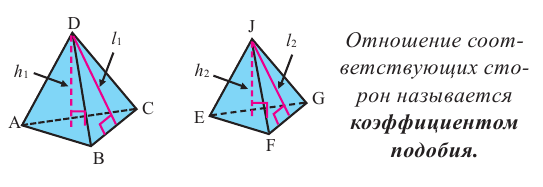
Подобные фигуры
Если при преобразовании расстояние между любыми двумя точками, меняется в одинаковое число раз, то такое преобразование называется подобием. Одна и другая, полученная при преобразовании подобием, фигура называются подобными фигурами. Коэффициент подобия равен отношению расстояний между парой любых двух соответсвующих точек.
Пример №2
Определим подобны или нет фигуры на рисунке.
Площади поверхностей и объёмы подобных фигур
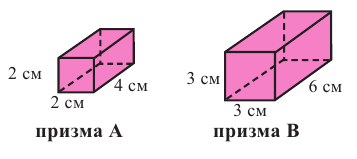
Исследование. Покажите подобны или нет следующие фигуры.
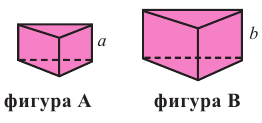
Призмы А и В (прямоугольные параллелепипеды) подобные призмы
с коэффициентом подобия равным 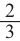
Для данных призм найдите:
а)отношение площадей полных поверхностей;
а)площадь полной поверхности призмы А
площадь полной поверхности призмы В
Отношение полной поверхности призмы А к полной поверхности призмы В
б)объём призмы А
объём призмы В
Отношение объёма призмы А к объёму призмы В
Если коэффициент подобия двух пространственных фигур равен 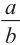
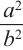
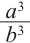
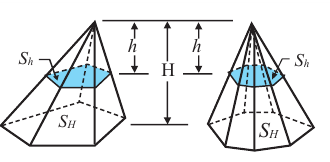
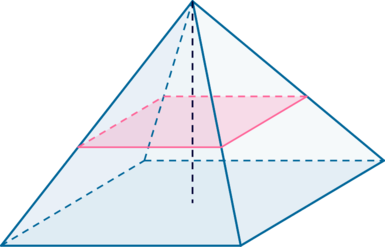
Пирамида, полученная сечением плоскости параллельной основанию, подобна данной. Коэффициент подобия можно найти из отношения соответствующих линейных размеров.
Например, на рисунке даны высоты. Тогда, отношения их боковых поверхностей, основании и полных поверхностей равно квадрату отношения высот.
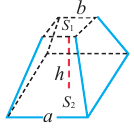
Объём усечённой пирамиды
Исследование. В древнем Египте объём правильной усечённой четырёхугольной пирамиды вычисляли по формуле 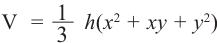
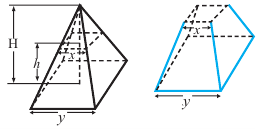
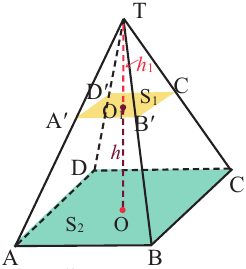
Объём усечённой пирамиды можно также найти как разность объёмов пирамид, при сечении плоскостью параллельной основанию.
Здесь V — объём усечённой пирамиды, S2 и S1 площади нижнего и верхнего оснований. h — высота усечённой пирамиды, h1 — высота меньшей пирамиды.
Так как эти пирамиды подобны, то отношение площадей равно квадрату отношений высот. Запишем это равенство и найдём высоту меньшей пирамиды.
Учитывая выражение
в равенстве
Объём усечённой призмы
Объём усечённой пирамиды с площадями оснований 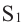
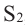
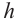
Задачи на сечение плоскостью
Пример:
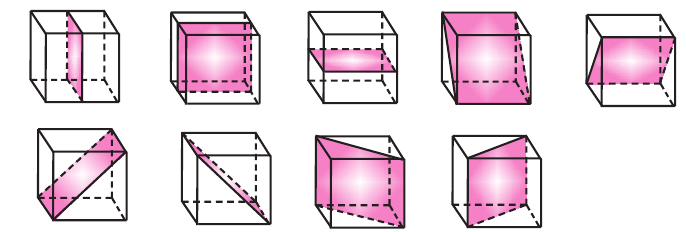
На рисунке показано сечение куба, с ребром а, плоскостью АВDО. Точки D и С являются серединами рёбер. Найдём площадь сечения.
Решение:
Дано: куб, длина ребра которого равна а точки D и С середины рёбер.
Найдите:
Для удобства повернём куб и отметим данные задачи на рисунке. Из 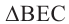
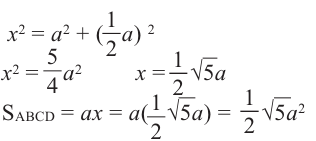
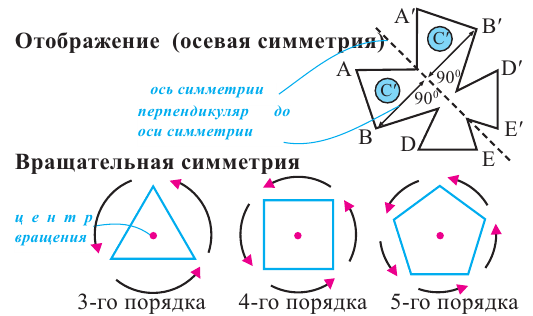
Симметрия в пространстве
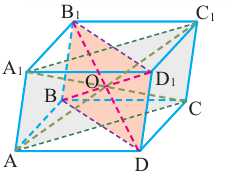
В пространственных фигурах также можно наблюдать различную симметрию. Известно, что в параллелепипеде диагональные сечения являются параллелограммами и диагонали ВD1 и DВ1 пересекаясь в точке О делятся пополам.
Можно показать, что другие диагонали также пересекаются в точке О и делятся пополам. Значит, точка пересечения диагоналей параллелепипеда является центром его симметрии.
В пространстве, помимо симметрии относительно точки и прямой, рассматривается симметрия относительно плоскости.
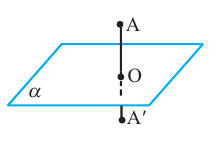
Если отрезок АА’ пересекает плоскость а посередине, и перпендикулярен плоскости, то говорят, что точки А и А’ симметричны относительно плоскости а.
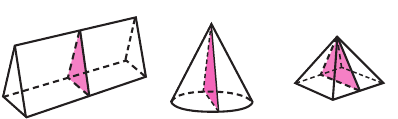
Если точки фигуры, симметричные некоторой плоскости, также принадлежат этой фигуре,то эту плоскость называют плоскостью симметрии, а фигуру называют симметричной относительно плоскости.
Прямоугольный параллелепипед, у которого все линейные размеры разные, кроме центра симметрии имеет ещё три оси и три плоскости симметрии. Прямая, проходящая через точку пересечения диагоналей противоположных граней, называется осью симметрии,а плоскость, проходящая перпендикулярно через середину рёбер называется плоскостью симметрии. Параллелепипед, у которого два линейных размера равны, имеет 5 плоскостей симметрии. Данные изображения нарисуйте в тетрадь.
Точка пересечения диагоналей куба является его центром симметрии. Прямые, проходящие через середину параллельных рёбер, не принадлежащих одной грани (их всего 6) и прямые, проходящие через центры противоположных граней(их всего три), являются осями симметрии куба. У куба 9 плоскостей симметрии. Они изображены на следующих рисунках.
Вращательная симметрии
Вращательная симметрия пространственных фигур похожа на вращательную симметрию плоских фигур. Однако, для объёмных фигур она определяется при помощи оси вращения.
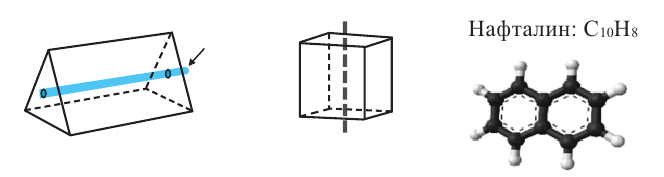
Вращательная и осевая симметрия широко применяется при изучении строения молекул веществ.
Пример №3
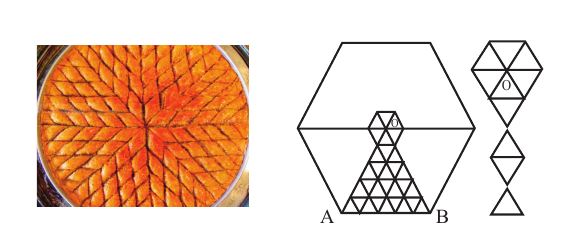
На рисунке показан вид сверху деталей, в виде правильных треугольных призм. Из них сконструирована правильная шестиугольная призма с центром основания О. Сколько деталей понадобилось для этого?
Основанием призмы является правильный шестиугольник, состоящий их 6 конгруэнтных треугольников. Каждый треугольник заполнен призмами. По изображению видно, что в один треугольник помещено 1+3 + 5 + 7 + 9 = 25 призм . Для правильной шестиугольной призмы таких призм нужно будет 6 • 25 = 150.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Подобные треугольники
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Подобные треугольники
Подобные треугольники — это треугольники, у которых все три угла равны, а все стороны одного треугольника в одно и то же число раз длиннее (или короче) сторон другого треугольника, то есть треугольники подобны если их углы равны, а сходственные стороны пропорциональны.
Сходственные стороны — это стороны двух треугольников, лежащие против равных углов.
Рассмотрим два треугольника ABC и A1B1C1, у которых ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1:
Стороны AB и A1B1, BC и B1C1, CA и C1A1, лежащие напротив равных углов, называются сходственными сторонами. Следовательно, отношения сходственных сторон равны:
| AB | = | BC | = | AC | = k, |
| A1B1 | B1C1 | A1C1 |
k — это коэффициент подобия ( число, равное отношению сходственных сторон подобных треугольников). Если k = 1, то треугольники равны, то есть равенство треугольников – это частный случай подобия.
Подобие треугольников обозначается знаком
: ABC
A1B1C1.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S1, то:
Первый признак подобия треугольников
Если два угла одного треугольника равны двум углам другого, то треугольники подобны.
то ABC
A1B1C1.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.
| Если | AB | = | AC | , ∠A = ∠A1, |
| A1B1 | A1C1 | |||
| то ABC
A1B1C1. |
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.
http://izamorfix.ru/matematika/planimetriya/podob_treug.html
Тело плавает в жидкости при условии, что сила Архимеда равна силе тяжести:
FА=Fтяж.
.
Чтобы найти архимедову (выталкивающую) силу, действующую на тело в жидкости, надо плотность жидкости умножить на ускорение свободного падения ((g=9,8) Н/кг) и на объём погружённой в жидкость части тела:
Силу тяжести вычислим по формуле:
Fтяж.=m⋅g=ρтела⋅Vвсего тела⏟∥m⋅g
Подставив соответствующие значения в первую формулу, получим:
ρж⋅g⋅Vчасти тела=ρтела⋅Vвсего тела⋅gρж⋅Vчасти тела=ρтела⋅Vвсего тела⇒Vчасти телаVвсего тела=ρтелаρж
Отношение объёма погружённой части тела к полному объёму тела равно отношению плотности тела к плотности жидкости.
.
На иллюстрации бревно наполовину погружено в воду, потому что его плотность меньше плотности воды в (2) раза.
Айсберг состоит из льда. Его плотность на (10) (%) меньше плотности воды.
Это означает, что часть айсберга, которая находится под водой, в (9) раз больше части айсберга, находящейся над водой. По этой причине айсберги опасны для судов.
Тема 2.
Геометрия в пространстве (стереометрия)
2
.
16
Отношение площадей поверхностей и отношение объемов тел
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
геометрия в пространстве (стереометрия)
Решаем задачи
Во сколько раз уменьшится объем конуса, если радиус его основания останется прежним, а высота уменьшится в 3
раза?
Показать ответ и решение
Пусть площадь основания конуса равна а его высота равна
Тогда объём конуса равен
Если высота уменьшится в 3 раза, то объем конуса станет равен
Тогда объем конуса уменьшится в 3 раза.
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Показать ответ и решение
Пусть — изначальный радиус шара. Площадь поверхности шара вычисляется по формуле
После увеличения радиуса шара в 2 раза площадь поверхности равна
Это в 4 раза больше, чем изначальная площадь поверхности.
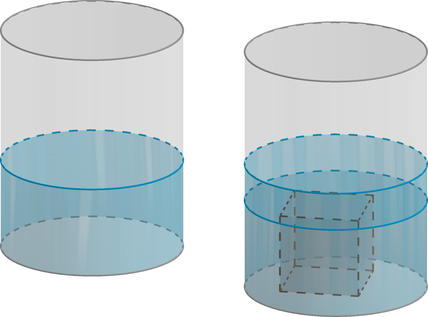
В сосуд цилиндрической формы, объем которого 2400 см, налили жидкость, заполнив сосуд
на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего
уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических
сантиметрах.
Показать ответ и решение
Объем цилиндра вычисляется по формуле , где
– радиус основания,
– высота. Таким
образом, во сколько раз увеличивается/уменьшается высота цилиндра, во столько же раз
увеличивается/уменьшается объем цилиндра.
Следовательно, если жидкость заполнила сосуд лишь на треть, то есть высота жидкости в 3 раза
меньше высоты сосуда, то и объем жидкости в 3 раза меньше объема сосуда, следовательно, объем
жидкости равен см
.
Так как после погружения в жидкость предмета уровень повысился на четверть, то и занимаемый в
сосуде объем повысился на четверть.
Закон Архимеда гласит, что объем вытесненной жидкости равен объему погруженного в нее предмета.
Следовательно, объем предмета равен четверти объема жидкости, то есть см
.
В цилиндрическом сосуде уровень жидкости достигает см. На какой
высоте будет находиться уровень жидкости, если её перелить во второй
цилиндрический сосуд, диаметр которого в раза больше диаметра первого?
Ответ дайте в сантиметрах.
В цилиндрическом сосуде уровень воды достигает 384 см. На какой высоте будет находиться уровень воды, если её перелить во
второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ дайте в сантиметрах.
Показать ответ и решение
Пусть уровень воды в первом цилиндрическом сосуде равен см, а во втором —
см.
Пусть диаметр первого сосуда равен см. Тогда площадь дна этого сосуда равна
Значит, объем воды в сосуде равен
По условию диаметр второго сосуда равен см. Тогда площадь его дна равна
Так как количество воды не изменилось, то
Тогда искомый уровень воды равен
В правильной четырехугольной пирамиде с высотой через точку на боковом ребре, лежащую на расстоянии
от плоскости
основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите
объем полученной меньшей пирамиды, если объем исходной пирамиды равен 54.
Показать ответ и решение
Также отсюда следует, что .
, следовательно,
Таким образом, объемы маленькой и большой пирамид относятся как
Следовательно, объем маленькой пирамиды равен
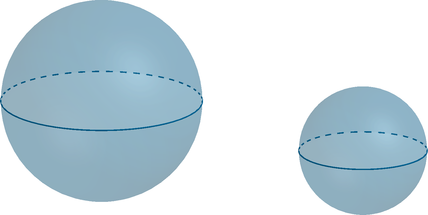
Радиус первого шара в 5 раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади
поверхности первого шара?
Показать ответ и решение
Площадь поверхности шара радиуса ищется по формуле
Следовательно, площадь поверхности первого шара
относится к площади поверхности второго шара как
Так как радиус первого шара больше радиуса второго шара в 5 раз, то Следовательно,
Тогда площадь поверхности второго шара в 25 раз меньше площади поверхности первого.
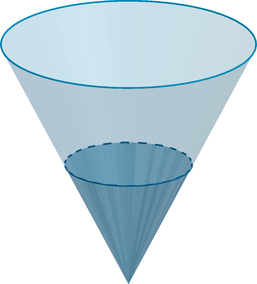
Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости
налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.
Показать ответ и решение
Тогда объем налитой жидкости к объему всего сосуда относится как
Следовательно объем жидкости равен
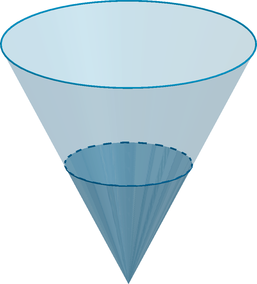
В сосуд, имеющий форму конуса, налили 75 грамм жидкости до половины высоты сосуда. Сколько
грамм этой же жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Показать ответ и решение
так
как по условию высота жидкости в два раза меньше высоты сосуда. Тогда для жидкости
имеем:
Следовательно, весь сосуд вмещает этой же жидкости
Значит, долить нужно
Заметим, что в данной задаче использование плотности – чистая формальность.
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного
параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго,
ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины
второго.
Объем первого цилиндра равен 16, причем известно, что его радиус в 7 раз меньше радиуса второго цилиндра, а высота второго
цилиндра в 8 раз меньше высоты первого. Найдите объем второго цилиндра.
Показать ответ и решение
Объем цилиндра с высотой и радиусом основания
ищется по формуле
Тогда объем первого относится к объему
второго цилиндра как
Из условия следует, что
следовательно,
Площадь боковой поверхности первого цилиндра равна . Найдите площадь боковой поверхности
второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты
первого цилиндра.
Площадь боковой поверхности первого конуса относится к площади боковой
поверхности второго конуса как Найдите отношение образующей первого
конуса к образующей второго конуса, если радиус первого конуса относится к
радиусу второго как
Показать ответ и решение
Площадь боковой поверхности конуса с образующей и радиусом основания
ищется по формуле
Тогда площадь бок.
поверхности первого конуса относится к площади бок. поверхности второго как
Так как радиус первого конуса относится к радиусу второго как то есть
то
Следовательно,
Даны два конуса. Радиус второго конуса в 3 раза больше радиуса первого конуса, а высота второго конуса в 6 раз меньше высоты
первого конуса. Найдите объем первого конуса, если объем второго конуса равен 18.
Показать ответ и решение
Объем конуса с высотой и радиусом основания
вычисляется по формуле
Следовательно, объем первого конуса
относится к объему второго конуса как
Так как радиус второго в 3 раза больше радиуса первого, то Так как высота второго в 6 раз меньше высоты первого,
то Следовательно,
Объем первого шара равен равен 54. Найдите объем второго шара, если его радиус в 3 раза меньше радиуса первого
шара.
Показать ответ и решение
Объем шара радиуса ищется по формуле
Следовательно, объем первого шара относится к объему второго
как
Так как радиус второго шара в 3 раза меньше радиуса первого шара, то следовательно,
Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в 343 раза больше объема второго
шара?
Показать ответ и решение
Объем шара радиуса ищется по формуле
Следовательно, объем первого шара относится к объему второго
как
Значит,
Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.
Радиус первого шара равен 6, а радиус второго шара равен 2. Во сколько раз объем первого шара больше объема второго
шара?
Показать ответ и решение
Объем шара радиуса ищется по формуле
Следовательно, объем первого шара относится к объему второго
как
Следовательно, объем первого шара в 27 раз больше объема второго шара.
Показать ответ и решение
Пусть – объём шара, ограниченного первой сферой. Так как радиус
в два раза больше, чем
радиус , то
.
следовательно, .
Урок
Тема: Отношение
площадей поверхностей и объемов подобных тел.
Цель урока: изучить понятия равновеликих
и подобных тел, выучить значения отношений площадей поверхностей и объемов
подобных тел.
Задачи урока:
формировать навыков и умения применения формул вычисления объемов и площадей
геометрических тел при решении задач.
Ход урока
1.
Организационный момент
2.
Актуализация опорных знаний
Фигура, все точки которой не находятся на
одной плоскости, называется объёмной фигурой.
Ограниченная часть пространства
называется геометрическим телом, а множество точек, ограничивающих
его от окружающего пространства, называется поверхностью этого тела.
Шар — геометрическое тело, его
поверхность — сфера.

Шар Сфера
Винтовая линия — объёмная фигура, но
это не тело.
Пирамида — геометрическое тело, которое
ограничено плоскими многоугольниками.

Пирамида Плоские
многоугольники
Две фигуры (или тела) называются равными, если их можно
совместить наложением.
Два тела подобны, если одно из них может быть получено
из другого путём увеличения (или уменьшения) всех его линейных размеров
в одном и том же отношении.
Пример 1:
Автомобиль и его модель – подобные тела.
Пример 2. Два
тела (фигуры) зеркально подобны, если одно из них подобно зеркальному
отражению другого.
Пример 3:
Картина и её фотонегатив зеркально подобны друг другу.
В подобных
и зеркально подобных фигурах все соответственные углы (линейные и
двугранные) равны.
Пример 4:
Две правильные призмы или пирамиды с одинаковым числом граней подобны, если
радиусы их оснований пропорциональны их высотам. Два круглых цилиндра или конуса
подобны, если радиусы их оснований пропорциональны их высотам.
3. Изучение нового материала
Главная величина
геометрических тел — это их объём.
Объём
геометрического тела — это величина, которая описывает занимающую этим телом часть пространства.
ИЛИ Объем тела – это положительная величина
той части пространства, которую занимает геометрическое тело.
Задача 1.
Три
латунных куба 6 м, 8 м и 10 м переплавлены в один куб. Чему равно ребро этого
куба.
Решение:
1. Найдем объем каждого куба:
V1= 63=
216 м3 V2= 83= 512 м3 V3=
103= 1000 м3
2.
Отсюда следует, что общий объем равен:
Vобщ = V1+
V2+ V3= 216 + 512 + 1000 = 1728 м3
3. Сторону куба можно найти из формулы:
V = a3,
Ответ:
12 м.
Объемы равных
тел равны.
Если тело разбито на несколько тел, не
имеющих общих внутренних точек, то его объем равен сумме объемов этих тел.
Из определения следует, что объём не
зависит ни от местонахождения тела в пространстве, ни от того, как это тело делится
на части.
Величину объёма вычисляют, основываясь на
аксиомах:
1) равные тела имеют равные объёмы.
2) Объём тела равен сумме объёмов его отдельных частей.
Чтобы объём можно было измерить, т. е.
чтобы объём можно было бы выразить в виде числа, необходимо выбрать единицу
измерения объёма.
Единица объёма — это объём такого куба, ребро
которого равно одной единице длины.
Если ребро куба равно 1 см, то его объём
обозначается кубическими сантиметрами — см3, если ребро куба равно1 м,
то объём обозначается кубическими метрами — м3.
Тела с равными
объёмами называются равновеликими.
Равные тела

Равные тела с объёмом 8 см3

Равновеликие тела
с объёмом 6 см3
Все равные тела равновелики, но не все
равновеликие тела равны.
Отношение площадей поверхностей
подобных тел
УТВЕРЖДЕНИЕ 1: Если
два и более тел подобны, то площади всех соответствующих плоских и кривых
поверхностей этих тел пропорциональны квадратам любых соответствующих
отрезков.
Задача
2.
Даны
два шара с радиусами 3 и 1. Во сколько раз площадь поверхности первого шара
больше площади поверхности второго?
Решение.
Радиус
первого шара в 3 раза больше радиуса второго шара. Площадь поверхности шара
выражается через его радиус формулой S = 4πr2, поэтому при увеличении радиуса втрое
площадь увеличится в 32 = 9 раз.
Ответ: 9.
Самостоятельная
работа
Задача 3.
Даны два шара с радиусами 14 и 2.
Во сколько раз площадь поверхности большего шара больше площади поверхности
другого?
Решение.
Площади поверхности шаров относятся как
квадрат отношения их радиусов. Радиус большего шара в 7 раз больше радиуса
меньшего, поэтому их площади относятся как 72= 49.
Ответ: 49.
Задача 4.
Даны
два шара с радиусами 8 и 4. Во сколько раз площадь поверхности первого шара
больше площади поверхности второго?
Решение.
Найдём
площадь поверхности первого шара: S1 = 4πr2 = 4π82 = 256π
Найдём
площадь поверхности второго шара: S2 = 4πr2 = 4π42 = 64π
Найдём
отношение площадей: S1/S2=256π/64π=4
Ответ: 4.
Отношение объемов подобных тел
УТВЕРЖДЕНИЕ 2: Если
два и более тел подобны, то их объёмы, а также объёмы любых их соответствующих частей,
пропорциональны кубам любых соответствующих отрезков.
Вывод:
Отношение объемов подобных
тел равно кубу коэффициента подобия.
ИЛИ
Объемы подобных тел
пропорциональны кубам соответствующих линейных размеров.

Объём куба – это
произведение трех его измерений.
Пример 5: На рисунке выше
показаны два куба, сторона одного из которых в 3 раза больше стороны другого.
Объем тела с рисунка
а) V=x*x*x=x3
Объем тела с рисунка
б) V=3x*3x*3x=27x3
Следовательно, тело на
рис. б) имеет объем 33, т.е. его объем в 27 раз больше объема тела
на рис. а).
Задача 5. Чашка диаметром 8 см и высотой 10 см вмещает
0,5 литра воды. Каких размеров должна быть подобная чашка, вмещающая 4 литра
воды ?
Решение:
Чашки – подобные цилиндры, значит отношение их
объёмов равно отношению кубов соответствующих отрезков
(в нашем случае – высот и диаметров чашек).
Следовательно, высота h новой чашки находится из отношения:
1)
(h/10 )3=
4/0,5; то есть h3 = 8*103, откуда h = 20 см;
аналогично, для диаметра d получим:
2)
(d/8)3=4/0,5
, то есть d3= 8*83, откуда d = 16 см.
Ответ: h = 20 см; d = 16 см.
Задача 6.
Масса автомобиля 1050 кг. Изготовлена модель автомобиля в масштабе
1:60. Определить массу модели автомобиля, если она сделана из того же
материала, что и сам автомобиль.
Решение:
1.
(Объем
модели)/(объем автомобиля)=(1/60)3, поскольку объемы подобных тел
пропорциональны кубам соостветствующих линейных размеров.
2.
Масса
=плотность*объем, а так как автомобиль и модель сделаны из одного материала,
значит:
(Масса модели)/(Масса автомобиля)=(1/60)3
Следовательно,
3.
Масса модели =
(Масса автомашины) *(1/60)3=(1050)/(603)=
0,0049 кг=4,9г.
Ответ: 4,9г.
Задача 7.
Однородный шар
диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из
того же материала, с диаметром 2 см? Ответ дайте в граммах.
Решение.
Масса шара прямо
пропорциональна его объёму. Объёмы шаров относятся как кубы их радиусов:
Следовательно, масса
второго, меньшего шара равна 162*8/27=48 грамм.
Ответ:48.
Задача 8
Даны два шара с радиусами
8 и 2. Во сколько раз объём большего шара больше объёма меньшего?
Решение.
Объёмы шаров относятся как кубы отношений их радиусов. Радиус
большего шара в 4 раза больше радиуса меньшего, поэтому их объёмы относятся как
43= 64.
Приведём другое решение.
Найдём
отношение объёмов шаров:
Ответ:
64.
4.
Домашнее
задание
1) Выучить теоретический материал
урока
2) Решить задачи
Задача 1.
Даны два шара с
радиусами 5 и 1. Во сколько раз площадь поверхности первого шара больше площади
поверхности второго?
Задача 2.
Даны
два шара с радиусами 12 и 4. Во сколько раз объём большего шара больше объёма
меньшего?
Источники:
1. https://www.yaklass.ru/p/geometria/10-klass/osnovnye-poniatiia-stereometrii-10438/aksiomy-stereometrii-i-ikh-prosteishie-sledstviia-9252/re-325b23ad-df13-4cb3-ac0f-397dc7ba8da4
2. https://www.yaklass.ru/p/geometria/10-klass/osnovnye-poniatiia-stereometrii-10438/aksiomy-stereometrii-i-ikh-prosteishie-sledstviia-9252/re-325b23ad-df13-4cb3-ac0f-397dc7ba8da4
3. https://mathb-ege.sdamgia.ru/problem?id=506288

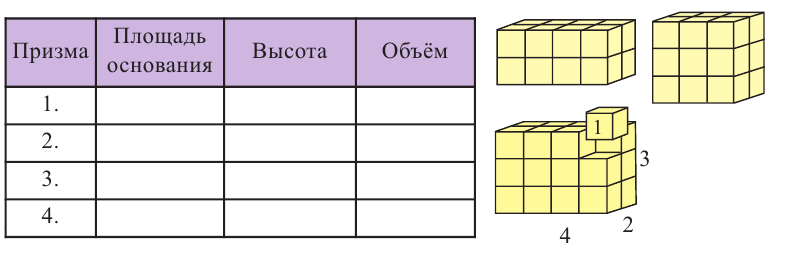
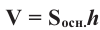
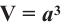
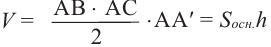
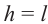 , основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.