Обратное отношение в математике — это отношение, взятое в обратном порядке по отношению к данному.
Определение
Пусть на множестве 


Свойства
- Если отношение
обладает одним из перечисленных свойств: рефлексивностью, нерефлексивностью, симметрией, антисимметрией, асимметрией, транзитивностью или полнотой, то и обратное отношение
также обладает им.
- Если
инъективно, сюръективно или функционально, то
, вообще говоря, не обязано обладать таким же свойством.
Примеры
|
п·о·р Бинарное отношение |
|---|
| между двумя множествами: инъективное · сюръективное · биективное · полное слева · полное справа · функциональное |
| на множестве: рефлексивное · нерефлексивное · симметричное · антисимметричное · асимметричное · транзитивное · полное · евклидово |
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Эта информация доступна зарегистрированным пользователям
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как (mathbf{a div b}) или же через дробную черту: (mathbf{frac{a}{b}})
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
- может получиться натуральное число
- обыкновенная дробь
- смешанное число
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
(mathbf{256div8=32})
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
- если отношение получилось больше 1, значит, первое число больше второго
- если меньше 1, то второе число больше первого
- если отношение оказалось равно 1, значит, числа равны
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
(mathbf{15div12=frac{15}{12}=frac{5cdot3}{4cdot3}=frac{5}{4}=1frac{1}{4}})
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в (mathbf{1frac{1}{4}}) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
(mathbf{16div24=frac{16}{24}=frac{8cdot2}{8cdot3}=frac{2}{3}})
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в (mathbf{frac{2}{3}}) раза.
Мы можем сформулировать вывод и так: 16 составляет (mathbf{frac{2}{3}}) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
(mathbf{14div28=frac{14}{28}=frac{14cdot1}{14cdot2}=frac{1}{2}})
И посчитаем отношение 28 к 14
(mathbf{28div14=2})
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно (mathbf{frac{2}{5}}), найдем отношение b к a
Для этого надо найти обратное число к (mathbf{frac{2}{5}})
(mathbf{1divfrac{2}{5}=frac{5}{2}=2frac{1}{2}})
Значит, отношение b к a равняется (mathbf{2frac{1}{2}})
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно (mathbf{frac{1}{3}})
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно (mathbf{frac{1}{3}})
Эта информация доступна зарегистрированным пользователям
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него (mathbf{frac{3}{8}})
Перемножив, мы получим:
(mathbf{4cdotfrac{3}{8}=frac{4cdot3}{8}=frac{4cdot3}{4cdot2}=frac{3}{2}=1frac{1}{2}})
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
(mathbf{1frac{1}{2}div4=frac{3}{2}div4=frac{3}{2cdot4}=frac{3}{8}})
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна (mathbf{2frac{1}{2}})
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
(mathbf{2frac{1}{2}div10=frac{2cdot2+1}{2}div10=frac{5}{2}div10=frac{5}{2cdot10}=frac{1}{2cdot2}=frac{1}{4}})
Ответ: дробь, взяв которую от 10 получили (mathbf{2frac{1}{2}}), равняется (mathbf{frac{1}{4}})
Пример 2
Отношение первого числа ко второму равно (mathbf{1frac{1}{5}}), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к (mathbf{1frac{1}{5}})
(mathbf{1div1frac{1}{5}=1divfrac{6}{5}=1cdotfrac{5}{6}=frac{5}{6}})
Теперь можно найти второе число, домножим первое на эту дробь:
(mathbf{6cdotfrac{5}{6}=frac{6cdot5}{6}=5})
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
(mathbf{6div5=frac{6}{5}=1frac{1}{5}})
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно (mathbf{1frac{1}{2}})
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
(mathbf{1div1frac{1}{2}=1divfrac{3}{2}=frac{2}{3}})
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
(mathbf{8divfrac{2}{3}=8cdotfrac{3}{2}=frac{8cdot3}{2}=4cdot3=12})
Ответ: число a равняется 12
Эта информация доступна зарегистрированным пользователям
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Эта информация доступна зарегистрированным пользователям
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
(mathbf{15div25=frac{15}{25}=frac{3cdot5}{5cdot5}=frac{3}{5}})
Значит, длина освещенного участка составляет (mathbf{frac{3}{5}}) от длины всей улицы.
Во втором вопросе нас спрашивают: «Во сколько раз больше?» — это соответствует отношению большего числа к меньшему.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
(mathbf{25div15=frac{25}{15}=frac{5cdot5}{3cdot5}=frac{5}{3}=1frac{2}{3}})
Что отвечает на вопрос второго пункта.
Ответ: a) (mathbf{frac{3}{5}}), б) (mathbf{1frac{2}{3}})
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Эта информация доступна зарегистрированным пользователям
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
(mathbf{frac{350}{2000}=frac{35}{200}=frac{7cdot5}{5cdot40}=frac{7}{40}})
Ответ: (mathbf{frac{7}{40}}).
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Эта информация доступна зарегистрированным пользователям
Эта информация доступна зарегистрированным пользователям
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц.
Отношение, обратное данному.
ПРИМЕР:
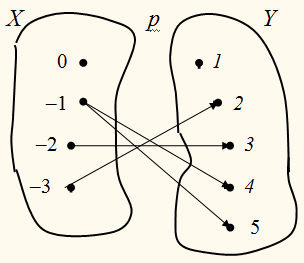
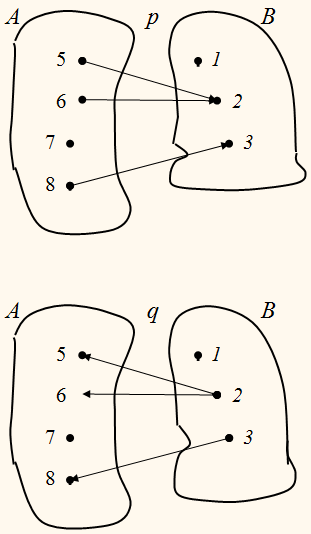
На рисунке отношение р между элементами множества Х и элементами множества Y задано с помощью стрелок.
Поменяем направление стрелок.
Получим другое отношение –
отношение q между элементами множества Y и элементами
множества Х.
Говорят, что q есть отношение,
обратное отношению р. В свою очередь отношение р является обратным отношению q.
Областью определения
отношения p является множество
{–3; –2; –1},
а областью значений –
множество
{2; 3; 4; 5}
Для отношения q,
обратного отношению р,
областью определения служит множество
{2; 3; 4; 5},
а областью значений –
множество
{–3; –2; –1}.
Таким образом, область определения и область значений взаимно-обратных
отношений меняются ролями.
Отношение p между элементами
множеств Х и Y определяется множеством пар:
{(–3; 2); (–2; 3); (–1; 4); (–1; 5)}
Поменяв в каждой паре местами
её элементы, получим множество пар, которым задаётся отношение q, обратное р:
{(2; –3); (3; –2); (4; –1); (5; –1)}
Если отношение
определяется некоторым множеством пар, то обратное ему отношение определяется множеством
пар, которое получено из первого перестановкой элементов в каждой паре.
ПРИМЕР:
Вернёмся к рассмотренным выше
взаимно-обратным отношениям р и q.
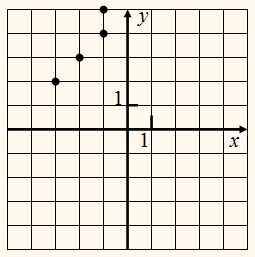
На рисунке построен график
отношения р.
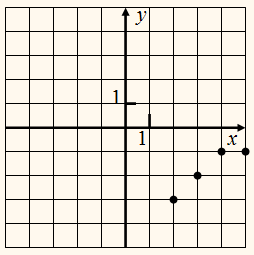
На рисунке построен график
отношения q.
Построим теперь графики
отношений р и q в одной и той же системе координат.
Нетрудно заметить, что точки с координатами
(–3; 2) и (2; –3), (–1;
4) и (4; –1) и т. д.,
т. е. точки, у которых абсцисса первой является ординатой
второй и ордината первой является абсциссой второй, симметричны относительно
прямой
у = х.
Каждой точке графика отношения р
соответствует симметричная относительно прямой у = х
точка графика отношения q,
и наоборот, каждой точке графика отношения
q соответствует
симметричная относительно прямой у
= х точка графика
отношения р.
Поэтому графики отношений р и q симметричны относительно прямой у = х.
Вообще справедлива
следующая теорема:
Графики взаимно-обратных отношений между числами
симметричны относительно прямой у
= х.
Приведём примеры взаимно-обратных отношений
ПРИМЕР:
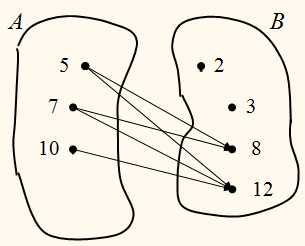
На рисунке с помощью стрелок
показано отношение <<меньше>> между элементами множества
А = {5; 7; 10}
В = {2; 3; 8; 12}
Обратное ему отношение является отношением <<больше>>
между элементами множества В и элементами множества А.
ПРИМЕР:
Отношение <<быть делителем>> и <<быть кратным>> между
натуральными числами – взаимно-обратные отношения.
Действительно, если а и b – некоторые натуральные числа и а делитель b,
то b кратно
а, и наоборот, если b кратно а,
то а делитель
b. Например, из того, что
<<2
делитель 6>>,
следует, что <<6 кратно 2>>; из того, что <<24
кратно 8>>,
следует, что <<8 делитель 24>>.
Понятие функции, обратной данной.
ПРИМЕР:
На рисунку с помощью стрелок
задано отношение р между элементами множеств А и В. Это
отношение – функция, так как каждому элементу множества А соответствует не более одного множества В.
Отношение q между элементами множества В и А,
обратное р,
не является функцией: в множестве
В существует
элемент (число 2), которому
соответствует более одного элемента из множества А (элементы 5 и 6).
ПРИМЕР:
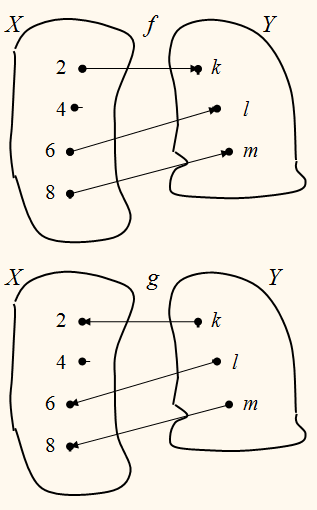
На рисунках с помощью стрелок
задано отношение f между элементами множеств X и Y и обратное ему отношение g между элементами
множеств Y и X.
Отношение f – функция, отношение
g, обратное f,
тоже функция.
Приведённые примеры показывают, что отношение, обратное функции, может быть
функцией, а может и не быть функцией.
Функция f называется обратимой, если обратное ей
отношение – функция.
В этом случае отношение, обратное функции
f,
называют функцией, обратной f.
Мы рассмотрели примеры функций p и f,
заданных с помощью стрелок. Обратимой оказалась функция в том случае, когда к
любому элементу области её значений было проведено не более одной стрелки, т.
е. когда каждое своё значение функции принимала только при одном значении
аргумента.
Функция
обратима тогда и только тогда, когда каждое своё значение она принимает лишь
при одном значении аргумента.
ПРИМЕР:
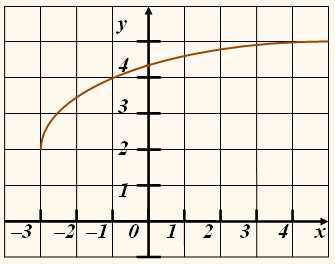
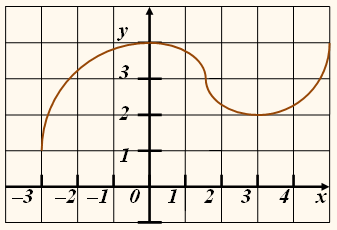
На рисунках изображены графики
функций g и h.
Функция g обратима, так как нет такого значения
функции, которое соответствовало бы различным значениям аргумента (любая прямая,
параллельная оси х,
пересекает график не более чем в одной точке).
Функция h необратима, так как существует такое значение
функции, например у
= 3, которое соответствует трём различным значениям
переменной х (прямая у = 3 пересекает график в трёх точках).
Всякая
возрастающая функция обратима.
Функция,
обратная возрастающей, является возрастающей.
Всякая убывающая
функция обратима.
Функция,
обратная убывающей, является убывающей.
Если некоторое
отношение f задано уравнением с двумя
переменными х и у,
то для задания уравнением отношения, обратного
f,
достаточно в данном уравнении поменять обозначения х на у и у на х.
ПРИМЕР:
Функция f,
заданная формулой
у = –2х + 3,
убывающая. Поэтому она
обратима. Обратная ей функция также убывающая.
Чтобы задать формулой функцию,
обратную f,
поменяем в уравнении
у = –2х + 3,
обозначения х на у и у на х. Получим
уравнение
х = –2у + 3,
Обычно при задании функции
уравнением с переменными х и у переменную
у выражают через
переменную х.
В данном случае имеем:
2у = –х + 3,
у = –0,5х + 1,5.
Мы получили формулу, которой
задаётся функция, обратная f.
ПРИМЕР:
Пусть дана функция:
у = 3х – 2.
Если определить х через у и в полученном равенстве вместо х написать
у, а вместо у написать
х, будем иметь:
Эта
функция, обратная данной. Данную функцию также можно назвать обратной по
отношению к полученной. Эти функции взаимно обратные.
ПРИМЕР:
Для функции, заданной равенством:
у = х2
На
]–∞; +∞
[,
обратной не существует. А для
функции:
у = х2
заданной на промежутке
[0; +∞ [,
обратная функция существует.
Графики двух взаимно обратных функций симметричны друг к другу относительно
биссектрисы первого и третьего координатных углов, то есть относительно прямой
у = х.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Обратно пропорциональная зависимость
- Урок 23. График обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х — m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований
Содержание
- — Как найти отношение чисел объяснение?
- — Что значит вычислить отношение?
- — Как определить соотношение?
- — Что такое отношение двух величин?
- — Что такое соотношение чисел?
- — Что такое пропорция В математике 6 класс?
- — Что такое обратное отношение?
- — Как посчитать в процентном соотношении?
- — Чем отличается отношение от дроби?
- — Как посчитать соотношение 1 к 2?
- — Как понять пропорция 1 к 3?
- — Как рассчитать соотношение 1 к 3?
- — Что такое отношение 2 к 3?
- — Как рассчитать отношение одного числа к другому?
Частное двух чисел и , отличных от нуля, называют отношением числа к числу . Отношение числа к числу записывается как или .
Как найти отношение чисел объяснение?
Отношением двух чисел называют их частное.
…
- отношение a к b — это результат от деления a на b;
- если a > b, то отношение a : b обозначает, во сколько раз a больше b;
- если a отношение a : b обозначает, какую часть составляет a от b;
- процентное отношение a к b — это отношение a : b, умноженное на 100 процентов.
Что значит вычислить отношение?
Отношение двух чисел — это их частное. Отношение двух чисел показывает: во сколько раз одно число больше другого; какую часть одно число составляет от другого.
Как определить соотношение?
Правило. Чтобы найти процентное отношение двух чисел , нужно одно число разделить на другое, а результат умножить на 100. Например, вычислить, сколько процентов составляет число 52 от числа 400. По правилу: 52 : 400 * 100 — 13 (%).
Что такое отношение двух величин?
Отношение (математич.)
— Отношение двух чисел, частное от деления первого числа на второе. О. двух однородных величин называется число, получающееся в результате измерения первой величины, когда вторая выбрана за единицу меры.
Что такое соотношение чисел?
, а иногда выражаемое арифметически как безразмерное отношение (результат деления) двух чисел, непосредственно отображающее, сколько раз первое число содержит второе (не обязательно целое). … Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого.
Что такое пропорция В математике 6 класс?
Пропорция — это равенство двух отношений. Соединив их знаком равенства, мы получим пропорцию. В пропорции различают крайние и средние члены. 8 и 5 называют крайними членами.
Что такое обратное отношение?
Обратное отношение в математике — это отношение, взятое в обратном порядке по отношению к данному.
Как посчитать в процентном соотношении?
Процентное отношение определяет, какой процент от целого составляет данное число. Для нахождения процента нужно разделить одно число на другое и умножить на 100%. Пример: Процентное соотношение числа 25 от 50 будет составлять 50%, так как 25/50×100%=50%.
Чем отличается отношение от дроби?
Отношение двух чисел — это их частное. Дробь— число, состоящее из одной или нескольких частей единицы.
Как посчитать соотношение 1 к 2?
Рецепт строят из соотношений между продуктами. Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).
Как понять пропорция 1 к 3?
Ответ: Пошаговое объяснение: 1:3 это когда первое число в 3 раза меньше второго. 3:1 это когда первое число в 3 раза больше второго.
Как рассчитать соотношение 1 к 3?
Это обозначает, что, например, на два литра молока вы должны класть две столовые ложки соли и шесть столовых ложек сахара, чтобы сохранялась требуемая пропорция: 2/6=1/3.
Что такое отношение 2 к 3?
Понимание «Отношение чисел» используется для сравнения двух величин и показывает во сколько раз первое число больше второго, либо какую часть первое число составляет от второго. В нашем примере отношение показывает, что число 2 составляет 2/3 от числа 3. Отношение показывает, что число 5 составляет 1/2 от числа 10.
Как рассчитать отношение одного числа к другому?
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100. Например, вычислить, сколько процентов составляет число 52 от числа 400. По правилу: 52: 400 × 100 — 13 (%).
Интересные материалы:
Что такое канифоль скрипка?
Что такое каппа?
Что такое хронологический возраст?
Что такое кислотные дожди чем они опасны для всего живого?
Что такое кластер по литературе?
Что такое климатические показатели?
Что такое кмс по художественной гимнастике?
Что такое конструктор слайдов?
Что такое коррекция ногтей?
Что такое Круизер скейт?
В математике, обратное отношение или транспонирование, бинарного отношения — это отношение, которое возникает при изменении порядка элементов в отношении. Например, отношение «дочерний элемент», обратное отношению «родительский элемент». Формально, если X и Y — множества и L ⊆ X × Y — отношение от X к Y, то L — отношение, определенное так, что y L x тогда и только тогда, когда x L y. В нотации конструктора множеств L = {(y, x) ∈ Y × X | (x, y) ∈ L}.
Обозначения аналогичны обозначениям для обратной функции. Хотя многие функции не имеют обратного, каждое отношение имеет уникальное обратное. Унарная операция , отображающая отношение в обратное отношение, является инволюцией, поэтому она индуцирует структуру полугруппы с инволюцией на бинарных отношениях на множестве, или, в более общем смысле, вызывает категорию кинжала в категории отношений как, подробно описанное ниже. Как унарная операция, взятие обратного (иногда называемого преобразованием или транспонированием ) коммутирует с операциями, связанными с порядком исчисления отношений, то есть коммутирует с объединением, пересечением и дополнением.
Обратное отношение также называется отношением или транспонированием — последнее ввиду его сходства с транспонированием матрицы. Его также называли противоположным или двойным исходного отношения, или обратным исходному отношению, или обратным L ° отношения L.
Другие обозначения для обратного отношения включают L, L, L, L ˘ { displaystyle { breve {L}}}
Содержание
- 1 Примеры
- 2 Свойства
- 3 Инверсии
- 3.1 Обратное отношение функции
- 4 См. также
- 5 Ссылки
Примеры
Для обычных (может быть, строгих или частичных) отношений порядка обратным является наивно ожидаемый «противоположный» порядок, например, ≤ T = ≥, < T =>. { displaystyle { leq ^ { mathsf {T}}} = { geq}, quad {<^{mathsf {T}}}={>}.}
Отношение может быть представлено в виде логической матрицы например
- (1 1 1 1 0 1 0 1 0 0 1 0 0 0 0 1). { displaystyle { begin {pmatrix} 1 1 1 1 1 \ 0 1 0 1 \ 0 0 1 0 \ 0 0 0 1 end {pmatrix}}.}
Тогда обратное отношение представлено его транспонированной матрицей :
- (1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 1). { Displaystyle { begin {pmatrix} 1 0 0 0 \ 1 1 0 0 \ 1 0 1 0 \ 1 1 0 1 end {pmatrix}}.}
Обратные отношения родства называются: «A является дочерним элементом B» имеет обратное «B является родительским элементом A «.» A является племянником или племянницей из B «имеет обратное выражение» B является дядей или тетей из A «. Отношение» A является родственник из B «является его собственным обратным, поскольку это симметричное отношение.
В теории множеств предполагается универсум U дискурса, а фу Основное отношение принадлежности к множеству x ∈ A, когда A является подмножеством U. мощный набор всех подмножеств U является областью обратного ∋ = ∈ T. { displaystyle { ni} = { in ^ { mathsf {T}}}.}
Свойства
В моноиде двоичных эндореляций на множестве (с бинарной операцией на отношениях, являющейся композицией отношений ), обратное отношение не удовлетворяет определению обратного из теории групп, т. е. если L — произвольное отношение на X, тогда L ∘ LT { displaystyle L circ L ^ { mathsf {T}}}


Так как обычно можно рассматривать отношения между различными наборами (которые образуют категорию, а не моноид, а именно категория отношений Rel ), в этом контексте обратное отношение соответствует аксиомам категории кинжала (также известной как категория с инволюцией). Отношение, равное его обратному, является симметричным отношением ; на языке категорий кинжала это самосопряженный.
Кроме того, полугруппа эндореляций на множестве также является частично упорядоченной структурой (с включением отношений как множеств) и фактически инволютивным квантом. Аналогично, категория разнородных отношений, Rel также является упорядоченной категорией.
В исчислении отношений преобразование (унарная операция перехода к обратному отношению) коммутирует с другими бинарными операциями объединения и пересечения. Преобразование также коммутируется с унарной операцией дополнения, а также с взятием suprema и infima. Преобразование также совместимо с упорядочением отношений по включению.
Если отношение рефлексивное, иррефлексивное, симметричное, антисимметричное, асимметричный, транзитивный, всего, трихотомический, частичный порядок, всего порядок, строгий слабый порядок, общий предварительный порядок (слабый порядок) или отношение эквивалентности, его обратное тоже.
Инверсия
Если I представляет отношение идентичности, то отношение R может иметь обратное следующим образом:
- Отношение R называется правообратимым, если существует существует отношение X с R ∘ X = I { displaystyle R circ X = I}
, и обратимое слева, если существует Y с Y ∘ R = I { стиль отображения Y circ R = I}
. Тогда X и Y называются правым и левым обратными R соответственно. Обратимые вправо и влево отношения называются обратимыми . Для обратимых однородных отношений все обратные справа и слева совпадают; используется понятие инверсия R. Тогда R = R.
Обратное отношение функции
A function является обратимым тогда и только тогда, когда его обратное отношение является функцией, и в этом случае обратное отношение является обратной функцией.
Обратное отношение функции f: X → Y { displaystyle f: X to Y}


Это не обязательно функция: одно необходимое условие — чтобы f была injective, поскольку else f — 1 { displaystyle f ^ {- 1}}



Например, функция f (x) = 2 x + 2 { displaystyle f (x) = 2x + 2}

Однако функция g (x) = x 2 { displaystyle g (x) = x ^ {2}}

См. Также
- Биекция
- График транспонирования
Ссылки
- Халмос, Пол Р. (1974), Наивная теория множеств, стр. 40, ISBN 978-0-387-90092-6




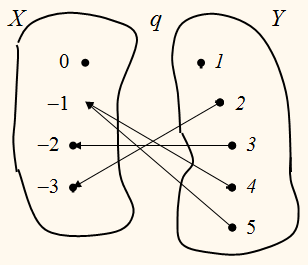


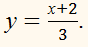





 , и обратимое слева, если существует Y с Y ∘ R = I { стиль отображения Y circ R = I}
, и обратимое слева, если существует Y с Y ∘ R = I { стиль отображения Y circ R = I} . Тогда X и Y называются правым и левым обратными R соответственно. Обратимые вправо и влево отношения называются обратимыми . Для обратимых однородных отношений все обратные справа и слева совпадают; используется понятие инверсия R. Тогда R = R.
. Тогда X и Y называются правым и левым обратными R соответственно. Обратимые вправо и влево отношения называются обратимыми . Для обратимых однородных отношений все обратные справа и слева совпадают; используется понятие инверсия R. Тогда R = R.