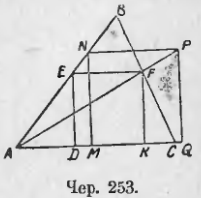Как найти отношение периметров четырехугольников

Как найти отношение периметров четырехугольников

Изучение зависимостей площадей и периметров в четырехугольниках

Автор работы награжден дипломом победителя III степени

С понятием периметр и площадь я познакомилась в 3 классе. Э ти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.

Актуальность темы . Понятия «площади» и «периметра» необходимы человеку в окружающей жизни постоянно, например – сделать ремонт в доме или красиво оформить клумбу на даче. И то и другое понятие связывают стороны многоугольников. Знание зависимостей между этими величинами очень важно для современного человека.

Цель проекта: установить некоторые зависимости между площадью и периметром, увидеть их применение в практических ситуациях.

Задачи:повторить понятия по теме исследования, а именно: «площадь фигуры» и «периметр фигуры»; провести необходимые исследования и опыты; сделать выводы о зависимости площадей и периметров ; рассмотреть практическое применение полученных результатов.

Определение предмета исследования. Что нужно выяснить:

Как связаны периметры и площади прямоугольников?

Зависит ли площадь прямоугольника от его периметра?

Какой прямоугольник имеет наибольшую площадь при заданном периметре?

Если известен периметр прямоугольника, то нельзя ли однозначно установить его площадь?

Что можно сказать о зависимости площади квадрата от его периметра?

Проблема. Никаких зависимостей связывающих площади и периметры фигур мы пока не изучили.

Вот, самый простой пример, который задает проблему: «Есть два участка земли 80 м на 100 м и 50 м на 160 м. Вроде, площадь одинаковая – 8000 м 2 , а первый участок выгоднее купить, чем второй, забор то на 60 м короче строить». С точки зрения математики, все ясно, а вот логически – странно, периметр это замкнутая воображаемая нить, и то, что внутри нее не должно меняться, как ее не крути. Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?

Гипотеза. Предполагаем, что некоторые зависимости существуют. С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника. Можно даже предположить, что если площадь больше, то периметр больше. Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?

Периметр – величина, равная сумме длин всех сторон многоугольника.

Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.

Свойства площадей нам тоже известны:

Равные фигуры имеют равные площади.

Площадь всей фигуры равна сумме площадей ее частей.

За единицу площади принимают площадь квадрата, сторона которого равна единичному отрезку.

Исследования начнем с простой и хорошо знакомой нам фигуры – прямоугольника.

Заполним таблицу, считая площадь одной клеточки равной 1 см 2

Как найти отношение периметров четырехугольников

Периметры двух подобных многоугольников относятся как 3 : 5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.

Отношение площадей подобных многоугольников равно квадрату отношения их периметров. Пусть периметр и площадь меньшего многоугольника соответственно равны P₁ и S₁, периметр и площадь большего многоугольника соответственно равны P₂ и S₂. Поэтому

Математика

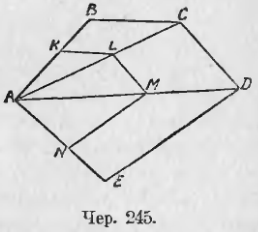
252. Понятие о подобии треугольников распространяется и на многоугольники. Пусть дан многоугольник ABCDE (чер. 245); выполним построение аналогичное п. 206. Построим диагонали AC и AD и, выбрав какую-либо точку K на стороне AB между точками A и B или вне отрезка AB, построим KL || BC до пересечения с диагональю AC, затем LM || CD до пересечения с AD и, наконец, MN || DE до пересечения с AE. Тогда получится многоугольник AKLMN, который связан с ABCD следующими зависимостями:

1) Углы одного многоугольника равны попарно углам другого: угол A у них общий, ∠K = ∠B (как соответственные), ∠KLM = ∠BCD, ибо ∠KLA = ∠BCA и ∠ALM = ∠ACD и т. д.

2) Сходственные стороны этих многоугольников пропорциональны, т. е. отношение одной пары сходственных сторон равно отношению другой пары, равно отношению третьей пары и т. д.

«Сходственные» стороны здесь надо понимать несколько иначе, чем для треугольников: здесь считаем сходственными сторонами те, которые заключены между равными углами, например, BC и KL.

Справедливость указанной пропорциональности видна следующим образом:

∆ABC, следовательно, AK/AB = KL/BC = AL/AC
∆ALM

∆ACD, следовательно, AL/AC = LM/CD = AM/AD
∆AMN

∆ADE, следовательно, AM/AD = MN/DE = AN/AE

Мы видим, что среди первых трех равных отношений и среди вторых трех равных отношений имеется одно одинаковое AL/AC; также и последние три отношения связываются с предыдущими отношением AM/AD. Поэтому, пропуская отношения диагоналей, получим:

AK/AB = KL/BC = LM/CD = MN/DE = AN/AE

Все это остается, как легко видеть, справедливым и для многоугольника с большим, чем у нас, числом сторон.

Если мы многоугольник AKLMN перенесем в другое место плоскости, то найденные выше 2 соотношения этого многоугольника с ABCDE останутся в силе; такие многоугольники называются подобными. Итак, два многоугольника называются подобными, если углы одного равны попарно углам другого и если сходственные стороны их пропорциональны .

Мы, следовательно, умеем строить многоугольник, подобный данному. Мы построили AKLMN

Мы видим еще, что в многоугольниках ABCDE и AKLMN построены диагонали из их соответственных вершин,причем получилось два ряда подобных треугольников: ∆AKL

∆ADE — треугольники эти одинаково расположены в обоих многоугольниках.

Возникает вопрос, останется ли в силе последнее свойство, если мы построим многоугольник, подобный данному, каким-либо еще способом, не тем, которым мы пользовались здесь.

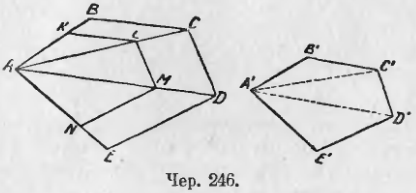
253. Пусть как-либо построен многоугольник A’B’C’D’E’ подобный многоугольнику ABCDE (чер. 246), т. е. так, что

∠A’ = ∠A, ∠B’ = ∠B, ∠C’ = ∠C, ∠D’ = ∠D, ∠E’ = ∠E (1)

A’B’/AB = B’C’/BC = C’D’/CD = D’E’/DE = E’A’/EA (2)

Вопрос конца предыдущего п. равносилен другому: можно ли привести эти два многоугольника в положение, чтобы, например, точка A’ совпала с A, а остальные вершины были бы расположены попарно на прямых, идущих из этой общей точки, и чтобы сходственные стороны их или были параллельны, или сторона одного многоугольника расположилась бы на стороне другого.

Решим этот вопрос. Для этого отложим на стороне AB от точки A отрезок AK = A’B’ и, пользуясь предыдущим п., построим многоугольник AKLMN

Остается выяснить, может ли многоугольник A’B’C’D’E’ совпасть при наложении с AKLMN.

Мы имеем: AK/AB = KL/BC = LM/CD = MN/DE = NA/EA.

Сравнивая эти равенства с равенствами (2) и принимая во внимание, что AK = A’B’, легко получаем KL = B’C’, LM = C’D’ и т. д., т. е. все стороны многоугольников A’B’C’D’E’ и AKLMN попарно равны. Наложим многоугольник A’B’C’D’E’ на AKLMN так, чтобы A’ попала в A и сторона A’B’ совпала бы с AK (мы ведь строили AK = A’B’); тогда, в силу равенства углов B’ и K, сторона B’C’ пойдет по KL, в силу равенства сторон KL и B’C’, точка C’ попадет в L и т. д.

Итак, A’B’C’D’E’ совпадает с AKLMN, а следовательно, если построим диагонали A’C’ и A’D’, получим ряд треугольников, подобных и одинаково расположенных с ∆ABC, ∆ACD и т. д.

Поэтому заключаем: Если построить в подобных многоугольниках диагонали из соответственных вершин, то получим 2 ряда подобных и одинаково расположенных треугольников.

Легко увидать справедливость и обратного заключения: если, ∆A’B’C’

∆ADE, то многоугольник A’B’C’D’E’

многоугольнику ABCDE. Тогда ∆A’B’C’ = ∆AKL, ∆A’C’D’ = ∆ALM и ∆A’D’E’ = ∆AMN, откуда следует равенство многоугольников A’B’C’D’E’ и AKLMN и, следовательно, подобие A’B’C’D’E’ и ABCDE.

254. То положение (две соответственных вершины сливаются в одной точке, остальные вершины попарно лежат на прямых, проходящих чрез эту точку, а сходственные стороны параллельны), в которое нам удалось привести два подобных многоугольника, является частным случаем другого более общего положения двух подобных многоугольников.

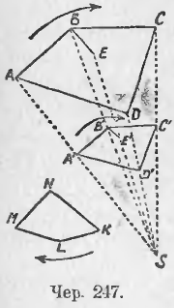
Пусть имеем KLMN

ABCD (чер. 247). Возьмем какую-либо точку S и соединим ее со всеми вершинами A, B, C и D первого многоугольника. Постараемся построить многоугольник, равный многоугольнику KLMN, так, чтобы его вершины лежали на прямых SA, SB, SC и SD и стороны были бы параллельны сторонам многоугольника ABCD.

Для этого отложим на стороне AB отрезок AP = KL (полагаем, что KL и AB сходственные стороны) и построим PB’ || AS (на чертеже точка P и прямая PB’ не даны). Чрез точку B’, где SB пересекается с PB’, построим B’A’ || AB. Тогда A’B’ = AP = KL, затем построим B’C’ || BC, чрез точку C’, где B’C’ пересекается с SC, проведем C’D’ || CD и точку D’, где C’D’ пересекается с SD, соединим с A’. Получим многоугольник A’B’C’D’, который, как это сейчас увидим, подобен многоугольнику ABCD.

Так как A’B’ || AB, то ∆SA’B’

SA’/SA = A’B’/AB = SB’/SB (1)

Так как B’C’ || BC, то ∆SB’C’

SB’/SB = B’C’/BC = SC’/SC (2)

Так как C’D’ || CD, то ∆SC’D’

SC’/SC = C’D’/CD = SD’/SD (3)

Отсюда можно вывести, что SA’/SA = SD’/SD, а следовательно ∆SA’D’

∆SAD, так как две стороны одного пропорциональны двум сторонам другого и углы между ними равны (∠S общий), — A’D’ || AD и

SD’/SD = D’A’/DA = SA’/SA (4)

Из равенств отношений (1), (2), (3) и (4) легко получаем:

A’B’/AB = B’C’/BC = C’D’/CD = D’A’/DA (5)

Кроме того, ∠A’ = ∠A, ∠B’ = ∠B и т. д., как углы с параллельными сторонами. Следовательно, A’B’C’D’

Далее легко увидать, что KLMN = A’B’C’D’. В самом деле, ∠K = ∠A, но ∠A = ∠A’, следовательно, ∠K = ∠A’; также ∠L = ∠B’ и т. д. — углы у наших многоугольников равны. Креме того, из подобия KLMN

KL/AB = LM/BC = MN/CD = NK/DA.

Сравнивая эти равные отношения с равенствами (5) и имея в виду, что A’B’ = KL, находим: B’C’ = LM, C’D’ = MN, D’A’ = NK. Теперь легко, как это делали выше, увидать, что KLMN при наложении совместится с A’B’C’D’. Следовательно, нам удалось поместить данные подобные многоугольники в такое положение, что их вершины расположены попарно на прямых, проходящих чрез точку S и их сходственные стороны параллельны, к чему мы и стремились.

Заметим еще, что соответственные вершины в наших многоугольниках следуют друг за другом в одном направлении (см. стрелки около многоугольников ABCD, KLMN и A’B’C’D’) — по часовой стрелке.

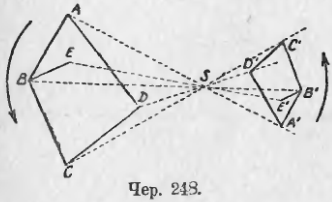
Если бы вершины одного многоугольника, соответствующие последовательным вершинам другого, шли друг за другом в направлении, обратном тому, как они расположены в другом, то удалось бы поместить наши многоугольники так, чтобы соответствующие вершины располагались по разные стороны от точки S (см. чер. 248).

Точка S, где сходятся прямые, соединяющие пары соответственных вершин многоугольников, называется центром подобия; в первом случае (чер. 247), когда обе соответственные вершины (например, A и A’) расположены в одной стороне от S, центр подобия называется внешним , а во втором (чер. 248), когда соответствующие вершины расположены по разные стороны точки S, центр подобия называется внутренним . Если подобные многоугольники расположены так, что они имеют центр подобия, то говорят, что они подобно расположены .

255. Если нам дан многоугольник ABCD (чер. 247 или 248), — будем данный многоугольник называть оригиналом , — мы можем, выбрав произвольную точку S, получать его изображения, подобные ему в каком угодно масштабе , — этим именем называют отношение какого-либо отрезка изображения к соответствующему отрезку в оригинале (в данном многоугольнике). Это отношение называют еще коэффициентом подобия — обозначим его через k. Пока еще для нас коэффициентом подобия является отношение стороны изображения к стороне оригинала, т. е.

A’B/AB = B’C/BC = … = k.

В дальнейшем мы распространим это понятие на отношение всяких двух отрезков изображения и оригинала, сходственных между собою.

Из равенства (1), (2), (3) и (4) предыдущего п., имеем:

SA’/SA = SB’/SB = SC’/SC = SD’/SD = A’B’/AB = k,

т. е. отношение расстояний от центра подобия соответственных вершин изображения и оригинала = коэффициенту подобия.

Под именем фигура (плоская) мы понимаем совокупность точек и линий плоскостей. Многоугольники ABCD — есть фигура. Присоединим еще одну точку (выбранную по произволу) E — получим новую фигуру состоящую из многоугольника ABCD и точки E, — найдем изображение точки E. Для этого построим прямую SE и на ней отложим отрезок SE так, чтобы SE’/SE = k (такой отрезок легко построить, пользуясь п. 214); этот отрезок мы можем отложить по направлению SE (чер. 247); или в обратном направлении (чер. 248). Полученная точка E’ и есть изображение точки E — другими словами точки E’ и E суть соответственные точки в наших двух подобных и подобно расположенных фигурах.

Соединив точку E, например, с B и точку E’ с B’ (B и B’ суть тоже соответственные точки), получим два соответствующих друг другу отрезка BE и B’E’.

Легко увидать, что ∆SBE

∆SB’E’ (так как ∠BSE = ∠B’SE и стороны, составляющие эти углы, пропорциональны: SB’/SB = k и SE’/SE = k, — следовательно, SB’/SB = SE’/SE), отсюда вытекает:

1) B’E’ || BE и 2) B’E’/BE = SB’/SB = k

т. е. соответствующие друг другу отрезки в изображении и оригинале 1) параллельны между собою и 2) их отношение равно коэффициенту подобия .

Отсюда вытекает возможность следующего построения для нахождения точки, соответствующей данной в оригинале точке, если уже имеем одну пару соответствующих точек и известен центр подобия: пусть имеем пару соответствующих точек B и B’ и требуется найти точку, соответствующую точке E, — строим прямые SE и BE и чрез B’ строим прямую, параллельную BE, ее точка пересечения E’ с SE и даст искомую точку.

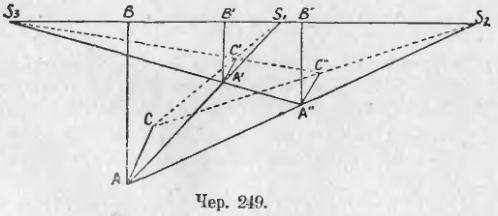
256. Построим для какой-либо фигуры, одна точка которой есть A (чер. 249), ее изображения, принимая две произвольных точки S₁ и S₂ за внешние центры подобия и числа k₁ и k₂ за коэффициенты подобия. Пусть в первом изображении точке A соответствует точка A’ и во втором изображении этой же точке соответствует точка A».

Присоединим еще к данной фигуре какую-либо точку B, лежащую на прямой S₁S₂; тогда этой точке B соответствуют в первом изображении точка B’ и во втором точка B», причем точки B’ и B» должны лежать на той же прямой S₁S₂ и прямые AB, A’B’ и A»B» должны быть параллельны и одинаково направлены.

Соединим точки A’ и A», найдем точку пересечения S₃ прямых A»A’ и S₂S₁. Тогда из подобия треугольников S₃A’B’ и S₂A»B» находим:

Соединив точки A’ и A», найдем точку пересечения S₃ прямых A»A’ и S₂S₁. Тогда из подобия треугольников S₃A’B’ и S₂A»B» находим:

т. е. точка S₂ должна делить отрезок B’B» внешним образом в отношении, равном данному числу k₁/k₂. Мы знаем (п. 217), что существует только одна точка, которая делит данный отрезок B’B» в данном отношении внешним образом. Если мы возьмем какую-либо еще точку C данной фигуры и построим ее изображения C’ и C», то, соединив точки C’ и C» и взяв точку пересечения, назовем ее опять S₃, прямой C’C» с прямой S₁S₂, получим, что ∆S₃B’C’

∆S₃B»C» (B»C» || BC и B’C’ || BC, следовательно, B»C» || B’C’), откуда опять найдем, что S₃B’/S₃B» = k₁/k₂, т. е. новая точка S₃ совпадает с прежнею. Следовательно, S₃ есть центр подобия фигур (A’B’C’. ) и (A»B»C». ) и притом внешний, ибо направления, в котором следуют друг за другом соответствующие точки в обеих фигурах, одинаковы. Из этого заключаем, что фигуры (A’B’C’. ) и (A»B»C». ) также имеют внешний центр подобия и он расположен на одной прямой с центрами S₁ и S₂.

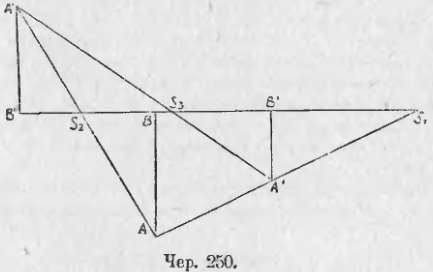
Если одни из центров подобия S1 взять внешний, а другой S2 внутренний (чер. 250), то направления соответствующих отрезков таковы: A’B’ одинаково с направлением AB, но A»B» обратно направлению AB, — следовательно, направление A»B» обратно A’B’ и S3 является внутренним центром подобия фигур (A’B’. ) и (A»B». ).

Если взять оба центра подобия внутренними (например, S₂ и S₃ на чер. 250), то легко увидать, что третий центр подобия окажется внешним. Итак, вообще:

Если три фигуры попарно подобно расположены, то три центра подобия расположены на одной прямой, причем или все три они внешние, или два из них внутренних, а один внешний.

257. Отношение периметров и площадей подобных многоугольников.
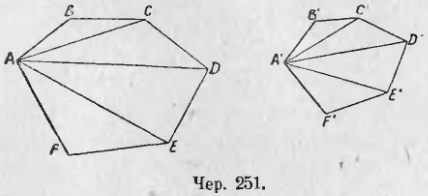
Пусть имеем два подобных многоугольника ABCDEF и A’B’C’D’E’F’ (чер. 251). Назовем коэффициент подобия чрез k.

A’B’/AB = k, B’C’/BC = k и т. д.,

A’B’ = k · AB, B’C’ = k · BC, C’D’ = k · CD, …

Сложив эти равенства по частям и вынеся множитель k во второй части за скобку, получим:

A’B’ + B’C’ + C’D’ + … = k(AB + BC + CD + …),

(A’B’ + B’C’ + C’D’ …) / (AB + BC + CD + …) = k = A’B’/AB,

т. е. отношение периметров подобных треугольников равно отношению сходственных сторон (или равно коэффициенту подобия).

Выберем две соответственных вершины, напр., A и A’, и построим проходящие чрез них диагонали. Тогда мы знаем: 1) (из п. 253) ∆ABC

∆A’C’D’ и т. д. 2) (из п. 212). Отношение площадей подобных треугольников равно квадрату отношения их сходственных сторон, следовательно,

пл. ∆A’B’C’ / пл. ∆ABC = (A’B’/AB) 2 = k 2 ; пл. ∆A’C’D’ / пл. ∆ACD = (C’D’/CD) 2 = k 2 и т. д.,

пл. ∆A’B’C’ = k 2 · пл. ∆ABC; пл. ∆A’C’D’ = k 2 · пл. ∆ACD;
пл. ∆A’D’E’ = k 2 · пл. ∆ADE .

Сложив эти равенства по частям и вынеся общего множителя k 2 во второй части за скобку получим:

пл. ∆A’B’C’ + пл. ∆A’C’D’ + ∆A’D’E’ + … = k 2 (пл. ∆ABC + пл. ∆ACD + пл. ∆ADE + …),

пл. A’B’C’D’E’F’ / пл. ABCDEF = k 2 = (A’B’/AB) 2 ,

т. е. отношение площадей подобных многоугольников равно квадрату отношения их сходственных сторон (или равно квадрату коэффициента подобия).

258. Два правильных одноименных многоугольника всегда подобны. В самом деле, углы у одноименных многоугольников одинаковы (п. 248), а так как все стороны каждого равны между собою, то, очевидно, отношение любой стороны одного к любой стороне другого есть число постоянное.

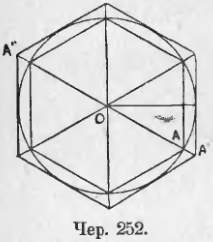
Если в круг впишем какой-либо правильный многоугольник (чер. 252) и чрез середины дуг, стягиваемых его сторонами, построим касательные к кругу, то получим правильный одноименный многоугольник, описанный около этого круга. Не трудно выяснить (предоставляем это желающим), что полученные два правильные многоугольника подобно расположены, и центр круга служит их внешним центром подобия, – внешним потому, что каждая пара соответствующих точек (напр., A и A’) расположена в одном направлении от центра (если многоугольник имеет четное число сторон, то центр круга можно считать и внутренним центром подобия, надо лишь считать, что, например, точке A соответствует точка A»).

259. Упражнения.

1. Стороны одного пятиугольника равны соответственно 12, 14, 10, 8 и 16 дм. Найти стороны другого пятиугольника, подобного первому, если его периметр = 80 дм.

2. Сумма площадей двух подобных многоугольников равна 250 кв. дм., а отношение двух сходственных сторон = ¾. Вычислить площадь каждого из них.

3. Показать, что если в круг вписан правильный многоугольник с нечетным числом сторон и в его вершинах построены касательные к кругу, то получится описанный многоугольник, подобно расположенный с вписанным, – центр круга служит их внутренним центром подобия.

4. Дан треугольник; построить другой треугольник, подобно расположенный с первым так, чтобы центр тяжести первого служил внутренним центом подобия и чтобы коэффициент подобия = ½. Выяснить при помощи этого, как расположены точки высот, центр тяжести и центр описанного круга данного треугольника.

5. В данный треугольник вписан квадрат.

Пусть ABC данный треугольник (чер. 253) и DEFK искомый квадрат. Построим еще квадрат MNPQ, чтобы одна сторона MQ лежала на стороне AC треугольника и точка N на стороне AB. Легко видеть, что квадрат MNPQ подобно расположен с искомым квадратом DEFK и внешним их центром подобия является точка A; следовательно, точка F лежит на прямой AP. После нахождения точки F искомый квадрат легко построить.

6. Дан угол и точка внутри его. Найти на одной стороне угла точку, равноудаленную от данной точки и от другой стороны.

Задача решается тем же приемом.

7. Построить треугольник по его высотам.

Легко получить, называя стороны треугольника чрез a, b и c и соответствующие высоты чрез h_a, h_b и h_c, следующую зависимость:

Легко построить отрезок x = (h_bh_a)/h_c (x/h_a = h_b/h_c — построение 4-го пропорционального), после чего построим треугольник со сторонами h_b, h_a и x. Этот треугольник подобен искомому, так как a : h : c = h_b : h_a : x; остается построить треугольник подобный только что построенному так, чтобы одна его высота была равна данной.

1. Отношение площадей подобных фигур равно квадрату коэффициента подобия, т.е. 25:64=k^2. Отсюда k=5/8, отношение периметров подобных фигур равно коэффициенту подобия, т.е. 5/8.
2. Очевидно, символ «0» в записи условия задачи означает «градусов», так как два отрезка не могут образовывать угол в 370 градусов. 

Тогда угол ABD=ABC + ADC = 15 + 37 = 52 градуса. Больший угол в сумме с меньшим дают 180 градусов, т.е. больший угол равен 180 — 52 = 128 градусов.

3. Внутренние односторонние углы в сумме дают 180 градусов, т.е. мы имеем два числа, сумма которых равна 180, а разность 52. Большее из чисел равно (180+52)/2 = 116, поэтому больший из углов равен 116 градусам.

Содержание

• Как узнать, похожи ли два многоугольника
• Пример 1: Определение длины и периметра с учетом масштабного коэффициента
• Пример 2: Определение длины соответствующих сторон похожих многоугольников
• Пример 3: Определение площади меньшего многоугольника по диагоналям и площадям
• Пример 4: Нахождение масштабных коэффициентов, длин сторон и периметров похожих многоугольников
• Пример 5: Нахождение масштабного коэффициента по периметрам подобных параллелограммов
• Пример 6: Решение проблемы похожих многоугольников с учетом соотношения площадей
• Пример 7: Определение площади большего треугольника с учетом периметров похожих многоугольников
• Пример 8: Подобные многоугольники с учетом суммы площадей и периметров
• Пример 9: Проблема с похожими многоугольниками
• Пример 10: Коэффициенты масштабирования и длины сторон похожих многоугольников
• Изучите другие статьи о геометрии

Похожие полигоны

А_L = площадь большего многоугольника

А_s = площадь меньшего многоугольника

S_L = длина более длинной соответствующей стороны

S_S = длина более короткой соответствующей стороны

d_L = длина более длинной соответствующей диагонали

d_S = длина более короткой соответствующей диагонали

На показанных рисунках предполагается, что шестиугольник ABCDEF и PQRSTU подобны. Из определения подобных многоугольников можно сказать, что A P, B Q, C R, D S, E T и F U.

Например, рассмотрим следующие четырехугольники с учетом их сторон. Отметим, что A P, B Q, C R, D S. Находя отношения соответствующих сторон, получаем следующее.

Из приведенного выше решения следует, что AB / PQ = BC / QR = CD / RS = DA / SP = 5. По определению похожих многоугольников мы можем заключить, что четырехугольники ABCD и PQRS подобны. В символах ABCD ~ PQRS.

Как вы можете заметить, обычное отношение 5 — это масштабный коэффициент от ABCD до PQRS. Это означает, что все длины сторон PQRS должны быть умножены на масштабный коэффициент 5, чтобы получить размер сторон ABCD, поскольку ABCD — это больший четырехугольник.

Как узнать, похожи ли два многоугольника

Чтобы гарантировать, что n-сторонние многоугольники, n> 3, подобны, необходимо, чтобы выполнялись оба условия в определении похожих многоугольников. Даже если известно, что соответствующие углы двух многоугольников совпадают, из этого не следует, что многоугольники подобны. Итак, чтобы мы могли проверить, похожи ли два многоугольника, должны быть выполнены два условия.

1. Соответствующие углы двух многоугольников совпадают.
2. Длины соответствующих сторон пропорциональны.

Обратите внимание на рисунок A. Обратите внимание, что все соответствующие углы являются прямыми углами и, следовательно, конгруэнтны, но соответствующие стороны не пропорциональны. Кроме того, пропорциональность соответствующих сторон двух многоугольников не гарантирует схожести многоугольников. Также обратите внимание на рисунок B. Квадрат PQRS и ромб XYZW имеют пропорциональные стороны, но не идентичны.

Пример 1: Определение длины и периметра с учетом масштабного коэффициента

Четырехугольники ABCD и EFGH схожи с масштабным коэффициентом.

1. Найдите длины a, b, c, d четырехугольника EFGH.
2. Найдите отношение периметров четырехугольника ABCD и EFGH.

Решение

Учитывая масштабный коэффициент, вычислите значения a, b, c и d четырехугольника EFGH, умножив заданные длины сторон ABCD на масштабный коэффициент. Обратите внимание, что масштабный коэффициент равен делению большей длины на меньшую длину.

Масштабный коэффициент = большая длина / меньшая длина

= a / EF

= а / 5

а = 5 / ()

а = 5 х 3

а = 15

= b / BC

= b / 2

б = 2 / ()

б = 2 х 3

б = 6

= c / DC

= c / 3

с = 3 / ()

с = 3 х 3

с = 9

= d / AD

= d / 4

d = 4 / ()

г = 4 х 3

d = 12

Для отношения периметров ABCD и EFGH вычислите значение ребер.

P (ABCD) = 2 + 3 + 4 + 5

P (ABCD) = 14

P (EFGH) = 6 + 9 + 12 + 15

P (EFGH) = 42

Соотношение периметров = меньший периметр / больший периметр

Соотношение периметров = 14/42

Соотношение периметров =

Как видите, отношение периметра равно заданному коэффициенту масштабирования.

Окончательный ответ

Длины a, b, c, d четырехугольника EFGH равны 15, 6, 9 и 12 соответственно. Отношение периметров ABCD и EFGH равно заданному масштабному коэффициенту.

Пример 2: Определение длины соответствующих сторон похожих многоугольников

Площадь двух одинаковых многоугольников 120 см.² и 30 см². Если сторона меньшего многоугольника имеет длину 3 сантиметра, найдите длину соответствующей стороны большего многоугольника.

Решение

Пусть A_L — площадь большего многоугольника, а A_S — площадь меньшего многоугольника. Обратите внимание, что заданная длина стороны меньшего многоугольника S_S составляет 3 сантиметра. Подставьте указанные величины в уравнение.

А_L = 120 см²

А_S = 30 см²

S_S = 3 см

А_L / А_S = (S_L/ S_S)²

120/30 = (S_L/3)²

4 = (S_L/3)²

4 = S_L² / 9

S_L² = 9 х 4

S_L² = 36

S_L² = 36

S_L = 6 см

Окончательный ответ

Длина соответствующей стороны большего многоугольника S_L равен 6 сантиметрам.

Пример 3: Определение площади меньшего многоугольника по диагоналям и площадям

Соответствующие диагонали двух одинаковых многоугольников имеют длину 4 см и 7 см. Если площадь большего многоугольника составляет 147 квадратных сантиметров, найдите значение A_s.

Решение

Пусть d_L — длина диагонали большего многоугольника, а d_S соответствующей диагонали меньшего многоугольника. Учитывая, что A_L = 147 см², вычислите площадь меньшего многоугольника, используя упомянутые ранее формулы.

А_L = 147 см²

d_s = 4 см

d_L = 7 см

А_L / А_S = (d_L/ д_S)2

147 / А_S = (7/4)2

147 / А_S = 49/16

А_S = 147 (16) / (49)

А_S = 48 см²

Окончательный ответ

Площадь меньшего многоугольника равна As = 48 см.².

Пример 4: Нахождение масштабных коэффициентов, длин сторон и периметров похожих многоугольников

Учитывая, что PQRS ~ JKLM, найдите следующее.

1. Коэффициент масштабирования от PQRS до JKLM
2. Коэффициент масштабирования от JKLM до PQRS
3. Значения x, y и w
4. Периметр каждого многоугольника
5. Отношение суммы граней PQRS к сумме сторон JKLM

Решение

При получении масштабного коэффициента от PQRS до JKLM постарайтесь найти длины сторон, указанные на рисунке. Разделите заданную длину PQRS на соответствующую длину стороны JKLM. С другой стороны, найдите коэффициент масштабирования JKLM в PQRS, изменив указанную процедуру в обратном порядке, разделив размер соответствующих сторон JKLM на размер PQRS.

PQ / JK = 15/12

PQ / JK = 4/3

JK / PQ = 12/15

JK / PQ = ¾

Поскольку мы получили масштабные коэффициенты JKLM в PQRS и PQRS в JKLM, теперь мы можем вычислить значения x, y и w.

х = KL х (4/3)

х = 10 х (4/3)

x = 40/3 единицы

у = LM x (4/3)

у = 16 х (4/3)

y = 64/3 единицы

w = PS x (¾)

ш = 25 х (¾)

w = 75/4 единицы

Теперь, когда все стороны одинаковых многоугольников завершены, определите периметр, просто добавив все стороны по отдельности. Затем получите отношение периметра PQRS к периметру JKLM.

P (PQRS) = 25 + 15 + 40/3 + 64/3

P (PQRS) = 224/3 = 74,6 единиц

P (JKLM) = 12 + 10 + 16 + 75/4

P (JKLM) = 227/4 = 56,75 единиц

Соотношение периметров = Периметр PQRS / Периметр JKLM

Соотношение периметров = 74,6 / 56,75

Соотношение периметров = 4/3

Окончательный ответ

Масштабные коэффициенты от PQRS до JKLM и от JKLM до PQRS составляют 4/3 и ¾ соответственно.

Значения x, y и w равны 40/3, 64/3 и 75/4 соответственно.

Периметр PQRS составляет 74,6 единицы.

Периметр JKLM составляет 56,75 единиц.

Отношение периметра PQRS к JKLM составляет 4/3, что равно масштабному коэффициенту PQRS к JKLM.

Пример 5: Нахождение масштабного коэффициента по периметрам подобных параллелограммов

Периметр параллелограммов PQRS и JKLM составляет 94 см и 18,8 см соответственно. Если два параллелограмма похожи, найдите масштабный коэффициент параллелограмма PQRS к параллелограмму JKLM.

Решение

Помните, что соотношение периметров двух одинаковых многоугольников равно их масштабному коэффициенту. Чтобы получить масштабный коэффициент параллелограмма от PQRS до JKLM, разделите периметр PQRS, равный 94 сантиметрам, на окружность JKLM, которая составляет 18,8 сантиметра.

Коэффициент масштабирования от PQRS до JKLM = P (PQRS) / P (JKLM)

Масштабный коэффициент от PQRS до JKLM = 94 / 18,8

Масштабный коэффициент от PQRS до JKLM = 5

Окончательный ответ

Коэффициент масштабирования параллелограмма PQRS на параллелограмм JKLM равен пяти.

Пример 6: Решение проблемы похожих многоугольников с учетом соотношения площадей

Площади двух одинаковых треугольников находятся в соотношении 25:16.

1. Найдите длину стороны большего треугольника, если соответствующая сторона меньшего треугольника имеет длину 80 единиц.
2. Найдите длину медианы большего треугольника, если соответствующая медиана меньшего треугольника имеет длину 10 единиц.
3. Найдите длину биссектрисы меньшего треугольника, если соответствующая биссектриса большего треугольника имеет длину 15 единиц.
4. Найдите периметр меньшего треугольника, если периметр большего треугольника равен 125.

Решение

Нам дано соотношение площадей двух одинаковых треугольников, которое составляет 25:16. При нахождении длины стороны большего треугольника по соответствующей стороне меньшего треугольника S_S = 80 единиц, используйте формулу для соотношения площадей и соответствующих сторон.

А_L / А_S = (S_L/ S_S)²

25/16 = (S_L/80)²

S_L = 100 единиц

Относительно вопросов, касающихся медиан и биссектрис угла, помните, что два треугольника подобны, если отношение любых двух соответствующих сегментов (высоты, медианы или биссектрисы угла) равно доле любых двух соответствующих сторон. Теперь, когда мы получили значение более короткой стороны, создайте формулу пропорции для длин сторон и соответствующих сегментов, таких как медианы и биссектрисы.

S_L / S_S = M_L / М_S

100/80 = М_L / 10

M_L = 12,5 единиц

S_L / S_S = AB_L / AB_S

100/80 = 15 / AB_S

AB_S = 12 единиц

Наконец, решите периметр меньшего треугольника с учетом периметра большего треугольника P_L = 125. Напомним, что отношение периметров двух одинаковых многоугольников равно отношению длин двух соответствующих сторон.

п_L / П_S = S_L / S_S

125 / P_S = 100 / 80

п_S = 100 единиц

Окончательный ответ

Длина стороны большего треугольника равна 100 единицам.

Длина медиан большего треугольника равна 12,5 единицам.

Длина биссектрисы меньшего треугольника равна 12 единицам.

Периметр меньшего треугольника равен 100 единицам.

Пример 7: Определение площади большего треугольника с учетом периметров похожих многоугольников

Два одинаковых многоугольника имеют периметр 32 см и 24 см. Если площадь меньшего треугольника составляет 27 квадратных сантиметров, найдите площадь большего треугольника.

Решение

Учитывая периметры двух похожих многоугольников, вычислите отношение соответствующих сторон. Когда отношение соответствующих сторон станет доступным, вычислите площадь меньшего треугольника, используя формулу для отношения площадей и соответствующих сторон.

п_L / П_S = S_L / S_S

32/24 = S_L / S_S

S_L / S_S = 4/3

А_L / А_s = (S_L/ S_S)²

А_L / 27 = (4/3)²

А_L = 48 квадратных сантиметров

Окончательный ответ

Площадь большего треугольника равна 48 квадратным сантиметрам.

Пример 8: Подобные многоугольники с учетом суммы площадей и периметров

Сумма площадей двух одинаковых многоугольников составляет 65 квадратных единиц. Если их периметр равен 12 единицам и 18 единицам, найдите площадь большего многоугольника.

Решение

Составьте математическое уравнение, описывающее сумму площадей двух похожих многоугольников. Оттуда выразите площадь меньшего многоугольника через большой многоугольник.

А_L + А_S = 65 квадратных единиц

А_S = 65 — А_L

Вычислите пропорцию соответствующих длин двух похожих многоугольников, используя заданные периметры.

п_L = 18 единиц

п_S = 12 единиц

п_L / П_S = S_L / S_S

18/12 = S_L / S_S

S_L / S_S = 3/2

Воспользуйтесь формулой соотношения площадей и соответствующих сторон. Подставьте полученное уравнение для площади меньшего многоугольника в уравнение.

А_L / А_S = (S_L/ S_S)2

А_L / (65 — А_L) = (3/2)2

А_L = 45 квадратных единиц

Окончательный ответ

Площадь большего многоугольника составляет 45 квадратных единиц.

Пример 9: Проблема с похожими многоугольниками

Предположим, Альфред хочет, чтобы фотография размером с бумажник была похожа на фотографию 8 x 10. Если бы фотография размером с бумажник была шириной 2,5 дюйма, какой длины она была бы?

Решение

Больший многоугольник имеет размер 8 дюймов на 10 дюймов на основе данной фотографии размером с бумажник. Напомним, что похожие многоугольники подобны, если длины соответствующих сторон пропорциональны. Вычислите высоту фотографии размера бумажника, создав уравнение пропорций.

8 / 2,5 = 10 / год

y = 3,125 дюйма

Окончательный ответ

Размер фото кошелька составляет 2,5 дюйма и 3,125 дюйма.

Пример 10: Коэффициенты масштабирования и длины сторон похожих многоугольников

Определите расширение и найдите его масштабный коэффициент. Затем найдите значения x, y и z.

Решение

Расширение — это состояние расширения, расширения или расширения. Следовательно, расширенные многоугольники можно рассматривать как аналогичные многоугольники. Вычислите масштабный коэффициент многоугольника и расширенного многоугольника, получив отношение двух соответствующих сторон. После вычисления вычислите значения x, y и z, найдя отношения соответствующих сторон.

Масштабный коэффициент = PQ / PQ

Масштабный коэффициент = 10/20

Масштабный коэффициент = ½

Масштабный коэффициент = 8 / x

½ = 8 / х

x = 16 единиц

Масштабный коэффициент = 10 / год

½ = 10 / год

y = 20 единиц

Масштабный коэффициент = 8 / z

½ = 8 / z

z = 16 единиц

Окончательный ответ

Значение масштабного коэффициента составляет ½. Полученные значения для x, y и z равны 16, 8 и 16 единиц.

Изучите другие статьи о геометрии

• Методы калькуляции многоугольников в плоской геометрии
  Решение проблем, связанных с плоской геометрией, особенно с полигонами, можно легко решить с помощью калькулятора. Вот исчерпывающий набор задач о многоугольниках, решаемых с помощью калькуляторов.
• Методы калькуляции четырехугольников в плоской геометрии
  Узнайте, как решать задачи, связанные с четырехугольниками в плоской геометрии. Он содержит формулы, методы калькулятора, описания и свойства, необходимые для интерпретации и решения задач Четырехугольника.
• Нахождение площади поверхности и объема створок пирамиды и конуса
  Узнайте, как рассчитать площадь поверхности и объем усеченных углов правильного кругового конуса и пирамиды. В этой статье рассказывается о концепциях и формулах, необходимых для решения площади поверхности и объема усеченных твердых тел.
• Определение площади поверхности и объема усеченных цилиндров и призм
  Узнайте, как вычислить площадь поверхности и объем усеченных твердых тел. В этой статье рассматриваются концепции, формулы, проблемы и решения, касающиеся усеченных цилиндров и призм.
• Полное руководство по треугольнику 30-60-90 (с формулами и примерами)
  Эта статья представляет собой полное руководство по решению задач на 30-60-90 треугольниках. Он включает формулы паттернов и правила, необходимые для понимания концепции треугольников 30-60-90. Также приведены примеры, показывающие пошаговую процедуру, как это сделать.
• Односторонние внутренние углы: теорема, доказательство и примеры
  В этой статье вы можете изучить концепцию теоремы об односторонних внутренних углах в геометрии, решая различные приведенные примеры. В статье также содержится обращение к теореме о односторонних внутренних углах и ее доказательство.

Изучение зависимостей площадей и периметров в четырехугольниках

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

С понятием периметр и площадь я познакомилась в 3 классе. Эти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.

Актуальность темы. Понятия «площади» и «периметра» необходимы человеку в окружающей жизни постоянно, например – сделать ремонт в доме или красиво оформить клумбу на даче. И то и другое понятие связывают стороны многоугольников. Знание зависимостей между этими величинами очень важно для современного человека.

Цель проекта: установить некоторые зависимости между площадью и периметром, увидеть их применение в практических ситуациях.

Задачи:повторить понятия по теме исследования, а именно: «площадь фигуры» и «периметр фигуры»; провести необходимые исследования и опыты; сделать выводы о зависимости площадей и периметров; рассмотреть практическое применение полученных результатов.

Основнаячасть

Определение предмета исследования. Что нужно выяснить:

Как связаны периметры и площади прямоугольников? 

Зависит ли площадь прямоугольника от его периметра?

Какой прямоугольник имеет наибольшую площадь при заданном периметре?

Если известен периметр прямоугольника, то нельзя ли однозначно установить его площадь?

Что можно сказать о зависимости площади квадрата от его периметра?

Проблема. Никаких зависимостей связывающих площади и периметры фигур мы пока не изучили.

Вот, самый простой пример, который задает проблему: «Есть два участка земли 80 м на 100 м и 50 м на 160 м. Вроде, площадь одинаковая – 8000 м ², а первый участок выгоднее купить, чем второй, забор то на 60 м короче строить». С точки зрения математики, все ясно, а вот логически – странно, периметр это замкнутая воображаемая нить, и то, что внутри нее не должно меняться, как ее не крути. Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?

Гипотеза.Предполагаем, что некоторые зависимости существуют. С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника. Можно даже предположить, что если площадь больше, то периметр больше. Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?

Мы уже знаем: 

Периметр – величина, равная сумме длин всех сторон многоугольника.

Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.

Свойства площадей нам тоже известны:

Равные фигуры имеют равные площади.

Площадь всей фигуры равна сумме площадей ее частей.

За единицу площади принимают площадь квадрата, сторона которого равна единичному отрезку.

Проверка гипотезы.

Исследования начнем с простой и хорошо знакомой нам фигуры – прямоугольника.

Исследование №1.   

Заполним таблицу, считая площадь одной клеточки равной 1 см ²

Таблица №1

№	Фигуры	Площадь (S, см 2)	Периметр (Р, см)
1		1	4
2		2	6
3		3	8
4		4	10
5		4	8
6		5	12
7		6	14
8		6	10
9		7	16
10		8	12
11		8	18
12		9	20
13		9	12
14		10	22
15		10	14

Исследуя результаты измерений, делаем вывод, что не всегда увеличение площади означает, что периметр тоже увеличивается, например фигуры №3 и №5 или фигуры №4 и №8, или фигуры №6 и №10 и №13. Если периметры равны, то площади могут быть различны. (Приложение 1, стр.14-16)

Мы заметили, если периметр одного прямоугольника больше, то и его площадь больше чем у других, например фигуры №2 и №3 или фигуры №4 и №6. Однако, если периметр одного прямоугольника больше, то его площадь не всегда больше, например фигуры №6 и №8.

При одинаковом периметре и площади бывают разные! Отчего же так происходит?

Продолжим наблюдения. 

Исследование №2.                

Таблица №2

№ фигуры	1 сторона (длина, см)	2 сторона (ширина, см)	Площадь (S, см 2)	Периметр (Р, см)
1	1	100	100	202
2	2	50	100	104
3	4	25	100	58
4	5	20	100	50
5	10	10	100	40
6	20	5	100	50
7	25	4	100	58
8	50	2	100	104
9	100	1	100	202

Замечаем, что при равных площадях периметры не равны, самый маленький периметр из всех прямоугольников с равными площадями – у квадрата. Вот какое замечательное свойство у квадрата! Оказывается, что среди всех прямоугольников одинаковой площади у квадрата самый маленький периметр!

Какой же из всех прямоугольников заданного периметра имеет наибольшую площадь? Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в книге Евклида.

Исследование №3.                

Таблица №3

№ фигуры	1 сторона (длина, см)	2 сторона (ширина, см)	Площадь (S, см 2)	Периметр (Р, см)
1	1	49	49	100
2	2	48	96	100
3	5	45	225	100
4	10	40	400	100
5	20	30	600	100
6	25	25	625	100

Очевидно, можно сделать вывод, что при одинаковом периметре, самая выгодная площадь у квадрата. Запомним это замечательное свойство квадрата, заключать в своих границах наибольшую площадь при постоянном периметре. Отчего же возникают такие зависимости, в чем причина? Чтобы лучше разобраться в этом вопросе, проведем опыт.

Опыт.

Я взяла четырехугольник – квадрат. Измерила его стороны, вычислила площадь и периметр. Разрезала фигуру пополам и составила новую фигуру (Приложение 2, стр.17).  Результаты измерений занесла в таблицу №4.

Таблица №4

№ фигуры	1 сторона (длина, см)	2 сторона (ширина, см)	Площадь (S, см 2)	Периметр (Р, см)
1	8	8	64	32
2	16	4	64	40

Таблица №5

1 фигура
2 фигура

Количество квадратиков не изменилось. Наблюдаем, что происходит со сторонами, когда периметр увеличивается. У фигуры появились дополнительные стороны, которые стали границами, это дополнительные 8+8=16 см, и исчезла граница 4+4=8 см. Итого: 16-8=8 см. Вот и дополнительные 8 см. Периметр увеличится.

Практические задачи.

А что можно сказать о зависимости площади квадрата от его периметра?

Задача №1. Если известен периметр квадрата, то можно ли однозначно установить его площадь?

Решим задачу для квадрата, периметр которого равен 40 см. Можно, поскольку по известному периметру можно вычислить сторону квадрата. А вычислив его сторону, можно потом вычислить площадь по этой найденной стороне.

1) 40 : 4 = 10 (см) – одна сторона

2) 10 • 10 = 100 (см ²) – площадь

Площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.

Задача №2. Начертите какой-нибудь квадрат. Как надо изменить его стороны, чтобы построить квадрат, площадь которого была бы: 1) в 4 раза больше? 2) в 9 раз больше? 3) в 16 раз больше?

Проверим решение построением (Приложение 3, стр.18). 

Таблица №6

№	Фигуры	Вывод
1		Стороны увеличить в 2 раза
2		Стороны увеличить в 3 раза
3		Стороны увеличить в 4 раза

Задача №3. Начертите три прямоугольника, у одного из которых стороны имеют длину 7 см и 3 см, у второго соответственно 8 см и 2 см, а у третьего – 9 см и 1 см. Вычислите периметр и площадь каждого из этих прямоугольников. Сравните получившиеся периметры между собой и получившиеся площади между собой.

Проиллюстрируем на примере.

Первый прямоугольник: Р = (7 + 3) • 2 = 20 (см), S = 7 • 3= 21 (см ²).


Второй прямоугольник: Р = (8 + 2) • 2 = 20 (см), S = 8 • 2 = 16 (см ²).


Третий прямоугольник: Р = (9 + 1) • 2 = 20 (см), S = 9 • 1 = 9 (см ²).


Периметры прямоугольников равны, а площадь первого прямоугольника больше площади второго прямоугольника и площадь второго – больше площади третьего: 21 > 16 > 9 . Если известен периметр прямоугольника, то нельзя однозначно установить его площадь. Площадь прямоугольника не будет однозначно зависеть от его периметра.

А, что можно сказать о зависимости периметра квадрата от длины его стороны?

Задача №4. Может ли периметр квадрата не измениться, если длина стороны квадрата изменилась? Могут ли получиться разные значения периметра квадрата при одном и том же значении длины его стороны?

Таблица №7

Длина стороны квадрата α, см	1	2	3	4	5
Периметр квадрата Р, см	4	8	12	16	20

Из таблицы видно, что с изменением стороны квадрата изменяется и периметр. Периметр квадрата однозначно зависит от длины его стороны, поскольку периметр квадрата – 4 • α, то есть при изменении значения α, изменится значение выражения. Если изменить длину стороны квадрата, то это обязательно приведёт к изменению его периметра, то есть Р зависит от а. 

Если длина стороны квадрата увеличивается, то его периметр тоже увеличивается.
Если длина стороны квадрата уменьшается, то его периметр тоже уменьшается.

Заключение

Практические результаты и выводы, полученные мною, могут быть использованы при подготовке домашних заданий и в бытовых вопросах, постоянно возникающих в жизни. Мои исследования помогли узнать о том, что по известному периметру прямоугольника нельзя однозначно установить его площадь.
Потому, что у прямоугольников с одинаковым периметром могут быть разные площади, как выяснилось выше.
 Я выяснила, что площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.

Основные выводы.

Если периметры прямоугольников равны, то площади могут быть различны. 

Не всегда увеличение площади прямоугольников означает, что периметр тоже увеличивается.

Если площади прямоугольников равны, то периметры могут быть различны.

Из всех прямоугольников с равными площадями наименьший периметр имеет квадрат.

Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.

Площадь квадрата однозначно зависит от его периметра.

Основные выводы я разместила на памятках-закладках (Приложение 4.1 и 4.2, стр.19-20)

Списокиспользованныхисточниковилитературы

А. Г. Мерзляк. Математика: 5 кл.: учебник для общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. −  2-е изд., перераб. — М.: Вентана-Граф, 2018

М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, Математика — 4 класс, учебник для общеобразовательных организаций, в двух частях, М: Просвещение, 2018 г.-148 с.

3. Я.И. Перельман, Занимательная геометрия, Изд.: Терра-Книжный клуб, 2008 г., 384 стр.

4. Я.И. Перельман: Занимательная геометрия на вольном воздухе и дома , Издательство: Центрополиграф, 2017 г.

5. М.Г. Нефедова, Рабочая тетрадь по математике, Периметр и площадь — 3-4 классы. М: Издательство «Экзамен», 2014 г.- 46 стр.

6. М.И. Башмаков, М.Г. Нефедова, Математика, 3 класс, учебник, АСТ-Астрель, Москва, 2010 г.

7. О.В. Узорова, М.Г. Нефедова: Математика. 4 класс. Простые и составные задачи площади и периметра, Тренинговая тетрадь, ФГОС: издательства АСТ, 2015 г.

Приложение 4.1

Приложение 4.2

Просмотров работы: 7201