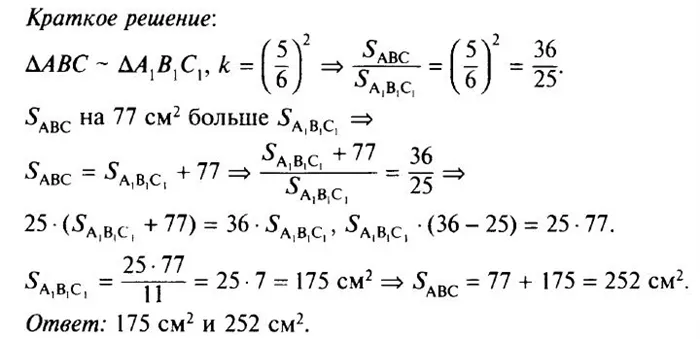Основные сведения об отношении площадей подобных треугольников
Понятие подобия треугольников
Два треугольника называются подобными, если их углы попарно равны, а стороны, лежащие напротив соответственных углов пропорциональны.
A B / K L = B C / L M = A C / K M = k , ∠ A = ∠ K , ∠ B = ∠ L , ∠ C = ∠ M ⇒ Δ A B C
Отношение длин подобных треугольников называют коэффициентом подобия (k).
Также пропорциональные стороны подобных треугольников могут быть названы сходственными сторонами.
В подобных треугольниках, кроме сторон, подобны и другие величины: биссектрисы, медианы, высоты и т.д.
Теорема об отношении площадей подобных треугольников
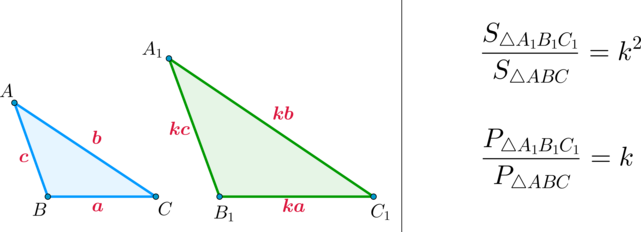
Формулировка теоремы: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
В геометрии существует три признака подобия треугольников:
1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.
Свойства подобных треугольников:
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных элементов равно коэффициенту подобия.
Доказательство теоремы
Докажем теорему об отношении площадей подобных треугольников.
Теорема: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство: изобразим подобные треугольники Δ A B C
Из подобия треугольников по определению следует: A B / K L = B C / L M = A C / K M = k .
Воспользуемся следующей теоремой: если у двух треугольников равны углы (∠A=∠K), то их площади относятся, как произведение сторон, заключающих данные углы. Запишем в виде формулы:
Что и требовалось доказать.
Примеры решения задач
Площади подобных треугольников ΔABC и ΔA1B1C1 равны соответственно 200 см² и 50 см². Сторона A1B1=5 см. Найдите сходственную ей сторону AB треугольника ABC.
По теореме об отношении площадей подобных треугольников: S a b c / S a 1 b 1 c 1 = k ² ⇒ 200 / 50 = k ² ⇒ k = 2 .
A B / A 1 B 1 = 2 , A B = A 1 B 1 * 2 , A B = 5 * 2 = 10 с м .
ΔABC и ΔA1B1C1 — подобны. Сходственные стороны AC и A1C1 соответственно равны 13 см и 0,1 м.
Найдите отношение периметров ΔABC и ΔA1B1C1.
A 1 C 1 = 0 , 1 м = 10 с м
A C / A 1 C 1 = 13 / 10 = 1 , 3 ⇒ P a b c / P a 1 b 1 c 1 = 1 , 3
Задача для самостоятельной работы
Треугольники Δ A B C
Δ K L M подобны. Площадь ΔABC равна 500 см², площадь ΔKLM равна 125 см². Сторона AC равна 18 см, найти сходственную ей сторону KM.
Проверьте, насколько верный или неверный ваш ответ.
Советуем составить краткий конспект для подготовки к уроку.
Основные свойства площадей треугольников
Факт 1.
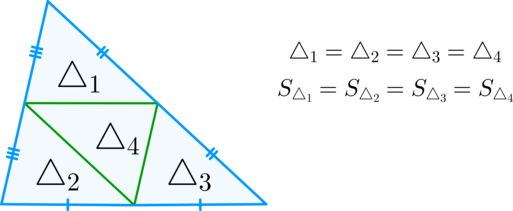
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
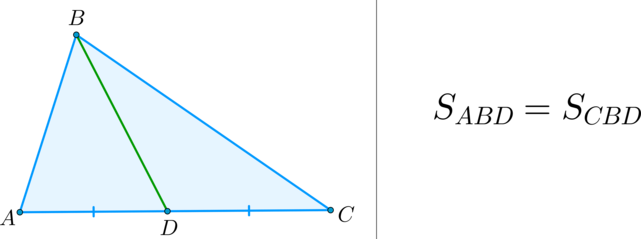
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
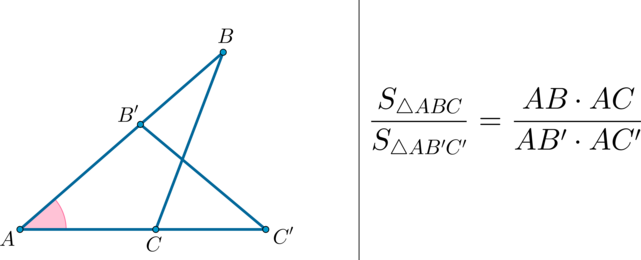
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Факт 7.
(bullet) Если прямые (p) и (q) параллельны, то
Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.
Найдите отношение площадей двух равносторонних треугольников если их периметры равны 9 см и 27?
Математика | 5 — 9 классы
Найдите отношение площадей двух равносторонних треугольников если их периметры равны 9 см и 27.
Равносторонние треугольники подобны, их периметры относятся друг к другу с коэффициентом подобия k = 9 / 27 = 1 / 3
Площади относятся друг к другу как квадрат коэффициента подобия :
Ответ : 1 / 9 (меньшая к большей, или 9 : 1, если большая к меньшей).
Периметр равностороннего треугольника равна 30 ?
Периметр равностороннего треугольника равна 30 .
Найдите его площадь , делённую на корень 3 .
Периметр равностороннего треугольника равна 21 ?
Периметр равностороннего треугольника равна 21 .
Из двух таких треугольников составили ромб, чему равен периметр ромба?
В равностороннем треугольнике ABC сторона равна 18см, а медиана 15?
В равностороннем треугольнике ABC сторона равна 18см, а медиана 15.
6см. Найди площадь и периметр треугольника ABD.
Сторона равностороннего треугольника равна а?
Сторона равностороннего треугольника равна а.
Найдите отношение медианы равностороннего треугольника к его высоте.
Помогите решить пожалуйста!
Найди периметр треугольника?
Найди периметр треугольника.
Составь из двух таких треугольников прямоугольник.
Найди его периметр и площадь.
Найди площадь треугольника.
Высота равностороннего треугольника равна 27 корней из 3?
Высота равностороннего треугольника равна 27 корней из 3.
Найдите его периметр.
Отношение площадей подобных треугольников равно 16 / 9?
Отношение площадей подобных треугольников равно 16 / 9.
Чему равно отношение периметров?
Отношение площадей подобных треугольников равно 16 / 9?
Отношение площадей подобных треугольников равно 16 / 9.
Чему равно отношение периметров?
Периметр равностороннего треугольника равен 21см?
Периметр равностороннего треугольника равен 21см.
Из двух таких треугольников составили ромб.
Найди его периметр.
Запиши решение задачи.
Периметр равностороннего треугольника равен 84 найдите его площадь деленную на корень из 3?
Периметр равностороннего треугольника равен 84 найдите его площадь деленную на корень из 3.
Если вам необходимо получить ответ на вопрос Найдите отношение площадей двух равносторонних треугольников если их периметры равны 9 см и 27?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
Наименьшее общее кратное 1. 3 ; 2. 4 ; 3. 2 ; 4. 5 ; 5. 3 ; 6. 2 ; 7. 2 ; 8. 2 ; 9. 3 ; 10. 3 ; 11. 3 ; 12. 7. 1)3 и 7 ; 3 и 6. 2)4 и 6 ; 4 и 8. 3)2 и 8 ; 2 и 10. 4)5 и 4 ; 5 и 7. 5)3 и 25 ; 3 и 30. 6)2и 3 ; 2 и 6. 5. 7)2 и 7 ; 2 и ..
http://shkolkovo.net/theory/119
http://matematika.my-dict.ru/q/7050869_najdite-otnosenie-plosadej-dvuh-ravnostoronnih-treugolnikov/
math-public:otnoshenie_ploshchadej_treugolnikov_s_ravnymi_ehlementami
Содержание
Отношение площадей треугольников с равными элементами
Теорема
-
Если высоты двух треугольников равны, то их площади относятся, как основания.
-
Если основания двух треугольников равны, то их площади относятся, как высоты, проведенные к этим основаниям.
-
Если угол одного треугольника равен углу другого треугольника, то их площади относятся, как произведения сторон, заключающих равные углы.
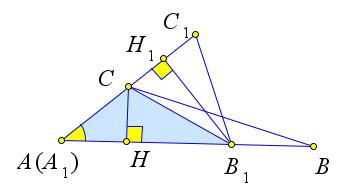
Докажем первый пункт теоремы.
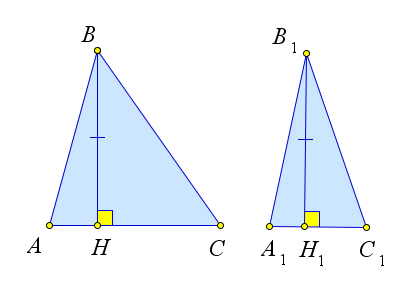
Рассмотрим треугольники $triangle ABC$ и $triangle A_1B_1C_1$ в которых высоты $BH$ и $B_1H_1$ равны.
Тогда $dfrac{S_{ABC}}{S_{A_1B_1C_1}}=dfrac{frac{1}{2}BHcdot
AC}{dfrac{1}{2}B_1H_1cdot A_1C_1}=dfrac{AC}{A_1C_1}$.
Докажем второй пункт теоремы.
Рассмотрим треугольники $triangle ABC$ и $triangle A_1B_1C_1$ в которых основания $AC$ и $A_1C_1$ равны.
Тогда $dfrac{S_{ABC}}{S_{A_1B_1C_1}}=dfrac{dfrac{1}{2}BHcdot
AC}{dfrac{1}{2}B_1H_1cdot A_1C_1}=dfrac{BH}{B_1H_1}$.
Докажем третий пункт теоремы.
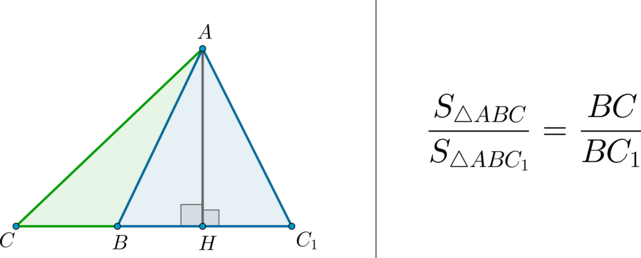
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$ в которых углы $A$ и $A_1$ равны.
Докажем, что их площади относятся как произведения сторон, заключающих эти углы.
Наложим треугольник $A_1B_1C_1$ на треугольник $ABC$ так, чтобы вершина $A_1$ совместилась с вершиной $A$, а стороны $A_1B_1$ и $A_1C_1$ наложились соответственно на лучи $AB$ и $AC$.
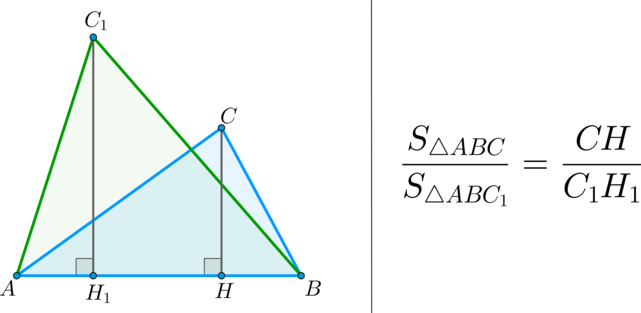
Треугольники $ABC$ и $AB_1C$ имеют общую высоту $CH$, поэтому
$dfrac{S_{ABC}}{S_{AB_1C}}=dfrac{AB}{AB_1}$.
Треугольники $AB_1C$ и $AB_1C_1$ имеют общую высоту $B_1H_1$, поэтому
$dfrac{S_{AB_1C}}{S_{AB_1C_1}}=dfrac{AC}{AC_1}$.
Перемножая полученные равенства, находим: $dfrac{S_{ABC}}{S_{A_1B_1C_1}}=dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1}$.
Свойство биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки,
пропорциональные двум другим его сторонам.
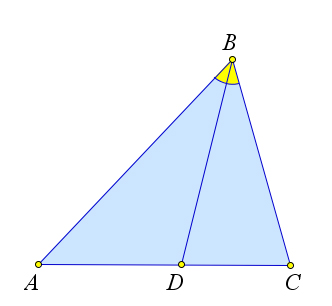
Доказательство
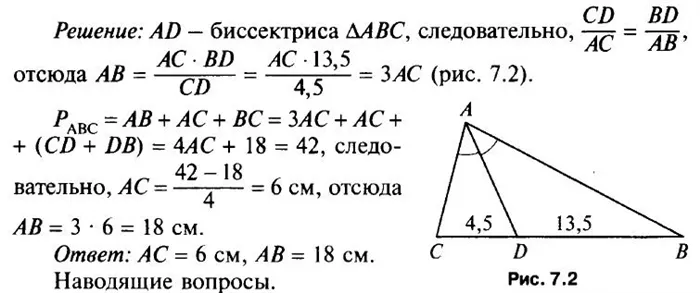
Рассмотрим треугольник $ABC$, в котором проведена биссектриса $BD$.
Докажем, что $dfrac{AD}{DC}=dfrac{AB}{BC}$.
Действительно, так как у треугольников $ABD$ и $BDC$ высота,
проведенная из вершины $B$, общая, то $S_{ABD}:S_{BDC}=AD:DC$.
Кроме того у этих треугольников есть равные углы, следовательно их площади
относятся, как произведения сторон: $S_{ABD}:S_{BDC}=dfrac{ABcdot
BD}{BDcdot BC}=dfrac{AB}{BC}$.
Сравнивая полученные равенства для отношения площадей, получаем: $dfrac{AD}{DC}=dfrac{AB}{BC}$.
Теорема об инцентре
-
Инцентр делит биссектрису $l_c$ в отношении $(a+b):c$
-
Все биссектрисы треугольника пересекаются в одной точке.
Доказательство
Докажем первый пункт теоремы
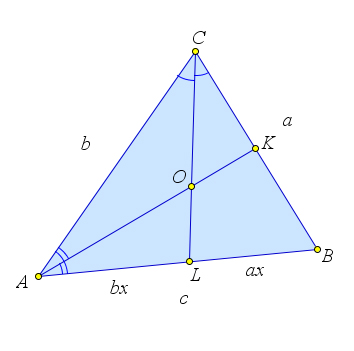
Рассмотрим треугольник $ABC$, в котором проведены биссектрисы $AK$ и $CL$.
Пусть $BC=a, AC=b, AB=c$.
Пусть $AK$ пересекает $CL$ в точке $O$.
По теореме $AL:LB=b:a$.
Тогда $AL=ccdotdfrac{b}{a+b}$
Кроме того в треугольнике $ACL$, $AO$ – биссектриса.
Тогда $CO:OL=b:AL=b:left(dfrac{bc}{a+b}right)=dfrac{a+b}{c}$.
Докажем второй пункт теоремы
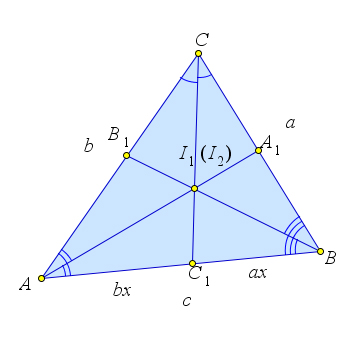
Рассмотрим треугольник $ABC$, в котором проведены биссектрисы $AA_1$, $BB_1$ и $CC_1$.
Пусть $BC=a, AC=b, AB=c$.
Пусть $AA_1cap CC_1=I_1$, $BB_1cap CC_1=I_2$.
Тогда по теореме $CI_1:I_1C_1=dfrac{a+b}{c}$ и $CI_2:I_2C_1=dfrac{a+b}{c}$.
А это означает, что точки $I_1$ и $I_2$ совпадают (так как они обе лежат на отрезке $CC_1$).
Таким образом все биссектрисы пересекаются в одной точке.
Доптеоремы
О шести треугольниках и медианах
О боковых треугольниках трапеции
О произведении площадей в четырехугольнике с диагоналями и следствие для трапеции
· Последнее изменение: 2019/11/18 18:08 —
labreslav
Факт 1.
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Факт 7.
(bullet) Если прямые (p) и (q) параллельны, то 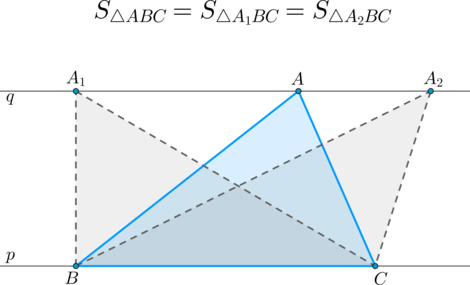
Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.
Если стороны одного треугольника равны 8 см, 10 см и 6 см, а стороны другого треугольника равны 12 см, 15 см и 9 см, найдите отношение площадей этих двух треугольников.
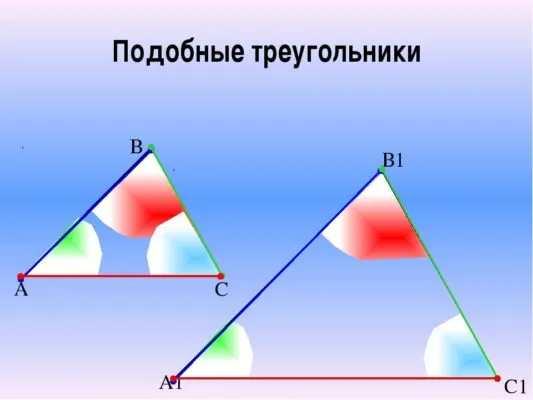
Подобные треугольники
Подобные треугольники — это треугольники, углы которых равны между собой, а одна сторона пропорциональна другой.
Коэффициентом подобия является k, который равен отношению сходных сторон подобных треугольников.
Стороны (или сопряженные стороны) подобных треугольников являются противоположными сторонами равных углов.
Признаки подобия треугольников
I Принцип подобия треугольников
Если два угла треугольника равны двум углам другого треугольника, то эти треугольники одинаковы.
II Принцип подобия треугольников
Если две стороны треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные в этих сторонах, равны, то эти треугольники одинаковы.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники одинаковы.
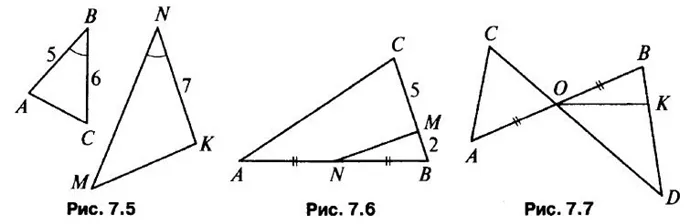
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
1. линия, параллельная одной стороне треугольника, пересекает подобный ей треугольник.
2. треугольники, образованные отрезком диагонали и основанием трапеции, подобны. Степень сходства
3. в прямоугольном треугольнике высота, проведенная из вершины прямого угла, делит треугольник на два треугольника, подобных исходному треугольнику.
Здесь вы найдете подборку задач, похожих на «Подобные треугольники».
Работа. Прямая, параллельная AB в BCABC, пересекает BC и AC в точках E и P. Найдем, что EC = 2, BE = 3 и EP = 3,2. Какова длина отрезка AB?
Подобие
Идентичные треугольники — это треугольники, у которых длины всех сторон пропорциональны друг другу, а углы равны. Отношение соответствующих сторон подобных треугольников всегда равно одному и тому же числу, которое называется коэффициентом подобия.
Рисунок 1. Подобные треугольники
Коэффициенты подобия часто используются для решения задач на подобие треугольников, так как коэффициенты можно найти из оснований после того, как неизвестные стороны представлены известными сторонами. Сходство представлено буквой k.
Не обязательно концентрироваться на треугольниках. Все фигуры в геометрии имеют сходство, хотя символ сходства появляется только на них. То же самое справедливо и для эквивалентности формы. Все фигуры в геометрии эквивалентны, так как эквивалентность является частным случаем сходства с коэффициентом k=1.
Рисунок 2.Похожие элементы
Признаки подобия
В настоящее время для любого треугольника существует три варианта подобия.
- По двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- По сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.
- По трем сторонам. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Чтобы доказать пропорциональность сторон, необходимо вычислить отношение длин каждой стороны. Тот же результат применим и к аналоговой стороне.
Аналоговые треугольники также имеют аналоговые треугольники и все характерные части, такие как высоты, медианы и биссектрисы. Коэффициенты сходства одинаковы для всех сегментов треугольника. Этот факт необходимо помнить. Это важно для решения многих задач и извлечения формул, поскольку существуют площади подобных треугольников.
Площади подобных треугольников
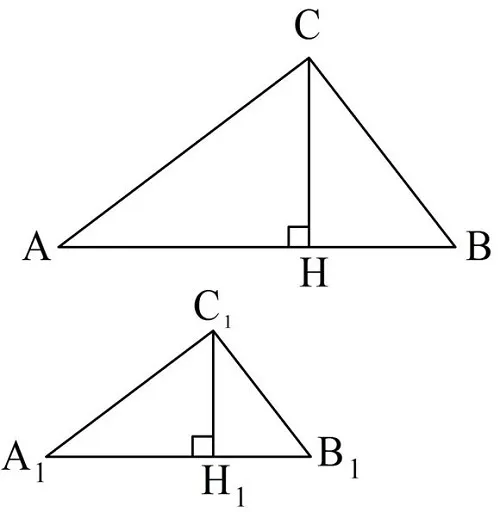
Рассмотрим два одинаковых треугольника ABC и $A_1B_1C_1$. Площадь треугольника равна половине произведения его основания и высоты.
$ S =.<1over<2>> h * AB $, тогда площадь второго треугольника:.
Деление одной поверхности на вторую поверхность дает следующее соотношение.
$> = over> $ Вспоминая, что отношение сторон подобных треугольников равно коэффициенту подобия, получаем.
$> = k * k = k ^ 2 $- т.е. области подобных треугольников взаимосвязаны в соотношении, равном коэффициенту подобия квадратов.
Проведите перпендикуляр к вертикальному прямоугольному треугольнику (рис. 166, а). Сделайте из него квадрат со сторонами квадрата. Итак: ^
Работа по теме урока
(Учитель делит класс на группы для решения творческой работы. По завершении задаются и обсуждаются решения).
Работа. Треугольники ABC и A1B1C1 подобны коэффициенту K. Найдите причину в их районе.
Заключение Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Закрепление изученного материала
- Работа в рабочих тетрадях. Решить задачу № 54. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
- Решить задачу № 545 (работа в парах). (После завершения работы заслушиваются и обсуждаются варианты решений.)
Вопрос нет. 545
- Чему равно отношение площадей подобных треугольников, если их сходственные стороны относятся как 6 : 5?
- Верно ли составлено уравнение исходя из условий задачи?
- Решить задачи № 547, 548 (работа в группах). (После завершения работы заслушиваются и обсуждаются варианты решений.)
Самостоятельная работа
I уровень сложности
II уровень сложности
III уровень сложности
Научитесь правильно писать задачи, делайте записи короткими и не тратьте время на то, чтобы написать все идеи и названия теорий.
Самый главный «секрет» подобия треугольников
Плита научила вас находить подобные треугольники, но как теперь использовать те, которые вы нашли?
А что бы вы хотели с ним сделать? Что же тогда …
Все элементы одного треугольника ровно в ዄ (⌘ displaystyle 2 ) (или во столько раз, во сколько получится) больше элементов других треугольников.
Не только стороны, но и высоты, дихотомии, интерстиции, зарегистрированные, граничные лучи цикла и т.д.
Есть важное исключение: площадь.
Открыть ответы…
Чтобы открыть все выпуски всех учебников, охваченных синим баннером (например, этот), зарегистрируйтесь следующим образом.
Чтобы управлять им, просто разделите длину сторон между ними. Разделите наибольшую сторону одного треугольника на другую и наименьшую сторону на наименьшую. Если результат одинаков для всех трех сторон, то треугольники подобны.
Второй и третий признаки подобия треугольников
Существуют еще два подобия треугольника, которые реже используются при решении задач. Идите прямо от первого участка.
Докажите второе сходство. Пусть DABC и DA1В1Больше.1, мы удовлетворяем соотношению:.
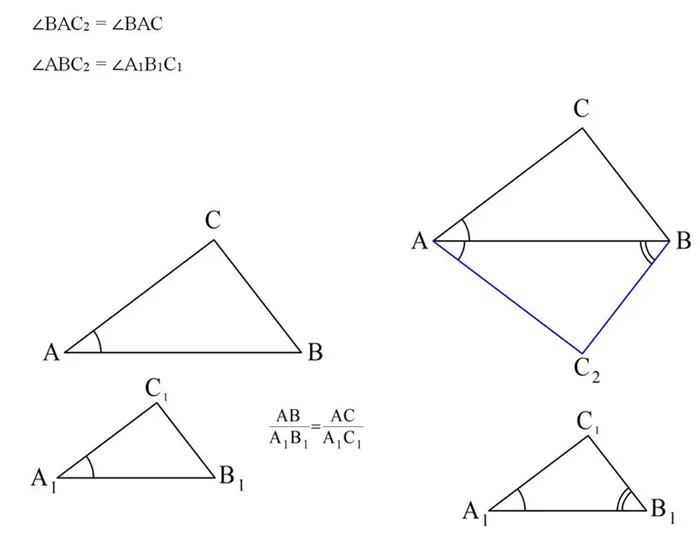
Докажите, что они похожи. Для этого мы построим еще один DABC2которая имеет общие аспекты с DABC.2 Выберите точку C так, чтобы условие было выполнено.
DM1В1Больше.1 Затем слегка постучите.2 Поскольку два угла одинаковы, они подобны. Поэтому необходимо применить следующие уравнения
Но потом ДАБК и ДАБК2 равны, так как углы, образованные двумя сторонами и двумя сторонами, одинаковы.
В результате, DB и DA1В1Больше.1 имеют два одинаковых угла, т.е. похожи друг на друга
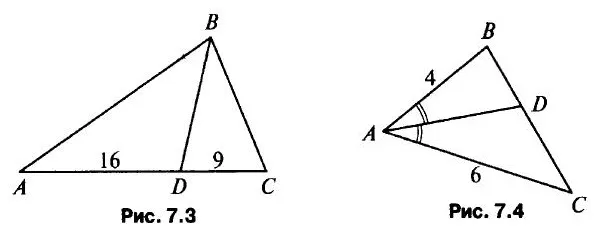
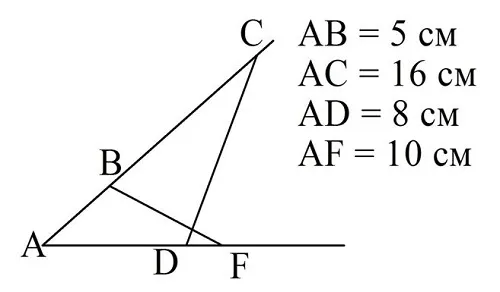
Выпуск. На стороне угла отмечены точки a и b, так что ab = 5 см и ag = 16 см. На другой стороне того же угла отмечены точки c и d, такие, что AD = 8 см и AF = 10 см. Похожи ли ΔACD и D AFB?
Рассмотренные треугольники имеют общий угол.
Отношения одинаковы, поэтому треугольники симметричны.
ПРИМЕЧАНИЯ. В этом случае важно понять, какую сторону нужно разделить. У DGD стороны AC и AD равны 16 и 8 см. У DAFB стороны AF и AB равны 10 и 5 см. Наибольшая сторона одного треугольника делится на наибольшую сторону другого треугольника, т.е. 16 x 10, или 8 на 8. Сходство и взятое число — это просто коэффициент сходства.
Рассмотрим третье свойство подобия треугольников.
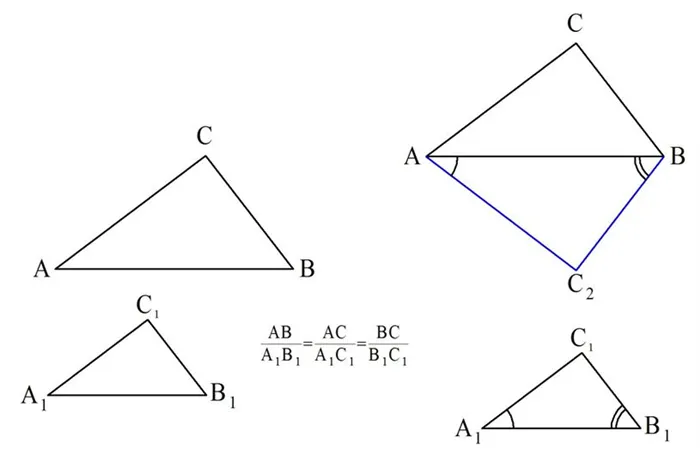
Давайте докажем это. Пусть DABC и DA1В1Больше.1 Это соизмеримо с их сторонами:.
Мы видим, что DABC2 И да1В1Больше.1 Они похожи, потому что два угла одинаковы. Тогда пропорции верны:.
Отношение площадей подобных треугольников
Если треугольники подобны, то их стороны зависят от коэффициента K. Здесь K — коэффициент. И как соотносятся между собой их высоты, промежуточные и другие характерные длины? Легко предположить, что они также зависят от коэффициента K.
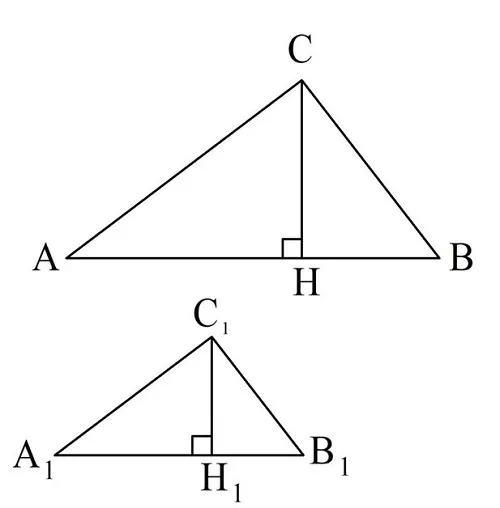
Докажем это на примере высоты. Предположим, что у нас есть аналогичные DABC и DA1В1Больше.1и их коэффициент сходства равен k.
ch и c, которые построены на этих высотах1н1:.
Аналогично, мы можем доказать, что длины и расщепления промежуточных продуктов отличаются по времени k.
В чем причина одинаковой площади треугольника? Получается, что дважды по k. Докажите это.
Пусть DABC и DA1В1Больше.1 аналогично коэффициенту сходства k. Снова постройте высоты Ch и Ch1:.
Запишите очевидное уравнение: .
В результате площади одного и того же треугольника могут отличаться на коэффициент k 2.
Задание. Площадь DABC равна 10, и мы знаем, что отрезок AB равен 5. Сторона DE, которая подобна AB, равна 15. чтобы вычислить площадь DEF, DEF DB подобна DAB.
Решение. Согласно описанию проблемы, мы находим сходство между DABC и DDEF следующим образом
Задание. Два подобных треугольника имеют площади 75 м 2 и 300 м 2. Одна сторона второго треугольника равна 9 м. Вычислите одинаковую сторону первого треугольника.
Решение. Если известны площади треугольников, то коэффициент подобия легко найти.
Если коэффициент подобия равен 2, то сторона первого треугольника меньше стороны второго.
Коэффициенты подобия часто используются для решения задач на подобие треугольников, так как коэффициенты можно найти из оснований после того, как неизвестные стороны представлены известными сторонами. Сходство представлено буквой k.
Как найти отношение площадей двух треугольников, если стороны одного равны 5 см, 8 см, 12 см, а стороны другого 15 см, 24 см, 36 см?
Как найти отношение двух треугольников, если одна сторона равна 5 см, 8 см или 12 см, а другая сторона равна 15 см, 24 см или 36 см.
Треугольники, приведенные в задаче, подобны. Это объясняется тем, что их стороны соизмеримы.
Два треугольника подобны, если три стороны одного треугольника подобны другой стороне.
Площадь подобных треугольников равна квадрату их подобия.
Площадь этих треугольников объясняется следующими причинами.
Найдите отношение двух треугольников, если одна сторона равна 5 см, 8 см или 12 см, а другая сторона равна 15 см, 24 см или 36 см.
Если стороны одного треугольника равны 8 см, 10 см и 6 см, а стороны другого треугольника равны 12 см, 15 см и 9 см, найдите отношение площадей этих двух треугольников.
Если стороны одного треугольника равны 12 см и 21 см 27 см, а другого треугольника — 4 см 7 см и 9 см, найдите причину возникновения двух треугольников.
На этой странице вы найдете ответ на вопрос, как найти отношение двух треугольников, если одна сторона равна 5 см, 8 см и 12 см, а другая 15 см, 24 см, 36 см и 36 см. Он относится к категории геометрии. Сложность вопроса соответствует базовым знаниям учащихся в классе5-9.Для получения дополнительной информации воспользуйтесь поисковой системой, чтобы найти другие вопросы, связанные с этим. Кроме того, нажмите на кнопку в верхней части страницы и задайте новый вопрос, используя ключевые слова, соответствующие критериям. Поговорите с посетителями вашей страницы и обсудите эту тему. Возможно, их ответы помогут вам найти информацию, которую вы ищете.
ДОКАЗАТЕЛЬСТВО: Предположим, что отрезки AC и BD пересекаются в точке o треугольника. Первое начало согласно треугольнику aob = sod (угол aob, угол SOD перпендикулярны, bo = od, ao = os, где o — середина ac и ua) треугольник abc = треугольник SOD (ac) является общим …
AC = 16 + 2 = 18 (см) BC = 18-8 = 10 (см) P = 16 + 18 + 10 = 44 (см) Ответ: 44 см.
Да, потому что это проекция и поэтому может иметь отображение.
AC = AD + DC = 6 + 8 = 14.Построим график CH, который является высотой ABC. Это также высота треугольника ABD. Sabc = 1/2 AC-BHBH = 2Sabc / AC = 2-42/14 = 6Sabd = 1/2 AB-BH = 1/2-6-6 = 18Sq.
Решение. Эта диаграмма показывает, что ∠BCA = CESCE и ∠A = ∠E = 90°. Это означает, что BCABC и CESCE похожи, потому что у них два одинаковых угла. Стороны AB и EC похожи, используйте их для нахождения коэффициентов подобия.
Применение площадей
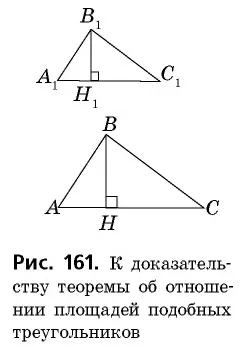
Теорема (Соотношение площадей подобных треугольников).
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Предположим, мы докажем, что с этим коэффициентом.
Проведем в данных треугольниках высоты
Прямоугольные треугольники Это означает, что
Средняя линия отсекает от данного треугольника треугольник с площадью 8
Давайте сделаем сторону, параллельную
Треугольники подобны по двум сторонам и углу между ними, причем Тогда по доказанной теореме откуда Ответ:
Метод площадей
Понятие площади и формула для ее вычисления также могут быть применены к задачам, в которых условия не относятся к площадям. Рассмотрим такой пример.
Стороны прямоугольника равны 16 см и 12 см. Высота прямоугольника, начерченного по самой длинной стороне, равна 3 см. Найдите высоту меньшего из них.
Предположим, что вам дан прямоугольник со сторонами, высоты которых нарисованы, а длины нужно найти (рис. 163).
Используйте формулу для площади прямоугольника
Итак.
Для решения этой задачи площадь прямоугольника вычислялась двумя разными способами. Поскольку площадь полигона определялась однозначно, независимо от метода расчета, полученное уравнение было уравнено, чтобы соотнести известные значения с требуемыми. Этот метод, использующий площадь в качестве вспомогательного размера, называется методом вспомогательной площади или просто методом площади.
Отметим, что для прямоугольного типа площади следует сделать важный вывод: в прямоугольниках высота, нарисованная на малой стороне, больше, а высота, нарисованная на большой стороне, меньше.
Метод сайта используется как для вычислительных задач, так и для доказательств утверждений.
Сумма расстояний от внутренних точек равностороннего треугольника до его сторон равна высоте треугольника, независимо от выбора точек. Доказательство.
Пусть точка находится на расстоянии одной стороны от этой точки до стороны треугольника (рис. 164).
Точка соединения равна сумме площадей треугольника и возвышения. У нас есть:.
Отсюда т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки
Другие доказательства теоремы Пифагора
Исторически появление и доказательство теоремы Пифагора связано с вычислением площадей. Таким образом, классическая формулировка этой теоремы относится не к квадратам сторон прямоугольного треугольника, а к площади соответствующей фигуры.
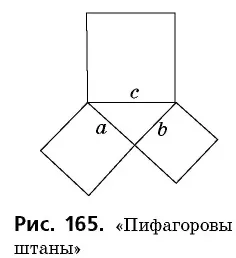
- площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рисунок 165, на котором наглядно представлена эта формулировка, стал отличительным символом геометрии и был назван школьниками прошлого века «пифагорейскими брюками».
Ученики на всю жизнь запомнили забавные стихи о пифагорейских брюках.
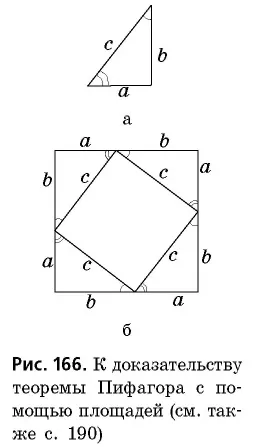
Используйте площадь для доказательства теоремы Пифагора.
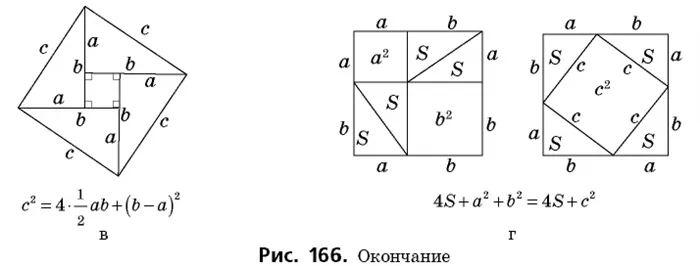
Проведите перпендикуляр к вертикальному прямоугольному треугольнику (рис. 166, а). Сделайте из него квадрат со сторонами квадрата. Итак: ^
т.е.
На рисунках 166, C и D показаны другие способы доказательства теоремы Пифагора с помощью площадей. В работе индийского математика XII века Бхаскари, один из них: «Смотрите!». сопровождается только словом «Смотри!». В целом, в настоящее время существует более 150 различных способов доказательства этой знаменитой теоремы. Однако каждый из вас может изобрести свой собственный метод.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей стороны
Сумма углов многоугольника Сумма углов выпуклости
Сумма внешних углов выпуклой фигуры
Внешние углы выпуклого многоугольника
Если все вершины лежат на окружности, многоугольник регистрируется как окружность.
Полигон описан как зарегистрированный.
Если все стороны принадлежат этому циклу, то многоугольник называется циклом периметра многоугольника.
Аксиомы площади
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата со стороной, равной единице длины, равна единице площади