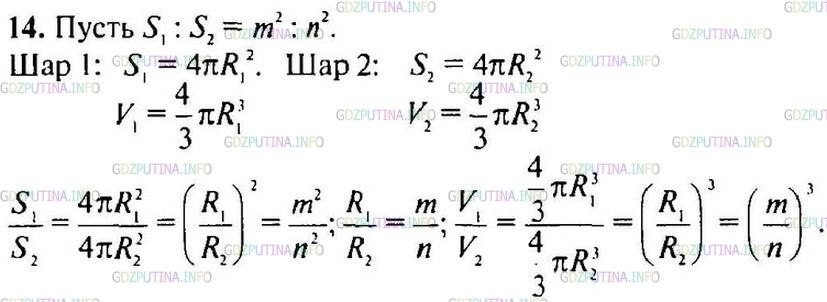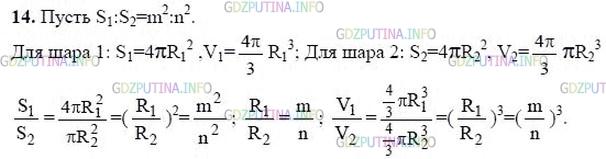Объёмы двух шаров относятся как 8 : 125. Найдите отношение площадей их поверхностей

Светило науки — 3713 ответов — 0 раз оказано помощи
Ответ:
4/25
Решение:
V1/V2=k³
k=³√(V1/V2)=³√(8/125)=2/5
S1/S2=k²
S1/S2=(2/5)²=4/25

Светило науки — 1606 ответов — 6543 помощи
Ответ:
Объяснение:
Два шара всегда подобны. Коэффициент подобия линейных величин равен отношению радиусов (диаметров, длин окружностей). Отношение площадей — квадрат коэффициента подобия. Отношение объемов — куб коэффициента подобия. Следовательно: отношение площадей поверхности шаров — (∛(V1/V2))²=(∛(8/125))²=(2/5)²=4/25.
Ответ:
Объяснение:
Объемы относятся как куб коэффициента подобия. Поэтому коэффициент подобия:
k =
Площади относятся как квадрат коэффициента подобия, то есть
Рисунок не нужен, но да ладно.
Приложения:
Площадь поверхности шара определяется по формуле
S = 4 * п * ρ^2.
Тогда для двух шаров радиусами r и R отношение площадей будет равно
S1 / S2 = (4 * п * r^2) / (4 * п * R^2) = (r / R) ^2.
По условию площади относятся как
S1 / S2 = 16 / 25,
тогда радиусы шаров относятся как
r / R = √ (16 / 25) = 4 / 5.
Объем шара определяется по формуле
V = 4/3 * п * ρ^3.
Тогда для двух шаров радиусами r и R отношение объемов будет равно
V1 / V2 = (4/3 * п * r^3) / (4/3 * п * R^3) = (r / R) ^3.
Зная отношение радиусов, получим:
V1 / V2 = (4 / 5) ^3 = 64 / 125.
Урок
Тема: Отношение площадей поверхностей и объемов подобных тел.
Цель урока: изучить понятия равновеликих и подобных тел, выучить значения отношений площадей поверхностей и объемов подобных тел.
Задачи урока: формировать навыков и умения применения формул вычисления объемов и площадей геометрических тел при решении задач.
Ход урока
1. Организационный момент
2. Актуализация опорных знаний
Фигура, все точки которой не находятся на одной плоскости, называется объёмной фигурой.
Ограниченная часть пространства называется геометрическим телом, а множество точек, ограничивающих его от окружающего пространства, называется поверхностью этого тела.
Шар — геометрическое тело, его поверхность — сфера.
Шар Сфера
Винтовая линия — объёмная фигура, но это не тело.
Пирамида — геометрическое тело, которое ограничено плоскими многоугольниками.

Пирамида Плоские многоугольники
Две фигуры (или тела) называются равными, если их можно совместить наложением.
Два тела подобны, если одно из них может быть получено из другого путём увеличения (или уменьшения) всех его линейных размеров в одном и том же отношении.
Пример 1: Автомобиль и его модель – подобные тела.
Пример 2. Два тела (фигуры) зеркально подобны, если одно из них подобно зеркальному отражению другого.
Пример 3: Картина и её фотонегатив зеркально подобны друг другу.
В подобных и зеркально подобных фигурах все соответственные углы (линейные и двугранные) равны.
Пример 4: Две правильные призмы или пирамиды с одинаковым числом граней подобны, если радиусы их оснований пропорциональны их высотам. Два круглых цилиндра или конуса подобны, если радиусы их оснований пропорциональны их высотам.
3. Изучение нового материала
Главная величина геометрических тел — это их объём.
Объём геометрического тела — это величина, которая описывает занимающую этим телом часть пространства.
ИЛИ Объем тела – это положительная величина той части пространства, которую занимает геометрическое тело.
Задача 1.
Три латунных куба 6 м, 8 м и 10 м переплавлены в один куб. Чему равно ребро этого куба.
Решение:
1. Найдем объем каждого куба:
V1= 63= 216 м3 V2= 83= 512 м3 V3= 103= 1000 м3
Отсюда следует, что общий объем равен:
Vобщ = V1+ V2+ V3= 216 + 512 + 1000 = 1728 м3
3. Сторону куба можно найти из формулы: V = a3,
Ответ: 12 м.
Объемы равных тел равны.
Если тело разбито на несколько тел, не имеющих общих внутренних точек, то его объем равен сумме объемов этих тел.
Из определения следует, что объём не зависит ни от местонахождения тела в пространстве, ни от того, как это тело делится на части.
Величину объёма вычисляют, основываясь на аксиомах:
1) равные тела имеют равные объёмы.
2) объём тела равен сумме объёмов его отдельных частей.
Чтобы объём можно было измерить, т. е. чтобы объём можно было бы выразить в виде числа, необходимо выбрать единицу измерения объёма.
Единица объёма — это объём такого куба, ребро которого равно одной единице длины.
Если ребро куба равно 1 см, то его объём обозначается кубическими сантиметрами — см3, если ребро куба равно1 м, то объём обозначается кубическими метрами — м3.
Тела с равными объёмами называются равновеликими.
Равные тела
Равные тела с объёмом 8 см3
Равновеликие тела
Равновеликие тела с объёмом 6 см3
Все равные тела равновелики, но не все равновеликие тела равны.
Отношение площадей поверхностей подобных тел
УТВЕРЖДЕНИЕ 1: Если два и более тел подобны, то площади всех соответствующих плоских и кривых поверхностей этих тел пропорциональны квадратам любых соответствующих отрезков.
Задача 2.
Даны два шара с радиусами 3 и 1. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение.
Радиус первого шара в 3 раза больше радиуса второго шара. Площадь поверхности шара выражается через его радиус формулой S = 4πr2, поэтому при увеличении радиуса втрое площадь увеличится в 32 = 9 раз.
Ответ: 9.
Самостоятельная работа
Задача 3.
Даны два шара с радиусами 14 и 2. Во сколько раз площадь поверхности большего шара больше площади поверхности другого?
Решение.
Площади поверхности шаров относятся как квадрат отношения их радиусов. Радиус большего шара в 7 раз больше радиуса меньшего, поэтому их площади относятся как 72= 49.
Ответ: 49.
Задача 4.
Даны два шара с радиусами 8 и 4. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение.
Найдём площадь поверхности первого шара: S1 = 4πr2 = 4π82 = 256π
Найдём площадь поверхности второго шара: S2 = 4πr2 = 4π42 = 64π
Найдём отношение площадей: S1/S2=256π/64π=4

Отношение объемов подобных тел
УТВЕРЖДЕНИЕ 2: Если два и более тел подобны, то их объёмы, а также объёмы любых их соответствующих частей, пропорциональны кубам любых соответствующих отрезков.
Вывод:
Отношение объемов подобных тел равно кубу коэффициента подобия.
ИЛИ
Объемы подобных тел пропорциональны кубам соответствующих линейных размеров.
Объём куба – это произведение трех его измерений.
Пример 5: На рисунке выше показаны два куба, сторона одного из которых в 3 раза больше стороны другого.
Объем тела с рисунка а) V=x*x*x=x3
Объем тела с рисунка б) V=3x*3x*3x=27x3
Следовательно, тело на рис. б) имеет объем 33, т.е. его объем в 27 раз больше объема тела на рис. а).
Задача 5. Чашка диаметром 8 см и высотой 10 см вмещает
0,5 литра воды. Каких размеров должна быть подобная чашка, вмещающая 4 литра воды ?
Решение:
Чашки – подобные цилиндры, значит отношение их
объёмов равно отношению кубов соответствующих отрезков
(в нашем случае – высот и диаметров чашек).
Следовательно, высота h новой чашки находится из отношения:
(h/10 )3= 4/0,5; то есть h3 = 8*103, откуда h = 20 см;
аналогично, для диаметра d получим:
(d/8)3=4/0,5 , то есть d3= 8*83, откуда d = 16 см.
Ответ: h = 20 см; d = 16 см.
Задача 6.
Масса автомобиля 1050 кг. Изготовлена модель автомобиля в масштабе 1:60. Определить массу модели автомобиля, если она сделана из того же материала, что и сам автомобиль.
Решение:
(Объем модели)/(объем автомобиля)=(1/60)3, поскольку объемы подобных тел пропорциональны кубам соостветствующих линейных размеров.
Масса =плотность*объем, а так как автомобиль и модель сделаны из одного материала, значит:
(Масса модели)/(Масса автомобиля)=(1/60)3
Следовательно,
Масса модели = (Масса автомашины) *(1/60)3=(1050)/(603)=
0,0049 кг=4,9 г.
Ответ: 4,9 г.
Задача 7.
Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
Решение.
Масса шара прямо пропорциональна его объёму. Объёмы шаров относятся как кубы их радиусов:
Следовательно, масса второго, меньшего шара равна 162*8/27=48 грамм.
Ответ:48.
Задача 8
Даны два шара с радиусами 8 и 2. Во сколько раз объём большего шара больше объёма меньшего?
Решение.
Объёмы шаров относятся как кубы отношений их радиусов. Радиус большего шара в 4 раза больше радиуса меньшего, поэтому их объёмы относятся как 43= 64.
Приведём другое решение.
Найдём отношение объёмов шаров:
Ответ: 64.
4. Домашнее задание
1. Выучить теоретический материал урока
2. Решить задачи
Задача 1.
Даны два шара с радиусами 5 и 1. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Задача 2.
Даны два шара с радиусами 12 и 4. Во сколько раз объём большего шара больше объёма меньшего?
Источники:
https://www.yaklass.ru/p/geometria/10-klass/osnovnye-poniatiia-stereometrii-10438/aksiomy-stereometrii-i-ikh-prosteishie-sledstviia-9252/re-325b23ad-df13-4cb3-ac0f-397dc7ba8da4
https://www.yaklass.ru/p/geometria/10-klass/osnovnye-poniatiia-stereometrii-10438/aksiomy-stereometrii-i-ikh-prosteishie-sledstviia-9252/re-325b23ad-df13-4cb3-ac0f-397dc7ba8da4
https://mathb-ege.sdamgia.ru/problem?id=506288
ГДЗ (готовое домашние задание из решебника) на Вопрос №14, Глава 7 по учебнику Геометрия. 10-11 классы: учебник для общеобразовательных учреждений : базовый и профильный уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. — 22-е изд. — Просвещение, 2013-2019г
Условие
В каком отношении находятся объемы двух шаров, если площади их поверхностей относятся как m2:n2?
Решение 1
Решение 2
Другие задачи из этого учебника
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено