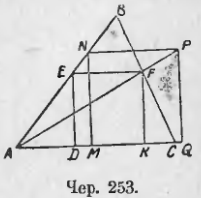Как найти отношение разных прямоугольников

Как найти отношение сторон прямоугольника? Помоги себе сам [5.5K] 4 года назад  Эта задачка для семиклассника. Но мы ведь с Вами учились дольше! Задачу решить просто даже для семиклассника. Сначала нужно произвести анализ условия и определить алгоритм достижения цели. Нужно найти соотношение сторон. Но соотношение должно быть выражено в числовых величинах. Для этого нужно узнать размеры сторон АВ и ВС. Известно количество равных прямоугольников, из которых состоит прямоугольник ABCD. Известно, что в прямоугольнике противоположные стороны равны между собой. Еще у нас есть число 7, которое будет частью ответа. Думаю, что решение понятно. Успехов! Кстати, задача решается, как говорят, в уме, числового ответа не даю, потому что нужно понять и получить знания для решения подобных задач. в избранное ссылка отблагодарить Вл50 [179K] Ответ выдали, но на чертеже нет обозначений сторон малых прямоугольников. Поэтому обойдемся без иксов и игреков. ВС = AD 1. Находим значение АВ, AB = BC/4 + BC/3. 2. Приведем выражение к общему знаменателю, который равен 12. 12AB = 3BC + 4BC. 12AB = 7BC. 3. Теперь математика. АВ : ВС = 7 : 12.  —  4 года назад  Гэнда­льф [50.5K] 4 года назад  Обозначим короткую сторону маленького прямоугольника «х», а длинную его сторону «у». Тогда АВ = х + у, ВС = 4х, а АД = 3у. Но так как ВС=АД, то 4х = 3у. Отсюда находим х = 3у/4. Подставим этот икс в полученное выше уравнение АВ = х + у, получим АВ = 3у/4 + у = 7у/4. Теперь находим соотношение искомое АВ/ВС. АВ = 7у/4, ВС = 3у. Поэтому соотношение будет АВ/ВС = 7у/4 / 3у. Делим одну дробь на другую, сокращаем игреки и получаем, что соотношение равно 7/12. комментировать в избранное ссылка отблагодарить Евген­ий трохо­в [56.5K] 4 года назад  Рассмотрим стороны ВС и АД .Так вот,если принять длинную сторону маленького прямоугольника за 1, то другая меньшая сторона будет равна 3/4.Теперь найдём соотношение АВ/ВС=(1+3/4)/(4*(3/­4)=7/12.Можно и по другому.У нас ВС=АД.Тогда АВ/ВС=АВ/АД=(1+(3/4)­)/3=7/12.Ответ-7/12 комментировать в избранное ссылка отблагодарить габба­с [215K] 4 года назад  Обозначим стороны маленького прямоугольника через х и у. Тогда АВ = х+у, ВС = 4*у. По рисунку видно, что 4*у = 3*х, то есть х = (4*у)/3. Получим АВ = (4*у)/3 +у = (7*у)/3. Значит искомое отношение АВ:ВС = (7*у)/3 : 4*у = 7/12. Ответ: 7:12. в избранное ссылка отблагодарить Вл50 [179K] Нужно решить без X и Y.  —  4 года назад  SIlm [8.4K] В седьмом классе не знают решение задачи подстановкой неизвестного?  —  4 года назад  Видно, что соотношение стороне маленьких прямоугольников составляет 3/4, а тогда соотношение сторон большого прямоугольника составит (3+4)/(3+3+3+3), или 7/12 комментировать в избранное ссылка отблагодарить Знаете ответ?

Rectangles have four sides, and generally the adjacent sides are not equal. Knowing the measurements of the two sides allows you to create a ratio of the rectangle. This tells you how much bigger one side is compared to the other side. This is used in basic geometry and helps students understand properties of a rectangle. If you know the ratio of a rectangle and know the measurement of one side, you can calculate the adjacent side.

Measure your rectangle’s sides. For example, assume your rectangle has a side of 8 inches and another of 4 inches.

Set up a ratio where your large side is on top of the fraction and the smaller side is on the bottom of the fraction. In the example, 8 inches / 4 inches.

Divide the ratio, then set the bottom number to one. In the example, 8 divided by 4 equals 2. So your ratio is 2 to 1.

Tips

• Rectangles with the same length-to-width ratios are considered similar.

Прямоугольники имеют четыре стороны, и, как правило, смежные стороны не равны. Знание измерений двух сторон позволяет создать соотношение прямоугольника. Это говорит вам, насколько больше одна сторона по сравнению с другой стороной. Это используется в базовой геометрии и помогает студентам понять свойства прямоугольника. Если вы знаете соотношение прямоугольников и знаете размеры одной стороны, вы можете рассчитать соседнюю сторону.

Измерьте стороны вашего прямоугольника. Например, предположим, что у вашего прямоугольника есть сторона 8 дюймов, а другая — 4 дюйма.

Установите соотношение, где ваша большая сторона находится сверху фракции, а меньшая — снизу фракции. В примере 8 дюймов / 4 дюйма.

Разделите соотношение, затем установите нижнее число на единицу. В этом примере 8, деленное на 4, равно 2. Таким образом, ваше соотношение составляет 2 к 1.

подсказки

• Прямоугольники с одинаковым отношением длины к ширине считаются одинаковыми.

Как найти отношение периметров четырехугольников

Изучение зависимостей площадей и периметров в четырехугольниках

Автор работы награжден дипломом победителя III степени

С понятием периметр и площадь я познакомилась в 3 классе. Э ти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.

Актуальность темы . Понятия «площади» и «периметра» необходимы человеку в окружающей жизни постоянно, например – сделать ремонт в доме или красиво оформить клумбу на даче. И то и другое понятие связывают стороны многоугольников. Знание зависимостей между этими величинами очень важно для современного человека.

Цель проекта: установить некоторые зависимости между площадью и периметром, увидеть их применение в практических ситуациях.

Задачи:повторить понятия по теме исследования, а именно: «площадь фигуры» и «периметр фигуры»; провести необходимые исследования и опыты; сделать выводы о зависимости площадей и периметров ; рассмотреть практическое применение полученных результатов.

Определение предмета исследования. Что нужно выяснить:

Как связаны периметры и площади прямоугольников?

Зависит ли площадь прямоугольника от его периметра?

Какой прямоугольник имеет наибольшую площадь при заданном периметре?

Если известен периметр прямоугольника, то нельзя ли однозначно установить его площадь?

Что можно сказать о зависимости площади квадрата от его периметра?

Проблема. Никаких зависимостей связывающих площади и периметры фигур мы пока не изучили.

Вот, самый простой пример, который задает проблему: «Есть два участка земли 80 м на 100 м и 50 м на 160 м. Вроде, площадь одинаковая – 8000 м 2 , а первый участок выгоднее купить, чем второй, забор то на 60 м короче строить». С точки зрения математики, все ясно, а вот логически – странно, периметр это замкнутая воображаемая нить, и то, что внутри нее не должно меняться, как ее не крути. Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?

Гипотеза. Предполагаем, что некоторые зависимости существуют. С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника. Можно даже предположить, что если площадь больше, то периметр больше. Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?

Периметр – величина, равная сумме длин всех сторон многоугольника.

Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.

Свойства площадей нам тоже известны:

Равные фигуры имеют равные площади.

Площадь всей фигуры равна сумме площадей ее частей.

За единицу площади принимают площадь квадрата, сторона которого равна единичному отрезку.

Исследования начнем с простой и хорошо знакомой нам фигуры – прямоугольника.

Заполним таблицу, считая площадь одной клеточки равной 1 см 2

Как найти отношение периметров четырехугольников

Периметры двух подобных многоугольников относятся как 3 : 5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.

Отношение площадей подобных многоугольников равно квадрату отношения их периметров. Пусть периметр и площадь меньшего многоугольника соответственно равны P₁ и S₁, периметр и площадь большего многоугольника соответственно равны P₂ и S₂. Поэтому

Математика

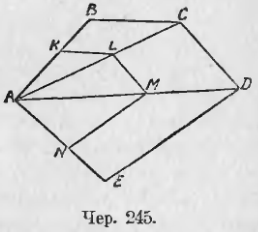
252. Понятие о подобии треугольников распространяется и на многоугольники. Пусть дан многоугольник ABCDE (чер. 245); выполним построение аналогичное п. 206. Построим диагонали AC и AD и, выбрав какую-либо точку K на стороне AB между точками A и B или вне отрезка AB, построим KL || BC до пересечения с диагональю AC, затем LM || CD до пересечения с AD и, наконец, MN || DE до пересечения с AE. Тогда получится многоугольник AKLMN, который связан с ABCD следующими зависимостями:

1) Углы одного многоугольника равны попарно углам другого: угол A у них общий, ∠K = ∠B (как соответственные), ∠KLM = ∠BCD, ибо ∠KLA = ∠BCA и ∠ALM = ∠ACD и т. д.

2) Сходственные стороны этих многоугольников пропорциональны, т. е. отношение одной пары сходственных сторон равно отношению другой пары, равно отношению третьей пары и т. д.

«Сходственные» стороны здесь надо понимать несколько иначе, чем для треугольников: здесь считаем сходственными сторонами те, которые заключены между равными углами, например, BC и KL.

Справедливость указанной пропорциональности видна следующим образом:

∆ABC, следовательно, AK/AB = KL/BC = AL/AC
∆ALM

∆ACD, следовательно, AL/AC = LM/CD = AM/AD
∆AMN

∆ADE, следовательно, AM/AD = MN/DE = AN/AE

Мы видим, что среди первых трех равных отношений и среди вторых трех равных отношений имеется одно одинаковое AL/AC; также и последние три отношения связываются с предыдущими отношением AM/AD. Поэтому, пропуская отношения диагоналей, получим:

AK/AB = KL/BC = LM/CD = MN/DE = AN/AE

Все это остается, как легко видеть, справедливым и для многоугольника с большим, чем у нас, числом сторон.

Если мы многоугольник AKLMN перенесем в другое место плоскости, то найденные выше 2 соотношения этого многоугольника с ABCDE останутся в силе; такие многоугольники называются подобными. Итак, два многоугольника называются подобными, если углы одного равны попарно углам другого и если сходственные стороны их пропорциональны .

Мы, следовательно, умеем строить многоугольник, подобный данному. Мы построили AKLMN

Мы видим еще, что в многоугольниках ABCDE и AKLMN построены диагонали из их соответственных вершин,причем получилось два ряда подобных треугольников: ∆AKL

∆ADE — треугольники эти одинаково расположены в обоих многоугольниках.

Возникает вопрос, останется ли в силе последнее свойство, если мы построим многоугольник, подобный данному, каким-либо еще способом, не тем, которым мы пользовались здесь.

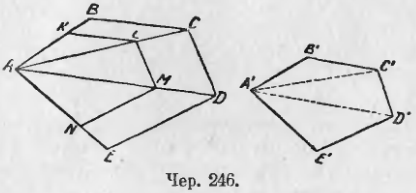
253. Пусть как-либо построен многоугольник A’B’C’D’E’ подобный многоугольнику ABCDE (чер. 246), т. е. так, что

∠A’ = ∠A, ∠B’ = ∠B, ∠C’ = ∠C, ∠D’ = ∠D, ∠E’ = ∠E (1)

A’B’/AB = B’C’/BC = C’D’/CD = D’E’/DE = E’A’/EA (2)

Вопрос конца предыдущего п. равносилен другому: можно ли привести эти два многоугольника в положение, чтобы, например, точка A’ совпала с A, а остальные вершины были бы расположены попарно на прямых, идущих из этой общей точки, и чтобы сходственные стороны их или были параллельны, или сторона одного многоугольника расположилась бы на стороне другого.

Решим этот вопрос. Для этого отложим на стороне AB от точки A отрезок AK = A’B’ и, пользуясь предыдущим п., построим многоугольник AKLMN

Остается выяснить, может ли многоугольник A’B’C’D’E’ совпасть при наложении с AKLMN.

Мы имеем: AK/AB = KL/BC = LM/CD = MN/DE = NA/EA.

Сравнивая эти равенства с равенствами (2) и принимая во внимание, что AK = A’B’, легко получаем KL = B’C’, LM = C’D’ и т. д., т. е. все стороны многоугольников A’B’C’D’E’ и AKLMN попарно равны. Наложим многоугольник A’B’C’D’E’ на AKLMN так, чтобы A’ попала в A и сторона A’B’ совпала бы с AK (мы ведь строили AK = A’B’); тогда, в силу равенства углов B’ и K, сторона B’C’ пойдет по KL, в силу равенства сторон KL и B’C’, точка C’ попадет в L и т. д.

Итак, A’B’C’D’E’ совпадает с AKLMN, а следовательно, если построим диагонали A’C’ и A’D’, получим ряд треугольников, подобных и одинаково расположенных с ∆ABC, ∆ACD и т. д.

Поэтому заключаем: Если построить в подобных многоугольниках диагонали из соответственных вершин, то получим 2 ряда подобных и одинаково расположенных треугольников.

Легко увидать справедливость и обратного заключения: если, ∆A’B’C’

∆ADE, то многоугольник A’B’C’D’E’

многоугольнику ABCDE. Тогда ∆A’B’C’ = ∆AKL, ∆A’C’D’ = ∆ALM и ∆A’D’E’ = ∆AMN, откуда следует равенство многоугольников A’B’C’D’E’ и AKLMN и, следовательно, подобие A’B’C’D’E’ и ABCDE.

254. То положение (две соответственных вершины сливаются в одной точке, остальные вершины попарно лежат на прямых, проходящих чрез эту точку, а сходственные стороны параллельны), в которое нам удалось привести два подобных многоугольника, является частным случаем другого более общего положения двух подобных многоугольников.

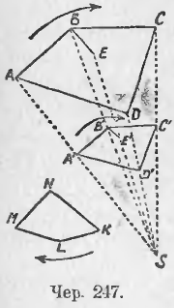
Пусть имеем KLMN

ABCD (чер. 247). Возьмем какую-либо точку S и соединим ее со всеми вершинами A, B, C и D первого многоугольника. Постараемся построить многоугольник, равный многоугольнику KLMN, так, чтобы его вершины лежали на прямых SA, SB, SC и SD и стороны были бы параллельны сторонам многоугольника ABCD.

Для этого отложим на стороне AB отрезок AP = KL (полагаем, что KL и AB сходственные стороны) и построим PB’ || AS (на чертеже точка P и прямая PB’ не даны). Чрез точку B’, где SB пересекается с PB’, построим B’A’ || AB. Тогда A’B’ = AP = KL, затем построим B’C’ || BC, чрез точку C’, где B’C’ пересекается с SC, проведем C’D’ || CD и точку D’, где C’D’ пересекается с SD, соединим с A’. Получим многоугольник A’B’C’D’, который, как это сейчас увидим, подобен многоугольнику ABCD.

Так как A’B’ || AB, то ∆SA’B’

SA’/SA = A’B’/AB = SB’/SB (1)

Так как B’C’ || BC, то ∆SB’C’

SB’/SB = B’C’/BC = SC’/SC (2)

Так как C’D’ || CD, то ∆SC’D’

SC’/SC = C’D’/CD = SD’/SD (3)

Отсюда можно вывести, что SA’/SA = SD’/SD, а следовательно ∆SA’D’

∆SAD, так как две стороны одного пропорциональны двум сторонам другого и углы между ними равны (∠S общий), — A’D’ || AD и

SD’/SD = D’A’/DA = SA’/SA (4)

Из равенств отношений (1), (2), (3) и (4) легко получаем:

A’B’/AB = B’C’/BC = C’D’/CD = D’A’/DA (5)

Кроме того, ∠A’ = ∠A, ∠B’ = ∠B и т. д., как углы с параллельными сторонами. Следовательно, A’B’C’D’

Далее легко увидать, что KLMN = A’B’C’D’. В самом деле, ∠K = ∠A, но ∠A = ∠A’, следовательно, ∠K = ∠A’; также ∠L = ∠B’ и т. д. — углы у наших многоугольников равны. Креме того, из подобия KLMN

KL/AB = LM/BC = MN/CD = NK/DA.

Сравнивая эти равные отношения с равенствами (5) и имея в виду, что A’B’ = KL, находим: B’C’ = LM, C’D’ = MN, D’A’ = NK. Теперь легко, как это делали выше, увидать, что KLMN при наложении совместится с A’B’C’D’. Следовательно, нам удалось поместить данные подобные многоугольники в такое положение, что их вершины расположены попарно на прямых, проходящих чрез точку S и их сходственные стороны параллельны, к чему мы и стремились.

Заметим еще, что соответственные вершины в наших многоугольниках следуют друг за другом в одном направлении (см. стрелки около многоугольников ABCD, KLMN и A’B’C’D’) — по часовой стрелке.

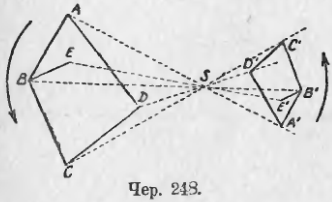
Если бы вершины одного многоугольника, соответствующие последовательным вершинам другого, шли друг за другом в направлении, обратном тому, как они расположены в другом, то удалось бы поместить наши многоугольники так, чтобы соответствующие вершины располагались по разные стороны от точки S (см. чер. 248).

Точка S, где сходятся прямые, соединяющие пары соответственных вершин многоугольников, называется центром подобия; в первом случае (чер. 247), когда обе соответственные вершины (например, A и A’) расположены в одной стороне от S, центр подобия называется внешним , а во втором (чер. 248), когда соответствующие вершины расположены по разные стороны точки S, центр подобия называется внутренним . Если подобные многоугольники расположены так, что они имеют центр подобия, то говорят, что они подобно расположены .

255. Если нам дан многоугольник ABCD (чер. 247 или 248), — будем данный многоугольник называть оригиналом , — мы можем, выбрав произвольную точку S, получать его изображения, подобные ему в каком угодно масштабе , — этим именем называют отношение какого-либо отрезка изображения к соответствующему отрезку в оригинале (в данном многоугольнике). Это отношение называют еще коэффициентом подобия — обозначим его через k. Пока еще для нас коэффициентом подобия является отношение стороны изображения к стороне оригинала, т. е.

A’B/AB = B’C/BC = … = k.

В дальнейшем мы распространим это понятие на отношение всяких двух отрезков изображения и оригинала, сходственных между собою.

Из равенства (1), (2), (3) и (4) предыдущего п., имеем:

SA’/SA = SB’/SB = SC’/SC = SD’/SD = A’B’/AB = k,

т. е. отношение расстояний от центра подобия соответственных вершин изображения и оригинала = коэффициенту подобия.

Под именем фигура (плоская) мы понимаем совокупность точек и линий плоскостей. Многоугольники ABCD — есть фигура. Присоединим еще одну точку (выбранную по произволу) E — получим новую фигуру состоящую из многоугольника ABCD и точки E, — найдем изображение точки E. Для этого построим прямую SE и на ней отложим отрезок SE так, чтобы SE’/SE = k (такой отрезок легко построить, пользуясь п. 214); этот отрезок мы можем отложить по направлению SE (чер. 247); или в обратном направлении (чер. 248). Полученная точка E’ и есть изображение точки E — другими словами точки E’ и E суть соответственные точки в наших двух подобных и подобно расположенных фигурах.

Соединив точку E, например, с B и точку E’ с B’ (B и B’ суть тоже соответственные точки), получим два соответствующих друг другу отрезка BE и B’E’.

Легко увидать, что ∆SBE

∆SB’E’ (так как ∠BSE = ∠B’SE и стороны, составляющие эти углы, пропорциональны: SB’/SB = k и SE’/SE = k, — следовательно, SB’/SB = SE’/SE), отсюда вытекает:

1) B’E’ || BE и 2) B’E’/BE = SB’/SB = k

т. е. соответствующие друг другу отрезки в изображении и оригинале 1) параллельны между собою и 2) их отношение равно коэффициенту подобия .

Отсюда вытекает возможность следующего построения для нахождения точки, соответствующей данной в оригинале точке, если уже имеем одну пару соответствующих точек и известен центр подобия: пусть имеем пару соответствующих точек B и B’ и требуется найти точку, соответствующую точке E, — строим прямые SE и BE и чрез B’ строим прямую, параллельную BE, ее точка пересечения E’ с SE и даст искомую точку.

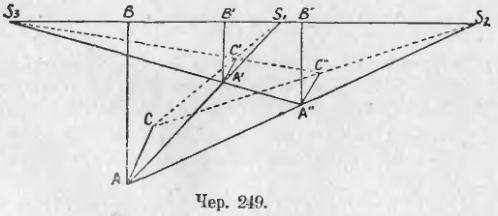
256. Построим для какой-либо фигуры, одна точка которой есть A (чер. 249), ее изображения, принимая две произвольных точки S₁ и S₂ за внешние центры подобия и числа k₁ и k₂ за коэффициенты подобия. Пусть в первом изображении точке A соответствует точка A’ и во втором изображении этой же точке соответствует точка A».

Присоединим еще к данной фигуре какую-либо точку B, лежащую на прямой S₁S₂; тогда этой точке B соответствуют в первом изображении точка B’ и во втором точка B», причем точки B’ и B» должны лежать на той же прямой S₁S₂ и прямые AB, A’B’ и A»B» должны быть параллельны и одинаково направлены.

Соединим точки A’ и A», найдем точку пересечения S₃ прямых A»A’ и S₂S₁. Тогда из подобия треугольников S₃A’B’ и S₂A»B» находим:

Соединив точки A’ и A», найдем точку пересечения S₃ прямых A»A’ и S₂S₁. Тогда из подобия треугольников S₃A’B’ и S₂A»B» находим:

т. е. точка S₂ должна делить отрезок B’B» внешним образом в отношении, равном данному числу k₁/k₂. Мы знаем (п. 217), что существует только одна точка, которая делит данный отрезок B’B» в данном отношении внешним образом. Если мы возьмем какую-либо еще точку C данной фигуры и построим ее изображения C’ и C», то, соединив точки C’ и C» и взяв точку пересечения, назовем ее опять S₃, прямой C’C» с прямой S₁S₂, получим, что ∆S₃B’C’

∆S₃B»C» (B»C» || BC и B’C’ || BC, следовательно, B»C» || B’C’), откуда опять найдем, что S₃B’/S₃B» = k₁/k₂, т. е. новая точка S₃ совпадает с прежнею. Следовательно, S₃ есть центр подобия фигур (A’B’C’. ) и (A»B»C». ) и притом внешний, ибо направления, в котором следуют друг за другом соответствующие точки в обеих фигурах, одинаковы. Из этого заключаем, что фигуры (A’B’C’. ) и (A»B»C». ) также имеют внешний центр подобия и он расположен на одной прямой с центрами S₁ и S₂.

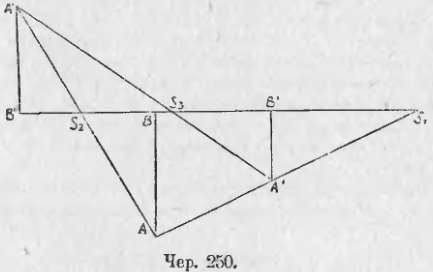
Если одни из центров подобия S1 взять внешний, а другой S2 внутренний (чер. 250), то направления соответствующих отрезков таковы: A’B’ одинаково с направлением AB, но A»B» обратно направлению AB, — следовательно, направление A»B» обратно A’B’ и S3 является внутренним центром подобия фигур (A’B’. ) и (A»B». ).

Если взять оба центра подобия внутренними (например, S₂ и S₃ на чер. 250), то легко увидать, что третий центр подобия окажется внешним. Итак, вообще:

Если три фигуры попарно подобно расположены, то три центра подобия расположены на одной прямой, причем или все три они внешние, или два из них внутренних, а один внешний.

257. Отношение периметров и площадей подобных многоугольников.
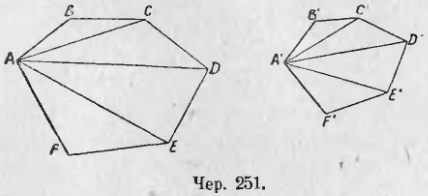
Пусть имеем два подобных многоугольника ABCDEF и A’B’C’D’E’F’ (чер. 251). Назовем коэффициент подобия чрез k.

A’B’/AB = k, B’C’/BC = k и т. д.,

A’B’ = k · AB, B’C’ = k · BC, C’D’ = k · CD, …

Сложив эти равенства по частям и вынеся множитель k во второй части за скобку, получим:

A’B’ + B’C’ + C’D’ + … = k(AB + BC + CD + …),

(A’B’ + B’C’ + C’D’ …) / (AB + BC + CD + …) = k = A’B’/AB,

т. е. отношение периметров подобных треугольников равно отношению сходственных сторон (или равно коэффициенту подобия).

Выберем две соответственных вершины, напр., A и A’, и построим проходящие чрез них диагонали. Тогда мы знаем: 1) (из п. 253) ∆ABC

∆A’C’D’ и т. д. 2) (из п. 212). Отношение площадей подобных треугольников равно квадрату отношения их сходственных сторон, следовательно,

пл. ∆A’B’C’ / пл. ∆ABC = (A’B’/AB) 2 = k 2 ; пл. ∆A’C’D’ / пл. ∆ACD = (C’D’/CD) 2 = k 2 и т. д.,

пл. ∆A’B’C’ = k 2 · пл. ∆ABC; пл. ∆A’C’D’ = k 2 · пл. ∆ACD;
пл. ∆A’D’E’ = k 2 · пл. ∆ADE .

Сложив эти равенства по частям и вынеся общего множителя k 2 во второй части за скобку получим:

пл. ∆A’B’C’ + пл. ∆A’C’D’ + ∆A’D’E’ + … = k 2 (пл. ∆ABC + пл. ∆ACD + пл. ∆ADE + …),

пл. A’B’C’D’E’F’ / пл. ABCDEF = k 2 = (A’B’/AB) 2 ,

т. е. отношение площадей подобных многоугольников равно квадрату отношения их сходственных сторон (или равно квадрату коэффициента подобия).

258. Два правильных одноименных многоугольника всегда подобны. В самом деле, углы у одноименных многоугольников одинаковы (п. 248), а так как все стороны каждого равны между собою, то, очевидно, отношение любой стороны одного к любой стороне другого есть число постоянное.

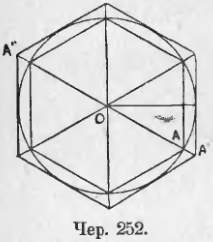
Если в круг впишем какой-либо правильный многоугольник (чер. 252) и чрез середины дуг, стягиваемых его сторонами, построим касательные к кругу, то получим правильный одноименный многоугольник, описанный около этого круга. Не трудно выяснить (предоставляем это желающим), что полученные два правильные многоугольника подобно расположены, и центр круга служит их внешним центром подобия, – внешним потому, что каждая пара соответствующих точек (напр., A и A’) расположена в одном направлении от центра (если многоугольник имеет четное число сторон, то центр круга можно считать и внутренним центром подобия, надо лишь считать, что, например, точке A соответствует точка A»).

259. Упражнения.

1. Стороны одного пятиугольника равны соответственно 12, 14, 10, 8 и 16 дм. Найти стороны другого пятиугольника, подобного первому, если его периметр = 80 дм.

2. Сумма площадей двух подобных многоугольников равна 250 кв. дм., а отношение двух сходственных сторон = ¾. Вычислить площадь каждого из них.

3. Показать, что если в круг вписан правильный многоугольник с нечетным числом сторон и в его вершинах построены касательные к кругу, то получится описанный многоугольник, подобно расположенный с вписанным, – центр круга служит их внутренним центром подобия.

4. Дан треугольник; построить другой треугольник, подобно расположенный с первым так, чтобы центр тяжести первого служил внутренним центом подобия и чтобы коэффициент подобия = ½. Выяснить при помощи этого, как расположены точки высот, центр тяжести и центр описанного круга данного треугольника.

5. В данный треугольник вписан квадрат.

Пусть ABC данный треугольник (чер. 253) и DEFK искомый квадрат. Построим еще квадрат MNPQ, чтобы одна сторона MQ лежала на стороне AC треугольника и точка N на стороне AB. Легко видеть, что квадрат MNPQ подобно расположен с искомым квадратом DEFK и внешним их центром подобия является точка A; следовательно, точка F лежит на прямой AP. После нахождения точки F искомый квадрат легко построить.

6. Дан угол и точка внутри его. Найти на одной стороне угла точку, равноудаленную от данной точки и от другой стороны.

Задача решается тем же приемом.

7. Построить треугольник по его высотам.

Легко получить, называя стороны треугольника чрез a, b и c и соответствующие высоты чрез h_a, h_b и h_c, следующую зависимость:

Легко построить отрезок x = (h_bh_a)/h_c (x/h_a = h_b/h_c — построение 4-го пропорционального), после чего построим треугольник со сторонами h_b, h_a и x. Этот треугольник подобен искомому, так как a : h : c = h_b : h_a : x; остается построить треугольник подобный только что построенному так, чтобы одна его высота была равна данной.

Получи верный ответ на вопрос 🏆 «Длина прямоугольника 8 см ширина 3 см. Длина другого прямоугольника 7 см ширина 5 см. Найдите отношения площади первого прямоугольника к …» по предмету 📕 Математика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!

Найти готовые ответы