В статистике вероятность относится к вероятности того, что какое-то событие произойдет. Он рассчитывается как:
ВЕРОЯТНОСТЬ:
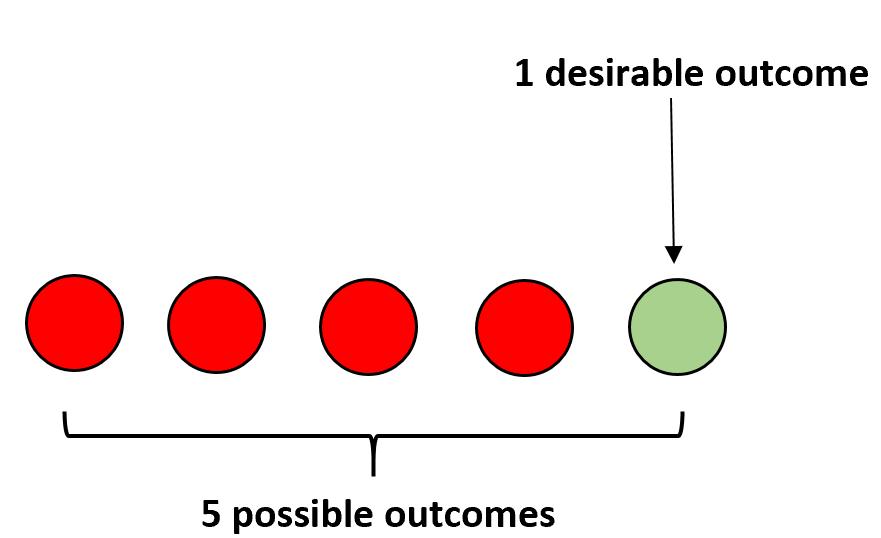
P(событие) = (# желаемых результатов) / (# возможных результатов)
Например, предположим, что у нас есть четыре красных мяча и один зеленый мяч в мешке. Если вы закроете глаза и случайным образом выберете мяч, вероятность того, что вы выберете зеленый мяч, рассчитывается как:
P(зеленый) = 1/5 = 0,2 .
Шансы на то, что какое-то событие произойдет, можно рассчитать как:
ШАНСЫ:
Коэффициенты (событие) = P (событие происходит) / 1-P (событие происходит)
Например, вероятность того, что выпадет зеленый шар, равна (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .
Отношение шансов – это отношение двух шансов.
КОЭФФИЦИЕНТ СООТНОШЕНИЯ:
Отношение шансов = шансы события A / шансы события B
Например, мы могли бы рассчитать отношение шансов между выбором красного и зеленого шаров.
Вероятность того, что выпадет красный шар, равна 4/5 = 0,8 .
Вероятность того, что выпадет красный шар, равна (0,8)/1-(0,8) = 0,8/0,2 = 4 .
Отношение шансов выбора красного шара по сравнению с зеленым шаром рассчитывается как:
Шансы (красный) / Шансы (зеленый) = 4 / 0,25 = 16 .
Таким образом, шансы выбрать красный шар в 16 раз больше, чем шансы выбрать зеленый мяч.
Когда в реальном мире используются отношения шансов?
В реальном мире отношения шансов используются в различных условиях, когда исследователи хотят сравнить шансы двух событий. Вот несколько примеров.
Пример №1: интерпретация отношения шансов
Исследователи хотят знать, повышает ли новое лечение шансы пациента на положительный результат для здоровья по сравнению с существующим лечением. В следующей таблице показано количество пациентов с положительным или отрицательным результатом лечения в зависимости от лечения.
Вероятность того, что пациент испытает положительный результат при новом лечении, можно рассчитать как:
Коэффициенты = P(положительные) / 1 — P(положительные) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25
Шансы пациента получить положительный результат при существующем лечении можно рассчитать как:
Шансы = P (положительный) / 1 — P (положительный) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875
Таким образом, отношение шансов получить положительный результат при новом лечении по сравнению с существующим лечением можно рассчитать как:
Отношение шансов = 1,25 / 0,875 = 1,428 .
Мы бы интерпретировали это как означающее, что вероятность того, что пациент испытает положительный результат при использовании нового лечения, в 1,428 раза превышает вероятность того , что пациент получит положительный результат при использовании существующего лечения.
Другими словами, шансы на положительный результат увеличиваются на 42,8% при новом лечении.
Пример № 2: интерпретация отношения шансов
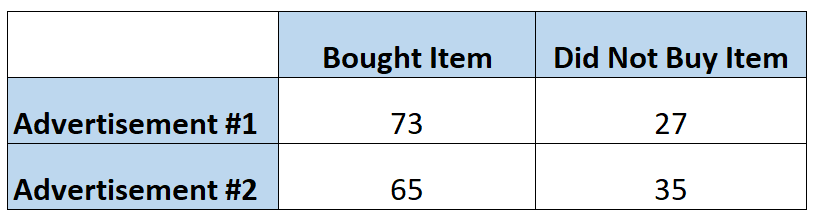
Маркетологи хотят знать, побуждает ли одна реклама покупателей покупать определенный товар чаще, чем другая реклама, поэтому они показывают каждую рекламу 100 людям. В следующей таблице показано количество людей, купивших товар, в зависимости от того, какую рекламу они видели:
Вероятность того, что человек купит товар после того, как увидит первую рекламу, можно рассчитать как:
Шансы = P(куплено) / 1 – P(куплено) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704
Вероятность того, что человек купит товар после просмотра второй рекламы, можно рассчитать как:
Шансы = P(куплено) / 1 – P(куплено) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857
Таким образом, отношение шансов для покупателя, купившего товар после просмотра первой рекламы, по сравнению с покупкой после просмотра второй рекламы, можно рассчитать как:
Отношение шансов = 2,704 / 1,857 = 1,456 .
Мы бы интерпретировали это так, что вероятность того, что человек купит товар после просмотра первой рекламы, в 1,456 раз превышает вероятность того , что человек купит товар после просмотра второй рекламы.
Другими словами, шансы купить предмет увеличиваются на 45,6% при использовании первой рекламы.
Дополнительные ресурсы
Как рассчитать отношение шансов и относительный риск в Excel
Как интерпретировать отношение шансов меньше 1
Как интерпретировать относительный риск
22 ноября 2021 г.
Расчет шансов — это математический способ делать прогнозы и анализировать данные. В области медицины и эпидемиологии вероятность представляет собой математический расчет, который позволяет ученым узнать вероятность и степень распространения вируса или другого заболевания. Знание того, каковы шансы и как их рассчитать, может помочь вам быть в курсе распространения болезней, что может повлиять как на медицинские, так и на политические решения. В этой статье мы обсудим, что значит вычислять шансы, посмотрим, почему шансы важны, и поговорим о том, как рассчитать шансы на примерах.
Что значит рассчитать шансы?
Расчет шансов — это математический принцип, связанный с вероятностью, но отличный от нее. Коэффициенты выражают количество благоприятных и неблагоприятных исходов ситуации. Вы можете выразить это число в виде отношения, например 1:3, дроби, например 1/3, десятичной дроби, например 0,33, или процента, например 33%. Расчет шансов также означает учет различных частей ситуации, таких как общее количество результатов и то, как вы определяете эти результаты. При расчете шансов нужно учитывать как можно больше информации, так как это поможет получить более точные результаты.
В медицине и профилактике заболеваний важно знать относительное возникновение события, такого как болезнь, по сравнению с другой переменной, такой как история болезни или индивидуальная характеристика здоровья. В этих полях также используются отношения шансов, чтобы определить, вызывает ли конкретное воздействие увеличение факторов риска для других исходов. Вы можете рассчитать вероятность возникновения определенного исхода, например болезни или расстройства, с помощью следующих формул:
Н = А + В + С + D
ИЛИ = (AD) / (BC)
Где:
-
N — общее количество людей, включенных в исследование, также известное как размер выборки.
-
ИЛИ — отношение шансов для определенного исхода
-
A — общее количество выявленных случаев
-
D — общее количество неэкспонированных не-случаев
-
B — общее количество выставленных не-случаев
-
C — общее количество невыявленных случаев
В этих переменных «воздействие» относится к тому, когда кто-то подвергается риску возникновения заболевания или расстройства.
Когда важно рассчитывать шансы?
Для ученых важно рассчитывать шансы при изучении вирусов и других инфекционных заболеваний, таких как простуда или грипп. Это может помочь им информировать общественность об опасностях болезней, разрабатывать способы борьбы с распространением этих болезней, а также обезопасить себя. Знание того, как рассчитать вероятность заражения болезнью, также помогает экспертам подготовиться к будущим сценариям, когда болезнь широко распространена и население обращается за рекомендациями к экспертам в области здравоохранения.
Нахождение отношения шансов для повторяющихся заболеваний также позволяет исследователям разрабатывать теории о профилактических мерах для болезни. Например, исследователи, изучающие вирус гриппа, могут определить шансы заражения на основе четырех категорий, которые помогают им подготовиться к будущим повторениям той же болезни:
-
Люди, которые контактировали с вирусом и заразились им
-
Люди, которые контактировали с вирусом, но остались здоровыми
-
Люди, которые не контактировали с вирусом и остались здоровыми
-
Люди, которые не контактировали с вирусом, но заразились им
Исследователи также могут рассчитать отношение шансов, чтобы учесть распространение определенных болезней среди вакцинированного и непривитого населения. Вся эта информация помогает исследователям предоставлять информативные рекомендации, когда болезни быстро распространяются.
Как рассчитать шансы
Ниже приведены шаги, которые вы можете использовать для расчета шансов:
1. Определите числа, которые представляют каждую переменную
Первым шагом к определению отношения шансов для воздействия конкретной переменной является определение чисел для переменных формулы A, B, C, D и N. В таблице ниже показано количество случаев гриппа с использованием факторов, описанных выше:
Значение Случай или не случай Подвергшийся или неподвергшийся воздействию 75 Выявленный случай 47 Незараженный подвергшийся воздействию 23 Случайный случай Не подвергшийся воздействию 17 Неслучай Не подвергшийся воздействию 162 Общее количество проб
2. Определите, что означают переменные для исследования отношения шансов.
Используя приведенный выше пример, каждая из переменных представляет определенный сегмент выборки. В исследовании используется выборка из 162 человек. Это означает, что каждая переменная представляет следующую информацию:
-
A = количество людей, больных гриппом, которые контактировали с этим заболеванием.
-
B = количество людей, которые не болели гриппом и подверглись воздействию этой болезни.
-
C = количество людей, больных гриппом, которые не подвергались воздействию этой болезни.
-
D = количество людей, не болеющих гриппом, которые не подвергались воздействию этой болезни.
3. Используйте формулу для ввода чисел для каждой переменной
После того, как вы установили, что представляет каждая переменная, вы можете добавить найденные значения в формулу. Ниже приведен пример формулы с использованием значений из таблицы:
-
ИЛИ = (75 х 17) / (47 х 23)
-
ИЛИ = (1275) / (1081)
-
ОШ = 1,18
4. Определите, что представляет собой отношение шансов для исследования
После того как вы рассчитали отношение шансов для выборки, вы можете использовать это значение в качестве основы для аргумента. Используя приведенный выше пример, отношение шансов представляет собой шансы того, что человек, подвергшийся воздействию гриппа, заразится по сравнению с тем, кто не подвергался воздействию вируса. Вероятность заражения гриппом при контакте с больным выше в 1,18 раза.
5. Определите доверительный интервал для ваших данных
Последний шаг, который делают исследователи, — это вычисление доверительного интервала для своих данных. Доверительные интервалы — это два значения, которые инкапсулируют данные на основе размера выборки. Как правило, из-за реального применения этих исследований исследователи используют доверительный интервал 95%. Это означает, что с вероятностью 95% найденное значение является точным и надежным.
Две формулы для расчета доверительного интервала:
Верхний 95% ДИ = e ^ [ln (OR) + 1.96√ (1/A + 1/B + 1/C + 1/D)]
Нижний 95% ДИ = e ^ [ln (OR) — 1.96√ (1/A + 1/B +1/C + 1/D)]
Где:
-
ln = натуральный логарифм
-
e = число Эйлера, или 2,71828
Использование этих формул обеспечивает диапазон интервалов для данных независимо от значений для A, B, C и D.
An odds ratio (OR) is a statistic that quantifies the strength of the association between two events, A and B. The odds ratio is defined as the ratio of the odds of A in the presence of B and the odds of A in the absence of B, or equivalently (due to symmetry), the ratio of the odds of B in the presence of A and the odds of B in the absence of A. Two events are independent if and only if the OR equals 1, i.e., the odds of one event are the same in either the presence or absence of the other event. If the OR is greater than 1, then A and B are associated (correlated) in the sense that, compared to the absence of B, the presence of B raises the odds of A, and symmetrically the presence of A raises the odds of B. Conversely, if the OR is less than 1, then A and B are negatively correlated, and the presence of one event reduces the odds of the other event.
Note that the odds ratio is symmetric in the two events, and there is no causal direction implied (correlation does not imply causation): an OR greater than 1 does not establish that B causes A, or that A causes B.[1]
Two similar statistics that are often used to quantify associations are the relative risk (RR) and the absolute risk reduction (ARR). Often, the parameter of greatest interest is actually the RR, which is the ratio of the probabilities analogous to the odds used in the OR. However, available data frequently do not allow for the computation of the RR or the ARR, but do allow for the computation of the OR, as in case-control studies, as explained below. On the other hand, if one of the properties (A or B) is sufficiently rare (in epidemiology this is called the rare disease assumption), then the OR is approximately equal to the corresponding RR.
The OR plays an important role in the logistic model.
Definition and basic properties[edit]
A motivating example, in the context of the rare disease assumption[edit]
Suppose a radiation leak in a village of 1,000 people increased the incidence of a rare disease. The total number of people exposed to the radiation was 





The risk of developing the disease given exposure is 

The odds ratio is different. The odds of getting the disease if exposed is 

As illustrated by this example, in a rare-disease case like this, the relative risk and the odds ratio are almost the same. By definition, rare disease implies that 



Relative risk is easier to understand than the odds ratio, but one reason to use odds ratio is that usually, data on the entire population is not available and random sampling must be used. In the example above, if it were very costly to interview villagers and find out if they were exposed to the radiation, then the prevalence of radiation exposure would not be known, and neither would the values of 

The odds in this sample of getting the disease given that someone is exposed is 20/10 and the odds given that someone is not exposed is 6/16. The odds ratio is thus 


It is standard in the medical literature to calculate the odds ratio and then use the rare-disease assumption (which is usually reasonable) to claim that the relative risk is approximately equal to it. This not only allows for the use of case-control studies, but makes controlling for confounding variables such as weight or age using regression analysis easier and has the desirable properties discussed in other sections of this article of invariance and insensitivity to the type of sampling.[3]
Definition in terms of group-wise odds[edit]
The odds ratio is the ratio of the odds of an event occurring in one group to the odds of it occurring in another group. The term is also used to refer to sample-based estimates of this ratio. These groups might be men and women, an experimental group and a control group, or any other dichotomous classification. If the probabilities of the event in each of the groups are p1 (first group) and p2 (second group), then the odds ratio is:
where qx = 1 − px. An odds ratio of 1 indicates that the condition or event under study is equally likely to occur in both groups. An odds ratio greater than 1 indicates that the condition or event is more likely to occur in the first group. And an odds ratio less than 1 indicates that the condition or event is less likely to occur in the first group. The odds ratio must be nonnegative if it is defined. It is undefined if p2q1 equals zero, i.e., if p2 equals zero or q1 equals zero.
Definition in terms of joint and conditional probabilities[edit]
The odds ratio can also be defined in terms of the joint probability distribution of two binary random variables. The joint distribution of binary random variables X and Y can be written
where p11, p10, p01 and p00 are non-negative «cell probabilities» that sum to one. The odds for Y within the two subpopulations defined by X = 1 and X = 0 are defined in terms of the conditional probabilities given X, i.e., P(Y |X):
Thus the odds ratio is
The simple expression on the right, above, is easy to remember as the product of the probabilities of the «concordant cells» (X = Y) divided by the product of the probabilities of the «discordant cells» (X ≠ Y). However note that in some applications the labeling of categories as zero and one is arbitrary, so there is nothing special about concordant versus discordant values in these applications.
Symmetry[edit]
If we had calculated the odds ratio based on the conditional probabilities given Y,
we would have obtained the same result
Other measures of effect size for binary data such as the relative risk do not have this symmetry property.
Relation to statistical independence[edit]
If X and Y are independent, their joint probabilities can be expressed in terms of their marginal probabilities px = P(X = 1) and py = P(Y = 1), as follows
In this case, the odds ratio equals one, and conversely the odds ratio can only equal one if the joint probabilities can be factored in this way. Thus the odds ratio equals one if and only if X and Y are independent.
Recovering the cell probabilities from the odds ratio and marginal probabilities[edit]
The odds ratio is a function of the cell probabilities, and conversely, the cell probabilities can be recovered given knowledge of the odds ratio and the marginal probabilities P(X = 1) = p11 + p10 and P(Y = 1) = p11 + p01. If the odds ratio R differs from 1, then
where p1• = p11 + p10, p•1 = p11 + p01, and
In the case where R = 1, we have independence, so p11 = p1•p•1.
Once we have p11, the other three cell probabilities can easily be recovered from the marginal probabilities.
Example[edit]
A graph showing how the log odds ratio relates to the underlying probabilities of the outcome X occurring in two groups, denoted A and B. The log odds ratio shown here is based on the odds for the event occurring in group B relative to the odds for the event occurring in group A. Thus, when the probability of X occurring in group B is greater than the probability of X occurring in group A, the odds ratio is greater than 1, and the log odds ratio is greater than 0.
Suppose that in a sample of 100 men, 90 drank wine in the previous week (so 10 did not), while in a sample of 80 women only 20 drank wine in the same period (so 60 did not). This forms the contingency table:
The odds ratio (OR) can be directly calculated from this table as:
Alternatively, the odds of a man drinking wine are 90 to 10, or 9:1, while the odds of a woman drinking wine are only 20 to 60, or 1:3 = 0.33. The odds ratio is thus 9/0.33, or 27, showing that men are much more likely to drink wine than women. The detailed calculation is:
This example also shows how odds ratios are sometimes sensitive in stating relative positions: in this sample men are (90/100)/(20/80) = 3.6 times as likely to have drunk wine than women, but have 27 times the odds. The logarithm of the odds ratio, the difference of the logits of the probabilities, tempers this effect, and also makes the measure symmetric with respect to the ordering of groups. For example, using natural logarithms, an odds ratio of 27/1 maps to 3.296, and an odds ratio of 1/27 maps to −3.296.
Statistical inference[edit]
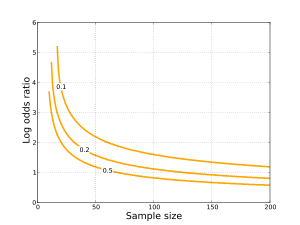
A graph showing the minimum value of the sample log odds ratio statistic that must be observed to be deemed significant at the 0.05 level, for a given sample size. The three lines correspond to different settings of the marginal probabilities in the 2×2 contingency table (the row and column marginal probabilities are equal in this graph).
Several approaches to statistical inference for odds ratios have been developed.
One approach to inference uses large sample approximations to the sampling distribution of the log odds ratio (the natural logarithm of the odds ratio). If we use the joint probability notation defined above, the population log odds ratio is
If we observe data in the form of a contingency table
then the probabilities in the joint distribution can be estimated as
where ︿pij = nij / n, with n = n11 + n10 + n01 + n00 being the sum of all four cell counts. The sample log odds ratio is
.
The distribution of the log odds ratio is approximately normal with:
The standard error for the log odds ratio is approximately
.
This is an asymptotic approximation, and will not give a meaningful result if any of the cell counts are very small. If L is the sample log odds ratio, an approximate 95% confidence interval for the population log odds ratio is L ± 1.96SE.[4] This can be mapped to exp(L − 1.96SE), exp(L + 1.96SE) to obtain a 95% confidence interval for the odds ratio. If we wish to test the hypothesis that the population odds ratio equals one, the two-sided p-value is 2P(Z < −|L|/SE), where P denotes a probability, and Z denotes a standard normal random variable.
An alternative approach to inference for odds ratios looks at the distribution of the data conditionally on the marginal frequencies of X and Y. An advantage of this approach is that the sampling distribution of the odds ratio can be expressed exactly.
Role in logistic regression[edit]
Logistic regression is one way to generalize the odds ratio beyond two binary variables. Suppose we have a binary response variable Y and a binary predictor variable X, and in addition we have other predictor variables Z1, …, Zp that may or may not be binary. If we use multiple logistic regression to regress Y on X, Z1, …, Zp, then the estimated coefficient 
so 

Insensitivity to the type of sampling[edit]
If the data form a «population sample», then the cell probabilities 
The odds ratio p11p00 / p01p10 for this distribution does not depend on the value of f. This shows that the odds ratio (and consequently the log odds ratio) is invariant to non-random sampling based on one of the variables being studied. Note however that the standard error of the log odds ratio does depend on the value of f.[citation needed]
This fact is exploited in two important situations:
- Suppose it is inconvenient or impractical to obtain a population sample, but it is practical to obtain a convenience sample of units with different X values, such that within the X = 0 and X = 1 subsamples the Y values are representative of the population (i.e. they follow the correct conditional probabilities).
- Suppose the marginal distribution of one variable, say X, is very skewed. For example, if we are studying the relationship between high alcohol consumption and pancreatic cancer in the general population, the incidence of pancreatic cancer would be very low, so it would require a very large population sample to get a modest number of pancreatic cancer cases. However we could use data from hospitals to contact most or all of their pancreatic cancer patients, and then randomly sample an equal number of subjects without pancreatic cancer (this is called a «case-control study»).
In both these settings, the odds ratio can be calculated from the selected sample, without biasing the results relative to what would have been obtained for a population sample.
Use in quantitative research[edit]
Due to the widespread use of logistic regression, the odds ratio is widely used in many fields of medical and social science research. The odds ratio is commonly used in survey research, in epidemiology, and to express the results of some clinical trials, such as in case-control studies. It is often abbreviated «OR» in reports. When data from multiple surveys is combined, it will often be expressed as «pooled OR».
Relation to relative risk[edit]
As explained in the «Motivating Example» section, the relative risk is usually better than the odds ratio for understanding the relation between risk and some variable such as radiation or a new drug. That section also explains that if the rare disease assumption holds, the odds ratio is a good approximation to relative risk[5] and that it has some advantages over relative risk. When the rare disease assumption does not hold, the unadjusted odds ratio can overestimate the relative risk,[6][7][8] but novel methods can easily use the same data to estimate the relative risk, risk differences, base probabilities, or other quantities.[9]
If the absolute risk in the unexposed group is available, conversion between the two is calculated by:[6]
where RC is the absolute risk of the unexposed group.
If the rare disease assumption does not apply, the odds ratio may be very different from the relative risk and can be misleading.
Consider the death rate of men and women passengers when the Titanic sank.[3] Of 462 women, 154 died and 308 survived. Of 851 men, 709 died and 142 survived. Clearly a man on the Titanic was more likely to die than a woman, but how much more likely? Since over half the passengers died, the rare disease assumption is strongly violated.
To compute the odds ratio, note that for women the odds of dying were 1 to 2 (154/308). For men, the odds were 5 to 1 (709/142). The odds ratio is 9.99 (4.99/.5). Men had ten times the odds of dying as women.
For women, the probability of death was 33% (154/462). For men the probability was 83% (709/851). The relative risk of death is 2.5 (.83/.33). A man had 2.5 times a woman’s probability of dying.
Which number correctly represents how much more dangerous it was to be a man on the Titanic? Relative risk has the advantage of being easier to understand and of better representing how people think.
Confusion and exaggeration[edit]
Odds ratios have often been confused with relative risk in medical literature. For non-statisticians, the odds ratio is a difficult concept to comprehend, and it gives a more impressive figure for the effect.[10] However, most authors consider that the relative risk is readily understood.[11] In one study, members of a national disease foundation were actually 3.5 times more likely than nonmembers to have heard of a common treatment for that disease – but the odds ratio was 24 and the paper stated that members were ‘more than 20-fold more likely to have heard of’ the treatment.[12] A study of papers published in two journals reported that 26% of the articles that used an odds ratio interpreted it as a risk ratio.[13]
This may reflect the simple process of uncomprehending authors choosing the most impressive-looking and publishable figure.[11] But its use may in some cases be deliberately deceptive.[14] It has been suggested that the odds ratio should only be presented as a measure of effect size when the risk ratio cannot be estimated directly,[10] but with newly available methods it is always possible to estimate the risk ratio, which should generally be used instead.[15]
Invertibility and invariance[edit]
The odds ratio has another unique property of being directly mathematically invertible whether analyzing the OR as either disease survival or disease onset incidence – where the OR for survival is direct reciprocal of 1/OR for risk. This is known as the ‘invariance of the odds ratio’. In contrast, the relative risk does not possess this mathematical invertible property when studying disease survival vs. onset incidence. This phenomenon of OR invertibility vs. RR non-invertibility is best illustrated with an example:
Suppose in a clinical trial, one has an adverse event risk of 4/100 in drug group, and 2/100 in placebo… yielding a RR=2 and OR=2.04166 for drug-vs-placebo adverse risk. However, if analysis was inverted and adverse events were instead analyzed as event-free survival, then the drug group would have a rate of 96/100, and placebo group would have a rate of 98/100—yielding a drug-vs-placebo a RR=0.9796 for survival, but an OR=0.48979. As one can see, a RR of 0.9796 is clearly not the reciprocal of a RR of 2. In contrast, an OR of 0.48979 is indeed the direct reciprocal of an OR of 2.04166.
This is again what is called the ‘invariance of the odds ratio’, and why a RR for survival is not the same as a RR for risk, while the OR has this symmetrical property when analyzing either survival or adverse risk. The danger to clinical interpretation for the OR comes when the adverse event rate is not rare, thereby exaggerating differences when the OR rare-disease assumption is not met. On the other hand, when the disease is rare, using a RR for survival (e.g. the RR=0.9796 from above example) can clinically hide and conceal an important doubling of adverse risk associated with a drug or exposure.[citation needed]
Estimators of the odds ratio[edit]
Sample odds ratio[edit]
The sample odds ratio n11n00 / n10n01 is easy to calculate, and for moderate and large samples performs well as an estimator of the population odds ratio. When one or more of the cells in the contingency table can have a small value, the sample odds ratio can be biased and exhibit high variance.
Alternative estimators[edit]
A number of alternative estimators of the odds ratio have been proposed to address limitations of the sample odds ratio. One alternative estimator is the conditional maximum likelihood estimator, which conditions on the row and column margins when forming the likelihood to maximize (as in Fisher’s exact test).[16] Another alternative estimator is the Mantel–Haenszel estimator.
Numerical examples[edit]
The following four contingency tables contain observed cell counts, along with the corresponding sample odds ratio (OR) and sample log odds ratio (LOR):
| OR = 1, LOR = 0 | OR = 1, LOR = 0 | OR = 4, LOR = 1.39 | OR = 0.25, LOR = −1.39 | |||||
|---|---|---|---|---|---|---|---|---|
| Y = 1 | Y = 0 | Y = 1 | Y = 0 | Y = 1 | Y = 0 | Y = 1 | Y = 0 | |
| X = 1 | 10 | 10 | 100 | 100 | 20 | 10 | 10 | 20 |
| X = 0 | 5 | 5 | 50 | 50 | 10 | 20 | 20 | 10 |
The following joint probability distributions contain the population cell probabilities, along with the corresponding population odds ratio (OR) and population log odds ratio (LOR):
| OR = 1, LOR = 0 | OR = 1, LOR = 0 | OR = 16, LOR = 2.77 | OR = 0.67, LOR = −0.41 | |||||
|---|---|---|---|---|---|---|---|---|
| Y = 1 | Y = 0 | Y = 1 | Y = 0 | Y = 1 | Y = 0 | Y = 1 | Y = 0 | |
| X = 1 | 0.2 | 0.2 | 0.4 | 0.4 | 0.4 | 0.1 | 0.1 | 0.3 |
| X = 0 | 0.3 | 0.3 | 0.1 | 0.1 | 0.1 | 0.4 | 0.2 | 0.4 |
Numerical example[edit]
| Quantity | Experimental group (E) | Control group (C) | Total |
|---|---|---|---|
| Events (E) | EE = 15 | CE = 100 | 115 |
| Non-events (N) | EN = 135 | CN = 150 | 285 |
| Total subjects (S) | ES = EE + EN = 150 | CS = CE + CN = 250 | 400 |
| Event rate (ER) | EER = EE / ES = 0.1, or 10% | CER = CE / CS = 0.4, or 40% | — |
| Variable | Abbr. | Formula | Value |
|---|---|---|---|
| Absolute risk reduction | ARR | CER − EER | 0.3, or 30% |
| Number needed to treat | NNT | 1 / (CER − EER) | 3.33 |
| Relative risk (risk ratio) | RR | EER / CER | 0.25 |
| Relative risk reduction | RRR | (CER − EER) / CER, or 1 − RR | 0.75, or 75% |
| Preventable fraction among the unexposed | PFu | (CER − EER) / CER | 0.75 |
| Odds ratio | OR | (EE / EN) / (CE / CN) | 0.167 |
[edit]
There are various other summary statistics for contingency tables that measure association between two events, such as Yule’s Y, Yule’s Q; these two are normalized so they are 0 for independent events, 1 for perfectly correlated, −1 for perfectly negatively correlated. Edwards (1963) studied these and argued that these measures of association must be functions of the odds ratio, which he referred to as the cross-ratio.
See also[edit]
- Cohen’s h
- Cross-ratio
- Diagnostic odds ratio
- Forest plot
- Hazard ratio
- Likelihood ratio
- Rate ratio
References[edit]
Citations[edit]
- ^ Szumilas, Magdalena (August 2010). «Explaining Odds Ratios». Journal of the Canadian Academy of Child and Adolescent Psychiatry. 19 (3): 227–229. ISSN 1719-8429. PMC 2938757. PMID 20842279.
- ^ LaMorte WW (May 13, 2013), Case-Control Studies, Boston University School of Public Health, retrieved 2013-09-02
- ^ a b Simon, Stephen (July–August 2001). «Understanding the Odds Ratio and the Relative Risk». Journal of Andrology. 22 (4): 533–536. PMID 11451349.
- ^ Morris JA, Gardner MJ (May 1988). «Calculating confidence intervals for relative risks (odds ratios) and standardised ratios and rates». British Medical Journal (Clinical Research Ed.). 296 (6632): 1313–6. doi:10.1136/bmj.296.6632.1313. PMC 2545775. PMID 3133061.
- ^ Viera AJ (July 2008). «Odds ratios and risk ratios: what’s the difference and why does it matter?». Southern Medical Journal. 101 (7): 730–4. doi:10.1097/SMJ.0b013e31817a7ee4. PMID 18580722.
- ^ a b Zhang J, Yu KF (November 1998). «What’s the relative risk? A method of correcting the odds ratio in cohort studies of common outcomes». JAMA. 280 (19): 1690–1. doi:10.1001/jama.280.19.1690. PMID 9832001.
- ^ Robbins AS, Chao SY, Fonseca VP (October 2002). «What’s the relative risk? A method to directly estimate risk ratios in cohort studies of common outcomes». Annals of Epidemiology. 12 (7): 452–4. doi:10.1016/S1047-2797(01)00278-2. PMID 12377421.
- ^ Nurminen M (August 1995). «To use or not to use the odds ratio in epidemiologic analyses?». European Journal of Epidemiology. 11 (4): 365–71. doi:10.1007/BF01721219. PMID 8549701. S2CID 11609059.
- ^ King, Gary; Zeng, Langche (2002-05-30). «Estimating risk and rate levels, ratios and differences in case-control studies». Statistics in Medicine. 21 (10): 1409–1427. doi:10.1002/sim.1032. ISSN 0277-6715. PMID 12185893. S2CID 11387977.
- ^ a b Taeger D, Sun Y, Straif K (10 August 1998). «On the use, misuse and interpretation of odds ratios».
- ^ a b A’Court C, Stevens R, Heneghan C (March 2012). «Against all odds? Improving the understanding of risk reporting». The British Journal of General Practice. 62 (596): e220-3. doi:10.3399/bjgp12X630223. PMC 3289830. PMID 22429441.
- ^ Nijsten T, Rolstad T, Feldman SR, Stern RS (January 2005). «Members of the national psoriasis foundation: more extensive disease and better informed about treatment options». Archives of Dermatology. 141 (1): 19–26. doi:10.1001/archderm.141.1.19. PMID 15655138.
- ^ Holcomb, W (2001). «An odd measure of risk: Use and misuse of the odds ratio». Obstetrics & Gynecology. 98 (4): 685–688. doi:10.1016/S0029-7844(01)01488-0. PMID 11576589. S2CID 44782438.
- ^ Taylor HG (January 1975). «Social perception of the mentally retarded». Journal of Clinical Psychology. 31 (1): 100–2. doi:10.1136/bmj.316.7136.989. PMC 1112884. PMID 9550961.
- ^ King, Gary; Zeng, Langche (2002-05-30). «Estimating risk and rate levels, ratios and differences in case-control studies». Statistics in Medicine. 21 (10): 1409–1427. doi:10.1002/sim.1032. ISSN 0277-6715. PMID 12185893. S2CID 11387977.
- ^ Rothman KJ, Greenland S, Lash TL (2008). Modern Epidemiology. Lippincott Williams & Wilkins. ISBN 978-0-7817-5564-1.[page needed]
Sources[edit]
- Edwards, A. W. F. (1963). «The Measure of Association in a 2 × 2 Table». Journal of the Royal Statistical Society. A (General). 126 (1): 109–114. doi:10.2307/2982448. JSTOR 2982448.
External links[edit]
- Odds Ratio Calculator – website
- Odds Ratio Calculator with various tests – website
- OpenEpi, a web-based program that calculates the odds ratio, both unmatched and pair-matched
Медстатистика, медицинская статистика 👁 Прочитано 13 255 раз
А. Радостный, NewsForLife.info
- Доверительный интервал
- Отношение шансов
- Шанс
- Отношение шансов
- Пример
- Относительный риск (ОР)
- Достоверность, статистическая значимость (P – уровень)
- Критика
- Графическое представление результатов мета-анализа (блобограмма)
- Литература
Доверительный интервал
Доверительный интервал ДИ (confidence interval, CI ) — это диапазон значений, который с заданной степенью вероятности включает полученные данные.
Пример. Исследуемая величина — количество заболеваний на тысячу человек. Выяснилось, что в среднем было 60 заболеваний, а ДИ 95% (52, 73). Это означает, что, с вероятностью 95% заболеет не менее 52 и не более 73 человека.
Клиническая значимость эффекта велика, когда доверительный интервал узок.
Отношение шансов
Сначала давайте обсудим понятие «шанс», а потом перейдём к отношению шансов.
Шанс
Существует несколько дефиниций, однако в целях вычисления отношения шансов используется понятие «шансы в пользу». Вы часто слышали выражение типа: «пять к одному, что он выиграет». Это как раз шансы в пользу.
Итак, в рассматриваемом контексте:
шанс — это отношение вероятности того, что событие произойдёт, к вероятности того, что событие не произойдёт: да/нет, выиграет/проиграет, упадёт/вырастет и т.п.
Увеличь свои шансы!
ТОП-10 реально выполнимых методов продления ТВОЕЙ жизни
Хотя в русском языке слова «шанс» и «вероятность» часто используются как синонимы, но здесь шанс не равен вероятности.
Например, вероятность того, случайная карта, извлечённая из колоды, в которой 36 карт, окажется красной масти составит 0,5 = 50% = (16 карт красных мастей / 32 карты в колоде). А шанс того, что такая карта будет красной масти составит: 1:1 = (16 карт красных мастей / 32 карты в колоде) : (16 не красных / 32 карты).
ВАЖНО! Врачи склонны рассматривать риск с точки зрения группы пациентов, тогда как пациенты интерпретируют риск применительно к себе-любимому.
Например, психиатр сообщал пациентам, что при приеме флуоксетина была «30–50% вероятность развития сексуальной проблемы». При этом оказалось, что, по мнению пациентов, это означало трудности во время половины их сексуальных контактов. Между тем доктор желал проинформировать, что из каждых десяти человек, принимающих флуоксетин, три-пять будут испытывать затруднения [1].
Отношение шансов
Отношение шансов ОШ (OR — odds ratio) – это величина, которая количественно определяет силу связи между двумя событиями (признаками) A и B в пределах одной и той-же выборки (пример см. далее).
OШ=(A+/А-) : (В+/В-).
|
есть |
нет |
|
|
Событие А |
A+ |
А- |
|
Событие В |
B+ |
B- |
Два события независимы тогда и только тогда, когда OШ=1. Чем ближе значение OШ к 1, тем меньше различий в эффективности сравниваемых вмешательств.
Если OШ>1, то появление B повышает шансы наличия A (по отношению к отсутствию B).
Если OШ<1, то наличие одного события (признака) уменьшает шансы другого события (признака).
Пример
Допустим, что 100 добровольцам задают два вопроса:
-
Каково Ваше артериальное давление?
-
Сколько алкоголя Вы употребляете?
Далее, для каждого участника можно определить обладает ли он свойством
А — часто употребляет алкоголь
и свойством
B — высоким артериальным давлением.
В результате опроса всей сотни участников можно построить показатель, который количественно характеризует связь между признаками A и B в изучаемой группе.
|
В: высокое давление |
норма |
Всего |
|
|
А: часто употребляет алкоголь |
12 |
20 |
32 |
|
не часто употребляет алкоголь |
4 |
64 |
68 |
Отношение шансов (ОШ):
OШ=(A+/А-) : (В+/В-).
-
A+/А- = 12/20=0,6.
-
В+/В-=4/64= 0,0625
-
Разделим шансы, полученные в п. 1, на шансы, полученные в п.2, — это и будет отношение шансов (ОШ). ОШ = 0,6/0,0625 = 9,6.
Если ОШ превышает 1, наличие признака А ассоциируется с признаком B в том смысле, что наличие B повышает (по отношению к отсутствию В) шансы наличия A. В нашем умозрительном примере это означает, что частое употребление алкоголя почти десятикратно повышает шансы появления гипертонии.
Опасность для клинической интерпретации ОШ возникает когда вероятность случая высока, при этом преувеличиваются имеющиеся различия, если предположение о редком заболевании не выполняется.
Важно знать, что отношение шансов является симметричным относительно обоих событий, а потому и не отражает причинно-следственных связей. Оно не доказывает, что B вызывает A, или A вызывает B.
Для расчёта отношения шансов с 95% доверительным интервалом см. онлайн калькулятор.
В медицинской литературе отношение шансов нередко путают с относительным риском.
РАССЫЛКА «ЗДОРОВЬЕ И АНТИСТАРЕНИЕ»
Относительный риск (ОР)
Риск события (или заболевания) — это просто количество случаев, когда оно произошло, делённое на общее число случаев, когда оно может произойти. В нашем примере для тех, кто часто употребляет алкоголь риск высокого давления 12/32 = 0,375=37,5%. А для малопьющих он будет 4/(68)= 0,059=5,9%.
Относительный риск ОР (RR — relative risk) — отношение рисков появления определённого события в группах сравнения.
Для нашего примера
ОР = 0,375/0,059 = 6,4.
Если ОР > 1, то частота развития изучаемого исхода выше в основной группе, чем в контрольной.
При ОР < 1 — частота развития изучаемого исхода ниже в основной группе, чем в контрольной.
Т.е. в рассматриваемом случае риск развития гипертонии выше в 6,4 раз при употреблении алкоголя.
Для расчёта относительного риска с 95% доверительным интервалом — см. онлайн калькулятор.
Достоверность, статистическая значимость (P – уровень)
P-значение (англ. P-value), p-уровень значимости, p-критерий — это мера уверенности в «истинности» результата.
Чем меньше p-критерий, тем выше уверенность в правильности результатов, полученных при анализе выборки.
Во многих медицинских исследованиях p- уровень, равный 0,05 (5%) считается приемлемым.
Критика
Применение p-значений для проверки нулевых гипотез в работах по медицине и естественным наукам подвергается критике со стороны многих специалистов. Отмечается, что их использование нередко приводят к ситуации, когда отвергается правильная нулевая гипотеза, иными словами, исследователи находят связь там, где её нет вовсе.
Нулевая гипотеза — принимаемое по умолчанию предположение о том, что не существует связи между двумя наблюдаемыми событиями.
В частности, журнал Basic and Applied Social Psychology (BASP) в 2015 году вовсе запретил публикацию статей, в которых используются p-значения. Редакторы журнала мотивировали это тем, что сделать исследование, в котором получено p < 0,05 не очень сложно, и такие низкие значения p слишком часто становятся оправданием для низкопробных исследований.
Графическое представление результатов мета-анализа (блобограмма)
Не буду специально изощряться и придумывать картинки и объяснения. Возьму готовые материалы [2], которые многократно можно встретить в интернете, например, здесь. Далее идёт большая цитата из указанного источника.
На рисунке даётся пример результатов мета-анализа, рассматривающего побочные эффекты со стороны печени при интенсивной терапии статинами по сравнению со стандартной схемой назначения у пациентов, перенёсших острый коронарный синдром и пациентов со стабильной стенокардией. В качестве регистрируемого события было принято трёхкратное (и более) повышение активности печёночных трансаминаз.
Результаты, полученные в каждом из исследований показаны на блобограмме в виде квадратов. От каждого квадрата отходит горизонтальная линия, показывающая доверительный интервал (в данном случае он равен 95%) для зафиксированного в этом исследовании исхода.
Вертикальная линия по центру рисунка — линия «отсутствия различий», которая в данном случае соответствует отношению шансов 1,0.
Если горизонтальная линия (доверительный интервал) результатов исследования не пересекает линию «отсутствия различий», то существует 95% вероятность того, что различия между сравниваемыми группами действительно существуют. Если же доверительный интервал результата пересекает вертикальную линию, это означает что:
1) либо нет достоверных различий между изучаемыми вмешательствами;
2) либо размер выборки недостаточен для определения истинного результата;
3) ромб отображает обобщённый результат всех анализируемых исследований. Ширина ромба отображает доверительный интервал для обобщённого результата;
4) поскольку ромб не пересекает линию «отсутствие различий», результат можно считать статистически значимым, т.е. назначение высоких доз статинов достоверно сопровождается повышенным риском развития побочных эффектов со стороны печени по сравнению с умеренными дозами.
Сегодня пользователи сайта особенно интересуются этим:
- >>> Свежие новости
- >>> Таурин. Когда, сколько, какой, кому, побочки. Как…
- >>> Глутатион. Когда, сколько глутатиона, какой, кому,…
- >>> Кремний. Когда, сколько, какой, кому, побочки. Как…
- >>> Цинк. Когда, сколько, какой, кому, побочки. Дефицит. Избыток
ПОДЕЛИСЬ ЭТОЙ ИНФОРМАЦИЕЙ С ДРУГОМ!
Литература
- A’Court C, Stevens R, Heneghan C. Against all odds? Improving the understanding of risk reporting. Br J Gen Pract. 2012;62(596):e220‐e223. doi:10.3399/bjgp12X630223.
- Клиническая фармакология и фармакотерапия в реальной врачебной практике : мастер-класс : учебник / В. И. Петров. — М. : ГЭОТАР-Медиа, 2014.
медицинская статистика, медстатистика
Отношение шансов (OR, odds ratio) — это широко используемый статистический показатель, позволяющий сравнивать частоту воздействия факторов риска в эпидемиологических исследованиях. Отношение шансов является ретроспективным сравнением влияния данного фактора риска на две группы лиц.
Термин «шанс» пришёл из азартных игр и означает отношение числа выигрышей к числу проигрышей или, другими словами, отношение числа случаев, когда событие наступило, к числу случаев, когда оно не наступило.
Расчёт отношения шансов
Расчёт отношения шансов для набора данных несложен: необходимо построить таблицу сопряжённости так, чтобы в первой строке стояла группа испытуемых, а в первом столбце — фактор риска.
Рассмотрим первый пример
Представьте, что Вы решили провести обследование мутации в гене X, предположительно вызывающего некую болезнь. Вы проанализировали гены однородных групп заболевших и здоровых и нашли, что распределение мутаций выглядит так (табл. 1):
Таблица 1.
| Наличие мутации | Отсутствие мутации | Всего | |
| Группа заболевших | A = 332 | B = 164 | 496 |
| Контрольная группа (оставшиеся здоровыми) | C = 230 | D = 262 | 492 |
| Всего | 562 | 426 | 988 |
Сначала необходимо вычислить вероятность воздействия факторов риска (в данном случае, наличия мутации) в группе заболевших и в группе оставшихся здоровыми. Шанс того, что фактор риска есть в этих группах, рассчитывается так:
Шанс найти мутацию в группе заболевших = (A x (A + B))/(B x (A + B)) = A/B = 332/164 = 2.0244
Шанс найти мутацию в контрольной группе = (C x (C + D))/(D x (C + D)) = C/D = 230/262 = 0.8779
Затем следует найти OR путём деления шансов найти мутацию в группе заболевших и в контрольной группе:
OR = 2.0244/0.8779 = 2.306
Если свести все эти действия в одну формулу, то получим
OR = (A/B)/(C/D) = (А x D)/(В х С) = (332×262)/(164×230) = 2.306
… и это именно та формула, которая используется для определения OR.
Рассмотрим второй пример
Предположим, что в выборке из 100 мужчин 90 пили вино в предыдущую неделю, а в выборке из 100 женщин только 20 пили вино в тот же период (табл. 2).
Таблица 2.
| Пили | Не пили | Всего | |
| Мужчины | A = 90 | B = 10 | 100 |
| Женщины | C = 20 | D = 80 | 100 |
| Всего | 110 | 90 | 200 |
Шанс мужчины быть в группе пивших вино 90:10 или 9:1, в то время как шанс женщины быть в группе пивших только 20:80 или 1:4 (0.25:1). Отношение шансов, таким образом, 9/0.25 = 36 показывает, что мужчины склонны гораздо чаще пить вино, чем женщины.
Расчет OR (воздействия фактора риска) является хорошим инструментом, но поскольку он основан на выборке, то он является не более чем оценкой. Точность этой оценки отчасти зависит от размера выборки, и, в целом, чем больше выборка, тем правдоподобнее оценка (хотя следует с большой осторожностью подходить к интерпретации OR в исследованиях с огромными размерами выборки). По этой причине кроме расчёта OR обычно вычисляют и стандартное отклонение (SE) с доверительным интервалом (p) 95%.
Есть несколько различных способов расчёта SE при заданном p для отношения шансов. Приведём один из них:
при p = 95% ln(SE) = 1.96(1/A + 1/B + 1/C + 1/D)^0.5
Для первого примера:
при p = 95% ln(SE) = 1.96(1/332 + 1/164 + 1/230 + 1/262)^0.5 = 0.25760567, соответственно
OR ± SE = от e^0.57790875 до e^0.25760567 или от 1.7823073 до 2.9835686
Для второго примера:
при p = 95% ln(SE) = 1.96(1/90 + 1/10 + 1/20 + 1/80)^0.5 = 0.817
OR ± SE = 36 ± 2.26
В этих примерах доверительный интервал составляет 95%, но если нужно воспользоваться другой шириной доверительного интервала, то следует заменить 1.96 в уравнении соответствующим стандартным для нормального распределения значением.
Интерпретация отношения шансов
Предполагаемый фактор риска является значимым (т. е. с большой вероятностью вызовет наступление события, напр. болезнь), если OR больше единицы.
Следует иметь в виду, что само по себе значение OR нечувствительно к размеру выборки (напр., если во втором примере мы используем вдесятеро меньшие значения, то тоже получим OR = 36), однако от размера выборки зависит размер стандартного отклонения (так, во втором примере при вдесятеро меньших значениях мы вместо 2.26 получим SE = 13, т. е. ошибка измерения составит 37%).
Примечания
1. Этот материал является вольным переводом странички http://slack.ser.man.ac.uk/theory/association_odds.html с добавлением примера из http://en.wikipedia.org/wiki/Odds_ratio
2. В доступной форме эти вопросы изложены в Британском медицинском журнале за 2000 г.
3. Ошибки, возникающие при некритичном применении OR, рассмотрены в статье http://www.jstor.org/pss/3582428
4. Cм. тж. материал «Odds ratio. Отношение шансов и логистическая регрессия» Александра Виноградова.