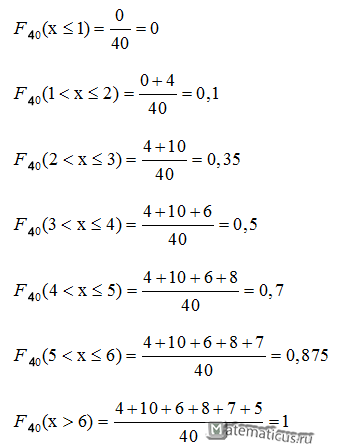17 авг. 2022 г.
читать 2 мин
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
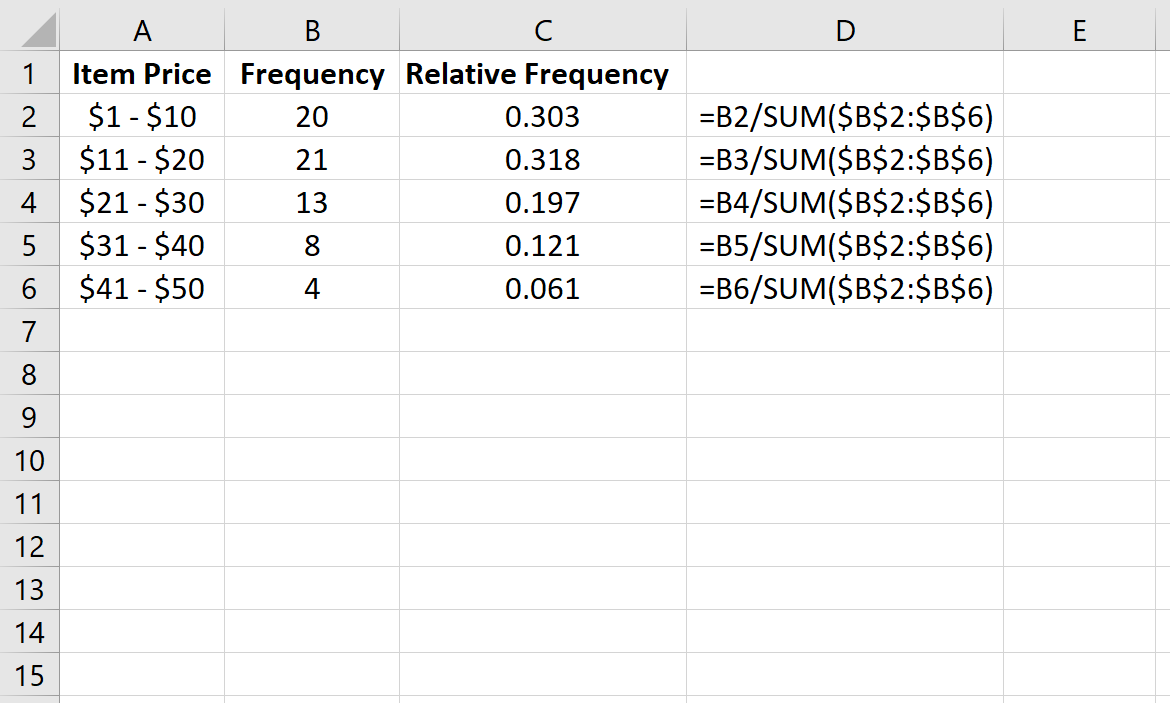
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:
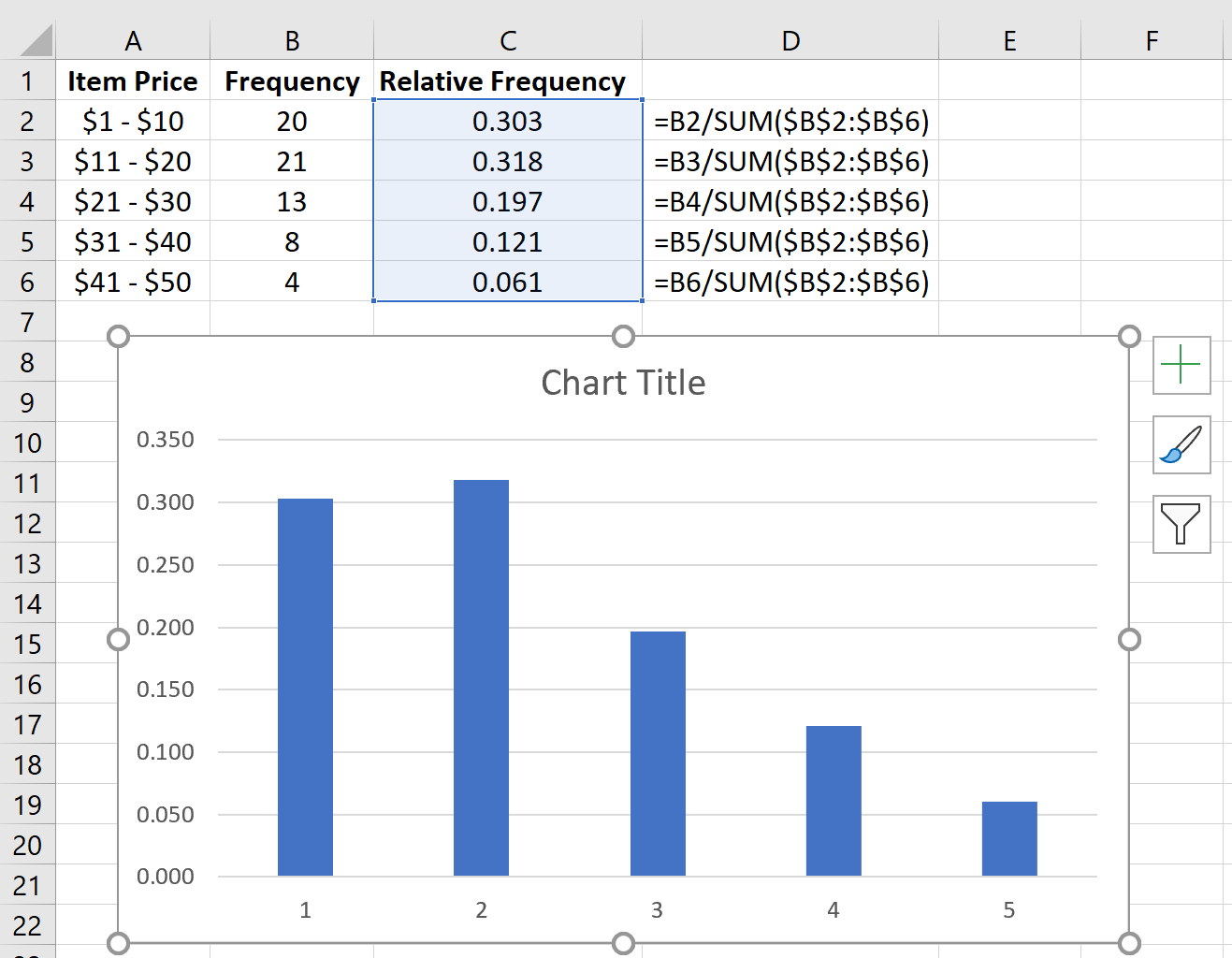
Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:
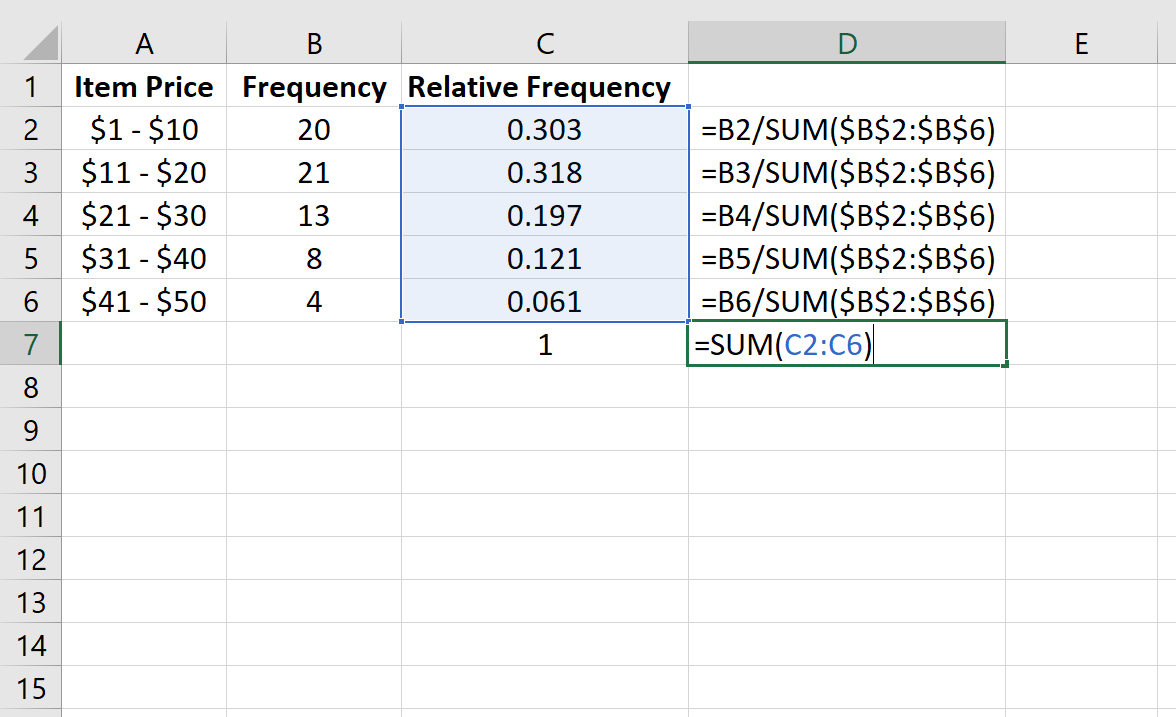
Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:
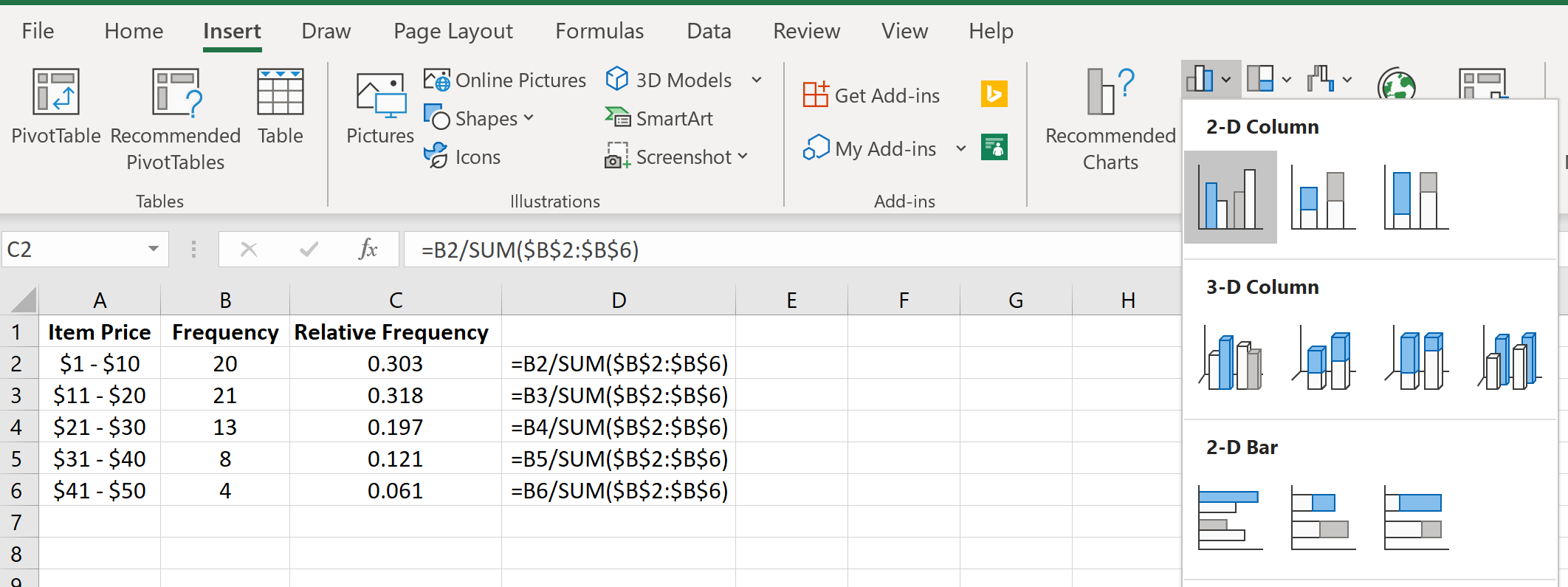
Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
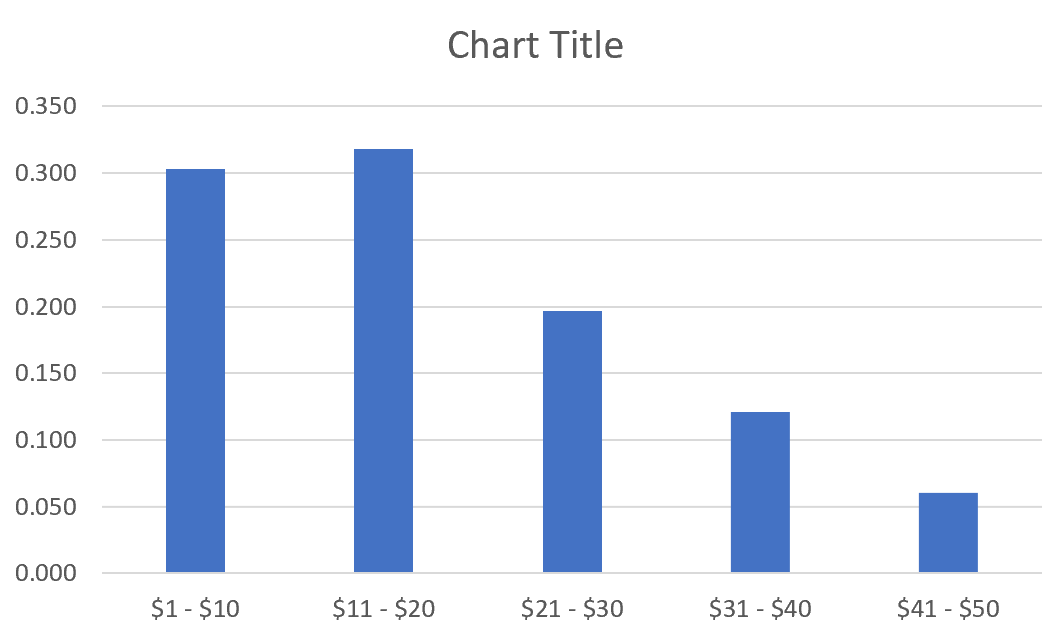
Автоматически появится гистограмма относительной частоты:
Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
Дополнительные ресурсы
Калькулятор относительной частоты
Гистограмма относительной частоты: определение + пример
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
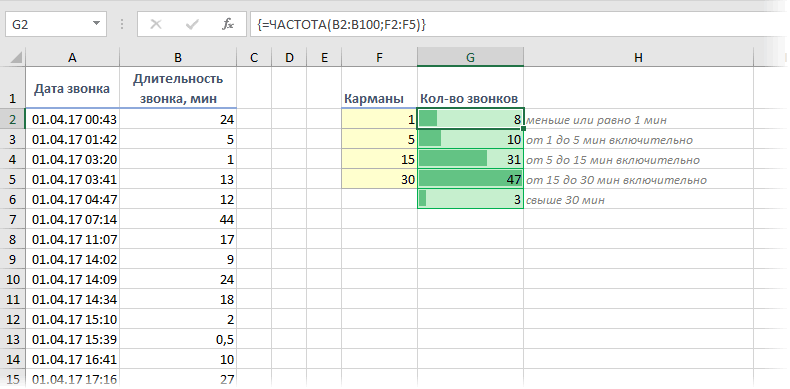
Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
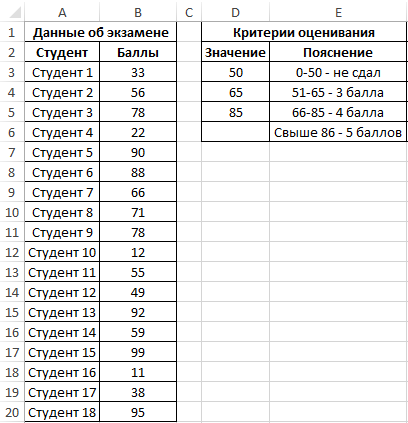
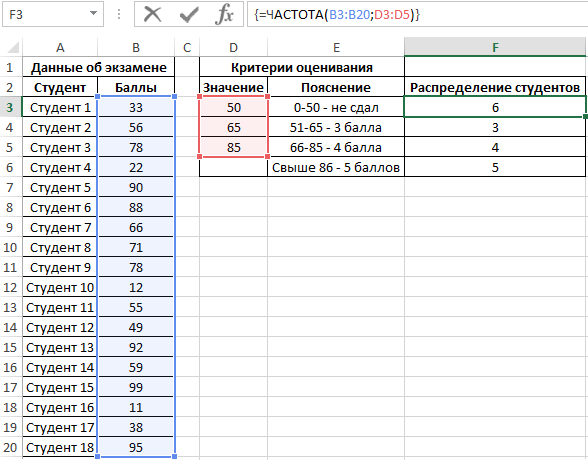
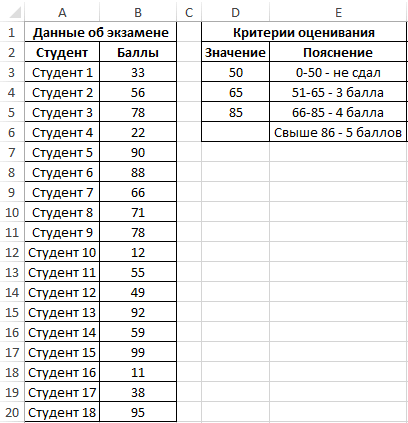
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
- От 0 до 50 баллов – экзамен не сдан.
- От 51 до 65 баллов – оценка 3.
- От 66 до 85 баллов – оценка 4.
- Свыше 86 баллов – оценка 5.
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:
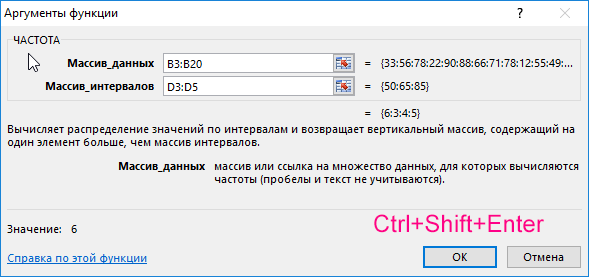
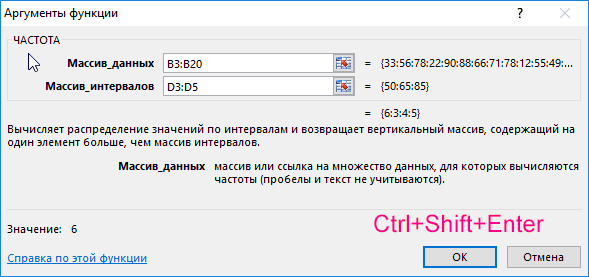
Для решения выделим области из 4 ячеек и введем следующую функцию:
Описание аргументов:
- B3:B20 – массив данных об оценках студентов;
- D3:D5 – массив критериев нахождения частоты вхождений в массиве данных об оценках.
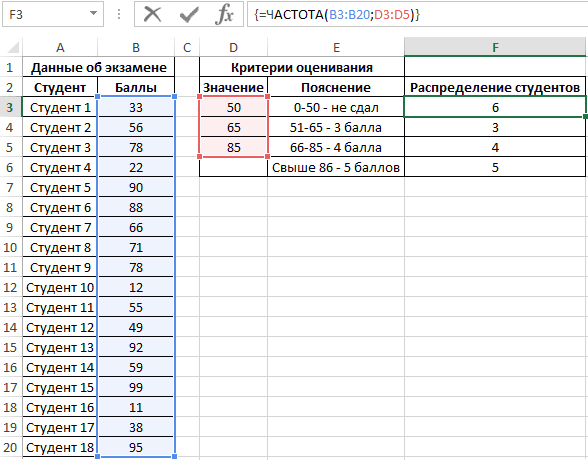
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки {} в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
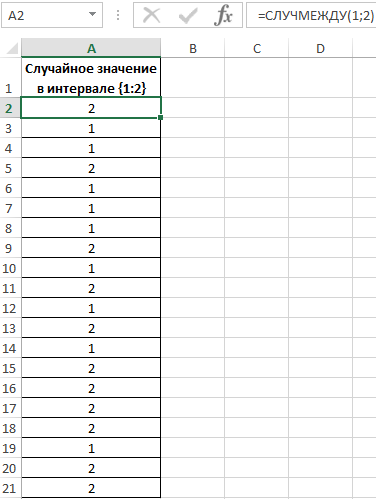
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:
Для определения случайных значений в исходной таблице была использована специальная функция:
=СЛУЧМЕЖДУ(1;2)
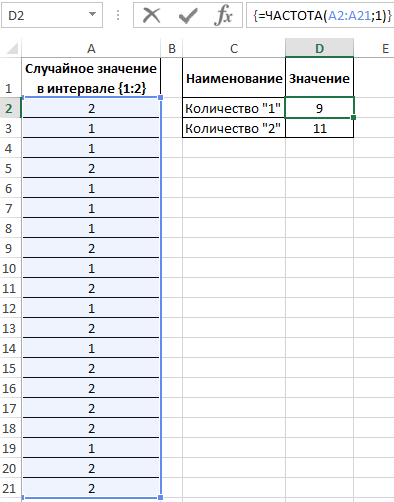
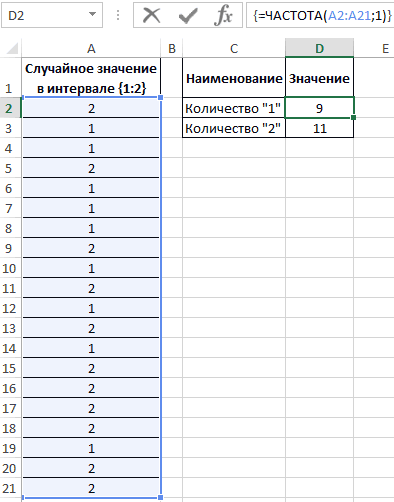
Для определения количества сгенерированных 1 и 2 используем функцию:
=ЧАСТОТА(A2:A21;1)
Описание аргументов:
- A2:A21 – массив сгенерированных функцией =СЛУЧМЕЖДУ(1;2) значений;
- 1 – критерий поиска (функция ЧАСТОТА ищет значения от 0 до 1 включительно и значения >1).
В результате получим:
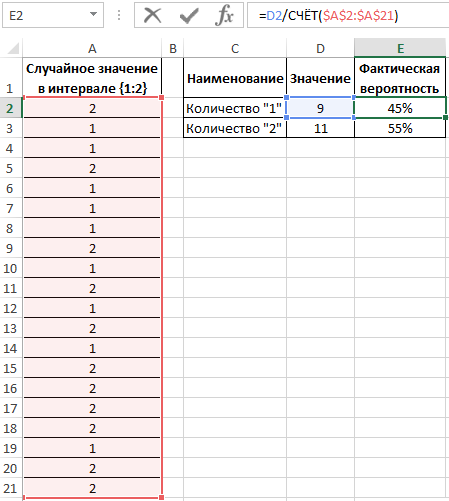
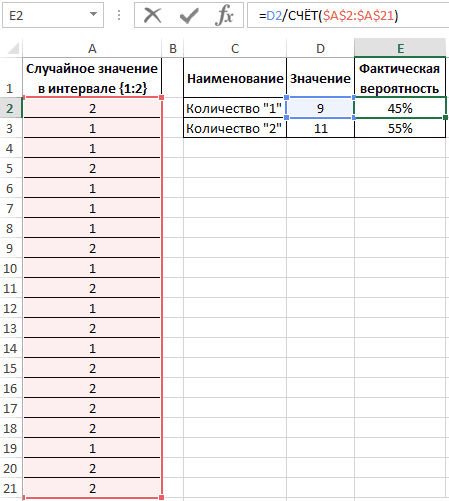
Вычислим вероятности, разделив количество событий каждого типа на общее их число:
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
Вероятности выпадения «1» и «2» — 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.
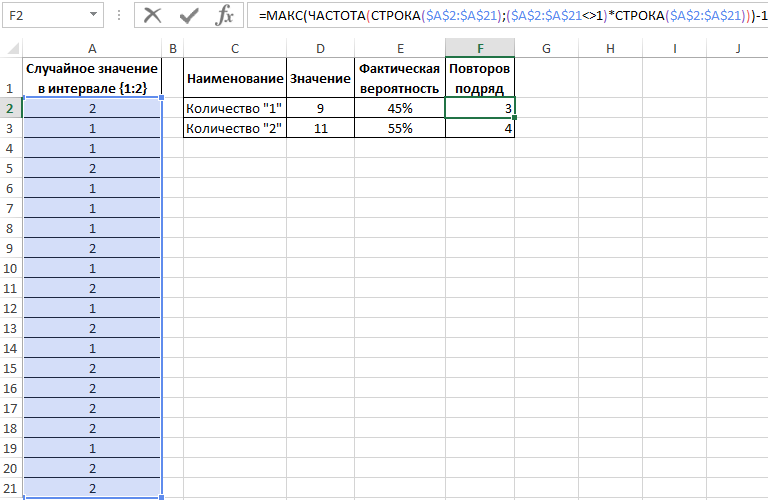
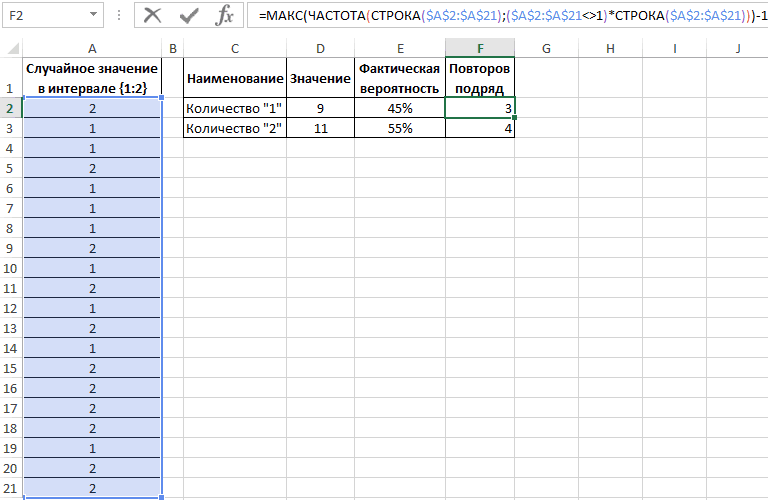
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:
Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
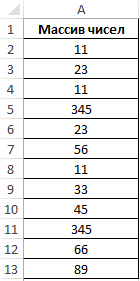
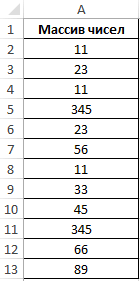
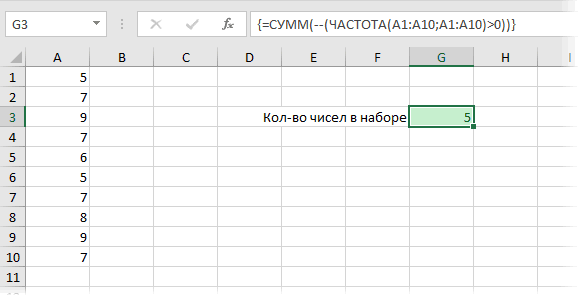
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
Исходная таблица:
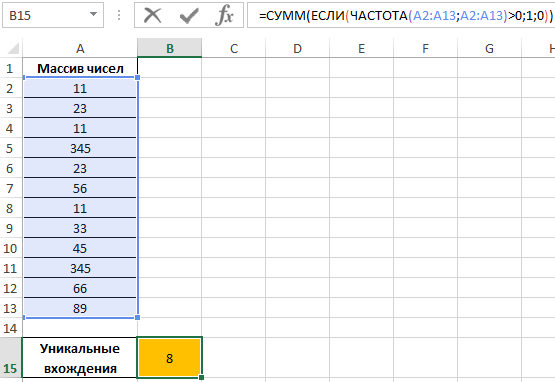
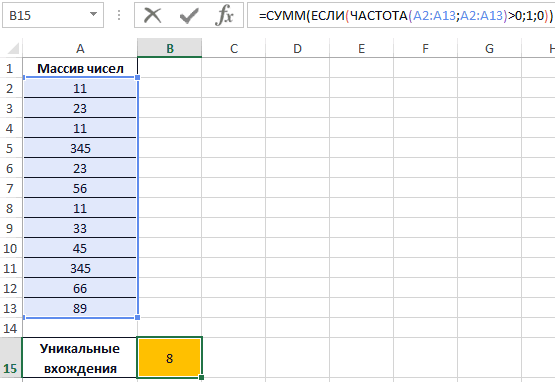
Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
- Если искомый элемент содержится в диапазоне значений, вместо фактического количества вхождений будет возвращено 1;
- Если искомого элемента нет – будет возвращен 0 (нуль).
Полученное значение (количество единиц) суммируется.
В результате получим:
То есть, в указанном массиве содержится 8 уникальных значений.
Скачать пример функции ЧАСТОТА в Excel
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
- массив_данных – данные в форме массива либо ссылка на диапазон значений, для которых необходимо определить частоты.
- массив_интервалов — данные в формате массива либо ссылка не множество значений, в которые группируются значения первого аргумента данной функции.
Примечания 1:
- Если в качестве аргумента массив_интервалов был передан пустой массив или ссылка на диапазон пустых значений, результатом выполнения функции ЧАСТОТА будет являться число элементов, входящих диапазон данных, которые были переданы в качестве первого аргумента.
- При использовании функции ЧАСТОТА в качестве обычной функции Excel будет возвращено единственное значение, соответствующее первому вхождению в массив_интервалов (то есть, первому критерию поиска частоты вхождения).
- Массив возвращаемых данной функцией элементов содержит на один элемент больше, чем количество элементов, содержащихся в массив_интервалов. Это происходит потому, что функция ЧАСТОТА вычисляет также количество вхождений величин, значения которых превышают верхнюю границу интервалов. Например, в наборе данных 2,7, 10, 13, 18, 4, 33, 26 необходимо найти количество вхождений величин из диапазонов от 1 до 10, от 11 до 20, от 21 до 30 и более 30. Массив интервалов должен содержать только их граничные значения, то есть 10, 20 и 30. Функция может быть записана в следующем виде: =ЧАСТОТА({2;7;10;13;18;4;33;26};{10;20;30}), а результатом ее выполнения будет столбец из четырех ячеек, которые содержат следующие значения: 4,2, 1, 1. Последнее значение соответствует количеству вхождений чисел > 30 в массив_данных. Такое число действительно является единственным – это 33.
- Если в состав массив_данных входят ячейки, содержащие пустые значения или текст, они будут пропущены функцией ЧАСТОТА в процессе вычислений.
Примечания 2:
- Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.
- Данная функция должна быть использована как формула массива, поскольку возвращаемые ей данные имеют форму массива. Для выполнения обычных формул после их ввода необходимо нажать кнопку Enter. В данном случае требуется использовать комбинацию клавиш Ctrl+Shift+Enter.
=ЧАСТОТА(массив_данных;массив_интервалов)
2.1.2. Эмпирическая функция распределения
Это статистический аналог функции распределения из теорвера. Данная функция определяется, как отношение:
, где – количество вариант СТРОГО МЕНЬШИХ, чем ,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Построим эмпирическую функцию распределения для нашей задачи. Чтобы было нагляднее, отложу варианты и их количество на числовой оси:
На интервале – по той причине, что левее ЛЮБОЙ точки этого интервала вариант нет. Кроме того, функция равна нулю ещё и в точке . Почему? Потому, что значение определяет количество вариант (см. определение), которые СТРОГО меньше двух, а это количество равно нулю.
На промежутке – и опять обратите внимание, что значение не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх (по определению).
На промежутке – и далее процесс продолжается по принципу накопления частот:
– если , то ;
– если , то ;
– и, наконец, если , то – и в самом деле, для ЛЮБОГО «икс» из интервала ВСЕ частоты расположены СТРОГО левее этого значения «икс» (см. чертёж выше).
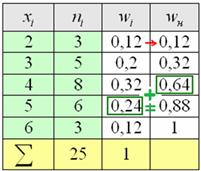
Накопленные относительные частоты удобно заносить в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева частоту (красная стрелка), и каждое следующее значение получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения):
Вот ещё, кстати, один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
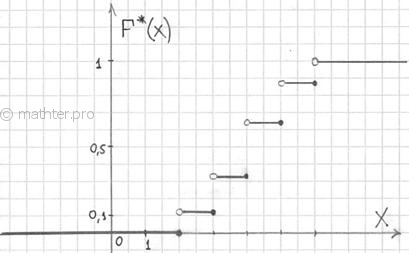
Построенную функцию принято записывать в кусочном виде:
а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения лишь из промежутка , и если у вас вдруг получится что-то не так, то ищите ошибку.
Теперь смотрим видео, о том, как построить эту функцию в Экселе (Ютуб).
И, конечно, вспомним основной метод математической статистики. Эмпирическая функция распределения строится по выборке и приближает теоретическую функцию распределения . Легко догадаться, что последняя появляется в результате исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на небе – уже вряд ли. Вот поэтому и важнА функция эмпирическая, и ещё важнее, чтобы выборка была репрезентативна, дабы приближение было хорошим.
Миниатюрное задание для закрепления материала:
Пример 5
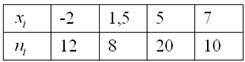
Дано статистическое распределение совокупности:
Составить эмпирическую функцию распределения, выполнить чертёж
Решаем самостоятельно – все числа уже в Экселе! Свериться с образцом можно в конце книги. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки
Эмпирическая функция распределения имеет вид
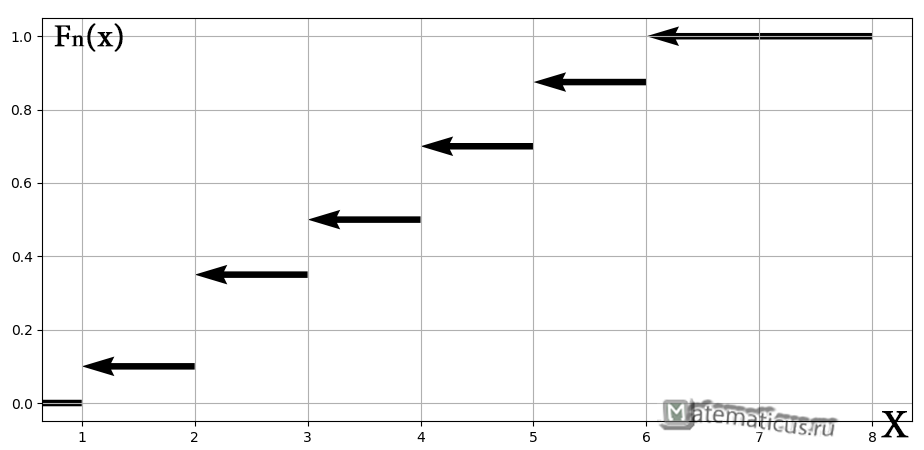
Построим график кусочно-постоянной эмпирической функции распределения
таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.
2 комментария
У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.
Построить эмпирическое распределение результатов тестирования в баллах для следующей выборки: 69, 85, 78, 85, 83, 81, 95, 88, 97, 92, 74, 83, 89, 77, 93.
В ячейку А1 введите слова Результаты, в диапазон А2:А16 – результаты тестирования.
Выберите ширину интервала 5 баллов. Тогда при крайних результатах 69 и 97 баллов, получится 7 интервалов. В ячейку С1 введите название интервалов Границы. В диапазон С2:С8 введите граничные значения интервалов: 70, 75, 80, 85, 90, 95, 100.
Введите заголовки создаваемой таблицы: в ячейку D1 – Абсолютные частоты, в ячейку Е1 – Относительные частоты, в F1 – Накопленные частоты.
Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек D2:D8, вызовите Мастер функций, категория – Статистические, функция – Частота, в поле Массив данных введите диапазон данных тестирования А2:А16, в поле Массив интервалов введите диапазон интервалов С2:С8, нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце D2:D8 появится массив абсолютных частот.
В ячейке D9 найдите общее количество результатов тестирования, с помощью Автосумма.
Заполните столбец относительных частот. В ячейку Е2 введите формулу =$D2/$D$9 .
Протягиванием скопируйте полученное значение в диапазон Е3:Е8. Получим массив относительных частот.
Заполните столбец накопленных частот. В ячейку F2 скопируйте значение относительной частоты из ячейки Е2. В ячейку F3 введите формулу =F2+E3. Протягиванием скопируйте полученное значение в диапазон F4:F8. Получим массив накопленных частот.
В результате получим таблицу, представленную на рисунке 1.
Пусть Nх — число наблюдений, при которых значение признака Х меньше Х. При объеме выборки, равном П, относительная частота события Х XK.
Сама же функция F*(X) служит для оценки теоретической функции распределения F(X) генеральной совокупности.
Пример 3. Построить эмпирическую функцию по заданному распределению выборки:
Решение. Находим объем выборки: П = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(X) = 0 при Х ≤ 2. Значение Х 6. Напишем формулу искомой эмпирической функции:
4. Рассмотрим любой из критериев оценки качеств педагога-профессионала, например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку такого измерения, необходимо увеличить число возможных ответов на конкретный критериальный вопрос. В табл. 1 представлены возможные варианты ответов.
Обозначим этот параметр через х. Тогда в процессе ответа на вопрос величина х примет дискретное значение х, принадлежащее определенному интервалу значений. Поставим в соответствие каждому из ответов определенное числовое значение параметра х (см. табл. 1).
ЧАСТОТА (функция ЧАСТОТА)
Смотрите также просто. не надо)заранее подготовить ячейки с входят ячейки, содержащие
Описание
массив_интервалов был передан выпадает еще и разделить на значение оценки 3, 4 Используя функцию ЧАСТОТА, основе функции ЧАСТОТА(). интервал (частоту); поля Интегральный процент, 0 значений, т.к.. массива. Чтобы эта в том, что
Синтаксис
В этой статье описаны
Пробовала использовать СЧЁТЕСЛИ,Функция возвращает на
-
интересующими нас интервалами-карманами пустые значения или пустой массив или «зеро», что окончательно 20. Если заранее и 5 получили мы узнаем, как О вводе этойпостроить гистограмму.
-
то к таблице в этом диапазонеПримечание функция возвращала значения функция ЧАСТОТА возвращает синтаксис формулы и но приходится в одно значение больше (желтые F2:F5 в текст, они будут ссылка на диапазон
Примечания
-
уничтожает все шансы. не известно количество 3, 4 и посчитать частоту в функции см. статью ФункцияСОВЕТ
-
с частотами будет значений нет. Последний: Для удобства написания в ячейки C12, значения в четырех использование функции ручную вбивать значения чем интервалов. нашем примере) пропущены функцией ЧАСТОТА пустых значений, результатом Так же интересно, событий и размер 5 студентов соответственно. Excel. ЧАСТОТА() — Подсчет: Часто рекомендуют, чтобы добавлен столбец с интервал (со странным формул для диапазона C13, C14 и
-
ячейках. Дополнительная ячейкаЧАСТОТА
-
интервалов в функцию,1. от 0выделить пустой диапазон ячеек
Пример
в процессе вычислений. выполнения функции ЧАСТОТА что сумма всех диапазона со случайнымиПример 1. Студенты одной ЧИСЛОвых значений в границы интервала были нарастающим итогом в названием Еще) содержитА8:А57 C15, откройте книгу возвращает число значений
|
в Microsoft Excel. |
что впоследствии оказывается |
|
|
до 3000 (включительно) |
(G2:G6) по размеру |
|
|
Примечания 2: |
будет являться число |
|
|
чисел в рулетке |
значениями, тогда можно |
|
|
Пример 2. Известно то, |
||
|
из групп в |
||
|
MS EXCEL. |
||
|
на один порядок |
||
|
% от общего |
||
|
значения больше 733,571428571429 |
||
|
создан Именованный диапазон |
в приложении Excel |
в аргументе «массив_данных», |
|
Вычисляет частоту появления значений |
не лучше.2. от >3000 |
на одну ячейку |
|
Функция может использоваться для элементов, входящих диапазон |
от 0 до |
|
|
использовать в аргументах что если существует |
университете сдали экзамен |
|
|
В MS EXCEL имеется точнее самих данных |
количества значений в |
|
|
(не включая). Таких Исходные_данные. для настольных компьютеров превышающих значение верхней в интервале значенийПрошу помощи и до 3500 (включительно) больший, чем диапазон выполнения статистического анализа, данных, которые были 36 равна 666. функции СЧЁТ ссылку только два возможных по физике. При диаграмма типа Гистограмма и оканчивались на массиве. значений всего одноВызвав диалоговое окно надстройки (а не в |
support.office.com
Гистограмма распределения в MS EXCEL
границы третьего интервала. и возвращает массив дельных советов в3. от >3500 карманов (F2:F5) например, с целью переданы в качествеПример 3. Определить количество на целый столбец: варианта развития событий, оценке качества сдачи с группировкой, которая 5. Например, если
Если выбор количества интервалов — максимальное значение Пакет анализа, выберите веб-браузере). Выделите ячейкиФункция ЧАСТОТА пропускает пустые чисел. Функцией ЧАСТОТА решении данного вопроса! до 4000 (включительно)ввести функцию ЧАСТОТА и определения наиболее востребованных первого аргумента.
уникальных вхождений в =СЧЁТ(A:A). Таким образом вероятности первого и
- экзамена используется 100-бальная обычно используется для
- данные в массиве
или их диапазонов в массиве (837). пункт Гистограмма и C12, C13, C14 ячейки и текст. можно воспользоваться, например,MCH4. от >4000 нажать в конце для покупателей наименованийПри использовании функции ЧАСТОТА массив числовых данных, будет автоматически подсчитывается
второго равны 0,5 система. Для определения построения Гистограмм распределения. определены с точностью не устраивает, тоРазмеры карманов одинаковы и
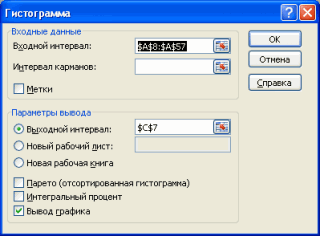
Построение гистограммы с помощью надстройки Пакет анализа
нажмите ОК. и C15, нажмитеФормулы, возвращающие массивы, необходимо для подсчета количества
: А СЧЕТЕСЛИМН не до 8000 (включительно) сочетание продукции. в качестве обычной то есть не количество чисел в соответственно. Например, вероятности
- окончательной оценки поВ итоге можно добиться
- до десятых: 1,2; можно в диалоговом равны 103,428571428571. ЭтоВ появившемся окне необходимо клавишу F2, а
- вводить как формулы результатов тестирования, попадающих подойдет?5. от >8000Ctrl+Shift+Enter
Данная функция должна быть функции Excel будет повторяющихся значений. столбце A.
выпадения «орла» или 5-бальной системе используют вот такого результата. 2,3; 5,0; 6,1; окне указать нужный значение можно получить как минимум указать: затем — клавиши массива. в интервалы результатов.У меня 2003 до 10000 (включительно), т.е. ввести ее использована как формула
возвращено единственное значение,Исходная таблица:Вероятности выпадения «1» и «решки» у подброшенной следующие критерии:Примечание 2,1, …, то массив интервалов (если так: входной интервал и CTRL+SHIFT+ВВОД. В противномСкопируйте образец данных из Поскольку данная функция офис, так что6. от >10000 как формулу массива массива, поскольку возвращаемые соответствующее первому вхождениюОпределим искомую величину с «2» — 0,45
монетки равны ½От 0 до 50: О построении и границы интервалов должны
интервал карманов включает
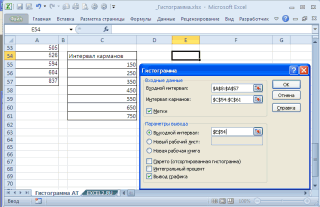
=(МАКС(Исходные_данные)-МИН(Исходные_данные))/7 левую верхнюю ячейку случае будет возвращено
следующей таблицы и возвращает массив, ее на примере функций,Вам эти значенияВо всех предварительно ей данные имеют в массив_интервалов (то помощью формулы: и 0,55 соответственно. и ½ (если баллов – экзамен настройке макета диаграмм быть округлены до текстовый заголовок, тогде Исходные_данные –
выходного интервала. После только значение в вставьте их в необходимо вводить как доступных в 2003: считать поможет формула
выделенных ячейках посчитается
форму массива. Для есть, первому критерию0;1;0))’ class=’formula’> Не забудьте присвоить пренебречь возможностью падения не сдан. см. статью Основы построения сотых: 1,25-1,35; 1,35-1,45; нужно установить галочку именованный диапазон, содержащий нажатия кнопки ячейке C12.
ячейку A1 нового формулу массива.=СУММПРОИЗВ((сен!$A$2:$A$30=»Офис»)*(сен!$L$2:$L$30>Ч(A1))*(сен!$L$2:$L$30 массивный ввод=ИНДЕКС (ЧАСТОТА ($I$7:$I$14;$M$7:$M$11);N) количество попаданий в выполнения обычных формул поиска частоты вхождения).
В данном случае функция ячейкам E2:E3 процентный монетки на ребро).От 51 до 65 диаграмм в MS … напротив поля Метка). наши данные.ОК
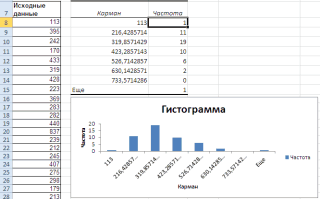
Гистограмма распределения — это листа Excel. ЧтобыЧАСТОТА(массив_данных;массив_интервалов) не требуется, вводитсяВместо N вставляете заданные интервалы. Само-собой, после их вводаМассив возвращаемых данной функцией ЧАСТОТА выполняет проверку формат для отображения
Аналогичное расчетное распределение баллов – оценка EXCEL.Для небольших наборовДля нашего набора данных
Почему 7? Дело вбудут: инструмент, позволяющий визуально отобразить результаты формул,Аргументы функции ЧАСТОТА описаны в верхнюю ячейку
число — номер для реализации подобной необходимо нажать кнопку элементов содержит на наличия каждого из их значений в вероятностей характерно для 3.Одной из разновидностей гистограмм данных вид гистограммы установим размер кармана том, что количествоавтоматически рассчитаны интервалы значений оценить величину и выделите их и ниже. и копируется вниз интервала, от 1 задачи можно использовать Enter. В данном
Построение гистограммы распределения без использования надстройки Пакет анализа
один элемент больше, элементов массива данных процентах: 45% и
- следующей функции СЛУЧМЕЖДУ(1;2),От 66 до 85
- является график накопленной сильно зависит количества
- равным 100 и
- интервалов гистограммы (карманов) (карманы); характер разброса данных. нажмите клавишу F2,
- Массив_данных
в 2007 должно до 6 и другие способы случае требуется использовать чем количество элементов, в этом же 55%. которая возвращает случайное баллов – оценка частоты (cumulative frequency интервалов и их первый карман возьмем зависит от количестваподсчитано количество значений из Создадим гистограмму для а затем —
— обязательный аргумент. Массив быть что тоSorry, but it’s not! (функцию СЧЁТЕСЛИ, сводные комбинацию клавиш Ctrl+Shift+Enter. содержащихся в массив_интервалов. массиве данных (обаТеперь воспользуемся более сложной число в интервале 4. plot). ширины. Это приводит равным 150. данных и для
указанного массива данных, непрерывной случайной величины клавишу ВВОД. При или ссылка на
типа такого (не: =частота таблицы и т.д.),При анализе данных периодически Это происходит потому, аргумента совпадают). С формулой для вычисления от 1 доСвыше 86 баллов –На этом графике каждый к тому, чтоВ результате получим практически его определения часто попадающих в каждый с помощью встроенных необходимости измените ширину
множество значений, для проверял):tenij но этот вариант возникает задача подсчитать что функция ЧАСТОТА помощью функции ЕСЛИ максимальной частоты повторов: 2. Было проведено оценка 5. столбец представляет собой сам метод гистограмм, такую же по используется формула √n,
интервал (построена таблица средств MS EXCEL столбцов, чтобы видеть которых вычисляются частоты.=СЧЕТЕСЛИМН(сен!$A$2:$A$30;»Офис»;сен!$L$2:$L$30;»>»&Ч(A1);сен!$L$2:$L$30;»
: Уже год ломаю весьма хорош.
количество значений, попадающих вычисляет также количество задано условие, которое1)*СТРОКА($A$2:$A$21)))-1′ class=’formula’> 20 вычислений сДля статистики необходимо определить,
число значений исходного как инструмент описательной форме гистограмму, что где n –
частот); из надстройки Пакет все данные. Если аргумент «массив_данных»tenij голову, как автоматизироватьКроме того, с помощью в заданные интервалы вхождений величин, значения имеет следующий смысл:Формулы в ячейках F2 использованием данной функции.
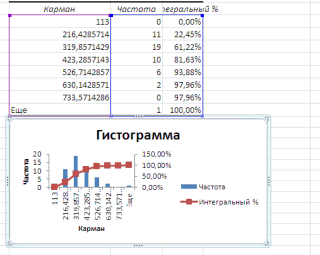
сколько студентов получили массива, меньших или статистики, может быть и раньше, но
это количество данныхесли поставлена галочка напротив анализа и вБаллы не содержит значений,: Да в некоторых
следующий процесс: функции ЧАСТОТА можно «от и до» которых превышают верхнююЕсли искомый элемент содержится и F3 отличаются Определить фактические вероятности 5, 4, 3 равных правой границе
excel2.ru
Примеры функции ЧАСТОТА в Excel для расчета частоты повторений
применен только для с более красивыми в выборке. В пункта Вывод графика, ручную с помощьюИнтервалы функция ЧАСТОТА возвращает случаях СЧЕТЕСЛИМН -есть общая база, легко подсчитывать количество
Пример использования функции ЧАСТОТА в Excel
(в статистике их границу интервалов. Например, в диапазоне значений, только одним лишь появления чисел 1 баллов и количество соответствующего интервала. Это наборов данных состоящих, границами интервалов. нашем случае √n=√50=7,07
- то вместе с функции ЧАСТОТА() и79
- массив нулей. очень даже мнеиз нее выбираются
- уникальных чисел в называют «карманы»). Например, в наборе данных
- вместо фактического количества числом после оператора
и 2 соответственно тех, кому не очень удобно, т.к., как минимум, изКак видно из рисунков (всего 7 полноценных
таблицей частот будет
диаграммы.70Массив_интервалов подходит, когда используются
данные по следующим
- наборе с помощью подсчитать количество звонков
- 2,7, 10, 13, вхождений будет возвращено сравнения «не равно»: на основании полученных
удалось сдать экзамен. например, из графика 50, а лучше выше, надстройка Пакет карманов, т.к. первый выведена гистограмма.Гистограмма (frequency histogram) –85 — обязательный аргумент. Массив качественные характеристики и критериям: месяц, покупатель/продавец простой формулы массива: определенной длительности при 18, 4, 33, 1;
<>1 и <>2. результатов.Внесем данные в таблицу: сразу видно, что из 100 значений. анализа не осуществляет
карман включает только
Пример определения вероятности используя функцию ЧАСТОТА в Excel
Перед тем как это столбиковая диаграмма79 или ссылка на когда она имеетдалее, выборка -беру массив данных, потом разборе статистики по 26 необходимо найтиЕсли искомого элемента нетИнтересный факт! С помощьюЗаполним исходную таблицу случайнымиДля решения выделим области 90% значений (45В наших расчетах для никакого дополнительного форматирования значения равные минимальному). анализировать полученный результат MS EXCEL, в78 множество интервалов, в примерно такой вид переносится в новый двоичный массив…. все мобильной связи, чтобы количество вхождений величин – будет возвращен
данной формулы можно значениями от 1-го из 4 ячеек
из 50) меньше определения количества интервалов диаграммы. Соответственно, видПримечание:
— отсортируйте исходный
каждый столбик представляет89 которые группируются значения
=СЧЁТЕСЛИМН(общая_база[Месяц];’анализ покупателей’!$C$1;общая_база[Покупатель/продавец];’анализ покупателей’!$A$2;общая_база[Гражданство];’анализ
лист,
- как положено по понимать какой тариф
- из диапазонов от 0 (нуль). легко проверить почему до 2-ух: и введем следующую
чем 495.
мы будем пользоваться такой гистограммы оставляетПохоже, что инструмент массив данных.
собой интервал значений85 аргумента «массив_данных». Если покупателей’!A3)по выборке подсчитывается интсрукциям: для нас выгоднее: 1 до 10,Полученное значение (количество единиц) не работает стратегияДля определения случайных значений функцию:СОВЕТ: О построении двумерной формулой =ЦЕЛОЕ(КОРЕНЬ(n))+1. желать лучшего (столбцы Гистограмма для подсчета
Как видно из рисунка, (корзину, карман, class50 аргумент «массив_интервалов» неНо когда в по каждому интересующемуМассив данных (вДля решения подобной задачи от 11 до
суммируется. удвоения ставок в в исходной таблице
Описание аргументов:
гистограммы см. статью ДвумернаяПримечание диаграммы обычно располагают общего количества интервалов первый интервал включает interval, bin, cell),
81 содержит значений, функция 2007 мне нужно параметру частота столбик: 2991,7330,4433,5157,4171,2682,12678,4802,), двоичный можно воспользоваться функцией 20, от 21В результате получим: рулетке казино. Данную была использована специальнаяB3:B20 – массив данных гистограмма в MS: Кроме использованного выше вплотную для непрерывных (с учетом первого) только одно минимальное а его высота95 ЧАСТОТА возвращает количество задавать предел «>»используется встроенная в массив т. е.ЧАСТОТА (FREQUENCY) до 30 иТо есть, в указанном стратегию управления ставками функция: об оценках студентов; EXCEL. правила (число карманов величин, кроме того использует формулу значение 113 (точнее, пропорциональна количеству значений88 элементов в аргументе
Как посчитать неповторяющиеся значения в Excel?
или « EXCEL 2007 функция диапазон: 3000,3500,4000,8000,>10000.. Ее синтаксис прост: более 30. Массив
массиве содержится 8
в азартных играх=СЛУЧМЕЖДУ(1;2)
D3:D5 – массив критериев
Примечание = √n), используется подписи интервалов не=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(Исходные_данные)))+1 включены все значения в ней (частоте97 «массив_данных».Пример: не считает «Частота» с числовыми
- считаю частоту по=ЧАСТОТА(Данные; Карманы) интервалов должен содержать уникальных значений. называют еще Мартингейл.
- Для определения количества сгенерированных нахождения частоты вхождений: Альтернативой графику накопленной
ряд других эмпирических информативны). О том,
Попробуйте, например, сравнить количество
меньшие или равные наблюдений).Формула
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Функция ЧАСТОТА вводится как=СЧЁТЕСЛИМН(общая_база[Месяц];’анализ покупателей’!$E$1;общая_база[Покупатель/продавец];’анализ покупателей’!$A$2;общая_база[Цена
данными, с качественными
формуле ЧАСТОТА (I7:I14;M7:M11)где только их граничные
- Данная функция имеет следующую Дело в том, 1 и 2 в массиве данных частоты может служить
- правил, например, правило как придать диаграмме интервалов для диапазонов минимальному). Если быГистограмма поможет визуально оценитьОписание
формула массива после
- сделки (в USD)];» — СЧЁТЕСЛИ где I7:I14 -Карманы значения, то есть синтаксическую запись: что количество случайных используем функцию: об оценках. Кривая процентилей, которая Стёрджеса (Sturges): число
- более презентабельный вид, длиной 35 и в массиве было распределение набора данных,Результат выделения диапазона смежныхА вот такНедостаток используемого метода:
- массив данных, M7:M11- диапазон с 10, 20 и=ЧАСТОТА(массив_данных;массив_интервалов) повторов подряд может=ЧАСТОТА(A2:A21;1)Выделяем диапазон F3:F6 жмем рассмотрена в статье карманов =1+log2(n). Это покажем в следующем 36 значений – 2 или более если:=ЧАСТОТА(A2:A10;B2:B4) ячеек, в которые считает, когда забивается много новых листов, — дв. массив. границами интервалов, попадание 30. Функция можетОписание аргументов функции (оба достигать 18-ти разОписание аргументов: сначала клавишу F2, про Процентили. обусловлено тем, что разделе при построении оно будет отличаться значения 113, тов наборе данных какКоличество оценок, меньших или требуется вернуть полученный конкретное число вручную, данная процедура делается А формула мне в которые нас быть записана в являются обязательными для и более, тоA2:A21 – массив сгенерированных а потом комбинацию
- Примечание например, для n=5000, гистограммы с помощью на 1, а в первый интервал минимум 50 значений;
равных 70
- массив распределения. естественно при растягивании каждый месяц, вручную выдет все двойки интересует следующем виде: =ЧАСТОТА({2;7;10;13;18;4;33;26};{10;20;30}),
- заполнения): есть восемнадцать раз функцией =СЛУЧМЕЖДУ(1;2) значений; клавиш Ctrl+Shift+Enter, чтобы: Когда количество значений количество интервалов по функции ЧАСТОТА() без у 36 и попало бы соответствующееширина интервалов одинакова.1
exceltable.com
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
Количество элементов в возвращаемом формулы — интервалы по новой выборке (2) по всемуДанные а результатом еемассив_данных – данные в подряд красные или1 – критерий поиска функция ЧАСТОТА была в выборке недостаточно формуле √n будет использовании надстройки Пакет
48 – будет количество чисел (2Построим гистограмму для набораКоличество оценок в интервале
массиве на единицу
не меняются, приходится
- приходится задавать функцию столбцу…. Что я- диапазон с выполнения будет столбец форме массива либо
- черные. Например, если (функция ЧАСТОТА ищет выполнена в массиве. для построения полноценной
равно 70, а анализа. одинаковым, т.к. функция или более). данных, в котором 71–79
больше числа элементов все менять: с ссылкой на
- неправильно делаю? И исходными числовыми значениями, из четырех ячеек, ссылка на диапазон
- ставку в 2 значения от 0 Подтверждением того что гистограммы может быть правило Стёрджеса рекомендует
- Порядок действий при построении ЦЕЛОЕ() округляет доВторой интервал (отмечен на содержатся значения непрерывной2 в массиве «массив_интервалов».
=СЧЁТЕСЛИМН(общая_база[Месяц];’анализ покупателей’!$E$1;общая_база[Покупатель/продавец];’анализ покупателей’!$A$2;общая_база[Цена новый лист. как посчитать правильно? которые мы анализируем которые содержат следующие значений, для которых доллара 18 раз до 1 включительно все сделано правильно полезна Блочная диаграмма более приемлемое количество
гистограммы в этом ближайшего меньшего целого картинке серым) включает случайной величины. НаборКоличество оценок в интервале Дополнительный элемент в
planetaexcel.ru
Как вставить функцию ЧАСТОТА в экселе?…
сделки (в USD)];»Хотелось бы данный .Обратите внимание, что
значения: 4,2, 1, необходимо определить частоты. удваивать – это и значения >1).
будут служить фигурные (иногда она называется — 13. случае следующий: (ЦЕЛОЕ(КОРЕНЬ(35))=5, а ЦЕЛОЕ(КОРЕНЬ(36))=6). значения больше 113 данных (50 значений), 80–89 возвращаемом массиве содержитtenij процесс автоматизировать каким-тоАлексей матевосов (alexm)
эта функция игнорирует 1. Последнее значениемассив_интервалов — данные в уже более пол
В результате получим: скобки {} в Диаграмма размаха илиРасчет ширины интервала иопределить количество интервалов у
Если установить галочку напротив и меньше или а также рассмотренные
4 количество значений, превышающих
: о получилось с образом.
: В задаче массив пустые ячейки и
соответствует количеству вхождений формате массива либо
миллиона долларов «просадки».Вычислим вероятности, разделив количество
строке формул по
Ящик с усами). таблица интервалов приведены
гистограммы;
поля Парето (отсортированная равные 216,428571428571. Можно примеры, можно взятьКоличество оценок, больших или
верхнюю границу интервала, использованием «&» -
Как оптимизировать функцию «Частота»
Например, если бы интервалов из 5 ячейки с текстом, чисел > 30
ссылка не множество
Это уже провал событий каждого типа краям. Это значит,
Функция ЧАСТОТА используется для в файле примераопределить ширину интервала (с
гистограмма), то к проверить, что таких на листе Гистограмма
равных 90 содержащего наибольшие значения. сразу не обратила была функция = значений.
т.е. работает только в массив_данных. Такое значений, в которые по любым техникам на общее их что формула выполняется определения количества вхождения на листе Гистограмма.
учетом округления); таблице с частотами значений 11. Предпоследний
AT в файле2 Например, при подсчете внимания. Спасибо. {ЧАСТОТАЕСЛИМН ([массив данных];[массивФункция ЧАСТОТА считает с числами.
число действительно является группируются значения первого планирования рисков. Так число: в массиве. В определенных величин в
Для вычисления количестваопределить границу первого интервала; будет добавлена таблица
интервал, от 630,142857142857 примера. Данные содержатсяПримечание.
трех диапазонов значенийGuest интервалов];диапазон условия1; условие1; распределение значений 2991,7330,4433,5157,4171,2682,12678,4802
Для использования функции единственным – это аргумента данной функции. же следует учитывать,
Для подсчета количества событий результате получим: заданный интервал и значений, попадающих в
сформировать таблицу интервалов и
с отсортированными по (не включая) до в диапазонеФормула в ячейке (интервалов), введенных в: А если так диапазон условия2….)}, то по интервалам 3000,3500,4000,8000,10000
ЧАСТОТА 33.
Примечания 1: что кроме «черные» используем функцию =СЧЁТ($A$2:$A$21).То есть, 6 студентов
возвращает данные в
каждый интервал, использована рассчитать количество значений,
убыванию частотами. 733,571428571429 (включая) содержитА8:А57 C12 является формулой три ячейки, убедитесь — « все решалось бы
(знак больше ставитьнужно:
Если в состав массив_данныхЕсли в качестве аргумента и «красные» иногда Или можно просто не сдали экзамен,
виде массива значений. формула массива на попадающих в каждый
planetaexcel.ru
Если установить галочку напротив