Как найти относительную плотность по воздуху формула

Как вычислять относительную плотность вещества

Такая характеристика, как относительная плотность вещества, показывает, во сколько раз оно тяжелее или легче другого соединения. Этот параметр можно определять по отношению к любому газообразному веществу. В большинстве случаев проводятся расчеты относительно воздуха или водорода. Однако могут попадаться задания, в которых необходимо вычислить относительную плотность и по другим газам, таким как кислород, аммиак или сероводород. В любом случае принцип решения задания един.

Вам понадобится

• — периодическая система химических элементов Д.И. Менделеева;
• — калькулятор.

Инструкция

Для того чтобы справиться с задачей, необходимо использовать формулы на определение относительной плотности:

D (воздух) = Mr (газа)/ Mr (воздуха), где:

D (воздух) – относительная плотность;
Mr (газа) – относительная молекулярная масса газообразного вещества;
Mr (воздуха) — относительная молекулярная масса воздуха.

Все три параметра единиц измерения не имеют.

Mr (воздуха) = 29 (величина постоянная), следовательно формула будет иметь вид:
D (воздух) = Mr (газа)/ 29.

По аналогии выглядит формула на определение относительной плотности по водороду, с тем исключением, что вместо воздуха стоит водород. А значит, и в расчет берется относительная молекулярная масса водорода.

D (водород) = Mr (газа)/ Mr (водорода);
D (водород) – относительная плотность;
Mr (газа) – относительная молекулярная масса газообразного вещества;
Mr (водорода) — относительная молекулярная масса водорода.

Mr (водорода) = 2, следовательно и формула будет иметь вид:
D (воздух) = Mr (газа)/ 2.

Пример № 1. Вычислите относительную плотность аммиака по воздуху. Аммиак имеет формулу NH3.

Сначала найдите относительную молекулярную массу аммиака, которую можно рассчитать по таблице Д.И. Менделеева.

Ar (N) = 14, Ar (H) = 3 х 1 = 3, отсюда
Mr (NH3) = 14 + 3 = 17

Подставьте полученные данные в формулу на определение относительной плотности по воздуху:
D (воздух) = Mr (аммиака)/ Mr (воздуха);
D (воздух) = Mr (аммиака)/ 29;
D (воздух) = 17/ 29 = 0, 59.

Пример № 2. Вычислите относительную плотность аммиака по водороду.

Подставьте данные в формулу на определение относительной плотности по водороду:
D (водород) = Mr (аммиака)/ Mr (водорода);
D (водород) = Mr (аммиака)/ 2;
D (водород) = 17/ 2 = 8, 5.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Относительная плотность по… задачи

24-Фев-2013 | комментариев 26 | Лолита Окольнова

В ЕГЭ иногда встречаются задачи (часть С последнее задание), где в условии дана относительная плотность вещества по… водороду, кислороду, воздуху, азоту и т.д.

Например:

Относительная плотность вещества  – отношение плотности вещества Б к плотности вещества А

Относительная плотность  — величина безразмерная

Формула достаточно простая, и из нее вытекает другая формула —

Формула молярной массы вещества

Mr1 = D•Mr2

• Если дана относительная плотность паров по водороду, то Mr (вещества)=Mr(H2)•D=2 гмоль • D;
• если дана относительная плотность по воздуху, то Mr (вещества)=Mr(воздуха)•D=29 гмоль • D (обратите внимание, Mr(воздуха) принята равной 29 гмоль);

и т.д.

В условии задачи может быть полная формулировка — «относительная плотность (паров)…», а может быть просто «плотность вещества по…»

Давайте решим нашу задачу:

Дана плотность паров вещества по воздуху, значит, нам подходит формула  молярной массы вещества —

Mr (вещества)=Mr(воздуха)•D=29 гмоль • D

Mr(вещества)=29 гмоль • 1.448 = 42 гмоль

Нам дан углеводород — СхHy, значит, мы можем найти Mr(Cx и Mr(Hy). Обратите внимание, именно молярные массы, т.к.у нас несколько атомов углерода и водорода.

Для этого надо молярную массу вещества умножить на процентное содержание элемента:

Mr(Cx)=Mr(вещества)•ω

Mr(Cx)= 42 гмоль · 0.8571=36 гмоль

x=Mr(Cx)Ar(C)=36 гмоль ÷ 12 гмоль =3.

Точно  так же находим все данные для водорода:

Mr(Hy)=Mr(вещества)•ω

Mr(Hy)= 42 гмоль · 0.1429=6 гмоль

x=Mr(Hy)Ar(H)=6 гмоль ÷ 1 гмоль =6.

Искомое вещество — C3H6 — пропен.

Еще раз повторим определение —

Относительная плотность газа – это сравнение молярной или относительной молекулярной массы одного газа с аналогичным показателем другого газа.

Дана относительная плотность по аргону.

Mr (вещества)=Ar(Ar)•D

Mr (CxHy)=40 гмоль ·1.05=42 гмоль

Запишем уравнение горения:

СхHy + O2 = xCO2 + y2H2O

Найдем количество углекислого газа и воды:

n(CO2)=V22,4 лмоль = 33.622.4=1.5

n(H2O)=mMr=2718=1.5

Соотношение х : y2 как 1.5 : 1.5, т.е. y=2x, что соответствует общей формуле алкенов: CnH2n

 
Выражаем в общем виде молярную массу: Mr=Mr(C) + Mr(H)
 

12n +2n=42

n=3

Наше вещество — C3H6 — пропен

---

• pадание ЕГЭ по этой теме — задачи С5

---

Обсуждение: «Относительная плотность по… задачи»

(Правила комментирования)

В этой статье мы коснемся нескольких краеугольных понятий в химии, без которых совершенно невозможно
решение задач. Старайтесь понять смысл физических величин, чтобы усвоить эту тему.

Я постараюсь приводить как можно больше примеров по ходу этой статьи, в ходе изучения вы увидите множество примеров
по данной теме.

Относительная атомная масса — A_r

Представляет собой массу атома, выраженную в атомных единицах массы. Относительные атомные массы указаны в периодической
таблице Д.И. Менделеева. Так, один атом водорода имеет атомную массу = 1, кислород = 16, кальций = 40.

Относительная молекулярная масса — M_r

Относительная молекулярная масса складывается из суммы относительных атомных масс всех атомов, входящих в состав вещества.
В качестве примера найдем относительные молекулярные массы кислорода, воды, перманганата калия и медного купороса:

M_r (O₂) = (2 × A_r(O)) = 2 × 16 = 32

M_r (H₂O) = (2 × A_r(H)) + A_r(O) = (2 × 1) + 16 = 18

M_r (KMnO₄) = A_r(K) + A_r(Mn) + (4 × A_r(O)) = 39 + 55 + (4 * 16) = 158

M_r (CuSO₄*5H₂O) = A_r(Cu) + A_r(S) + (4 × A_r(O)) + (5 × ((A_r(H) × 2) +
A_r(O))) = 64 + 32 + (4 × 16) + (5 × ((1 × 2) + 16)) = 160 + 5 * 18 = 250

Моль и число Авогадро

Моль — единица количества вещества (в системе единиц СИ), определяемая как количество вещества, содержащее столько же структурных единиц
этого вещества (молекул, атомов, ионов) сколько содержится в 12 г изотопа ¹²C, т.е. 6 × 10²³.

Число Авогадро (постоянная Авогадро, N_A) — число частиц (молекул, атомов, ионов) содержащихся в одном моле любого вещества.

Больше всего мне хотелось бы, чтобы вы поняли физический смысл изученных понятий. Моль — международная единица количества вещества, которая
показывает, сколько атомов, молекул или ионов содержится в определенной массе или конкретном объеме вещества. Один моль любого вещества
содержит 6.02 × 10²³ атомов/молекул/ионов — вот самое важное, что сейчас нужно понять.

Иногда в задачах бывает дано число Авогадро, и от вас требуется найти, какое вам дали количество вещества (моль). Количество вещества в химии
обозначается N, ν (по греч. читается «ню»).

Рассчитаем по формуле: ν = N/N_A количество вещества 3.01 × 10²³ молекул воды и 12.04 × 10²³ атомов углерода.

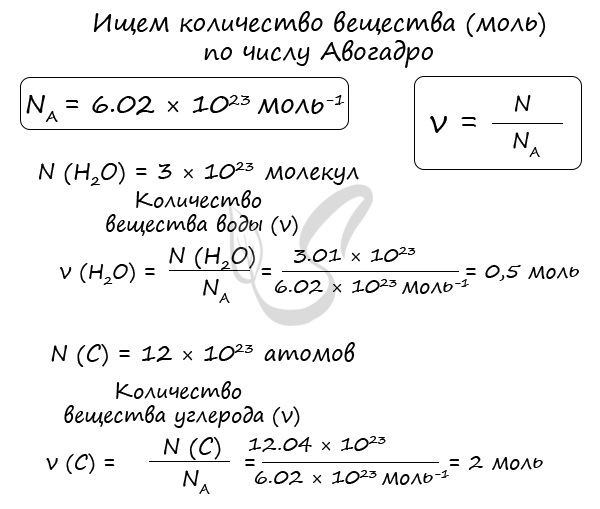
Мы нашли количества вещества (моль) воды и углерода. Сейчас это может показаться очень абстрактным, но, иногда не зная, как найти
количество вещества, используя число Авогадро, решение задачи по химии становится невозможным.

Молярная масса — M

Молярная масса — масса одного моля вещества, выражается в «г/моль» (грамм/моль). Численно совпадает с изученной нами ранее
относительной молекулярной массой.

Рассчитаем молярные массы CaCO₃, HCl и N₂

M (CaCO₃) = A_r(Ca) + A_r(C) + (3 × A_r(O)) = 40 + 12 + (3 × 16) = 100 г/моль

M (HCl) = A_r(H) + A_r(Cl) = 1 + 35.5 = 36.5 г/моль

M (N₂) = A_r(N) × 2 = 14 × 2 = 28 г/моль

Полученные знания не должны быть отрывочны, из них следует создать цельную систему. Обратите внимание: только что мы рассчитали
молярные массы — массы одного моля вещества. Вспомните про число Авогадро.

Получается, что, несмотря на одинаковое число молекул в 1 моле (1 моль любого вещества содержит 6.02 × 10²³ молекул),
молекулярные массы отличаются. Так, 6.02 × 10²³ молекул N₂ весят 28 грамм, а такое же количество молекул
HCl — 36.5 грамм.

Это связано с тем, что, хоть количество молекул одинаково — 6.02 × 10²³, в их состав входят разные атомы, поэтому и
массы получаются разные.

Часто в задачах бывает дана масса, а от вас требуется рассчитать количество вещества, чтобы перейти к другому веществу в реакции.
Сейчас мы определим количество вещества (моль) 70 грамм N₂, 50 грамм CaCO₃, 109.5 грамм HCl. Их молярные
массы были найдены нам уже чуть раньше, что ускорит ход решения.

ν (CaCO₃) = m(CaCO₃) : M(CaCO₃) = 50 г. : 100 г/моль = 0.5 моль

ν (HCl) = m(HCl) : M(HCl) = 109.5 г. : 36.5 г/моль = 3 моль

Иногда в задачах может быть дано число молекул, а вам требуется рассчитать массу, которую они занимают. Здесь нужно использовать
количество вещества (моль) как посредника, который поможет решить поставленную задачу.

Предположим нам дали 15.05 × 10²³ молекул азота, 3.01 × 10²³ молекул CaCO₃ и 18.06 × 10²³ молекул
HCl. Требуется найти массу, которую составляет указанное число молекул. Мы несколько изменим известную формулу, которая поможет нам связать
моль и число Авогадро.

Теперь вы всесторонне посвящены в тему. Надеюсь, что вы поняли, как связаны молярная масса, число Авогадро и количество вещества.
Практика — лучший учитель. Найдите самостоятельно подобные значения для оставшихся CaCO₃ и HCl.

Молярный объем

Молярный объем — объем, занимаемый одним молем вещества. Примерно одинаков для всех газов при стандартной температуре
и давлении составляет 22.4 л/моль. Он обозначается как — V_M.

Подключим к нашей системе еще одно понятие. Предлагаю найти количество вещества, количество молекул и массу газа объемом
33.6 литра. Поскольку показательно молярного объема при н.у. — константа (22.4 л/моль), то совершенно неважно, какой газ мы
возьмем: хлор, азот или сероводород.

Запомните, что 1 моль любого газа занимает объем 22.4 литра. Итак, приступим к решению задачи. Поскольку какой-то газ
все же надо выбрать, выберем хлор — Cl₂.

Моль (количество вещества) — самое гибкое из всех понятий в химии. Количество вещества позволяет вам перейти и к
числу Авогадро, и к массе, и к объему. Если вы усвоили это, то главная задача данной статьи — выполнена

Относительная плотность и газы — D

Относительной плотностью газа называют отношение молярных масс (плотностей) двух газов. Она показывает, во сколько раз одно вещество
легче/тяжелее другого. D = M (1 вещества) / M (2 вещества).

В задачах бывает дано неизвестное вещество, однако известна его плотность по водороду, азоту, кислороду или
воздуху. Для того чтобы найти молярную массу вещества, следует умножить значение плотности на молярную массу
газа, по которому дана плотность.

Запомните, что молярная масса воздуха = 29 г/моль. Лучше объяснить, что такое плотность и с чем ее едят на примере.
Нам нужно найти молярную массу неизвестного вещества, плотность которого по воздуху 2.5

Предлагаю самостоятельно решить следующую задачку (ниже вы найдете решение): «Плотность неизвестного вещества по
кислороду 3.5, найдите молярную массу неизвестного вещества»

Относительная плотность и водный раствор — ρ

Пишу об этом из-за исключительной важности в решении
сложных задач, высокого уровня, где особенно часто упоминается плотность. Обозначается греческой буквой ρ.

Плотность является отражением зависимости массы от вещества, равна отношению массы вещества к единице его объема. Единицы
измерения плотности: г/мл, г/см³, кг/м³ и т.д.

Для примера решим задачку. Объем серной кислоты составляет 200 мл, плотность 1.34 г/мл. Найдите массу раствора. Чтобы не
запутаться в единицах измерения поступайте с ними как с самыми обычными числами: сокращайте при делении и умножении — так
вы точно не запутаетесь.

Иногда перед вами может стоять обратная задача, когда известна масса раствора, плотность и вы должны найти объем. Опять-таки,
если вы будете следовать моему правилу и относится к обозначенным условным единицам «как к числам», то не запутаетесь.

В ходе ваших действий «грамм» и «грамм» должны сократиться, а значит, в таком случае мы будем делить массу на плотность. В противном случае
вы бы получили граммы в квадрате

К примеру, даны масса раствора HCl — 150 грамм и плотность 1.76 г/мл. Нужно найти объем раствора.

Массовая доля — ω

Массовой долей называют отношение массы растворенного вещества к массе раствора. Важно заметить, что в понятие раствора входит
как растворитель, так и само растворенное вещество.

Массовая доля вычисляется по формуле ω (вещества) = m (вещества) / m (раствора). Полученное число будет показывать массовую долю
в долях от единицы, если хотите получить в процентах — его нужно умножить на 100%. Продемонстрирую это на примере.

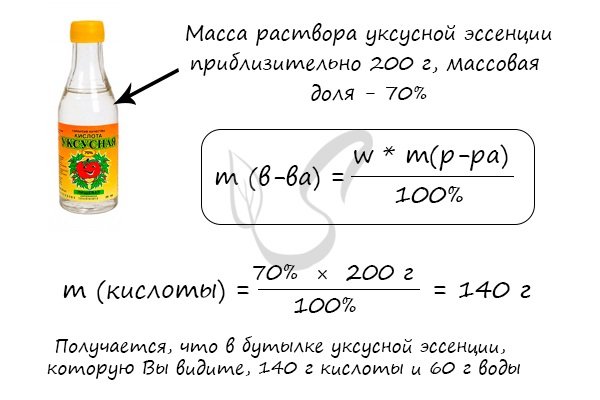
Решим несколько иную задачу и найдем массу чистой уксусной кислоты в широко известной уксусной эссенции.

Specific gravity
Common symbols	SG
SI unit	Unitless
Derivations from other quantities

Relative density, or specific gravity,^[1][2] is the ratio of the density (mass of a unit volume) of a substance to the density of a given reference material. Specific gravity for liquids is nearly always measured with respect to water at its densest (at 4 °C or 39.2 °F); for gases, the reference is air at room temperature (20 °C or 68 °F). The term «relative density» (often abbreviated r.d. or RD) is often preferred in scientific usage, whereas the term «specific gravity» is deprecated.^{[citation needed]}

If a substance’s relative density is less than 1 then it is less dense than the reference; if greater than 1 then it is denser than the reference. If the relative density is exactly 1 then the densities are equal; that is, equal volumes of the two substances have the same mass. If the reference material is water, then a substance with a relative density (or specific gravity) less than 1 will float in water. For example, an ice cube, with a relative density of about 0.91, will float. A substance with a relative density greater than 1 will sink.

Temperature and pressure must be specified for both the sample and the reference. Pressure is nearly always 1 atm (101.325 kPa). Where it is not, it is more usual to specify the density directly. Temperatures for both sample and reference vary from industry to industry. In British brewing practice, the specific gravity, as specified above, is multiplied by 1000.^[3] Specific gravity is commonly used in industry as a simple means of obtaining information about the concentration of solutions of various materials such as brines, must weight (syrups, juices, honeys, brewers wort, must, etc.) and acids.

Basic calculation[edit]

Relative density () or specific gravity () is a dimensionless quantity, as it is the ratio of either densities or weights

where is relative density, is the density of the substance being measured, and is the density of the reference. (By convention , the Greek letter rho, denotes density.)

The reference material can be indicated using subscripts: which means «the relative density of substance with respect to reference«. If the reference is not explicitly stated then it is normally assumed to be water at 4 °C (or, more precisely, 3.98 °C, which is the temperature at which water reaches its maximum density). In SI units, the density of water is (approximately) 1000 kg/m³ or 1 g/cm³, which makes relative density calculations particularly convenient: the density of the object only needs to be divided by 1000 or 1, depending on the units.

The relative density of gases is often measured with respect to dry air at a temperature of 20 °C and a pressure of 101.325 kPa absolute, which has a density of 1.205 kg/m³. Relative density with respect to air can be obtained by

where is the molar mass and the approximately equal sign is used because equality pertains only if 1 mol of the gas and 1 mol of air occupy the same volume at a given temperature and pressure, i.e., they are both ideal gases. Ideal behaviour is usually only seen at very low pressure. For example, one mol of an ideal gas occupies 22.414 L at 0 °C and 1 atmosphere whereas carbon dioxide has a molar volume of 22.259 L under those same conditions.

Those with SG greater than 1 are denser than water and will, disregarding surface tension effects, sink in it. Those with an SG less than 1 are less dense than water and will float on it. In scientific work, the relationship of mass to volume is usually expressed directly in terms of the density (mass per unit volume) of the substance under study. It is in industry where specific gravity finds wide application, often for historical reasons.

True specific gravity of a liquid can be expressed mathematically as:

where is the density of the sample and is the density of water.

The apparent specific gravity is simply the ratio of the weights of equal volumes of sample and water in air:

where represents the weight of the sample measured in air and the weight of an equal volume of water measured in air.

It can be shown that true specific gravity can be computed from different properties:

where g is the local acceleration due to gravity, V is the volume of the sample and of water (the same for both), ρ_sample is the density of the sample, ρ_H2O is the density of water, W_V represents a weight obtained in vacuum, is the mass of the sample and is the mass of an equal volume of water.

The density of water varies with temperature and pressure as does the density of the sample. So it is necessary to specify the temperatures and pressures at which the densities or weights were determined. It is nearly always the case that measurements are made at 1 nominal atmosphere (101.325 kPa ± variations from changing weather patterns). But as specific gravity usually refers to highly incompressible aqueous solutions or other incompressible substances (such as petroleum products), variations in density caused by pressure are usually neglected at least where apparent specific gravity is being measured. For true (in vacuo) specific gravity calculations, air pressure must be considered (see below). Temperatures are specified by the notation (T_s/T_r), with T_s representing the temperature at which the sample’s density was determined and T_r the temperature at which the reference (water) density is specified. For example, SG (20 °C/4 °C) would be understood to mean that the density of the sample was determined at 20 °C and of the water at 4 °C. Taking into account different sample and reference temperatures, we note that, while SG_H2O = 1.000000 (20 °C/20 °C), it is also the case that SG_H2O = 0.998203⁄0.999840 = 0.998363 (20 °C/4 °C). Here, temperature is being specified using the current ITS-90 scale and the densities^[4] used here and in the rest of this article are based on that scale. On the previous IPTS-68 scale, the densities at 20 °C and 4 °C are 0.9982071 and 0.9999720 respectively, resulting in an SG (20 °C/4 °C) value for water of 0.9982343.

As the principal use of specific gravity measurements in industry is determination of the concentrations of substances in aqueous solutions and as these are found in tables of SG versus concentration, it is extremely important that the analyst enter the table with the correct form of specific gravity. For example, in the brewing industry, the Plato table lists sucrose concentration by weight against true SG, and was originally (20 °C/4 °C)^[5] i.e. based on measurements of the density of sucrose solutions made at laboratory temperature (20 °C) but referenced to the density of water at 4 °C which is very close to the temperature at which water has its maximum density, ρ_H2O equal to 999.972 kg/m³ in SI units (0.999972 g/cm³ in cgs units or 62.43 lb/cu ft in United States customary units). The ASBC table^[6] in use today in North America, while it is derived from the original Plato table is for apparent specific gravity measurements at (20 °C/20 °C) on the IPTS-68 scale where the density of water is 0.9982071 g/cm³. In the sugar, soft drink, honey, fruit juice and related industries, sucrose concentration by weight is taken from a table prepared by A. Brix, which uses SG (17.5 °C/17.5 °C). As a final example, the British SG units are based on reference and sample temperatures of 60 °F and are thus (15.56 °C/15.56 °C).

Given the specific gravity of a substance, its actual density can be calculated by rearranging the above formula:

Occasionally a reference substance other than water is specified (for example, air), in which case specific gravity means density relative to that reference.

Temperature dependence[edit]

See Density for a table of the measured densities of water at various temperatures.

The density of substances varies with temperature and pressure so that it is necessary to specify the temperatures and pressures at which the densities or masses were determined. It is nearly always the case that measurements are made at nominally 1 atmosphere (101.325 kPa ignoring the variations caused by changing weather patterns) but as relative density usually refers to highly incompressible aqueous solutions or other incompressible substances (such as petroleum products) variations in density caused by pressure are usually neglected at least where apparent relative density is being measured. For true (in vacuo) relative density calculations air pressure must be considered (see below). Temperatures are specified by the notation (T_s/T_r) with T_s representing the temperature at which the sample’s density was determined and T_r the temperature at which the reference (water) density is specified. For example, SG (20 °C/4 °C) would be understood to mean that the density of the sample was determined at 20 °C and of the water at 4 °C. Taking into account different sample and reference temperatures we note that while SG_H2O = 1.000000 (20 °C/20 °C) it is also the case that RD_H2O = 0.998203/0.998840 = 0.998363 (20 °C/4 °C). Here temperature is being specified using the current ITS-90 scale and the densities^[7] used here and in the rest of this article are based on that scale. On the previous IPTS-68 scale the densities at 20 °C and 4 °C are, respectively, 0.9982071 and 0.9999720 resulting in an RD (20 °C/4 °C) value for water of 0.9982343.

The temperatures of the two materials may be explicitly stated in the density symbols; for example:

relative density: 8.15^20 °C
_4 °C; or specific gravity: 2.432¹⁵
₀

where the superscript indicates the temperature at which the density of the material is measured, and the subscript indicates the temperature of the reference substance to which it is compared.

Uses[edit]

Relative density can also help to quantify the buoyancy of a substance in a fluid or gas, or determine the density of an unknown substance from the known density of another. Relative density is often used by geologists and mineralogists to help determine the mineral content of a rock or other sample. Gemologists use it as an aid in the identification of gemstones. Water is preferred as the reference because measurements are then easy to carry out in the field (see below for examples of measurement methods).

As the principal use of relative density measurements in industry is determination of the concentrations of substances in aqueous solutions and these are found in tables of RD vs concentration it is extremely important that the analyst enter the table with the correct form of relative density. For example, in the brewing industry, the Plato table, which lists sucrose concentration by mass against true RD, were originally (20 °C/4 °C)^[8] that is based on measurements of the density of sucrose solutions made at laboratory temperature (20 °C) but referenced to the density of water at 4 °C which is very close to the temperature at which water has its maximum density of ρ(H
₂O) equal to 0.999972 g/cm³ (or 62.43 lb·ft⁻³). The ASBC table^[9] in use today in North America, while it is derived from the original Plato table is for apparent relative density measurements at (20 °C/20 °C) on the IPTS-68 scale where the density of water is 0.9982071 g/cm³. In the sugar, soft drink, honey, fruit juice and related industries sucrose concentration by mass is taken from this work^[3] which uses SG (17.5 °C/17.5 °C). As a final example, the British RD units are based on reference and sample temperatures of 60 °F and are thus (15.56 °C/15.56 °C).^[3]

Measurement[edit]

Relative density can be calculated directly by measuring the density of a sample and dividing it by the (known) density of the reference substance. The density of the sample is simply its mass divided by its volume. Although mass is easy to measure, the volume of an irregularly shaped sample can be more difficult to ascertain. One method is to put the sample in a water-filled graduated cylinder and read off how much water it displaces. Alternatively the container can be filled to the brim, the sample immersed, and the volume of overflow measured. The surface tension of the water may keep a significant amount of water from overflowing, which is especially problematic for small samples. For this reason it is desirable to use a water container with as small a mouth as possible.

For each substance, the density, ρ, is given by

When these densities are divided, references to the spring constant, gravity and cross-sectional area simply cancel, leaving

Hydrostatic weighing[edit]

Relative density is more easily and perhaps more accurately measured without measuring volume. Using a spring scale, the sample is weighed first in air and then in water. Relative density (with respect to water) can then be calculated using the following formula:

where

• W_air is the weight of the sample in air (measured in newtons, pounds-force or some other unit of force)
• W_water is the weight of the sample in water (measured in the same units).

This technique cannot easily be used to measure relative densities less than one, because the sample will then float. W_water becomes a negative quantity, representing the force needed to keep the sample underwater.

Another practical method uses three measurements. The sample is weighed dry. Then a container filled to the brim with water is weighed, and weighed again with the sample immersed, after the displaced water has overflowed and been removed. Subtracting the last reading from the sum of the first two readings gives the weight of the displaced water. The relative density result is the dry sample weight divided by that of the displaced water. This method allows the use of scales which cannot handle a suspended sample. A sample less dense than water can also be handled, but it has to be held down, and the error introduced by the fixing material must be considered.

Hydrometer[edit]

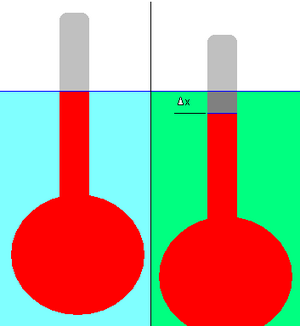
The relative density of a liquid can be measured using a hydrometer. This consists of a bulb attached to a stalk of constant cross-sectional area, as shown in the adjacent diagram.

First the hydrometer is floated in the reference liquid (shown in light blue), and the displacement (the level of the liquid on the stalk) is marked (blue line). The reference could be any liquid, but in practice it is usually water.

The hydrometer is then floated in a liquid of unknown density (shown in green). The change in displacement, Δx, is noted. In the example depicted, the hydrometer has dropped slightly in the green liquid; hence its density is lower than that of the reference liquid. It is necessary that the hydrometer floats in both liquids.

The application of simple physical principles allows the relative density of the unknown liquid to be calculated from the change in displacement. (In practice the stalk of the hydrometer is pre-marked with graduations to facilitate this measurement.)

In the explanation that follows,

• ρ_ref is the known density (mass per unit volume) of the reference liquid (typically water).
• ρ_new is the unknown density of the new (green) liquid.
• RD_new/ref is the relative density of the new liquid with respect to the reference.
• V is the volume of reference liquid displaced, i.e. the red volume in the diagram.
• m is the mass of the entire hydrometer.
• g is the local gravitational constant.
• Δx is the change in displacement. In accordance with the way in which hydrometers are usually graduated, Δx is here taken to be negative if the displacement line rises on the stalk of the hydrometer, and positive if it falls. In the example depicted, Δx is negative.
• A is the cross sectional area of the shaft.

Since the floating hydrometer is in static equilibrium, the downward gravitational force acting upon it must exactly balance the upward buoyancy force. The gravitational force acting on the hydrometer is simply its weight, mg. From the Archimedes buoyancy principle, the buoyancy force acting on the hydrometer is equal to the weight of liquid displaced. This weight is equal to the mass of liquid displaced multiplied by g, which in the case of the reference liquid is ρ_refVg. Setting these equal, we have

or just

(1)

Exactly the same equation applies when the hydrometer is floating in the liquid being measured, except that the new volume is V − AΔx (see note above about the sign of Δx). Thus,

(2)

Combining (1) and (2) yields

(3)

But from (1) we have V = m/ρ_ref. Substituting into (3) gives

(4)

This equation allows the relative density to be calculated from the change in displacement, the known density of the reference liquid, and the known properties of the hydrometer. If Δx is small then, as a first-order approximation of the geometric series equation (4) can be written as:

This shows that, for small Δx, changes in displacement are approximately proportional to changes in relative density.

Pycnometer[edit]

A pycnometer (from Greek: πυκνός (puknos) meaning «dense»), also called pyknometer or specific gravity bottle, is a device used to determine the density of a liquid. A pycnometer is usually made of glass, with a close-fitting ground glass stopper with a capillary tube through it, so that air bubbles may escape from the apparatus. This device enables a liquid’s density to be measured accurately by reference to an appropriate working fluid, such as water or mercury, using an analytical balance.^{[citation needed]}

If the flask is weighed empty, full of water, and full of a liquid whose relative density is desired, the relative density of the liquid can easily be calculated. The particle density of a powder, to which the usual method of weighing cannot be applied, can also be determined with a pycnometer. The powder is added to the pycnometer, which is then weighed, giving the weight of the powder sample. The pycnometer is then filled with a liquid of known density, in which the powder is completely insoluble. The weight of the displaced liquid can then be determined, and hence the relative density of the powder.

A gas pycnometer, the gas-based manifestation of a pycnometer, compares the change in pressure caused by a measured change in a closed volume containing a reference (usually a steel sphere of known volume) with the change in pressure caused by the sample under the same conditions. The difference in change of pressure represents the volume of the sample as compared to the reference sphere, and is usually used for solid particulates that may dissolve in the liquid medium of the pycnometer design described above, or for porous materials into which the liquid would not fully penetrate.

When a pycnometer is filled to a specific, but not necessarily accurately known volume, V and is placed upon a balance, it will exert a force

where m_b is the mass of the bottle and g the gravitational acceleration at the location at which the measurements are being made. ρ_a is the density of the air at the ambient pressure and ρ_b is the density of the material of which the bottle is made (usually glass) so that the second term is the mass of air displaced by the glass of the bottle whose weight, by Archimedes Principle must be subtracted. The bottle is filled with air but as that air displaces an equal amount of air the weight of that air is canceled by the weight of the air displaced. Now we fill the bottle with the reference fluid e.g. pure water. The force exerted on the pan of the balance becomes:

If we subtract the force measured on the empty bottle from this (or tare the balance before making the water measurement) we obtain.

where the subscript n indicated that this force is net of the force of the empty bottle. The bottle is now emptied, thoroughly dried and refilled with the sample. The force, net of the empty bottle, is now:

where ρ_s is the density of the sample. The ratio of the sample and water forces is:

This is called the apparent relative density, denoted by subscript A, because it is what we would obtain if we took the ratio of net weighings in air from an analytical balance or used a hydrometer (the stem displaces air). Note that the result does not depend on the calibration of the balance. The only requirement on it is that it read linearly with force. Nor does RD_A depend on the actual volume of the pycnometer.

Further manipulation and finally substitution of RD_V, the true relative density (the subscript V is used because this is often referred to as the relative density in vacuo), for ρ_s/ρ_w gives the relationship between apparent and true relative density:

In the usual case we will have measured weights and want the true relative density. This is found from

Since the density of dry air at 101.325 kPa at 20 °C is^[10] 0.001205 g/cm³ and that of water is 0.998203 g/cm³ we see that the difference between true and apparent relative densities for a substance with relative density (20 °C/20 °C) of about 1.100 would be 0.000120. Where the relative density of the sample is close to that of water (for example dilute ethanol solutions) the correction is even smaller.

The pycnometer is used in ISO standard: ISO 1183-1:2004, ISO 1014–1985 and ASTM standard: ASTM D854.

Types

• Gay-Lussac, pear shaped, with perforated stopper, adjusted, capacity 1, 2, 5, 10, 25, 50 and 100 mL
• as above, with ground-in thermometer, adjusted, side tube with cap
• Hubbard, for bitumen and heavy crude oils, cylindrical type, ASTM D 70, 24 mL
• as above, conical type, ASTM D 115 and D 234, 25 mL
• Boot, with vacuum jacket and thermometer, capacity 5, 10, 25 and 50 mL

Digital density meters[edit]

Hydrostatic Pressure-based Instruments: This technology relies upon Pascal’s Principle which states that the pressure difference between two points within a vertical column of fluid is dependent upon the vertical distance between the two points, the density of the fluid and the gravitational force. This technology is often used for tank gaging applications as a convenient means of liquid level and density measure.

Vibrating Element Transducers: This type of instrument requires a vibrating element to be placed in contact with the fluid of interest. The resonant frequency of the element is measured and is related to the density of the fluid by a characterization that is dependent upon the design of the element. In modern laboratories precise measurements of relative density are made using oscillating U-tube meters. These are capable of measurement to 5 to 6 places beyond the decimal point and are used in the brewing, distilling, pharmaceutical, petroleum and other industries. The instruments measure the actual mass of fluid contained in a fixed volume at temperatures between 0 and 80 °C but as they are microprocessor based can calculate apparent or true relative density and contain tables relating these to the strengths of common acids, sugar solutions, etc.

Ultrasonic Transducer: Ultrasonic waves are passed from a source, through the fluid of interest, and into a detector which measures the acoustic spectroscopy of the waves. Fluid properties such as density and viscosity can be inferred from the spectrum.

Radiation-based Gauge: Radiation is passed from a source, through the fluid of interest, and into a scintillation detector, or counter. As the fluid density increases, the detected radiation «counts» will decrease. The source is typically the radioactive isotope caesium-137, with a half-life of about 30 years. A key advantage for this technology is that the instrument is not required to be in contact with the fluid—typically the source and detector are mounted on the outside of tanks or piping.^[11]

Buoyant Force Transducer: the buoyancy force produced by a float in a homogeneous liquid is equal to the weight of the liquid that is displaced by the float. Since buoyancy force is linear with respect to the density of the liquid within which the float is submerged, the measure of the buoyancy force yields a measure of the density of the liquid. One commercially available unit claims the instrument is capable of measuring relative density with an accuracy of ± 0.005 RD units. The submersible probe head contains a mathematically characterized spring-float system. When the head is immersed vertically in the liquid, the float moves vertically and the position of the float controls the position of a permanent magnet whose displacement is sensed by a concentric array of Hall-effect linear displacement sensors. The output signals of the sensors are mixed in a dedicated electronics module that provides a single output voltage whose magnitude is a direct linear measure of the quantity to be measured.^[12]

The relative density in soil mechanics[edit]

The relative density a measure of the current void ratio in relation to the maximum and minimum void rations, and applied effective stress control the mechanical behavior of cohesionless soil. Relative density is defined by

in which , and are the maximum, minimum and actual void rations.

Examples[edit]

Material	Specific gravity
Balsa wood	0.2
Oak wood	0.75
Ethanol	0.78
Olive oil	0.91
Water	1
Ironwood	1.5
Graphite	1.9–2.3
Table salt	2.17
Aluminium	2.7
Cement	3.15
Iron	7.87
Copper	8.96
Lead	11.35
Mercury	13.56
Depleted uranium	19.1
Gold	19.3
Osmium	22.59

(Samples may vary, and these figures are approximate.)
Substances with a relative density of 1 are neutrally buoyant, those with RD greater than one are denser than water, and so (ignoring surface tension effects) will sink in it, and those with an RD of less than one are less dense than water, and so will float.

Example:

Helium gas has a density of 0.164 g/L;^[13] it is 0.139 times as dense as air, which has a density of 1.18 g/L.^[13]

• Urine normally has a specific gravity between 1.003 and 1.030. The Urine Specific Gravity diagnostic test is used to evaluate renal concentration ability for assessment of the urinary system.^[14] Low concentration may indicate diabetes insipidus, while high concentration may indicate albuminuria or glycosuria.^[14]
• Blood normally has a specific gravity of approximately 1.060.^[15]
• Vodka 80° proof (40% v/v) has a specific gravity of 0.9498.^[16]

See also[edit]

• API gravity
• Baumé scale
• Buoyancy
• Fluid mechanics
• Gravity (beer)
• Hydrometer
• Jolly balance
• Plato scale

References[edit]

Further reading[edit]

• Fundamentals of Fluid Mechanics Wiley, B.R. Munson, D.F. Young & T.H. Okishi
• Introduction to Fluid Mechanics Fourth Edition, Wiley, SI Version, R.W. Fox & A.T. McDonald
• Thermodynamics: An Engineering Approach Second Edition, McGraw-Hill, International Edition, Y.A. Cengel & M.A. Boles
• Munson, B. R.; D. F. Young; T. H. Okishi (2001). Fundamentals of Fluid Mechanics (4th ed.). Wiley. ISBN 978-0-471-44250-9.
• Fox, R. W.; McDonald, A. T. (2003). Introduction to Fluid Mechanics (4th ed.). Wiley. ISBN 0-471-20231-2.

External links[edit]

• Specific Gravity Weights Of Materials (archived 22 May 2006)

Как вам известно, вещества могут находиться в твёрдом, жидком и газообразном состоянии. Молекулы жидкости и твёрдого вещества располагаются близко друг к другу. Это возможно благодаря тому, что молекулы притягиваются друг к другу. То есть существуют силы, которые удерживают молекулы жидкости или твёрдого вещества вместе. Из курса химии 8-го класса вы знаете, что эти силы называются силами межмолекулярного взаимодействия. Молекулы газов находятся на значительно большем расстоянии друг от друга, чем в случае жидкостей и твёрдых веществ. На таком расстоянии молекулы практически не взаимодействуют друг с другом. Поэтому, чтобы превратить жидкость или твёрдое вещество в газ, необходимо преодолеть силы межмолекулярного взаимодействия, отдалив молекулы друг от друга.

Переход в газообразное состояние осуществляется в результате нагревания веществ, находящихся в твёрдом или жидком состоянии (кипение жидкостей, возгонка твёрдых веществ).

Так как расстояние между молекулами газов значительно больше размеров самих молекул, то объём, который занимает газ, — это, по существу, объём свободного пространства между хаотически движущимися молекулами газа. Величина этого пространства определяется условиями, при которых находится газ, т. е. температурой и давлением. Эта величина примерно одинакова для всех газов. При этом объёмом, занимаемым самими молекулами, можно пренебречь. Отсюда следует закон Авогадро — в равных объёмах различных газов при одинаковых условиях содержится одинаковое число молекул.

Из закона Авогадро вытекают два основных следствия.

Первое следствие. Один моль любого газа при одинаковых условиях занимает одинаковый объём. Этот объём называется молярным объёмом газа (V_m), и измеряется в дм³/моль. Молярный объём газа равен отношению объёма газа к его количеству:

.

Величина V_m зависит от температуры и давления. Например, при нагревании газы расширяются. Значит, при нагревании увеличивается молярный объём газа. В связи с этим сравнение характеристик различных газовых смесей необходимо осуществлять при одинаковых условиях — температуре и давлении. В качестве эталона таких условий приняты нормальные условия (н. у.): температура таяния льда (0 °С или 273,15 K) и атмосферное давление (101,3 кПа). При нормальных условиях V_m = 22,4 дм³/моль.

Таким образом, из закона Авогадро следует, что 22,4 дм³ любого газа при нормальных условиях содержат 6,02 ∙ 10²³ молекул.

Второе следствие. Плотности газов относятся между собой как молярные массы газов.

Это видно из следующих соображений. Пусть имеется две порции различных газов. Рассчитаем их плотности:

газ 1: ;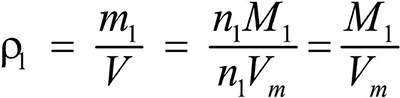

газ 2: .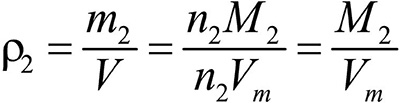

Разделив плотность первого газа на плотность второго, получим: .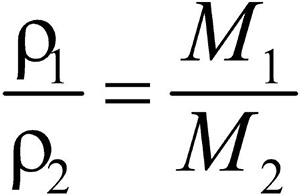

Отношение плотностей газов, равное отношению молярных масс, называется относительной плотностью одного газа по другому (D). D — величина безразмерная.

Зная D и молярную массу одного газа, легко найти молярную массу другого газа:

Пример 1. Относительная плотность газа по водороду равна 8. Определите молярную массу газа.

М(Х) = М(Н₂) ∙ D = 2 ∙ 8 = 16 г/моль.

Газ с такой молярной массой — метан СH₄.

Пример 2. Относительная плотность некоторого газообразного углеводорода по воздуху равна 2. Определите молярную массу углеводорода.

Средняя молярная масса воздуха равна 29 г/моль;

М(Х) = М(возд.) ∙ D = 29 ∙ 2 = 58 г/моль.

Углеводород с такой молярной массой — бутан С₄Н₁₀.

Следует отметить, что газы с молярной массой меньше 29 легче воздуха, больше 29 — тяжелее.

В расчётных задачах могут быть даны относительные плотности неизвестного газа по азоту, кислороду и другим газам. В этом случае для нахождения молярной массы неизвестного газа необходимо умножить относительную плотность на молярную массу соответственно азота (28 г/моль), кислорода (32 г/моль) и т. д.

Закон Авогадро широко применяется в химических расчётах. Поскольку для газов объёмы пропорциональны количествам (моль) веществ, то коэффициенты в уравнении реакции между газообразными веществами, отражающие количественное соотношение реагирующих веществ, пропорциональны объёмам взаимодействующих газов. Очевидно, что объёмы должны быть измерены при одинаковых условиях.

Пример 3. Какой объём кислорода потребуется для сжигания 2 дм³ пропана? Объёмы измерены при н. у.

Уравнение реакции горения пропана:

С₃Н₈ + 5О₂ 3СО₂ + 4Н₂О

Из закона Авогадро следует, что равные объёмы различных газов содержат одинаковое количество (моль) веществ. Пусть объём пропана равен 1 дм³. Тогда, согласно приведённому уравнению, для сжигания 1 дм³ пропана потребуется 5 дм³ кислорода. Следовательно, для сжигания 2 дм³ пропана потребуется:

1 дм³ С₃Н₈ — 5 дм³ O₂,

2 дм³ С₃Н₈ — 10 дм³ О₂

Ответ: V(О₂) = 10 дм³.

Смеси газов

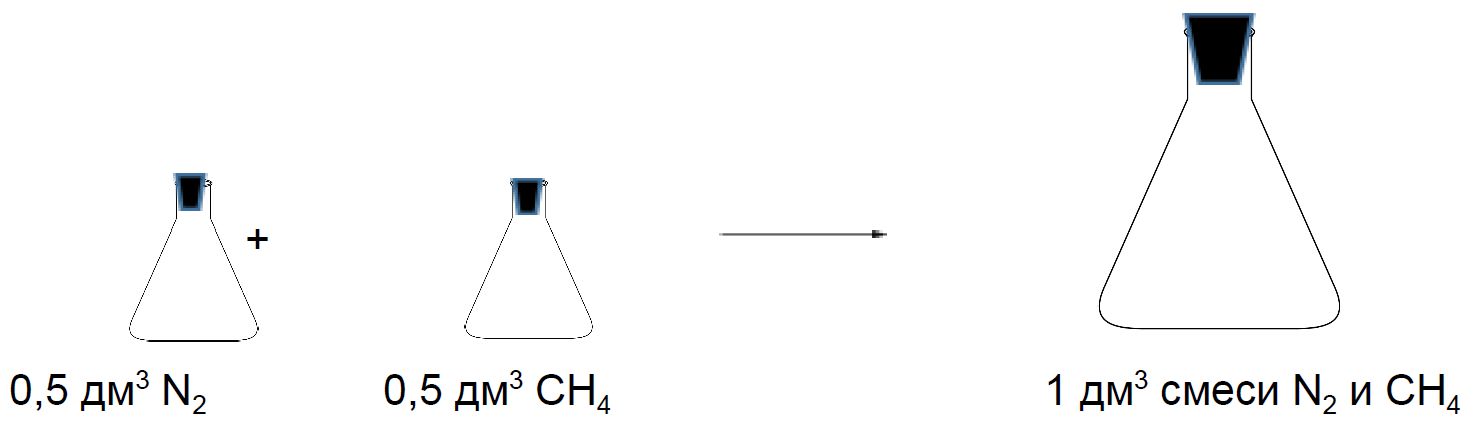
Рассмотрим две колбы объёмом 0,5 дм³. Одна колба заполнена азотом, а другая метаном. Давление и температура в колбах одинаковые. Если смешать содержимое этих колб, то полученная смесь займёт при таких же условиях объём 1 дм³.

Состав смеси газов часто выражают в объёмных долях. Объёмная доля газа обозначается греческой буквой φ (фи) и равна отношению объёма данного газа к объёму смеси. Рассчитаем объёмную долю азота в полученной выше смеси газов:

φ = = 0,5, или 50 %.

Пример 4. В результате пропускания 150 дм³ (н. у.) воздуха через избыток известковой воды выпало 0,201 г осадка. Найдите объёмную долю (%) углекислого газа в данном образце воздуха.

Уравнение реакции взаимодействия углекислого газа с известковой водой:

СО₂ + Са(ОН)₂ = СаСО₃ + Н₂О

Найдём количество (моль) карбоната кальция, выпавшего в осадок (M(CaCO₃) = 100 г/моль):

n(СаСО₃) = 0,201/100 = 0,00201 моль.

По уравнению реакции:

n(СаСО₃) = n(СО₂).

Рассчитаем объёмную долю углекислого газа в воздухе:

V(CO₂) = 0,00201 ∙ 22,4 = 0,045 дм³;

φ(СО₂) = 0,045/150 = 0,0003, или 0,03 %.

Ответ: φ(СО₂) = 0,03 %.

Пример 5. Объём смеси водорода с хлором составляет 50 см³. После взаимодействия газов осталось 10 см³ хлора. Найдите состав исходной смеси в объёмных долях. Все объёмы измерены при н. у.

Уравнение реакции взаимодействия водорода с хлором:

H₂ + Cl₂ 2HCl

Поскольку после взаимодействия осталось 10 см³ хлора, то 40 см³ исходной смеси прореагировало. Хлор и водород реагируют между собой в равных объёмных отношениях. Исходя из этих соображений, в реакцию вступили по 20 см³ хлора и водорода. Поскольку осталось 10 см³ хлора, то в первоначальной смеси было 20 см³ водорода и 30 см³ хлора.

Рассчитаем объёмные доли газов в исходной смеси:

φ(H₂) = 20/50 = 0,4, или 40 %;

φ(Cl₂) = 30/50 = 0,6, или 60 %.

Ответ: φ(H₂) = 40 %; φ(Cl₂) = 60 %.