Как найти относительную погрешность измерения массы - Исправление недочетов и поиск решений вместе с Examum.ru

ЛАБОРАТОРНАЯ РАБОТА 2

Прямые измерения
массы тела с помощью рычажных весов и определение полной погрешности измерений

Цель работы:
измерить массы трёх предложенных тел прямым способом и рассчитать полную погрешность
результатов прямых измерений.

Оборудование: три тела разной плотности, рычажные весы, разновес (набор гирь)

ТАОРЕТИЧЕСКИЕ СВЕДЕНИЯ

При определении
полной погрешности измеренного значения массы необходимо учитывать погрешность
весов , погрешность гирь
, и погрешность подбора гирь
.

Погрешность весов зависит от нагрузки линейно и
определяется по графику зависимости . Смотрите об этом §
75 учебника «физика-10» Пинский А.А. Вам необходимо построить такой график
самостоятельно в отчёте по следующим данным: при нагрузке погрешность весов ,
а при нагрузке погрешность весов (см.§ 75). Зная, что зависимость линейная, построение графика не составит
никакого труда.

Погрешность гирь ,
входящих в набор гирь (разновес) приводится в таблице 1. Смотрите также
§ 75 учебника «физика-10» Пинский А.А.

Таблица 1 Погрешность гирь

НОМИНАЛЬНОЕ ЗНАЧЕНИЕ МАССЫ ГИРИ	ГРАНИЦЫ ПОГРЕШНОСТИ
10 мг; 20 мг; 50 мг; 100 мг	1 мг
200 мг	2 мг
500 мг	3 мг
1г	4 мг
2г	6 мг
5 г	8 мг
10 г	12 мг
20 г	20 мг
50 г	30 мг
100 г	40 мг

Погрешность гирь
равна сумме погрешностей всех использованных гирь (формула 1)

(1)

Погрешность подбора гирь аналогична погрешности отсчёта и половине
значения наименьшей гири, находящейся на весах, или той, которая выводит весы
из равновесия (формула 2)

(2)

Таким образом, при прямом измерении массы тела
на весах граница абсолютной погрешности измерений (формула 3)

(3)

Ниже смотрите пример определения полной
погрешности массы тела, измеренной прямым способом на рычажных весах.

Пример определения полной погрешности
массы тела

Пусть весы
находятся в равновесии, если на чашке лежат гири со значениями массы: , , . Тогда за результат измерения массы тела
принимается значение

(4)

Погрешность
весов при нагрузке равна . Как было сказано выше, это определяется
по графику зависимости , который уже
необходимо построить.

Таким образом:

(5)

Погрешность
всех гирь определим, пользуясь таблицей 1,
(см. формулу 1):

(6)

Погрешность
подбора гирь определяем по значению наименьшей
гири на весах (см. формулу 2)

(7)

Полная
погрешность массы тела определяется как сумма всех
погрешностей (см. формулу 3)

(8)

Полная погрешность
округляется до одной значащей цифры (общее правило для любых измерений), поэтому
в нашем примере для погрешности получаем окончательно:

(9)

Результат измерения
массы записывается в интервальной форме:

Не забывайте, что
разряд последней цифры измеренного значения и разряд погрешности должны совпадать
(правило Брадиса-Крылова), поэтому в данном примере измеренное значение массы (см. формулу 4) округляется до разряда
десятых, т.к. погрешность находится в этом разряде (см. формулу 9)

Относительная
погрешность измерения массы определяется по
известной формуле:

ПРАКТИЧЕСКАЯ
ЧАСТЬ РАБОТЫ

ВНИМАНИЕ! Прежде
чем приступать к работе, вам необходимо изучить правила работы с весами. Обратитесь
к учебникам 7-го класса (Пёрышкин А.В. или Громов С.В.) и 10-го (Пинский А.А.).
Без знаний этих правил вас не допустят к работе.

Порядок
выполнения работы

Определите массу
первого тела. Запишите значение массы в виде суммы масс всех гирь
находящихся на весах. Смотрите пример выше.

(результат в граммах)

Постройте график
зависимости погрешности весов от нагрузки (смотрите теоретическую часть
работы) и по графику определите погрешность весов

(результат в миллиграммах)

Пользуясь таблицей
1, определите погрешность всех гирь

(результат в миллиграммах)

По значению наименьшей гири на весах (не в
наборе) определите погрешность подбора гирь

= (результат в миллиграммах)

Полная
погрешность определяется как сумма всех погрешностей

= (результат выразите в граммах и
округлите до одной значащей цифры)

Округлите
результат измерения массы (см. пункт 1 практической части) так, чтобы
последняя цифра в округлённом результате принадлежала тому же разряду, в
котором находится значащая цифра полной абсолютной погрешности (пункт 2).

Результат
запишите в интервальной форме в соответствии с правилом Брадиса-Крылова

Определите относительную погрешность
измерения массы

ПОВТОРИТЬ ИЗМЕРЕНИЯ
В СООТВЕТСТВИИ С ПУНКТАМИ 1-8 ДЛЯ ДВУХ ДРУГИХ ТЕЛ

ВСЕ ЗАПИСИ И
РАСЧЁТЫ ВЫПОЛНЯТЬ В ЛАБОРАТОРНАОЙ ТЕТРАДИ

ОТЧЁТ К РАБОТЕ ПОДГОТОВИТЬ
ПО ПЕРДЛАГАЕМОЙ ФОРМЕ (СМ.НИЖЕ)

ОТЧЁТ К РАБОТЕ № 2 ВЫПОЛНИЛ________________________

Цель работы:_____________________________________________________________________________

_________________________________________________________________________________________

Оборудование:_____________________________________________________________________________

Расчёт погрешности измерения массы первого
тела

(Выполняется в
соответствии с пунктами 1-8)

Расчёт погрешности измерения массы второго
тела

(Выполняется в
соответствии с пунктами 1-8)

Расчёт погрешности измерения массы третьего
тела

(Выполняется в
соответствии с пунктами 1-8)

Вывод

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

КОНТРОЛЬНЫЕ ВОПРОСЫ (ОТВЕТИТЬ ПИСЬМЕННО И СДАТЬ С ОТЧЁТОМ)

1 Как определяется погрешность весов?

Ответ на вопрос 1__________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2 Как определяется погрешность гирь?

Ответ на вопрос
2__________________________________________________________________________

3 Как определяется погрешность подбора
гирь?

Ответ на вопрос
3__________________________________________________________________________

4 Как определяется полная абсолютная
погрешность измерения массы?

Ответ на вопрос
4__________________________________________________________________________

5 Как определяется относительная
погрешность и что она показывает?

Ответ на вопрос
5__________________________________________________________________________

6 Какие цифры числа являются значащими? В
чём состоит правило Брадиса-Крылова?

Ответ на вопрос
6__________________________________________________________________________

Источник

ЛАБОРАТОРНАЯ РАБОТА № 3.

ИЗМЕРЕНИЕ МАССЫ ТЕЛА НА РЫЧАЖНЫХ ВЕСАХ.

ЦЕЛЬ РАБОТЫ: — Научиться пользоваться рычажными весами и с их

помощью определить массу тела.

— Оценить погрешность данного измерения.

ПРИБОРА И МАТЕРИАЛЫ: — Весы с разновесом

— Тело, массу которого необходимо определить.

ХОД РАБОТЫ.

Изучите правила взвешивания при помощи рычажных весов по учебнику.

1. Уравновесим весы.

2. Придерживаясь правил взвешивания, измерим массу твердого тела.

mизм. = … + … + + … = …г (При определении массы, обязательно запишите массы всех гирек, которые уравновесили тело. Это понадобиться нам при дальнейших расчетах).

3. Определим абсолютную погрешность данного измерения.

Наиболее сложным случаем определения погрешности является определение погрешности измерения массы тела при работе с рычажными весами.

m = весов + всех гирь + подбора гирь , где m – абсолютная погрешность при взвешивании.

а). весов – абсолютная погрешность весов, определяется чувствительностью весов и зависит от нагрузки. Её определяют по графику.

m,мг

200

150

100

0 10 50 100 150 200 m,г

График зависимости погрешности весов

от их нагрузки.

mвесов = … г (Определите погрешность весов по графику и запишите её.)

б). всех гирь – это сумма абсолютных погрешностей каждой гирьки, которая использовалась при взвешивании. Эти данные вы возьмёте из таблицы.

Таблица зависимости погрешности гирь от их массы.

mгири	mгири	mгири	mгири
100мг	1мг	5г	8мг
200мг	2мг	10г	12мг
500мг	3мг	20г	20мг
1г	4мг	50г	30мг
2г	6мг	100г	40мг

mвсех гирь = … г (Определите погрешность всех гирь, пользуясь таблицей.)

ОБРАТИТЕ ВНИМАНИЕ! Если, предположим, тело имеет массу 20г, и мы воспользуемся гирями: 10г и 10г, то абсолютная погрешность всех гирь будет равна – 12мг + 12мг = 24мг.

А если одной гирькой 20г, то абсолютная погрешность будет равна – 20мг.

КАК ВЫ ДУМАЕТЕ, как предпочтительнее поступить?

в). mподбора гирь – абсолютная погрешность подбора гирь, не превосходит половины минимальной массы гири, выводящей весы из равновесия. В нашем подборе гирь самая маленькая гирька имеет массу 100мг (0,1г).

mподбора гирь = 0.1г / 2 = 0,05г

m = … + … + 0,05г = …г (Подставьте численные значения в формулу для определения абсолютной погрешности при взвешивании. Округлите полученный результат до десятых.

ОБРАТИТЕ ВНИМНИЕ! Второе слагаемое мало по сравнению с остальными, поэтому в дальнейшем им можно будет пренебрегать. (Это соответствует закону сложения погрешностей.)

ВЫВОДЫ ПО РАБОТЕ:

Научились ли Вы пользоваться рычажными весами и с их помощью определить массу тела?

1. Запишите, чему равна масса тела с учетом абсолютной погрешности с точностью до десятых.

m = ( …  …)г

Что эта запись означает?

2. Какие меры предосторожности необходимо выполнять при работе с рычажными весами и разновесом?

3. Почему определение погрешности при взвешивании оказалось таким сложным?

ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ.

1.Определите, чему равна относительная погрешность данного измерения. Что Вы можете сказать о точности этих весов?

Источник

Погрешности измерений, представление результатов эксперимента

Шкала измерительного прибора
Цена деления
Виды измерений
Погрешность измерений, абсолютная и относительная погрешность
Абсолютная погрешность серии измерений
Представление результатов эксперимента
Задачи

п.1. Шкала измерительного прибора

Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.

Примеры шкал различных приборов:

п.2. Цена деления

Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.

Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.

Пример определения цены деления:

Определим цену деления основной шкалы секундомера.
Два ближайших пронумерованных деления на основной шкале:a = 5 c
b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*}

п.3. Виды измерений

Вид измерений

Определение

Пример

Прямое измерение

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Косвенное измерение

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.

Составляющие погрешности измерений

Причины

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$

Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$

Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$

Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.

Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

определение длины с помощью линейки или мерной ленты;
определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями.
Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см})
Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями.
Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см})
Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}

п.6. Представление результатов эксперимента

Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то

абсолютная погрешность их суммы равна сумме абсолютных погрешностей

$$ triangle (a+b)=triangle a+triangle b $$

абсолютная погрешность их разности также равна сумме абсолютных погрешностей

$$ triangle (a-b)=triangle a+triangle b $$

Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:

относительная погрешность их произведения равна сумме относительных погрешностей

$$ delta_{acdot b}=delta_a+delta_b $$

относительная погрешность их частного также равна сумме относительных погрешностей

$$ delta_{a/b}=delta_a+delta_b $$

Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:

относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности

$$ delta_{a^2}=2delta_a $$

относительная погрешность куба (a^3) равна утроенной относительной погрешности

$$ delta_{a^3}=3delta_a $$

относительная погрешность произвольной натуральной степени (a^n) равна

$$ delta_{a^n}=ndelta_a $$

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	(triangle=frac{b-a}{n+1}), мл
1	20	40	4	(frac{40-20}{4+1}=4)
2	100	200	4	(frac{200-100}{4+1}=20)
3	15	30	4	(frac{30-15}{4+1}=3)
4	200	400	4	(frac{400-200}{4+1}=40)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем (V_0), мл	Абсолютная погрешность (triangle V=frac{triangle}{2}), мл	Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%})
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})

Источник

Как найти абсолютную и относительную погрешность

При измерении какой-либо величины всегда есть некоторое отклонение от истинного значения, поскольку ни один прибор не может дать точного результата. Для того, чтобы определить возможные отклонения полученных данных от точного значения, используют понятия относительной и абсолютной погрешности.

Вам понадобится

— результаты измерений;
— калькулятор.

Инструкция

В первую очередь, проведите несколько измерений прибором одной и той же величины, чтобы иметь возможность посчитать действительное значение. Чем больше будет проведено измерений, тем точнее будет результат. Например, взвесьте яблоко на электронных весах. Допустим, вы получили результаты 0,106, 0,111, 0,098 кг.

Теперь посчитайте действительное значение величины (действительное, поскольку истинное найти невозможно). Для этого сложите полученные результаты и разделите их на количество измерений, то есть найдите среднее арифметическое. В примере действительное значение будет равно (0,106+0,111+0,098)/3=0,105.

Для расчета абсолютной погрешности первого измерения вычитайте из результата действительное значение: 0,106-0,105=0,001. Таким же образом вычислите абсолютные погрешности остальных измерений. Обратите внимание, независимо от того, получится результат с минусом или с плюсом, знак погрешности всегда положительный (то есть вы берете модуль значения).

Чтобы получить относительную погрешность первого измерения, разделите абсолютную погрешность на действительное значение: 0,001/0,105=0,0095. Обратите внимание, обычно относительная погрешность измеряется в процентах, поэтому умножьте полученное число на 100%: 0,0095х100%=0,95%. Таким же образом считайте относительные погрешности остальных измерений.

Если истинное значение уже известно, сразу принимайтесь за расчет погрешностей, исключив поиск среднего арифметического результатов измерений. Сразу вычитайте из истинного значения полученный результат, при этом вы найдете абсолютную погрешность.

Затем делите абсолютную погрешность на истинное значение и умножайте на 100% — это будет относительная погрешность. Например, количество учеников 197, но его округлили до 200. В таком случае рассчитайте погрешность округления: 197-200=3, относительная погрешность: 3/197х100%=1,5%.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Обработка результатов измерений

Любая
лабораторная работа по физической химии
сводится к определению численных
значений конкретных физико-химических
величин. Последние находятся путем
расчётов по уравнениям с использованием
результатов измерений, которые всегда
содержат некоторую погрешность
(ошибку).
Погрешность имеют и табличные данные.

Погрешности,
в зависимости от источников их
происхождения, подразделяются на грубые,
систематические
и случайные.
Грубые
ошибки (промахи)
связаны обычно с невнимательностью
экспериментатора, и их довольно легко
обнаружить при повторных измерениях.
В дальнейшем предполагается, что грубые
промахи студентом не допускаются.

Систематические
погрешности обусловлены дефектами
измерительной аппаратуры, её
неправильной установкой, применением
недостаточно чистых реактивов,
использованием приближённых уравнений
и недостаточно точных констант,
отсутствием контроля постоянства
условий проведения эксперимента,
например температуры. При повторных
измерениях систематические ошибки
обычно остаются постоянными. Если же в
процессе проведения эксперимента
условия, определяющие состояние системы,
изменяются, возможно существенное
изменение систематической ошибки.

Исключить
систематические ошибки можно проверкой
оборудования по эталонным образцам,
его калибровкой, использованием других,
более точных методов и уравнений,
введением соответствующих поправок.

Часто
при повторных измерениях одной и той
же величины получаются несколько
отличающиеся друг от друга результаты,
что связано с невозможностью поддержания
строгого постоянства условий эксперимента.
Последние испытывают случайные колебания
и являются причиной появления случайных
погрешностей
измерений. Случайные
погрешности независимы друг от друга.
Они
обусловлены факторами, которые практически
невозможно контролировать и учесть и
которые при повторных измерениях могут
действовать на результаты измерений
по-разному. Исключить эти ошибки нельзя,
но их можно учесть, проведя серию
повторных измерений и статистическую
обработку результатов последних.

Разделение
ошибок на систематические и случайные
весьма условно. Например, если для
приготовления серии растворов использовать
несколько колб, то погрешность их объёмов
выступает как случайная ошибка. Но если
эта серия растворов приготовлена с
использованием лишь одной колбы, то
погрешность её объёма является
систематической, поскольку во всех
случаях постоянна и её значение
присутствует во всех результатах.

При
определении величины погрешности
физико-химического параметра, измеряемого
в ходе конкретного эксперимента, характер
погрешности, как правило, безразличен,
важна величина общей погрешности, равная
сумме систематической и случайной
ошибок.

Результаты
измерений и вычислений характеризуются
правильностью
и воспроизводимостью.
Под воспроизводимостью
понимают разброс результатов параллельных
измерений относительно среднего
значения. Чем этот разброс меньше, тем
воспроизводимость выше. При отсутствии
систематических ошибок воспроизводимость
определяется случайными ошибками. Если
чувствительность прибора недостаточна,
случайные погрешности могут не проявиться
и тогда бессмысленно говорить об учёте
случайных ошибок. Из теории ошибок
следует, что если они подчиняются
распределению Гаусса (в дальнейшем это
подразумевается), среднее арифметическое
результатов достаточно большого числа
отдельных измерений наиболее близко к
истинному значению измеряемой величины.

Правильность
результата характеризуется отклонением
среднего арифметического от истинного
значения и определяется наличием
систематических ошибок. Хорошая
воспроизводимость результатов не
означает их правильности, поскольку
результат может содержать очень большую
постоянную систематическую погрешность.

Погрешность
конкретного результата измерения
величины х_i
(если
произведено n
измерений) можно выразить через абсолютную
ошибку x_i,
являющуюся разностью между х_i
и истинным значением х
(средним арифметическим
=х_i/n,
если ошибки случайные). Относительная
погрешность _i=x_i/

более наглядно характеризует точность
измерения. Для серии из n
измерений величины х
средняя абсолютная ошибка х=х_i/
.
Абсолютная погрешность имеет размерность
измеряемой величины, относительная
погрешность безразмерная.

В
физико-химическом эксперименте значение
определяемой величины обычно рассчитывают
из некоторого уравнения, в которое
входят параметры, имеющие определённую
погрешность. Для нахождения относительной
погрешности

величины у,
являющейся функцией независимых
переменных ,,
и т.д., выражаемой уравнением у=f(,,,…)
при условии, что

,
необходимо прологарифмировать это
уравнение и продифференцировать
полученный натуральный логарифм, т.е.

Так
как знаки отдельных погрешностей
неизвестны, предполагается наихудший
вариант, когда они одинаковы и вклады
всех ошибок складываются. Поэтому, если
после описанных выше математических
операций получается полином, отдельные
слагаемые в котором отрицательные, то
знак минус перед ними заменяется плюсом.

Относительные
погрешности некоторых простых функций
приведены в таблице 1, в которой а
– точная константа. В случае более
сложного уравнения (например, выражение
для энтальпии реакции Н
через ЭДС и её температурный коэффициент),
его необходимо представить как комбинацию
более простых соотношений.

Таблица 1

Погрешности
некоторых функций

№

Функция

Относительная
погрешность

№

Функция

Относительная
погрешность

y = ах

y = x + z

y = x — z

_у= _х

y = xz

y
= x^a

y
= ln x

Если
определяемая величина является
логарифмической функцией (в том числе
рН, рК), то обычно находят её абсолютную
погрешность, а не относительную. Как
следует из формулы (7), абсолютная
погрешность натурального логарифма
равна относительной погрешности
логарифмируемого выражения.
Если логарифм десятичный, то сначала
необходимо перейти к натуральному,
после чего воспользоваться формулой
(7).

Погрешность
исходных данных определяется погрешностью
используемых приборов (указывается в
паспорте прибора). Если она неизвестна,
то обычно принимается равной половине
наименьшего деления шкалы. Погрешность
приборов соответствует паспортному
значению лишь при правильном их
использовании.

Погрешность
весов зависит от их конструкции.
Погрешность мерной посуды, в соответствии
с ГОСТом, не должна превышать значений,
указанных в таблице 2. Погрешность
бюреток объёмом 50 и 25 мл равна соответственно
0,12 и 0,10 мл.

Погрешность
табличных величин учитывается так же,
как и погрешность результатов измерений.
При этом, если она не оговаривается, то
принимается равной половине единицы
последнего десятичного разряда. Например,
подвижность иона Н₃О⁺
равна 349,8, следовательно, её абсолютная
погрешность 0,05.

Часто
некоторые величины приходится определять
графически, например, путем экстраполяции,
интерполяции, через тангенс угла наклона
линейного участка графика или касательной
к кривой. В подобных случаях при построении
графика необходимо выбрать такой
масштаб, чтобы график не был источником
значительной погрешности, т.е. для
построения необходим достаточно большой
лист бумаги^¹.

Таблица 2

Допустимая
абсолютная погрешность объема мерной
посуды

Колбы

Пипетки

с одной меткой

Пипетки

с подразделениями

Ёмкость, мл

V,

мл

Ёмкость,

мл

V,

мл

Ёмкость,

мл

V,

мл

1000

500

250

200

100

0,60

0,30

0,20

0,10

50; 40

20; 15

2; 1

0,12

0,10

0,06

0,04

0,03

0,015

0,06

0,04

0,02

Если
точки графика укладываются
на прямую, т.е. выполняется уравнение

y
= а + bx,

то
для определения величин а
и b
выбирают на графике две точки с
координатами х₁,у₁
и
х₂,у₂
, расположенные,
по возможности, дальше друг от друга, и
константы а
и
b находят из
выражений

Погрешности
величин а и
b
можно найти, используя формулы (3) – (5)
таблицы 1, зная погрешности величин х
и у
и учитывая, что х
= _хх.
Поскольку при определении х₁, у₁
,х₂,
и у₂
производится отсчёт их значений на
координатных осях, результат отсчёта
содержит соответствующую погрешность,
равную половине наименьшего деления,
и которую необходимо прибавить к
погрешности величины, изображаемой на
оси.

Численные
значения величин, имеющих погрешность,
выражаются приближёнными
числами. Используя приближённые числа,
следует соблюдать определённые правила.
При записи приближённого числа
предпоследняя цифра должна быть точной,
а последняя – сомнительной (т. е. содержать
погрешность). Большее число цифр,
записанных с отступлением от этого
правила, не увеличивает точности.
Точность величины выражается числом
значащих цифр в её численном выражении.
Значащими^²
цифрами являются все цифры приближённого
числа, записанного правильно, кроме
первых нулей. Нули в конце числа значащие,
если они стоят на своем месте, а не
записаны вместо отсутствующих цифр.
Так, числа 628, 6,28, 0,00628, 6,2810^–5,
6,2810⁴
содержат три значащие цифры. Если вместо
последнего из приведенных чисел записать
62800, в этом числе останется три значащие
цифры.

Произведение
и частное приближенных чисел должно
содержать столько значащих цифр, а сумма
и разность – столько знаков после
запятой, сколько их имеется в наименее
точном исходном числе. Например, 42,6 
73,503 = 3,1310³,
а не 3131,2278, и 36,823 – 22,4 = 14,4, а не 14,423. У
логарифма значащие только цифры мантиссы,
т.е. его дробной части^¹,
и последняя должна иметь столько цифр,
сколько их в логарифмируемом числе.
Поскольку при выполнении арифметических
действий погрешность накапливается,
необходимо стремиться сокращать, если
это возможно число таких действий. При
проведении цепочки вычислений оставляют
лишнюю цифру в промежуточных результатах,
конечный же результат округляется в
соответствии с изложенными выше
правилами. Применяя для вычислений
калькулятор, следует использовать его
память для исключения необоснованных
округлений промежуточных результатов.

В
качестве примера рассмотрим расчёт
относительной погрешности молярной
концентрации приготовленного раствора.
На технических весах взята навеска
хлорида натрия массой 3,28 г, которая была
растворена в воде в мерной колбе объёмом
250 мл. Молярная концентрация с
рассчитывается по уравнению

где
g
– масса навески, г, М
– молярная масса растворённого вещества,
V
– объём колбы, мл.

Как
следует из уравнений (4) и (5) таблицы 1,
относительная погрешность концентрации
равна сумме относительных погрешностей
всех величин, входящих в правую часть
формулы для концентрации. Однако 1000 –
число миллилитров в одном литре – по
определению величина точная, следовательно,
её погрешность равна нулю.

Относительная
погрешность массы навески _g
равна отношению абсолютной погрешности
взвешивания g
к массе навески. Последняя же находится
как разность между массой навески вместе
с сосудом, в котором производилось
взвешивание (бюкс, стаканчик), и массой
пустого сосуда. Поэтому погрешность
массы навески рассчитывается по уравнению
(3) таблицы 1, в котором абсолютные
погрешности обоих взвешиваний одинаковы
(так как использовались одни и те же
весы) и равны 0,02 г для технических весов.
Следовательно, абсолютная погрешность
массы навески g
равна 20,02
= 0,04 г. Поэтому относительная погрешность
массы навески составляет 0,04: 3,28 = 0,012.

Молярная
масса вещества – постоянная величина,
поэтому часто студенты ошибочно считают
её точной. Однако атомные массы элементов
определены с большей или меньшей
погрешностью, которая для разных
элементов различна, что следует из
разного числа значащих цифр в их
величинах. Если молярная масса вещества
рассчитана по атомным массам элементов,
входящих в его состав, то для нахождения
относительной погрешности следует
воспользоваться формулой (2), причём
абсолютные погрешности атомных масс
элементов необходимо умножать на число
этих атомов в молекуле. Поэтому удобнее
брать величину молярной массы из
справочника. Тогда её абсолютная
погрешность равна пяти в первом
отсутствующем разряде. Молярная масса
хлорида натрия равна 58,44, следовательно,
её абсолютная погрешность составляет
0,005, а относительная погрешность –
0,005/58,44 = 0,000086.

В
соответствии с таблицей 2 абсолютная
погрешность объёма мерной колбы на
250 мл равна 0,20 мл, поэтому относительная
погрешность объёма составит 0,20:250 =
0,0008.

Суммируя
найденные погрешности, для относительной
погрешности концентрации приготовленного
раствора получим: 0,012 + 0,000086 + 0,0008 = 0,012886

0,013 = 1,3 %. Оценивая вклад погрешностей
исходных величин, можно заметить, что,
во-первых, погрешность концентрации
определяется, в основном, погрешностью
взвешивания. Если найденная погрешность
концентрации оказывается слишком
большой, то для её уменьшения необходимо
навеску брать с использованием
аналитических весов, погрешность
которых^¹
составляет 0,0002 г. Тогда относительная
погрешность массы навески составит
0,00012 и определяющей станет погрешность
объёма колбы. Если и теперь точность
определения концентрации окажется
недостаточной, необходимо калибровать
используемую мерную колбу, т.е. более
точно определить её объём. Методика
калибровки мерной посуды описана в
пособиях по аналитической химии.

Во-вторых,
все величины, используемые в расчётных
формулах, следует определять с максимально
возможной точностью, поскольку даже
одна величина, имеющая большую погрешность,
обесценивает труд по определению
остальных величин с высокой точностью.

В-третьих,
погрешность молярной массы в рассмотренном
примере практически не влияет на
погрешность концентрации. Это является
следствием большого числа значащих
цифр в величине М
по сравнению с другими величинами.
Отсюда следует, что если некоторые
величины, используемые в расчётной
формуле, содержат значащих цифр больше,
чем другие, т.е. являются более точными,
то их погрешность можно не учитывать,
считая их точными числами. Конечно, при
расчётах необходимо и использовать эти
величины с большим числом значащих
цифр, не округляя.

При
построении графиков необходимо правильно
выбрать размеры листа бумаги. Обе
координатные оси не должны сильно
различаться в размерах. Вместе с тем
всё поле графика должно быть использовано,
т.е. если первое значение координаты
точки сильно отличается от нуля, разметку
соответствующей оси необходимо начинать
с ближайшего меньшего целого значения.
При этом точка пересечения координатных
осей не будет соответствовать нулям на
осях координат.

Координаты
изображаемых точек не записываются на
осях координат, где необходимо указать
лишь целые значения изображаемой
величины, т.е. построить шкалу этих
значений. На осях должны быть указаны
обозначения величин и их размерность.

Точки
на графике должны быть выделены отчётливо.
Если изображается несколько зависимостей,
то точки каждой из них необходимо
изображать разными символами. Кривую
проводить плавно так, чтобы число точек,
не попадающих на кривую, по разные её
стороны было одинаково. Используя для
построения графиков компьютер, следует
не соединять точки между собой, а
аппроксимировать зависимость плавной
кривой, подобрав соответствующую
функциональную зависимость.

Одной
из наиболее удобных и распространённых
программ для построения графиков функций
и их обработке является компьютерная
программа Origin.
В настоящее время доступна седьмая
версия этой программы, которая имеет
незначительные отличия от предыдущей
шестой версии. Изменения коснулись в
основном стиля работы программы, он
стал более приближен к стилю, принятому
в программах Microsoft
Excel
и Microsoft
Word.
Несмотря на то, что работа в программе
Origin
рассматривается в курсах «Информатика»
и «Новые информационные технологии»
есть смысл кратко напомнить основные
моменты работы с данной программой, её
возможности, ограничившись при этом
лишь самыми необходимыми функциями.

Программа
Origin
позволяет строить различные двухмерные
графики в декартовой или полярной
системе координат, кроме того, имеется
возможность построения треугольных
диаграмм (используются для описания
поведения трехкомпонентных систем) и
трехмерных (3D)
поверхностей.

При
запуске Origin сначала открывается новое
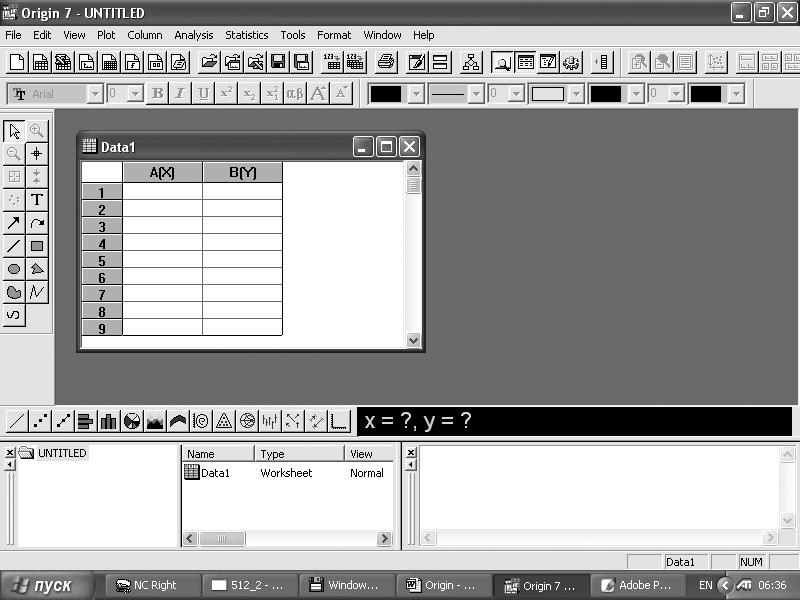
окно в виде рабочего листа в рабочем
пространстве Origin. Рабочий лист (рис. 1)
является одним из типов окон, доступных
в этой программе. В самом верху окна в
строке заголовка указывается версия
Origin
7 и имя проекта (в
начальный момент Untitled
– без имени), в правом верхнем углу
расположены стандартные для WINDOWS
элементы управления, позволяющие
свернуть окно в кнопку на панели задач,
свернуть в окно и закрыть приложение.

Ниже
расположена стандартная для WINDOWS
строка меню: File,
Edit,
View,
Plot,
Column,
Analysis,
Statistics,
Tools,
Format,
Window,
Help,
элементы которого раскрываются после
щелчка по ним мышью. Перечень меню
меняется в зависимости от того, какое
окно активно. Под строкой меню расположены
кнопки быстрого доступа к определенным
функциям программы, например, сохранить
проект (кнопка с изображением дискеты),
распечатать (кнопка с изображением
принтера) и т.д. Узнать назначение той
или иной кнопки можно, поместив на неё
указатель мыши; при этом рядом с кнопкой
появляется соответствующее пояснение.
Количество выводимых кнопок может
меняться, в зависимости от настройки
конкретной программы, а доступ к
соответствующим функциям может быть
осуществлен через общее меню программы.

Ещё ниже находится
панель форматирования, позволяющая
выбрать шрифт надписей, его начертание
и размер, толщину линий.

Рис.1. Вид окна
программы Origin

В
основном поле окна находится Окно
рабочий лист
– пустая таблица со столбцами A[X]
и B[Y],
в каждую строку которых попарно вносятся
результаты измерений. При
необходимости количество столбцов
может быть добавлено, для чего необходимо
открыть меню Column
и щелкнуть мышью по пункту Add
New
Columns…
или, не заходя, в меню нажать комбинацию
клавиш Ctrl
+ D
(плюс в
данном случае означает одновременное
нажатие указанных клавиш). В поле
открывшегося окна Add
New
Columns
указать необходимое количество
добавляемых колонок.

При
наборе данных с клавиатуры или их
копировании из других приложений
(например, Excel)
необходимо помнить, что разделителем
целой и дробной части числа в программе
Origin
является точка, а не запятая, как во
многих русифицированных программах.
Набор запятой в числе в качестве
разделителя приводит к тому, что введенные
данные воспринимаются программой как
текстовые, а не числовые, без какой либо
диагностики. Ввод каждого числа в ячейку
заканчивается нажатием клавиши “Enter”,
при этом происходит переход к следующей
ячейке.

После
ввода всех исходных данных необходимо
построить график, для чего следует войти
в меню Plot
и выбрать в открывшемся перечне вариант
построения графика: только линии (Line),
только точки – маркеры (Skatter)
или маркеры, соединенные линиями (Line
+ Symbol).
Если планируется аппроксимировать
экспериментальные данные методом
наименьших квадратов, то целесообразно
строить только маркеры. Если под таблицей
в нижней части рабочего окна Origin
открыта панель кнопок 2D Graphs,
то для построения графика достаточно
щелкнуть указателем мыши по соответствующей
кнопке.

Открывается
окно Select
Columns
for
Plotting,
в котором необходимо выбрать, какая
колонка будет аргументом (ось X),
какая функцией (ось Y).
Для этого, щёлкнув в окне по названию
колонки значений аргумента (например,
A[X]),
щёлкнуть по кнопке <–>X
, находящейся рядом справа. Затем выбрать
щелчками колонку функции (например,
B[Y]) и кнопку <–>Y
.После нажатия на кнопку “OK”
мышью появляется окно Graph,
в котором будет построен график. Один
из вариантов построения представлен
на рис.2.

В
рабочем окне Origin
одновременно может быть отображено
несколько окон, но активным может быть
только одно. Для того, чтобы сменить
активное окно, необходимо щелкнуть
мышью по нужному окну. Любое окно может
быть свернуто кнопкой и тогда оно не
заслоняет другие окна, либо развернуто
во всю площадь окна Origin
(соответствующие элементы управления
находятся в правом верхнем углу). В тех
случаях, когда на одном графике
представлено несколько зависимостей,
для редактирования, аппроксимации,
сглаживания и других типов обработки,
необходимо выделить активный набор
данных, для чего нужно зайти в меню
“Data”,
если активно окно Graph
и выбрать из представленных там наборов
данных.

Для
аппроксимации экспериментальных данных
методом наименьших квадратов необходимо
выделить активный набор данных (если
их несколько) и зайти в меню “Analysis”,
где из списка выбрать подходящую функцию
из набора, либо задать пользовательскую
функцию. После выполнения расчётов
выдается отчёт, в котором указывается
вид функции и значения всех её
коэффициентов. Сама аппроксимирующая
кривая обычно строится красным цветом,
который может быть изменен пользователем.

Рис.2

График
функции, построенный в Origin,
не имеет подписей под координатными
осями (точнее, там указано, что это
соответственно ось X
и ось Y).
Для изменения подписей необходимо
щелкнуть по ним указателем мыши, при
этом становится активной панель
форматирования. После чего можно набирать
на клавиатуре название осей. Необходимо
помнить, что в программе Origin
для перехода на русский язык недостаточно
переключить клавиатуру, надо выбрать
шрифт, поддерживающий кириллицу (типа
“Courier
New
Cyr“
или другой, но обязательно Cyr).
Origin позволяет в произвольном месте
графика выполнить любую надпись, для
этого необходимо щелкнуть по кнопке с
буквой T на панели Tools
и набрать текст, который можно перетащить
мышью в любое место.

При
сохранении информации вся работа в
данной секции сохраняется, как проект
Origin.
Он включает в себя все окна на экране
(включая также свернутые окна) а также
все файлы, связанные с информацией в
окнах. Кроме сохранения проектов, можно
также сохранить окно или шаблон как
отдельный файл.

Источник