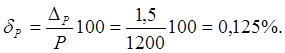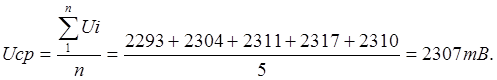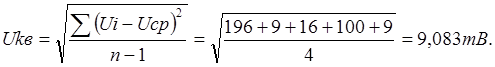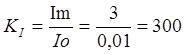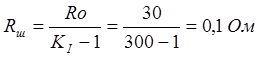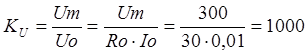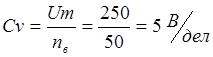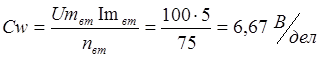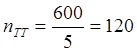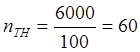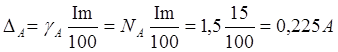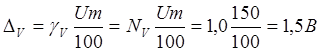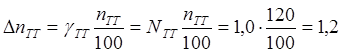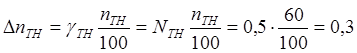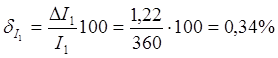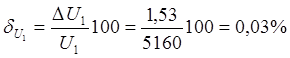Как найти относительную погрешность мощности

Задача 1

Для
определения мощности в цепи постоянного тока были измерены напряжение сети U вольтметром класса точности N_B
с пределом измерений U_m, ток I амперметром класса точности N_a
с пределом измерений I_m. Определить
мощность, потребляемую приёмником, а также относительную и абсолютную
погрешности её определения.

Дано:

Найти:

Решение:

1)  Найдем
мощность, потребляемую приемником

2)  Класс
точности определяет приведенную погрешность

3)  Найдем
абсолютную погрешность измерения тока и напряжения

,

.

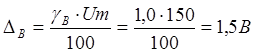
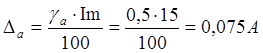
4)  Найдем
абсолютную погрешность измерения мощности при косвенном измерении

5)  Найдем
относительную погрешность измерения мощности

6)  Доверительный
интервал результата измерения с вероятностью .

Задача 2

Проведено пять
независимых наблюдений одного и того же напряжения U.
Найти результат измерения и доверительную вероятность того, что абсолютная
погрешность измерения не превышает по модулю DU. Систематической погрешностью можно пренебречь.

Дано:

Найти:

Решение:

1)  Определим
среднее арифметическое результатов измерения

2)  Определяем
среднее квадратичное результатов измерения

3)  Для
определения интервала и вероятности пользуются распределением Стьюдента, где
доверительный интервал равняется     , где

— коэффициент Стьюдента,

 — среднее квадратичное отклонение
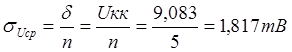
результата измерения.

4)  Находим
доверительный интервал

5)  Результат
измерения

Задача 3

Обмотка
магнитоэлектрического измерительного механизма имеет сопротивление R_O  и рассчитана на предельный длительный ток I_O, при котором подвижная часть получает
наибольшее отклонение. Каким образом на базе указанного измерительного
механизма сделать амперметр с пределом измерений I_m
и вольтметр с пределом измерений U_m?

Дано:

Найти: ,

Решение:

1)  Расчет
измерительной цепи амперметра

1.1 
Определяем коэффициент расширения пределов измерения по току

1.2     Определяем сопротивление
шунта

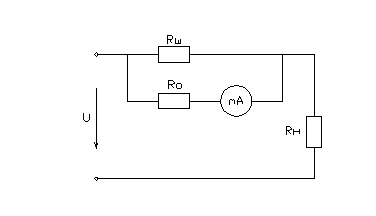
1.3 
 Схема измерительной цепи

2)  Расчет
цепи вольтметра

2.1 Определяем коэффициент
расширения пределов измерения по напряжению

2.2  Определяем добавочное
сопротивление

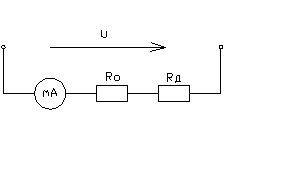
2.3 
Схема включения

Задача 4

Определить
цену деления измерительных приборов:

1) амперметра, имеющего на шкале n_a делений и предел измерения I_m;

2)вольтметра, имеющего n_в делений шкалы и предел измерения U_m;

3) ваттметра, имеющего n_ВТ делений шкалы и пределы измерений по току I_{m ВТ} и напряжению U_m
ВТ.

Дано:

Найти:

Решение:

1) Цена деления
амперметра

2) Цена деления
вольтметра

3) Цена
деления ваттметра

Задача 5

У вольтметра и
амперметра с пределами измерений U_m и I_m, включенных соответственно через измерительные
трансформаторы напряжения 6000/100 и тока 600/5, отчёт по шкале составил U₂ и I₂.
Определить напряжение и ток в сети, а также предел допускаемой абсолютной и
относительной погрешностей измерения, если известны класс точности приборов N_a и N_в и
измерительных трансформаторов N_тн и N_тт. Привести схему измерения.

Дано:

Найти:

Решение:

1) Определим
коэффициенты трансформации трансформатора напряжения и тока

2) Определим
ток и напряжение в сети

3) Определим
абсолютные погрешности амперметра и вольтметра

4) Определяем
абсолютные погрешности коэффициентов трансформации трансформатора тока и
напряжения

5) Результирующие
абсолютные погрешности измерения тока и напряжения равны

6)
Относительные погрешности измерения тока и напряжения

Задача 6

Определить
относительные погрешности измерения сопротивления R_x
в цепи постоянного тока с помощью амперметра и вольтметра при подключении их
двумя возможными способами. Сопротивление амперметра – R_a,
вольтметра – R_в. Сделать вывод о
целесообразности использования той или иной схемы.

Дано:

Найти: .

Решение:

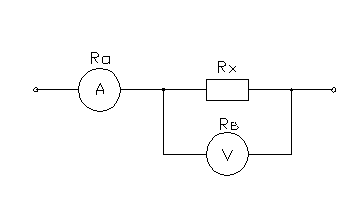
Принципиальные
схемы

 

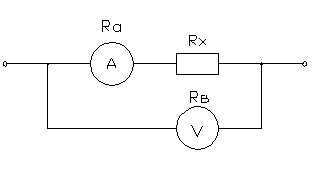
Схема
1                                              Схема 2

1)  Для
схемы включения 1.

1.1. 
Измеренное сопротивление.

1.2. 
Определяем абсолютную погрешность.

1.3. 
Определяем относительную погрешность.

Лабораторная работа № 1.

Расчет погрешностей емкости с помощью коэффициента Стьюдента.

Расчет погрешности измерения мощности и сопротивления

Цели занятия:

1. Общеобразовательная – Умение решать задачи по теме погрешности.

2. Развивающая — Углубление знаний .

3. Воспитательная – Проверить сформированность качеств знаний.

Теоретическая часть

Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:

ΔА = Ах – А (1)

Действительная относительная погрешность представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:

(2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению исследуемой величины,

т .е. к показанию прибора

(3)

Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к максимальному значению измерительного прибора

(4)

Для приборов с двухсторонней шкалой А_макс определяется как сумма абсолютных величин положительного и отрицательного пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального значения, то А_макс равно разности между конечным и начальным значениями шкалы.

Случайными называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя исключить опытным путем, т. к. они возникают случайно. Для того, чтобы исключить случайные погрешности производят неоднократные измерения и определяют среднее арифметическое из полученных значений, определяемое как

,

где а₁, а₂, …, а_n – результаты отдельных измерений;

n – число измерений.

Для оценки точности результата измерений необходимо знать закон распределения случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдения Р:

где Р₁ = а₁ – А_ср; Р₂ = а₂ – А_ср; Р_n = а_n – А_ср.

Этот способ определения доверительных интервалов справедлив толко для больших количеств измерений (20-30). Для небольшого количества измерений для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента t_n, которые зависят от задаваемой доверительной вероятности Р и количества измерений n.

Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:

А = Аср t_n

Контрольное задание

Задача 1. Для уменьшения влияния случайных погрешностей на результат измерения, емкость конденсатора С измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерения (табл. 1, табл. 2):

• Действительное значение измеряемой емкости;

• Среднюю квадратическую и максимальную погрешности однократного измерения;

• Доверительный интервал для результата измерения при доверительной вероятности Р_д (табл.3).

• Имеется ли систематическая составляющая в погрешности измерения емкости и с какой доверительной вероятностью ее можно оценить, если принять в качестве действительного значения емкости значения С_ср (таб.1, таб.2).

Таблица 1

№№из мере ния	1	2	3	4	5	6	7	8	9	10
С, пФ	2430	2440	2435	2438	2439	2441	2438	2440	2441	2439
№№из мере ния	11	12	13	14	15	16	17	18	19	20
С, пФ	2500	2564	2550	2480	2450	2528	2440	2556	2562	2550

Таблица 2

№ вари анта	1	2	3	4	5	6	7	8	9	10
№№из мере ния	1-3	6-10	2-6	1-4	2-8	2-4	7-9	4-7	3-5	5-7
С0, пФ	2428	2429	2430	2432	2436	2424	2440	2441	2440	2442
Рд	0,89	0,9	0,99	0,95	0,85	0,94	0,97	0,9	0,96	0,98
№ вари анта	11	12	13	14	15	16	17	18	19	20
№№из мере ния	11-14	12-15	16-19	13-16	14-17	17-20	15-18	11-13	12-16	15-20

Примечание. Количество и номера наблюдений значений емкости для каждого варианта определяются данными таблицы 1 и 2, например для варианта 1 следует взять результаты измерений 1-3 табл.2.

Указания к решению

1. Для удобства выполнения и проверки расчетов по заданию целесообразно представить промежуточное вычисление в виде таблицы

Таблица 3

№№ пп	№№ наблюдения	Сi, пФ	Сi – Cср, пФ	(Сi – Cср)2, пФ
1 2 3 4
		Сумма Сi, пФ	Сумма Сi – Cср, пФ	Сумма (Сi – Cср)2, пФ

1. Далее определить среднеквадратическую погрешность :

1. По таблице (4) определить коэффициент Стьюдента.

2. В конце решения следует записать окончательный (с учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р

Задание 2._. Используя формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей измерения мощности и сопротивления. Расчет выполняется в соответствии с вариантами указанными в задании.

Задача 1. Для определения сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены напряжение и ток. Зная основные параметры измерительных приборов (амперметра и вольтметра), определить ошибку косвенных измерений мощности и сопротивления.

Пример. Определить абсолютную и относительную погрешности измерения мощности, выделяемой на резисторе, если известны показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности К_А = 1,0, номинальное значение шкалы 10 _МА, показания 6 _МА.

Решение:

1. Определяем мощность Р = U * I ( Вт)

2. Абсолютная ошибка измерения напряжения, В

1. Абсолютная ошибка измерения тока, _М А

1. В соответствии с таблицей абсолютная ошибка измерения мощности, Вт

Относительная ошибка

1. Формула для сопротивления R = U / I

2. 

3. Относительная погрешность

Примечание:

1. Для вычисления погрешностей измерения мощности используются формулы 1,2,3,4,

2. Для вычисления погрешностей измерения сопротивления используются формулы 2,3,5,6,7.

Формулы для выполнения контрольной работы и письменного экзамена по предмету «Электрические измерения»

1.Абсолютная погрешность измерения

ΔА = Ах – А

2. Действительная относительная погрешность

3 Номинальная относительная погрешность

4.Приведенная относительная погрешность

1. Сопротивление шунта

R_Ш = R_А / Р-1 (Ом)

6 .Добавочное сопротивление

R_ДОБ = R_V * ( Р-1) (Ом)

1. Коэффициент трансформации по току:

Кi = I ₁/ I₂

8 Коэффициент трансформации по напряжению:

К_U = U ₁ /U₂

9. Ток сети:

I_C = K_{i *} I (А)

1. Напряжение сети:

U_C = K_U* U (В)

1. Активная мощность сети:

P_C = K_i * K_U *P (Вт)

1. Реактивная мощность сети :

Q = U*I* sinφ (Вар)

1. Полная мощность сети:

S = U*I (ВА)

14. Полное сопротивление сети :

Z_C = U_C/ I_C (Ом)

15 Коэффициент мощности:

Cosφ = P_C / S_C

1. Номинальная постоянная счетчика:

С_НОМ = W _НОМ/ N_НОМ (Вт*с/об)

1. Действительная постоянная счетчика:

С = (U*I*t / N) (Вт*с/об)

18 Поправочный коэффициент:

К= С / С_НОМ

1. Относительная погрешность счетчика

Β = [(С_НОМ – С) /C_НОМ] * 100%

Задача 1. Определить
абсолютную и относительную погрешность
косвенного метода измерения мощности
при следующих данных приборов и их
показаниях:

%;

%.

Решение:

1. значение мощности по показаниям приборов
   Вт;

б) предельные абсолютные погрешности
измерительных приборов:

амперметра А;

вольтметра В;

в) абсолютная погрешность косвенного
измерения мощности

д) действительное значение мощности
Вт.

Задача 2.
Для определения напряжения смещения
нуля исследуется схема измерительного
усилителя, представленного на рис. 1.10.
Известны математическое ожидание и
средние квадратические отклонения
источников тока и ЭДС, определяющих
дрейф:m_I
= 1 мкА,m_E
= 1 мВ,мкА,мВ. Определить математическое ожиданиеmи среднее квадратическое
отклонениенапряжения смещения нуляU_вых(при отсутствии входного напряжения),
считая операционный усилитель идеальным,
причемR1 = 1 кОм,R2 = 10 кОм.

Решение.
Напряжение на выходе выражается
зависимостью

. (1.14)

Искомые величины можно рассчитать по
формулам:

; (1.15)

21мВ;

; (1.16)

;
(1.17)

= 7 мВ.

1.4. Лабораторная
работа 1

ОПРЕДЕЛЕНИЕ
МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК

ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ

Цель работы: изучение и определение
погрешностей измерительных

приборов и их технических характеристик.

1.4.1. Основные теоретические положения

Погрешность измерений – это отклонение
результата измерения от истинного
значения измеряемой величины. Различают
абсолютную, относительную и приведенную
погрешность измерительных приборов.

Абсолютная погрешность прибора – это разность между показанием прибора
X и истинным значениемX₀измеряемой величины:

.
(1.18)

Относительная погрешность прибора –
это отношение абсолютной погрешности
к истинному значению измеряемой
величины, выраженное в процентах:

%.
(1.19)

Для практических расчетов в знаменателе
формулы (1.19) истинное значение X₀заменяется результатом измеренияX.

Отношение абсолютной погрешности к
нормирующему значению X_N,
выраженное в процентах, называется
приведенной погрешностью:

%.
(1.20)

Для приборов с нулевой отметкой на краю
шкалы нормирующее значение X_Nравно конечному значению диапазона
измерений.

Основная наибольшая допустимая
приведенная погрешность характеризует
цифру класса точности прибора:

, (1.21)

где _max– наибольшая допустимая абсолютная
погрешность;

К_п– цифра класса точности
средства измерения.

Постоянной
прибора С (ценой деления) называется
количество единиц измеряемой величины,
приходящееся на одно деление шкалы:

для амперметра, А/дел., ;

для вольтметра, В/дел., ;
(1.22)

для ваттметра, Вт/дел., ,

где I_ном,U_ном–
номинальные значения тока и напряжения
приборов;

_max –
максимальное число делений шкалы
прибора.

Величина S, обратная постоянной
прибора, называется чувствительностью
прибора:

. (1.23)

1.4.2. Порядок выполнения работы

1) Собрать электрическую цепь по схеме,
представленной на рис. 1.11.

Рис. 1.11. Схема проведения эксперимента

2)
Снять показания амперметра, вольтметра
и ваттметра при двух значениях нагрузки,
указанных преподавателем.

3)
Используя обозначения на шкалах
измерительных приборов, для каждого
из них вычислить постоянную С,
чувствительность S,
наибольшую допустимую абсолютную
погрешность _max.

4) По результатам измерений вычислить
относительную погрешность по (1.16) в
числителе, в качестве выбрать_max
, Х₀принять равным
измеренному значениюХ,предполагая,
что показания приборов являются
достоверными.

5) По результатам измерений и вычислений
заполнить табл. 1.4 и 1.5.

6) Провести анализ относительной
погрешности
в зависимости от
измеряемой величиныX. Сделать вывод о подборе предела
измерения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  10.04.20152.72 Mб61Учебник 1 История бухучета.rtf

• #
• #
• #
• #
• #
• #
• #
• #

Лабораторная работа № 1.

Расчет погрешностей емкости с
помощью коэффициента Стьюдента.

Расчет погрешности измерения
мощности и сопротивления

Цели занятия:

1.     Общеобразовательная – Умение решать задачи по
теме погрешности.

2.     Развивающая —  Углубление знаний .

3.     Воспитательная – Проверить сформированность
качеств знаний.

Теоретическая часть

Отклонение результата измерения от истинного измеряемой
величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности
между результатом измерения Ах и истинным значением измеренной величины А:

ΔА = Ах – А                                                                                      
                          (1)

Действительная относительная погрешность  представляет собой отношение абсолютной
погрешности измерения к действительному значению измеряемой величины,
выраженное в процентах:

                                                                                                                  
       (2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению
исследуемой величины,

т
.е. к показанию прибора

                                                                      
                                               (3)

Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности
измерения к максимальному значению измерительного прибора

                                                                                                          (4)

Для приборов с двухсторонней шкалой А_макс
определяется как сумма абсолютных величин положительного и отрицательного
пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального
значения, то А_макс равно разности между конечным и начальным
значениями шкалы.

Случайными называются
погрешности, изменяющиеся случайным образом при повторных измерениях одной и
той же величины. Случайные погрешности нельзя исключить опытным путем, т. к.
они возникают случайно. Для того, чтобы исключить случайные погрешности
производят неоднократные измерения и определяют среднее арифметическое из
полученных значений, определяемое как

 ,

где
а₁, а₂, …, а_n –
результаты отдельных измерений;

n
– число измерений.

            Для
оценки точности результата измерений необходимо знать закон распределения
случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее
квадратическое отклонение может быть выражено через случайные отклонения
результатов наблюдения Р:

где
Р₁ = а₁ – А_ср; Р₂ = а₂ –
А_ср; Р_n = а_n – А_ср.

            Этот
способ определения доверительных интервалов справедлив толко для больших
количеств измерений (>20-30). Для небольшого количества измерений для
определения доверительного интервала нужно пользоваться коэффициентами
Стьюдента t_n, которые зависят от задаваемой
доверительной вероятности Р и количества измерений n.

            Для
определения доверительного интервала среднюю квадратическую погрешность  надо умножить на коэффициент Стьюдента.
Окончательный результат измерения можно записать так:

А
= Аср  t_n

Контрольное задание

Задача 1. Для уменьшения
влияния случайных погрешностей на результат измерения, емкость конденсатора С
измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные
погрешности имеют нормальный закон распределения, определить на основании
заданного количества измерения (табл. 1, табл. 2):

• Действительное
  значение измеряемой емкости;
• Среднюю
  квадратическую и максимальную погрешности однократного измерения;
• Доверительный
  интервал для результата измерения при доверительной вероятности Р_д
  (табл.3).
• Имеется
  ли систематическая составляющая в погрешности измерения емкости и с какой
  доверительной вероятностью ее можно оценить, если принять в качестве
  действительного значения емкости значения С_ср  (таб.1, таб.2).

Таблица
1

№№из мере ния	1	2	3	4	5	6	7	8	9	10
С, пФ	2430	2440	2435	2438	2439	2441	2438	2440	2441	2439
№№из мере ния	11	12	13	14	15	16	17	18	19	20
С, пФ	2500	2564	2550	2480	2450	2528	2440	2556	2562	2550

Таблица
2

№ вари анта	1	2	3	4	5	6	7	8	9	10
№№из мере ния	1-3	6-10	2-6	1-4	2-8	2-4	7-9	4-7	3-5	5-7
С0, пФ	2428	2429	2430	2432	2436	2424	2440	2441	2440	2442
Рд	0,89	0,9	0,99	0,95	0,85	0,94	0,97	0,9	0,96	0,98
№ вари анта	11	12	13	14	15	16	17	18	19	20
№№из мере ния	11-14	12-15	16-19	13-16	14-17	17-20	15-18	11-13	12-16	15-20

Примечание.
Количество и номера наблюдений значений емкости для каждого варианта
определяются данными таблицы 1 и 2, например для варианта 1 следует взять
результаты измерений 1-3 табл.2.

Указания к решению

1.     
Для удобства выполнения и проверки расчетов по
заданию целесообразно представить промежуточное вычисление в виде таблицы

Таблица
3

№№ пп	№№ наблюдения	Сi, пФ	Сi – Cср, пФ	(Сi – Cср)2, пФ
1 2 3 4
		Сумма Сi, пФ	Сумма Сi – Cср, пФ	Сумма (Сi – Cср)2, пФ

2.     
Далее определить среднеквадратическую погрешность :

3.     
По таблице  (4) определить коэффициент Стьюдента.

4.     
В конце решения следует записать окончательный  (с
учетом округления) результат измерения в требуемой форме, например: С = 1231 12 пФ, Р

Задание
2._. Используя
формулы (1-7 примера) произвести расчет абсолютной и относительной погрешностей
измерения мощности и сопротивления. Расчет выполняется в соответствии с
вариантами указанными в задании.

Задача 1. Для определения
сопротивления резистора и мощности, выделяемой на этом сопротивлении, измерены
напряжение и ток. Зная основные параметры измерительных приборов (амперметра и
вольтметра), определить ошибку косвенных измерений  мощности и сопротивления.

Пример. Определить абсолютную и
относительную погрешности измерения мощности, выделяемой на резисторе, если известны
показания вольтметра класс точности Кв = 2,5, номинальное значение Umax = 150 В, показание 120 В и амперметра – класс точности К_А =
1,0, номинальное значение шкалы 10 _МА, показания 6 _МА.

Решение:

1. Определяем
   мощность Р = U * I  ( Вт)
2. Абсолютная
   ошибка измерения напряжения, В

1. Абсолютная
   ошибка измерения тока, _М А

1. В
   соответствии с таблицей абсолютная ошибка измерения мощности, Вт

            Относительная
ошибка

1. Формула
   для сопротивления R = U / I
2. 
3. Относительная
   погрешность

  

Примечание:

1.     
Для  вычисления погрешностей измерения мощности
используются формулы 1,2,3,4,

2.     
Для вычисления погрешностей измерения сопротивления
используются формулы 2,3,5,6,7.

Формулы для выполнения
контрольной работы и письменного экзамена по предмету «Электрические измерения»

1.Абсолютная погрешность измерения

ΔА = Ах – А

2. Действительная относительная погрешность

          3    Номинальная относительная погрешность

          4.Приведенная относительная погрешность

5.     
Сопротивление шунта

R_Ш = R_А / Р-1  (Ом)

6 .Добавочное сопротивление

R_ДОБ = R_V * ( Р-1)  (Ом)

7       
Коэффициент трансформации по току:

Кi = I ₁/ I₂

8 Коэффициент трансформации по напряжению:

К_U = U ₁ /U₂

9. Ток сети:

I_C = K_{i *} I (А)

10   
Напряжение сети:

U_C = K_U* U (В)

11   
Активная мощность сети:

P_C = K_i * K_U *P (Вт)

12   
Реактивная мощность сети :

Q = U*I* sinφ (Вар)

13   
Полная мощность сети:

S = U*I (ВА)

14. Полное сопротивление
сети :

Z_C  = U_C/ I_C (Ом)

15 Коэффициент мощности:

Cosφ = P_C  / S_C

16   
Номинальная постоянная счетчика:

С_НОМ = W _НОМ/ N_НОМ (Вт*с/об)

17   
Действительная постоянная счетчика:

С = (U*I*t / N) (Вт*с/об)

18 Поправочный коэффициент:

К= С / С_НОМ

18   
Относительная погрешность счетчика

Β = [(С_НОМ – С) /C_НОМ] * 100%