Точное значение величины
Приближенное значение величины
Как вычислить относительную погрешность
Относительная погрешность приближенного числа – это отношение абсолютной погрешности к приближенному числу.
Для того чтобы вычислить относительную погрешность необходимо:
1. Вычислить абсолютную погрешность, то есть найти разность между приближенным числом и его точным значением.
2. Разделить абсолютную погрешность на точное значение величины.
3. Для получения округленного результата в процентах разделить абсолютную погрешность на приближенное значение величины и умножить получившееся частное на 100%.
Приведем пример, в помещении 23 человека, округлим это значение до 25. Тогда абсолютная погрешность = 25 – 23 = 2.
Относительная погрешность =
= 0.086956521739
ВИДЕО УРОК
Абсолютная погрешность.
Разность между истинным значением измеряемой величины
и её приближённым значением называется абсолютной погрешностью.
Для подсчёта
абсолютной погрешности необходимо из большего числа вычесть меньшее число.
Существует формула
абсолютной погрешности. Обозначим точное число буквой А, а буквой а –
приближение к точному числу. Приближённое число – это число, которое
незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда
формула будет выглядеть следующим образом:
∆а = А – а.
ПРИМЕР:
В школе учится 374 ученика. Если округлить это число до 400,
то абсолютная погрешность измерения равна:
400 – 374 = 26.
ПРИМЕР:
На предприятии 1284 рабочих и
служащих. При округлении этого числа до 1300 абсолютная
погрешность составляет
1300 – 1284 = 16.
При округлении до 1280 абсолютная
погрешность составляет
1284 – 1280 = 4.
Редко когда можно
точно знать значение измеряемой величины, чтобы рассчитать абсолютную
погрешность. Но при выполнении различных измерений мы обычно представляем себе
границы абсолютной погрешности и всегда можем сказать, какого определённого
числа она не превосходит.
ПРИМЕР:
Торговые весы могут дать абсолютную погрешность, не
превышающую 5 г, а аптекарские – не превышающую одной сотой грамма.
Записывают
абсолютную погрешность числа, используя знак
±.
ПРИМЕР:
Длина рулона обоев составляет.
30 м ± 3
см.
Границу абсолютной
погрешности называют предельной абсолютной погрешностью.
Но абсолютная
погрешность не даёт нам представление о качестве измерения, то есть о том,
насколько тщательно это измерение выполнено. Чтобы понять эту мысль, достаточно
разобраться в таком примере.
ПРИМЕР:
Допустим, что при измерении коридора длиной в 20
м мы допустили абсолютную погрешность
всего только в 1 см. Теперь представим себе, что, измеряя корешок книги,
имеющий 18
см длины, мы тоже допустили абсолютную
погрешность в 1 см. Тогда понятно, что первое измерение нужно признать
превосходным, но зато второе – совершенно неудовлетворительным. Это значит, что
на 20
м ошибка в 1
см вполне допустима и неизбежна, но
на 18
см такая ошибка является очень грубой.
Отсюда ясно, что для оценки качества измерения
существенна не сама абсолютная погрешность, а та доля, какую она составляет от
измеряемой величины. При измерении коридора длиной в 20 м погрешность в 1 см
составляет
долю
измеряемой величины, а при измерении корешка книги погрешность в 1 см составляет
долю
измеряемой величины.
Делаем вывод, что измеряя корешок книги, имеющий 18
см длины и допустив погрешность в 1
см, можно считать измерение с большой ошибкой. Но если погрешность в 1
см была допущена при измерении коридора
длиной в 20
м, то это измерение можно считать максимально точным.
Если ошибка,
возникающая при измерении линейкой или каким либо другим измерительным
инструментом, значительно меньше, чем деления шкалы этой линейки, то в качестве
абсолютной погрешности измерения обычно берут половину деления. Если деления на
линейке нанесены достаточно точно, то ошибка при измерении близка к нулю.
Тогда
значение измеряемой длины предмета будет значение ближайшей метки линейки.
Поэтому, если измерение выполнено аккуратно, то истинная длина предмета может
отличаться от измеренной длины не более чем на половину деления шкалы, то есть 0,5 мм.
ПРИМЕР:
Для измерения длины болта использованы метровая линейка с
делениями 0,5 см и линейка с
делениями 1 мм. В обоих случаях получен результат 3,5
см. Ясно, что в первом случае отклонение найденной длины 3,5
см от истинной, не
должно по модулю превышать 0,5 см, во втором случае
0,1 см.
Если этот же результат получится при измерении
штангенциркулем, то
p(l; 3,5) = |l – 3,5 ≤ 0,01|.
Данный пример показывает зависимость абсолютной
погрешности и границ, в которых находится точный результат, от точности
измерительных приборов. В одном случае ∆l = 0,5 и, следовательно,
3
≤ l ≤ 4,
в другом – ∆l = 0,1 и
3,4
≤ l ≤ 3,6.
ПРИМЕР:
Длина листа бумаги формата А4 равна (29,7 ± 0,1)
см. А расстояние от Санкт-Петербурга до Москвы равно (650 ± 1) км. Абсолютная погрешность в первом случае
не превосходит одного миллиметра, а во втором – одного километра. Необходимо
сравнить точность этих измерений.
РЕШЕНИЕ:
Если вы думаете, что длина листа измерена точнее потому,
что величина абсолютной погрешности не
превышает 1 мм, то вы ошибаетесь.
Напрямую сравнить эти величины нельзя. Проведём некоторые рассуждения.
При измерении длины листа абсолютная погрешность не
превышает 0,1 см на 29,7 см, то есть в процентном отношении это составляет
0,1
: 29,7 ∙ 100% ≈ 0,33%
измеряемой величины.
Когда мы измеряем расстояние от Санкт-Петербурга до
Москвы, то абсолютная погрешность не превышает
1 км
на 650 км, что в процентном соотношении составляет
1
: 650 ∙ 100% ≈ 0,15%
измеряемой величины.
Видим, что расстояние между городами измерено точнее, чем
длинна листа формата А4.
Истинное значение
измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и
действительная величина абсолютной погрешности почти никогда не может быть вычислена.
На практике абсолютной погрешности недостаточно для точной оценки измерения.
Поэтому на практике более важное значение имеет определение относительной
погрешности измерения.
Относительная погрешность.
Абсолютная
погрешность, как мы убедились, не даёт возможности судить о качестве измерения.
Поэтому для оценки качества приближения вводится новое понятие – относительная
погрешность. Относительная погрешность позволяет судить о качестве измерения.
Относительная погрешность –
это частное от деления абсолютной погрешности на модуль приближённого значения
измеряемой величины, выраженная в долях или процентах.
Относительная
погрешность величина всегда положительная. Это следует из того, что абсолютная погрешность
всегда положительная величина, и мы делим её на модуль приближённого значения
измеряемой величины, а модуль тоже всегда положителен.
ПРИМЕР:
Округлим дробь 14,7 до целых и найдём относительную погрешность приближённого
значения:
14,7 ≈ 15,
Для вычисления
относительной погрешности, кроме приближённого значения, нужно знать ещё и
абсолютную погрешность. Обычно абсолютная погрешность неизвестна, поэтому
вычислить относительную погрешность нельзя. В таких случаях ограничиваются
оценкой относительной погрешности.
ПРИМЕР:
При измерении в (сантиметрах) толщины
b
стекла и длины l книжной полки
получили следующие результаты:
b ≈ 0,4 с
точностью до 0,1,
l ≈ 100 с
точностью до 0,1.
Абсолютная погрешность каждого из этих измерений не
превосходит 0,1. Однако 0,1 составляет
существенную часть числа 0,4 и
ничтожную часть числа 100. Это показывает, что качество второго
измерения намного выше, чем первого.
В результате измерения нашли,
что b ≈ 0,4 с точностью до 0,1, то
есть абсолютная погрешность измерения не превосходит 0,1.
Значит, отношение абсолютной погрешности к приближённому значению меньше или равно
то есть относительная погрешность приближения не превосходит 25%.
Аналогично найдём, что
относительная погрешность приближения, полученного при измерении длины полки,
не превосходит
Говорят, что в первом случае измерение выполнено с
относительной точностью до 25%,
а во втором – с относительной точностью до 0,1%.
ПРИМЕР:
Если взять абсолютную погрешность в 1
см, при измерении длины отрезков 10
см и 10
м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для
отрезка длиной в 10 см погрешность
в 1
см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, эта ошибка всего в 0,1%.
Чем меньше относительная погрешность
измерения, тем оно точнее.
Различают
систематические и случайные погрешности.
Систематической погрешностью называют ту погрешность, которая остаётся неизменной при
повторных измерениях.
Случайной погрешностью называют ту погрешность, которая возникает в результате
воздействия на процесс измерения внешних факторов и может изменять своё
значение.
В большинстве
случаев невозможно узнать точное значение приближённого числа, а значит, и
точную величину погрешности. Однако почти всегда можно установить, что
погрешность (абсолютная или относительная) не превосходит некоторого числа.
ПРИМЕР:
Продавец взвешивает арбуз на чашечных весах. В наборе
наименьшая гиря – 50
г. Взвешивание показало 3600 г. Это число – приближённое. Точный вес арбуза
неизвестен. Но абсолютная погрешность не превышает 50
г. Относительная погрешность не превосходит
50/3600 ≈
1,4%.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной
погрешностью.
Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной
погрешностью.
В предыдущем примере
за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность 1,4%.
Величина предельной
погрешности не является вполне определённой. Так в предыдущем примере можно
принять за предельную абсолютную погрешность
100 г, 150 г и вообще всякое
число, большее чем 50 г.
На практике берётся по возможности меньшее значение предельной погрешности. В
тех случаях, когда известна точная величина погрешности, эта величина служит
одновременно предельной погрешностью. Для каждого приближённого числа должна
быть известна его предельная погрешность (абсолютная или относительная). Когда
она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено
приближённое число 4,78 без указания предельной погрешности, то подразумевается,
что предельная абсолютная погрешность составляет 0,005. В следствии этого соглашения всегда можно обойтись без указания
предельной погрешности числа.
Предельная
абсолютная погрешность обозначается греческой буквой ∆ (<<дельта>>),
предельная относительная погрешность – греческой буквой δ
(<<дельта малая>>). Если приближённое число обозначить буквой а,
Правила округления.
На практике
относительную погрешность округляют до двух значащих цифр, выполняя округление
с избытком, то есть, всегда увеличивая последнюю значащую цифру на единицу.
ПРИМЕР:
Для х = 1,7 ± 0,2 относительная погрешность измерений равна:
ПРИМЕР:
Длина карандаша измерена линейкой с миллиметровым
делением. Измерение показало 17,9 см. Какова предельная относительная погрешность этого
измерения ?
РЕШЕНИЕ:
Здесь а =
17,9 см. Можно принять ∆ = 0,1 см, так как с точностью
до 1 мм
измерить карандаш нетрудно, а значительно уменьшить предельную
погрешность не удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но
у самого карандаша рёбра могут отличаться на большую величину). Относительная погрешность равна
Округляя, находим
ПРИМЕР:
Цилиндрический поршень имеет около 35
мм в диаметре. С какой точностью нужно
его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05% ?
РЕШЕНИЕ:
По условию, предельная относительная
погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная абсолютная
погрешность равна
или, усиливая, 0,02
мм.
Можно воспользоваться
формулой
Подставляя в формулу
а = 35,
𝛿 = 0,0005,
имеем
Значит,
∆
= 35 × 0,0005 = 0,0175 мм.
Действия над приближёнными числами.
Сложение и вычитание приближённых чисел.
Абсолютная погрешность суммы двух величин равна сумме
абсолютных погрешностей отдельных слагаемых.
ПРИМЕР:
Складываются приближённые числа
265 и 32.
РЕШЕНИЕ:
Пусть предельная погрешность первого есть 5,
а второго 1. Тогда предельная погрешность суммы равна
5
+ 1 = 6.
Так, если истинное значение первого есть 270,
а второго 33, то приближённая сумма
265
+ 32 = 297
на 6 меньше истинной
270
+ 33 = 303.
ПРИМЕР:
Найти сумму приближённых чисел:
0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Предельная погрешность каждого слагаемого
0,00005.
Предельная погрешность суммы:
0,00005
∙ 9 = 0,00045.
Значит, в последнем (четвёртом) знаке суммы возможна ошибка до 5
единиц. Поэтому округляем сумму до третьего знака, то есть до тысячных.
Получаем 0,619,
здесь все знаки верные.
При значительном
числе слагаемых обычно происходит взаимная компенсация погрешностей, поэтому
истинная погрешность суммы лишь в исключительных случаях совпадает с предельной
погрешностью или близка к ней. Насколько редки эти случаи, видно из предыдущего
примера, где 9 слагаемых. Истинная величина каждого из них может
отличаться в пятом знаке от взятого приближённого значения на 1, 2, 3, 4 или даже на 5 единиц в ту и в другую сторону.
Например, первое
слагаемое может быть больше своего истинного значения на 4 единицы пятого знака, второе – на две, третье – меньше
истинного на одну единицу и так далее.
Расчёт показывает,
что число всех возможных случаев распределения погрешностей составляет около
одного миллиарда. Между тем лишь в двух случаях погрешность суммы может
достигнуть предельной погрешности 0,00045,
это произойдёт:
– когда истинная величина каждого слагаемого больше
приближённой величины на 0,00005;
– когда истинная величина каждого слагаемого меньше
приближённой величины на 0,00005.
Значит, случаи,
когда погрешность суммы совпадает с предельной, составляют только 0,0000002% всех возможных случаев.
Дальнейший расчёт
показывает, что случаи, когда погрешность суммы девяти слагаемых может
превысить три единицы последнего знака, тоже очень редки. Они составляют
лишь 0,07%
из числа всех
возможных. Две единицы последнего знака погрешность может превысить 2% всех возможных случаев, а одну единицу –
примерно в 25%.
В остальных 75% случаев погрешность девяти слагаемых не
превышает одной единицы последнего знака.
ПРИМЕР:
Найти сумму точных чисел:
0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Округлим их до тысячных и сложим:
0,091
+ 0,083 + 0,077 + 0,071 + 0,067
+ 0,062 + 0,059 + 0,056 + 0,053 = 0,619.
Предельная погрешность суммы:
0,0005
∙ 9 = 0,0045.
Приближённая сумма отличается от истинной на 0,0003,
то есть на треть единицы последнего знака приближённых чисел. Все три знака
приближённой суммы верны, хотя теоретически последняя цифра могла быть грубо
неверной.
Произведём в наших слагаемых округление до сотых. Теперь
предельная погрешность суммы будет:
0,005
∙ 9 = 0,045.
Между тем получим:
0,09
+ 0,08 + 0,08 + 0,07 + 0,07
+ 0,06 + 0,06 + 0,06 + 0,05 = 0,62.
Истинная погрешность составляет только 0,0013.
Предельная абсолютная погрешность разности двух величин
равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.
ПРИМЕР:
Пусть предельная погрешность приближённого
уменьшаемого 85 равна 2,
а предельная погрешность вычитаемого 32 равна 3.
Предельная погрешность разности
85
– 32 = 53
есть
2
+ 3 = 5.
В самом деле, истинное значение уменьшаемого и
вычитаемого могут равняться
85
+ 2 = 87 и
32
– 3 = 29.
Тогда истинная разность есть
87
– 29 = 58.
Она на 5 отличается от
приближённой разности 53.
Относительная погрешность суммы и разности.
Предельную
относительную погрешность суммы и разности легко найти, вычислив сначала
предельную абсолютную погрешность.
Предельная
относительная погрешность суммы (но не разности!) лежит между наименьшей и
наибольшей из относительных погрешностей слагаемых. Если все слагаемые имеют
одну и ту же (или примерно одну и ту же) предельную относительную погрешность,
то и сумма имеет ту же (или примерно ту же) предельную относительную
погрешность. Другими словами, в этом случае точность суммы (в процентном
выражении) не уступает точности слагаемых. При значительном же числе слагаемых
сумма, как правило, гораздо точнее слагаемых.
ПРИМЕР:
Найти предельную абсолютную и предельную относительную
погрешность суммы чисел:
24,4
+ 25,2 + 24,7.
РЕШЕНИЕ:
В каждом слагаемом суммы
24,4
+ 25,2 + 24,7 = 74,3
предельная относительная погрешность примерно одна и та
же, а именно:
0,05
: 25 = 0,2%.
Такова же она и для суммы.
Здесь предельная абсолютная погрешность равна 0,15,
а относительная
0,15
: 74,3 ≈ 0,15 : 75 = 0,2%.
В противоположность
сумме разность приближённых чисел может быть менее точной, чем уменьшаемое и
вычитаемое. <<Потеря точности>> особенно велика в том случае, когда
уменьшаемое и вычитаемое мало отличаются друг от друга.
Относительные погрешности при сложении и вычитании
складывать нельзя.
Умножение и деление приближённых чисел.
При делении и умножении чисел требуется сложить
относительные погрешности.
ПРИМЕР:
Пусть перемножаются приближённые числа 50 и 20, и пусть предельная относительная погрешность первого
сомножителя есть 0,4%, а второго
0,5%.
Тогда предельная относительная погрешность произведения
50
× 20 = 1000
приближённо равна 0,9%.
В самом деле предельная абсолютная погрешность первого сомножителя есть
50
× 0,004 = 0,2,
а второго
20
× 0,005 = 0,1.
Поэтому истинная величина произведения не больше чем
(50
+ 0,2)(20 + 0,1) = 1009,02,
и не меньше, чем
(50
– 0,2)(20 – 0,1) = 991,022.
Если истинная величина произведения есть 1009,2,
то погрешность произведения равна
1009,2
– 1000 = 9,02,
а если 991,02, то погрешность произведения равна
1000
– 991,02 = 8,98.
Рассмотренные два случая – самые неблагоприятные. Значит,
предельная абсолютная погрешность произведения есть 9,02.
Предельная относительная погрешность равна
9,02
: 1000 = 0,902%,
то есть приближённо 0,9%.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
- Урок 1. Числовые неравенства
- Урок 2. Свойства числовых неравенств
- Урок 3. Сложение и умножение числовых неравенств
- Урок 4. Числовые промежутки
- Урок 5. Линейные неравенства
- Урок 6. Системы линейных неравенств
- Урок 7. Нелинейные неравенства
- Урок 8. Системы нелинейных неравенств
- Урок 9. Дробно-рациональные неравенства
- Урок 10. Решение неравенств с помощью графиков
- Урок 11. Неравенства с модулем
- Урок 12. Иррациональные неравенства
- Урок 13. Неравенства с двумя переменными
- Урок 14. Системы неравенств с двумя переменными
- Урок 15. Приближённые вычисления
Абсолютная и относительная погрешности
Абсолютная погрешность приближения
Имея дело в вычислениях с бесконечными десятичными дробями, приходится для удобства выполнять приближение этих чисел, т. е. округлять их. Приблизительные числа получаются также при различных измерениях.
Бывает полезно узнать, как сильно приближенное значение числа отличается от его точного значения. Понятно, что чем это различие меньше, тем лучше, тем точнее выполнено измерение или вычисление.
Для определения точности измерений (вычислений) вводят такое понятие как погрешность приближения. По-другому его называют абсолютной погрешностью.
Абсолютной погрешностью приближения называется модуль разности между точным значением числа и его приближенным значением.
где х — это точное значение числа, а — его приближенное значение.
Например, в результате измерений было получено число 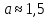
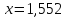
В случае с бесконечными дробями погрешность приближения определяется по той же формуле. На месте точного числа записывается сама бесконечная дробь. Например, 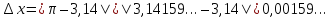
Приближение может выполняться как по недостатку, так и по избытку.
То же число π при приближении по недостатку с точностью до 0,01 равно 3,14, а при приближении по избытку с точностью до 0,01 равно 3,15.
Правило округления: если первая отбрасываемая цифра равна пяти или больше пяти, то выполняется приближение по избытку; если же меньше пяти, то по недостатку.
Например, т.к. третьей цифрой после запятой у числа π является 1, то при приближении с точностью до 0,01 оно выполняется по недостатку.
Вычислим абсолютные погрешности приближения до 0,01 числа π по недостатку и по избытку:
Как видим, абсолютная погрешность приближения по недостатку меньше, чем по избытку. Значит, приближение по недостатку в этом случае обладает более высокой точностью.
Относительная погрешность приближения
Абсолютная погрешность обладает одним важным недостатком – оно не позволяет оценить степень важности ошибки.
Например, покупаем мы на рынке 5 кг картофеля, а недобросовестный продавец при измерении веса ошибся на 50 г в свою пользу. Т.е. абсолютная погрешность составила 50 г. Для нас такая оплошность будет сущей мелочью и мы даже не обратим на неё внимания. А если при приготовлении лекарства произойдёт подобная ошибка? Тут уже всё будет намного серьёзней. А при загрузке товарного вагона наверняка возникают отклонения намного больше данного значения.
Поэтому сама по себе абсолютная погрешность малоинформативная. Кроме неё очень часто дополнительно рассчитывают относительное отклонение.
Относительной погрешностью приближения называется отношение абсолютной погрешности к точному значению числа.
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
Приведём несколько примеров.
Пример 1. На предприятии 1284 рабочих и служащих. Округлить количество работающих до целых с избытком и с недостатком. Найти их абсолютные и относительные погрешности (в процентах). Сделать вывод.
Итак, 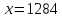
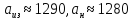
Абсолютная погрешность:
Относительная погрешность:
Значит, точность приближения с недостатком выше, чем точность приближения с избытком.
Пример 2. В школе 197 учащихся. Округлить количество учащихся до целых с избытком и с недостатком. Найти их абсолютные и относительные погрешности (в процентах). Сделать вывод.
Итак, 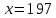
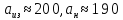
Абсолютная погрешность:
Относительная погрешность:
Значит, точность приближения с избытком выше, чем точность приближения с недостатком.
-
Найдите абсолютную погрешность приближения:
-
числа 2,87 числом 2,9; числом 2,8;
-
числа 0,6595 числом 0,7; числом 0,6;
-
числа
числом
;
-
числа
числом 0,3;
-
числа 4,63 числом 4,6; числом 4,7;
-
числа 0,8535 числом 0,8; числом 0,9;
-
число
числом
;
-
число
числом 0,2.
-
Приближённое значение числа х равно а. Найдите абсолютную погрешность приближения, если:
|
|
|
|
|
|
|
|
|
|
|
|
-
Запишите в виде двойного неравенства:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Найдите приближённое значение числа х, равное среднему арифметическому приближений с недостатком и избытком, если:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Докажите, что среднее арифметическое чисел а и b является приближённым значением каждого из этих чисел с точностью до
.
-
Округлите числа:
|
|
|
|
|
|
|
|
|
|
|
|
-
Представьте обыкновенную дробь в виде десятичной и округлите её до тысячных и найдите абсолютную погрешность:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Докажите, что каждое из чисел 0,368 и 0,369 является приближённым значением числа
с точностью до 0,001. Какое из них является приближённым значением числа
с точностью до 0,0005?
-
Докажите, что каждое из чисел 0,38 и 0,39 является приближённым значением числа
с точностью до 0,01. Какое из них является приближённым значением числа
с точностью до 0,005?
-
Округлите число до единиц и найдите относительную погрешность округления:
|
|
|
|
|
|
|
|
-
Представьте каждое из чисел
и
в виде десятичной дроби. Округлив полученные дроби до десятых, найдите абсолютную и относительную погрешности приближений.
-
Представьте каждое из чисел
и
в виде десятичной дроби. Округлив полученные дроби до десятых, найдите абсолютную и относительную погрешности приближений.
-
Радиус Земли равен 6380 км с точностью до 10 км. Оцените относительную погрешность приближённого значения.
-
Наименьшее расстояние от Земли до Луны равно 356400 км с точностью до 100 км. Оцените относительную погрешность приближения.
-
Сравните качества измерения массы М электровоза и массы т таблетки лекарства, если
т (с точностью до 0,5 т), а
г (с точностью до 0,01 г).
-
Сравните качества измерения длины
реки Волги и диаметра
мячика для настольного тенниса, если
км (с точностью до 5 км) и
мм (с точностью до 1 мм).
3
☰
Погрешность приближения
Имея дело в вычислениях с бесконечными десятичными дробями, приходится для удобства выполнять приближение этих чисел, т. е. округлять их. Приблизительные числа получаются также при различных измерениях.
Бывает полезно узнать, как сильно приближенное значение числа отличается от его точного значения. Понятно, что чем это различие меньше, тем лучше, тем точнее выполнено измерение или вычисление.
Для определения точности измерений (вычислений) вводят такое понятие как погрешность приближения. По-другому его называют абсолютной погрешностью. Погрешность приближения представляет собой взятую по модулю разность между точным значением числа и его приближенным значением.
Если a — это точное значение числа, а b — его приближенное значение, то погрешность приближения определяется по формуле |a – b|.
Допустим, что в результате измерений было получено число 1,5. Однако в результате вычисления по формуле точное значение этого числа равно 1,552. В таком случае погрешность приближения будет равна |1,552 – 1,5| = 0,052.
В случае с бесконечными дробями погрешность приближения определяется по той же формуле. На месте точного числа записывается сама бесконечная дробь. Например, |π – 3,14| = |3,14159… – 3,14| = 0,00159… . Здесь получается, что погрешность приближения выражена иррациональным числом.
Как известно, приближение может выполняться как по недостатку, так и по избытку. То же число π при приближении по недостатку с точностью до 0,01 равно 3,14, а при приближении по избытку с точностью до 0,01 равно 3,15. Причина, по которой в вычислениях используется его приближение по недостатку, заключается в применении правил округления. Согласно этим правилам, если первая отбрасываемая цифра равна пяти или больше пяти, то выполняется приближение по избытку. Если меньше пяти, то по недостатку. Так как третьей цифрой после запятой у числа π является 1, то поэтому при приближении с точностью до 0,01 оно выполняется по недостатку.
Действительно, если вычислить погрешности приближения до 0,01 числа π по недостатку и по избытку, то получим:
|3,14159… – 3,14| = 0,00159…
|3,14159… – 3,15| = 0,0084…
Так как 0,00159…
Говоря о погрешности приближения, также как и в случае с самим приближением (по избытку или недостатку), указывают его точность. Так в приводимом выше примере с числом π следует сказать, что оно равно числу 3,14 с точностью до 0,01. Ведь модуль разности между самим числом и его приближенным значением не превышает 0,01 (0,00159… ≤ 0,01).
Точно также π равно 3,15 с точностью до 0,01, так как 0,0084… ≤ 0,01. Однако если говорить о большей точности, например до 0,005, то мы можем сказать, что π равно 3,14 с точностью до 0,005 (так как 0,00159… ≤ 0,005). Сказать же это по отношению к приближению 3,15 мы не можем (так как 0,0084… > 0,005).
Загрузить PDF
Загрузить PDF
Абсолютная погрешность – это фактическая ошибка, допущенная при измерении какой-либо величины. Относительная погрешность сравнивает абсолютную погрешность со значением измеряемой величины. Чтобы вычислить относительную погрешность, следует найти и абсолютную погрешность. Если вы измеряете предмет, длина которого равна 12 см, и вы допустили ошибку в 6 см, то относительная погрешность будет огромной. Но если длина измеряемого предмета равна 12 м, а ошибка – 6 см, то относительная погрешность будет значительно меньше, даже с учетом того, что абсолютная погрешность (6 см) не изменилась.[1]
-
1
Если вам дано ожидаемое значение, вычтите из него полученное вами значение, чтобы вычислить абсолютную погрешность. Как правило, ожидаемое значение находится в ходе тестовых или лабораторных испытаний. Ожидаемое значение является наиболее точным значением некоторой величины, которое используется при различных вычислениях. Чтобы получить абсолютную погрешность, сравните результаты ваших измерений с ожидаемым значением – так вы узнаете, насколько ваши результаты отличаются от ожидаемого значения. Для этого просто вычтите полученное вами значение из ожидаемого. Если разность отрицательная, превратите ее в положительную, проигнорировав знак «минус». Вы получите абсолютную погрешность.[2]
-
Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
-
Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
-
2
Теперь допустим, что абсолютная погрешность – это наименьшая единица измерения. Например, рулетка имеет миллиметровые деления, то есть ее наименьшей единицей является 1 мм. Таким образом, вы можете измерить расстояние с точностью до ± 1 мм; в этом случае абсолютная погрешность составляет 1 мм.
- Это верно для любых измерительных инструментов или систем. Например, на корпус многих научных инструментов, таких как прецизионные весы и измерительные приборы, наносят маркировку об абсолютной погрешности в виде «± ____».
-
3
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Используйте те же единицы измерения, которыми вы пользовались в ваших измерениях.[4]
-
4
Попрактикуйтесь на нескольких примерах. Это наилучший способ научиться вычислять погрешность. Решите следующие задачи (ответы приведены в конце каждой задачи).
- На уроке химии в результате реакции ученик получил вещество массой 32 г. Известно, что действительное значение выхода этой реакции равно 34 г. Абсолютная погрешность равна ± 2 г.
- На уроке химии ученику необходимо 10 мл воды, чтобы вызвать реакцию; при этом погрешность капельницы составляет «± 0,5 мл». В этом случае абсолютная погрешность измерений равна ± 0,5 мл.
-
5
Уясните, что приводит к появлению погрешности и как ее устранить. Всякое научное исследование подразумевает наличие ошибок – даже в научных работах, за которые вручаются Нобелевские премии, сообщается о допущениях или погрешностях. Но если вы определите причину появления погрешности, вы, возможно, сможете устранить ее.[5]
- Человеческий фактор – наиболее распространенная причина появления ошибок. Сюда относятся неподобающие условия для проведения измерений и плохо продуманные эксперименты.
- Одной из причин появления ошибок может являться внезапное отключение энергии, недостаточное количество рабочего материала или изменение других условий, например, нехватка воды в результате ее испарения, внезапное изменение температуры окружающей среды и так далее.
- Еще одной причиной является несовершенство оборудования, используемого для измерений или исследований, например, прецизионных инструментов или горелок, которые обеспечивают неравномерное распределение тепла.[6]
Реклама
-
1
Разделите абсолютную погрешность на действительное значение исследуемой величины. Так вы вычислите относительную погрешность. Эта формула позволит вам выяснить, насколько полученное вами значение отличается от действительного значения изучаемой величины. Конечно, прекрасно, если относительная погрешность мала. Продолжим рассматривать пример с измерением расстояния между двумя деревьями.
- Абсолютная погрешность равна 0,6 м, а действительное значение равно 6 м.
- 0,6 м / 6 м
- Относительная погрешность равна 0,1 м.[7]
-
2
Полученный результат умножьте на 100, чтобы выразить относительную погрешность в процентах. Вы можете представить относительную погрешность в виде обыкновенной дроби, десятичной дроби или в процентах – в этом случае умножьте десятичную дробь на 100. Так вы узнаете, какой процент от полученного вами значения составляет погрешность. Если вы измеряете длину 60 м лодки, а погрешность составляет 0,6 м, то процент ошибки будет значительно меньше, чем при вычислении расстояния между деревьями (6 м) с погрешностью 0,6 м. Погрешность представляет собой небольшой процент от экспериментального значения. [8]
- 0,6 м / 6 м = 0,1 м
- 0,1 * 100 = 10% – относительная погрешность.
-
3
Вычислите относительную погрешность без нахождения абсолютной погрешности. Для этого выражение для вычисления абсолютной погрешности запишите в числителе выражения для нахождения относительной погрешности. Уяснив разницу между абсолютной и относительной погрешностями, нет необходимости отдельно вычислять абсолютную погрешность. Просто замените значение абсолютной погрешности на выражение для ее вычисления. Обратите внимание, что вертикальные черты обозначают абсолютную величину, то есть любое полученное значение нужно превратить в положительное.
- Относительная погрешность:
, где Е — экспериментальное значение, D — действительное значение.
- Умножьте это выражение на 100, чтобы выразить относительную погрешность в процентах.[9]
- Относительная погрешность:
-
4
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Также не имеет смысла указывать погрешность в виде процентов от ошибки (10% от 0,6 м) – следует писать, например, так: относительная погрешность равна 10%.[10]
Реклама
Советы
- Удостоверьтесь, что экспериментальное значение и действительное значение измеряются в одних единицах измерения. Например, если экспериментальное значение измеряется в сантиметрах, а действительное значение – в миллиметрах, преобразуйте одну из этих единиц измерения в другую.
Реклама
Предупреждения
- Убедитесь, что вы правильно округляете числа.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 169 791 раз.















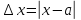
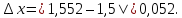
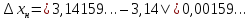
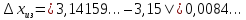
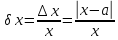
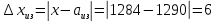
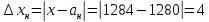
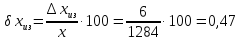
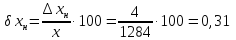
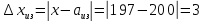
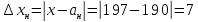
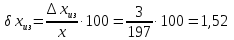
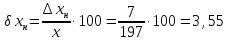
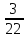 числом
числом 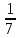 ;
;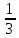 числом 0,3;
числом 0,3;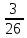 числом
числом 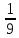 ;
;








