Как найти относительную точность приближения

При измерении
длин отрезков и площадей фигур, при взвешивании тел и других измерениях
получаются числа, выражающие эти величины.

Ввиду
погрешностей измерения полученные числа являются приближёнными значениями измеряемой
величины.

У каждого из
вас есть линейка и карандаш. Давайте попытаемся измерить длину карандаша.

Из рисунка
видно, что длина карандаша чуть меньше 10 см. Если бы на этой линейке не было
миллиметровых делений, то мы бы сказали, что длина карандаша равна 10 см. Но
это было бы не совсем точное измерение.

Такую
неточность называют погрешностью измерения.

В нашем случае,
на линейке есть миллиметровые деления, поэтому мы можем измерить длину
карандаша с более высокой точностью – 9,8 см.

Приближённое
значение отличается от точного значения в этом случае на 0,2 см. Чтобы узнать,
на сколько приближённое значение отличается от точного, надо из большего числа
вычесть меньшее, т.е. найти модуль разности точного и приближённого значений.
Этот модуль разности называют абсолютной погрешностью.

Определение:

Абсолютной
погрешностью приближённого значения называют модуль разности точного и приближённого значений.

Значение
абсолютной погрешности не всегда можно найти. Но обычно известна её оценка
сверху – например, при измерении длины отрезка линейкой с сантиметровыми
делениями абсолютная погрешность измерения не превышает 1 сантиметра, а при
взвешивании на весах с гирями 100 грамм, 200 грамм, 500 грамм и 1 килограмм
абсолютная погрешность взвешивания не превышает ста грамм.

Посмотрите, на слайде
изображён отрезок CD.

Его длина
расположена между цифрами 7 см и 8 см. Понятно, что 7 см – это приближённое
значение длины отрезка CD с недостатком, а 8 см – это приближённое значение длины отрезка CD с
избытком.

Если истинную длину
отрезка обозначить за х, то получим, что длина отрезка CD удовлетворяет
неравенству:

Пусть истинное
значение измеряемой величины равно .

Измерение дало
результат .

Тогда разность  – это абсолютная погрешность измерения.

Число  называют границей абсолютной погрешности
измерения, если выполняется неравенство:

Принято писать

Точность
приближённого значения зависит от многих причин. Если приближённое значение
получено в процессе измерения, то, конечно же, его точность будет зависеть от
прибора, с помощью которого выполнялось это измерение.

Вот, например,
комнатный термометр. На нём деления нанесены через один градус. Это даёт
возможность измерять температуру воздуха с точностью до 1 градуса. А на весах,
у которых цена деления шкалы 20 г, можно взвешивать с точностью до 20 г. Или, к примеру, ещё, механические часы. Цена одного
деления, которых 1 мин. По ним можно сказать время с точностью до 1 минуты.

Для оценки
качества измерения можно использовать относительную погрешность приближённого
значения.

Определение:

Относительной
погрешностью приближённого значения называется отношение абсолютной погрешности к модулю приближённого
значения.

Относительную
погрешность принято выражать в процентах. В тех случаях, когда абсолютная
погрешность приближенного значения неизвестна, а известна лишь его точность,
ограничиваются оценкой относительной погрешности.

Например: при измерении (в сантиметрах) длины книжной полки и
толщины компакт-диска получили следующие результаты:

Чем меньше
относительная погрешность измерения, тем оно точнее.

Итоги:

Абсолютной
погрешностью приближенного значения
называют модуль разности точного и приближенного значений.

Число  называют границей абсолютной погрешности измерения,
если выполняется неравенство:

Относительной
погрешностью приближенного значения называется
отношение абсолютной погрешности к модулю приближенного значения.

Чем меньше
относительная погрешность измерения, тем оно

точнее.

Автор: Софронова Наталия Андреевна,

учитель математики МОУ «Упшинская ООШ»

Оршанского района Республики Марий Эл

( К учебнику Ю.А.Макарычева Алгебра

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

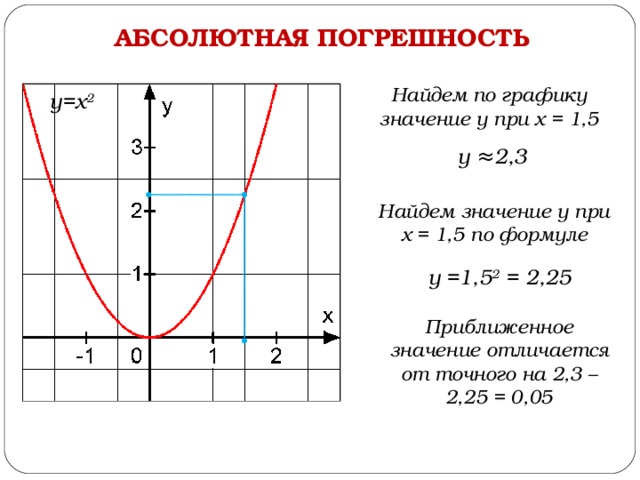
Найдем по графику значение у при х = 1,5

у=х 2

у ≈2,3

Найдем значение у при х = 1,5 по формуле

у =1,5 2 = 2,25

Приближенное значение отличается от точного на 2,3 – 2,25 = 0,05

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

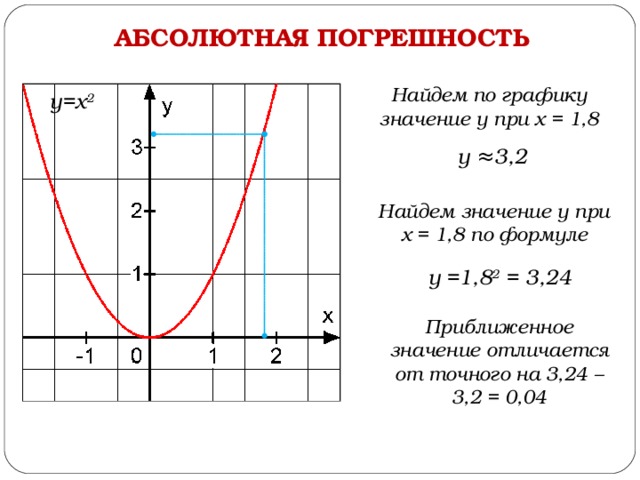
Найдем по графику значение у при х = 1,8

у=х 2

у ≈3,2

Найдем значение у при х = 1,8 по формуле

у =1,8 2 = 3,24

Приближенное значение отличается от точного на 3,24 – 3,2 = 0,04

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

х

1,5

Точное значение у

(по формуле)

1,8

2,25

Приближенное значение у (по графику)

3,24

2,3

3,2

у=х 2

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

у = 2,3 А.П. = |2,25 – 2,3| = |- 0,0 5| = 0,05

у = 3,2 А.П. = |3,24 – 3,2| = | 0,0 4| = 0,04

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 1 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите абсолютную погрешность приближенного значения.

Решение. 1 6 ,38 ≈ 16

16,38 – точное значение;

16 – приближенное значение.

А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 2 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите абсолютную погрешность приближенного значения.

Решение. 10 6 7 ≈ 1070

1067 – точное значение;

1070 – приближенное значение.

А.П. = | 1067 – 1070 | = |-3| = 3

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Пример 3 . Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до десятых и найдите абсолютную погрешность приближенного значения.

Решение. 2, 1 3 ≈ 2,1

2,13 – точное значение;

2,1 – приближенное значение.

А.П. = | 2,13 – 2,1 | = | 0,03 | = 0,03

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Пример 4 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите абсолютную погрешность приближенного значения.

Решение.

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

Всегда ли можно найти абсолютную погрешность ?

АВ ≈ 5,3 см

Найдем длину отрезка АВ

А

В

Точного значения длины отрезка АВ мы определить не можем, поэтому и абсолютную погрешность приближенного значения найти невозможно.

В подобных случаях в качестве погрешности указывают такое число, больше которого абсолютная погрешность быть не может.

В нашем примере в качестве такого числа можно взять число 0,1.

ПОЧЕМУ? Цена деления линейки равна 0,1 см и поэтому абсолютная погрешность приближенного значения 5,3 не больше 0,1.

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

А

В

Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в санти-метрах) с точностью до 0,1

АВ ≈ 5,3 см

t ≈ 28 0 с точностью до 1

t ≈ 14 0 с точностью до 2

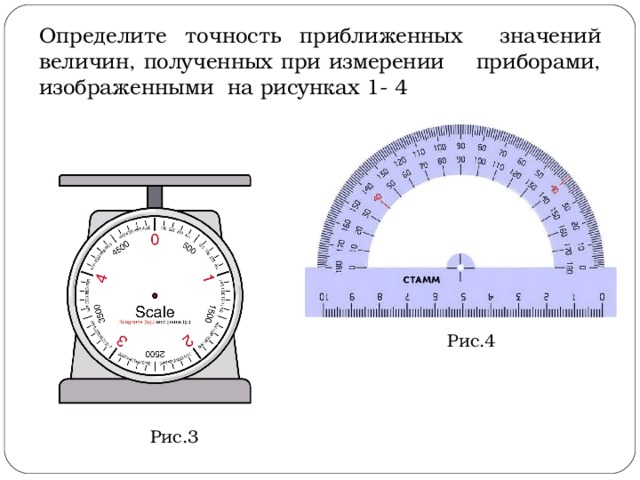
Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4

Рис.2

Рис.1

Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4

Рис.4

Рис.3

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в сантиметрах) с точностью до 0,1

АВ ≈ 5,3 см

Если х ≈ а и абсолютная погрешность приближенного значения не превосходит некоторого числа h , то число а называют приближенным значением х с точностью до h

х ≈ а с точностью до h

х = а ± h

Длина рулона 10,5 ± 0,5

ТОЧНОСТЬ ПРИБЛИЖЕНИЯ

А

В

АВ ≈ 5,3 см

с точностью до 0,1

t ≈ 28 0 с точностью до 1

t ≈ 14 0

с точностью до 2

Определение . Относительной погрешностью (точностью) приближенного значения называется отношение абсолютной погрешности (точности) к модулю приближенного значения

Для оценки качества измерения можно использовать определения относительной погрешности и относительной точности

l = 100,0 ± 0,1

b = 0,4 ± 0,1

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения

Пример 5 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите относительную погрешность приближенного значения.

Решение. 1 6 ,38 ≈ 16

16,38 – точное значение;

16 – приближенное значение.

А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения

Пример 6 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите относительную погрешность приближенного значения.

Решение. 10 6 7 ≈ 1070

1067 – точное значение;

1070 – приближенное значение.

А.П. = | 1067 – 1070 | = |-3| = 3

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Пример 7 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите относительную погрешность приближенного значения.

Решение.

Содержание:

1. Приближённые вычисления
2. Абсолютная и относительная погрешности
3. Выполнение действий над приближёнными числами
4. Выполнение действий без точного учёта погрешности

Приближённые вычисления

Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность

Абсолютная и относительная погрешности

При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.

Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.

Абсолютной погрешностью  приближённой называется модуль разности между точным значением величины  и её приближённым значением х, то есть

Пример.

Абсолютная погрешность приближённого числа  числом 0,44 составляет

Если точное число неизвестно, то найти абсолютную погрешность  невозможно. На практике вводят оценку допустимой при данных измерениях или вычислениях абсолютной погрешности, которую называют пределом абсолютной погрешности и обозначают буквой h. Считают, что h. Как правило, предел абсолютной погрешности устанавливают из практических соображений, например, при измерениях  пределом абсолютной погрешности считают наименьшее деление прибора.

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.

Цифра  называется верной, если предел абсолютной погрешности данного приближения не превышает единицы того разряда, в котором записана эта цифра. В другом случае цифра называется  сомнительной.

Например: в числе две цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых. Цифры 9 и 7 верны, поскольку  а цифры 4 и 6 являются сомнительными, поскольку 

В конечной записи приближённого числа сохраняют только верные цифры. Так число  можно записать в виде  , число  в виде  Если в десятичной дроби последние верные цифры — нули, то их оставляют в записи числа.

Например: если , то правильной записью числа будет 0,260.

Если в целом числе последние нули являются сомнительными, их исключают из записи числа.

Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.

Например: в числе  верными являются три первые цифры, а два последних нуля — сомнительные цифры. Запись числа возможна только в виде: 

Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.

Например:

1. Запись  означает, что , то есть предел абсолютной погрешности h=0,01.

2. Запись 

3. Если 

В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.

Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25_*10³ — две значимых цифры.

При таком подходе к записи приближенного числа необходимо уметь округлять числа.

Правила округления чисел:

— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.

— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.

— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.

— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.

Абсолютная погрешность не полностью характеризует точность приближения. Например,  будет грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже самое можно сказать и про предел абсолютной погрешности. Качество (точность) приближённости лучше характеризуется относительной погрешностью.

Относительной погрешностью  (омега) приближённости х величины  называется отношением абсолютной погрешности  этого приближения к модулю приближённого значения х, то есть 

Поскольку абсолютная погрешность  обычно бывает неизвестна, то на практике оценивают модуль относительной погрешности некоторым числом, которое не меньше чем этот модуль: 

Число  называется пределом относительной погрешности.

Предел относительной погрешности можно вычислить по формуле: 

Конечно относительная погрешность выражается в процентах.

С помощью относительной погрешности легко установить точность приближённости.

Пример 1. Найти относительную погрешность числа 

Решение: Имеем 

Следовательно 

Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что  .

Решение: 

Как видим, точность измерения высоты стола значительно выше.

Выполнение действий над приближёнными числами

Результат арифметических действий над приближёнными числами является также приближённым числом.

Необходимо уметь устанавливать погрешности результатов вычислений. Их находят с точным и без точного учёта погрешностей исходных данных. Правила нахождения погрешностей результатов действий с точным учётом погрешности приведены в таблице (обозначения —  исходные данные;  пределы абсолютных погрешностей относительно чисел; пределы относительных погрешностей).

Пример 3. Вычислить приближение значения выражения  и найти предел погрешностей результата.

Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.

Найдём границу относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ: 

Пример 4. Вычислить приближение значения выражения   и найти предел погрешностей результата.

Решение: находим значение квадратного корня из числа 6,24 и , имеем:

Граница относительной погрешности результата:

Граница абсолютной погрешности результата: 

Ответ: 

Выполнение действий без точного учёта погрешности

Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила. 

Сложение и вычитание приближённых вычислений рекомендуется выполнять так:

а) выделить слагаемое с наименьшим числом верных десятичных знаков;

б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;

в) выполнить действия, учитывая все сохранённые десятичные знаки;

г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.

Умножение и деление приближённых вычислений рекомендуется выполнять так:

а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;

б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;

в) выполнить действия — сохранить все значимые цифры;

г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.

При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.

При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.

Погрешность и точность приближения.

Найдем значение функции у = х² при х=1,5 и при х=2,1.

Можно найти значение функции двумя способами: по формуле и с помощью графика.

С помощью графика приближенные значения функции равны:

при х = 1,5 у ≈ 2,3;

при х = 2,1 у ≈ 4,4.

По формуле:

при х = 1,5 у = 1,5² = 2,25;

при х = 2,1 у = 2,1² = 4,41.

Приближенное значение отличается от точного, так как по графику мы не можем определить с точностью до сотых значение функции.

В первом случае приближенное значение отличается от точного на 0,05, а во втором – на 0,01.

Чтобы узнать, на сколько приближенное значение отличается от точного, надо из большего числа вычесть меньшее, т.е. найти модуль разности точного и приближенного значений.

Модуль разности точного и приближенного значений называется абсолютной погрешностью.

Но найти абсолютную погрешность не всегда возможно. Пусть, например, при измерении длины некоторого отрезка получен результат АВ ≈ 4,3 см. Мы не можем найти абсолютную погрешность приближенного значения, так как не знаем точного значения длины отрезка АВ. В таких случаях важно указать такое число, больше которого абсолютная погрешность быть не может. В рассматриваемом случае это 0,1 см, то есть 1 мм – цена деления линейки.

Если х ≈ a и абсолютная погрешность этого приближенного значения не превосходит некоторого числа h, то число а называют приближенным значением х с точностью до h.

Пишут х ≈ a с точностью до h.

Используют также такую запись:

x = а±h

Запись х= а±h означает, что точное значение переменной х заключено между числами a-h и a+h.

То есть a-h ≤ х ≤ a+h.

Для оценки качества измерения можно использовать относительную погрешность приближенного значения.

Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения.

Относительную погрешность принято выражать в процентах.

В тех случаях, когда абсолютная погрешность приближенного значения неизвестна, а известна только его точность, ограничиваются оценкой относительной погрешности.

Рассмотрим пример. При измерении в сантиметрах толщины стекла b получаем такой результат

b = 0,4±0,1.

В этом случае относительная погрешность не превосходит 0,10,4·100% , то есть 25%. Говорят, что измерение выполнено с относительной точностью 25%.

ПРИМЕР:

Для измерения длины болта использованы метровая линейка с
делениями  0,5 см  и линейка с
делениями  1 мм. В обоих случаях получен результат  3,5
см. Ясно, что в первом случае отклонение найденной длины  3,5
см  от истинной, не
должно по модулю превышать  0,5 см, во втором случае 
0,1 см.

Если этот же результат получится при измерении
штангенциркулем, то

p(l; 3,5) = |l – 3,5 ≤ 0,01|.

Данный пример показывает зависимость абсолютной
погрешности и границ, в которых находится точный результат, от точности
измерительных приборов. В одном случае  ∆l = 0,5  и, следовательно,

3
≤ l ≤ 4,

в другом – ∆l = 0,1  и

3,4
≤ l ≤ 3,6.

ПРИМЕР:

Длина листа бумаги формата  А4  равна  (29,7 ± 0,1)
см. А расстояние от Санкт-Петербурга до Москвы равно  (650 ± 1) км. Абсолютная погрешность в первом случае
не превосходит одного миллиметра, а во втором – одного километра. Необходимо
сравнить точность этих измерений.

РЕШЕНИЕ:

Если вы думаете, что длина листа измерена точнее потому,
что величина абсолютной  погрешности не
превышает  1 мм, то вы ошибаетесь.
Напрямую сравнить эти величины нельзя. Проведём некоторые рассуждения.

При измерении длины листа абсолютная погрешность не
превышает  0,1 см на  29,7 см, то есть в процентном отношении это составляет

0,1
: 29,7 ∙ 100% ≈ 0,33%

измеряемой величины.

Когда мы измеряем расстояние от Санкт-Петербурга до
Москвы, то абсолютная погрешность не превышает 
1 км 
на  650 км, что в процентном соотношении составляет

1
: 650 ∙ 100% ≈ 0,15%

измеряемой величины.

Видим, что расстояние между городами измерено точнее, чем
длинна листа формата  А4.

Истинное значение
измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и
действительная величина абсолютной погрешности почти никогда не может быть вычислена.
На практике абсолютной погрешности недостаточно для точной оценки измерения.
Поэтому на практике более важное значение имеет определение относительной
погрешности измерения.

Относительная погрешность.

Абсолютная
погрешность, как мы убедились, не даёт возможности судить о качестве измерения.
Поэтому для оценки качества приближения вводится новое понятие – относительная
погрешность. Относительная погрешность позволяет судить о качестве измерения.

Относительная погрешность –
это частное от деления абсолютной погрешности на модуль приближённого значения
измеряемой величины, выраженная в долях или процентах. 

Относительная
погрешность величина всегда положительная. Это следует из того, что абсолютная погрешность
всегда положительная величина, и мы делим её на модуль приближённого значения
измеряемой величины, а модуль тоже всегда положителен.

ПРИМЕР:

Округлим дробь  14,7 до целых и найдём относительную погрешность приближённого
значения:

14,7 ≈ 15,

Для вычисления
относительной погрешности, кроме приближённого значения, нужно знать ещё и
абсолютную погрешность. Обычно абсолютная погрешность неизвестна, поэтому
вычислить относительную погрешность нельзя. В таких случаях ограничиваются
оценкой относительной погрешности.

ПРИМЕР:

При измерении в (сантиметрах) толщины 
b 
стекла и длины  l  книжной полки
получили следующие результаты:

b ≈ 0,4 с
точностью до  0,1,

l ≈ 100 с
точностью до  0,1.

Абсолютная погрешность каждого из этих измерений не
превосходит  0,1. Однако  0,1  составляет
существенную часть числа  0,4  и
ничтожную часть числа  100. Это показывает, что качество второго
измерения намного выше, чем первого.

В результате измерения нашли,
что  b ≈ 0,4  с точностью до  0,1, то
есть абсолютная погрешность измерения не превосходит  0,1.
Значит, отношение абсолютной погрешности к приближённому значению меньше или равно

то есть относительная погрешность приближения не превосходит  25%.

Аналогично найдём, что
относительная погрешность приближения, полученного при измерении длины полки,
не превосходит

Говорят, что в первом случае измерение выполнено с
относительной точностью до  25%,
а во втором – с относительной точностью до  0,1%.

ПРИМЕР:

Если взять абсолютную погрешность в  1
см,  при измерении длины отрезков  10
см  и  10
м, то относительные погрешности будут соответственно равны  10%  и  0,1%. Для
отрезка длиной в  10 см  погрешность
в  1
см  очень велика, это ошибка в  10%. А для десятиметрового отрезка  1 см  не имеет значения, эта ошибка всего в   0,1%.

Чем меньше относительная погрешность
измерения, тем оно точнее.

Различают
систематические и случайные погрешности.

Систематической погрешностью называют ту погрешность, которая остаётся неизменной при
повторных измерениях.

Случайной погрешностью называют ту погрешность, которая возникает в результате
воздействия на процесс измерения внешних факторов и может изменять своё
значение.

В большинстве
случаев невозможно узнать точное значение приближённого числа, а значит, и
точную величину погрешности. Однако почти всегда можно установить, что
погрешность (абсолютная или относительная) не превосходит некоторого числа.

ПРИМЕР:

Продавец взвешивает арбуз на чашечных весах. В наборе
наименьшая гиря – 50
г. Взвешивание показало  3600 г. Это число – приближённое. Точный вес арбуза
неизвестен. Но абсолютная погрешность не превышает  50
г. Относительная погрешность не превосходит 

⁵⁰/₃₆₀₀ ≈
1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной
погрешностью.

Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной
погрешностью.

В предыдущем примере
за предельную абсолютную погрешность можно взять  50 г, а за предельную относительную погрешность  1,4%.

Величина предельной
погрешности не является вполне определённой. Так в предыдущем примере можно
принять за предельную абсолютную погрешность 
100 г, 150 г  и вообще всякое
число, большее чем  50 г.
На практике берётся по возможности меньшее значение предельной погрешности. В
тех случаях, когда известна точная величина погрешности, эта величина служит
одновременно предельной погрешностью. Для каждого приближённого числа должна
быть известна его предельная погрешность (абсолютная или относительная). Когда
она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено
приближённое число  4,78  без указания предельной погрешности, то подразумевается,
что предельная абсолютная погрешность составляет  0,005. В следствии этого соглашения всегда можно обойтись без указания
предельной погрешности числа.

Предельная
абсолютная погрешность обозначается греческой буквой  ∆ (<<дельта>>),
предельная относительная погрешность – греческой буквой  δ
(<<дельта малая>>). Если приближённое число обозначить буквой  а,