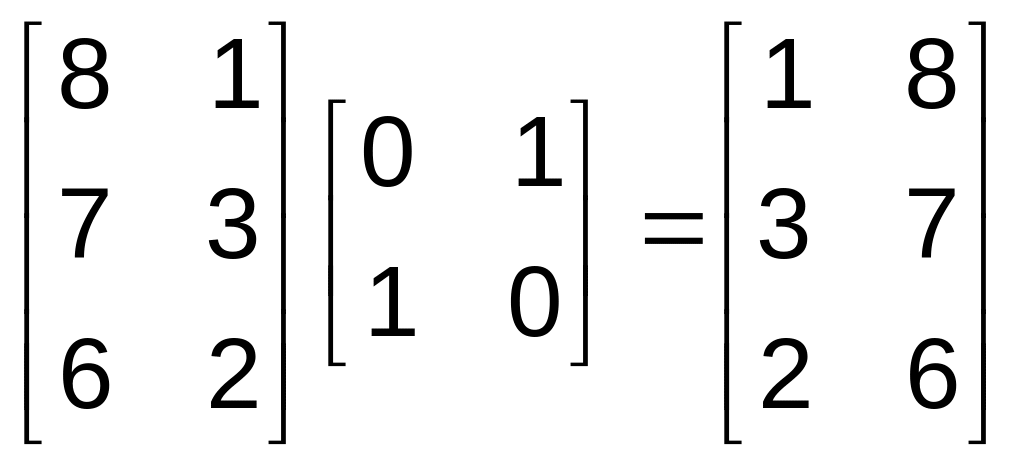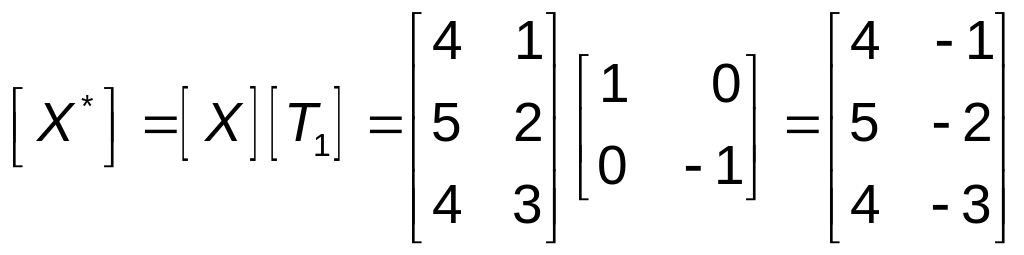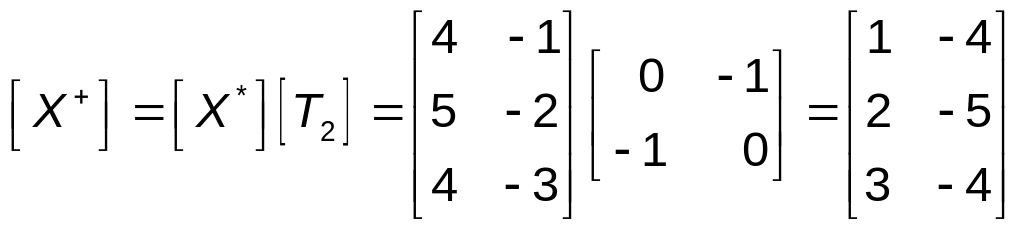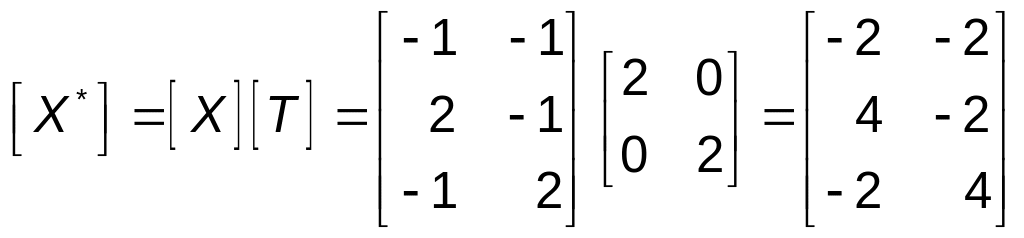Как найти точку, симметричную относительно прямой
Пусть даны некоторая прямая, заданная линейным уравнением, и точка, заданная своими координатами (x0, y0) и не лежащая на этой прямой. Требуется найти точку, которая была бы симметрична данной точке относительно данной прямой, то есть совпадала бы с ней, если плоскость мысленно согнуть пополам вдоль этой прямой.
Инструкция
Ясно, что обе точки — заданная и искомая — должны лежать на одной прямой, причем эта прямая должна быть перпендикулярна данной. Таким образом, первая часть задачи заключается в том, чтобы найти уравнение прямой, которая была бы перпендикулярна некоторой данной прямой и при этом проходила бы через данную точку.
Прямая может быть задана двумя способами. Каноническое уравнение прямой выглядит так: Ax + By + C = 0, где A, B, и C — константы. Также прямую можно определить при помощи линейной функции: y = kx + b, где k — угловой коэффициент, b — смещение.
Эти два способа взаимозаменяемы, и от любого можно перейти к другому. Если Ax + By + C = 0, то y = — (Ax + C)/B. Иными словами, в линейной функции y = kx + b угловой коэффициент k = -A/B, а смещение b = -C/B. Для поставленной задачи удобнее рассуждать, исходя из канонического уравнения прямой.
Если две прямые перпендикулярны друг другу, и уравнение первой прямой Ax + By + C = 0, то уравнение второй прямой должно выглядеть Bx — Ay + D = 0, где D — константа. Чтобы найти конкретное значение D, нужно дополнительно знать, через какую точку проходит перпендикулярная прямая. В данном случае это точка (x0, y0).
Следовательно, D должно удовлетворять равенству: Bx0 — Ay0 + D = 0, то есть D = Ay0 — Bx0.
После того как перпендикулярная прямая найдена, нужно вычислить координаты точки ее пересечения с данной. Для этого требуется решить систему линейных уравнений:
Ax + By + C = 0,
Bx — Ay + Ay0 — Bx0 = 0.
Ее решение даст числа (x1, y1), служащие координатами точки пересечения прямых.
Искомая точка должна лежать на найденной прямой, причем ее расстояние до точки пересечения должно быть равно расстоянию от точки пересечения до точки (x0, y0). Координаты точки, симметричной точке (x0, y0), можно, таким образом, найти, решив систему уравнений:
Bx — Ay + Ay0 — Bx0 = 0,
√((x1 — x0)^2 + (y1 — y0)^2 = √((x — x1)^2 + (y — y1)^2).
Но можно поступить проще. Если точки (x0, y0) и (x, y) находятся на равных расстояниях от точки (x1, y1), и все три точки лежат на одной прямой, то:
x — x1 = x1 — x0,
y — y1 = y1 — y0.
Следовательно, x = 2×1 — x0, y = 2y1 — y0. Подставив эти значения во второе уравнение первой системы и упростив выражения, легко убедиться, что правая его часть становится идентична левой. Дополнительно учитывать первое уравнение уже нет смысла, поскольку известно, что точки (x0, y0) и (x1, y1) ему удовлетворяют, а точка (x, y) заведомо лежит на той же прямой.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
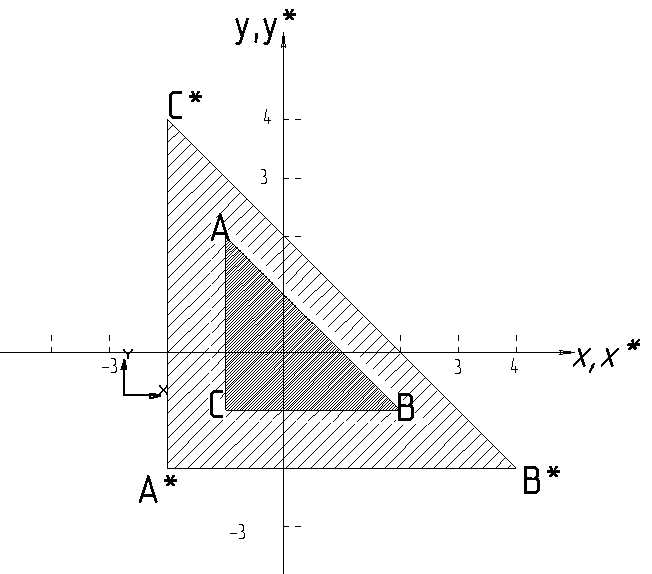
I’ve been doing some problems on the topic Reflection.And struggling with it when I am doing it graphically. I have solved it using Reflection Matrix but graphically it is giving the wrong answer. Please enlighten me where I am wrong?
I solved it for the equation Y = X correctly like
I have to find the reflection of the point
(2,5)aboutY = X, whose answer will definitely be(5,2)HOW I DID IT.
First of All I find the corresponding point on the line
Y = x, which will be(5,5) and (2,2), and the corresponding reflected point will have the same value of x coordinate as (5,5) and same value of Y coordinate as (2,2) so the answer will be(5,2)which is correct.
I am attaching an image in my support
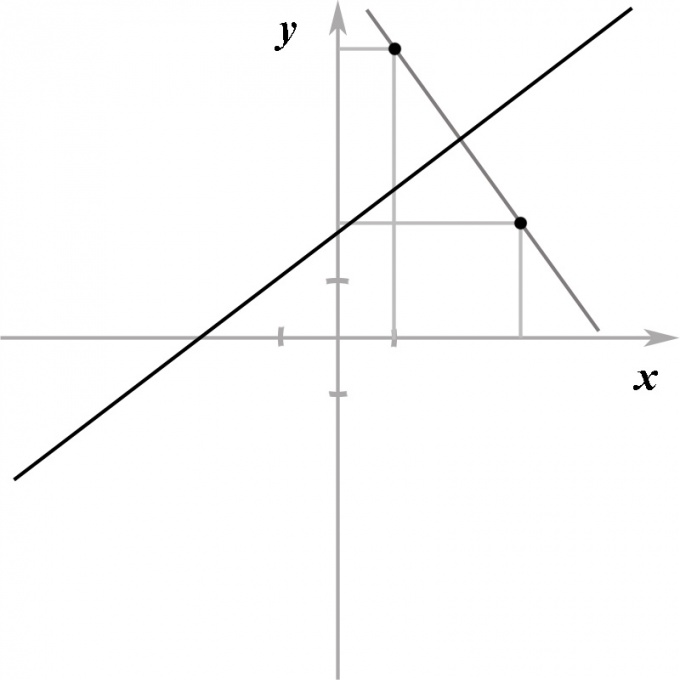
But when I solve it for equation 2Y = X + 1 it gives me wrong result
I have to find the reflection of the point
(3,-3)about2Y = X + 1, whose answer is (-1,5) but my answer is(7,2)HOW I DID IT.
First of All I find the corresponding point on the line
2Y = X + 1, which will be(3,2) and (-7,-3), and the corresponding reflected point will have the same value of x coordinate as (-7,-3) and same value of Y coordinate as (3,2) so the answer will be(-7,2)which is incorrect.
attached an image in my support
Please tell me where am I doing wrong?
Any other requirements or doubt in question?
Please ask me in comments.
В то
время, как полный поворот на плоскости
ху обычно осуществляется в двумерном
пространстве относительно нормали к
плоскости, отражение представляет собой
тот же поворот на угол 180º
в трехмерном пространстве и обратно на
плоскость относительно оси, лежащей на
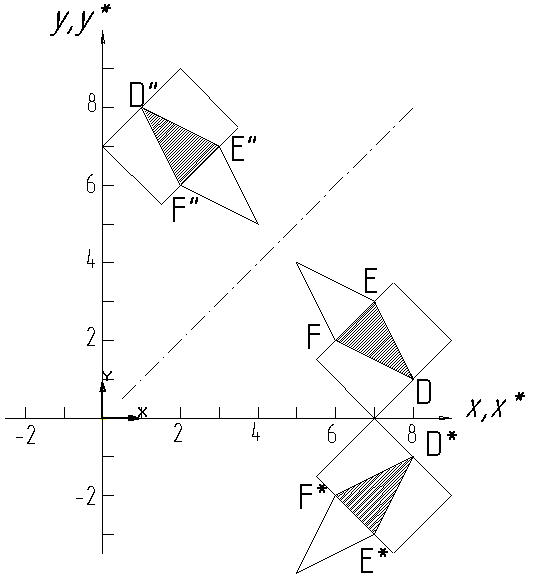
плоскости ху. На рис. 4.6 приведены
примеры двух отражений на плоскости
треугольника DEF.
Отражение относительно прямой у =
0 (ось х) получено с использованием
матрицы
(4.39)
В этом
случае новые вершины треугольника
D*E*F*
будут определяться преобразованием
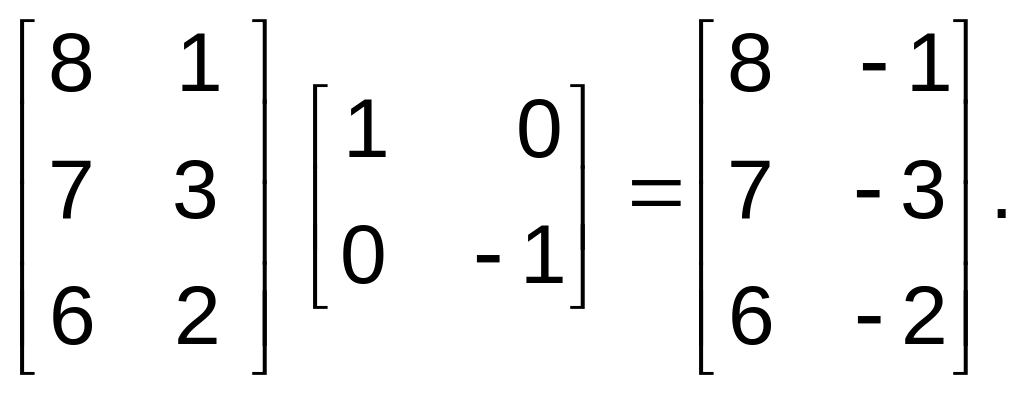
Подобным
образом отражение относительно оси у
при х = 0 будет иметь вид
(4.40)
Рис. 4.6
Отражение
относительно прямой у = х осуществляется
с помощью матрицы
.
(4.41)
Выполнив преобразования,
получим координаты вершин треугольника
D*E*F*
.
Аналогичным
образом отражение относительно оси х
будет иметь вид
.
(4.42)
У каждой
из этих матриц определитель равен –1.
В общем случае, если определитель равен
–1, то преобразование дает полное
отражение.
Если
оба полных отражения осуществляются
последовательно относительно прямых,
проходящих через начало координат, то
результатом будет полный поворот
относительно начала координат. Это
можно увидеть, обратившись к следующему
примеру.
Пример 3. Отражение и вращение
Рассмотрим
плоскость треугольника АВС, показанную
на рис. 4.7. Первоначально отобразим
относительно оси х (уравнение
(4.39)), а затем относительно прямой у =
–х (см. выражение (4.42)). Результатом
первого отображения будет
.
Результатом
второго будет
.
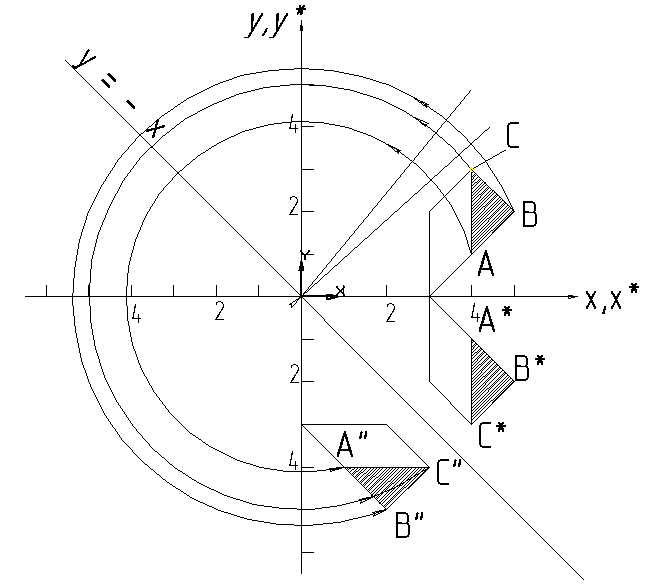
Рис. 4.7
Повернем
треугольник относительно начала
координат на угол θ
= 270º (4.35)
и получим аналогичный результат

Отметим,
что матрицы отражения из (4.39) и (4.42)
ортогональны,
т. е. транспонированная
матрица одновременно является обратной.
Например,
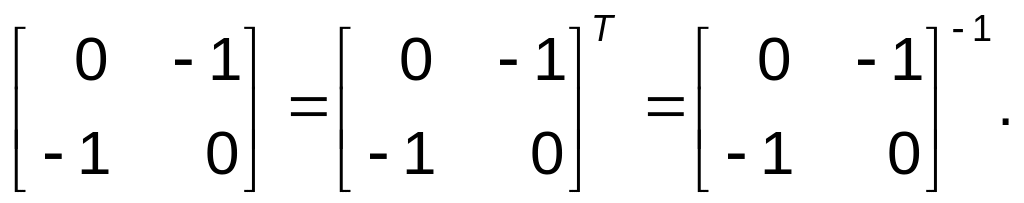
4.1.3.3. Масштабирование
Из
рассуждений относительно преобразования
точек следует, что величина масштабирования
определяется значением элементов
исходной диагональной матрицы. Если
матрица
используется
в качестве оператора воздействия на
вершины треугольника, то имеет место
«двукратное» расширение или равномерное
масштабирование относительно точки
начала координат. Если значения элементов
не равны, то треугольник искажается,
что проиллюстрировано на рис. 4.8.
Рис. 4.8
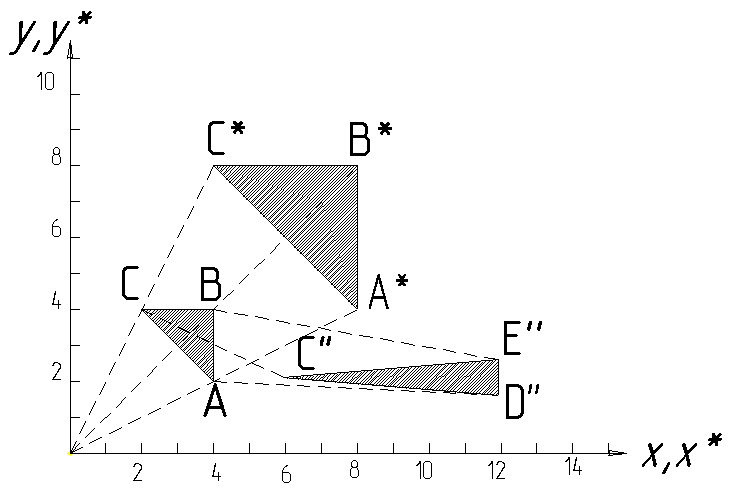
Треугольник
АВС, преобразованный с помощью
матрицы
,
переходит
в пропорционально увеличенный треугольник
А*В*С*.
Тот же треугольник, но преобразованный
с помощью матрицы
переходит
в треугольник D*E*F*,
имеющий искажение, вызванное разными
коэффициентами масштабирования.
В общем
случае при матрице
, (4.43)
в которой
а = d, b
= c = 0, выполняется
пропорциональное масштабирование; если
a ≠ d,
b = c
= 0, то масштабирование будет проведено
непропорционально. В первом случае для
a = d
> 1 происходит расширение, т. е.
увеличение изображения. Если a
= d < 1, то
происходит равномерное сжатие, т. е.
фигура уменьшается. Непропорциональное
расширение и сжатие возникают в
зависимости от значений a
и d, которые могут быть
меньше либо больше, чем 1, независимо
друг от друга.
Из рис.
4.8 видно также, что на первый взгляд
преобразование треугольника является
перемещением. Это объясняется тем, что
относительно начала координат
масштабируются координатные векторы,
а не точки.
Для
того чтобы лучше понять этот факт,
рассмотрим преобразования АВС в
D*E*F*
более внимательно. В частности,
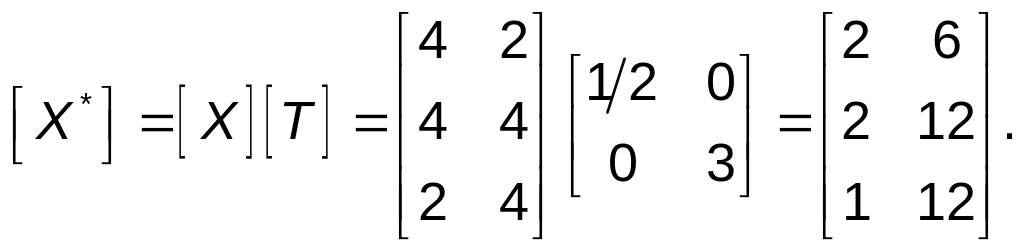
Заметим,
что каждая из компонент х
координатных векторов треугольника
DEF
умножалась на масштабный коэффициент
3, а компоненты у
– на 2.
Для
того чтобы получить чистое масштабирование
без эффекта перемещения, центр фигуры
надо поместить в начало координат. Это
видно на рис. 4.9, на котором треугольник
АВС
увеличивается в два раза при масштабировании
относительно его центра с координатами,
равными 1/3 основания и 1/3 высоты. Конкретная
матрица преобразования имеет вид
.
Рис. 4.9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #