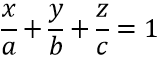Как найти отрезки отсекаемые от осей координат - Исправление недочетов и поиск решений вместе с Examum.ru

Общее уравнение
плоскости

Всякое уравнение
первой степени определяет в заданной
прямоугольной системе координат
плоскость.

Уравнение вида:

(27)

называется общим
уравнением плоскости. Вектор
,
перпендикулярный плоскости, называется
нормальным вектором плоскости.

Уравнение
плоскости, проходящей через точку
перпендикулярную вектору

Если плоскость
проходит через точку
перпендикулярно вектору,
то её уравнение имеет вид:

(28)

Уравнение
плоскости, проходящей через три точки
в отрезках

Пусть плоскость
проходит через точки
,,.

Имеет вид:

(29)

Если плоскость
отсекает по осям координат соответственно
отрезку
,,
и,
то её уравнение имеет вид:

(30)

Угол между
плоскостями. Условия параллельности
и перпендикулярности плоскостей

Угол
между плоскостямииопределяется по формуле:

(31)

Условие параллельности
плоскостей:

(32)

Условие
перпендикулярности плоскостей:

(33)

Расстояние
от точки до плоскости

Расстояние от
точки
до плоскостинаходится по формуле:

(34)

Пример 1. Составить
уравнение плоскости, проходящей через
точку
перпендикулярно вектору.

Решение. Воспользуемся
уравнением (28). Здесь
;;;;;.

Получим:
или.

Пример 2. Найти
отрезки, отсекаемые плоскостью
на осях координат.

Решение. Преобразуем
данноё уравнение плоскости к уравнению
в отрезках (30) следующим образом:

;

Следовательно,
величины отрезков, отсекаемых на осях,
равны:

;
;

Пример 3. Найти
расстояние между параллельными
плоскостями
и

Решение. Возьмём
на одной из плоскостей произвольную
точку и определим её расстояние от
другой плоскости. Например, на первой
плоскости выберем точку
и найдём её расстояние до плоскости,
пользуясь формулой (33):

Пример 4. Определить
угол, образованный плоскостями
и.

Решение. Воспользуемся
формулой (31)

Вопросы для
самопроверки

Как определяется
общее уравнение плоскости?

Какой вектор
называется нормальным к плоскости и
как определяются его координаты из
общего уравнения плоскости?

Как записывается
уравнение плоскости, проходящей через
точку перпендикулярно вектору?

Запишите уравнения
плоскости через три точки; в отрезках.

Как определяется
угол между плоскостями? Сформулируйте
условия параллельности и перпендикулярности
плоскостей.

Как определяется
расстояние от точки до плоскости?

Примеры для
самостоятельного решения
1. Составить
  уравнение плоскости, проходящей через
  точку
  м перпендикулярной вектору.
2. Составить
  уравнение плоскости, проходящей через
  точку
  и отсекающей равны отрезки на осях
  координат.
3. Составить
  уравнение плоскости, проходящей через
  точки
  .
  Через точкупровести плоскость, параллельно
  плоскости.
4. Составить
  уравнение плоскости, проходящей через
  точку
  перпендикулярно плоскостями.
5. Найти угол между
  плоскостями
  и.
6. При каких
  значениях
  иуравненияиопределяют параллельные плоскости?
7. При каком значении
  уравнениеиопределяют взаимно перпендикулярные
  плоскости?
8. Найти высоту
  пирамиды
  ,
  опущенную из вершинына грань АВС, если,,,.
  Указание. Данную высоту можно найти
  как расстояние от точкидо плоскости АВС.
9. Найти длину
  перпендикуляра, опущенного из точки
  на плоскость.
10. Составить
  уравнение плоскостей, параллельных
  плоскости
  и отстоящих от неё на расстоянии

Ответы к
примерам

4.7.1.
. 4.7.2..

4.7.3.
. 4.7.4..

4.7.5.
. 4.7.6..

4.7.7.
;. 4.7.8..

4.7.9.
.
4.7.10.,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Чтобы определить длину отрезков, отсекаемых на осях прямой, необходимо найти точки пересечения прямой с осями координат.

Найдём точку пересечения прямой с осью абсцисс. Для этого подставим координату y=0:

2 — 3x = 0;

3x = 2;

x=2/3.

Длина искомого отрезка на оси абсцисс равна 2/3.

Найдём точку пересечения прямой с осью ординат. Для этого подставим координату x=0:

y = 2 — 0;

y = 2.

Длина искомого отрезка на оси ординат равна 2.

Ответ: На оси абсцисс отсекается отрезок 2/3; на оси ординат — 2.

Источник

Ответ:

Пошаговое объяснение:

2x+4y-3z-12=0

уравнение в отрезках

а = -D/A = -12/2 = -6

b= -D/B = -12/4 = -3

c= -D/C = -12/(-3) = 4

абсолютные величины чисел a, b и c равны длинам отрезков, которые плоскость отсекает на координатных осях Ox, Oy и Oz соответственно, считая от начала координат

точки (-6,0.0) (0,-3,0) (0,0,4) — точки пересечения плоскости и координатных осей

Источник

Расстояние от точки до плоскости, как найти, пример, решение, формула, в пространстве, от точки до плоскости, расстояние, длина
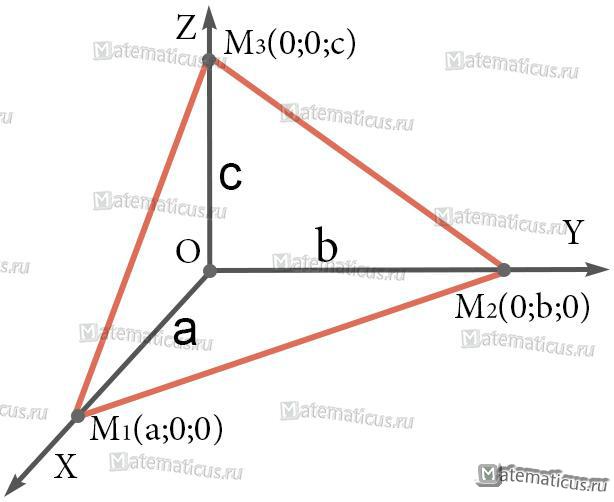
Если плоскость Ax + By + Cz + D = 0 отсекает на осях отрезки (не равные нулю) а, b, с, то ее можно представить в виде уравнения:

Это уравнение и есть уравнение плоскости в отрезках

а, b, с — отрезки, отсекаемые плоскостью на координатных осях и находятся по формулам:

отрезок на осях OX:

$a = — frac{D}{A}$, A≠0

отрезок на осях OY:

$b = — frac{D}{B}$, B≠0

отрезок на осях OZ:

$c = — frac{D}{C}$, C≠0

На рисунке точки M₁(a; 0; 0), M₂(0; b; 0) и M₃(0; 0; c) являются точками пересечения плоскости с координатными осями

Примечание

Плоскость, проходящую через начало координат, нельзя представить уравнением в отрезках

Пример
Написать уравнение плоскости 4x-6y+z-12=0 в отрезках.

$a = — frac{-12}{4}$, $b = — frac{-12}{-6}$, $c = — frac{-12}{1}$

Находим a=3, b=−2, c=12.
Уравнение в отрезках есть:

$frac{x}{3} + frac{y}{{ — 2}} + frac{z}{{12}} = 1$

3075

Источник

вторник, 08 января 2008

Не могу решить несколько задач…а завтра уже надо их сдать. Помогите, пожалуйста, с решением или посоветуйте, где найти метод решения подобных…

1. Найти отрезки, отсекаемые на осях координат прямой у=4х-2.
2. Даны две стороны ромба 5х-3у+14=0 и 5х-3у-20=0 и диагональ х-4у-4=0. Найти уравнения двух других сторон ромба.
3. Найти точку М1, симметричную точке М относительно плоскости.
М(2,1,0); y+z+2=0

(1 курс)

← Предыдущая запись
Следующая запись →

Комментарии

а я и не знаю, где ты и с кем

в 1 как я понимаю надо подставить сначал у=0 потом х=0.

1. «отсекаемые на осях» — значит, образуемые при пересечении указанной прямой и осей Ox, Oy.
Что такое ось Ox? это прямая, заданная уравнением y=0. Аналогично для оси Oy x=0.
Следовательно, пересечение с осью Ox происходит, когда в заданной прямой координата y равна нулю. Подставим: 0 = 4x-2, откуда x = 1/2. Отрезок, отсекаемый прямой на оси Ox, равен 1/2. Аналогично Oy.

а я и не знаю, где ты и с кем

> 2. Даны две стороны ромба 5х-3у+14=0 и 5х-3у-20=0 и диагональ х-4у-4=0. Найти уравнения двух других сторон ромба.

Найти точки пересечения х-4у-4=0 с первыми двумя прямыми (решить две системы)
Найти середину диагонали.
Найти прямую, перпендикулярную диагонали, проходящую через середины.
Найти точки пересечения этой прямой со сторонами
По двум точкам построить уравния прямых других сторон.

Вариант два:
Найти угол между диагональю и прямой и точку их пересечения
Найти прямые, составляющую с диагональю такой же угол.
Одна прямая будет уже известна, другая — будет искомая.

Я одна, но всё же я есть. Я не могу сделать всё, но всё же могу сделать что-то. И я не откажусь сделать то немногое, что могу (c)

Образец

Но вообще-то совсем недавно я похожую задачу в сообществе решала, можно поискать по теме Аналитическая геометрия

В данном случае направляющий вектор прямой , перпенд. плоскости, а(0,1,1) — коэффициенты при неизвестных в уравнении плоскости
Параметрические уравения этой прямой
х=2
у=1+t
z=t
Их надо подставить в уравнение плоскости, найти t, вернуться и найти х,у,z координаты точки пересечения этой прямой и плоскости
Это будет точка М как в образце и далее по нему

Источник