Как найти отрезок медианы в правильном треугольнике

Определение и свойства медианы равностороннего треугольника

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.

Определение медианы

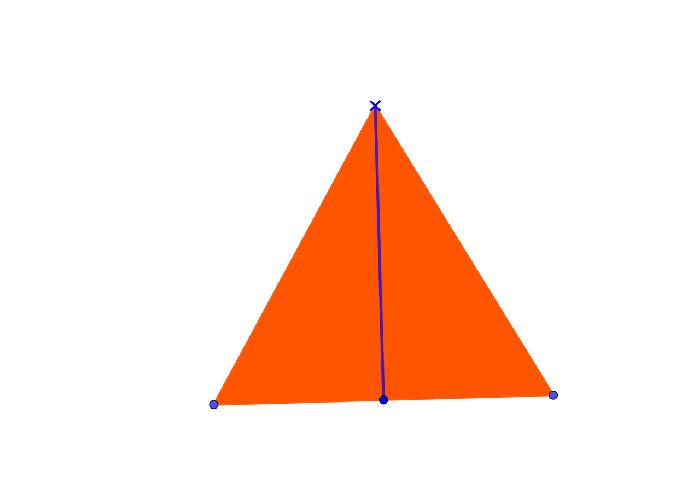
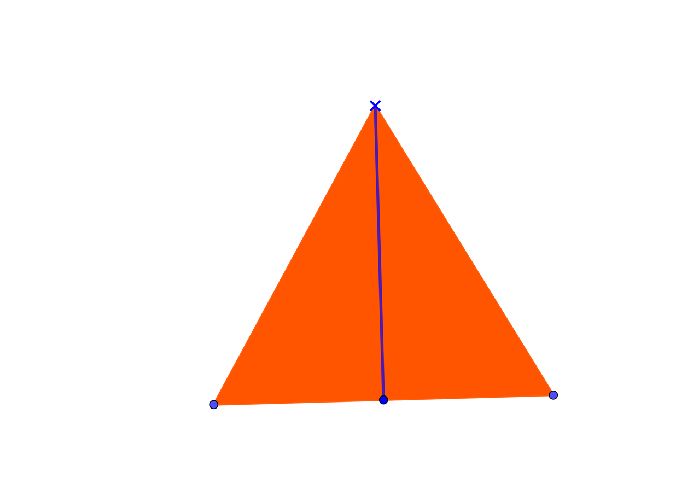
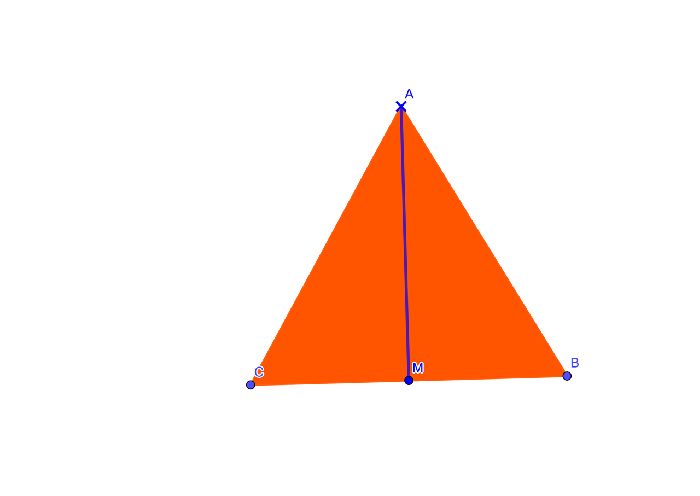
Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).

Свойства медианы равностороннего треугольника

Свойство 1

Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

    BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;

Свойство 2

Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3

Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Свойство 4

Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S1 = S2.

Свойство 5

Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S1 = S2 = S3 = S4 = S5 = S6.

Свойство 6

Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

  • r – радиус вписанной окружности;
  • R – радиус описанной окружности;
  • R = 2r (следует из Свойства 3).

Свойство 7

Длину медианы равностороннего треугольника можно вычислить по формуле:

a – сторона треугольника.

Примеры задач

Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Для нахождения требуемого значения применим формулу выше:

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

  • BG = 8 см (самая большая сторона, является гипотенузой △BFG);
  • FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 .
Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

Медиана равностороннего треугольника

Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?

(свойство медианы равностороннего треугольника)

В равностороннем треугольнике медиана, проведённая к любой стороне, является также его биссектрисой и высотой.

Пусть в треугольнике ABC AB=BC=AC.

Проведём медиану BF.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.

Аналогично, так как AB=AC, треугольник ABC — равнобедренный с основанием BC, AK — его медиана, биссектриса и высота;

так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.

Что и требовалось доказать .

(свойство медиан равностороннего треугольника)

Все три медианы равностороннего треугольника равны между собой.

Пусть в треугольнике ABC AB=BC=AC,

AK, BF, CD — его медианы.

Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон:

Что и требовалось доказать .

Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.

1) Выразим длину медианы равностороннего треугольника через его сторону.

Так как медиана равностороннего треугольника является также его высотой, треугольник ABF- прямоугольный.

Обозначим AB=a, BF=m, тогда AF=a/2.

Таким образом, формула медианы равностороннего треугольника по его стороне:

2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.

Центр правильного треугольника является центром его вписанной и описанной окружностей.

Так как центр вписанной окружности лежит в точке пересечения биссектрис треугольника, а медианы равностороннего треугольника являются также его биссектрисами, в равностороннем треугольнике ABC OF — радиус вписанной, BO — радиус описанной окружностей:

Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,

Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна

Найти медиану биссектрису высоту равностороннего треугольника

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L — высота=биссектриса=медиана

a — сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, ( L ):

Калькулятор — вычислить, найти медиану, биссектрису, высоту

источники:

Медиана равностороннего треугольника

http://www-formula.ru/bisectormedianheightequipotentialtriangles

Источник

Длина медианы правильного треугольника


Длина медианы правильного треугольника

3.9

Средняя оценка: 3.9

Всего получено оценок: 132.

3.9

Средняя оценка: 3.9

Всего получено оценок: 132.

Медиана – это один из характеризующих отрезков треугольника, наравне с биссектрисой и высотой. Особую сложность у учеников часто вызывают задачи на нахождение медианы. В обычном случае приходится применять формулу, но для правильного треугольника можно вывести упрощенную версию нахождения медианы.

Необходимые данные

Для вывода формул потребуется вспомнить несколько теоретических выкладок:

  • Медиана это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке.
  • В равнобедренном треугольнике, медиана, проведенная к основанию, является биссектрисой и высотой. А правильный треугольник это частный случай равнобедренного треугольника, у которого основанием может выступать любая из сторон. Значит каждая медиана равностороннего треугольника будет совпадать с соответствующей биссектрисой и высотой.
  • В правильном треугольнике все стороны равны, а каждый из углов равен 60 градусам.

Нахождение медианы по общей формуле

Для начала воспользуемся общей формулой. Вспомним формулу длины медианы через длины сторон треугольника:

Медиана в правильном треугольнике

Рис. 1. Медиана в правильном треугольнике.

$$m_c={{sqrt{2a^2+2b^2-c^2}}over{2}}$$

Но в правильном треугольнике все стороны равны между собой:

a=b=c

Подставим условия равенства в формулу и приведем подобные слагаемые:

$$m_c={{sqrt{2a^2+2а^2-а^2}}over{2}}$$

$$m_c={{sqrt{3a^2}}over{2}}$$

Значение $ {a^2} $ можно вынести за пределы корня. Тогда:

$$m_c={{sqrt{3a^2}}over{2}}$$

$$m_c={{sqrt{3}}over{2}*а}$$

Нахождением медианы через теорему Пифагора

Теперь попробуем вывести ту же формулу через теорему Пифагора.

В имеющемся правильном треугольнике АВС проведем медиану АМ. Она совпадет с биссектрисой и высотой. Тогда по теореме Пифагора из треугольника АВМ найдем сторону АМ, которая и будет являться медианой большого треугольника.

Рисунок к задаче

Рис. 2. Рисунок к задаче.

$$АМ=sqrt{AB^2-BM^2}$$

Но все стороны треугольника равны, а точка М является серединой стороны ВС. Значит:

$$АВ=а$$

$$ВМ={1over2}BC={1over2}a$$

Подставим эти значения в начальную формулу:

$$АМ={sqrt{AB^2-BM^2}}= {sqrt{а^2-{{а}over{2}}^2}}= sqrt{а^2-{{а^2}over{4}}}=sqrt{{3a^2}over{4}}$$

Вынесем значения $a^2$ и 4 за знак корня.

$$АМ=sqrt{{3a^2}over{4}}=a*{{3}over{sqrt{2}}}$$

Получилась та же формула длины медианы правильного треугольника. Значит, вывод первым способом был осуществлен верно и можно использовать любой из двух способов, если вы вдруг забыли формулу нахождения медианы правильного треугольника.

Точка пересечения медиан правильного треугольника

Рис. 3. Точка пересечения медиан правильного треугольника.

Последний метод очень часто используется не только для вывода формул правильного треугольника, но и для решения задач.

Заключение

Что мы узнали?

Мы несколькими методами вывели формулу длины медианы правильного треугольника. Указали на метод решения простых задач на нахождение характеристик правильного треугольника, а так же вспомнили основные свойства медианы.

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда — пройдите тест.

  • Милана Швецова

    3/5

  • Оксана Шмидт

    3/5

Оценка статьи

3.9

Средняя оценка: 3.9

Всего получено оценок: 132.

А какая ваша оценка?

Источник

Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?

Теорема 1

(свойство медианы равностороннего треугольника)

В равностороннем треугольнике медиана, проведённая к любой стороне, является также его  биссектрисой и высотой.

Доказательство:

mediana-ravnostoronnego-treugolnikaПусть в треугольнике ABC AB=BC=AC.

Проведём медиану BF.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.

mediana-ravnostoronnego-treugolnika-yavlyaetsyaАналогично, так как AB=AC, треугольник ABC — равнобедренный с основанием BC, AK — его медиана, биссектриса и высота;

так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.

Что и требовалось доказать.

Теорема 2

(свойство медиан равностороннего треугольника)

Все три медианы равностороннего треугольника равны между собой.

Доказательство:

mediany-ravnostoronnego-treugolnika-ravny Пусть в треугольнике ABC AB=BC=AC,

AK, BF, CD — его медианы.

Тогда AF=FC=BK=CK=AD=BD.

vse-mediany-ravnostoronnego-treugolnika-ravny

∠BAF=∠BFC=∠ABC (как углы равностороннего треугольника).

Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон:

AK=BF=CD.

Что и требовалось доказать.

Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.

1) Выразим длину медианы равностороннего треугольника через его сторону.

mediana-ravnostoronnego-treugolnika-cherez-storonuТак как медиана равностороннего треугольника является также его высотой, треугольник ABF- прямоугольный.

Обозначим AB=a,  BF=m, тогда AF=a/2.

По теореме Пифагора

    [m = sqrt {{a^2} - {{(frac{a}{2})}^2}} = sqrt {frac{{4{a^2} - {a^2}}}{4}} = sqrt {frac{{3{a^2}}}{4}} = frac{{asqrt 3 }}{2}.]

Таким образом, формула медианы равностороннего треугольника по его стороне:

    [m = frac{{asqrt 3 }}{2}.]

2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.

Центр правильного треугольника является центром его вписанной и описанной окружностей.

mediana-ravnostoronnego-treugolnika-cherez-radiusТак как центр вписанной окружности лежит в точке пересечения биссектрис треугольника, а медианы равностороннего треугольника являются также его биссектрисами, в равностороннем треугольнике ABC OF — радиус вписанной, BO — радиус описанной окружностей:

OF=r, BO=R.

Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,

    [OF = frac{1}{3}BF,BO = frac{2}{3}BF,]

    [ Rightarrow BF = 3 cdot OF;BF = frac{3}{2} cdot BO.]

Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна

    [m = 3r,]

через радиус описанной окружности —

    [m = frac{{3R}}{2}.]

Источник

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.

  • Определение медианы

  • Свойства медианы равностороннего треугольника

    • Свойство 1

    • Свойство 2

    • Свойство 3

    • Свойство 4

    • Свойство 5

    • Свойство 6

    • Свойство 7

  • Примеры задач

Определение медианы

Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Медиана в равностороннем треугольнике

  • BD – медиана, проведенная к стороне AC;
  • AD = DC.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).

Свойства медианы равностороннего треугольника

Свойство 1

Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

Медиана в равностороннем треугольнике

  • BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;
  • ∠ABD = ∠CBD.

Свойство 2

Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Равенство медиан в равностороннем треугольнике

Свойство 3

Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Деление медиан в точке пересечения в равностороннем треугольнике

  • G – центр тяжести (центроид) треугольника;
  • AG = 2GF;
  • BG = 2GD;
  • CG = 2GE.

Свойство 4

Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S1 = S2.

Деление равностороннего треугольника медианой на два равновеликих прямоугольных треугольника

Свойство 5

Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S1 = S2 = S3 = S4 = S5 = S6.

Деление равностороннего треугольника медианами на шесть равновеликих прямоугольных треугольников

Свойство 6

Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

Центры описанной и вписанной в равносторонний треугольник окружностей на пересечении медиан

  • r – радиус вписанной окружности;
  • R – радиус описанной окружности;
  • R = 2r (следует из Свойства 3).

Свойство 7

Длину медианы равностороннего треугольника можно вычислить по формуле:

Формула нахождения медианы равностороннего треугольника через длину его стороны

a – сторона треугольника.

Примеры задач

Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Для нахождения требуемого значения применим формулу выше:

Нахождение медианы равностороннего треугольника через длину его стороны (пример)

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение
Нарисуем чертеж согласно условиям задачи.

Медианы равностороннего треугольника (пример)

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

  • BG = 8 см (самая большая сторона, является гипотенузой △BFG);
  • FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF2 = BG2 – FG2 = 82 – 42 = 48 см2.
Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

Источник

Найти медиану биссектрису высоту равностороннего треугольника

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

Найти медиану биссектрису высоту равностороннего треугольника

L — высота=биссектриса=медиана

a — сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Формула длины высоты, биссектрисы и медианы равностороннего треугольника

Калькулятор — вычислить, найти медиану, биссектрису, высоту

Подробности

Автор: Administrator

Опубликовано: 07 октября 2011

Обновлено: 13 августа 2021

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти на резине год выпуска
  • Как составить звуковую схему слова машина
  • Как найти группу стим по аббревиатуре
  • Как найти работу в татарске
  • Как быстро найти наречие в тексте