Как найти отрезок отсекаемый высотой

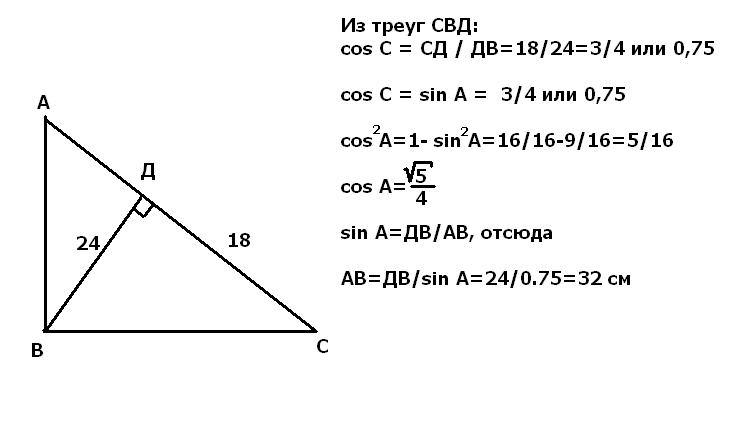
В Прямоугольном треугольнике ABC высота BD равна 24 см и отсекает от гипотенузы АС отрезок DC, равный 18 см. Найдите АВ и cos A.

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,061
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Высота bd прямоугольного треугольника abc равна 24 см и отсекает от гипотенузы AC отрезок DC равный 18 см Найти AB и cos A?

Геометрия | 5 — 9 классы

Высота bd прямоугольного треугольника abc равна 24 см и отсекает от гипотенузы AC отрезок DC равный 18 см Найти AB и cos A.

Смотри вложение, но только рисунок, решение верное вот :

гипотенуза ВС = корень из (18 * 18 + 24 * 24) = корень из 900 = 30 см

cos C = 18 / 30 = 3 / 5, тогда

sin A = 3 / 5, тогда

cos ^ 2 A = 1 — (3 / 5) ^ 2 = 1 — (9 / 25) = (16 / 25)

АВ = ВД / sin A = 24 * 5 / 3 = 120 / 3 = 40 cм.

В прямоугольном треугольнике ABC высота BD равна 24 см и отсекает от гипотенузы AC отрезок DC, равный 18 см?

В прямоугольном треугольнике ABC высота BD равна 24 см и отсекает от гипотенузы AC отрезок DC, равный 18 см.

Найдите AC И cos A.

Высота BD прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы АС отрезок DC, равный 18см?

Высота BD прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы АС отрезок DC, равный 18см.

Найти АВ и cos А.

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы AC отрезок DC?

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы AC отрезок DC.

НАйдите AB и cos A.

Только подробно и понятно!

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы АС отрезоr DC, равный 18 см?

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы АС отрезоr DC, равный 18 см.

Найти отрезок АB и Cos.

Высота BD прямоугольного треугольника ABC равна 24см и отсекает от гипотенузы AC отрезок DC, равный 18см?

Высота BD прямоугольного треугольника ABC равна 24см и отсекает от гипотенузы AC отрезок DC, равный 18см.

Найдите AB и cosA.

. Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы АС отрезок DC, равный 18 см?

. Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы АС отрезок DC, равный 18 см.

Найдите АВ и cos A.

Высота BD прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы АС отрезок DC, равный 18см?

Высота BD прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы АС отрезок DC, равный 18см.

Найдите АВ и cosA.

Высота ВД прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы отрезок ДС, равный 18см?

Высота ВД прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы отрезок ДС, равный 18см.

Найдите АВ и cosA.

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы AC отрезок DC?

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы AC отрезок DC.

НАйдите AB и cos A.

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы AC отрезок DC, равный 18 см?

Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы AC отрезок DC, равный 18 см.

Найдите AB и cos A.

На этой странице вы найдете ответ на вопрос Высота bd прямоугольного треугольника abc равна 24 см и отсекает от гипотенузы AC отрезок DC равный 18 см Найти AB и cos A?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть

Свойства высоты в прямоугольном треугольнике

Свойство 1

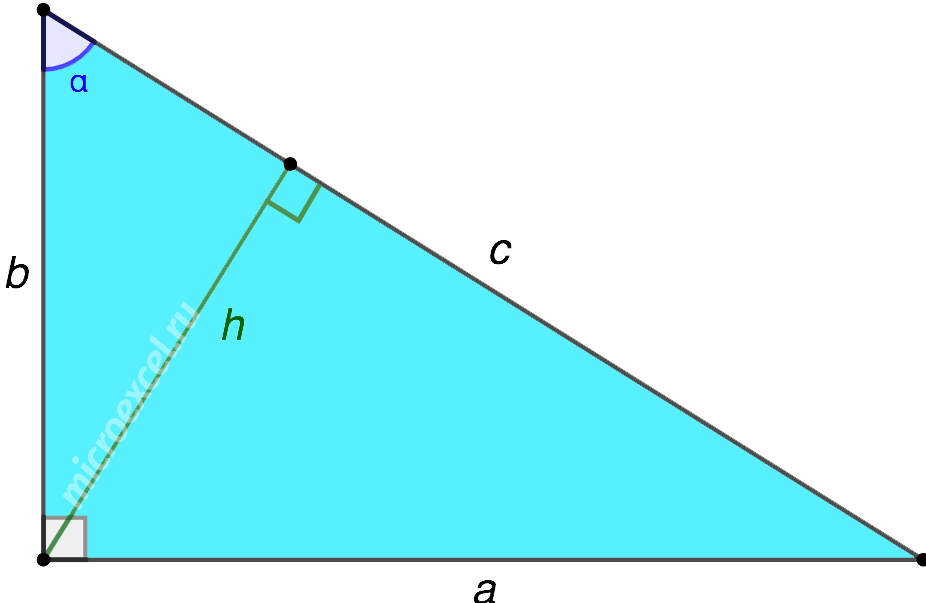
В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

Светило науки — 13 ответов — 310 раз оказано помощи

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые (<90°).

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

1. △ABD ∼ △ABC по двум равным углам: ∠ADB = ∠BAC (прямые), ∠ABD = ∠ABC.

2. △ADC ∼ △ABC по двум равным углам: ∠ADC = ∠BAC (прямые), ∠ACD = ∠ACB.

3. △ABD ∼ △ADC по двум равным углам: ∠ABD = ∠DAC, ∠BAD = ∠ACD.
Доказательство: ∠BAD = 90° – ∠ABD (ABC). В то же время ∠ACD (ACB) = 90° – ∠ABC.
Следовательно, ∠BAD = ∠ACD.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c² = a² + b² = 9² + 12² = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

1. Общее уравнение
   плоскости

Всякое уравнение
первой степени определяет в заданной
прямоугольной системе координат
плоскость.

Уравнение вида:

(27)

называется общим
уравнением плоскости. Вектор
,
перпендикулярный плоскости, называется
нормальным вектором плоскости.

1. Уравнение
   плоскости, проходящей через точку
   перпендикулярную вектору

Если плоскость
проходит через точку
перпендикулярно вектору,
то её уравнение имеет вид:

(28)

1. Уравнение
   плоскости, проходящей через три точки
   в отрезках

Пусть плоскость
проходит через точки
,,.

Имеет вид:

(29)

Если плоскость
отсекает по осям координат соответственно
отрезку
,,
и,
то её уравнение имеет вид:

(30)

1. Угол между
   плоскостями. Условия параллельности
   и перпендикулярности плоскостей

Угол
между плоскостямииопределяется по формуле:

(31)

Условие параллельности
плоскостей:

(32)

Условие
перпендикулярности плоскостей:

(33)

1. Расстояние
   от точки до плоскости

Расстояние от
точки
до плоскостинаходится по формуле:

(34)

Пример 1. Составить
уравнение плоскости, проходящей через
точку
перпендикулярно вектору.

Решение. Воспользуемся
уравнением (28). Здесь
;;;;;.

Получим:
или.

Пример 2. Найти
отрезки, отсекаемые плоскостью
на осях координат.

Решение. Преобразуем
данноё уравнение плоскости к уравнению
в отрезках (30) следующим образом:

;

Следовательно,
величины отрезков, отсекаемых на осях,
равны:

;
;

Пример 3. Найти
расстояние между параллельными
плоскостями
и

Решение. Возьмём
на одной из плоскостей произвольную
точку и определим её расстояние от
другой плоскости. Например, на первой
плоскости выберем точку
и найдём её расстояние до плоскости,
пользуясь формулой (33):

Пример 4. Определить
угол, образованный плоскостями
и.

Решение. Воспользуемся
формулой (31)

1. Вопросы для
   самопроверки

Как определяется
общее уравнение плоскости?

Какой вектор
называется нормальным к плоскости и
как определяются его координаты из
общего уравнения плоскости?

Как записывается
уравнение плоскости, проходящей через
точку перпендикулярно вектору?

Запишите уравнения
плоскости через три точки; в отрезках.

Как определяется
угол между плоскостями? Сформулируйте
условия параллельности и перпендикулярности
плоскостей.

Как определяется
расстояние от точки до плоскости?

1. Примеры для
   самостоятельного решения

   1. Составить
      уравнение плоскости, проходящей через
      точку
      м перпендикулярной вектору.

   2. Составить
      уравнение плоскости, проходящей через
      точку
      и отсекающей равны отрезки на осях
      координат.

   3. Составить
      уравнение плоскости, проходящей через
      точки
      .
      Через точкупровести плоскость, параллельно
      плоскости.

   4. Составить
      уравнение плоскости, проходящей через
      точку
      перпендикулярно плоскостями.

   5. Найти угол между
      плоскостями
      и.

   6. При каких
      значениях
      иуравненияиопределяют параллельные плоскости?

   7. При каком значении
      уравнениеиопределяют взаимно перпендикулярные
      плоскости?

   8. Найти высоту
      пирамиды
      ,
      опущенную из вершинына грань АВС, если,,,.
      Указание. Данную высоту можно найти
      как расстояние от точкидо плоскости АВС.

   9. Найти длину
      перпендикуляра, опущенного из точки
      на плоскость.

   10. Составить
       уравнение плоскостей, параллельных
       плоскости
       и отстоящих от неё на расстоянии

1. Ответы к
   примерам

4.7.1.
. 4.7.2..

4.7.3.
. 4.7.4..

4.7.5.
. 4.7.6..

4.7.7.
;. 4.7.8..

4.7.9.
.
4.7.10.,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Математика,


вопрос задал li5173835,


4 года назад

Ответы на вопрос

Ответил user4812789431

3

Ответ:

2.4

Пошаговое объяснение:

Фоксфорд

---

alexpardue2007:
Лучший

Новые вопросы

Математика,
4 месяца назад

пж помогите дам 10 б​…

Українська мова,
4 месяца назад

СРОЧНО ПОЖАЛУЙСТА ДАЮ 20 БАЛОВОберіть правильні твердження (2 відповіді):
а) у словосполученні слова можуть бути поєднані лише за…

Математика,
4 года назад

Прямые m и n параллельны (см. рисунок). Найдите ∠3, если ∠1 = 58°, ∠2 = 115°. Ответ дайте в градусах.​

Українська мова,
4 года назад

Відредагуйте подані речення. 8.Ми прийшли до переконання, що попереджати хворобу легше, ніж її лікувати. 9. Так, я, звичайно, погоджуюся з тим, що добро завжди мае перемагати вдача повинна бути лише…

Биология,
6 лет назад

Среди перечисленных клеток организма человека укажите те, которые имеют эктодермальное происхождение.
исчерченные миоциты
гепатоциты
эпителий ротовой полости
фибробласты
нейроны
эпителий…

Биология,
6 лет назад

какую добычу ловит лягушка широким липким языком?