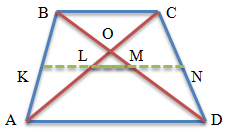
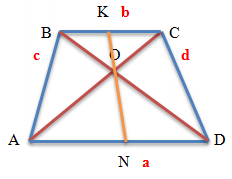
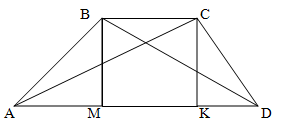
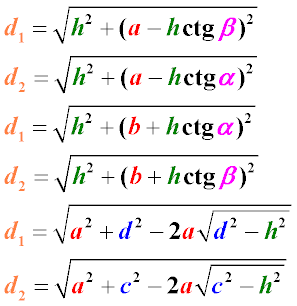Как найти отрезок соединяющий середины диагоналей трапеции

Свойства трапеции: отрезок, соединяющий середины диагоналей

Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

Пусть точка М – середина диагонали АС, N – середина диагонали ВD, Р и Q – середины боковых сторон АВ и СD.
Тогда РМ – средняя линия треугольника АВС, РМ параллельна ВС. Это значит, что точка М лежит на средней линии РQ трапеции, поскольку через точку Р можно провести на плоскости единственную прямую, параллельную прямой ВС. При этом PM=frac{BC}{2}.
Аналогично, точка N – середина диагонали BD – также лежит на РQ, то есть на средней линии трапеции, и QN=frac{BC}{2} . Поскольку  PQ=frac{AD+BC}{2}, MN=frac{AD+BC}{2}-PM-QN=frac{AD+BC}{2}-frac{BC}{2}-frac{BC}{2}=frac{AD-BC}{2}.

Задача ЕГЭ по теме: «Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований».

Основания трапеции равны 10 и 6. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ – среднюю линию трапеции, PQ = 8. Как мы доказали, отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.
PM – средняя линия треугольника ABC, значит, PM = 3.
NQ – средняя линия треугольника BCD, значит, NQ = 3.

Тогда MN = PQ − PM − NQ = 8 − 3 − 3 = 2
Ответ: 2.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Свойства трапеции: отрезок, соединяющий середины диагоналей» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Свойства отрезка, соединяющего середины диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции

1) лежит на средней линии трапеции,

2) равен полуразности оснований трапеции.

otrezok-soedinyayushchij-serediny-diagonalej-trapeciiДано: ABCD — трапеция, AD||BC,

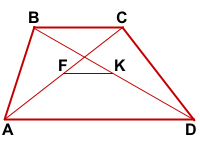
F — середина AC, K — середина BD,

MN — средняя линия трапеции

Доказать: FK∈MN,

    [ FK = frac{{AD - BC}}{2}. ]

Доказательство:

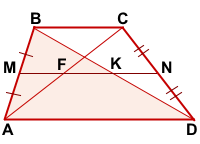
rasstoyanie-mezhdu-seredinami-diagonalej-trapeciiТак MN — средняя линия трапеции ABCD, то M — середина AB, N — середина CD, и MN||AD, MN||BC.

Рассмотрим угол ABD.

Так как AM=BM и MN||AD, то по теореме Фалеса, отрезки, на которые прямая MN делит BD, также равны, то есть MN пересекает отрезок BD в его середине, то есть в точке K.

Аналогично, для угла BAC:

AM=BM, MN||AD, следовательно, по теореме Фалеса прямая MN пересекает отрезок AC в его середине, то есть в точке F.

Таким образом, отрезок, соединяющий середины диагонали трапеции, параллелен основаниям трапеции и лежит на её средней линии.

MK — средняя линия треугольника ABD. Поэтому

    [ MK = frac{1}{2}AD. ]

MF — средняя линия треугольника ABC. Поэтому

    [ MF = frac{1}{2}BC. ]

    [ FK = MK - MF = frac{1}{2}AD - frac{1}{2}BC = frac{1}{2}(AD - BC). ]

Что и требовалось доказать.

Если использовать обозначения AD=a, BC=b, то формула длины отрезка, соединяющего середины диагоналей трапеции, примет вид

    [ FK = frac{{a - b}}{2}. ]

Источник
  • Печать

Отрезок, соединяющий середины диагоналей трапеции

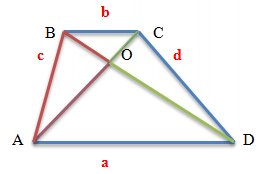
Одним из общих свойств трапеции является следующее: отрезок, соединяющий середины диагоналей равен половине разности оснований и лежит на средней линии.

Школьный курс геометрии включает в себя следующую задачу:

Докажите, что отрезок, соединяющий середины диагоналей трапеции, является параллельным ее основаниям и равен половине их разности.

Исходные данные:

  • Трапеция АВCD;
  • М принадлежит АС, АМ = МС;
  • N принадлежит BD, BM=ND;

Необходимо доказать следующее:

  1. MN параллельна AD;
  2. MN = (AD-BC)/2.

Доказательство:

  1. Исходя из теоремы Фалеса, средняя линия KF данной трапеции проходит через средины сторон AC и BD, из этого получаем, что MN принадлежит KF, а отрезок MN параллелен стороне AD. Что и следовало доказать.
  2. Для доказательства второй половины задачи воспользуемся свойством средней линии трапеции: средняя линия трапеции является параллельной основаниям и равняется их полусумме.

    треугольник АСD:
    MF = AD/2;

    треугольник BCD:
    NF=BC/2.

    Исходя из этого, получаем выражение MN = MF- NF. Подставляем в формулу значение отрезков MF и NF:

    MN = (AD/2)-(BC/2) = (AD-BC)/2

    3. Теорема доказана.

Источник

math-public:srednyaya_liniya_trapecii

Содержание

Определение

Отрезок, соединяющий середины боковых сторон трапеции, называется
средней линией трапеции.

Свойства средней линии трапеции

Средняя линия трапеции параллельна основаниям трапеции и равна их
полусумме.

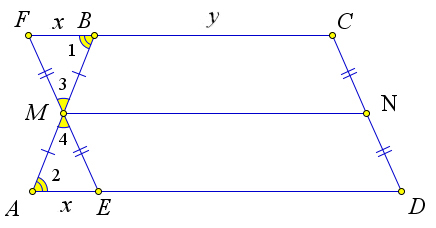
Доказательство

Рассмотрим трапецию $ABCD$, в которой проведена средняя линия $MN$.

Докажем, что $MNparallel AD$ и $MN=frac{AD+BC}{2}$.

Проведем через точку $M$ прямую $FE$ параллельно $CD$ ($Fin CB, Ein AD$).

Тогда $FCDE$ – параллелограмм ($FCparallel ED, FEparallel CD$).

Следовательно, $FE=CD$, $FC=ED$.

Кроме того $triangle FBM=triangle AME$, по второму признаку равенства ($angle
1=angle 2$, как накрест лежащие, $angle 3=angle 4$, как вертикальные,
$AM=MB$, так как $M$ – середина).

Следовательно, $FM=ME$.

Тогда $FMNC$ и $MNDE$ — параллелограммы ($FM=ME=ND=NC$ и $FEparallel
CD$).

Следовательно, $MNparallel BC$.

Кроме того, из равенства треугольников $triangle FBM=triangle AME$ следует,что $FB=AE$.

Пусть $FB=AE=x$ и $BC=y$.

Тогда $FC=ED=x+y$.

Следовательно, $MN=x+y$.

Кроме того, $BC+AD=BC+AE+ED=y+x+(x+y)=2x+2y$.

Таким образом, $MN=x+y=dfrac{BC+AD}{2}$.

Признаки средней линии трапеции

  1. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $M$ – середина боковой стороны, и $MN$ параллелен основаниям трапеции, то $MN$ – это средняя линия трапеции.

  2. Пусть отрезок $MN$ соединяет точки на боковых сторонах трапеции. Если $MN$ параллелен основанием трапеции и равен их полусумме, то $MN$ – средняя линия трапеции.

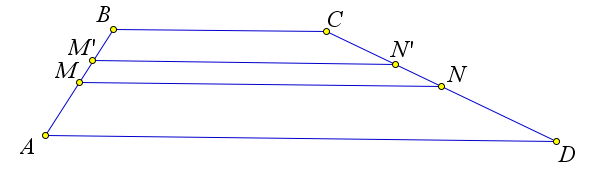
Доказательство

Первый пункт теоремы является прямым следствием теоремы Фалеса.

Докажем второй пункт теоремы.

Рассмотрим трапецию $ABCD$, в которой на боковых сторонах $AB$ и $CD$ выбраны точки $M$ и $N$ соответственно, и при этом $MN=dfrac{AD+BC}{2}$.

Докажем, что тогда $MN$ – средняя линия трапеции $ABCD$.

Предположим противное, то есть $MN$ – не средняя линия данной трапеции.

Если ровно одна из точек $M$ или $N$ является серединой, то по первому пункту теоремы $MN$ – это средняя линия, так как $MN$ параллельна основаниям трапеции.

Пусть точки $M$ и $N$ – не середины боковых сторон.

Тогда пусть $M’N’$ – средняя линия трапеции.

Следовательно, $M’N’=frac{BC+AD}{2}=MN$ и $MNparallel BCparallel MN$.

Но тогда $MNN’M’$ – параллелограмм, и, следовательно, $MM’parallel NN’$, что противоречит тому, что $ABCD$ – это трапеция.

Следовательно, $MN$ – средняя линия.

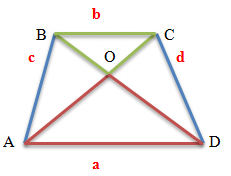
Теорема (об отрезке, соединяющем середины диагоналей трапеции)

Отрезок, соединяющий середины диагоналей трапеции, равен
полуразности ее оснований.

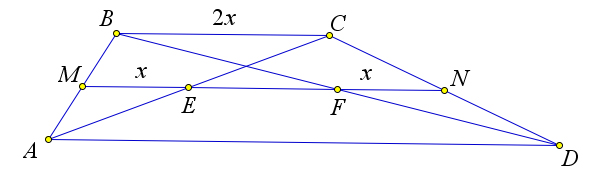
Доказательство

Рассмотрим трапецию $ABCD$, в которой точки $E$ и $F$ – это
середины диагоналей $AC$ и $BD$ соответственно.

Докажем, что $EF=frac{AD-BC}{2}$.

По теореме Фалеса средняя линия трапеции $MN$ делит диагонали $AC$ и $BD$ пополам, то есть точки $E$ и $F$ лежат на средней линии.

Тогда $ME$ и $FN$ – это средние линии треугольников $triangle ABC$ и $triangle DBC$.

Следовательно, если обозначить $BC=2x$, то $ME=FN=x$.

Тогда $EF=frac{2x+AD}{2}-x-x=frac{AD-2x}{2}=frac{AD-BC}{2}$.

math-public/srednyaya_liniya_trapecii.txt

· Последнее изменение: 2022/01/14 16:52 —

mesuslina

Источник

Диагонали трапеции

Свойства диагоналей трапеции

  1. Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
  2. Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
  3. Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
  4. Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
  5. Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
  6. Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

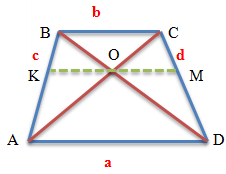
Свойства отрезка, соединяющего середины диагоналей трапеции

Трапеция со средней линией и отрезком соединяющим середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM. 

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.

Данный отрезок параллелен основаниям трапеции.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Подобие треугольников, образованных пересечением диагоналей трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны. 

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Свойства треугольников, образованных боковой стороной и диагоналями трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

Свойства трапеции, достроенной до треугольника

Свойства трапеции, достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований. 

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

  • Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
  • Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Свойства отрезка, соединяющего середины оснований трапеции и проходящего через точку пересечения диагоналей трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Свойство отрезка, параллельного основаниям трапеции и проходящего через точку пересечения диагоналей трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

  • Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
  • Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

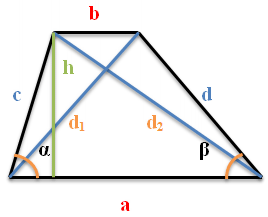
Формулы для нахождения диагоналей трапеции

Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»

Обозначения элементов произвольной трапеции для использования в формулах

Далее, в формулах используются следующие обозначения:

a, b — основания трапеции

c, d — боковые стороны трапеции

d1 d2 — диагонали трапеции

α β — углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Нахождение диагоналей трапеции через ее основания, стороны и углы при большем основании 

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции,  одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Формулы нахождения диагоналей трапеции через высоту трапеции, основания и углы при основании

Примечание. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.

Задача.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ: 16 см

Задача.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Неравнобокая трапеция

Решение.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину  KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

h2 + (24 — a)2 = (5√17)2

и

h2 + (24 — b)2 = 132

Учтем, что a = 16 — b , тогда в первом уравнении

h2 + (24 — 16 + b)2 = 425

h2  = 425 — (8 + b)2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 — (8 + b)2 + (24 — b)2  = 169

-(64 + 16b + b)2 + (24 — b)2 = -256

-64 — 16b — b2 + 576 — 48b + b2  = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h2  = 425 — (8 + b)2 = 425 — (8 + 12)2 = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

Площадь трапеции, где a b — основания трапеции, h — высота трапеции

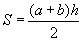
S = (24 + 8) * 5 / 2 = 80 см2

Ответ: площадь трапеции равна 80 см2.


0
 

 Трапеция (задачи про основания) |

Описание курса

| Прямоугольная трапеция 

Источник

Понравилась статья? Поделить с друзьями:
  • Как составить сборник игр
  • Как найти свой бланк осаго
  • Как найти напряженность магнитного поля в точке
  • 0x000025 как исправить
  • Как найти медиану в треугольнике зная периметр