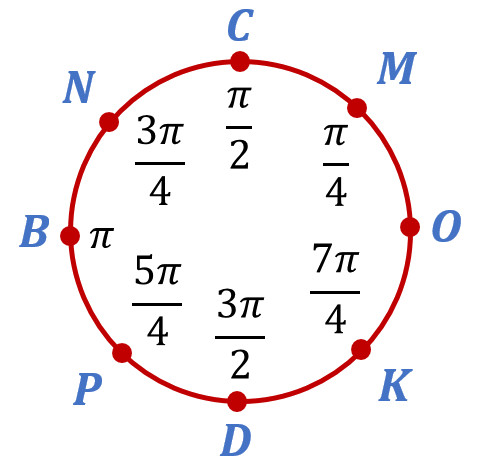
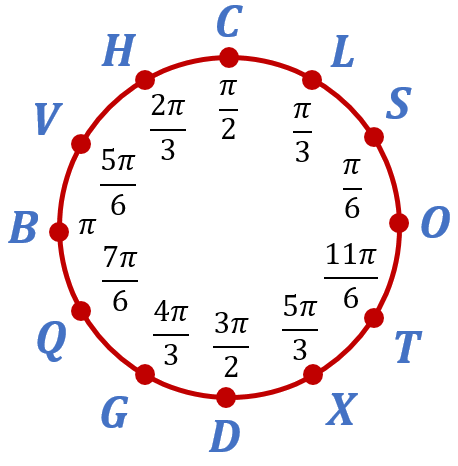
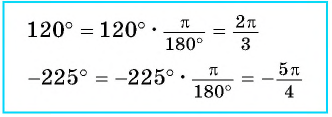
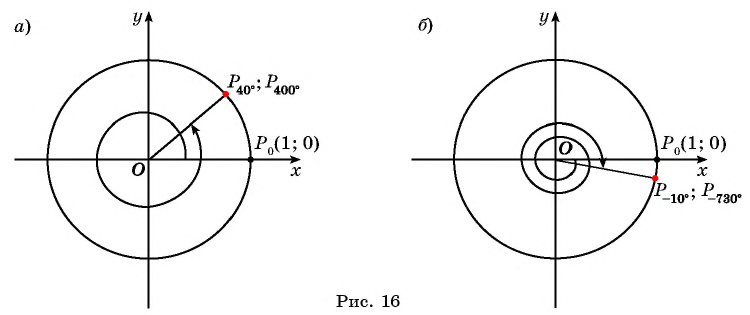
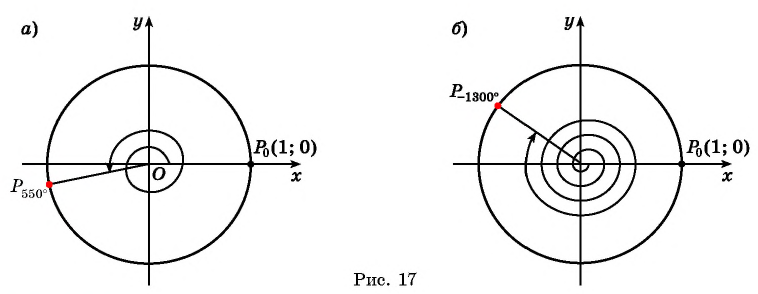
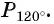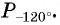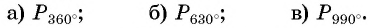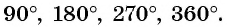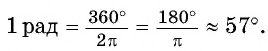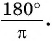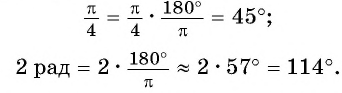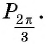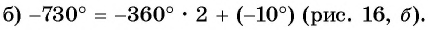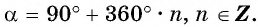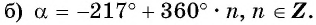Числовая окружность
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac<π><2>, frac<π><3>, frac<7π><4>, 10π, -frac<29π><6>)) разбирается в этой статье .
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:
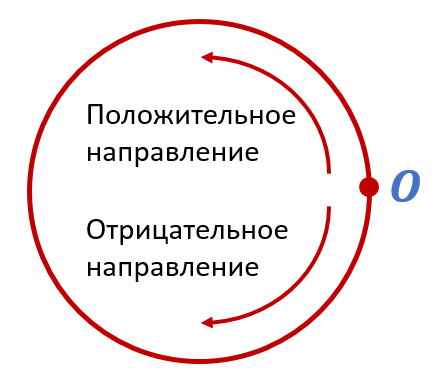
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.
Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
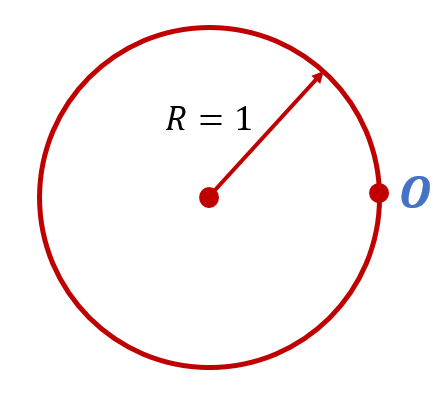
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).
Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
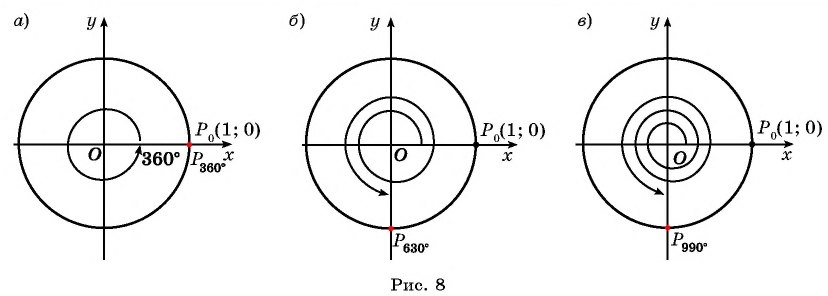
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
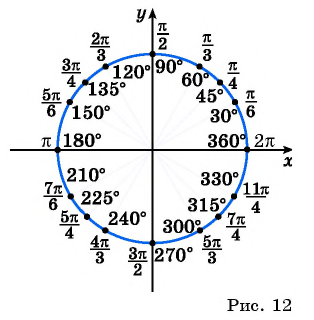
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac<π><2>),(-frac<π><2>),(frac<3π><2>), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .
Что надо запомнить про числовую окружность:
Урок «Числовая окружность»
Краткое описание документа:
Видеоуроки относятся к наиболее эффективным средствам обучения, особенно таких школьных дисциплин, как математика. Поэтому автор данного материала собрал в единое целое только полезную, важную и грамотную информацию.
Данный урок рассчитан на 11:52 минут. Практически столько же времени требуется учителю на уроке для объяснения нового материала по данной теме. Хотя главным достоинством видеоурока будет тот факт, что обучающиеся будут внимательно слушать то, о чем говорит автор, не отвлекаясь на посторонние темы и разговоры. Ведь если обучающиеся будут слушать не внимательно, то упустят важный момент урока. А если материал будет объяснять учитель сам, то его обучающиеся смогут легко отвлечь от главного своими разговорами на отвлеченные темы. И, конечно, становится понятно, какой способ будет боле рационален.
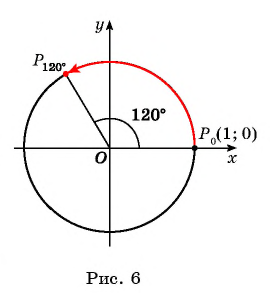
Начало урока автор посвящает повторению тех функций, с которыми обучающиеся знакомились ранее в курсе алгебры. И первыми предлагается начать изучать – тригонометрические функции. Чтобы их рассматривать и изучать требуется новая математическая модель. И этой моделью становится числовая окружность, которая, как раз, и заявлена в теме урока. Для этого вводится понятие единичной окружности, задается ее определение. Далее на рисунке автор показывает все компоненты такой окружности, и что пригодится обучающимся для дальнейшего обучения. Дугами обозначаются четверти.
Затем автор предлагает рассмотреть числовую окружность. Здесь же он делает замечание, что удобнее использовать единичную окружность. На этой окружности показано, как получается точка M, если t>0, t 0(тэ больше нуля), то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ (а эм) длины t. Точка М и будет искомой точкой М(t) (эм от тэ).
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 |
Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
 |
Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac<4>=frac<2pi r><4>=frac<pi r><2>.) Тогда радианная мера угла: $$ angle AOB=frac>=frac<pi r><2cdot r>=frac<pi> <2>$$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac<pi><6>) | (frac<pi><4>) | (frac<pi><3>) | (frac<pi><2>) | (frac<2pi><3>) | (frac<3pi><4>) | (frac<5pi><6>) | (pi) | (frac<3pi><2>) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
 |
Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<pi><4>, frac<pi><2>, frac<2pi><3>, pi), а также (-frac<pi><6>, -frac<pi><4>, -frac<pi><2>, -frac<2pi><3>, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |
 |
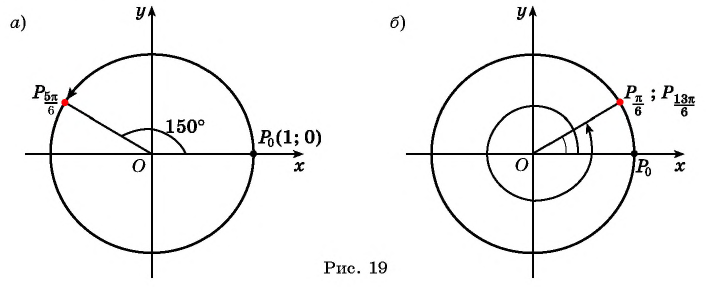
| Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<13pi><6>, frac<25pi><6>), и (-frac<11pi><6>). Все четыре точки совпадают, т.к. begin Mleft(frac<pi><6>right)=Mleft(frac<pi><6>+2pi kright)\ frac<pi><6>-2pi=-frac<11pi><6>\ frac<pi><6>+2pi=frac<13pi><6>\ frac<pi><6>+4pi=frac<25pi> <6>end |
 |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
$$ -frac<pi> <6>lt t lt frac<pi> <3>$$  а также, с учетом периода $$ -frac<pi><6>+2pi klt tltfrac<pi><3>+2pi k $$ |
 |
| Интервал | |
$$ -frac<pi> <6>leq t leq frac<pi> <3>$$  а также, с учетом периода $$ -frac<pi><6>+2pi kleq tleqfrac<pi><3>+2pi k $$ |
 |
| Полуинтервал | |
$$ -frac<pi> <6>leq t ltfrac<pi> <3>$$  а также, с учетом периода $$ -frac<pi><6>+2pi kleq tltfrac<pi><3>+2pi k $$ |
 |
п.6. Примеры
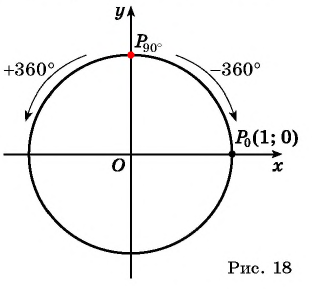
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^<circ>=frac<pi><6>.\ EC=60^<circ>=frac<pi><3>.\ AE=EC+CD=90^<circ>+30^<circ>=120^<circ>=frac<2pi><3>.\ ED=EC+CD=60^<circ>+90^<circ>=150^<circ>=frac<5pi><6>. end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<pi><2>; frac<3pi><4>; frac<7pi><6>; frac<7pi><4>).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac<pi><2>=-90^<circ>, frac<3pi><4>=135^<circ>\ frac<7pi><6>=210^<circ>, frac<7pi><4>=315^ <circ>end |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<11pi><2>; 5pi; frac<17pi><6>; frac<27pi><4>).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac<11pi><2>=frac<-12+1><2>cdotpi=-6pi+frac<pi><2>rightarrow frac<pi><2>=90^<circ>\ 5pi=4pi+pirightarrow pi=180^<circ>\ frac<17pi><6>=frac<18-1><6>pi=3pi-frac<pi><6>rightarrow pi-frac<pi><6>=frac<5pi><6>\ frac<27pi><4>=frac<28-1><4>pi=7pi-frac<pi><4>rightarrow pi-frac<pi><4>=frac<3pi> <4>end |
 |
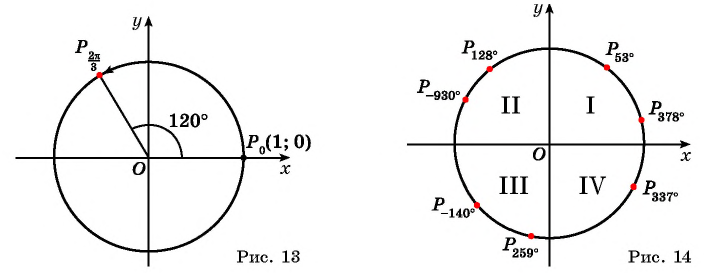
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 |
Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac<3,14><2>=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac<3pi><2>approx frac<3cdot 3,14><2>=4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac<3pi> <2>Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac<3pi><2>lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
http://urokimatematiki.ru/urok-chislovaya-okruzhnost-831.html
http://reshator.com/sprav/algebra/10-11-klass/edinichnaya-chislovaya-okruzhnost-na-koordinatnoj-ploskosti/
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac{π}{2}, frac{π}{3}, frac{7π}{4}, 10π, -frac{29π}{6})) разбирается в этой статье.
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам, расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π): ( frac{π}{2}),(-frac{π}{2}),(frac{3π}{2}),(2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье).

Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
(t_0+2πn), (n∈Z),
где (t_0) — любое значение это точки.
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео.
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь.
Что надо запомнить про числовую окружность:
Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
При изучении тригонометрии в школе каждый ученик сталкивается с весьма интересным понятием «числовая окружность». От умения школьного учителя объяснить, что это такое, и для чего она нужна, зависит, насколько хорошо ученик поймёт тригонометрию впоследствии. К сожалению, далеко не каждый учитель может доступно объяснить этот материал. В результате многие ученики путаются даже с тем, как отмечать точки на числовой окружности. Если вы дочитаете эту статью до конца, то научитесь делать это без проблем.
Итак, приступим. Нарисуем окружность, радиус которой равен 1. Самую «правую» точку этой окружности обозначим буквой O:
Поздравляю, вы только что нарисовали единичную окружность. Поскольку радиус этой окружности равен 1, то её длина равна .
Каждому действительному числу можно поставить в соответствие длину траектории вдоль числовой окружности от точки O. За положительное направление принимается направление движения против часовой стрелки. За отрицательное – по часовой стрелке:
Расположение точек на числовой окружности
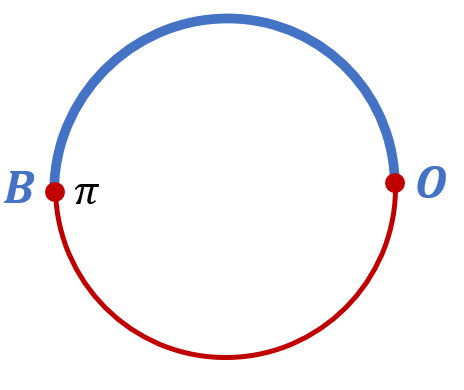
Как мы уже отмечали, длина числовой окружности (единичной окружности) равна . Где тогда будет располагаться на этой окружности число
? Очевидно, от точки O против часовой стрелки нужно пройти половину длины окружности, и мы окажемся в нужной точке. Обозначим её буквой B:
Обратите внимание, что в ту же точку можно было бы попасть, пройдя полуокружность в отрицательном направлении. Тогда бы мы отложили на единичной окружности число . То есть числам
и
соответствует одна и та же точка.
Причём этой же точке соответствуют также числа ,
,
,
и, вообще, бесконечное множество чисел, которые можно записать в виде
, где
, то есть принадлежит множеству целых чисел. Всё это потому, что из точки B можно совершить «кругосветное» путешествие в любую сторону (добавить или вычесть длину окружности
) и попасть в ту же самую точку. Получаем важный вывод, который нужно понять и запомнить.
Каждому числу соответствует единственная точка на числовой окружности. Но каждой точке на числовой окружности соответствует бесконечно много чисел.
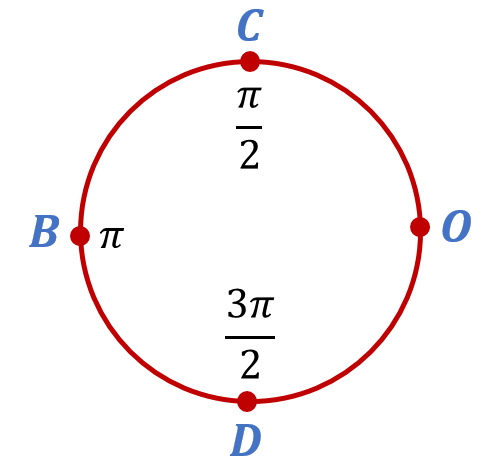
Разобьем теперь верхнюю полуокружность числовой окружности на дуги равной длины точкой C. Легко видеть, что длина дуги OC равна . Отложим теперь от точки C дугу той же длины в направлении против часовой стрелки. В результате попадём в точку B. Результат вполне ожидаемый, поскольку
. Отложим эту дугу в том же направлении ещё раз, но теперь уже от точки B. В результате попадём в точку D, которая будет уже соответствовать числу
:
Заметим опять, что эта точка соответствует не только числу , но и, например, числу
, потому что в эту точку можно попасть, отложив от точки O четверть окружности в направлении движения часовой стрелки (в отрицательном направлении).
И, вообще, отметим снова, что этой точке соответствует бесконечно много чисел, которые можно записать в виде . Но их также можно записать в виде
. Или, если хотите, в виде
. Все эти записи абсолютно равнозначны, и они могут быть получены одна из другой.
Разобьём теперь дугу на OC пополам точкой M. Сообразите теперь, чему равна длина дуги OM? Правильно, вдвое меньше дуги OC. То есть . Каким числам соответствует точка M на числовой окружности? Уверен, что теперь вы сообразите, что эти числа можно записать в виде
.
Но можно и иначе. Давайте в представленной формуле возьмём . Тогда получим, что
. То есть эти числа можно записать в виде
. Этот же результат можно было получить, используя числовую окружность. Как я уже говорил, оба записи равнозначны, и они могут быть получены одна из другой.
Теперь вы легко можете привести пример чисел, которым соответствуют точки N, P и K на числовой окружности. Например, числам ,
и
:
Часто именно минимальные положительные числа и берут для обозначения соответствующих точек на числовой окружности. Хотя это совсем не обязательно, и точке N, как вы уже знаете, соответствует бесконечное множество других чисел. В том числе, например, число .
Если разбить дугу OC на три равные дуги точками S и L, так что точка S будет лежать между точками O и L, то длина дуги OS будет равна , а длина дуги OL будет равна
. Используя знания, которые вы получили в предыдущей части урока, вы без труда сообразите, как получились остальные точки на числовой окружности:
Числа не кратные π на числовой окружности
Зададимся теперь вопросом, где на числовой прямой отметить точку, соответствующую числу 1? Чтобы это сделать, надо от самой «правой» точки единичной окружности O отложить дугу, длина которой была бы равна 1. Указать место искомой точки мы можем лишь приблизительно. Поступим следующим образом.
Мы знаем, где на числовой прямой находится точка L, соответствующая числу . Мы также знаем приблизительное значение числа
. Тогда, очевидно, число
чуть больше 1. Следовательно, точка, которая соответствует числу 1, расположена на числовой окружности чуть ближе к точке O, чем точка L:
Отмеченной точке, как мы уже знаем, соответствуют также числа .
Таким образом, на сегодняшнем уроке мы усвоили, что каждому числу соответствует какая-то точка на числовой окружности, но каждой точке числовой окружности соответствует бесконечное множество чисел. Запомните это, чтобы не путаться в дальнейшем при изучении тригонометрии.
Надеюсь, вы усвоили этот урок. Чтобы убедиться в этом, выполните самостоятельно следующие упражнения. Возникшие вопросы обсудим с вами в комментариях:
- Выделите на числовой окружности дугу, все точки которой удовлетворяют условию:
- Как расположены точки на числовой окружности, соответствующие числам:
a) и
;
б) и
;
в) и
;
г) и
?
Материал подготовил репетитор по физике и математике в Москве, Сергей Валерьевич
Единичная числовая окружность на координатной плоскости
- Понятие тригонометрии
- Числовая окружность
- Градусная и радианная мера угла
- Свойства точки на числовой окружности
- Интервалы и отрезки на числовой окружности
- Примеры
п.1. Понятие тригонометрии
Тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование.
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 |
Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета, ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным; по часовой стрелке – отрицательным. |
Например:
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
Радианной мерой угла называется отношение длины дуги окружности, заключенной между сторонами угла и центром в вершине угла, к радиусу этой окружности.
От радиуса окружности это отношение не зависит.
Например:
 |
Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_{AB}=frac{L}{4}=frac{2pi r}{4}=frac{pi r}{2}.) Тогда радианная мера угла: $$ angle AOB=frac{l_{AB}}{r}=frac{pi r}{2cdot r}=frac{pi}{2} $$ |
$$ 1^{circ}=frac{pi}{180}text{рад}, 1 text{рад}=frac{180^{circ}}{pi}approx 57,3^{circ} $$
Таблица соответствия градусных и радианных мер некоторых углов
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac{pi}{6}) | (frac{pi}{4}) | (frac{pi}{3}) | (frac{pi}{2}) | (frac{2pi}{3}) | (frac{3pi}{4}) | (frac{5pi}{6}) | (pi) | (frac{3pi}{2}) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
 |
Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t<0 двигаемся по окружности по часовой стрелке, описывая дугу ⌒ AM=t. Точка M — искомая. |
Например:
| Отметим на числовой окружности точки, соответствующие (frac{pi}{6}, frac{pi}{4}, frac{pi}{2}, frac{2pi}{3}, pi), а также (-frac{pi}{6}, -frac{pi}{4}, -frac{pi}{2}, -frac{2pi}{3}, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |
 |
Каждой точке M(t) на числовой окружности соответствует бесконечное множество действительных чисел t с точностью до полного периода 2π:
$$ M(t) = M(t+2pi k), kinmathbb{Z} $$
Например:
| Отметим на числовой окружности точки, соответствующие (frac{pi}{6}, frac{13pi}{6}, frac{25pi}{6}), и (-frac{11pi}{6}). Все четыре точки совпадают, т.к. begin{gather*} Mleft(frac{pi}{6}right)=Mleft(frac{pi}{6}+2pi kright)\ frac{pi}{6}-2pi=-frac{11pi}{6}\ frac{pi}{6}+2pi=frac{13pi}{6}\ frac{pi}{6}+4pi=frac{25pi}{6} end{gather*} |
 |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
Например:
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin{gather*} BE=30^{circ}=frac{pi}{6}.\ EC=60^{circ}=frac{pi}{3}.\ AE=EC+CD=90^{circ}+30^{circ}=120^{circ}=frac{2pi}{3}.\ ED=EC+CD=60^{circ}+90^{circ}=150^{circ}=frac{5pi}{6}. end{gather*}
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac{pi}{2}; frac{3pi}{4}; frac{7pi}{6}; frac{7pi}{4}).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin{gather*} -frac{pi}{2}=-90^{circ}, frac{3pi}{4}=135^{circ}\ frac{7pi}{6}=210^{circ}, frac{7pi}{4}=315^{circ} end{gather*} |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac{11pi}{2}; 5pi; frac{17pi}{6}; frac{27pi}{4}).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin{gather*} -frac{11pi}{2}=frac{-12+1}{2}cdotpi=-6pi+frac{pi}{2}rightarrow frac{pi}{2}=90^{circ}\ 5pi=4pi+pirightarrow pi=180^{circ}\ frac{17pi}{6}=frac{18-1}{6}pi=3pi-frac{pi}{6}rightarrow pi-frac{pi}{6}=frac{5pi}{6}\ frac{27pi}{4}=frac{28-1}{4}pi=7pi-frac{pi}{4}rightarrow pi-frac{pi}{4}=frac{3pi}{4} end{gather*} |
 |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 |
Сравниваем каждое число с границами четвертей: begin{gather*} 0, fracpi2approxfrac{3,14}{2}=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac{3pi}{2}approx frac{3cdot 3,14}{2}=4,71, 2piapprox 6,28 end{gather*} |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac{3pi}{2} Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac{3pi}{2}lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb{Z})), запишите количество полученных базовых точек.
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Содержание:
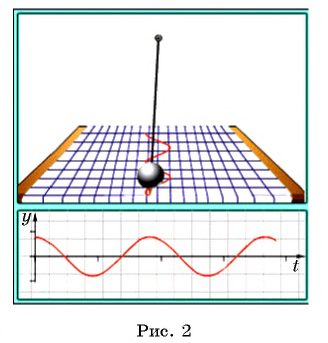
На рисунке 2 изображены колебания маятника и показан график функции, описывающей смещение маятника от положения равновесия в зависимости от времени. Изучение процесса колебания маятника, а также многих других процессов в физике (механические, электромагнитные колебания, волны и т. д.) приводит к необходимости рассматривать тригонометрические функции действительного аргумента.
Для изучения тригонометрических функций используется понятие единичной окружности.
Единичная окружность в тригонометрии
Единичную окружность называют также координатной окружностью.
Определение единичной окружности
Определение:
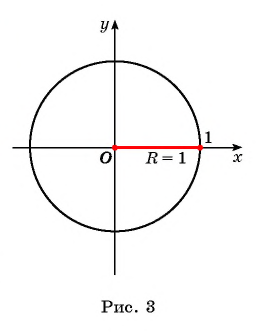
Окружность на координатной плоскости единичного радиуса с центром в начале координат (рис. 3) называется единичной окружностью.
Для того чтобы задать координатную окружность, нужно указать:
Точки на окружности будем получать путем поворота точки 
Точка 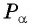
Таким образом, при повороте точки 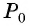
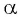
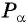
Пример №1
Построить на единичной окружности точку
Решение:
Точку 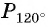
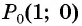
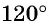
Пример №2
Построить на единичной окружности точку
Решение:
Точку 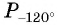
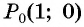
Пример №3
Построить на единичной окружности точку:
Решение:
а) Так как поворот на 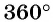
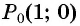
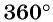
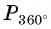
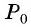
б) Так как 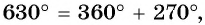
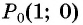
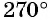
в) Так как 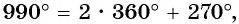
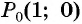
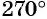
Пример №4
Построить на единичной окружности точку
Решение:
Так как 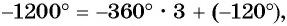
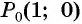
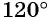
Радианное измерение углов
По формуле длины окружности 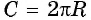
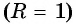
На единичной окружности (рис. 10) легко отметить точки 
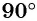
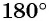
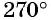
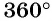
Числа 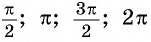
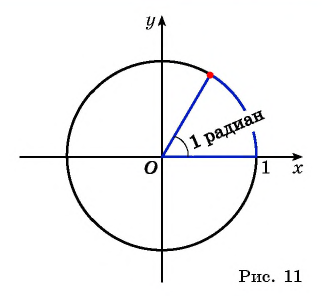
Угол в 1 радиан (от лат. radius — луч, радиус) — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
На рисунке 11 отмечена точка единичной окружности, соответствующая углу в 1 радиан. Длина дуги единичной окружности, соответствующей углу в 1 радиан, равна 1.
Так как 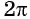
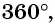
Сокращенное обозначение радиана «рад» чаще всего опускают.
Чтобы выразить радианную меру угла 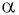
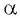
Например,
На рисунке 12 показано соответствие между градусной и радианной мерой некоторых углов.
- Заказать решение задач по высшей математике
Пример №5
Построить на единичной окружности точку
Решение:
Точку 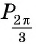
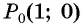
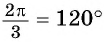
В зависимости от того, в какую четверть координатной плоскости попадает точка 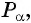
Например, углы 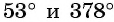
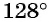
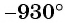
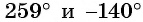
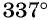
Углы 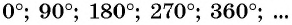
Пример №6
Определите, в какой четверти находится угол 3 рад.
Решение:
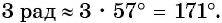
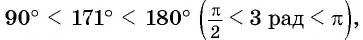
Примеры заданий и их решения
Пример №7
На единичной окружности отметьте точку, получаемую поворотом точки 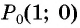
Решение.
а) Точку 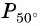
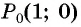
б) Точку 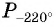
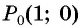
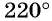
в) Точку 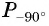
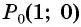
г) Точку 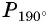
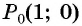
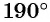
Пример №8
Покажите, что точки:

Решение:
а) Поскольку 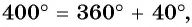
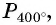
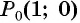
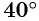
Пример №9
На единичной окружности отметьте точку, получаемую поворотом точки 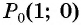
Решение:
а) Так как 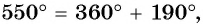
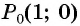
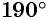
б) Так как 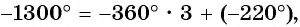
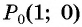
Пример №10
Запишите все углы 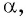
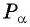
Решение:
а) Отметим на единичной окружности точку 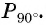
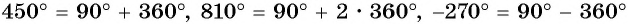
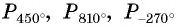
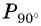
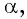
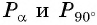
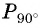
Пример №11
На единичной окружности отметьте точку, получаемую поворотом точки 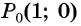
Решение:
а) Так как 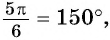
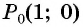
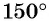
б) Поскольку 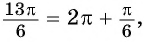
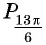
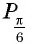
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая