Introduction: Calculating the Repelling Magnetic Force of Permanent Magnets
In this instructable you’re going to learn how to calculate the repelling magnetic force of two permanent magnets. Note that the magnetic force depends on the distance between the two, so in the end we will not get a single number but an equation.
This is very easily done using the law of balaced forces. You need the following supplies:
Supplies
- Magnets: you can use pretty much every two magnets that have the same shape
- some kind of (transparent) tube or rail where you can slide in your magnets. For example if you’re testing cylindrical shaped magnets like me, you can use a straw. You can also roll up or fold some transparencys to fit your magnets
- a measuring tool like a ruler or caliper
- kitchen scale
Step 1: Weighing the Magnets
First you need to weight your magnets. If you’re using a kitchen scale, don’t place them directly on the scale. Place them on a box to prevent affecting the scale’s sensor.
If you’ve got two (or more) identical magnets, weight them together and divide your result by the number of magnets. The more the better because kitchen scales are not very accurate.
Note the weight for the calculation.
Step 2: Setup and Measuring
Place your tube on a table vertically (just hold it upright) and slide in your magnets from the top so that they’re repelling each other. Depending on the weight and strength of the magnets there is a smaller or bigger gap between them. Measure and note the distance h as accurately as possible.
Step 3: Calculating
The upper (floating) magnet is experiencing the repelling force as well as gravitational force. As the lower magnet also experiences gravitational force, the gap between them is caused by the repelling force. That means that the repelling force of the magnets at the particular distance h equals the gravitational force of the upper (!) magnet:
Fm = Fg
=> Fm(h) = m * g
The potential energy of the upper magnet is calculated as follows: W = m * g * h
Since Energy is generally W = F * s, you can equalize the two equations and finally get:
W = F * s = m * g * h
=> F(s) = (m * g * h)/s
Just put in the measured mass (in kg), height (in m) and the location factor g = 9,81 kg/(m*s^2) and you get the repelling force in the pearticular distance s.
В современных учебниках по физике (см. например, [5], с. 303-307) формулу для силы тяготения F определяют так

где G=(6,6732±0,0031)•10-11Hм2кг-2 есть так называемая гравитационная постоянная, m1 и m2 – массы тяготеющих тел, а r – расстояние между этими телами. Силу F называют силой всемирного тяготения. При этом авторство формулы (1) приписывается Ньютону. Также считается, что численное определение гравитационной постоянной G выполнено английским физиком Кавендишем (1731 – 1810) в 1798 году.
Однако подробный анализ знаменитого сочинения Ньютона [4] свидетельствует о том, что формула (1) в этом сочинении отсутствует. Из приведённых рассуждений в [4] по поводу тяготения можно привести только следующую словесную формулировку закона тяготения.
Тяготение существует на всех планетах (с. 514 в [4]).
Тяготение, направляющееся к любой из планет, обратно пропорционально квадратам расстояний мест до центра её (с. 514 в [4]).
Тяготение существует ко всем телам и пропорционально массе каждого из них (с. 518 в [4]).
Следует обратить внимание на то, что в указанных формулировках Ньютон выражает физические закономерности не в виде равенств, а в форме пропорциональностей. Эта форма пропорциональности присутствует во всех закономерностях, полученных Ньютоном в [4].
Отсутствие в рассуждениях Ньютона аналитической формулы для закона тяготения позволило последующим исследователям при решении задач небесной механики создавать различные количественные соотношения для закона тяготения, в которых величины коэффициента пропорциональности различны.
Рассмотрим следующие две теоремы Ньютона, которые использовались в [1] при выводе аналитической формы закона тяготения.
Теорема 1. Два взаимно притягивающихся тела описывают и около своего общего центра тяжести и друг около друга подобные траектории (с. 217 в [4]).
Действительно, расстояние тел от их общего центра тяжести обратно пропорционально их массам, следовательно, отношение этих расстояний постоянно, тогда постоянно и отношение каждого из них к полному расстоянию между телами. Кроме того, эти расстояния обращаются около своего общего конца с одинаковым угловым движением, вследствие чего, не наклоняясь друг к другу, располагаются по одной прямой. Прямые же линии, отношение длин которых постоянно и которые поворачиваются около своих концов на равные углы, описывают вокруг этих концов на плоскостях, находящихся вместе в покое или движущихся без вращения, подобные фигуры. Следовательно фигуры, описываемые сказанными расстояниями, подобны между собой.
Рис. 1. Система двух взаимодействующих тел
Это доказательство рассматриваемой теоремы можно пояснить, используя рисунок 1. На нем показана система двух взаимодействующих тел S и P. При угловом движении двух тел S и P вокруг центра тяжести С углы φ1 и φ2 равна, а дуги ST и PQ подобны. Следовательно, траектории этих тел при движении вокруг центра тяжести подобны и центростремительная сила обоих тел будет направлена к точке С.
Если в этой системе движение тела Р рассматривать относительно тела S, то траектория такого движения будет подобна траектории тела Р относительно точки С. Аналогичное можно сказать и о траектории тела S относительно тела Р.
Таким образом, все возможные траектории в этой системе (рис.1) подобны и они могут быть представлены любой из плоских кривых второго порядка, а центростремительная сила как сила притяжения будет направлена по линии SP.
Далее Ньютон доказывает следующую теорем.
Теорема 2. Если два тела притягиваются взаимно с какой бы то ни было силою и поэтому обращаются около своего общего центра тяжести, тоя утверждаю, что под действием такой же силы каждое тело может описывать вокруг другого неподвижную фигуру, равную и подобную тем, которые они описывают друг около друга (с. 217-219 в [4]).
Доказательство Ньютон строит следующим образом.
Рис. 2. Движение двух тел вокруг их центра тяжести
Рис. 3. Относительное движение одного тела вокруг другого
Пусть два тела S и Р (рис. 2) обращаются около своего общего центра тяжести С на угол , перемещаясь от S к Т и от Р к Q.
Теперь в данном движении тел выделим движение тела Р относительно S. В таком случае тело S как бы остановлено и его положение фиксируется неподвижной точкой S1 (рис. 3). Из точки S1 проведем прямую S1Р1 = SР и прямую S1Q1 параллельную прямой ТQ. Так как S1Р1 = S1Q1, то дуга Р1Q1 (рис. 3) суть траектория движения тела Р в его перемещении относительно тела S.
Дуги Р1Q1, РQ, SТ подобны, так как они опираются на один тот же угол φ. Если учесть, что точка S1 подвижна и перемещается по дуге SТ (рис. 2), то дуга Р1Q1 не только подобна дуге РQ, но и равна ей.
Аналогичные рассуждения можно провести, рассмотрев движение тела S относительно тела Р.
Из предыдущих теорем следует, что если относительное движение тела Р происходит по эллиптической кривой, в фокусе которой находится тело S, то тело Р притягивается к телу S под действием центростремительной силы, направленной от Р к S и обратно пропорциональной квадрату расстояния между Р и S. Обозначим эту центростремительную силу через F1, а расстояние между рассматриваемыми телами через r.
Рассматривая относительное движение тела S по эллиптической орбите, в фокусе которой находиться тело Р, мы будем иметь силу F2, направленную от S к Р и также обратно пропорционально квадрату расстояния между телами S и Р.
Эти две силы F1 и F2, приложенные к телам Р и S, определяют силу взаимодействия между ними, которую Ньютон назвал силой притяжения.
Согласно третьему закону Ньютона, модули противоположно направленных сил F1 и F2 равны. Это может иметь место только в том случае, если

где m1 и m2 – массы тел S и Р, а F есть сила притяжения между двумя телами, движущимися по эллиптическим траекториям.
Направление силы F определяется выбором относительного движения одного из тел. Например, по второму закону Кеплера все планеты движутся по эллиптическим орбитам, в одном из фокусов которого находится Солнце. Следовательно, в данном случае рассматривается движение планет относительно неподвижного Солнца и центростремительная сила, приложенная к планете, направлена к Солнцу.
В формуле (2) множитель C суть коэффициент пропорциональности, который может содержать как размерную, так и безразмерную составляющую. Обычно размерные коэффициенты пропорциональности зависят от единиц измерения и позволяют правые и левые части физических формул свести к одинаковой размерности. Безразмерные же коэффициенты пропорциональности как отвлечённые числа определяют во сколько раз левая часть формулы больше или меньше правой и могут быть как положительными, так и отрицательными величинами.
Исходя из сказанного, в самом общем случае множитель C в (2) определим так

где G – гравитационная постоянная, которая представляет размерный коэффициент пропорциональности, а λ – безразмерный коэффициент пропорциональности. Знак минус в (3) отражает то, что силы F1 и F2 направлены в противоположные стороны.
Теперь после подстановки (3) в (2) получаем следующую формулу для закона тяготения

Формула (4) описывает две силы: одна из них – сила притяжения, а другая – отталкивания. Очевидно, что эти силы имеют разные знаки. Один из вариантов приписывания названным силам определённых знаков может быть таким.
Рассмотрим взаимодействие двух тел в условиях выполнения третьего закона Ньютона – действие равно противодействию. Пусть действие первого тела на второе осуществляется силой F1, приложенной к первому телу. Второе тело действует на первое силой F2, приложенной ко второму телу. Если теперь эти равные и противоположно направленные силы перенести в центр первого тела, то сила F1 будет притягивать первое тело ко второму, а сила F2 будет отталкивать первое тело от второго. В этом случае силу F1 назовём силой притяжения, припишем ей знак плюс и в рамках формулы (4) определим эту силу так

Силу F2 в данном рассмотрении назовём силой отталкивания, припишем ей знак минус и определим её так

Из формул (5) и (6) следует, что F1+F2=0, что означает выполнимость для этих сил третьего закона Ньютона.
Некоторые авторы силе притяжения приписывают знак минус, но это делается для того, чтобы потенциал этой силы был величиной положительной.
Для согласования знаков в формулах (5) и (6) с кинематическими характеристиками движения рассмотрим движение тела по эллиптической траектории, в левом фокусе которой находится Солнце. В этом случае большая ось эллипса пересекает траекторию в двух точках. Одна из них афелий является наиболее удалённой от фокуса. Расстояние афелия до левого фокуса вдоль большой оси эллипса обозначим через r1. Вторая точка перигелий есть ближайшая к левому фокусу. Расстояние до фокуса этой второй точки обозначим через r2. Скорости тела в указанных точках обозначим через v1 и v2. Можно показать, что скорости v1 и v2 обратно пропорциональны расстояниям r1 и r2, то есть справедливо соотношение v1∙ r1 v2 ∙ r2 = const, что в свою очередь означает: v1 = vmin есть минимальная скорость, а v2=v max – максимальная скорость, при этом r1 > r2.
Пусть тело начинает движение со скоростью v1 от точки афелия, удалённой от фокуса на расстоянии r1 до точки перигелия. Радиус вектор которой суть r2. Уже отмечалось, что скорость тела в перигелии равна v2. Так как v1 < v2, то тело на указанном участке траектории движется ускоренно. Работу силы тяготения F1 определим так

Так как r1 > r2, то на этом участке траектории работа A1 представляется отрицательной величиной.
Заметим, что на этом участке траектории тело приближается к левому фокусу, в котором расположено Солнце, следовательно сила F1, определяемая по формуле (5) суть сила притяжения.
Далее ввиду замкнутости траектории тело начинает удаляться от точки перигелия до точки афелия в результате чего скорость уменьшается от v2 до v1, то есть тело движется замедленно. Очевидно, то на этом участке траектории работа A2 силы F2 оказывается равной

Из формул (7) и (8) следует, что A1 A2, но величины этих работ – отрицательны.
Таким образом, сила притяжения F1, определяемая по формуле (5), вызывает ускорительное движение на участке эллиптической траектории от точки афелия до точки перигелия. При возвратном движении от перигелия до афелия тело движется замедленно под действием силы отталкивания F2, определяемой по (6).
Для изучения структуры формулы (4) выделим в ней в качестве множителя величину

размерность которой соответствует размерности ускорения. Если в ней в качестве m2 принять массу Земли, равную 5,9726 ∙ 1024 кг, r 6,378 ∙ 106 м считать радиусом Земли, а величину G полагать равной 6,6732 ∙ 10-11 Нм2кг-2 , то расчётом по (9) получаем 
Теперь силу притяжения (5) с учётом (9) переписываем так

которая при λ=1 переходит в силу тяжести тела массой m2. В формуле (4) введём дополнительное обозначение: α=±λ, после чего с учётом (9) ей придадим следующую форму

Формула (10) представляет уточнённую форму второго закона Ньютона, в которой введён коэффициент пропорциональности . Такое уточнение впервые выполнено в [2] и там же показано, что α > 0 для ускоренных движений, а для замедленных движений α < 0.
С помощью формулы (10) в [3] произведён аналитический анализ расчётов известного опыта Толмина и Стюарта, который доказывает электронную природу тока в металлах.
Старая цена —
{{(cart.totalPrice + cart.totalDiscountPrice) | rub}} руб.
Общая скидка — {{cart.totalDiscountPrice | rub}} руб.
Итого, без стоимости доставки:
{{cart.totalPrice | rub}} руб.
Общий вес: {{cart.totalWeight}} кг
До бесплатной доставки Boxberry или 5post (Пятерочка) осталось
{{(2000 — cart.totalPrice).toFixed(2)}}
{{2000 — cart.totalPrice.toFixed()|num2word:’рубль’:’рубля’:’рублей’}}
Поздравляем, вам доступна бесплатная доставка Boxberry или 5post (Пятерочка)
Только для предоплаченных заказов!
Немного истории
Происхождение слова «магнит» покрыто тайной. Ученые склоняются к версии названия, произошедшего от имени греческого пастуха Магнеса, пастух нашел минерал и был удивлен его свойствам. Другая неподтвержденная гипотеза: минерал назван так в честь региона Магнесия, находившегося в Малой Азии. В этом районе были открыты залежи магнетита.
Почему магниты имеют свойство притягиваться и отталкиваться
Магнетизм, как научное явление, вызывается перемещением электронов. Вещества и предметы состоят из мельчайших атомов, эта физическая единица представляет собой ядро и движущиеся вокруг него электроны. Поскольку электроны имеют отрицательные заряды, то создают магнитные поля. Вращение электрона по часовой стрелке направляет магнитное поле наверх, а вращение против часовой стрелки – вниз.
Если количество разнонаправленных полей совпадает, то магнитные поля отсутствуют. Если баланс нарушается, и электроны начинают вращение в одном направлении, возникает магнитное поле большой силы. Именно этот процесс и происходит в минерале под названием магнетит.
У магнита два полюса: северный и южный. Если два магнита расположить вблизи, они начинают направлять магнитные поля строго в одном направлении, другими словами, усиливать друг друга. Южный полюс первого магнита стремится к северному полюсу второго. Если вблизи оказываются пара северных или пара южных полюсов магнитов, их магнитные поля направляются в разные стороны, и магниты отталкиваются.
В структуре железа происходят приблизительно такие же процессы, электроны производят вращение в одну сторону. Если рядом появляется магнит, железо воспринимает его как близкий по структуре материал и стремится соединить свои магнитные поля с полями минерала. Железо само становится магнитом, находясь рядом с минералом. Пока железо и магнит притянуты друг к другу, их магнитные поля остаются в параллельном направлении. Как только они разъединяются, магнитные свойства железа исчезают.
Определение притяжения и отталкивания магнетизма
Если иметь в виду направление векторовv1, v2, а такжер, вы можете определить, является ли сила между ними притягивающей или отталкивающей. Например, если у вас есть частица, движущаяся вперед в направлении x со скоростьюv, то это значение должно быть положительным. Если он движется в другом направлении, то значение v должно быть отрицательным.
Эти две частицы отталкиваются друг от друга, если магнитные силы, определяемые их соответствующими магнитными полями между ними, нейтрализуют друг друга, указывая в разных направлениях друг от друга. Если две силы направлены в разные стороны друг к другу, магнитная сила притягивает. Магнитная сила вызвана этими движениями частиц.
Вы можете использовать эти идеи, чтобы показать, как магнетизм работает с повседневными предметами. Например, если вы поместите неодимовый магнит рядом со стальной отверткой и переместите его вверх, вниз по валу, а затем удалите магнит, отвертка может сохранить в нем некоторый магнетизм. Это происходит из-за взаимодействующих магнитных полей между двумя объектами, которые создают силу притяжения, когда они нейтрализуют друг друга.
Это определение «отталкивать и притягивать» справедливо во всех случаях использования магнитов и магнитных полей. Следите за тем, какие направления соответствуют отталкиванию и притяжению.
Отталкивающая сила магнита
Противоположности притягиваются. Чтобы объяснить, почему магниты отталкиваются друг от друга, северный конец одного магнита будет притягиваться к югу от другого магнита. Северный и северный концы двух магнитов, а также южный и южный концы двух магнитов будут отталкивать друг друга. Магнитная сила является основой электродвигателей и привлекательных магнитов для использования в медицине, промышленности и исследованиях.
Чтобы понять, как работает эта сила отталкивания, и объяснить, почему магниты отталкивают друг друга и притягивают электричество, важно изучить природу магнитной силы и множество форм, которые она принимает в различных явлениях в физика.
Расчет магнитных свойств
Магнитная индукция поля Земли составляет 0,5Ч10–4 Тл, тогда как поле между полюсами сильного электромагнита – порядка 2 Тл и более.
Магнитное поле, создаваемое какой-либо конфигурацией токов, можно вычислить, пользуясь формулой Био – Савара – Лапласа для магнитной индукции поля, создаваемого элементом тока. Расчет поля, создаваемого контурами разной формы и цилиндрическими катушками, во многих случаях весьма сложен. Ниже приводятся формулы для ряда простых случаев. Магнитная индукция (в теслах) поля, создаваемого длинным прямым проводом с током I (ампер), на расстоянии r (метров) от провода равна
Индукция в центре кругового витка радиуса R с током I равна (в тех же единицах):
Плотно намотанная катушка провода без железного сердечника называется соленоидом. Магнитная индукция, создаваемая длинным соленоидом c числом витков N в точке, достаточно удаленной от его концов, равна
Здесь величина NI/L есть число ампер (ампер-витков) на единицу длины соленоида. Во всех случаях магнитное поле тока направлено перпендикулярно этому току, а сила, действующая на ток в магнитном поле, перпендикулярна и току, и магнитному полю.
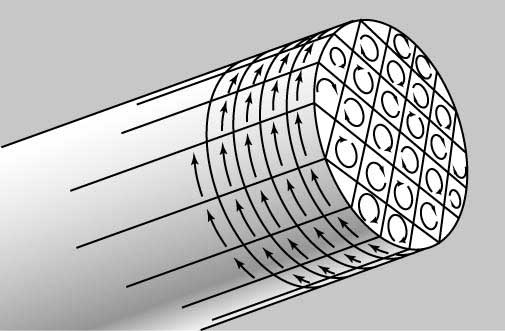
Поле намагниченного железного стержня сходно с внешним полем длинного соленоида с числом ампер-витков на единицу длины, соответствующим току в атомах на поверхности намагниченного стержня, поскольку токи внутри стержня взаимно компенсируются (рис. 12). По имени Ампера такой поверхностный ток называется амперовским. Напряженность магнитного поля Ha, создаваемая амперовским током, равна магнитному моменту единицы объема стержня M.
Если в соленоид вставлен железный стержень, то кроме того, что ток соленоида создает магнитное поле H, упорядочение атомных диполей в намагниченном материале стержня создает намагниченность M. В этом случае полный магнитный поток определяется суммой реального и амперовского токов, так что B = m0(H + Ha), или B = m0(H + M). Отношение M/H называетсямагнитной восприимчивостью и обозначается греческой буквой c; c– безразмерная величина, характеризующая способность материала намагничиваться в магнитном поле.
Величина B/H, характеризующая магнитные свойства материала, называется магнитной проницаемостью и обозначается через ma, причем ma = m0m, где ma – абсолютная, а m – относительная проницаемости,
В ферромагнитных веществах величина c может иметь очень большие значения –до 104ё106. Величина c у парамагнитных материалов немного больше нуля, а у диамагнитных – немного меньше. Лишь в вакууме и в очень слабых полях величины c и m постоянны и не зависят от внешнего поля. Зависимость индукции B от H обычно нелинейна, а ее графики, т.н. кривые намагничивания, для разных материалов и даже при разных температурах могут существенно различаться (примеры таких кривых приведены на рис. 2 и 3).
Магнитные свойства вещества весьма сложны, и для их глубокого понимания необходим тщательный анализ строения атомов, их взаимодействий в молекулах, их столкновений в газах и их взаимного влияния в твердых телах и жидкостях; магнитные свойства жидкостей пока наименее изучены.
Магнитная сила между проводами
Для токов, которые перемещают заряды по проводам, магнитная сила может быть определена как притягивающая или отталкивающий, основанный на расположении проводов относительно друг друга и направлении тока движется. Для токов в круглых проводах вы можете использовать правую руку, чтобы определить, как возникают магнитные поля.
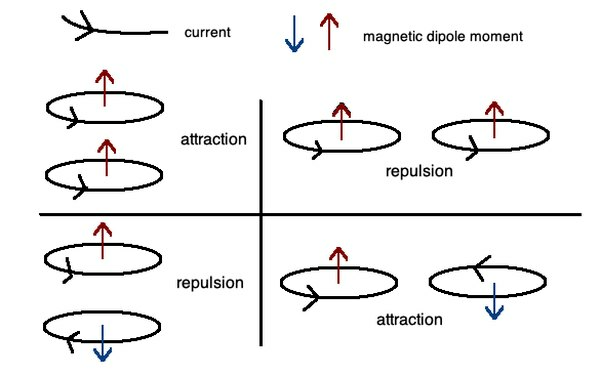
Правило правой руки для токов в петлях из проводов означает, что если вы поместите пальцы правой руки, согнутые в направлении проволочной петли, вы можете определить направление результирующего магнитного поля и магнитный момент, как показано на схеме выше. Это позволяет определить, насколько петли привлекательны или отталкивают друг друга.
Правило правой руки также позволяет определить направление магнитного поля, которое излучает ток в прямом проводе. В этом случае вы указываете большим пальцем правой руки в направлении тока через электрический провод. Направление сгибания пальцев правой руки определяет направление магнитного поля?
Из этих примеров магнитного поля, индуцированного токами, вы можете определить магнитную силу между двумя проводами в результате формирования этих силовых линий магнитного поля.
Определение притяжения и отталкивания электричества
Магнитные поля между витками токоведущих проводов являются либо притягивающими, либо отталкивающими, в зависимости от направления электрического тока и направления возникающих из них магнитных полей. Магнитный дипольный момент – это сила и ориентация магнита, создающего магнитное поле. На приведенной выше диаграмме результирующее притяжение или отталкивание показывает эту зависимость.
Вы можете представить себе силовые линии магнитного поля, излучаемые этими электрическими токами, как вьющиеся вокруг каждой части токовой петли. Если направления петли между двумя проводами противоположны друг другу, провода будут притягиваться друг к другу. Если они находятся в противоположных направлениях друг от друга, петли будут отталкивать друг друга.
Магнитная проницаемость и ее роль в магнетизме
Магнитная проницаемость m – это величина, характеризующая магнитные свойства материала. Ферромагнитные металлы Fe, Ni, Co и их сплавы обладают очень высокими максимальными проницаемостями – от 5000 (для Fe) до 800 000 (для супермаллоя). В таких материалах при сравнительно малых напряженностях поля H возникают большие индукции B, но связь между этими величинами, вообще говоря, нелинейна из-за явлений насыщения и гистерезиса, о которых говорится ниже. Ферромагнитные материалы сильно притягиваются магнитами. Они теряют свои магнитные свойства при температурах выше точки Кюри (770° С для Fe, 358° С для Ni, 1120° С для Co) и ведут себя как парамагнетики, для которых индукция B вплоть до очень высоких значений напряженности H пропорциональна ей – в точности так же, как это имеет место в вакууме. Многие элементы и соединения являются парамагнитными при всех температурах. Парамагнитные вещества характеризуются тем, что намагничиваются во внешнем магнитном поле; если же это поле выключить, парамагнетики возвращаются в ненамагниченное состояние. Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля.
На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1–2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1–3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)–(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант – участок 4–5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.
Магнитно-твердые материалы характеризуются широкой петлей гистерезиса, охватывающей значительную площадь на диаграмме и потому соответствующей большим значениям остаточной намагниченности (магнитной индукции) и коэрцитивной силы. Узкая петля гистерезиса (рис. 3) характерна для магнитно-мягких материалов – таких, как мягкая сталь и специальные сплавы с большой магнитной проницаемостью. Такие сплавы и были созданы с целью снижения обусловленных гистерезисом энергетических потерь. Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.
Магнитные материалы с высокой проницаемостью изготовляются путем отжига, осуществляемого выдерживанием при температуре около 1000° С, с последующим отпуском (постепенным охлаждением) до комнатной температуры. При этом очень существенны предварительная механическая и термическая обработка, а также отсутствие в образце примесей. Для сердечников трансформаторов в начале 20 в. были разработаны кремнистые стали, величина m которых возрастала с увеличением содержания кремния. Между 1915 и 1920 появились пермаллои (сплавы Ni с Fe) с характерной для них узкой и почти прямоугольной петлей гистерезиса. Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой – сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).
Почему сила магнита действует по-разному?
В других материалах электроны движутся в разных направлениях, поэтому не могут создать сильное магнитное поле, не способны притягивать магниты.
Магнит притягивается с разной силой к различным металлам. К примеру, к никелю, железу и другим сплавам магнит притягивается очень прочно. Подавляющая часть металлов не взаимодействует с магнитами с такой силой, взаимодействие иногда невозможно заметить в домашних условиях, а только в лабораториях, во время проведения опытов. Строение и связь атомов у других металлов отличны от строения и связей железа, поэтому притяжение столь малозаметно.
По какой причине не все материалы способны магнититься
Магнит взаимодействует с широким перечнем веществ. Вид взаимодействия не ограничивается притяжением или отталкиванием. Отдельные металлы и сплавы обладают специфическим строением, что дает возможность притягиваться к магниту с определенной мощностью.
Другие материалы также обладают данным свойством, но в меньших масштабах. Чтобы зафиксировать притяжение в таких условиях, необходимо создание очень сильного магнитного поля. Это невыполнимо в домашних условиях. Почему свойство притяжения есть у всех материалов, а магнититься доступно для восприятия только металл? Разгадка заключается в особом внешнем строении атомов.
Окружающие нас вещи состоят из атомов, связанных между собой. Тип связи между ними определяет материал. Атомы в большинстве веществ плохо сгруппированы, поэтому связь с магнитом формируется слабая. В металле атомы хорошо скоординированы, все атомы синхронно ощущают магнитное поле и тянутся к нему.
Предыдущая
ИнверторыЧто такое преобразователь напряжения
При межмолекулярном взаимодействии происходит взаимное влияние друг на друга соседних молекул или атомов. Эти частицы изначально должны быть нейтральными, т.е. электрически незаряженными.
Предположение о существование такого взаимодействия впервые высказал в 1873 году голландский ученый Я.Д. Ван-дер-Ваальс.
Изучая свойства газообразных веществ и жидкостей, он пришел к выводу, что есть особые силы, благодаря которым между молекулами возникает притяжение. Их существование через некоторое время было подтверждено, и они стали называться Ван-дер-Ваальсовыми силами (это одна из разновидностей межмолекулярного взаимодействия).
Силы, возникающие при межмолекулярном взаимодействии, подразделяются на две категории:
- силы притяжения;
- силы отталкивания.
Силы притяжения
Эти силы являются самыми значимыми для взаимодействия между частицами вещества. По своей природе они являются электростатическими. Силы притяжения, в свою очередь, подразделяются еще на две разновидности:
- Ван-дер-Ваальсовы силы: их действие распространяется сразу на всю молекулу;
- водородные связи: сфера их влияния ограничена отдельными участками.
Ван-дер-Ваальсовы силы
Эти силы по отношению к объему распространения их влияния являются близкодействующими. Их зона влияния распространяется на расстояние, не превышающее 0,3-0,5 нм.
Именно воздействием Ван-дер-Ваальсовых сил можно объяснить такие явления, как:
- сцепление в космическом пространстве между собой частиц, которые можно считать мелкими астероидами;
- кольца планет-гигантов, особенно планеты Сатурн (кольца Сатурна доступны для наблюдения с Земли даже в самый слабый телескоп);
- способность гекконов передвигаться по совершенно гладким поверхностям, таким как стекло.
Существует три их разновидности:
- дипольные (ориентационные) силы;
- индукционные (деформационные) силы;
- дисперсионные силы.
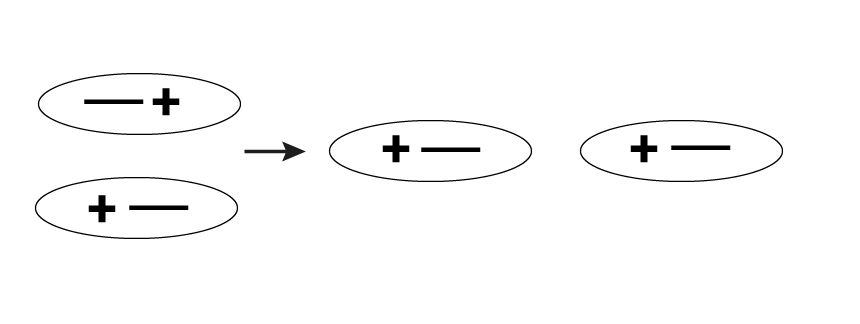
Дипольные силы можно наблюдать в полярных молекулах в процессе взаимодействия их диполей. Вокруг дипольной молекулы образуется электростатическое поле и происходит ориентация других диполей системы. Наибольшая сила притяжения между полярными молекулами отмечается в ситуации, когда их дипольные моменты расположены вдоль одной прямой. Возникновение такой силы обусловлено тем, что разноименные заряды отделены друг от друга несколько меньшим расстоянием, чем одноименные.
Значение энергии, высвобождающейся при подобном взаимодействии, находится в прямой зависимости от величины дипольных моментов и относительного положения диполей. Силой, противодействующей молекулярной ориентации, в данном случае является тепловое движение. Это значит, что энергия взаимодействия зависит в том числе и от температуры:
Eop=−23μ12μ22kTr6,E_{op} = — frac{2}{3} frac{mu^2_1 mu^2_2}{kTr^6},
где μ1mu_1 и μ2mu_2 – дипольные моменты молекул, которые участвуют во взаимодействии,
kk – постоянная Больцмана (ее значение 1,38066·1023 Дж/К),
TT – температура,
rr – расстояние, которым разделены молекулы.
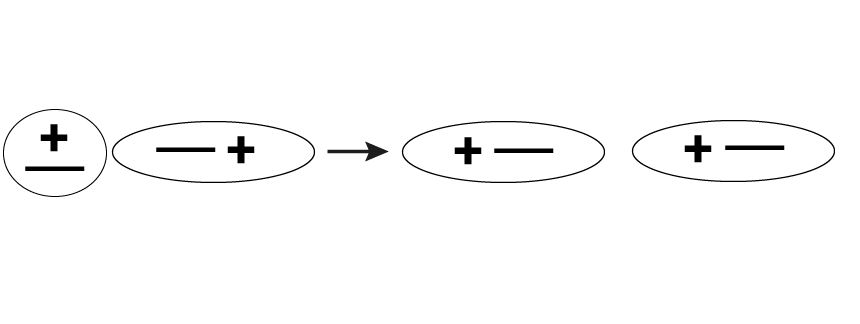
Индукционные силы возникают между двумя молекулами, одна из которых является полярной, а другая – неполярной. Вокруг полярной молекулы образуется электрическое поле. Оно способствует поляризации молекулы с электрическими зарядами. Положительные заряды движутся в сторону электрического поля, а отрицательные – в противоположном от него направлении.
Количество энергии при индукционном взаимодействии увеличивается вместе с возрастанием дипольного момента и стремительно сокращается при увеличении расстояний между частицами. С температурой индукционные силы никак не связаны.
EEинд =−2a2μ12r6,=- frac{2a_2 mu^2_1}{r^6},
где α2α_2 – значение степени поляризуемости неполярной молекулы.
Действие индукционных сил может наблюдаться также и между молекулами, обе из которых являются полярными.
Дисперсионные силы появляются вследствие движения электронов вокруг атомных ядер. Для правильного понимания их сущности атом можно представить в виде диполя, отрицательным полюсом которого является электрон, а положительным – протон. При этом наблюдается очень быстрое движение отрицательного полюса, т.е. электрона. В молекулах, расстояние между которыми небольшое, электроны движутся согласованно, и диполи оказываются расположенными по отношению друг к другу полюсами с противоположными значениями зарядов. Это приводит к тому, что они начинают притягиваться.
Природа дисперсионного взаимодействия была полностью раскрыта только после создания теории квантовой механики. С точки зрения этой теории получается, что в среднем по времени дипольные моменты у молекул, являющихся неполярными, имеют нулевое значение. Однако следует учитывать, что в любой момент времени каждый электрон занимает свое определенное положение. Из этого следует, что мгновенное значение дипольного момента не может быть равно нулю. Мгновенный диполь генерирует вокруг себя электрическое поле, вызывающее поляризацию расположенных по соседству молекул. Данные процессы приводят к взаимодействию мгновенных диполей.
Значение величины дисперсионного взаимодействия возрастает при ослаблении связи между электронами и ядром. Температура на ее значение влияния не оказывает.
EEдисп =−321r6I1I2I1+I2a1a2,= — frac{3}{2} frac{1}{r^6} frac{I_1 I_2}{I_1 + I_2} a_1a_2,
где α1α_1 и α2α_2 – показатели поляризуемости молекул, находящихся в состоянии взаимодействия.
Данный вид взаимодействия получил название дисперсионного по той причине, что дисперсия света в веществе обусловлена такими же характеристиками молекул, как и в случае рассматриваемого процесса.
Возникновение дисперсионных сил не связано с наличием или отсутствием постоянных дипольных моментов, они возникают между всеми атомами или молекулами. Из всех трех разновидностей Ван-дер-Ваальсовых сил они считаются самыми мощными, их величина в большинстве случаев превосходит величину дипольных и индукционных сил. Например, в процессе взаимодействия молекул таких соединений, как CO или HBr, дисперсионные силы больше всех прочих в несколько десятков или даже сотен раз.
Исключение составляют лишь молекулы веществ с большими значениями дипольных моментов. Так, у молекул воды дипольные силы превосходят дисперсионные примерно в 3 раза.
Водородная связь
Особой формой межмолекулярных взаимодействий считается так называемая водородная связь. Как следует из названия, она возникает между молекулами, в составе которых содержатся атомы водорода. Она может формироваться в ситуации, при которой атом водорода соединен ковалентной связью с другим атомом, обладающим значительной электроотрицательностью, вследствие чего формируется частичный положительный заряд на атоме водорода. Такая связь образуется между двумя молекулами, при этом одна из молекул должна содержать частично положительно заряженный атом водорода, а другая – атом элемента с частичным отрицательным зарядом, который содержит неподеленную пару электронов.
Рассмотрим характерные особенности водородной связи на примере молекулы воды. В ней связи O-H характеризуются сильной степенью полярности. Атом водорода обладает частичным положительным зарядом, а атом кислорода – частичным отрицательным. Отметим также, что у атома кислорода имеются 2 неподеленные электронные пары. В результате молекула H2O образует 4 водородные связи с находящимися рядом молекулами этого же вещества. Каждая молекула в 2 водородных связях является донором пары атомов водорода с частичным положительным зарядом, а в оставшихся 2 – донором 2 неподеленных пар электронов атома кислорода. В результате образуется сетчатая структура, которая может быть представлена в 3 измерениях.
Именно наличием водородной связи обусловлена межмолекулярная ассоциация таких соединений, как фторид водорода, аммиак, спирты, карбоновые кислоты.
Если учитывать степень электроотрицательности элементов, не составит труда понять, что формирование самых сильных водородных связей будет происходить с участием атомов фтора. Для атомов кислорода их сила меньше, далее, у атомов азота она становится еще меньше. Возникновение водородных связей возможно также и внутри молекулы, если в ней содержатся протонодонорные и протоноакцепторные группы.
По прочности водородные силы превосходят Ван-дер-Ваальсовы. Однако энергия их все же не настолько велика, чтобы связь между частицами оставалась стабильной. Без особых изменений параметров среды межмолекулярная связь может не только легко разрушаться, но и без труда восстанавливаться. Это играет огромную роль для жизни всех известных живых организмов. Большинство протекающих в них биохимических процессов основано на формировании или разрушении водородной связи.
Силы отталкивания
Силы отталкивания начинают действовать, когда межмолекулярное расстояние сокращается до предельно возможного минимума. При таком сближении начинают соприкасаться внешние уровни электронов двух атомов. Как следует из принципа Паули, являющегося одним из базовых положений квантовой механики, заполненные электронные оболочки не могут проникать одна внутрь другой. Величина таких сил в значительной степени зависит от особенностей строения молекулы определенного вещества.