Параболоиды: определение, виды, сечения
Определение параболоида
Эллиптическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
(4.51)
Гиперболическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
(4.52)
В уравнениях (4.51) и (4.52) и
— положительные параметры, характеризующие параболоиды, причем для эллиптического параболоида
.
Начало координат называют вершиной каждого из параболоидов ((4.50) или (4.51)).
Плоские сечения эллиптического параболоида
Плоскость пересекает эллиптический параболоид (4.51) по линии, имеющей в этой плоскости уравнение
, которое равносильно уравнению
параболы с фокальным параметром
. Сечение параболоида плоскостью
получаем, подставляя
в уравнение (4.51):
. Это уравнение равносильно уравнению
параболы с фокальным параметром
. Эти сечения называются главными параболами эллиптического параболоида (4.51).
Рассмотрим теперь сечение эллиптического параболоида плоскостями, параллельными плоскости . Подставляя
, где
— произвольная постоянная (параметр), в уравнение (4.51), получаем
При уравнение не имеет действительных решений, т.е. плоскость
при
не пересекает параболоид (4.51). При
уравнению (4.51) удовлетворяет одна вещественная точка
— вершина параболоида. При
уравнение определяет эллипс
с полуосями
. Следовательно, сечение эллиптического параболоида плоскостью
(при
) представляет собой эллипс, центр которого лежит на оси аппликат, а вершины — на главных параболах.
Таким образом, эллиптический параболоид можно представить как поверхность, образованную эллипсами, вершины которых лежат на главных параболах (рис.4.46,а).
Параболоид вращения
Эллиптический параболоид, у которого , называется параболоидом вращения. Такой параболоид является поверхностью вращения. Сечения параболоида вращения плоскостями
(при
), представляют собой окружности с центрами на оси аппликат (рис.4.46,б). Его можно получить, вращая вокруг оси
параболу
, где
.
Плоские сечения гиперболического параболоида
Сечения гиперболического параболоида координатными плоскостями и
представляют собой параболы (главные параболы)
или
с параметрами
или
соответственно. Поскольку оси симметрии главных парабол направлены в противоположные стороны, гиперболический параболоид называют седловой поверхностью.
Рассмотрим теперь сечения гиперболического параболоида плоскостями, параллельными плоскости . Подставляя
, где
— произвольная постоянная (параметр), в уравнение (4.52), получаем
При
уравнение равносильно уравнению гиперболы
полуосями
, то есть сечение гиперболического параболоида плоскостью
при
представляет собой гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе
. При
получаем уравнение сопряженной гиперболы
с полуосями
, т.е. сечение гиперболического параболоида плоскостью
при
представляет собой сопряженную гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе
. При
получаем уравнение пересекающихся прямых
, т.е. сечение гиперболического параболоида плоскостью
представляет собой пару пересекающихся в начале координат прямых.
Таким образом, гиперболический параболоид можно представить как поверхность, образованную гиперболами (включая и «крест» из их асимптот), вершины которых лежат на главных параболах (рис.4.47,а).
Сечение параболоида плоскостью , где
— произвольная постоянная, представляет собой параболу
равную главной параболе с параметром
, вершина которой лежит на другой главной параболе
с параметром
. Поэтому гиперболический параболоид можно представить как поверхность, получающуюся при перемещении одной главной параболы так, чтобы ее вершина «скользила» по другой главной параболе (рис.4.47,б).
Замечания 4.11.
1. Гиперболический параболоид является линейчатой поверхностью, т.е. поверхностью, образованной движением прямой (рис.4.47,в).
2. Ось аппликат канонической системы координат является осью симметрии параболоида, а координатные плоскости — плоскостями симметрии параболоида.
В самом деле, если точка принадлежит параболоиду (эллиптическому или гиперболическому), то точки с координатами
при любом выборе знаков также принадлежат параболоиду, поскольку их координаты удовлетворяют уравнению (4.51) или (4.52) соответственно. Поэтому параболоид симметричен относительно координатных плоскостей
и координатной оси
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
-
Поверхности вращения.
Начать изучение
-
Эллипсоид.
Начать изучение
-
Конус второго порядка.
Начать изучение
-
Однополостный гиперболоид.
Начать изучение
-
Двуполостный гиперболоид.
Начать изучение
-
Эллиптический параболоид.
Начать изучение
-
Гиперболический параболоид.
Начать изучение
Поверхности вращения.
Определение.
Поверхность (S) называется поверхностью вращения с осью (d), если она составлена из окружностей, которые имеют центры на прямой (d) и лежат в плоскостях, перпендикулярных данной прямой.
Рассмотрим линию (L), которая лежит в плоскости (P), проходящей через ось вращения (d) (рис. 43), и будем вращать ее вокруг этой оси. Каждая точка линии опишет окружность, а вся линия — поверхность вращения.
Выберем начало декартовой прямоугольной системы координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}) на оси (d), вектор (boldsymbol{e}_{3}) направим вдоль (d), а вектор (boldsymbol{e}_{1}) поместим в плоскости (P). Таким образом, (O, boldsymbol{e}_{1}, boldsymbol{e}_{3}) — декартова система координат в плоскости (P). Пусть линия (L) имеет в этой системе координат уравнение (f(x, y)=0).
Рассмотрим точку (M(x, y, z)). Через нее проходит окружность, которая имеет центр на оси (d) и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от (M) до оси, то есть (sqrt{x^{2}+y^{2}}). Точка (M) лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка Мь принадлежащая вращаемой линии (L).
Точка (M_{1}(x_{1}, y_{1}, z_{1})) лежит в плоскости (P), и потому (y_{1}=0). Кроме того, (z_{1}=z) и (|x|=sqrt{x^{2}+y^{2}}), так как (M_{1}) лежит на той же окружности, что и (M). Координаты точки (M_{1}) удовлетворяют уравнению линии (L): (f(x_{1}, z_{1})=0). Подставляя в это уравнение (x_{1}) и (z_{1}), мы получаем условие на координаты точки (M), необходимое и достаточное для того, чтобы (M) лежала на поверхности вращения (S): равенство
$$
fleft(pm sqrt{x^{2}+y^{2}}, zright)=0label{ref1}
$$
должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое можно записать также в виде
$$
fleft(sqrt{x^{2}+y^{2}}, zright)fleft(-sqrt{x^{2}+y^{2}}, zright)=0,label{ref2}
$$
и является уравнением поверхности вращения линии (L) вокруг оси (d).
Эллипсоид.
Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направив вектор (boldsymbol{e}_{3}) сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнения эллипса в следующих видах:
$$
frac{x^{2}}{a^{2}}+frac{z^{2}}{c^{2}}=1, frac{z^{2}}{a^{2}}+frac{x^{2}}{c^{2}}=1.nonumber
$$
(Здесь через (c) обозначена малая полуось эллипса.) В силу формулы eqref{ref1} уравнениями соответствующих поверхностей вращения будут
$$
frac{x^{2}+y^{2}}{a^{2}}+frac{z^{2}}{c^{2}}=1, frac{z^{2}}{a^{2}}+frac{x^{2}+y^{2}}{c^{2}}=1 (a > c).label{ref3}
$$
Поверхности с такими уравнениями называются соответственно сжатым и вытянутым эллипсоидами вращения (рис. 10.2).
Каждую точку (M(x, y, z)) на сжатом эллипсоиде вращения сдвинем к плоскости (y=0) так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении (lambda < 1). После сдвига точка попадет в положение (M'(x’, y’, z’)), где (x’=x), (y’=y), (z’=z).
Таким образом, точки эллипсоида вращения переходят в точки поверхности с уравнением
$$
frac{x’^{2}}{a^{2}}+frac{y’^{2}}{b^{2}}+frac{z’^{2}}{c^{2}}=1,label{ref4}
$$
где (b=lambda a). Поверхность, которая в некоторой декартовой системе координат имеет уравнение eqref{ref4}, называется эллипсоидом (рис. 10.3). Если случайно окажется, что (b=c), мы получим снова эллипсоид вращения, но уже вытянутый.
Эллипсоид так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения eqref{ref4} видно, что начало канонической системы координат — центр симметрии эллипсоида, а координатные плоскости — его плоскости симметрии.
Эллипсоид можно получить из сферы (x^{2}+y^{2}+z^{2}=a^{2}) сжатиями к плоскостям (y=0) и (z=0) в отношениях (lambda=b/a) и (mu=c/a).
В этой статье нам часто придется прибегать к сжатию, и мы не будем его каждый раз описывать столь подробно.
Конус второго порядка.
Рассмотрим на плоскости (P) пару пересекающихся прямых, задаваемую в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{3}) уравнением (a^{2}x^{2}-c^{2}z^{2}=0). Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение
$$
a^{2}(x^{2}+y^{2})-c^{2}z^{2}=0label{ref5}
$$
и носит название прямого кругового конуса (рис. 10.4). Сжатие к плоскости (y=0) переводит прямой круговой конус в поверхность с уравнением
$$
a^{2}x^{2}+b^{2}y^{2}-c^{2}z^{2}=0label{ref6}
$$
называемую конусом второго порядка.
Обратите внимание на то, что левая часть уравнения eqref{ref6} — однородная функция, и поверхность является конусом в смысле определения, введенного ранее.
Однополостный гиперболоид.
Однополостный гиперболоид вращения — это поверхность вращения гиперболы
$$
frac{x^{2}}{a^{2}}-frac{z^{2}}{c^{2}}=1nonumber
$$
вокруг той оси, которая ее не пересекает. По формуле eqref{ref1} мы получаем уравнение этой поверхности (рис. 10.5)
$$
frac{x^{2}+y^{2}}{a^{2}}-frac{z^{2}}{c^{2}}=1.label{ref7}
$$
В результате сжатия однополостного гиперболоида вращения к плоскости (y=0) мы получаем однополостный гиперболоид с уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}-frac{z^{2}}{c^{2}}=1.label{ref8}
$$
Интересное свойство однополостного гиперболоида — наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие, уравнения которых можно получить следующим образом.
Уравнение eqref{ref8} можно переписать в виде
$$
left(frac{x}{a}+frac{z}{c}right)left(frac{x}{a}-frac{z}{c}right)=left(1+frac{y}{b}right)left(1-frac{y}{b}right).nonumber
$$
Рассмотрим прямую линию с уравнениями
$$
begin{array}{cc}
& displaystylemuleft(frac{x}{a}+frac{z}{c}right)=lambdaleft(1+frac{y}{b}right),\
& \
& displaystylelambdaleft(frac{x}{a}-frac{z}{c}right)=muleft(1-frac{y}{b}right),
end{array}label{ref9}
$$
где (lambda) и (mu) — некоторые числа ((lambda^{2}+mu^{2} neq 0)). Координаты каждой точки прямой удовлетворяют обоим уравнениям, а следовательно, и уравнению eqref{ref8}, которое получается их почленным перемножением. Поэтому каковы бы ни были (lambda) и (mu), прямая с уравнениями eqref{ref9} лежит на однополостном гиперболоиде. Таким образом, система eqref{ref9} определяет семейство прямолинейных образующих.
Второе семейство прямолинейных образующих определяется системой
$$
begin{array}{cc}
& mu’left(frac{x}{a}+frac{z}{c}right)=lambda’left(1-frac{y}{b}right),\
& \
& lambda’left(frac{x}{a}-frac{z}{c}right)=mu’left(1+frac{y}{b}right),
end{array}label{ref10}
$$
Покажем на примере, как найти образующие, проходящие через данную точку поверхности. Рассмотрим поверхность (x^{2}+y^{2}-z^{2}=0) и точку (M_{0}(1, 1, 1)) на ней. Подставляя координаты (M_{0}) в уравнения eqref{ref9}, мы получаем условия на (lambda) и (mu): (2lambda=2mu) и (0 cdot lambda=0 cdot mu). Первое из них определяет (lambda) и (mu) с точностью до общего множителя, но только с такой точностью они и нужны. Подставляя эти значения в eqref{ref9}, получаем уравнения прямолинейной образующей
$$
x+z=1+y, x-z=1-y.nonumber
$$
Она проходит через (M_{0}), так как (lambda) и (mu) так и выбирались, чтобы координаты (M_{0}) удовлетворяли этой системе. Аналогично, подставляя координаты (M_{0}) в (10), находим условия на (lambda’) и (mu’): (2mu’=0) и (2mu’=0). Коэффициент (lambda’) можно взять любым ненулевым, и мы приходим к уравнению второй образующей: (x=z), (y=1).
Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.
Двуполостный гиперболоид.
Двуполостный гиперболоид вращения — это поверхность, получаемая вращением гиперболы
$$
frac{z^{2}}{c^{2}}-frac{x^{2}}{a^{2}}=1nonumber
$$
вокруг той оси, которая ее пересекает. По формуле eqref{ref1} мы получаем уравнение двуполостного гиперболоида вращения
$$
frac{z^{2}}{c^{2}}-frac{x^{2}+y^{2}}{a^{2}}=1.label{ref11}
$$
В результате сжатия этой поверхности к плоскости у=0 получается поверхность с уравнением
$$
frac{z^{2}}{c^{2}}-frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref12}
$$
Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида eqref{ref12}, называется двуполостным гиперболоидом (рис. 10.6). Двум ветвям гиперболы здесь соответствуют две не связанные между собой части (“полости”) поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывала всю поверхность.
Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.
Эллиптический параболоид.
Вращая параболу (x^{2}=2pz) вокруг ее оси симметрии, мы получаем поверхность с уравнением
$$
x^{2}+y^{2}=2pz.label{ref13}
$$
Она называется параболоидом вращения. Сжатие к плоскости (y=0) переводит параболоид вращения в поверхность, уравнение которой приводится к виду
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=2z.label{ref14}
$$
Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом (рис. 10.7).
Гиперболический параболоид.
По аналогии с уравнением eqref{ref14} мы можем написать уравнение
$$
frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=2z.label{ref15}
$$
Поверхность, которая имеет уравнение вида eqref{ref15} в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом.
Исследуем форму этой поверхности. Для этого рассмотрим ее сечение плоскостью (x=alpha) при произвольном (alpha). В этой плоскости выберем декартову прямоугольную систему координат (O’, boldsymbol{e}_{2}, boldsymbol{e}_{3}) с началом в точке (O'(alpha, 0, 0)). Относительно этой системы координат линия пересечения имеет уравнение
$$
-frac{y^{2}}{b^{2}}=2left(z-frac{alpha^{2}}{2a^{2}}right).label{ref16}
$$
Эта линия — парабола, в чем легко убедиться, перенеся начало координат в точку (O″) с координатами ((0, alpha^{2}/(2a^{2}))). (Координаты этой точки относительно исходной системы координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}) в пространстве равны ((alpha, 0, alpha^{2}/(2a^{2}))).)
Точка (O″), очевидно, является вершиной параболы, ось параболы параллельна вектору (boldsymbol{e}_{3}), а знак минус в левой части равенства eqref{ref16} означает, что ветви параболы направлены в сторону, противоположную направлению (boldsymbol{e}_{3}). Заметим, что после переноса начала координат в точку (O″) величина а не входит в уравнение параболы, и, следовательно, сечения гиперболического параболоида плоскостями (x=alpha) при всех (alpha) представляют собой равные параболы.
Будем теперь менять величину (alpha) и проследим за перемещением вершины параболы (O″) в зависимости от (alpha). Из приведенных выше координат точки (O″) следует, что эта точка перемещается по линии с уравнениями
$$
z=frac{x^{2}}{2a^{2}}, y=0nonumber
$$
в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}). Эта линия — парабола в плоскости (y=0). Вершина параболы находится в начале координат, ось симметрии совпадает с осью аппликат, а ветви параболы направлены в ту же сторону, что и вектор (boldsymbol{e}_{3}).
Теперь мы можем построить гиперболический параболоид следующим образом: зададим две параболы и будем перемещать одну из них так, чтобы ее вершина скользила по другой, оси парабол были параллельны, параболы лежали во взаимно перпендикулярных плоскостях и ветви их были направлены в противоположные стороны.
При таком перемещении подвижная парабола описывает гиперболический параболоид (рис. 10.8).
Сечения гиперболического параболоида плоскостями с уравнениями (z=alpha) при всевозможных (alpha) — гиперболы. Эти сечения нарисованы на рис. 10.9.
Гиперболический параболоид, как и однополостный гиперболоид, имеет два семейства прямолинейных образующих (рис. 10.10). Уравнения одного семейства —
$$
lambdaleft(frac{x}{a}-frac{y}{b}right)=mu, muleft(frac{x}{a}+frac{y}{b}right)=2lambda z,nonumber
$$
а другого —
$$
lambda’left(frac{x}{a}+frac{y}{b}right)=mu’, mu’left(frac{x}{a}-frac{y}{b}right)=2lambda’ z,nonumber
$$
Выводятся эти уравнения так же, как и уравнения прямолинейных образующих однополостного гиперболоида.
6.5. Параболоиды
Их два. Сначала рассмотрим мегапопулярный
Эллиптический параболоид
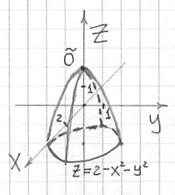
Каноничный эллиптический параболоид задаётся уравнением (система координат, напоминаю, везде декартова) 
. Данная поверхность выглядит бесконечной чашей:
Название «эллиптический параболоид» тоже произошло из результатов исследования сечений. В горизонтальных сечениях плоскостями 
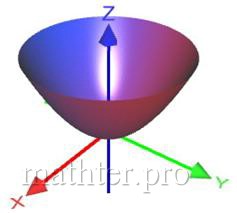
получаются различные эллипсы:
, в частности, при 
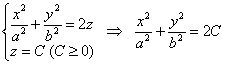
эллипс вырождается в точку (начало координат), которая называется вершиной эллиптического параболоида.
А вертикальные сечения плоскостями, параллельными оси 
, представляют собой различные параболы. Например, сечение координатной плоскостью 
:
– парабола, лежащая в плоскости 
.
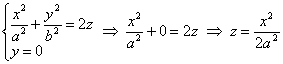
и сечение плоскостью 
:
– парабола, лежащая в плоскости 
.
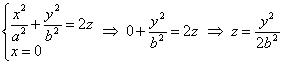
Отсюда и эллиптический параболоид.
На практике обычно встречается упрощенная версия поверхности с горизонтальными сечениями-окружностями. Перепишем каноническое уравнение в прикладном функциональном виде: 
– характерным признаком этой функции, как и в ситуации с конусом, является равенство коэффициентов при 
.
Задача 178
Построить поверхность 
. Записать неравенства, определяющие внутреннюю и внешнюю часть эллиптического параболоида.
Решение: используем ту же методику, что и при построении конической поверхности. Рассмотрим какое-нибудь не очень большое значение «зет», здесь удобно выбрать 
, и найдём сечение эллиптического параболоида этой плоскостью:
– окружность радиуса 2.
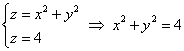
Теперь на высоте 
изобразим данную окружность и аккуратно соединим её с вершиной (началом координат) двумя параболами. В результате получится такая вот симпатичная чашка:
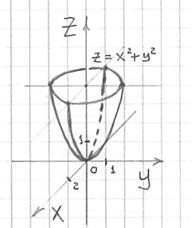
Рассматриваемый частный случай параболоида с сечениями-окружностями называют параболоидом вращения, поскольку его можно получить вращением параболы вокруг оси 
С неравенствами ничего нового. Нетрудно догадаться, что неравенство 
или, если развернуть запись в более привычном порядке, 
определяет множество точек внутри чаши (т.к. неравенство строгое, то сама поверхность не входит в решение). И, соответственно, неравенство 
задаёт множество внешних точек.
По моим наблюдениям, на практике часто встречается эллиптический параболоид вида 
, который выглядит точно так же, но мигрировал вершиной в точку 
.
Ещё одно типичное расположение эллиптического параболоида:
Задача 179
Построить поверхность 
Решение: если коэффициенты при 
отрицательны (сразу оба), то чаша параболоида «смотрит вниз». Вершина поверхности расположена в точке 
. Это понятно не только интуитивно, но и подкрепляется простым аналитическим рассуждением: очевидно, что, рассмотрев любую другую пару значений 
, мы уменьшим функцию 
. Таким образом, точка 
– это самая высокая точка (максимум).
В целях построения поверхность удобно «отсечь» плоскостью 
. Сечение представляет собой:
– окружность радиуса 2.
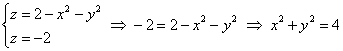
Отмечаем точку 
, проводим окружность 
на высоте 
и аккуратно завершаем конструкцию 4 направляющими (ветвями параболы).
Творческое задание для самостоятельного решения:
Задача 180
Построить эллиптический параболоид 
Теперь менее распространённый «собрат»:
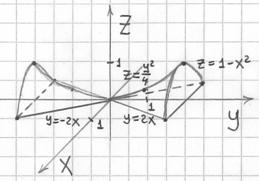
Гиперболический параболоид
Его каноническое уравнение имеет вид 
. Данную поверхность также называют седловой поверхностью, а всадники – седлом:
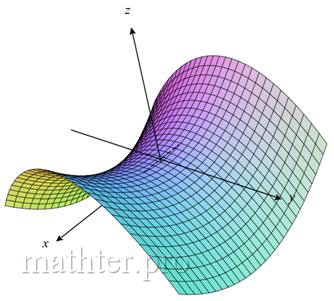
Если его рассекать плоскостями 
, то в общем случае будут получаться гиперболы 
, а при 
мы получим две пересекающиеся прямые: 
(на чертеже отсутствуют). Таким образом, гиперболический параболоид пересекает плоскость 
по двум прямым.
Если его рассекать плоскостями 
(параллельными плоскости 
), то в сечениях будут получаться параболы 
, ветви которых направлены вверх, и множество таких парабол легко увидеть на чертеже.
И, наконец, если параболоид рассекать плоскостями 
(параллельными плоскости 
), то в сечениях будут получаться параболы 
, ветви которых смотрят вниз, эти параболы тоже есть на чертеже.
Таким образом, происхождение гиперболического параболоида полностью расшифровано.
Как и конус, как и «чаша», седло симметрично относительно плоскостей 
и относительно оси 
. Рассмотрю один демонстрационный пример:
Задача 181
Построить тело, ограниченное поверхностями 
.
Решение: найдём линии пересечения параболоида с плоскостью 
. Слева и справа тело ограничено плоскостями 
, и ввиду его симметрии достаточно рассмотреть пересечение параболоида с плоскостью 
:
– изобразим эти параболы в плоскостях 
. Осталось «замкнуть» чертёж сверху, для этого найдем пересечение параболоида с фронтальной плоскостью 
– изобразим эту параболу в плоскости 
. Заметьте, что здесь под седлом скрылась ось 
, т.к. уравнение неканоническое.
6.6. Гиперболоиды
6.4. Коническая поверхность
| Оглавление |
Автор: Aлeксaндр Eмeлин
3.О поверхностях второго порядка
3.1.Поверхности вращения в координатах
Рис. 246
Пусть f(х, у, z) = 0 — уравнение с переменными х, y, z; Ф — некоторая поверхность (на рис. 246 изображена часть этой поверхности). Из курса 10 класса известно, что уравнение f(x, y, z) = 0 называется уравнением поверхности Ф, если этому уравнению удовлетворяют координаты х, у, z любой точки М этой поверхности и не удовлетворяют координаты ни какой точки пространства, не принадлежащей поверхности Ф.
Если f (x, y, z) — многочлен, то его степень называют порядком поверхности Ф.
Мы знаем, например, что сфера с центром K(a; b; с) и радиусом R > 0 в декартовой прямоугольной системе координат Oxyz задаётся уравнением
(x – a)2 + (y – b)2 + (z – c)2 = R2.
Из этого уравнения следует, что сфера — поверхность второго порядка.
Заметим, что уравнение второго порядка может задавать «поверхность», состоящую из двух плоскостей. Например, уравнение ху + у2 = 0 задаёт пару пересекающихся плоскостей, одна из которых имеет уравнение у = 0, другая — уравнение х + у = 0.
Eсли в пространстве некоторая линия γ является пересечением двух поверхностей Ф1 и Ф2, заданных уравнениями f1(x, y, z) = 0 и f2(х, у, z) = 0, то координаты х, у, z любой точки М линии γ удовлетворяют каждому из этих уравнений, т. е. удовлетворяют системе уравнений
(1)
В этом случае говорят, что система уравнений (1) задаёт линию γ.
Разрешив уравнения этой системы относительно х и у (если это возможно), получим систему уравнений
(2)
равносильную системе (1), следовательно, задающую ту же самую линию γ.
Если линию γ вращать вокруг некоторой прямой m, то при этом вращении образуется некоторая поверхность Ф, которую называют поверхностью вращения, а прямую m — осью вращения или осью симметрии этой поверхности (вспомните сферическую и сегментную поверхности).
Для получения уравнения поверхности Ф достаточно выбрать на ней любую точку M(X; Y; Z) и выразить в координатной форме свойство, которым обладают только точки M(X; Y; Z) ∈ Ф; в результате получим уравнение относительно X, Y, Z, которое и является искомым уравнением поверхности Ф.
Составим уравнение поверхности Ф, которая образуется вращением вокруг оси Oz линии γ, заданной системой уравнений (2). Для этого через произвольную точку M(X; Y; Z) ∈ Ф проведём плоскость, перпендикулярную оси Oz, т. е. плоскость z = Z (рис. 247). Эта плоскость пересекает поверхность Ф по окружности с центром K(0; 0; Z) на оси вращения Oz, а линию γ — в некоторой точке Р(х; у; z = Z). Так как KМ = KР, то
X2 + Y2 = x2 + y2.(3)
Учитывая, что z = Z, имеем для x и у в системе (2):
Рис. 247
После подстановки этих значений x и у в уравнение (3) получаем искомое уравнение поверхности Ф с осью вращения Oz в виде:
X2 + Y2 = 
+ 
.(4)
(Обратите внимание: правая часть уравнения (4) есть некоторая функция f переменной Z, т. е. f(Z) = 
+ 
.)
Справедливо обратное утверждение: любое уравнение X2 + Y2 = f(Z) задаёт поверхность вращения с осью Oz, так как сечением этой поверхности плоскостью Z = α (α = const) является окружность с центром на оси Oz.
Из сказанного следует: чтобы получить уравнение поверхности, которая образуется вращением вокруг оси Oz линии, заданной системой уравнений (1), достаточно выразить х и у через z, после чего сложить квадраты левых и правых частей полученных равенств.
Аналогично получаются уравнения поверхностей, образованных вращением линии вокруг осей Ох и Оу.
3.2.Поверхности вращения второго порядка
Рассмотрим некоторые поверхности, образованные вращением кривых второго порядка вокруг своих осей симметрии.
a) Сфера
Пусть окружность радиуса R с центром в начале системы координат Oxyz, расположенная в плоскости Oyz (рис. 248, а), задана системой уравнений:
Поверхностью, образованной вращением этой окружности вокруг оси Oz, является известная вам сфера (сферическая поверхность) (рис. 248, б).
Уравнение этой сферы
x2 + у2 + z2 = R2 (5)
Рис. 248
получим после сложения левых и правых частей равенств у2 = r2 – z2 и x2 = 0. Уравнение (5) называется каноническим (простейшим) уравнением сферы.
б) Эллипсоид вращения
Из планиметрии известно, что эллипсом называется множество всех точек М плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 той же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами (рис. 249, а).
Эллипс с центром в начале координат и осями симметрии Ох и Оу задаётся каноническим уравнением: 
= 1 (где а и b — длины полуосей эллипса).
Пусть эллипс расположен в плоскости Oyz и задан системой уравнений:
(6)
Поверхность, образованная вращением эллипса вокруг его оси симметрии, называется эллипсоидом вращения.
Рис. 249
Будем вращать эллипс, заданный системой уравнений (6), вокруг оси Oz. Чтобы получить уравнение образованного при этом эллипсоида вращения (рис. 249, б), из первого уравнения системы (6) находим y2 = 
a2. Тогда после сложения этого уравнения и уравнения х2 = 0 и последующего преобразования получаем искомое уравнение
= 1,(6a)
которое называется каноническим уравнением эллипсоида вращения.
Из уравнения (6а) видно, что любая плоскость z = m (m < b), перпендикулярная оси вращения эллипсоида, пересекает его по окружности с центром (0; 0; m) на оси Oz и радиусом
R = a 
.
в) Параболоид вращения
Из планиметрии известно, что параболой называется множество всех точек М плоскости, для каждой из которых расстояние до данной точки F, называемой фокусом, равно расстоянию до данной прямой а, называемой директрисой (рис. 250, а) параболы.
Парабола с вершиной в начале системы координат Оху и осью симметрии Ох задаётся каноническим уравнением: у2 = 2рх, где р — расстояние между фокусом и директрисой. При 2p = 1 парабола имеет уравнение y2 = x.
Поверхность, образованная вращением параболы вокруг её оси симметрии, называется параболоидом вращения (рис. 250, б). Вершина параболы при этом называется вершиной параболоида вращения.
Рис. 250
Парабола, расположенная в координатной плоскости Oyz и имеющая своей вершиной начало координат, а осью симметрии — координатную ось Oz, может быть задана в декартовой прямоугольной системе координат Oxyz системой уравнений:
(7)
Будем вращать эту параболу вокруг оси Oz. Уравнение
x2 + y2 = z(7a)
образованного при этом параболоида вращения (рис. 250, б) получим после почленного сложения уравнений
у2 = z и х2 = 0.
Уравнение (7а) называется каноническим уравнением параболоида вращения с осью вращения Oz. Из этого уравнения (7а) видно, что любая плоскость, перпендикулярная оси вращения (такая плоскость имеет уравнение z = m, m > 0), пересекает данный параболоид по окружности с центром (0; 0; m) на оси Oz и радиусом R = 
.
г) Гиперболоиды вращения
Из планиметрии известно, что гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Гипербола с действительной осью Ох и мнимой осью Oy (рис. 251, а) в системе координат Oxy задаётся каноническим уравнением: 
= 1.
Рис. 251
Пусть гипербола расположена в координатной плоскости Oyz и задана системой уравнений:
(8)
Координатная ось Oy является действительной осью данной гиперболы, а координатная ось Oz — её мнимой осью.
Если вращать данную гиперболу вокруг её действительной оси (оси Оу), то получим поверхность, состоящую из двух частей. Эти части называют полостями (или полами), а полученная при этом поверхность называется двуполостным гиперболоидом вращения (рис. 251, б).
Найдём уравнение этой поверхности.
Из уравнений (8) имеем:
После элементарных преобразований получаем искомое уравнение
= 1,(8а)
которое называется каноническим уравнением двуполостного гиперболоида вращения с осью Оу.
Вращая ту же самую гиперболу 
вокруг её мнимой оси (т. е. вокруг оси Oz), получим поверхность, которая называется однополостным гиперболоидом вращения (рис. 252, а). Рассуждениями, аналогичными предыдущим, получаем каноническое уравнение этого гиперболоида в виде
= 1.(8б)
Рис. 252
Любая плоскость z = m, перпендикулярная оси вращения однополостного гиперболоида (рис. 252, б), пересекает этот гиперболоид по окружности с центром (0; 0; m) на оси Oz и радиусом R = 
. Из выражения для вычисления радиуса окружности — сечения видно, что самым «узким» сечением нашего гиперболоида является окружность радиуса а. Эта окружность получается при пересечении данного гиперболоида плоскостью z = 0 и называется горловой окружностью (или горловиной) однополостного гиперболоида.
Если вращать вокруг оси Oz прямую
(8в)
(эта прямая лежит в плоскости х = а и не параллельна оси Oz, см. рис. 252, б), то при этом вращении образуется тот же однополостный гиперболоид.
В самом деле, из уравнений (8в) имеем:
После почленного сложения уравнений этой системы и последующего преобразования полученного уравнения приходим к уравнению
= 1,
совпадающему с уравнением (8б), следовательно, задающего тот же самый однополостный гиперболоид.
Но если вращать вокруг оси Oz прямую, заданную системой уравнений
(8г)
(эта прямая также лежит в плоскости х = а и не параллельна оси Oz, см. рис. 252, б), то при этом вращении вновь образуется однополостный гиперболоид, заданный уравнением (8б).
Поверхность, образованную движением прямой, называют линейчатой поверхностью, а прямые, целиком лежащие на этой поверхности, называют её прямолинейными образующими.
Из сказанногo следует, что однополостный гиперболоид является линейчатой поверхностью. При этом: множество всех прямых, образованное движением прямой (8в), представляет собой одну серию прямолинейных образующих однополостного гиперболоида (8б) («полуквадрику»), а множество всех прямых, образованное движением прямой (8г), — другую серию прямолинейных образующих этого гиперболоида (вторую «полуквадрику»).
Примечательным является тот факт, что любые две образующие разных серий однополостного гиперболоида пересекаются, а любые две его образующие одной серии скрещиваются (рис. 253).
Рис. 253
д) Коническая поверхность вращения
Пусть кривая второго порядка состоит из двух пересекающихся в начале координат прямых, расположенных в плоскости Oyz (рис. 254, а), и задана системой уравнений
(9)
Если эту пару пересекающихся прямых вращать вокруг оси Oz, то получим поверхность, которая состоит из двух частей, называемых полостями (или полами), а сама поверхность называется конической поверхностью вращения (рис. 254, б). Иногда эту поверхность в целях краткости называют простo конусом вращения.
Из определения конической поверхности следует, что она является линейчатой поверхностью.
Рис. 254
Чтобы получить уравнение этой конической поверхности, находим:
После почленного сложения уравнений системы и последующего преобразования полученного уравнения приходим к уравнению:
= 0,(9a)
которое называется каноническим уравнением конической поверхности вращения с осью вращения Oz.
Ecли жe вращать ту же пару прямых вокруг оси Оy (которая также является их осью симметрии), то получим вновь коническую поверхность вращения, но её каноническое уравнение имеет другой вид, а именно:
= 0.(9б)
Обратите внимание! Правая часть канонического уравнения конической поверхности равна нулю, а знак «–» в левой части уравнения «указывает» на ось вращения этой поверхности.
е) Цилиндрическая поверхность вращения
Пусть кривая второго порядка состоит из двух параллельных прямых, лежащих в плоскости Oyz (рис. 255, а), и задана системой уравнений
(10)
Если эту пару параллельных прямых вращать вокруг оси
Рис. 255
Oz 
координатная ось Oz является осью симметрии прямых 
и 
на которые распадается кривая второго порядка 
то получим поверхность, которая называется цилиндрической поверхностью вращения (рис. 255, б). Иногда эту поверхность в целях краткости называют просто цилиндром вращения.
Из определения цилиндрической поверхности следует, что она является линейчатой поверхностью.
После почленного сложения уравнений системы 
получаем искомое уравнение этой поверхности
x2 + y2 = a2,(10а)
которое называется каноническим уравнением цилиндрической поверхности вращения с осью вращения Oz.
Рис. 256
Если эту же пару параллельных прямых вращать вокруг оси Оу, то получим поверхность второго порядка, состоящую из двух параллельных плоскостей (рис. 256) (иногда говорят, распавшуюся на две параллельные плоскости). Их уравнение имеет вид
y2 – a2 = 0. (11)
Уравнение (11) нельзя получить из уравнений (10) по правилу, установленному в п. 1 «Дополнений», так как из этих уравнений у не выражается как функция z.
Цилиндрическую поверхность вращения с осью вращения Oz, заданную уравнением (10а), можно получить непрерывным движением прямой, параллельной оси Oz и пересекающей расположенную в плоскости Оху окружность 
Эта окружность называется направляющей цилиндрической поверхности.
Таким же образом можно получить другие цилиндрические поверхности. К ним относятся:
— эллиптический цилиндр, направляющей которого служит эллипс. Если образующие эллиптического цилиндра параллельны оси Oz, то его каноническое уравнение имеет вид:
= 1.(12)
Изображение этого цилиндра совпадает с изображением цилиндра вращения (см. рис. 255, б);
Рис. 257
— параболический цилиндр, направляющей которого служит парабола. Если образующие параболического цилиндра параллельны оси Oz, а парабола расположена в плоскости Оху (рис. 257), то такой цилиндр может быть задан уравнением:
x2 = y;(13)
— гиперболический цилиндр, направляющей которого служит гипербола. Если образующие гиперболического цилиндра параллельны оси Оz, а гипербола расположена в плоскости Оху (рис. 258), то он может быть задан уравнением:
= 1.(14)
Рис. 258
Мы получили только канонические (простейшие) уравнения каждой из рассмотренных выше поверхностей второго порядка. Такие уравнения имеют рассмотренные поверхности вследствие частного, наиболее «удобного», их расположения относительно системы координат Oxyz. Но если, например, сфера радиуса R = 4 имеет своим центром не начало координат, а точку А(2; –3; –1), то эта сфера задаётся уравнением
(х – 2)2 + (у + 3)2 + (z + 1)2 = 16,
которое после раскрытия скобок приводится также к уравнению второго порядка
x2 + y2 + z2 – 4х + 6у + 2z + 2 = 0.
В этом уравнении сферы число членов больше, чем в каноническом её уравнении (5). Аналогично, каждая из рассмотренных выше поверхностей второго порядка — эллипсоид, параболоид, гиперболоиды, цилиндр и конус, будучи расположенной общим образом относительно системы координат Oxyz, может быть задана общим уравнением второго порядка относительно переменных х, у, z. Поэтому вводится такое определение.
Поверхностью второго порядка называется множество всех точек М(x; y; z) пространства, координаты x, y, z которых удовлетворяют уравнению
a11x2 + a22y2 + a33z2 + 2a12xy + 2a13xz + 2a23yz + 2a14x +
+ 2
a24y + 2a34z + a44 = 0.
Это уравнение называется общим уравнением поверхности второго порядка (коэффициенты a11, a22, a33, a12, a13, a23 одновременно не равны нулю). Тaк кaк поверхности второго порядка задаются квадратными уравнениями, то эти поверхности кратко называют квадриками.
3.3.Линии второго порядка как плоские сечения конической поверхности
Рис. 259
Пусть дана коническая поверхность вращения с вершиной в точке S и осью вращения a. Из определения конической поверхности следует, что любая плоскость, проходящая через вершину S и ось а конической поверхности, пересекает эту поверхность по двум её линейным образующим (рис. 259, а), т. е. по кривой второго порядка, распавшейся на две пересекающиеся прямые.
Мы рассмотрим вопрос о пересечении конической поверхности вращения и любой плоскости, не проходящей через вершину этой поверхности. Из определения конической поверхности вращения следует, что любая плоскость, не проходящая через вершину S и перпендикулярная оси вращения a, пересекает эту коническую поверхность по окружности (рис. 259, б).
Далее мы рассмотрим три принципиально различных возможных расположения секущей плоскости α по отношению к конической поверхности вращения.
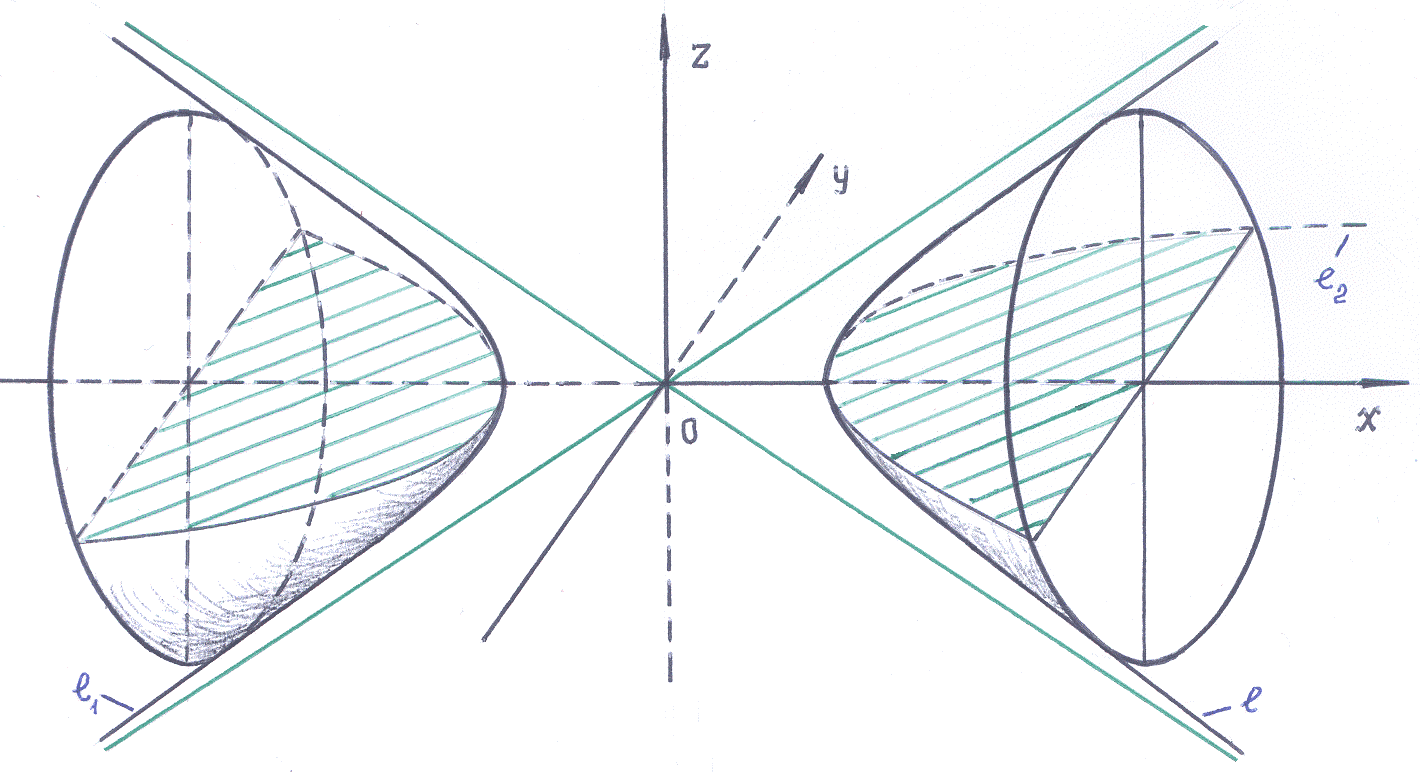
а) Плоскость α пересекает все линейные образующие конической поверхности и не перпендикулярна оси вращения а (рис. 260). Докажем, что полученная при этом в сечении конической поверхности кривая l является эллипсом.
Рис. 260
Проведём через ось а плоскость, перпендикулярную секущей плоскости α; она пересекает поверхность по двум прямолинейным образующим. Будем считать полученные образующие лежащими в плоскости чертежа, а точки их пересечения с плоскостью α обозначим через R и Т.
Впишем в угол, образованный этими образующими, две окружности, касающиеся прямой RT. Центры этих окружностей лежат на оси конической поверхности. Пусть одна из окружностей касается прямой RT в точке F1 и линейных образующих в точках Р и Q, а вторая касается прямой RT в точке F2 и линейных образующих — в точках P′ и Q′. При вращении этих окружностей вокруг оси конической поверхности образуются две сферы (I и II), вписанные в эту коническую поверхность (в одну её полость). Сфера I касается конической поверхности по окружности PQ, а сфера II — по окружности Р′Q′, которые лежат в параллельных между собой и перпендикулярных оси вращения а плоскостях. Для обеих сфер плоскость α является общей касательной плоскостью с точками касания соответственно F1 и F2.
Проведём теперь через любую точку M линии l прямолинейную образующую SM конической поверхности, и точки пересечения этой образующей с окружностями PQ и Р′Q′ обозначим соответственно А и В. Далее соединим отрезками точку М с точками F1 и F2. Тогда:
| MA | = | MF1 | (как отрезки касательных прямых, проведённых из точки М к сфере I);
| МВ | = | MF2 | (как отрезки касательных прямых, проведённых из точки М к сфере II).
Получаем: | MF1 | + | MF2 | = | MA | + | MB | = | AB |.
Так как плоскости окружностей PQ и P′Q′ перпендикулярны оси вращения конической поверхности, то длина отрезка AB постоянна для любой линейной образующей, т. е. не зависит от выбора точки M на кривой l. Это означает, что для любой точки M линии l сумма расстояний | MF1 | и | MF2 | до двух данных точек F1 и F2 есть величина постоянная, откуда, в свою очередь, следует, что кривая l — эллипс, что и требовалось доказать. ▼
б) Рассмотрим теперь случай, когда плоскость 
параллельна двум линейным образующим конической поверхности вращения.
В этом случае плоскость α пересекает обе полости конической поверхности (рис. 261), и в сечении получается линия l, состоящая, по-видимому, из двух ветвей. Интуитивно можно предположить, что этой линией окажется гипербола. Докажем, что это действительно так.
Рис. 261
Как и в предыдущем случае, проведём через ось а плоскость, перпендикулярную секущей плоскости α; она пересекает коническую поверхность по двум прямолинейным образующим. Будем считать полученные образующие лежащими в плоскости чертежа.
Впишем в различные полости конической поверхности две сферы (обозначим их опять I и II) так, чтобы они касались секущей плоскости α в некоторых точках F1 и F2. Пусть Р и Q — точки касания сферы I с прямолинейными образующими, лежащими в плоскости чертежа, а Р′ и Q′ — точки касания сферы II с этими образующими. Тогда сфера I касается конической поверхности по окружности PQ, а сфера II — по окружности Р′Q′, которые лежат в параллельных между собой и перпендикулярных оси вращения а плоскостях.
Проведём теперь через любую точку М линии l прямолинейную образующую SM конической поверхности, и точки пересечения этой образующей с окружностями PQ и P′Q′ обозначим соответственно А и В. Соединив отрезками точку М с точками F1 и F2, имеем:
| МA | = | MF1 | (как отрезки касательных прямых, проведённых из точки М к сфере I);
| MB | = | MF2 | (как отрезки касательных прямых, проведённых из точки М к сфере II).
Получаем:
|| mF2 | – | mF1 || = || МВ | – | МА || = | AB |.
Так как плоскости окружностей РQ и P′Q′ перпендикулярны оси вращения конической поверхности, то длина отрезка AВ, расположенного на образующей конуса, постоянна для любой его образующей, т. е. не зависит от выбора точки М на линии l. Это означает, что для любой точки М линии l модуль разности расстояний | MF2 | и | MF1 | до двух данных точек F1 и F2 есть величина постоянная, следовательно, кривая l — гипербола, что и требовалось доказать. ▼
в) Рассмотрим третий случай, когда секущая плоскость α, параллельна одной из образующих (обозначим её SX) конической поверхности вращения (рис. 262). В этом случае плоскость α перпендикулярна плоскости, проходящей через образующую SX и ось a конуса, а линия l пересечения плоскости α и конической поверхности состоит из одной ветви, простирающейся в бесконечность. Покажем, что эта линия является параболой.
Рис. 262
Впишем в коническую поверхность сферу, касающуюся плоскости α в некоторой точке F. Плоскость β, содержащая окружность ω соприкосновения этой сферы и конической поверхности, перпендикулярна оси a конуса и пересекает плоскость α по прямой KL.
Проведём через любую точку М линии l образующую конической поверхности и обозначим через Р точку её касания со сферой (точка P лежит на окружности ω). Тогда | MF | = | МР | (как отрезки касательных к сфере, проведённых из точки M). Далее проведём плоскость δ через точку М параллельно плоскости β, в которой лежит окружность ω, и обозначим точки пересечения данной образующей SX с плоскостями β и δ соответственно А и B (А = SX ∩ ω). Тогда | АВ | = | MP | (как длины отрезков образующих конической поверхности, заключённых между плоскостями, перпендикулярными к оси этой поверхности). Плоскость, проходящая через образующую SX перпендикулярно плоскости α, пересекает эту плоскость по прямой DE, параллельной АВ и перпендикулярной прямой KL. Причём | DE | = | АВ | (как отрезки параллельных прямых, заключённые между параллельными плоскостями). Eсли теперь провести в плоскости α перпендикуляр МC из точки М на прямую KL, то он будет параллелен и равен DE: | MC | = | DE |. Тогда получаем:
| MC | = | DE | = | AB | = | MP |.
Учитывая, что | MF | = | МР |, приходим к выводу: | MF | = | МС |. Из этого равенства следует, что точка М независимо от её положения на линии l одинаково удалена от точки F и от прямой KL, следовательно, линия l является параболой, что и требовалось доказать. ▼
На рисунке 263 изображены все возможные виды плоских сечений конической поверхности.
Рис. 263
Таким образом, изученные вами в планиметрии кривые второго порядка являются различными плоскими сечениями конической поверхности вращения, поэтому их называют коническими сечениями, а для краткости — просто кониками. При этом окружность, эллипс, гиперболу и параболу называют собственными или невырожденными коническими сечениями (невырожденными кониками). Они обладают многими интересными и красивыми свойствами, о которых вы узнаете в высшей школе.
Наиболее
просто получают поверхность вращением
плоской
кривой относительно некоторой неподвижной
оси.
☺☺
Пример 6–03:
Точнее было бы назвать это не примером,
а экспериментом. На прозрачной тонкой
прямоугольной пластине нарисуем
произвольную линию
.
Закрепим пластину на неподвижной оси
вращения
.
Станем достаточно быстро вращать
пластину при помощи рукоятки вокруг
оси вращения (боковые упоры не позволяют
пластине смещаться вдоль оси
).
Учитывая свойство инерции нервной
системы глаза, ожидаем увидеть
равномерно окрашенную поверхность,
описываемую произвольной линией
.
Замечание:
изготовить предложенный механизм
достаточно просто; если пользоваться
набором пластин с разными линиями
,
то это позволит сформировать устойчивый
образ процесса получения поверхностей
вращения!
Поверхностью
второго порядка называют совокупность
точек
пространства, координаты которых
удовлетворяют уравнению:
. (1)
Уравнение
(1) называют общим
уравнением
поверхности 2-го порядка. Присваивая
коэффициентам уравнения (1):
,
;
произвольные значения, можно получить
(мы в этом убедимся!) всё многообразие
поверхностей 2-го порядка.
Применяя
преобразование координат вращением
относительно общей точки (подробно
показано при рассмотрении темы
«Преобразование координат»), получают
более простое уравнение для поверхностей
2-го порядка:
. (2)
Прежде,
чем приступить к рассмотрению возможных
случаев дальнейшего упрощения уравнения
(2), рассмотрим получение простейших
поверхностей второго порядка.
П
оверхности
вращения:
поверхности, образованные вращением
плоской линии около некоторой оси.
Пусть
линия l
задана в пространстве (x,y,z)
уравнениями: 
(3)
Для
нахождения уравнения поверхности,
получаемой вращением линии
,
вокруг оси
,
берём на поверхности произвольную точку
и проводим через неё плоскость,
перпендикулярную оси
.
Так как плоскость пересекает поверхность
вращения, то линия пересечения плоскости
с поверхностью – окружность с центром
,
расположенным на оси
.
Уравнение этой окружности:
=
=
,
где
=
,
если уравнение плоскости:
=
.
Из вышесказанного
следует достаточно простой приём
получения уравнения поверхности
вращения:
▫ Пусть
задана плоская линия
:
.
Приводим её уравнение одному из видов
записи: 
(4)
▫ Составим
одно из уравнений: 
=
,
=
, (5)
=
.
▫ Учитывая
уравнения (5), получены поверхности
вращения относительно осей
,
,
,
соответственно.
П
оверхности
вращения 2-го порядка образуются вращением
линий 2-го порядка относительно ихосей
симметрии.
Рассмотрим применение выражений (4) и
(5) для всех известных нам кривых 2-го
порядка.
10.
Пусть имеем эллипс
:
Совершим вращение этого эллипса вокруг
оси
:
и сложим уравнения этой системы:
.
Последнее
уравнение легко приводится к виду:
– эллипсоид
вращения,
с осью вращения
.
☺☺
Пример 6–04:
Используя общие выражения и алгоритм
построения поверхностей вращения,
построить уравнение эллипсоида вращения
с осью вращения
.
Р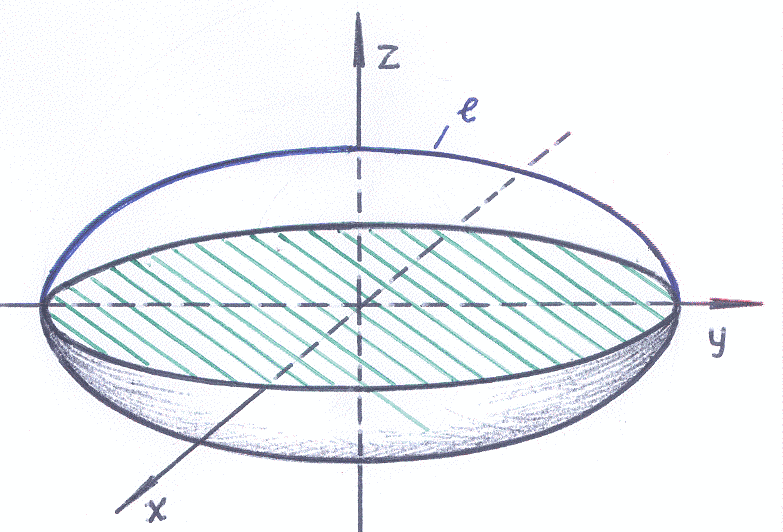
ешение:
20.
Пусть имеем эллипс
:
Совершим вращение этого эллипса вокруг
оси
:
и сложим уравнения этой системы:
.
Последнее
уравнение легко приводится к виду:
– эллипсоид
вращения,
с осью вращения
.
Ответ:
– эллипсоид
вращения,
с осью вращения
..
☻
Замечание:
нетрудно заметить, что вращение эллипса
вокруг оси
приводит к уравнению эллипсоида вращения,
в котором равными являются оси по
переменным
;
при вращении эллипса вокруг оси
равными являются оси по переменным
;
не рассматривая подробно случай вращения
эллипса вокруг оси
,
можем утверждать, что теперь равными
должны быть оси по переменным
!
В отличие
от эллипса, при вращении гиперболы
относительно действительной и мнимой
осей получаются принципиально различные
поверхности. И называются они по-разному:
однополостный гиперболоид и двуполостный
гиперболоид (имеется в виду количество
полостей в получающейся фигуре вращения).
Рассмотрим оба случая.
3
0. Пусть
имеем гиперболу 
:
Эта гипербола на рисунке выделена
красным цветом: расположена в плоскости
.
Совершим вращение линии 
вокруг оси
:
и сложим
уравнения этой системы:
.
Последнее
уравнение легко приводится к виду:
– однополостный
гиперболоид вращения
с осью вращения
.
На
рисунке выделена ещё одна линия
,
которая отличается только тем, что
теперь гипербола расположена в плоскости
.
В качестве
упражнения построим ещё одну поверхность
вращения.
☺☺
Пример 6–05:
Используя общие выражения и алгоритм
построения поверхностей вращения,
построить уравнение поверхности вращения
линии
с осью вращения
.
Решение:
1). Пусть
имеем гиперболу
:
Совершим вращение линии
вокруг оси
:
и сложим уравнения этой системы:
.
2).
Последнее уравнение легко приводится
к виду:
– однополостный
гиперболоид вращения
с осью вращения
.
Ответ:
– однополостный
гиперболоид вращения
с осью вращения
.
☻
Замечание: однотипность
построения поверхностей вращения
подсказывает: не требуется специально
запоминать конечные уравнения этих
поверхностей, следует помнить только
принцип их построения!
40. Пусть
имеем гиперболу 
:
Эта гипербола расположена в плоскости
.
Совершим вращение линии 
вокруг действительной оси
:
и сложим уравнения этой системы:
.
Последнее уравнение легко приводится
к виду:
– двуполостный
гиперболоид вращения
с осью вращения
.
На
рисунке выделена ещё одна линия
,
которая отличается только тем, что
теперь гипербола расположена в плоскости
.
В качестве
упражнения построим ещё одну поверхность
вращения
☺☺
Пример 6–06:
Используя общие выражения и алгоритм
построения поверхностей вращения,
построить уравнение поверхности вращения
линии
с осью вращения
.
Решение:
1). Пусть
имеем гиперболу
:
Совершим вращение линии
вокруг оси
:
и сложим уравнения этой системы:
.
2).
Последнее уравнение легко приводится
к виду:
– двуполостный
гиперболоид вращения
с осью вращения
.
Ответ:
– двуполостный
гиперболоид вращения
с осью вращения
.
☻
Рассмотрим
применение вращения кривой 2-го порядка
– параболы относительно осей
,
,
,
соответственно.
5
0.
Пусть имеем параболу
:
Эта парабола расположена в плоскости
.
Совершим вращение линии 
вокруг оси
:
и сложим уравнения этой системы:
– это уравнение параболоида
вращения
с осью вращения
.
Если
вращать параболу
:
расположенную в плоскости
вокруг той же оси
,
то получим параболоид вращения
,
ничем не отличающийся от параболоида,
рассмотренного выше.
А что
если вращать параболу
(или 
)
вокруг оси
(или
)?
Получится ли поверхность вращения 2-го
порядка?
Решим возникший
вопрос в качестве отдельного упражнения.
☺☺
Пример 6–07:
Пусть парабола 
:
вращается вокруг оси
.
Используя общие выражения и алгоритм
построения поверхностей вращения, найти
уравнение поверхности вращения для
этого случая.
Решение:
1). По
условию линия 
:
вращается вокруг оси
.
Отметим: ось
не является осью симметрии линии 
.
2). Так
как общий алгоритм построения поверхностей
вращения предполагает только вращение
плоских линий относительно осей
координат, то совершим вращение линии
:
вокруг оси
:
и сложим уравнения этой системы:
.
3).
Последнее уравнение легко приводится
к виду:
– алгебраическая
поверхность вращения:
представлена многочленом 4-й степени.
Ответ:
– алгебраическая
поверхность вращения.
☻
При
изучении кривых 2-го порядка были выделены
частные случаи:
– пара пересекающихся прямых, и
– пара параллельных прямых.
Оба
выделенных случая с прямыми линиями
можно было бы объединить: вокруг некоторой
оси вращаем произвольную
прямую линию. Требуется найти уравнение
образующейся при этом поверхности
вращения. Мы ограничимся
более простой задачей:
мы станем вращать прямую линию 
только тремя способами:
▫ вокруг
оси, пересекающей прямую линию
под некоторым острым углом;
▫ вокруг
оси, параллельной линии
;
▫ вокруг
оси, перпендикулярной линии
.
60.
Пусть задана линия, состоящая из двух
пересекающихся прямых:
Для того, чтобы детально наблюдать
процесс вращения линии представим эту
пару как:
Нетрудно заметить, что в этом случае
ось координат
является биссектрисой угла этих прямых!
Запишем отдельно эти прямые 
:
и 
:
С
овершим
вращение линии
вокруг оси
:
и сложим уравнения этой системы:
– это уравнение конуса
вращения
с осью вращения
.
Нетрудно
заметить, что вращение линии 
определяется
той же системой:
Это значит, что алгоритм вращения каждый
раз использует только одну линию. В
данном случае результаты совпали, так
как возведение в квадрат безразлично
к знаку числа!
Замечание: на
рисунке представлена только верхняя
часть конической поверхности, так как
получение уравнения поверхности
вращения:
сохраняет осевую симметрию (относительно
)
и симметрию относительно плоскости
;
представленная половина конуса в
наглядности не проигрывает!
Ниже
приводится пример, в котором определены
более общие начальные условия: точка,
определяющая вершину конуса, смещена,
но ось конуса остаётся параллельной
одной из осей координат. В этом случае
необходимо вспомнить простейшее
преобразование координат: параллельный
перенос.
☺☺
Пример 6–08:
Составить уравнение конуса с вершиной
в точке (0,0,
),
направляющая которого дана уравнениями
,
=0.
Решение:
1).
Образующая конуса есть вращающаяся
прямая, имеющая одну точку (0,0,
)
неподвижной, а вторую точку принадлежащей
эллипсу, расположенному в плоскости
.
Выделим одну из образующих точкой
(
,0,0).
Тогда уравнение вращающейся вокруг оси
линии можем записать в виде
:
=
.
2).
Применим преобразование координат:
,
,
.
Этим преобразованием задача преобразована
к виду, уже рассмотренному выше: вращается
линия:
построить поверхность вращения.
3). Легко
получаем уравнение:
– это уравнение конуса
вращения
с осью вращения
и вершиной в точке (0,0,
).
Ответ:
– конуса
вращения
с осью вращения
и вершиной, расположенной в точке
(0,0,
).
☻
П
усть
теперь имеем прямую, параллельную оси
вращения. Необходимо найти уравнение
поверхности вращения.
70.
Пусть задана линия, состоящая из двух
параллельных прямых:
Для того, чтобы детально наблюдать
процесс вращения линии представим эту
пару как:
Нетрудно заметить, что в этом случае
вращаемые прямые располагаются
симметрично относительно оси вращения
!
Запишем отдельно эти прямые 
:
и 
:
Совершим
вращение линии 
вокруг оси
:
и сложим уравнения этой системы:
– это уравнение цилиндра
вращения
с осью вращения
.
Нетрудно
заметить, что вращение линии 
определяется
той же системой:
Это значит, что алгоритм вращения каждый
раз использует только одну линию. В
данном случае результаты совпали, так
как возведение в квадрат безразлично
к знаку числа!
☺☺
Пример 6–09:
Пусть задана линия, состоящая из двух
параллельных прямых 
:
Вращением 
вокруг оси
найти уравнение поверхности вращения.
Решение:
1). По
условию линия 
распадается на две параллельные прямые:
Вращение осуществляется вокруг оси
.
2).
Вращением любой из двух прямых линий
получаем:
Складывая уравнения, получаем уравнение
поверхности вращения:
– это уравнение цилиндра
вращения
с осью вращения
.
Ответ:
– уравнение цилиндра
вращения
с осью вращения
.
☻
Пусть
теперь имеем прямую, перпендикулярную
оси вращения. Необходимо найти уравнение
поверхности вращения.
8
0.
Пусть задана линия, состоящая из двух
параллельных прямых:
Представим эту пару как:
Запишем отдельно эти прямые 
:
и 
:
В этом случае
получить поверхность вращения, применяя
алгоритм вращения, не удаётся.
Исходя
из геометрических соображений, нетрудно
записать уравнения двух параллельных
плоскостей:
и
.
Замечание: применение
общего алгоритма получения поверхности
вращения в рассматриваемом случае не
удаётся из-за того, что не может быть
установлена зависимость между переменными
и
.
Вывод: 1). Рассмотрен
класс поверхностей, уравнения которых
можно получить, применяя общий алгоритм
действий – это поверхности вращения.
2).
Получаемые вращением плоской кривой
уравнения поверхностей имеют отличительный
признак: все они имеют из трёх параметров
два равных. Такие уравнения не относят
к каноническим уравнениям.
3).
Большинство поверхностей вращения 2-го
порядка получаются вращением кривых
2-го порядка. Вращение прямой линии
относительно оси, составляющей с этой
линией некоторый острый угол (включая
ноль), тоже приводит к поверхности 2-го
порядка.
Соседние файлы в папке ЛА и АГ пособие
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #