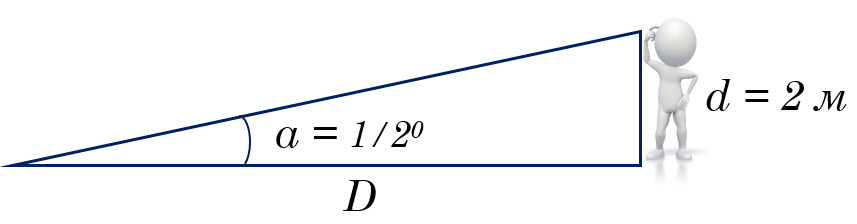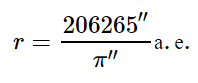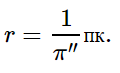Random converter
- Калькуляторы
- Астрономия
Калькулятор расстояния и годичного параллакса
Калькулятор определяет расстояние до недалекой звезды в световых годах и парсеках, если известен годичный параллакс этой звезды в угловых секундах. Можно также определить параллакс, если известно расстояние.
Пример: рассчитать расстояние в световых годах до самой яркой звезды звездного неба северного полушария Арктура (α Волопаса) в созвездии Волопаса, если известно что ее параллакс равен 88.83 угловым миллисекундам.
Параллакс
p
Расстояние
D
Поделиться ссылкой на этот калькулятор, включая входные параметры
Определение параллакса и формула для расчета расстояния
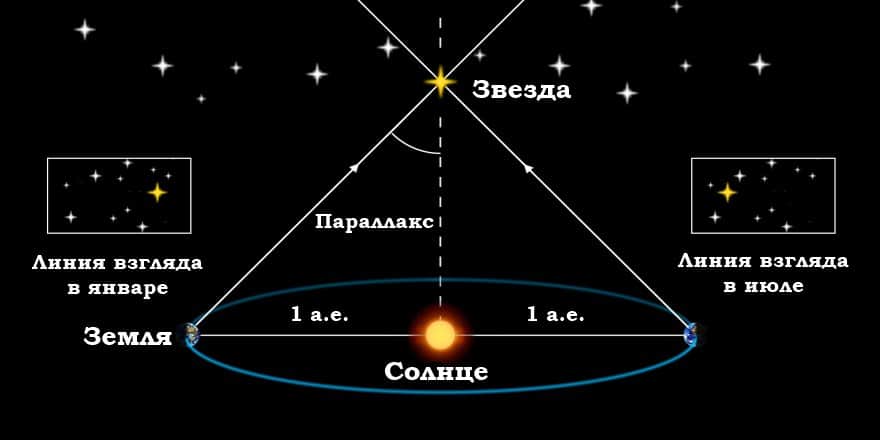
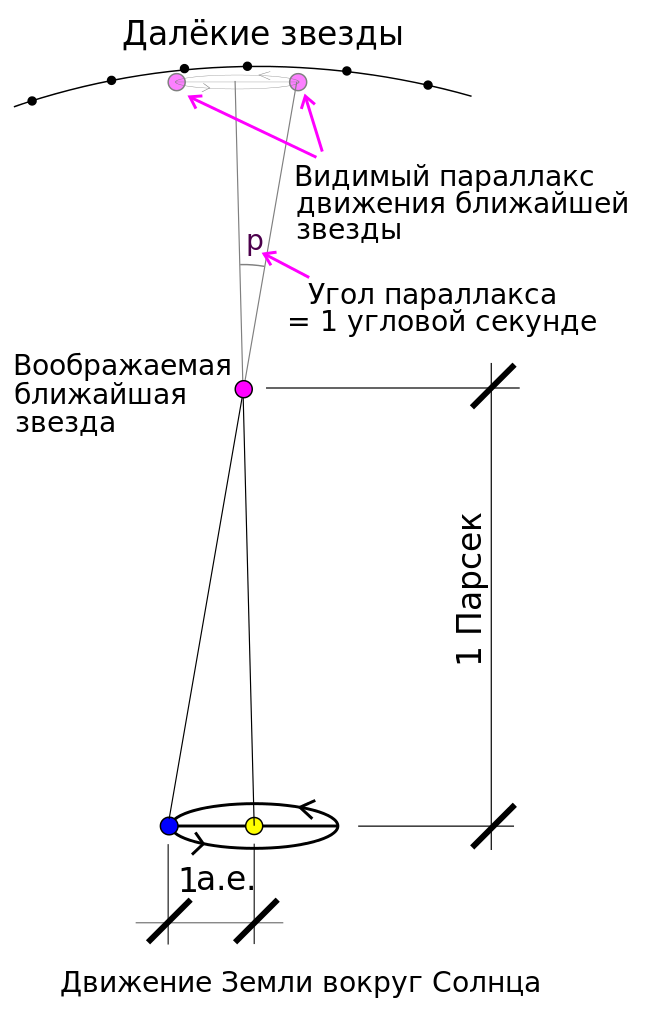
Параллакс — это изменение видимого кажущегося положения объекта, наблюдаемого с разных точек и измеренное как угол (или половинный угол) между направлениями от наблюдателя на объект. Годичный звездный параллакс — это изменение положения звезды, наблюдаемой с двух находящихся на большом расстоянии друг от друга точек. Эти две точки наблюдения расположены на земной орбите, как показано ниже. Параллакс небесного тела можно использовать для нахождения расстояния до него по формуле:
Здесь D — расстояние до небесного тела, измеренное в парсеках, и p — наблюдаемый годичный параллакс, измеренный в дуговых секундах. Эта формула и используется для расчетов в нашем калькуляторе. Парсек определяется как расстояние до объекта, годичный звездный параллакс которого равен 1 дуговой секунде. Иными словами, парсек — это расстояние, с которого диск размером в 1 а.е. будет иметь угловой размер в 1 угловую секунду.
Годичный параллакс звезды (чертеж не в масштабе); 1 — астрономическая единица (а.е.), то есть расстояние от Земли до Солнца; D — расстояние от центра земной орбиты до звезды S; p — параллакс, измеренный в угловых секундах («)
Подробнее о длине и расстоянии: измерение расстояний в космосе
Общие сведения
Космос огромен — поэтому космические расстояния измеряются не так, как это делается на Земле. В статье о длине и расстояниях мы говорили главным образом об измерении относительно небольших расстояний, которые не трудно себе представить. Однако расстояния в космосе представить себе очень трудно из-за их огромной величины, а привычные метры и километры едва ли годятся для использования в космосе. Для измерения расстояний между планетами и галактиками вряд ли можно использовать измерительные приборы типа рулетки или линейки. Спутниковая навигация в космосе тоже не работает. Поэтому для космоса придется ввести не только новые единицы измерения, но и новые методы измерения этих расстояний.
Измерения с помощью радиолокации
Расположенная на Земле радиолокационная станция (РЛС) посылает СВЧ-излучение в сторону астрономического объекта, расстояние до которого нужно вычислить. Затем измеряется время, которое необходимо, чтобы сигнал достиг объекта и вернулся назад, к РЛС. Зная это время и скорость света в вакууме, можно определить расстояние, умножая скорость на время.
Использовать РЛС для этих измерений удобно не только для определения расстояния до нужного астрономического объекта, но и для оценки скорости изменения этого расстояния (ведь объекты во Вселенной движутся друг относительно друга!). Это, в свою очередь, полезно при слежении за перемещениями объектов в космосе, например, для оценки возможности столкновения астероида с Землей.
Этот метод ограничен астрономическими объектами, которые находятся на небольших расстояниях от Земли. Можно сказать, что он пригоден для объектов, находящихся в пределах Солнечной системы. Это связано с тем, что радиосигнал ослабляется и рассеивается на больших расстояниях. Кроме того, чем больше расстояние, тем больше должен быть объект для того, чтобы его могла «увидеть» радиолокационная станция.
Годичный звездный параллакс
В статье о длине и расстоянии мы уже обсуждали годичный звездный параллакс. Здесь мы кратко рассмотрим это явление, потому что именно параллакс используется для измерения расстояний в космосе. Параллакс — геометрические явление, используемое для определения расстояний. Он хорошо выражен, если наблюдать объект с разных точек зрения относительно удаленного фона. Познать суть параллакса достаточно легко: вытяните перед собой палец или карандаш и закройте один глаз. Отметьте насколько далеко этот палец от другого объекта (скажем, от дерева, если вы на улице, или от шкафа, если вы находитесь в помещении). Теперь закройте этот глаз и откройте другой. Заметили, что палец или карандаш переместился относительно удаленного объекта? Это перемещение и является параллаксом. Если проделать аналогичный эксперимент, удерживая палец ближе к глазам, можно заметить, что расстояние, на которое перемещается палец или карандаш относительно удаленного объекта, стало больше. Чем ближе палец к глазам, тем больше он сдвигается относительно удаленного объекта при рассматривании пальца обоими глазами. Понятно, что это явление можно использовать для измерения расстояния до объекта, в данном случае — пальца.
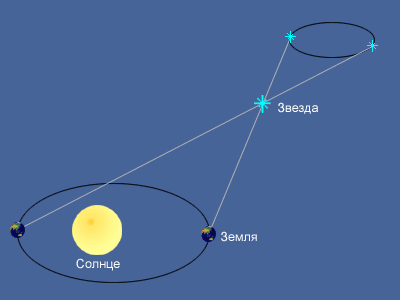
На этом рисунке два положения Земли обозначены голубыми кружками, а Солнце — оранжевое. А — реальное положение звезды, расстояние до которой необходимо измерить. А2 и А3 — кажущиеся положения этой звезды с двух точек наблюдения относительно удаленной белой звезды DS. Р — параллактический угол. Измеряемое расстояние между Солнцем и звездой, обозначенное оранжевой линией AS, равно одному парсеку, если угол Р равен одной дуговой секунде.
Более подробное математическое объяснение измерения расстояний с помощью параллакса приводится в статье о длине и расстоянии. В общем случае, можно сказать, что расстояния следует измерять, когда Земля находится в двух противоположных точках ее орбиты вокруг Солнца (с интервалом в шесть месяцев, так как Земля делает один оборот вокруг Солнца за один год). Мы используем известное расстояние от Земли до Солнца (точно измеренное и называемое астрономической единицей) и измерим угол, образованный линией, соединяющей Землю в точке первого измерения, звезду, расстояние до которой измеряется, и точкой, в которой находится Земля во время второго измерения. Фактически, нам нужно знать только половину этого угла, которая называется параллактическим углом и обозначена на рисунке буквой P. Таким образом, имеется достаточно информации, чтобы рассчитать расстояние от Земли до звезды с помощью тригонометрических уравнений.
С помощью описанного метода можно измерить расстояние в различных единицах длины, но астрономы предпочитают парсек. Один парсек — это расстояние от Солнца до рассматриваемой звезды, если параллактический угол равен 1 дуговой секунде. Другой единицей длины является световой год (1 парсек = 3,26 светового года), однако эту единицу чаще используют журналисты. Астрономы предпочитают парсеки.
Четыре звезды имеют один и тот же размер, но расположены на разных расстояниях от нас. Звезда в положении 1 находится ближе всего, а звезда в положении 4 на максимальном удалении от нас. В результате мы видим ближние к нам звезды как более яркие, а удаленные — как менее яркие. Если известная их реальная яркость, можно сравнить ее с их кажущейся яркостью и, таким образом, узнать расстояние до них
Как и при радиолокационных измерениях, этот метод ограничен расстоянием, на которое удалена звезда. Если она слишком далеко (более 500 парсеков), то угол, который нужно измерить, слишком мал и измерить его практически невозможно. Поэтому для больших расстояний данный метод не работает.
Цефеиды
Для измерения расстояний в космосе можно использовать определенные типы звезд, называемых Цефеидами. Цефеида — пульсирующая звезда с точной зависимостью светимости (яркости) от периода пульсации. Чем больше этот период, тем выше яркость Цефеид. Эта корреляция между периодом пульсации я светимостью хорошо известна и все Цефеиды ведут себя одинаково. Поэтому, если известен период пульсации, который несложно наблюдать, можно измерить светимость звезды. Мы знаем, что чем дальше звезда, тем меньше ее яркость. Таким образом, если сравнить реальную яркость с кажущейся, можно определить расстояние до звезды.
Пульсация цефеид обусловлена их сжатием и расширением. При этом их яркость изменяется, и для определения периода нужно измерить время между точками с максимальной яркостью. Ядро звезды не изменяет размеры, однако их внешние газовые слои расширяются и сжимаются вследствие флуктуаций давления газа в этих слоях. Сжатие и расширение происходит за счет двух сил: гравитационного притяжения, которое приводит к сближению молекул газа в направлении центра звезды, и давления газа, которое приводит к расширению внешнего слоя.
Схематическое изображение пульсирующей Цефеиды с периодом в два дня. Пики светимости 1 декабря 2010 г., когда звезда начинает постепенно терять яркость. 2 декабря яркость минимальная. Затем звезда снова достигает максимальной светимости 3 декабря и уменьшает светимость 4 декабря и так далее
Когда звезда находится в сжатом состоянии, ее фотоны имеют высокую энергию и в результате давление повышается, что приводит к расширению внешней оболочки звезды. Когда это давление падает и становится меньше гравитационных сил, сжимающих оболочку, звезда сжимается. Затем процесс повторяется.
Цефеиды можно использовать для измерения расстояний до 40 миллионов парсеков, то есть намного больших, чем позволяет метод параллакса. Недостаток метода — цефеиды не так уж часто встречаются.
Сверхновая типа Ia
Еще одним стандартным измерителем расстояния являются сверхновые типа Ia. Идея аналогичная использованию Цефеид: при известной реальной светимости сверхновой в момент взрыва, когда яркость максимальна, можно сравнить ее с видимой яркостью звезды и, таким образом, определить насколько далеко она от нас. Именно эта категория сверхновых интересует нас в связи с тем, что они наиболее хорошо изучены, а их поведение предсказуемо, поэтому максимальная светимость во время взрыва хорошо известна. Эти взрывы происходит с двумя астрономическими объектами — с белыми карликами и еще одним белым карликом или со звездой-гигантом. Белый карлик представляет собой звезду очень высокой плотности в конце ее жизненного цикла, когда эта звезда «всасывает» материю находящихся рядом звезд (в нашем случае — второй звезды) до тех пор, пока не взорвется. Эти взрывы сверхновых позволяет измерять расстояния до галактик, в которых они находятся.
Другие методы измерения расстояний
Имеется еще несколько методов измерения расстояний в космосе. Один из них основан на предположении, что вселенная расширяется с известной скоростью. Если известна скорость, с которой галактики удаляются от нашей галактики, то с помощью закона Хаббла можно рассчитать насколько далеко они от нас. Закон Хаббла гласит, что расстояние до галактики равно скорости галактики, деленной на постоянную Хаббла, которая является известной константой. Скорость галактики можно определить, изучая спектр галактики, а затем, учитывая эффект Доплера, можно определить расстояние. Эффект Доплера, более известный в астрономии как смещение Доплера — это изменение частоты электромагнитного излучения (в нашем случае — света), излучаемого объектом, который движется относительно наблюдателя. При движении в сторону от наблюдателя этот спектр сдвигается в сторону низких частот, то есть в красную сторону, причем степень сдвига зависит от скорости удаления галактики. По смещению можно рассчитать скорость, а затем вычислить расстояние.
Примеры расчета расстояния до некоторых звезд и их звездного параллакса
Параллакс в дуговых миллисекундах и расстояние в световых годах
Канопус (α Киля)
Ригель Кентаурус (α Центавра A)
Сириус (α Большого Пса)
Вега (α Лиры)
Капелла (α Возничего)
Ригель (β Ориона)
Альтаир (α Орла)
Альдебаран (α Тельца)
Антарес (α Скорпиона)
Арктур (α Волопаса)
Unit Converter articles were edited and illustrated by Анатолий Золотков
Астрономический словарик: параллакс, планета
Время на прочтение
7 мин
Количество просмотров 4.6K
Параллакс
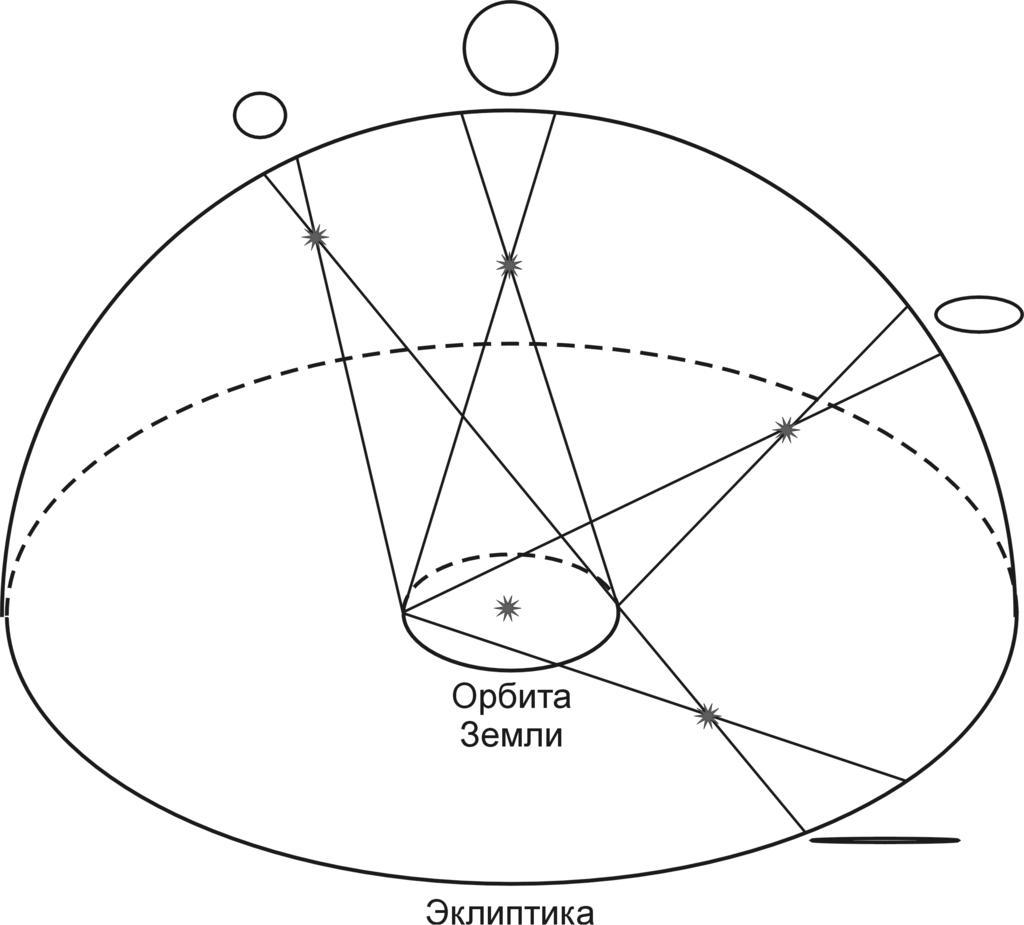
Параллактические эллипсы звёзд при различных расстояниях от плоскости эклиптики
Параллакс — это смещение видимого положения объекта, рассматриваемого с двух разных точек. Чем дальше объект от наблюдателя, тем меньше его видимое положение меняется при перемещении наблюдателя. На основе расстояния между точками наблюдения и углом смещения видимого положения объекта можно рассчитать расстояние до него.
В астрономии под параллаксом чаще всего понимается половина угла смещения видимого направления на звезду, измеряемого в моменты, когда Земля, двигающаяся вокруг Солнца по своей орбите, находится на её противоположных сторонах. Такое измерение расстояния иногда называют «годичным параллаксом». Это первая ступенька в «космической шкале расстояний» — метода измерения расстояний, похожего на лестницу, в которой каждая следующая «ступенька» опирается на предыдущую.
Расстояние до объекта, годичный тригонометрический параллакс которого равен одной угловой секунде, называют «парсеком» (сложив слова «параллакс» и «секунда»). Это расстояние равно 3,26 светового года. В 2015 году Международный астрономический союз определил парсек как расстояние, равное 648 000/π астрономических единиц.
Принцип параллакса дал человеку первый способ измерения расстояния от планеты Земля до звёзд. Впервые звёздный параллакс в 1838 году измерил Фридрих Вильгельм Бессель, немецкий математик и астроном, ученик Карла Фридриха Гаусса. Он выбрал звезду 61 Лебедя, и использовал для этой цели гелиометр – прибор для измерения небольших углов на небесной сфере, созданный в XVIII веке.
Точность измерения звёздного параллакса зависит от точности, с которой мы знаем расстояние от Земли до Солнца. В наши дни это расстояние мы измеряем при помощи сигналов радара, отражённых от других планет Солнечной системы.
Трудности точных измерений расстояний до звёзд при помощи параллакса связаны с его малыми значениями. К примеру, у ближайшей к Солнцу (и, следовательно, имеющей наибольший параллакс) звезды Проксима Центавра его величина составляет 0,7687 ± 0,0003 угловые секунды. Под таким углом объект диаметром 2 см будет виден с расстояния в 5,3 км. Именно по причине того, что такие маленькие параллаксы очень трудно измерить, философы долгое время отвергали теорию гелиоцентризма. То, что параллакс может быть маленьким из-за гигантского расстояния до звёзд, тогда казалось маловероятным.
Запущенный в 1989 году космический аппарат Hipparcos (High Precision Parallax Collecting Satellite — «высокоточный спутник для сбора параллаксов») был предназначен специально для измерения параллаксов различных звёзд и уточнения космических расстояний. Точность измерений для основного эксперимента (более 100 тыс. звёзд) составила 1 миллисекунду дуги. Успех программы позволил увеличить точность астрометрических измерений на порядок и тем самым совершить весьма значительный прорыв в астрономии. Но даже он смог измерить параллакс для звёзд, находящихся не далее 1600 световых лет от нас – что составляет чуть более 1% диаметра Млечного Пути.
Запущенный в 2013 году Европейским космическим агентством аппарат «Гайя» мог измерять параллакс с точностью до 10 угловых микросекунд, то есть определять расстояния до объектов, находящихся в нескольких десятках тысяч световых лет от нас.
Планета
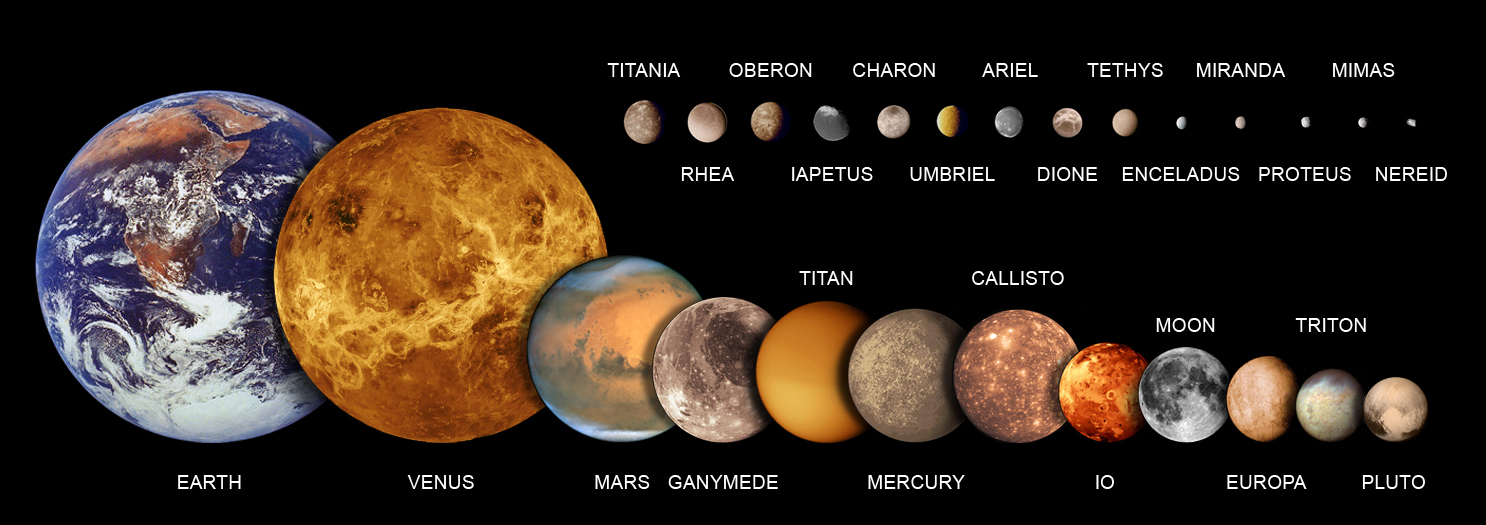
Объекты Солнечной системы с массой, сравнимой с планетной (в масштабе)
В древности люди, обращая взгляд к ночному небу, замечали, что большая часть картины, рисуемой яркими точками звёзд, не меняется по сути, а лишь периодически движется по небу на манер большого неделимого холста. Но кроме Солнца и Луны они видели ещё пять ярких объектов, движения которых не согласовывались с перемещением звёздного неба. Эти объекты двигались хоть и периодически, но по сложным траекториям. Их так и назвали – πλανήτης, «планеты», что означало «странники». Разные народы ассоциировали их с богами из своих пантеонов. До нашего времени сохранились древнеримские названия планет – Меркурий, Венера, Марс, Юпитер и Сатурн – получившие свои имена в честь римских богов.
Однако первой цивилизацией, у которой была документально подтверждённая теория планет, была Вавилонская, возникшая ещё 4 тысячи лет назад. Самый древний из дошедших до нас астрономических текстов, касающихся планет – это «таблички наблюдения за Венерой», датируемые приблизительно 1640 годом до н.э. времён правления вавилонского царя Амми-цадука.
Существуют две клинописные таблички под общим названием MUL.APIN от VII века до н.э., где описываются движение Солнца, Луны и планет в течение года. В Вавилоне зародилась не только астрономия, но и астрология – попытки описать происходящее на Земле и предсказывать события в соответствии с поведением небесных тел, несовместимые с наукой. Работы вавилонских астрологов заложили фундамент как для современной астрономии, так и для астрологии.
Остальные планеты Солнечной системы, известные на сегодня (Уран и Нептун) были открыты уже после изобретения телескопа, в XVIII веке. Тогда же определение планеты поменялось – вместо объектов, движущихся по небу относительно неподвижных звёзд, планетами стали называть небесные тела, вращающиеся вокруг звезды. Таким образом Землю причислили к планетам, а Солнце из их списка исключили.
Когда оказалось, что не только у Земли есть компаньон (Луна) – астрономы разглядели четыре спутника у Юпитера и пять у Сатурна – эти мелкие небесные тела стали называть «вторичными планетами» или «планетами-спутниками», а потом просто сократили до «спутников».
В начале XIX века были открыты новые «планеты» — Церера, Паллада, Юнона и Веста. Но быстро стало понятно, что они кардинально отличаются от обычных планет. Они находятся в одном участке космоса, между Марсом и Юпитером, их орбиты частично пересекаются, да и размера они небольшого. Английский астроном Уильям Гершель, открывший до этого Уран, назвал эти небольшие планеты «астероидами», что по-гречески означает «звездоподобные» — поскольку тогда даже при разглядывании в телескоп они были похожи на звёзды. Но когда подобные небольшие небесные тела начали находить регулярно, астероиды окончательно отделили в классификации от обычных планет.
Ещё одну планету, Нептун, открыли в конце XIX века.
Очередные сложности классификации подстерегали учёных в начале XX века, когда был открыт Плутон. Сначала астрономам показалось, что он превышает по размерам Землю, поэтому он мгновенно был возведён в ранг планет. Однако затем оказалось, что это далеко не так, а масса Плутона вообще составляет 0,2% от земной. Поскольку он всё равно значительно превышал по массе известные астероиды, а транснептуновые объекты ещё не были открыты, свой статус «планеты» он потерял позже.
После работ Койпера и исследования Солнечной системы при помощи космических зондов астероиды постепенно перестали считаться «малыми планетами», а крупные спутники планет, наоборот, возвели в этот ранг.
После того, как в 1990-х астрономы начали открывать экзопланеты – планеты, находящиеся за пределами Солнечной системы, и вращающиеся вокруг других звёзд – встал другой вопрос: какой максимальный размер может иметь небесное тело, чтобы считаться планетой? У других звёзд начали находить планеты, достаточно гигантские для того, чтобы приблизиться по размеру к коричневым карликам – а последние уже считаются звёздами, поскольку теоретически в них может идти синтез дейтерия.
В начале XXI века шли активные дебаты по поводу того, какие небесные тела можно считать планетами. Например, можно ли считать планетой тело, существующее в поясе астероидов, или тело, достаточно большое для того, чтобы внутри него шёл синтез дейтерия. Кроме того, некоторые небесные тела могут формироваться путём гравитационного сжатия газопылевого облака (вместо появления в протопланетном диске, согласно общепринятой гипотезе), но при этом не достигать размеров достаточных для старта ядерного синтеза в ядре – поэтому шли дискуссии, нужно ли учитывать способ формирования небесного тела при его классификации.
Также поднимался вопрос об исключении Плутона из состава планет, поскольку в том же регионе Солнечной системы нашлось уже достаточно много объектов, приближавшихся к нему по размеру. Кроме того, найденная в 2005 году карликовая планета Эрида была на 27% массивнее Плутона – и если он считался планетой, тогда и её стоило тоже записать в планеты.
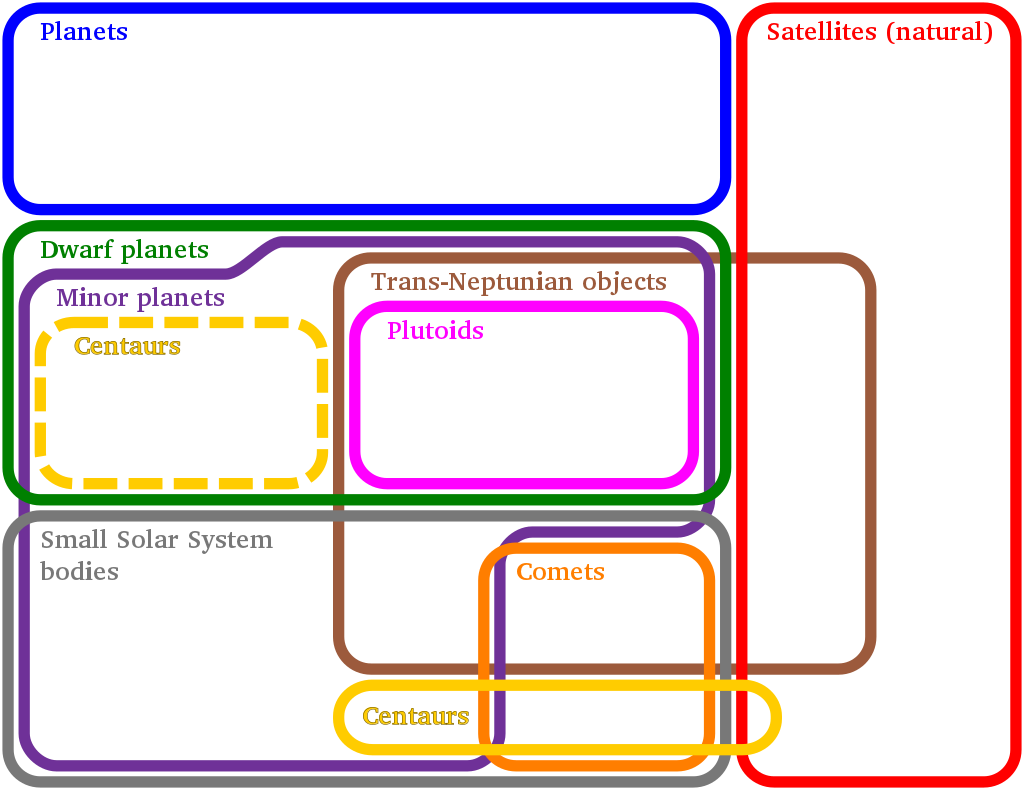
Диаграмма Эйлера, описывающая типы объектов в Солнечной системе
В результате в 2006 году на XXVI Ассамблее Международного астрономического союза было принято новое определение планеты. Теперь официально планетой Солнечной системы называется небесное тело, удовлетворяющее всем следующим условиям:
- обращающееся по орбите вокруг Солнца (то есть не являющееся спутником другого тела);
- обладающее достаточной гравитацией, чтобы иметь форму, близкую к шару;
- вблизи орбиты которого имеется «пространство, свободное от других тел» — то есть, там нет тел, не являющихся её спутниками (иными словами, планета «очищает» свою орбиту от других тел).
Однако в разных дисциплинах к определению «планета» подходят по-разному. Например, в планетарной геологии (изучающей геологию разных небесных тел) планетой считают объект массой меньше звёздной, в котором никогда не шли реакции ядерного синтеза, и гравитация которого оказалась достаточной для придания ему формы шара в результате гидростатического равновесия. Параметры орбиты этого тела в учёт не берутся. Исходя из этого определения, такие тела, как Плутон и Церера, можно считать планетами.
Также под официальное определение не попадают экзопланеты, вращающиеся вокруг других звёзд. Пока общепринятого определения экзопланеты не существует.
Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.
Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.
Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).
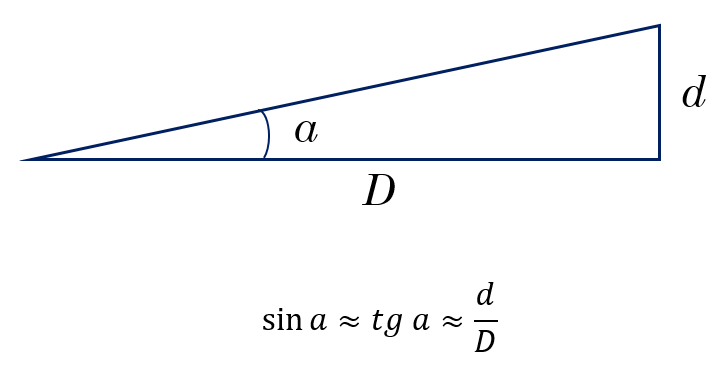
Уравнение малых углов
Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере.
Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a, выраженному в секундах дуги. Обозначим диаметр объекта как d, а расстояние до него как D. Тогда уравнение малого угла
a / 206 265 = d / D
Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3°, который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr, Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга.
Вот пример использования уравнения малого угла. Предположим, что ваш друг ростом в 2 метра стоит через поле от вас, где он виден под углом ½°, или 1800″. Как он далеко от вас? Мы хотим найти расстояние D, выразим эту величину из уранения:
D = 206 265 d / a
Используя метрические единицы, найдем
D = (2.1 x 105 x 2) / (1.8 x 103) = 2.3 х 102 метра = 230 метров
Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.
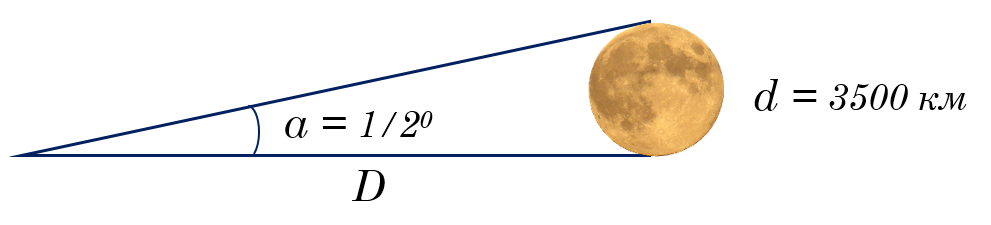
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½°, или 1800″.
Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 106 метров. Уравнение будет гласить:
D = (2.1 × 105 × 3.5 × 106) / (1.8 × 103) ≈ 4 х 108 метров ≈ 4 x 105 километров.
Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!
Методы определения расстояний до звезд
Годичный параллакс
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π).
Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.
Если CT = a есть средний радиус земной орбиты, SC = r — расстояние до звезды S от Солнца C, а угол π — годичный параллакс звезды, то
Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′, то расстояние до звезды можно определить из соотношения
При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины — парсек (пк), название которой происходит от слов «параллакс» и «секунда».
Парсек — это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.
1 пк = 206 265 а. е. = 3,086 · 1013 км.
Таким образом, расстояние до звезд в парсеках будет определяться выражением
В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 кпк = 103 пк) и мегапарсеках (1 Мпк = 106 пк), а также в световых годах (1 св. г. = 9,46 · 1012 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г.).
Световой год — расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.
Источник
Фотометрический метод определения расстояний
Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m — видимая, M — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний rф(пк):
Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.
Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5m. Эта погрешность соответствует относительной погрешности 30%.
Цефеиды (стандартные свечи)
Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5m. Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).

- Информация о материале
-
Просмотров: 15650
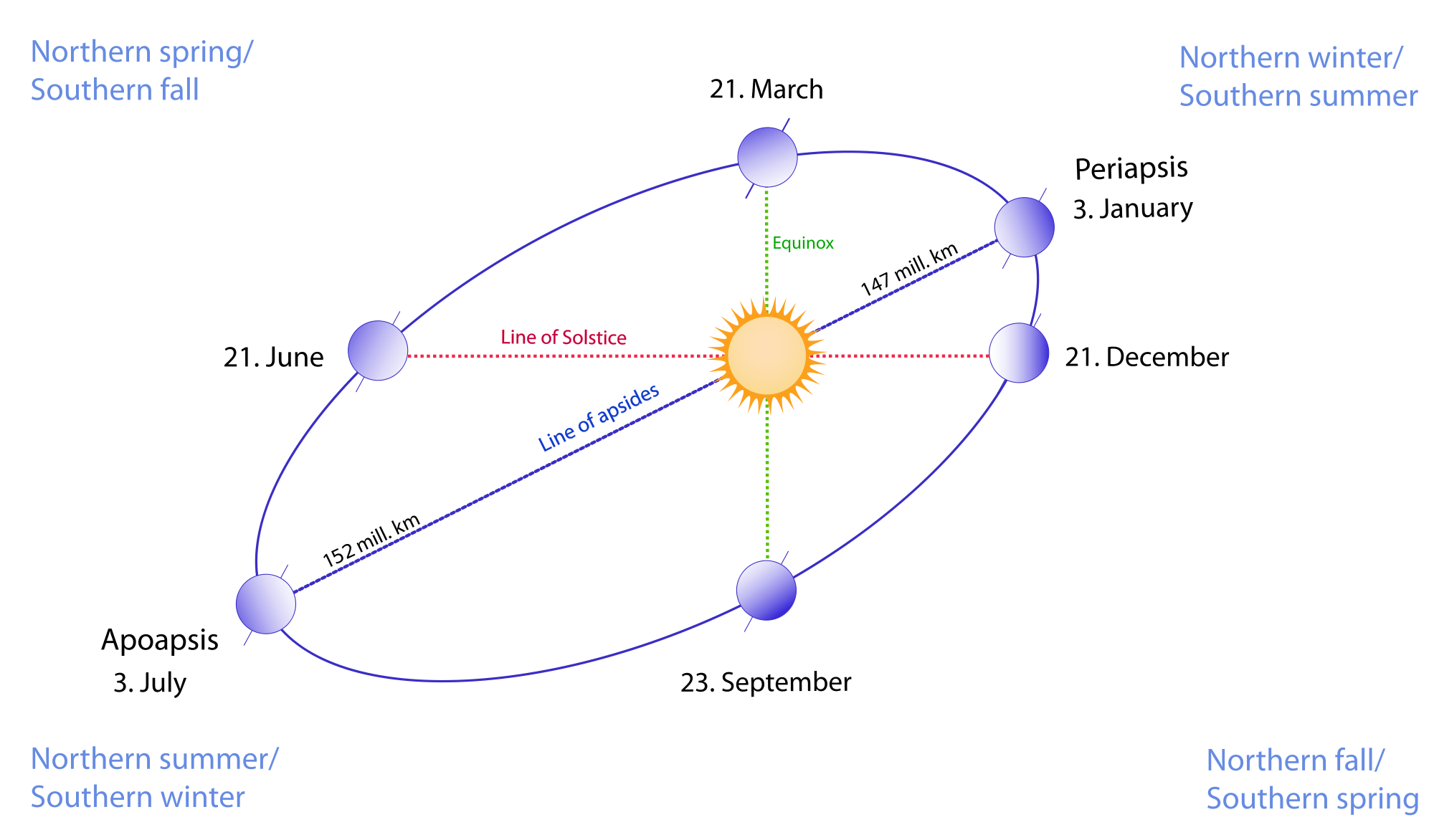
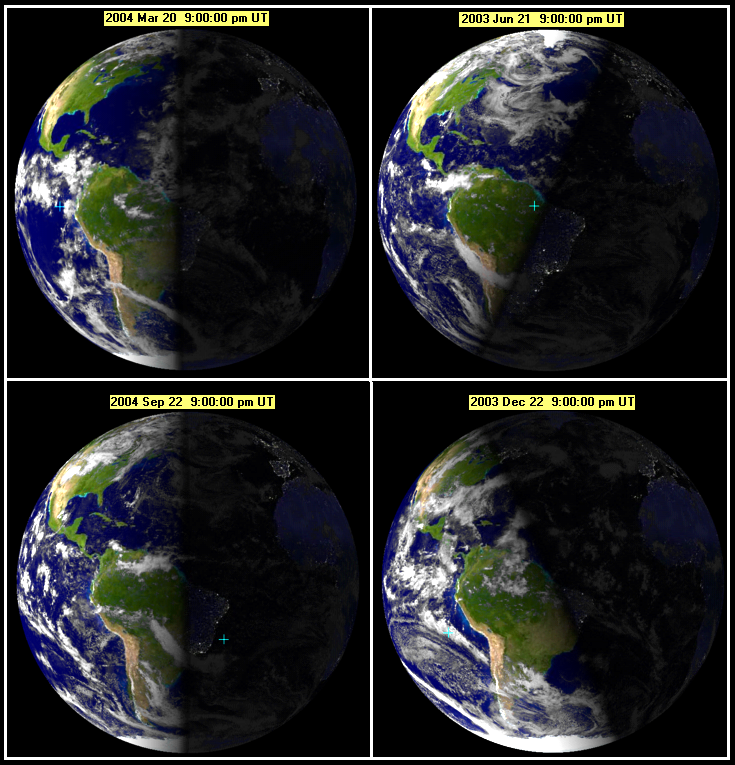
Смена времен года — вечное и неизменное явление природы. Причина его заключается в движении Земли вокруг Солнца.
Путь, по которому в космическом пространстве движется земной шар, имеет форму вытянутого круга — эллипса. Солнце находится не в центре этого эллипса, а в одном из его фокусов. Поэтому на протяжении года расстояние от Солнца до Земли периодически меняется: от 147,1 млн. км (в начале января) до 152,1 млн. км (в начале июля). Переход от тёплого времени года (весна, лето) к холодному (осень, зима) происходит вовсе не потому, что Земля то приближается к Солнцу, то удаляется от него.
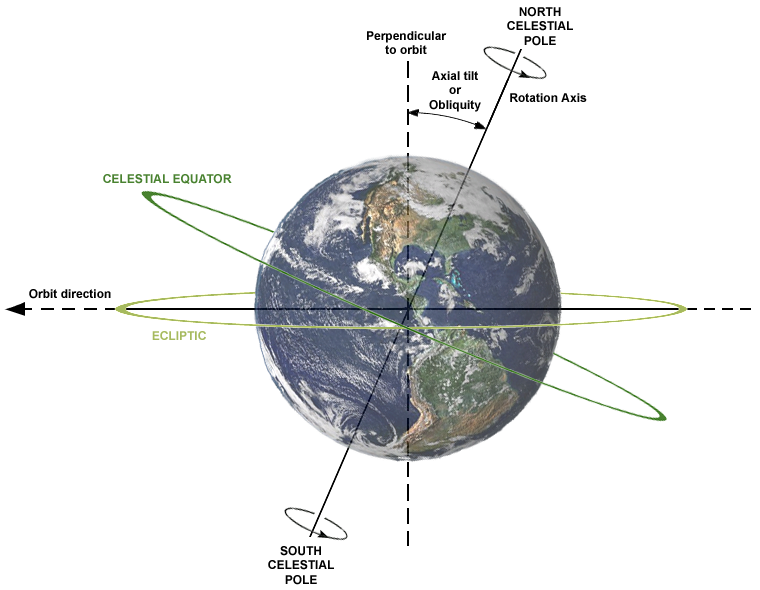
Истинная причина смены времен года — это наклон земной оси. Ось вращения, воображаемая линия, соединяющая северный и южный полюса Земли, не перпендикулярна плоскости земной орбиты, по которой она движется вокруг Солнца. И отклонение оси от перпендикуляра составляет 23,5°. Ось направлена на север в точку среди звезд возле Полярной звезды. (На самом деле, ось медленно меняет свое направление и со временем будет указывать не на Полярную, а на другую звезду.)
Лето приходит в Северное полушарие, когда ось, направленная через Северный полюс вверх, указывает примерно в сторону Солнца. В этой ситуации Солнце в полдень находится выше над горизонтом, чем во все остальные сезоны года, поэтому оно лучше освещает Северное полушарие и дает больше тепла. В это же самое время ось, проходящая вниз через Южный полюс, направлена от Солнца, поэтому Солнце в полдень находится ниже над горизонтом, чем в любое другое время года, и хуже освещает Южное полушарие. В это время в Австралии наступает зима.
Летом светлого времени суток больше, чем зимой, потому что Солнце находится выше над горизонтом. Поэтому ему требуется больше времени, чтобы сначала подняться на эту высоту, а потом — спуститься. И, поскольку день длится дольше, в это время года теплее.
По мере того как Земля движется по орбите вокруг Солнца, кажется, что Солнце перемещается по небу по некой окружности, которая называется эклиптикой. Плоскость эклиптики наклонена к плоскости экватора точно под таким же углом, как ось Земли — 23,5°.
Равноденствие — момент пересечения небесного экватора центром видимого солнечного диска. Весеннее равноденствие наступает, когда Солнце переходит из южного полушария небесной сферы в северное и обычно происходит около 21 марта. Осеннее равноденствие бывает около 23 сентября. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце переходит из южного полушария небесной сферы в северное, т. е. пересекает небесный экватор «снизу вверх», наступает первый день весны, который называется днем весеннего равноденствия. Он приходится на 20–21 марта. В Южном полушарии Земли наступает астрономическая осень, а в Северном — астрономическая весна. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце достигает самой высокой (северной) точки на эклиптике, это день летнего солнцестояния. Приходится примерно на 21–22 июня. С этого дня в Северном полушарии начинается астрономическое лето, а в Южном — астрономическая зима.
Когда Солнце переходит из северного полушария небесной сферы в южное, т. е. пересекает небесный экватор «сверху вниз», это начало осени, день осеннего равноденствия. Обычно он приходится примерно на 23 сентября. В Южном полушарии Земли наступает астрономическая весна, а в Северном — астрономическая осень.
Когда Солнце достигает самой нижней (южной) точки на эклиптике, это день зимнего солнцестояния. Приходится примерно на 21–22 декабря. С этого дня в Северном полушарии начинается астрономическая зима, а в Южном — астрономическое лето.
Источник

- Информация о материале
-
Просмотров: 8864
Расстояния звезд
Рис. 1. Определение параллаксов звезд (размеры орбиты Земли сильно преувеличены).
Рис. 2. Темная туманность.
Рис. З. Участок Млечного Пути.
Рис. 4. Схема строения нашей звездной системы (Галактики).
Рис.5. Туманность в созвездии Андромеды — далекая звездная система.
Рис. 6. Зависимость между наблюдаемыми скоростями удаления внегалактических туманностей и их расстояниями.
‹
›
Тот способ, которым определяются расстояния до Луны, Солнца и других тел солнечной системы (см. «Наука и жизнь» № 6, 1938) совершенно неприменим для измерения расстояний до звезд. Звезды настолько далеки от нас, что направления к какой-нибудь из них с двух противоположных точек земного шара практически параллельны между собою, и самыми точными инструментами нельзя установить, где эти направления пересекаются. Все базисы, доступные нам на Земле, слишком малы для измерения звездных расстояний, — для этой цели необходимо иметь базис гораздо большей длины. Действительно, снимки одного и того же участка неба, сделанные на двух возможно более далеких друг от друга обсерваториях, оказываются совершенно тождественными.
Но, двигаясь вокруг Солнца, Земля проходит большой путь в пространстве; летом она находится в противоположной стороне от Солнца по отношению к тому месту, где она была зимой. В июне и декабре мы смотрим на небо с двух точек, лежащих на расстоянии в 300 млн. км одна от другой.
Смотря из окна движущегося поезда, мы видим, что далекие предметы как бы стоят на месте, а близкие «бегут» в направлении, противоположном движению поезда. Видимые движения должны наблюдаться и у звезд; вследствие движения Земли каждая звезда должна описывать в течение года маленький эллипс (тем больший, чем меньше расстояние до нее). Однако таких движений звезд не наблюдалось, и еще Коперник, излагая свою теорию строения мира, указывал, что мы не замечаем их из-за больших расстояний звезд.
Астрономы последующих поколений искали видимые движения звезд; телескопы совершенствовались, но все попытки определить расстояния звезд от нас оставались безуспешными.
Около 1725 г. английский астроном Брадлей укрепил неподвижно в стене дома телескоп так, что ежедневно через поле зрения последнего проходила звезда гамма Дракона. Брадлей очень точно определял положение звезды и вскоре заметил видимые смещения ее. Но Дальнейшие наблюдения принесли разочарование: Брадлей открыл не параллакс звезды, а совершенно другое явление — аберрацию света, т. е. видимое отклонение светового луча, происходящее вследствие сложения скорости движения Земли со скоростью света. Было найдено физическое доказательство движения Земли, но расстояния звезд оставались неизвестными.
Очевидно, что гораздо легче заметить смещение звезды, если вблизи нее видна другая звезда, значительно более далекая. Пусть (рис. 1) звезда S1 значительно ближе к нам, чем звезда S2. Когда Земля находится в точке Т1, мы будем видеть обе звезды в одном направлении. Но через полгода Земля перейдет в Т2, на расстояние 300 млн. км от Т1, и звезды S1 и S2 как бы разойдутся. Измерив видимое расстояние между звездами, т. е. угол S1T2S2, и считая, что звезда S2 очень далека и не испытывает видимого смещения, можно найти угол, под которым с звезды S1 виден радиус орбиты Земли (параллакс звезды), а по нему и расстояние звезды от Земли (напомним, что для Солнца, Луны и планет параллаксом назывался угол, под которым с небесного тела виден радиус земного шара). По такому пути и пошли в дальнейшем астрономы: они стали искать относительное смещение двух звезд, одну из которых по тем или иным соображениям можно было считать близкой к Солнцу.
Сто лет назад работы астрономов, наконец, увенчались успехом: впервые удалось измерить расстояния до звезд. Почти одновременно 3 астронома — Бессель, Гендерсон и В. Струве (первый директор Пулковской обсерватории) — опубликовали найденные ими параллаксы звезд. Наибольший параллакс был найден Гендерсоном для звезды альфа Центавра (находящейся в южном полушарии неба), которая и до сих пор считается ближайшей к нам звездой. Но и ее параллакс равен всего 0″,76; видимое смещение ее за полгода равно 1»,52 или углу, под которым шарик диаметром в 1 мм виден с расстояния около 140 м. Параллаксы других звезд еще меньше. Становится понятным, почему так долго их не могли обнаружить.
Параллаксу в 0″,76 соответствует расстояние, в 270 тыс. раз большее расстояния от Земли до Солнца, или примерно 4 • 1013 км. Выражать такие расстояния в километрах уже неудобно, слишком мала и «астрономическая единица» — среднее расстояние от Земли до Солнца; пришлось вводить новые единицы. Одна из них «парсек» (от слов «параллакс-секунда») есть расстояние, соответствующее параллаксу в 1″. Парсек равен примерно 3,1 • 1013 км.
Свет проходит в секунду 300 тыс. км, следовательно, за год он пройдет 9,5 • 1012 км.
Расстояние это тоже принято за единицу измерения и названо «световым годом». Мы можем сказать, что ближайшая к нам звезда — альфа Центавра — находится на расстоянии 1,3 парсека, или 4,3 световых года. Наблюдая эту звезду, мы видим ее такой, какой она была 4 с лишним года назад.
За первыми определениями параллаксов звезд последовали все новые и новые; особенно успешно пошло дело после развития звездной фотографии. Сейчас звездные параллаксы определяются исключительно фотографическим методом.
Казалось бы, что достаточно сделать два снимка звезды, которую есть основание считать близкой к нам, с интервалом в полгода, определить ее положение относительно слабых, значительно более далеких звезд, чтобы, сравнив эти два снимка, найти параллакс. Однако дело обстоит более сложно. Звезды, которые мы называли неподвижными, несутся в пространстве с большими скоростями, и движение их незаметно нам лишь потому, что они очень далеки от нас. Далее, Земля, кроме вращения вокруг Солнца, движется вместе с ним в пространстве, что также вызывает видимое смещение близких звезд. Для выделения параллактического смещения звезды необходимы по меньшей мере три снимка, сделанные через полгода один после другого. На практике же в течение года делается не три, а больше снимков, с помощью которых и находится параллакс звезды.
В настоящее время удалось определить расстояния примерно 4000 звезд. Чем дальше звезда, чем меньше ее параллакс, тем менее точно удается измерить ее расстояние. Современные методы дают возможность определять параллаксы вплоть до 0″,005;
меньшие величины уже нельзя считать реальными, они меньше возможных ошибок наблюдения. Параллаксу 0″,005 соответствует расстояние в 200 парсек или 650 световых лет; свет, дошедший до нас в 1938 г., вышел от такой звезды в 1288 г.
Но это только самые близкие к нам звезды, наши «соседи». Огромное большинство звезд несравненно более далеки. Как же измерили расстояния до них, если обычный, так называемый тригонометрический метод уже не в состоянии дать ответ?
Определение расстояний по яркости звезд
Освещение уменьшается пропорционально квадрату расстояния от источника света: лампа в 1000 свечей на расстоянии в 10 м освещает так же, как лампа в 10 свечей на расстоянии 1 м. Пользуясь этим законом, мы можем найти действительную яркость звезд, если известно их расстояние до нас. Условились принимать за меру яркости звезды ту видимую яркость, которую звезда имела бы при наблюдении ее с расстояния в 10 парсек, или 32,6 световых лет. Яркость эту называют «абсолютной величиной»1 звезды. Так, «абсолютная величина» нашего Солнца 4,85 звездной величины, т. е. при удалении от него на 10 парсек оно будет видно как слабая звездочка 4,85 величины (самые слабые, еще видимые глазом звезды — 6-й величины). Если бы мы знали абсолютные величины звезд, мы могли бы по их видимым яркостям определять расстояния.
Оказалось, что такая задача разрешима. Для всех звезд, параллаксы которых измерены, можно найти абсолютные величины. Было сделано сопоставление абсолютных величин звезд и их спектров; установлено, что интенсивность некоторых фраунгоферовых линий в спектре зависит от абсолютной величины звезды. Астрономы получили в свои руки могучее орудие; сфотографировав спектр звезды, можно найти ее абсолютную величину, а сравнив эту последнюю с видимой, — найти расстояние звезды.
Например, из измерения спектра и яркости звезды получается, что ее яркость в миллион раз слабее той, которую она имела бы, если бы находилась на расстоянии 10 парсек. Отсюда легко найти расстояние звезды: оно равно 10 • √1 000 000 = 10 000 парсек, или 32 600 световых лет. Параллакс ее равен 0″,0001 (величина, которая непосредственно не может быть измерена). Такой способ, способ «спектроскопических параллаксов», годен для измерения каких угодно больших расстояний, лишь бы силы света звезды хватило для получения достаточно хорошего снимка спектра, пригодного для определения ее абсолютной яркости. Современные большие телескопы позволяют фотографировать очень слабые звезды.
Способ «спектроскопических параллаксов» хорош еще тем, что ошибка, полученная при определении расстояния, всегда около 20% и не зависит от самого расстояния, между тем как тригонометрические параллаксы определяются тем хуже, чем дальше звезда: при параллаксе 0″,5 ошибка в расстоянии будет порядка 2—5%, при параллаксе 0″,01 она может быть в 200%.
В настоящее время известны спектроскопические параллаксы многих тысяч звезд, на основании их сделан ряд весьма существенных выводов о строении нашего звездного мира.
Но работы последнего десятилетия принесли некоторое разочарование и заставили относиться к спектроскопическим параллаксам с большей осторожностью. Дело в том, что закон ослабления света пропорционально квадрату расстояния от его источника справедлив лишь в том случае, если пространство совершенно прозрачно и свет в нем не поглощается. Давно было известно существование областей, занятых темной, несветящейся материей, видимых на фоне более далеких звезд. Это так называемые темные туманности (рис. 2). Сейчас установлено, что темная материя имеется и во всем пространстве, и она ослабляет свет, доходящий к нам от звезд. Очень трудно учесть, насколько ослаблен свет звезды поглощением в темной материи, и всегда есть опасность недооценить или переоценить расстояние до нее. Поэтому при определении расстояний по абсолютной яркости всегда нужно тщательно учесть возможное влияние поглощения света.
Наша звездная система
Остановимся очень кратко на главных результатах, полученных из исследования расстояний до звезд.
Все знают полосу Млечного Пути — слабое сияние, пересекающее небо и особенно хорошо видимое у нас в ясные осенние и зимние вечера. Если навести на Млечный Путь телескоп, то можно убедиться, что это слабое сияние — свет многих миллионов звезд, расположенных настолько тесно, что для глаза они сливаются в общую массу (рис. 3).
Уже из одного вида Млечного Пути можно заключить, что звезды расположены в пространстве не равномерно и не беспорядочно, а по какому-то определенному закону.
Определение расстояний до звезд, с учетом межзвездного поглощения света и с применением статистических методов исследования, дало возможность построить картину окружающей нас звездной вселенной.
Несколько миллиардов звезд, в число которых входит и наше Солнце, образуют в пространстве как бы «чечевицу», диаметр которой раз в 5 больше ее толщины (рис. 4). Размеры чечевицы огромны, — диаметр ее около 30 000 парсек; иными словами, свет идет от одного ее края до другого примерно 100 000 лет. Смотря по направлению плоскости чечевицы, мы видим значительно больше звезд, чем в перпендикулярном направлении, — этим и объясняется полоса Млечного Пути. Солнце лежит не в центре системы, а примерно на 2/3 ее радиуса.
Центр системы расположен в направлении к созвездию Стрельца, там, где видны наиболее яркие «звездные облака» Млечного Пути. Кроме звезд, имеется много облаков темной несветящейся материи, видимой как темные туманности. Но если вблизи такого скопления материи расположена достаточно яркая звезда, — материя отражает ее свет или начинает светиться сама, и вместо темной туманности будет видна светлая. Такова, например, хорошо известная туманность в созвездии Ориона.
Коперник 400 лет назад доказал, что наша Земля лишь одна из планет; теперь мы знаем, что Солнце — одна из многих миллиардов звезд. Естественно возникает вопрос: существует ли только одна наша звездная система или есть много других таких же звездных групп.
Уже давно были известны небесные объекты, сходные по форме с Млечным Путем (как мы его себе представляем), — так называемые спиральные туманности. Самая большая и яркая из них находится в созвездии Андромеды (рис. 5). Смотря на Млечный Путь извне и издалека, мы видели бы его похожим на туманность Андромеды. Но не случайное ли это сходство? Подобна ли туманность Андромеды Млечному Пути?
Еще лет 20 назад такой вопрос вызывал большие споры. Чтобы ответить на него, надо знать размеры туманности Андромеды, что требует знания расстояния до нее.
Сильные телескопы показывают, что туманность Андромеды состоит из звезд, как
и многие другие подобные ей по виду туманности. Но быть может это тесные группы звезд, входящие в нашу звездную систему?
Звездные маяки
Давно известны звезды, меняющие свою яркость; такие звезды называются переменными. Причины изменения яркости переменных звезд различны. Среди них есть группа звезд, меняющих яркость строго периодически; причина этого связана с изменениями температуры и радиуса звезды; такие звезды названы цефеидами. Они-то и оказались теми «маяками», с помощью которых удалось определить расстояние до туманности Андромеды.
30 лет назад на Гарвардской обсерватории в Америке было сделано очень важное открытие: было установлено, что между периодом изменения яркости цефеид и их абсолютными яркостями существует определенная зависимость.
Наблюдая цефеиду, легко можно установить период изменения ее блеска и по нему найти ее абсолютную яркость. Сравнивая абсолютную величину с видимой, можно найти расстояние до звезды. Этот способ может быть применен и к слабым звездам, получить спектры которых для определения по ним абсолютных величин уже нельзя.
Среди звезд, видимых в туманности Андромеды и в других наиболее ярких туманностях, нашлось довольно много цефеид. Сравнение их с цефеидами в нашей звездной системе показало, что расстояние до туманности Андромеды около 700 000 световых лет. И отсюда определилась и ее величина: диаметр туманности Андромеды того же порядка, что и нашего Млечного Пути, она должна включать в себя миллиарды звезд.
Другие спиральные туманности находятся от нас дальше, размеры их того же порядка. Следовательно, наша звездная система не одна, есть очень много таких же звездных систем, расположенных далеко от нас.
Нашу звездную систему, систему Млечного Пути, часто называют Галактикой, от греческого слова галактос—молоко. Поэтому далекие звездные системы получили название «внегалактических туманностей», т. е. туманностей, лежащих за пределами нашей звездной системы. Часто называют их далекими галактиками.
Но цефеиды найдены далеко не во всех спиральных туманностях, зато во многих из них были замечены вспышки «новых» звезд. «Новая» звезда — вспышка слабой звездочки, происходящая от каких-то неизвестных пока причин. Вспыхнув, звезда светит ярко довольно короткое время, а затем ее свет снова ослабевает. Исследования «новых» звезд, вспыхивающих в нашей звездной системе, показали, что наибольшая абсолютная яркость их всегда примерно одинакова; такую же абсолютную яркость имели и «новые» звезды, вспыхивавшие в туманности Андромеды. Мы имеем право считать, что все процессы происходят так же и в других туманностях, следовательно, «новые» звезды в момент вспышки должны иметь ту же абсолютную яркость. «Новые» звезды тоже дают способ измерения расстояний далеких звездных систем; результаты определений расстояний по цефеидам и «новым» звездам сходятся достаточно хорошо.
Есть и еще одна возможность оценки расстояний. Самые яркие звезды в нашей и других системах должны быть примерно одинаковы. Следовательно, сравнив самые яркие звезды в двух туманностях, можно сказать, которая из них дальше и во сколько раз; обычно, во избежание ошибок берется 5—10 наиболее ярких звезд туманности, и оценка расстояния делается по ним. Так удалось узнать расстояния до других звездных систем и выяснить их природу и строение. Оказалось, что они тоже весьма сходны с системой Млечного Пути.
Все три описанных метода таят в себе, однако, некоторую опасность. Пространство между звездными системами света не поглощает, но внутри других звездных систем есть такая же темная материя, как и в нашей системе; свет цефеиды или «новой звезды» может быть из-за этого ослаблен, что приведет к преувеличенной оценке расстояния.
Статистические методы
К сожалению, выделить отдельные звезды можно лишь примерно в 10 самых близких туманностях, остальные же туманности, которых известно сейчас много тысяч, слишком далеки. Для определения их расстояний приходится пользоваться значительно менее точными статистическими методами.
По исследованию более близких туманностей установлено, что размеры их и полная абсолютная яркость колеблются сравнительно немного. Считая, что наблюдаемая туманность имеет средние размеры и среднюю яркость, можно по ее видимым размерам и яркости оценить расстояние.
Оценка расстояния по видимым размерам туманности менее точная, чем по видимой яркости; границы туманностей весьма неопределенны. Для более близких туманностей все же пользуются для контроля обоими способами. Расстояния очень далеких туманностей могут быть оценены лишь по видимой яркости этих туманностей.
Нельзя считать, что все внегалактические туманности построены совершенно одинаково, — и размеры и видимая яркость отдельной туманности могут отличаться от средних величин. Оценка расстояния до отдельной туманности может быть в значительной степени ошибочна, но средний результат для большого числа объектов будет близок к истине. В данное время приходится для далеких звездных систем удовольствоваться этим.
«Красное смещение»
Спектр звезды содержит многочисленные темные линии, называемые фраунгоферовыми, которые указывают на присутствие в атмосфере звезды известных химических элементов.
Каждая линия занимает в спектре определенное место, зависящее от длины ее волны. Но место линии может меняться под влиянием разных обстоятельств, из которых наиболее известное и хорошо изученное есть движение звезды по лучу зрения — к нам или от нас. По закону Допплера-Физо линии, соответствующие отдельным химическим элементам, сместятся к фиолетовому концу спектра, если звезда движется к нам, и к красному — при удалении от нас. По величине смещения можно найти скорость звезды относительно наблюдателя.
Спектр внегалактической туманности представляет собой сумму спектров входящих в нее звезд; движение, определенное по спектру туманности, будет движением системы как целого, движением ее центра тяжести. Исследование спектров туманностей показало удивительную вещь: линии в них всегда сильно смещены к красному концу, и если считать, что это смещение вызвано движением, то все внегалактические туманности удаляются от нас c большими скоростями.
В 1929 г. астроном Геббл обнаружил еще более удивительное обстоятельство: смещение линий каждой туманности пропорционально ее расстоянию от нас, далекие туманности имеют бо́льшие (рис. 6) смещения. Таким образом, определив смещение линий в спектре туманности, можно, воспользовавшись результатом Геббла, вычислить ее расстояние. В настоящее время известны у туманностей смещения, соответствующие расстояниям примерно в 100 и 200 млн. световых лет.
Чем вызывается это «красное смещение», пока еще не решено наукой. Несомненно, что здесь, кроме движения, замешаны еще другие влияния, — быть может свойства самого пространства. Но если только для очень далеких внегалактических туманностей пропорциональность наблюдаемого смещения расстоянию не нарушается, явление «красного смещения» дает средство для измерения расстояний предельно далеких звездных систем, свет от которых идет до нас сотни миллионов лет. Световой луч, давший на фотопластинке изображение самой далекой из исследованных внегалактической туманности в 1938 г., вышел из нее тогда, когда на Земле еще не существовало человека.
Комментарии к статье
1 Под «величиной» звезды в астрономии понимается ее яркость, а не линейные размеры.
Содержание:
- 1 Общие сведения
- 2 История открытия
- 3 Материалы по теме
- 4 Как определить парсек
- 5 Самые популярные примеры расстояний в парсеках
- 6 О расстояниях наглядно. Нажмите кнопку «Старт»
Общие сведения
Парсек (сокращенное «параллакс секунда») – это внесистемная единица измерений, при помощи которой в космологии измеряют расстояния к особенно отдаленным объектам космического пространства. Данная единица выполняет не только практическую функцию – помогает вычислить расстояние к тому или иному объекту во Вселенной, но и создает астрономам своеобразный комфорт. Судите сами, гораздо проще сказать, что расстояние от Солнца к ближайшей звезде равно 1,3 парсека, чем то, что оно равно 40,7 триллионов километров. Человек, который бы регулярно оперировал цифрами с таким огромным количеством нулей, рано или поздно бы сошел с ума. Таким образом, придумав парсек, ученые значительно упростили вычислительные процессы в астрономии.
Парсек
Парсек – популярная единица измерения в астрофизике. Любителям этой науки хорошо известно, что она равна 3,2616 световым годам. Многие из них свободно могут назвать расстояние к тому или другому отдаленному объекту в парсеках. Но, к сожалению, далеко не все понимают, как появилась на свет данная единица измерения и как ее правильно вычислять.
История открытия
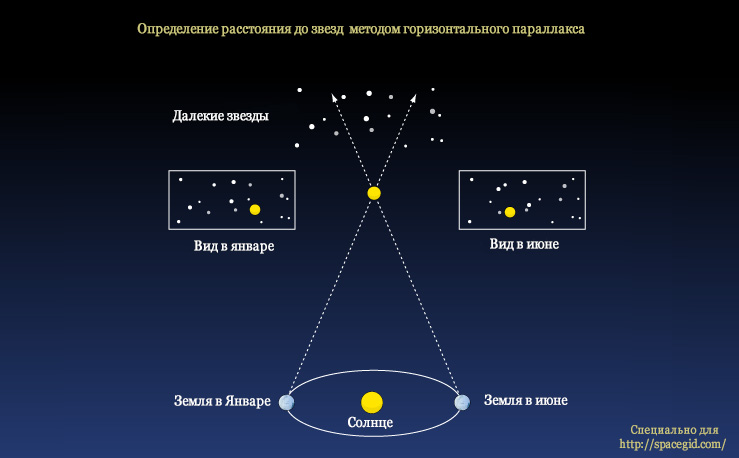
Если расстояния к близким объектам в космосе можно измерить при помощи радиотелескопа с точностью до нескольких сантиметров, то измерить расстояние к удаленным уголкам Вселенной намного сложнее. Тем не менее, ученым нужно было найти способ, как вычислить данную величину и они решили воспользоваться методом горизонтального параллакса, который хорошо известен в геометрии.
Материалы по теме
Суть метода горизонтального параллакса проста: если смотреть на отдаленный объект с разных мест, то на фоне других, более далеких объектов он будет менять свое положение. Зная расстояние между местами, с которых ведется наблюдение, а также угол смещения объекта на фоне отдаленных предметов, можно вычислить расстояние к нему путем геометрических подсчетов. Этой аксиомой решили воспользоваться астрономы; она послужила основой для открытия новой единицы измерения – парсек.
Как определить парсек
Допустим, вы смотрите на звезду и хотите определить расстояние к ней в парсеках. Но для этого вам необходимо знать, что собой являет расстояние в 1 парсек. Данное расстояние представляет собой смещение небесного тела на фоне других, более далеких объектов на угол равный одной угловой секунде при перемещении наблюдателя на половину диаметра земной орбиты.
Кому-то такое определение может показаться сложным для восприятия. В действительности суть определения парсека понять не так уж трудно. Возвращаясь к нашей звезде, расстояние в парсеках к которой мы хотим определить, нам придется произвести два наблюдения за этим объектом с разных точек земной орбиты. Сделать это можно без каких-нибудь космических приборов, а просто дождавшись, когда Земля сама пройдет половину своего годичного пути и станет на противоположную сторону Солнца.
Собственное движение 61 Лебедя за год
Зная длину между точками, откуда производились наблюдения (она равна 1 астрономической единице – расстоянию Земли от Солнца или радиусу орбиты Земли), а также смещение звезды на фоне более дальних звезд и галактик, мы можем вычислить расстояние к ней. Если в наблюдаемом диапазоне звезда сместилась на 1 угловую секунду, расстояние к ней составляет один парсек, если же она сместилась на полсекунды – два парсека. Вопреки догадкам, чем меньше параллакс (смещение) небесного тела, тем больше к нему парсеков.
Самые популярные примеры расстояний в парсеках
- Ближайшая к Солнцу звезда Проксима Центавра удалена от него на расстояние 1,3 парсека (пк);
- Диаметр нашей галактики Млечный Путь составляет 30 тыс. пк или 30 килопарсеков;
- 1 астрономическая единица при переводе в парсеки представляет собой очень маленькое число – всего 4,848·10−6 парсека;
- Расстояние к ближайшей к нам галактике Андромеда равно 0,77 мегапарсек или 770 000 парсек;
- 1 парсек равен 30,8568 трлн. км.;
- Согласно современным представлениям возраст вселенной 13.7 млрд. лет, а за это время Вселенная увеличилась в размерах до 27 млрд. парсек из-за того, что расширение пространства идет быстрее скорости света.