Параллельность плоскостей: признаки и свойства
Две плоскости параллельны, если они не имеют общих точек.
Это определение. Однако в практических целях чаще используется признак параллельности плоскостей:
Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
Свойства параллельных плоскостей:
- Если две плоскости параллельны третьей, то они параллельны друг другу.
- Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
- Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Читаем дальше: Угол между плоскостями.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Параллельность плоскостей: признаки и свойства» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит, две плоскости или пересекаются, или не пересекаются.
Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости
α
и
β
обозначаются
α∥β
.
Пример:
любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.
Рис. (1). Стены здания.
Признак параллельности плоскостей.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Рис. (2). Доказательство признака параллельности плоскостей.
Доказательство.
Пусть
α
и
β
— данные плоскости,
a1
и
a2
— пересекающиеся прямые в плоскости
α
, а
b1
и
b2
— соответственно параллельные им прямые в плоскости
β
.
Допустим, что плоскости
α
и
β
не параллельны, то есть, они пересекаются по некоторой прямой (c).
Прямая
a1
параллельна прямой
b1
, значит, она параллельна и самой плоскости
β
.
Прямая
a2
параллельна прямой
b2
, значит, она параллельна и самой плоскости
β
(признак параллельности прямой и плоскости).
Прямая (c) принадлежит плоскости
α
, значит, хотя бы одна из прямых —
a1
или
a2
— пересекает прямую (c), то есть имеет с ней общую точку. Но прямая (c) также принадлежит и плоскости
β
, значит, пересекая прямую (c), прямая
a1
или
a2
пересекает плоскость
β
, чего быть не может, так как прямые
a1
и
a2
параллельны плоскости
β
.
Из этого следует, что плоскости
α
и
β
не пересекаются, то есть, они параллельны.
Свойства параллельных плоскостей
Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Рис. (3). Две параллельные плоскости пересечены третьей плоскостью..
Доказательство.
Пусть
α
и
β
— параллельные плоскости, а
γ
— плоскость, пересекающая их.
Плоскость
α
пересекается с плоскостью
γ
по прямой (a).
Плоскость
β
пересекается с плоскостью
γ
по прямой (b).
Линии пересечения (a) и (b) лежат в одной плоскости
γ
и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.
Теорема 2. Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны.
Рис. (4). Параллельные прямые пересекают две параллельные плоскости.
Доказательство.
Пусть
α
и
β
— параллельные плоскости, а (a) и (b) — параллельные прямые, пересекающие их.
Через прямые (a) и (b) можно провести плоскость — эти прямые параллельны, значит, определяют плоскость, причём только одну.
Проведённая плоскость пересекается с плоскостью
α
по прямой (AB), а с плоскостью
β
— по прямой (CD).
По предыдущей теореме прямые (AB) и (CD) параллельны. Четырёхугольник (ABCD) есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть (BC = AD).
Источники:
Рисунки 2-4. Теоремы о параллельных плоскостях, © ЯКласс.
Плоскости в пространстве
§ 13.Параллельность плоскостей
13.1. Признаки параллельности плоскостей
При взаимном расположении двух плоскостей в пространстве возможен один из двух взаимно исключающих случаев.
1. Две плоскости имеют общую точку. Тогда по аксиоме пересечения двух плоскостей они имеют общую прямую. Такие плоскости называются пересекающимися.
2. Две плоскости не имеют общей точки.
Определение. Две плоскости, не имеющие общей точки, называются параллельными.
Если плоскости α и β параллельны, то записывают: α ‖ β или β ‖ α. При этом также говорят, что плоскость α параллельна плоскости β или плоскость β параллельна плоскости α.
В п. 9.1 доказано, что в пространстве существуют параллельные плоскости. Но возникает вопрос: как определить, параллельны ли две данные плоскости? Ответить на этот вопрос помогают признаки параллельности двух плоскостей (т. 18, 19 и 24).

Дано: α, β, a ⊂ α, b ⊂ α, a ∩ b = M; a ‖ β, b ‖ β (рис. 82).
Доказать: α ‖ β.
Рис. 82
Доказательство. Рассуждаем методом от противного. Предположим, что плоскости α и β не параллельны. Тогда они пересекаются по некоторой прямой c (см. рис. 82).
В плоскости α расположены прямая c и данные пересекающиеся прямые a и b. Так как из двух пересекающихся прямых не более чем одна может быть параллельна данной прямой, то прямая c пересекает, по крайней мере, одну из прямых a и b. Пусть прямая c пересекает прямую a в некоторой точке K: a ∩ c = K.
Имеем: прямая c, следовательно, и точка K лежат в плоскости β. Значит, прямая a пересекает плоскость β. Это противоречит условию теоремы (a ‖ β).
Также к противоречию с условием теоремы придём, если допустим, что пересекаются прямые c и b или прямая c пересекает обе прямые a и b.
Таким образом, предположив, что плоскости α и β не параллельны, мы пришли к противоречию. Это означает, что предположение неверно. Следовательно, α ‖ β. Теорема доказана. ▼

Рис. 83
Доказательство. Пусть прямые a и b плоскости α пересекаются в точке M, прямые a1 и b1 плоскости β параллельны соответственно прямым a и b (рис. 83). Тогда по признаку параллельности прямой и плоскости имеем:
a ‖ a1, a1 ⊂ β ⇒ a ‖ β; b ‖ b1, b1 ⊂ β ⇒ b ‖ β.
Таким образом, пересекающиеся прямые a и b в плоскости α параллельны плоскости β. По предыдущей теореме плоскости α и β параллельны. Теорема доказана. ▼
Заметим, что доказанная теорема 19 также является признаком параллельности двух плоскостей и может быть доказана независимо от теоремы 18. Самостоятельно докажите теорему 19, не используя теорему 18.
Докажите самостоятельно, что две плоскости, перпендикулярные одной и той же прямой, параллельны.
13.2. Свойства параллельных плоскостей

Рис. 84
Дано: α ‖ β, γ ∩ α = a, γ ∩ β = b (рис. 84).
Доказать: a ‖ b.
Доказательство. Прямые a и b лежат в одной плоскости γ. Эти прямые не имеют общей точки, так как плоскости α и β параллельны. Следовательно, прямые a и b параллельны по определению. Теорема доказана. ▼

Дано: α ‖ β, a ∩ α = A (рис. 85).
Доказать: a пересекает β.
Доказательство. Выберем в плоскости β любую точку C. Через эту точку и прямую a проведём плоскость γ.
Рис. 85
Так как плоскость γ имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости γ прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости β, то точка B является точкой пересечения прямой a и плоскости β. Теорема доказана. ▼

Дано: α ‖ β, α и γ пересекаются (рис. 86).
Рис. 86
Доказать: β и γ пересекаются.
Доказательство. Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 21 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана. ▼
Вернёмся к вопросу о существовании параллельных плоскостей.

Дано: α, M; M ∉ α (рис. 87).
Доказать: существует единственная плоскость β такая, что M ∈ β, β ‖ α.
Рис. 87
Доказательство. В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a1 и b1, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a1 и b1, обозначим β. На основании теоремы 19 плоскость β параллельна плоскости α.
Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 22 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана. ▼
Данная теорема даёт способ построения в пространстве плоскости, параллельной данной плоскости.
ЗадаЧа. В кубе ABCDA1B1C1D1 через точку K — середину ребра A1D1 провести сечение, параллельное плоскости A1C1D.
Решение. Плоскость сечения пересекает плоскость AA1D1 по прямой KM, параллельной прямой A1D (почему?), а плоскость DCC1 — по прямой ME, параллельной прямой C1D (почему?). Треугольник KME — искомое сечение (рис. 88).
Самостоятельно постройте сечение этого куба плоскостью, проходящей через середину ребра AA1 параллельно плоскости A1C1D, и вы получите в сечении правильный шестиугольник.
Рис. 88

Рис. 89
Дано: α ‖ β, γ ‖ β (рис. 89).
Доказать: α ‖ γ.
Доказательство. Допустим, что плоскости α и γ пересекаются по некоторой прямой c. Выберем на прямой c произвольную точку M. Через эту точку проходят две различные плоскости α и γ, каждая из которых параллельна плоскости β. Это противоречит теореме 23. Значит, предположение было неверно. Поэтому α ‖ γ. Теорема доказана. ▼

Дано: α ‖ β; a ‖ b; a ∩ α = A1, a ∩ β = B1;
b ∩ α = A2, b ∩ β = B2 (рис. 90).
Рис. 90
Доказать: A1B1 = A2B2.
Доказательство. Проведём через параллельные прямые a и b плоскость γ (т. 3). Она пересекает параллельные плоскости α и β по параллельным прямым A1A2 и B1B2 (т. 20).
А так как a ‖ b, то четырёхугольник A1A2B2B1 — параллелограмм. Поэтому A1B1 = A2B2 (как противоположные стороны этого параллелограмма). Теорема доказана. ▼

Дано: α1 ‖ α2, l ⊥ α1.
Доказать: l ⊥ α2.
Рис. 91
Проведите доказательство самостоятельно, построив две любые плоскости γ1 и γ2, проходящие через прямую l (рис. 91).
ЗадаЧа 4.007. Построить сечение пятиугольной пирамиды PABCDE плоскостью α, которая проходит через внутреннюю точку M основания ABCDE параллельно грани PAB (рис. 92).
Решение. Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость α параллельна грани PAB, то: а) прямая пересечения плоскости α с плоскостью ABC (плоскостью основания пирамиды) должна быть параллельна AB; б) прямая пересечения плоскости α с гранью PAE — параллельна AP; в) прямая пересечения α с плоскостью грани PBC — параллельна PB; г) прямая пересечения плоскости α с плоскостью PAD — параллельна PA, поэтому проводим: 1) через точку M прямую KF ‖ AB, K ∈ BC, F ∈ AE; 2) прямую FH ‖ PA, H ∈ PE; 3) прямую KR ‖ PB, R ∈ PC; 4) прямую ML ‖ AP, L ∈ PD. Пятиугольник HLRKF — искомое сечение.
Доказательство проделайте самостоятельно.
Рис. 92
Рис. 93
Замечание. При внимательном анализе обнаруживается аналогия между свойствами параллельных плоскостей в пространстве и свойствами параллельных прямых на плоскости. Попробуйте, например, пользуясь рисунком 93, сформулировать и доказать «пространственный аналог теоремы Фалеса».
Геометрия, 10 класс
Урок №6. Параллельность плоскостей
Перечень вопросов, рассматриваемых в теме
- Определение параллельных плоскостей;
- Свойства параллельных плоскостей;
- Признак параллельности плоскостей.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Основная литература:
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
Дополнительная литература:
Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24
Теоретический материал для самостоятельного изучения
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются α∥β.
Изображение:
Пример 1.
Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

Доказательство.
Пусть α и β — данные плоскости, a1 и a2 – пересекающиеся прямые в плоскости α, а b1 и b2 соответственно параллельные им прямые в плоскости β.
Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.
Прямая a1 параллельна прямой b1, значит она параллельна и самой плоскости β.
Прямая a2 параллельна прямой b2, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a1 или a2 пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.
Теорема доказана.
Свойства параллельных плоскостей.

Доказательство.
Пусть α и β — параллельные плоскости, а γ- плоскость, пересекающая их.
Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.
Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Доказательство.
Пусть α и β — параллельные плоскости, а a и b – параллельные прямые, пересекающие их.
Через прямые a и b можно провести плоскость — эти прямые параллельны, значит определяют плоскость, причём только одну.
Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.
По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Доказательство.
Пусть α||β, a пересекает α в точке А.
Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.
Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.

Доказательство.
Пусть α||β, α и γ пересекаются.
Докажем, что плоскости β и γ пересекаются.
Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Доказательство.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана.
Рассмотрим несколько примеров на применение данных свойств.
Пример 2.
Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.
Доказательство.
Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А1, эти прямые единственным образом определяют плоскость α.
Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .
Пример 3.
Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.
Доказательство.
Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Примеры и разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Доказательство.
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Верное решение:
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
№2.
Тип задания: выделение цветом
Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.
Решение:
Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.
Ответ:
1) они параллельны
2) скрещиваются
3) пересекаются
Статья посвящена изучению вопросов геометрии по теме параллельность плоскостей. Будет изложено определение плоскостей, параллельных между собой, рассказано о признаках и достаточных условиях параллельности, описание теории на наглядных практических примерах и изображениях.
Основная информация о параллельных плоскостях
Плоскости именуются параллельными при отсутствии общих точек. Для обозначения параллельности используют такой знак: ∥. В случае двух заданных плоскостей: α и β, которые параллельны друг другу, их обозначение будет изображено таким образом: α ∥ β.
На чертежах принято иллюстрировать параллельные плоскости в виде двух равных параллелограммах, которые имеют смещение сравнительно друг друга.
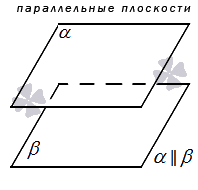
На словах параллельность обозначают таким образом: две плоскости α и β являются параллельными, а плоскость α будет параллельной плоскости β или, наоборот, плоскость β является параллельной плоскости α.
Признак и условие параллельности плоскостей
При процессе решения задач по геометрии часто появляется вопрос: являются ли заданные плоскости параллельными друг другу? Чтобы ответить на данный вопрос применяют признак параллельности, он в это же время означает достаточное условие параллельности двух плоскостей.
В форме теоремы звучит так: когда две пересекающиеся прямые плоскости параллельны двум пересекающимся прямым второй плоскости, тогда плоскости параллельны между собой. Доказательство теоремы можно найти в учебниках по геометрии 10 и 11 класса.
Теоремы 1 — 2
Также в практическом процессе чтобы доказать параллельность используют две такие теоремы:
- Первая звучит так: когда одна данная параллельная плоскость является параллельной третьей, то другая считается либо параллельной этой, либо соответствует ей;
- Вторая объясняется таким образом: когда две плоскости не совпадают и перпендикулярны какой-либо прямой, то они обозначаются параллельными.
Факт доказывающий параллельность двух разных плоскостей строится на основании озвученных теорем и признака параллельности.
Для лучшего понимания можно рассмотреть подробно достаточное и необходимое условия параллельности плоскости α и плоскости β, которые заданы в прямоугольной системе координат трёхмерного пространства.
Предположим, что в прямоугольной системе координат была задана плоскость α с общим уравнением A1x+B1y+C1z+D1=0, также есть плоскость β с общим уравнением A2x+B2y+C2z+D2=0. Для того, чтобы это доказать необходима теорема: для определения параллельности плоскости α и плоскости β нужно, чтобы линейные уравнения A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 не обладали решениями, то есть считались несовместными. Доказательство таково:
Допустим, что плоскости, которые определяются A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0 параллельные, а значит не обладают общими точками параллельных плоскостей. И ни одна координата точек не отвечает одновременно двум условиям заданных уравнений плоскостей, то есть решение отсутствует. Из этого следует, что также ни одна точка не отвечает условиям уравнений системы. Исходя из сказанного: плоскости, которые заданы уравнениями не обладают общими точками, то есть являются параллельными.
Теорема 3
Теорема о необходимом и достаточном условии параллельности плоскостей
Несовпадающие плоскости параллельны между собой, когда нормальные векторы двух плоскостей считаются коллинеарными. Доказательство сформировано на основе определения нормальных векторов плоскости:
Предположим n1→=(A1, B1, C1) и n2→=(A2, B2, C2) – это нормальные векторы α и β. Условие коллинеарности заданных векторов таково: n1→=t·n2⇀⇔A1=t·A2B1=t·B2C1=t·C2, t – действительное число.
Из вышесказанного следует, что несовпадающие α и β с данными векторами являются параллельными, если существует действительное t с верным равенством: n1→=t·n2⇀⇔A1=t·A2B1=t·B2C1=t·C2.
Условие параллельности и перпендикулярности плоскостей
Условие параллельности плоскостей в пространстве характеризуется так: плоскости параллельны между собой, когда нормальные векторы также параллельны. При этом, две плоскости являются параллельными, если коэффициенты пропорциональны при сопутствующих координатах.
Условие перпендикулярности звучит так: две плоскости являются перпендикулярными, когда нормальные векторы также перпендикулярны.
Подробнее на практическом примере:
Необходимо создать уравнение плоскости, которая проходит через точку M(-2; 1; 4) лежащая параллельно такой плоскости 3x+2y-7z+8=0.
Поиск уравнения будет проходить в форме Ax+By+Cz+D=0. Следуя условию параллельности известно следующее: [frac{A}{3}=frac{B}{2}=frac{C}{-7}]. Из этого предполагается, что A=3, B=2, C=-7. Вследствие чего уравнение принимает форму x+2y-7z+D=0. Помимо этого, точка M α, то-6+2-28+D=0, D=32. В итоге составленное уравнение выглядит так 3x+2y-7z+32=0.
Еще одно условие параллельности прямой и плоскости в пространстве. Прямая и плоскость будут параллельны, когда нормальный вектор плоскости и вектор направляющий прямой будут перпендикулярны, при этом скалярное произведение должно равняться нулю.
Сечение параллельных плоскостей
В геометрии чтобы построить сечение любой пространственной фигуры нужно учитывать теоремы и определения плоскостей и их свойства. Основные определения, которые помогут в построении:
- Две прямые пересекаются и параллельны, если невозможно прочертить плоскость;
- Плоскость и прямая являются параллельными при отсутствии общих точек;
- Прямые называются перпендикулярными при условии, что образующийся между ними угол равен 90°;
- Прямая именуется перпендикулярной заданной плоскости, когда она перпендикулярна другой прямой, которая лежит в этой же плоскости.
Нет времени решать самому?
Наши эксперты помогут!
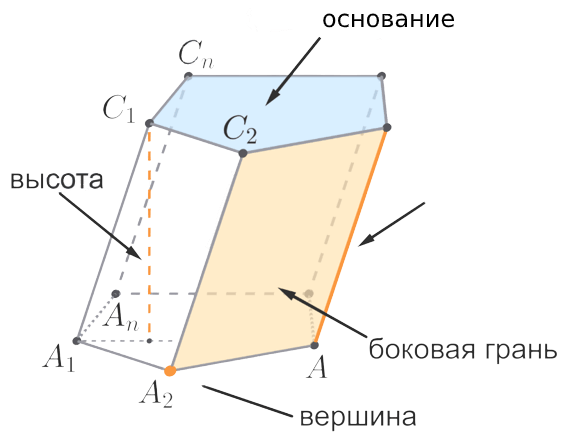
Параллельные плоскости призмы
Определения
Фигура призма – многогранник, который состоит из плоских многоугольников, совмещённые параллельным переносом и отрезками, которые соединяют точки данных многоугольников. То есть грани призмы – равные многоугольники, которые лежат в параллельных плоскостях, другие грани являются параллелограммами.
Многоугольники, которые лежат в плоскостях параллельных друг другу именуются основаниями, а отрезки, соединяющие вершины – боковыми ребрами. То есть боковые ребра равны и параллельны между собой.