Как найти параллельную плоскость в кубе - Исправление недочетов и поиск решений вместе с Examum.ru

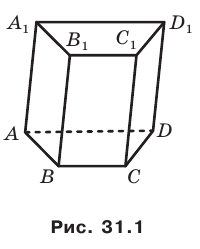
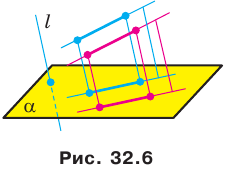
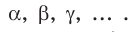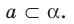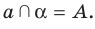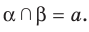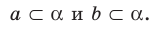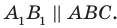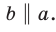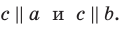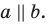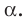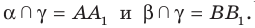Две различные плоскости в пространстве либо параллельны, либо пересекаются.

Параллельность двух плоскостей

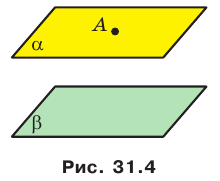
Определение. Две плоскости в пространстве называются параллельными, если они не пересекаются.

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.

Основные свойства параллельности плоскостей.

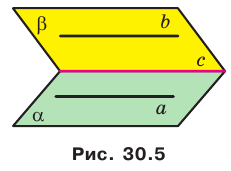
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны по длине.

Пересечение двух плоскостей

Две плоскости пересекаются по прямой. Общая прямая двух плоскостей называется ребром двугранного угла, образованного при пересечении данных плоскостей. При пересечении двух плоскостей образуются четыре двугранных угла. Если все они равны, то плоскости называются перпендикулярными.

Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Из признака перпендикулярности плоскостей следует, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Угол между плоскостями — наименьший из двугранных углов, образованных при пересечении плоскостей.

Угловая величина двугранного угла — это величина линейного угла данного двугранного угла.

Чтобы найти линейный угол двугранного угла надо из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру. Все линейные углы двугранного угла равны друг другу.

Тренировочные задания

Дан куб $ABCDA_{1}B_{1}C_{1}D_{1}$ . Найдите угол между плоскостями $AD_{1}C_{1}$ и $A_{1}D_{1}C$ .
Дан куб $ABCDA_{1}B_{1}C_{1}D_{1}$ . Точка — середина ребра $C_{1}D_{1}$ . Найдите угол между плоскостями $KBA_{1}$ и $BCC_{1}$ .
В кубе $ABCDA_{1}B_{1}C_{1}D_{1}$ все рёбра равны . На его ребре $BB_{1}$ отмечена точка так, что . Через точки и $C_{1}$ построена плоскость , параллельная прямой $BD_{1}$ . Найдите угол наклона плоскости к плоскости грани $BB_{1}C_{1}C$ .
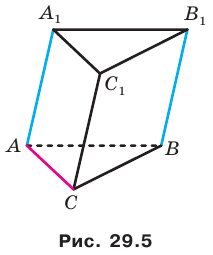
Дана правильная треугольная призма $ABCA_{1}B_{1}C_{1}$ , у которой сторона основания равна , а боковое ребро равно . Через точки , $C_{1}$ и середину ребра $A_{1}B_{1}$ проведена плоскость. Найдите угол между плоскостью сечения и плоскостью ABC.
Все рёбра правильной треугольной призмы $ABCA_{1}B_{1}C_{1}$ имеют длину . Точки и — середины рёбер $AA_{1}$ и $A_{1}C_{1}$ соответственно. Найдите угол между плоскостями и .
Основанием пирамиды является прямоугольник , в котором . Диагонали прямоугольника пересекаются в точке . Отрезок является высотой пирамиды . Из вершин и опущены перпендикуляры и на ребро . Найдите двугранный угол пирамиды при ребре , если .
В основании прямой призмы $ABCDA_{1}B_{1}C_{1}D_{1}$ лежит квадрат со стороной , а высота призмы равна . Точка лежит на диагонали $BD_{1}$ , причём . Найдите угол между плоскостью $A_{1}C_{1}E$ и плоскостью .

Источник

Две задачи на построение сечений

Здесь рассмотрено подробное решение двух наиболее сложных, на мой взгляд, задач из представленных в группе Задачи на построение сечений многогранников на этом сайте. Если Вы еще не выполняли подобных заданий, вернитесь на указанную страницу и попробуйте поработать самостоятельно.

Задача 6.

Замечание: куб на чертеже может быть повёрнут к нам любой гранью, но трудно предугадать, какой удобнее для построения. Поэтому, если совсем не получается решение какой-либо задачи по стереометрии, то я рекомендую начинать заново, перерисовав исходный чертёж. А зачастую бывает достаточно просто переставить символы, обозначающие вершины основания многоугольника (естественно, не произвольно, а согласовав между собой и с условием задачи).

Для начала вспомним признак перпендикулярности прямой и плоскости.

Теорема. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, то она перпендикулярна плоскости.

Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Поэтому для реализации нашей цели нужно найти две различные плоскости, содержащие прямую B₁D, и построить в них нужные перпендикуляры. В качестве таковых в кубе можно взять, например, плоскости B₁BDD₁ и B₁ADC₁

Построим сечение B₁BDD₁. Две противоположные стороны этого четырёхугольника являются рёбрами куба, а две другие — диагоналями его граней. По свойствам куба можем сделать вывод, что B₁BDD₁ – прямоугольник длина которого в √2 _ раз больше ширины. Делим диагональ на 4 части и ставим точку К, удовлетворяющую условию B₁K : B₁D = 1 : 4. Проводим через эту точку перпендикуляр к B₁D. Отрезок MN лежит на одной из искомых прямых.
При необходимости легко уточнить положение точек M и N на поверхности куба. Если задана длина ребра (или можно обозначить её, например, символом a), то длины отрезков B₁M и B₁N легко вычисляются из подобия прямоугольных треугольников, которое хорошо просматривается на плоском чертеже.

Получили четыре точки, принадлежащие искомой плоскости сечения и поверхности куба. Соединяем прямой линией точки M и F на грани BСС₁B₁. Соединяем точки F и N на грани A₁B₁С₁D₁ и продолжаем прямую до пересечения с ребром A₁B₁ в точке R. Соединяем точки R и E на грани A₁B₁BA и продолжаем прямую до пересечения с ребром B₁B в точке. M ? Но где гарантия, что именно в точке M, а не выше или ниже по ребру?

Если были проведены вычисления отрезков B₁F = B₁M и B₁N = B₁E в процессе анализа плоских прямоугольников, то ответ становится очевидным: так как прямоугольные треугольники B₁RF, B₁RM и B₁FM равнобедренные и равные.
Если же при построении положение точек M и F не вычислялось, а контролировался только факт их положения на рёбрах куба, то придётся произвести ряд вычислений на этапе доказательства верности построения.

Замечание I.
Возможен альтернативный подход к этой задаче. Так как куб является правильным многогранником и имеет центр симметрии, расположенный в точке пересечения диагоналей, а значит на линии B₁D, с которой мы работаем, то можно предположить, что сечение также будет симметричным и будет иметь форму равностороннего треугольника. Поэтому после анализа (жёлтого) прямоугольника на первом чертеже и получения точки М, можно сразу отложить от вершины B₁ на рёбрах куба равные отрезки B₁R = B₁F = B₁M, а затем доказать, что плоскость RMF перпендикулярна прямой B₁D. Для этого лучше всего воспользоваться теоремой о трёх перпендикулярах.

Теорема. Прямая, проведенная на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и самой наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Замечание II.
Вид сечения сильно зависит от положения точки K на диагонали куба. Попробуйте сместить точку K ближе к середине отрезка B₁D и построить MN ⊥ B₁D в прямоугольнике B₁BDD₁. На каких гранях и рёбрах куба теперь окажутся точки искомого сечения?

Ниже вы можете посмотреть маленькое видео о том, как изменяется сечение куба плоскостью, перпендикулярной его диагонали, в зависимости от положения их точки пересечения.

Задача 16.

При решении задачи предполагаем, что все операции на плоскости, в частности, построение параллельных и перпендикулярных прямых, нам известны из планиметрии и в подробном описании не нуждаются.

Решение.

Чтобы построить плоскость, параллельную заданной плоскости, нужно вспомнить признак параллельности двух плоскостей.

Теорема. Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости.

Теорема. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Кроме того, нам нужно, чтобы плоскость сечения проходила через заданную точку А₂. Значит, хорошо бы сразу найти две такие пересекающиеся прямые, параллельные каким-либо прямым в плоскости PQR, чтобы хотя бы одна из них содержала точку А₂. В этом и будет состоять первый этап решения задачи.

Через точки R и Р проводим РN || CC₁ и RM || CC₁ . Соединяем точки M и N прямой линией. По свойствам призмы получим MN || RР и MN = RР .

Терерь рассмотрим диагональное сечение призмы, проведенное через параллельные прямые AA₁ и СС₁. Плоскость AA₁C₁C содержит заданные точкии A₂ и Q и пересекает заданную плоскость PQR по линии QE. (Буквой Е обозначена общая точка линии пересечения плоскостей и прямой RP.) В этой плоскости (голубой на чертеже) через точку А₂ проводим прямую, параллельную QE до пересечения с верхним основанием призмы в точке F. А₂F || QE по построению.

На верхней грани призмы через точку F проводим прямую, параллельную линии MN, которая в нашем случае пересекает рёбра призмы A₁D₁ и B₁C₁ в точках H и G соответственно. HG || MN .
В зависимости от положения точки А₂ на ребре АА₁ положение точек H и G на рёбрах призмы может изменяться. Например, если бы точка А₂ располагалась ближе к вершине А₁, то точка G могла бы оказаться на ребре А₁В₁, а если бы она находилась близко к вершине А, то точка Н могла бы оказаться на ребре D₁С₁. От этого зависит окончательная форма искомого сечения призмы. Т.е. поскольку в условии задачи положение точек на рёбрах не фиксировано, то ваши ответы могут отличаться от приведенного мной не только формой на чертеже, но и количеством сторон получившегося многоугольника.

Обе прямые HG и RР параллельны прямой MN по построению, следовательно HG || RР . Для прямых в плоскости это вам уже известно давно. Для прямых в пространстве это тоже доказано.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Таким образом, прямые А₂F и HG и есть те самые прямые, которые мы искали. А₂F параллельна QE, следовательно параллельна плоскости PQR. HG параллельна RР, следовательно параллельна плоскости PQR. А₂F и HG пересекаются в точке F. Эти прямые определят секущую плоскость, параллельную заданной PQR.

Продолжим прямую HG до пересечения с ребром A₁B₁ в точке L. Точка L принадлежит верхней и фронтальной (на нашем чертеже) граням призмы, поскольку она принадлежит их общему ребру. Кроме того, точка L принадлежит плоскости сечения, поскольку находится на прямой HG. Следовательно, эта точка должна принадлежать и линии пересечения фронтальной грани с плоскостью сечения. Соединяем точку L с точкой А₂. Эта прямая будет принадлежать плоскости грани АА₁В₁В на основании следующей теоремы.

Теорема. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

Пользуясь этим же утверждением, соединяем и остальные две пары точек, принадлежащих одной грани призмы.

То, что оно удовлетворяет условию проходить через точку А₂ очевидно по построению. То, что плоскость A₂HGK параллельна плоскости RQP мы доказали, ссылаясь на соответствующие положения теории на каждом шаге построения.

Замечание.
Конечно, во время экзамена вы не будете делать несколько чертежей и так подробно описывать построение. Итоговый чертёж будет выглядеть примерно так.
Однако, не забывайте, что основное требование к заданиям второй части ЕГЭ профильного уровня это обоснованность решения. Поэтому, если вы просто выполнили все построения и представили на проверку итоговый чертёж, то к нему необходимо написать доказательство, которое содержит ссылки на теорию. При этом не обязательно цитировать теоремы полностью, можно упомянуть их названия.

Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.

Понравились материалы сайта?
Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Узнать ещё

Знание — сила. Познавательная информация

Сечение куба плоскостью

Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.

Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.

Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.

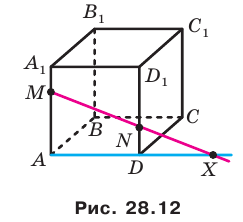
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.

Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.

2) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.

Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).

Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).

Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.

Пятиугольник MNLPS — искомое сечение.

3) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).

Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.

Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).

Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.

Шестиугольник MNHEPF — искомое сечение.

Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.

Работа с прямой PE дает то же сечение MNHEPF.

4) Построить сечение куба плоскостью, проходящей через точку M, N, P.

Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.

Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.

Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.

Урок 3. Линейная перспектива. Построения, часть 1.

Без знания законов линейной перспективы невозможно реалистично изобразить ни один объемный предмет, будь то человек или табуретка.

Но пугаться не стоит. Несмотря на громкое название, основных законов всего два и запомнить их очень просто.

Все вы когда-нибудь ездили на электричке и переходя железнодорожные пути, смотрели не идет ли поезд. Что вы видели в этот момент?

Сходящие на линии горизонта рельсы, очевидно, параллельные друг другу.

И одинаковой высоты столбы линии электропередач, ближний из которых кажется значительно больше дальнего.

Собственно, это и есть два основных закона линейной перспективы:

Параллельные прямые, удаляющиеся от нас мы видим сходящимися в одной точке. Эта точка называется точкой схода. Она, или ее проекция находится на линии горизонта
Предметы одинаковой величины кажутся тем меньше, чем дальше от нас они расположены.

Основные понятия перспективы.

Перед тем, как мы начнем применять эти законы на практике, я дам вам несколько определений. Это упростит объяснения и поможет вам легче понимать специальную литературу.

Горизонт ( линия горизонта) — плоскость, горизонтальная, бесконечная, находящаяся на высоте глаз наблюдателя и ВСЕГДА видимая в виде прямой горизонтальной линии.

Условно можно считать, что перспективный горизонт и горизонт географический в нашем зрении совпадают.

Все предметы, находящиеся ниже этой плоскости, ниже горизонта, мы видим сверху; все предметы, находящиеся выше горизонта,- видим снизу.

Важно запомнить, что линия горизонта всегда находится на уровне ваших глаз. Если вы сядете на землю, то перспективный горизонт опустится вместе с вами, при подъеме в гору он поднимается.

Точка зрения – условное расположение взгляда художника относительно изображаемого объекта.

Картинная плоскость — условная плоскость, на которую проецируется изображение. Она всегда вертикальна. Независимо от того, как расположен ваш лист.

Сокращения. Если поверхность находится под углом к картинной плоскости, она нам кажется более узкой, чем когда она параллельна картинной плоскости. Этот эффект называется — сокращения. Чем ближе угол между плоскостями к 90 градусам, тем больше сокращения. Если угол равен 90 градусам, мы видим поверхность, как линию.

Основные понятия. Тест.

Чтобы закрепить полученные знания, предлагаю вам пройти небольшой тест. Ответы присылайте, пожалуйста, мне в личном сообщении.

Где находится линия горизонта на картине.
1. А
2. Б
3. В
4. В натюрморте ее нет, горизонт виден только в пейзаже.
Картинная плоскость…
1. … всегда совпадает с плоскостью листа, на котором вы работаете.
2. … может совпадать, если лист расположен вертикально и прямо перед вами.
3. … никогда не совпадает.
Геометрические тела в натюрморте находятся …
1. … на линии горизонта.
2. … выше линии горизонта.
3. … ниже линии горизонта.
4. … и выше и ниже.

Перспектива с одной точкой схода.

Один из двух наиболее распространенных типов перспективных построений. Мы ее используем, когда рисуем объект с прямыми углами, передняя сторона которого параллельна картинной плоскости. Этот тип построений часто используется для изображений интерьеров и архитектуры.

Saint Jerome in His Study Albrecht Dürer 1514

Разберем построения перспективы с одной точкой схода на примере построения куба.

Нарисуем на нашем листе линию горизонта. Местоположение выбираем произвольно, лучше в середине или верхней трети листаю
Нарисуем переднюю сторону куба, ниже линии горизонта.Она будет видна нам без искажений, то есть как квадрат.

Зададим точку схода (Т.С.) на линии горизонта. Когда мы рисуем по воображению, мы ее задаем произвольно. При натурном рисовании, она зависит от нашей точки зрения и определяется по параллельным прямым в изображаемом объекте.

Уходящие от нас ребра куба параллельны друг другу, а значит сходятся на линии горизонта в точке схода. Проведем прямые из углов передней стороны куба в точку схода.

Определим на глаз длину уходящих от нас ребер куба. Мы видим их в сокращении. Справа от рисунка показаны ошибка при определении длины.

Достраиваем дальнюю сторону куба. Обратите внимание, что она тоже видна нам без искажений, то есть, как квадрат.

Упражнение 1.

Постройте кубы на линии горизонта и выше нее.

Дополнительное упражнение 1.

Распечатайте работы, восстановите построение и найдите, где проходит линия горизонта.

Дополнительное упражнение 2.

Постройте недостающие ножки у стола.

Перспектива с двумя точками схода.

Это более распространенный тип перспективных построений. Мы им пользуемся тогда, когда изображаем объекты, стороны которых расположены под прямым углом друг к другу. Сами эти объекты могут находиться под произвольными углом к картинной плоскости.

Обратите внимание, что несмотря на название типа построения, на одной работе точек схода может быть бесконечно много. Потому что для каждой группы параллельных прямых точка схода своя. Если у вас на работе несколько предметов, расположенных под разным углом к картинной плоскости, групп параллельных прямых тоже будет несколько.

View of Warsaw from the Terrace of the Royal Castle
Bernardo Bellotto1773

В одной работе могут совмещаться построение перспективы с одной и с двумя точками схода.

В системах построения с одной и с двумя точками схода мы условно считаем все вертикали строго вертикальны. Мы не учитываем, что вы смотрите на объект сверху или снизу и, соответственно, один из его краев ближе к вам, а вертикальные грани являются параллельными прямыми, удаляющимся от вас и должны иметь точку схода. Если вы хотите учитывать этот фактор, вам нужно использовать систему построения с тремя точками схода. Но о ней и о других системах построения объемных изображений мы будем говорить в следующем курсе.

Разберем построения перспективы с двумя точками схода на примере куба.

Проводим линию горизонта по центру листа или чуть выше.
Произвольно задаем длину переднего вертикального ребра куба.

Задаем направления горизонтальных, уходящих от нас, ребер куба. Углы выбираем произвольно, но стараемся, чтобы визуально угол между ребрами читался как прямой. (Он не будет прямым в геометрическом смысле, так как он находится не в плоскости, параллельной картинной, и мы видели его с перспективными искажениями)

Продлеваем горизонтальные ребра до линии горизонта. На пересечении получаем две точки схода (Т.С1 и Т.С.2).

От верхнего края переднего ребра проводим линии в точки схода.

На глаз определяем ширину боковых сторон куба. Обратите внимание, что их ширина будет меньше высоты, так как мы видим ее в сокращении, а высоту- нет. Чем на вашем рисунке меньше угол между горизонтальным и вертикальным ребром, тем уже соответствующая сторона.

От дальних углов боковых поверхностей проводим линии в точки схода.

На пересечении получаем верх и низ дальнего вертикального ребра. Соединяем их — строем ребро.

Упражнение 2.

Постройте кубы на и выше линии горизонта с теми же точками схода.

Задание. Воображаемый интерьер.

То, что окружает человека иногда говорит о нем больше, чем его внешность. Мне бы хотелось, чтобы вы придумали интерьер «с характером»: пространство, глядя на которое понимаешь, кто там обитает или что там произошло. Хотя ни обитателей ни событий мы не видим.

Как примеры тем предлагаю:

» комната, где прячется преступник»

«комната одинокого человека»

«комната, где находят ответы на вопросы»

Если вы боитесь не справиться с интерьером, можно взять упрощённый вариант задания — предмет мебели, по которому можно узнать владельца, Например: » любимое кресло старого профессора». Можно пофантазировать на тему любимых предметов мебели литературных героев.

Дополнительное упражнение 3.

Даже мастера путались в построениях.

Распечатайте картины, восстановите линии построения и найдите, где ошиблись художники.

Дополнительное задание.

Композиция из геометрических тел. Линейный рисунок без тона. Основные элементы строим напросвет( так, как будто они из стекла) Стараемся пока использовать только кубы или прямоугольные параллелепипеды.

Кубы построены напросвет

Предлагаю вам вообразить себя архитектором или скульптором-абстракционистом и придумать интересную и эстетичную конструкцию из геометрических тел. Вы можете создать просто гармоничную структуру или попробовать изобразить абстрактное понятие, например, тяжесть или легкость, величие, власть или угрозу. Любые, даже самые необычные варианты, приветствуются.

источники:

Сечение куба плоскостью

Урок 3. Линейная перспектива. Построения, часть 1.

Источник

Плоскости в пространстве

§ 13.Параллельность плоскостей

13.1. Признаки параллельности плоскостей

При взаимном расположении двух плоскостей в пространстве возможен один из двух взаимно исключающих случаев.

1. Две плоскости имеют общую точку. Тогда по аксиоме пересечения двух плоскостей они имеют общую прямую. Такие плоскости называются пересекающимися.

2. Две плоскости не имеют общей точки.

Определение. Две плоскости, не имеющие общей точки, называются параллельными.

Если плоскости α и β параллельны, то записывают: α ‖ β или β ‖ α. При этом также говорят, что плоскость α параллельна плоскости β или плоскость β параллельна плоскости α.

В п. 9.1 доказано, что в пространстве существуют параллельные плоскости. Но возникает вопрос: как определить, параллельны ли две данные плоскости? Ответить на этот вопрос помогают признаки параллельности двух плоскостей (т. 18, 19 и 24).

Теорема 18 (признак параллельности плоскостей). Если каждая из двух пересекающихся прямых одной плоскости параллельна другой плоскости, то данные плоскости параллельны.

Дано: α, β, a ⊂ α, b ⊂ α, a ∩ b = M; a ‖ β, b ‖ β (рис. 82).

Доказать: α ‖ β.

Рис. 82

Доказательство. Рассуждаем методом от противного. Предположим, что плоскости α и β не параллельны. Тогда они пересекаются по некоторой прямой c (см. рис. 82).

В плоскости α расположены прямая c и данные пересекающиеся прямые a и b. Так как из двух пересекающихся прямых не более чем одна может быть параллельна данной прямой, то прямая c пересекает, по крайней мере, одну из прямых a и b. Пусть прямая c пересекает прямую a в некоторой точке K: a ∩ c = K.

Имеем: прямая c, следовательно, и точка K лежат в плоскости β. Значит, прямая a пересекает плоскость β. Это противоречит условию теоремы (a ‖ β).

Также к противоречию с условием теоремы придём, если допустим, что пересекаются прямые c и b или прямая c пересекает обе прямые a и b.

Таким образом, предположив, что плоскости α и β не параллельны, мы пришли к противоречию. Это означает, что предположение неверно. Следовательно, α ‖ β. Теорема доказана. ▼

Теорема 19. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Рис. 83

Доказательство. Пусть прямые a и b плоскости α пересекаются в точке M, прямые a1 и b1 плоскости β параллельны соответственно прямым a и b (рис. 83). Тогда по признаку параллельности прямой и плоскости имеем:

a ‖ a1, a1 ⊂ β ⇒ a ‖ β; b ‖ b1, b1 ⊂ β ⇒ b ‖ β.

Таким образом, пересекающиеся прямые a и b в плоскости α параллельны плоскости β. По предыдущей теореме плоскости α и β параллельны. Теорема доказана. ▼

Заметим, что доказанная теорема 19 также является признаком параллельности двух плоскостей и может быть доказана независимо от теоремы 18. Самостоятельно докажите теорему 19, не используя теорему 18.

Докажите самостоятельно, что две плоскости, перпендикулярные одной и той же прямой, параллельны.

13.2. Свойства параллельных плоскостей

Теорема 20. Прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны.

Рис. 84

Дано: α ‖ β, γ ∩ α = a, γ ∩ β = b (рис. 84).

Доказать: a ‖ b.

Доказательство. Прямые a и b лежат в одной плоскости γ. Эти прямые не имеют общей точки, так как плоскости α и β параллельны. Следовательно, прямые a и b параллельны по определению. Теорема доказана. ▼

Теорема 21. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.

Дано: α ‖ β, a ∩ α = A (рис. 85).

Доказать: a пересекает β.

Доказательство. Выберем в плоскости β любую точку C. Через эту точку и прямую a проведём плоскость γ.

Рис. 85

Так как плоскость γ имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости γ прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости β, то точка B является точкой пересечения прямой a и плоскости β. Теорема доказана. ▼

Теорема 22. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.

Дано: α ‖ β, α и γ пересекаются (рис. 86).

Рис. 86

Доказать: β и γ пересекаются.

Доказательство. Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 21 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана. ▼

Вернёмся к вопросу о существовании параллельных плоскостей.

Теорема 23. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.

Дано: α, M; M ∉ α (рис. 87).

Доказать: существует единственная плоскость β такая, что M ∈ β, β ‖ α.

Рис. 87

Доказательство. В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a1 и b1, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a1 и b1, обозначим β. На основании теоремы 19 плоскость β параллельна плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.

Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.

Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 22 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана. ▼

Данная теорема даёт способ построения в пространстве плоскости, параллельной данной плоскости.

ЗадаЧа. В кубе ABCDA1B1C1D1 через точку K — середину ребра A1D1 провести сечение, параллельное плоскости A1C1D.

Решение. Плоскость сечения пересекает плоскость AA1D1 по прямой KM, параллельной прямой A1D (почему?), а плоскость DCC1 — по прямой ME, параллельной прямой C1D (почему?). Треугольник KME — искомое сечение (рис. 88).

Самостоятельно постройте сечение этого куба плоскостью, проходящей через середину ребра AA1 параллельно плоскости A1C1D, и вы получите в сечении правильный шестиугольник.

Рис. 88

Теорема 24. Две плоскости, параллельные третьей, параллельны.

Рис. 89

Дано: α ‖ β, γ ‖ β (рис. 89).

Доказать: α ‖ γ.

Доказательство. Допустим, что плоскости α и γ пересекаются по некоторой прямой c. Выберем на прямой c произвольную точку M. Через эту точку проходят две различные плоскости α и γ, каждая из которых параллельна плоскости β. Это противоречит теореме 23. Значит, предположение было неверно. Поэтому α ‖ γ. Теорема доказана. ▼

Теорема 25. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

Дано: α ‖ β; a ‖ b; a ∩ α = A1, a ∩ β = B1;

b ∩ α = A2, b ∩ β = B2 (рис. 90).

Рис. 90

Доказать: A1B1 = A2B2.

Доказательство. Проведём через параллельные прямые a и b плоскость γ (т. 3). Она пересекает параллельные плоскости α и β по параллельным прямым A1A2 и B1B2 (т. 20).

А так как a ‖ b, то четырёхугольник A1A2B2B1 — параллелограмм. Поэтому A1B1 = A2B2 (как противоположные стороны этого параллелограмма). Теорема доказана. ▼

Теорема 26. Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости.

Дано: α1 ‖ α2, l ⊥ α1.

Доказать: l ⊥ α2.

Рис. 91

Проведите доказательство самостоятельно, построив две любые плоскости γ1 и γ2, проходящие через прямую l (рис. 91).

ЗадаЧа 4.007. Построить сечение пятиугольной пирамиды PABCDE плоскостью α, которая проходит через внутреннюю точку M основания ABCDE параллельно грани PAB (рис. 92).

Решение. Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость α параллельна грани PAB, то: а) прямая пересечения плоскости α с плоскостью ABC (плоскостью основания пирамиды) должна быть параллельна AB; б) прямая пересечения плоскости α с гранью PAE — параллельна AP; в) прямая пересечения α с плоскостью грани PBC — параллельна PB; г) прямая пересечения плоскости α с плоскостью PAD — параллельна PA, поэтому проводим: 1) через точку M прямую KF ‖ AB, K ∈ BC, F ∈ AE; 2) прямую FH ‖ PA, H ∈ PE; 3) прямую KR ‖ PB, R ∈ PC; 4) прямую ML ‖ AP, L ∈ PD. Пятиугольник HLRKF — искомое сечение.

Доказательство проделайте самостоятельно.

Рис. 92

Рис. 93

Замечание. При внимательном анализе обнаруживается аналогия между свойствами параллельных плоскостей в пространстве и свойствами параллельных прямых на плоскости. Попробуйте, например, пользуясь рисунком 93, сформулировать и доказать «пространственный аналог теоремы Фалеса».

Источник

Ðассматривается отношение параллельности плоскостей, его свойства и применения.

Наглядное представление о расположении двух

плоскостей дает моделирование с помощью плоскостей поверхностей смежных стен, потолка и пола комнаты, двухъярусных кроватей, двух скрепленных листов бу-

маги и т. п. (рис. 242–244).

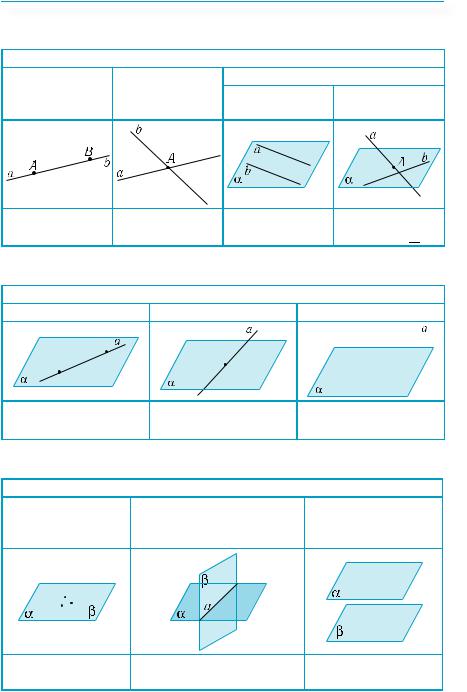
Хотя существует бесконечное множество вариантов взаимного расположения различных плоскостей, для установления и характеристики которых в последующем будут применены измерения углов и расстояний, мы сначала остановимся на таких, где в основу классификации (как и прямых с плоскостями) положено количество их общих точек.

1. Две плоскости имеют не менее трёх общих точек, не лежащих на одной прямой. Такие плоскости совпадают (аксиома С2, §7).

2. Общие точки двух плоскостей расположены на одной прямой, являющейся линией пересеченияэтихплоскостей(аксиомаС3,§7). Такие плоскости пересекаются.

Параллельность плоскостей

213

3.Две плоскости не имеют общих точек.

Вэтом случае их называют параллельны-

ми.

Две плоскости называются параллельными, если они не имеют общих точек.

Параллельность плоскостей обозначается знаком ||: α || β.

Как всегда, при введении геометрических понятий возника-

ет проблема их существования. Существование пересекающих-

ся плоскостей является характерным признаком пространства,

и этим мы уже многократно пользовались. Менее очевидным яв-

ляется существование параллельных плоскостей. Нет никакого

сомнения в том, что, например, плоскости противоположных гра-

ней куба параллельны, то есть не пересекаются. Но непосредс-

твенно, по определению, это установить невозможно. Для реше-

ния поставленного вопроса, а также других вопросов, связанных с

параллельностью плоскостей, необходимо иметь признак параллельности.

Для поиска признака целесообразно рассматривать плоскость,

«сотканную» из прямых. Очевидно, что каждая прямая одной из

параллельных плоскостей должна быть параллельна другой.

В противном случае плоскости будут иметь общую точку. Доста-

точно ли параллельности плоскости β одной прямой плоскости α

для того, чтобы плоскости α и β были параллельными? Безуслов-

но, нет (обоснуйте это!). Практический опыт свидетельствует, что

двух таких пересекающихся прямых достаточно. Чтобы закрепить

на мачте параллельную земле площадку, достаточно положить ее

на две прикрепленные к мачте балки, параллель-
ные земле (рис. 245). Можно привести еще много
примеров применения этого приема обеспечения
параллельности плоских поверхностей реальных
объектов (попробуйте это сделать!).
Приведенные рассуждения позволяют сформу-
лировать следующее утверждение.
Теорема	1	(признак параллельности плоскостей).
Если	две	пересекающиеся прямые одной плоско-

сти параллельны второй плоскости, то эти плоскости параллельны.

214	Параллельность прямых и плоскостей

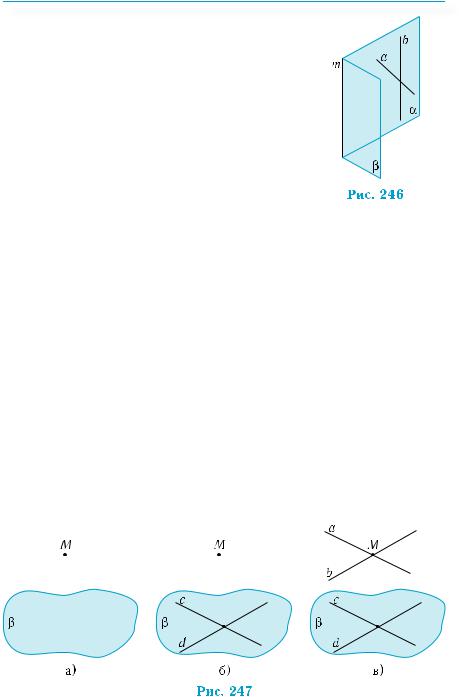
 Пусть пересекающиеся прямые а и b плоскости α параллельны плоскости β. Докажем, что плоскости α и β параллельны методом от противного. Для этого допустим, что плоскости α и β пересекаются по прямой

т (рис. 246). Прямые а и b пересекать прямую т не могут по условию. Однако тогда в плоскости α через одну точку проведены две прямые, не пересекающиеся с прямой т, то есть параллельные ей. Это противоречие

и завершает доказательство теоремы.

Признаком параллельности плоскостей пользуются при горизонтальном размещении плоских конструкций (бетонных плит, пола, диска угломерных приборов и т. п.) с помощью двух уровней, размещенных в плоскости конструкции на пересекающихся прямых. На основании этого признака можно выполнить построение плоскости, параллельной данной.

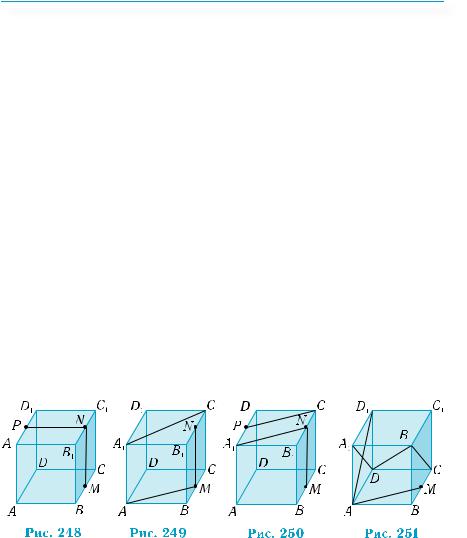
Задача 1. Через точку, лежащую вне данной плоскости, провести плоскость, параллельную данной.

Пусть даны плоскость β и точка М вне плоскости (рис. 247, а). Проведем через точку М две пересекающиеся прямые а и b, параллельные плоскости β. Для этого нужно взять в плоскости β две пересекающиеся прямые с и d (рис. 247, б). Потом через точку М провести прямые а и b, параллельные прямым с и d соответствен-

но (рис. 247, в).

Пересекающиеся прямые а и b параллельны плоскости β, по признаку параллельности прямой и плоскости (теорема 1 §11). Они определяют однозначно плоскость α. Согласно доказанному признаку, α || β.

Параллельность плоскостей

215

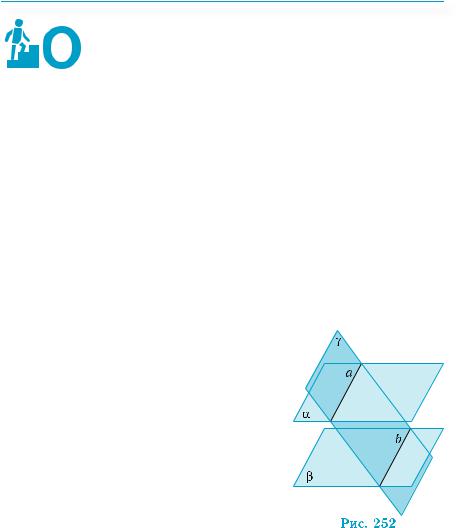
Пример 1. Дан куб ABCDA1B1C1D1, точки М, N, Р – середины ребер ВС, В1С1, А1D1 соответственно. Установить взаимное расположение плоскостей: 1) АВВ1 и PNM; 2) NMA и A1C1C; 3) A1NM

и РC1C; 4) МAD1 и DB1C.

 1) Плоскости ABB1 и РNM (рис. 248) параллельны, по признаку параллельности плоскостей (теорема 1). Действительно, прямые РN и NM пересекаются и параллельны плоскости ABB1, по признаку параллельности прямой и плоскости (теорема 1 §11), ведь отрезки РN и NM соединяют середины противоположных сторон квадратов, поэтому они параллельны сторонам квадратов:

РN || A1B1, NM || В1B.

2) Плоскости NMA и A1C1C пересекаются по прямой AA1 (рис. 249). Действительно, прямые AA1 и СC1 параллельны, по признаку параллельности прямых (AA1 || ВB1, ВB1 || СC1). Поэтому прямая AA1 лежит в плоскости A1C1C. Аналогично обосновывается принадлежность прямой AA1 плоскости NMA.

3) Плоскости A1NM и РC1C (рис. 250) параллельны, по признаку параллельности плоскостей. Действительно, NM || С1C. Поэтому прямая NM параллельна плоскости РC1C. Отрезки РC1 и A1N также параллельны, поскольку четырехугольник РC1NA1 – параллелограмм (А1P || NC1, A1P = NC1). Таким образом, прямая A1N параллельна плоскости РC1C. Прямые A1N и NM пересекаются.

4) Плоскости MAD1 и DB1C пересекаются (рис. 251). Хотя линию их пересечения построить непросто, но указать одну точку этой линии нетрудно. Действительно, прямые A1D и В1C — параллельны, поскольку четырехугольник A1B1CD – параллелограмм (A1B1 = AВ = СD, A1B1 || AВ, AВ || СD). Поэтому прямая A1D принадлежит плоскости DB1C. Прямые A1D и AD1 пересекаются в точке, общей для плоскостей MAD1, и DB1C.

216		Параллельность прямых и плоскостей
		Приведенный признак параллельности плоскостей

		иногда удобнее использовать в несколько другой
		форме.

Теорема	1′ (признак параллельности плоскостей).

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Пользуясь признаком параллельности прямой и плоскости (теорема 1 §11), нетрудно установить, что из условия теоремы 1′ вытекает условие теоремы 1. Применение теоремы, обратной признаку параллельности прямой и плоскости (теорема 2 §11) завершает обоснование эквивалентности условий теорем 1 и 1′.

Естественно возникает вопрос об однозначности приведенного в задаче 1 построения. Поскольку нам придется не раз воспользоваться этим свойством, то выделим его как отдельную теорему. Однако сначала рассмотрим другое утверждение.

Теорема 2 (о пересечении двух параллельных плоскостей третьей).

Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

 Пусть даны параллельные плоскости α, β и плоскость γ, их пересекающая (рис. 252). Обозначим линии пересечения

через а и b. Эти прямые лежат в плоскости γ и не пересекаются, поскольку плоскости α и β не имеют общих точек. Поэтому пря-

мые а и b — параллельны.

Теорема 3 (о существовании и единственности плоскости, параллельной данной).

Через точку, расположенную вне данной плоскости, можно провести единственную плоскость, параллельную данной.

 Построение такой плоскости выполнено в задаче 1. Однозначность построения докажем методом от противного. Допустим, что через точку М проведены две различные плоскости α и γ, па-

Параллельность плоскостей

217

раллельные плоскости β (рис. 253), и прямая т — линия их пересечения. Проведем через точку М плоскость δ, пересекающуюся с прямой

т и плоскостью β (как это можно сделать?). Обозначим через а и b

линии пересечения плоскости δ с плоскостями α и γ, а через с — линию пересечения плоскостей δ и β (рис. 253). Согласно теореме 2, а || с

и b|| с. То есть в плоскости δ через

точку М проходят две прямые, параллельные прямой с. Противоречие свидетельствует о неверности предположения.

Отношение параллельности плоскостей обладает рядом свойств, имеющих аналоги в планиметрии.

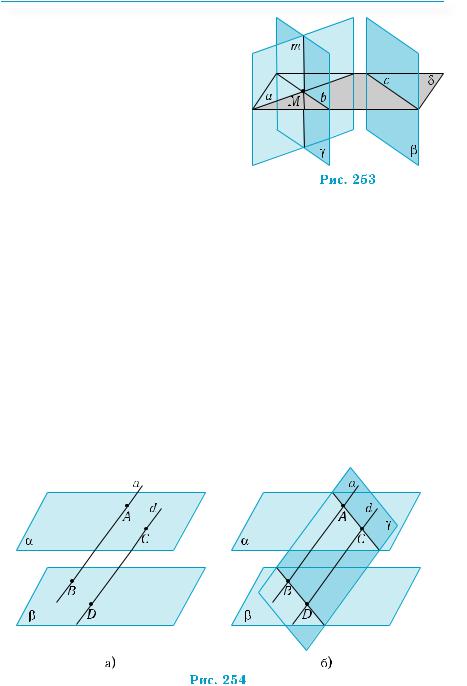
Теорема 4 (об отрезках параллельных прямых между параллельными плоскостями).

Отрезки параллельных прямых, отсекаемые параллельными плоскостями, равны между собой.

Пусть даны две параллельные плоскости α и β и отрезки АВ

иСD параллельных прямых a и d, отсекаемые этими плоскостями (рис. 254, а). Проведем через прямые a и d плоскость γ (рис. 254, б). Она пересекает плоскости α и β по прямым АС и BD, которые, согласно теореме 2, параллельны. Поэтому четырехугольник АBСD — параллелограмм, его противоположные стороны АС и BD равны.

218	Параллельность прямых и плоскостей

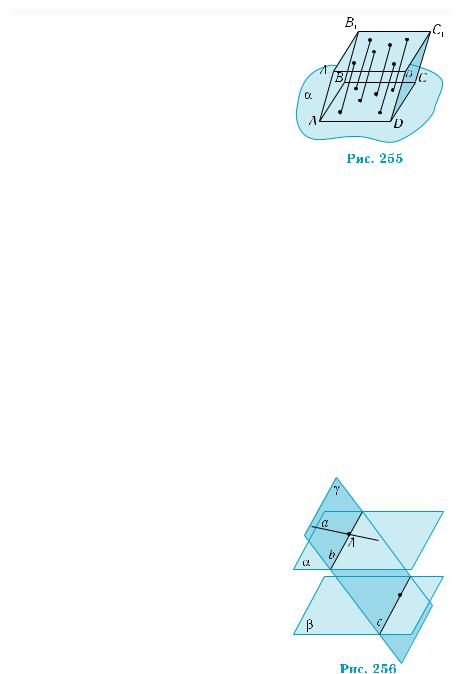
Из приведенного свойства вытекает, что если от всех точек плоскости отложить

по одну сторону от плоскости параллельные отрезки одинаковой длины, то концы этих отрезков образуют две параллельные плоскости. Именно на этом свойстве основано построение параллелепипеда с помощью отложения отрезков (рис. 255).

Теорема 5 (о транзитивности отношения параллельности плоскостей).

Если каждая из двух плоскостей параллельна третьей, то данные две плоскости параллельны между собой.

Пусть плоскости α и β параллельны плоскости γ. Допустим, что

αи β не параллельны. Тогда плоскости α и β имеют общую точку, и через эту точку проходят две различные плоскости, параллельные плоскости γ, что противоречит теореме 3. Поэтому плоскости α и β не имеют общих точек, то есть они параллельны.

Теорема 5 является еще одним признаком параллельности плоскостей. Она широко применяется как в геометрии, так и в практической деятельности. Например, в многоэтажном здании параллельность плоскостей пола и потолка на каждом этаже гарантирует их параллельность и на разных этажах.

Задача 2. Доказать, что если прямая а пересекает плоскость α, то она пересекает также каждую плоскость, параллельную плоскости α.

 Пусть плоскости α и β параллельны, а прямая а пересекает плоскость α в точке А. Докажем, что она пересекает и плоскость

β. Допустим, что это не так. Тогда прямая а параллельна плоскости β. Проведем плоскость γ через прямую а и произвольную точку плоскости β (рис. 256).

Эта плоскость пересекает параллельные плоскости α и β по прямым b и с. Со-

гласно теореме 2, b || с, то есть в плоскости γ через точку А проходят две прямые а и b, параллельные прямой с. Это противоречие и доказывает утверждение.

Параллельность плоскостей

219

Попробуйте доказать самостоятельно, что если плоскость α пересекает плоскость β, то она пересекает также каждую плоскость, параллельную плоскости β.

Пример 2. В тетраэдре АBCD точки K, F, Е — середины ребер DA, DС, DВ, а М и Р — центры масс граней АВD и ВСD соответственно.

1) Установить взаимное расположение плоскостей KEF и ABC;

DEF и ABC.

2) Построить линию пересечения плоскостей AFB и KEC.

3) Найти площадь сечения тетраэдра плоскостью, параллельной плоскости АВD и проходящей через точку Р, если все рёбра тетраэдра равны а.

 Построим рисунок, соответствующий условию (рис. 257, а). 1) Плоскости KEF и ABC параллельны, по признаку параллельности плоскостей (теорема 1’): пересекающиеся прямые KE и KF плоскости KEF параллельны пересекающимся прямым AB и AC плоскости ABC (на них лежат средние линии соответствую-

щих треугольников).

Плоскости DEF и ABC пересекаются по прямой BC, так как прямая BC принадлежит обеим плоскостям, а совпадать они не могут — точки А, В, С, D не лежат в одной плоскости.

2) Плоскость AFB пересекается с плоскостью KEC по прямой, содержащей точку Р, так как прямые СЕ и BF, лежащие в этих плоскостях, находятся в плоскости BCD и пересекаются в точке Р. Другой точкой является точка пересечения Q прямых AF и CK в плоскости ACD (рис. 257, б). Очевидно, что эта точка является центром масс грани ACD. Искомым пересечением является прямая PQ.

220	Параллельность прямых и плоскостей

3) Построим сечение, указанное в условии, пользуясь признаком параллельности плоскостей. Проведем через точки P и Q прямые, параллельные прямым DB и DA соответственно (рис. 257, в). Эти прямые пересекают отрезок CD в точке L. Последнее вытекает из свойства центра масс треугольника — он делит медианы треугольника в отношении 2 : 1, считая от вершины. Осталось применить теорему Фалеса. Таким образом, плоскости PLQ и BDA параллельны. Искомым сечением является треугольник LSN.

По построению, треугольники BCD и SCL подобны с коэффициентом подобия CECP = 32 . Поэтому LS = 32 BD . Аналогично уста-

навливаются равенства: LN = 32 AD , NS = 32 AB . Отсюда вытекает, что треугольники LSN и ABD подобны с коэффициентом подобия 32 . По свойствам площадей подобных треугольников,

SLNS = 49 SABD . Осталось найти площадь треугольника ABD. По-

скольку, по условию, все рёбра тетраэдра равны а, то SABD = 43 a2 .

Искомая площадь равна 313 a2.

Уместно обратить внимание на то, что ответ зависит лишь от площади грани ABD. Поэтому равенство всех рёбер является лишь средством найти эту площадь. Таким образом, данную задачу можно существенно обобщить.

Ответ. 1) KEF || ABC; 3) 313 a2 .

 Контрольные вопросы

1.Верно ли, что две плоскости параллельны, если каждая прямая, лежащая в одной плоскости, параллельна другой плоскости?

2.Плоскости α и β параллельны. Существуют ли скрещивающиеся прямые, лежащие в этих плоскостях?

3.Две стороны треугольника параллельны некоторой плоскости. Параллельна ли этой плоскости третья сторона треугольника?

Параллельность плоскостей

221

4.Две стороны параллелограмма параллельны некоторой плоскости. Верно ли, что плоскость параллелограмма параллельна данной плоскости?

5.Могут ли быть неравными отрезки двух прямых, отсекаемые параллельными плоскостями?

6.Может ли сечением куба быть равнобокая трапеция? Может ли сечением куба быть правильный пятиугольник? Верно ли, что две плоскости, параллельные одной и той же прямой, параллельны между собой?

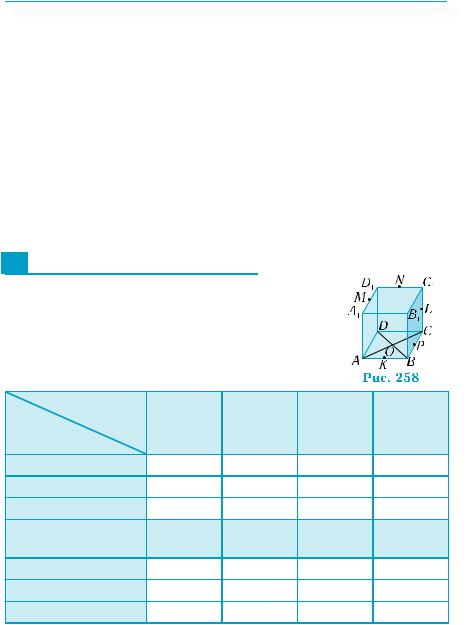
Линии пересечения плоскостей α и β плоскостью γ параллельны между собой. Параллельны ли плоскости α и β?

Могут ли три грани куба быть параллельными одной плоскости?

Графические упражнения

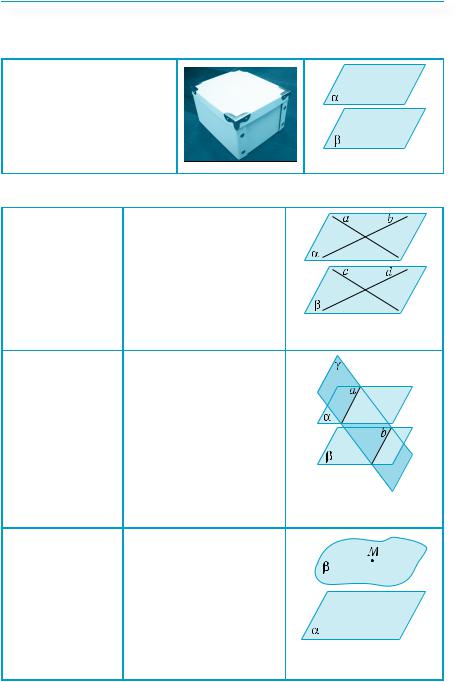
1. На рис.258 изображен куб ABCDA1B1C1D1, точки М, N, K, L, Р — середины соответствующих рёбер. Заполните по приведенному образцу таблицу, выбрав необходимое расположение плоскостей α и β.

α и β

Взаимное

расположение

α × β

α || β α = β

α × β α || β α = β

A1B1C1	MPK	MNK	D1KP
и ADC	и BB1D	и MNP	и BMN
+
MNK	B1KP	A1DC1	A1C1C
и PLN	и DMN	и AB1C	и MKP

222	Параллельность прямых и плоскостей

2. На рис. 259 изображен тетраэдр ABCD, точки K, F, M, N, Q — середины соответствующих рёбер. Укажите:

1) плоскость, проходящую через точку K параллельно плоскости ABC;

2) плоскость, проходящую через прямую BD параллельно плоскости MNQ.

3.Определите, чем является сечение фигуры плоскостью, проходящей через данные три точки, изображенные на рисун-

ках 260, а)–д) и 261, а)–г).

4. Постройте рисунок по приведенным данным.

1) Из вершин параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость соответственно в точках A1, B1, C1, D1.

2) Треугольник A1B1C1 является проекцией треугольника ABC на параллельную ему плоскость α. Точка М — середина ВС, М1 — проекция точки М на плоскость α.

Параллельность плоскостей

223

Задачи

207. В кубе ABCDA1B1C1D1 точки О, О1 — центры граней ABCD и A1B1C1D1 соответственно, М — середина ребра АВ.

1°) Определите взаимное расположение плоскостей МО1О

и ADD1, ABD1 и СО1С1.

2°) Постройте точку пересечения плоскости DCC1 и прямой МО1 и линию пересечения плоскостей МСС1 и A1D1C1.

3) Найдите площадь сечения куба плоскостью, параллельной плоскости AD1C1 и проходящей через точку О1, если ребро куба равно а.

208. В тетраэдре ABCD точки K, L, Р — центры масс граней ABD, BDC, ABC соответственно, а М — середина ребра AD.

1°) Определите взаимное расположение плоскостей ACD

и KLP; МLK и ABC.

2°) Постройте точку пересечения плоскости ABC и прямой МL и линию пересечения плоскостей МKL и ABC.

3) Найдите площадь сечения тетраэдра плоскостью, проходящей через точки K, L и М параллельно прямой AD, если все рёбра тетраэдра равны а.

209. Дан куб ABCDA1B1C1D1. Точки L, M, M1 — середины рёбер AB, AD и A1D1 соответственно.

1°) Определите взаимное расположение плоскостей B1D1D

и LMM1.

2) Постройте плоскость, проходящую через точку М параллельно плоскости ACC1.

3) Постройте сечение куба плоскостью, проходящей через точку M1 параллельно плоскости CDD1.

4) Определите взаимное расположение плоскостей МА1В1

и CDМ1.

5) Постройте плоскость, проходящую через прямую C1D1 параллельно плоскости CDM1.

210. В правильной четырехугольной пирамиде SABCD все рёбра равны между собой. Точки L, M и N — середины рёбер AS, BS, CS соответственно.

1°) Определите взаимное расположение: прямых LM и BC; прямой LN и плоскости ABD; плоскостей LMN и BDC.

2°) Докажите, что треугольники ABC и LMN подобны.

3) Постройте сечение пирамиды плоскостью AMN; плоскостью LMN; плоскостью LBC.

4*) Какое из сечений пирамиды, проходящих через вершину S, имеет наибольшую площадь?

224

211.

212.

213.

214.

215.

216.

Параллельность прямых и плоскостей

В тетраэдре SABC все грани — правильные треугольники. Точки L, M и N — середины рёбер AS, BS, CS соответственно. 1°) Определите взаимное расположение прямых LM и ВС. 2°) Определите взаимное расположение прямой LN и плоскости АВС.

3) Докажите, что треугольники LMN и AВС подобны.


Из вершин параллелограмма ABCD, лежащего в одной из
двух параллельных плоскостей, проведены попарно парал-
лельные прямые, пересекающие вторую плоскость соответс-
твенно в точках A1, В1, C1, D1.
1°) Докажите, что четырехугольник A1B1C1D1 – параллело-
грамм.
2°) Докажите, что параллелограммы ABCD и A1B1C1D1
равны между собой.
3°) Определите взаимное расположение плоскостей АВВ1
и DD1C1.
4) Проведите через середину отрезка АА1 плоскость так,
чтобы она пересекала данные прямые в точках, являющих-
ся вершинами параллелограмма, равного параллелограм-
му ABCD.
Даны две параллельные плоскости и точка О, не принадле-
жащая ни одной из этих плоскостей и не лежащая между
ними. Из точки О	проведены три луча, пересекающие плос-
кости соответственно в точках A, B, C и A1, B1, C1 ине лежа-
щие в одной плоскости.
1°) Определите взаимное расположение данных плоскостей
иплоскости,проходящейчерезсерединыотрезковAA1,BB1,CC1.
2) Найдите периметр треугольника A1B1C1, если OA = m,
AA1 = n, AB = c, AC = b, BC = а.
Треугольник А1В1С1 является проекцией треугольника АВС
на параллельную ему плоскость α. Точка M — середина сто-
роны ВС; М1 — проекция точки М	на плоскость α. Точка N
делит сторону АВ	в отношении 1:2.	плоскости M1MN и пря-
1) Постройте точку пересечения N1
мой А1В1.
2) Определите форму четырехугольника M1N1NM.
Точка	M лежит вне плоскости трапеции ABCB с основания-
ми AD	и BC. Постройте линию пересечения плоскостей:
1°) ABM и CDM;	2) CBM и ADM.

Постройте сечение куба, являющееся: 1°) равносторонним треугольником; 2) пятиугольником.

Параллельность плоскостей

225

217.Постройте сечение тетраэдра, являющееся параллелограммом.

218°. Докажите, что противоположные грани параллелепипеда параллельны.

219. Докажите, что множество всех прямых, проходящих через данную точку и параллельных данной плоскости, образует плоскость, параллельную данной.

220. Даны четыре точки A, B, C, D, не лежащие в одной плоскости. Докажите, что каждая плоскость, параллельная прямым AB и CD, пересекает прямые AC, AD, BD, BC в вершинах параллелограмма.

221. Докажите, что плоскость и прямая, не принадлежащая этой плоскости, параллельны между собой, если обе они параллельны одной и той же плоскости.

222. Через точку О пересечения диагоналей куба ABCDA1B1C1D1 проведена плоскость параллельно грани ABCD. Эта плоскость пересекает рёбра BB1 и CC1 в точках M и N соответственно. Докажите, что угол MON — прямой.

223. Докажите, что две плоскости параллельны между собой тогда и только тогда, когда каждая прямая, пересекающая одну из плоскостей, пересекает и вторую.

224*. В треугольной пирамиде SABC через отрезки AD и CE, где D — середина SB, а E — середина SA, проведите сечения пирамиды, параллельные между собой.

225. Найдите геометрические места:

1) середин всех отрезков с концами на двух данных параллельных плоскостях; 2*) середин отрезков с концами на двух данных скрещивающихся прямых.

226*.Сторона АВ треугольника АВС, лежащего в плоскости α, параллельна плоскости β. Равносторонний треугольник А1В1С1 является параллельной проекцией треугольника АВС на плоскость β; АВ = 5, ВС = 6, АС = 9.

1) Установите взаимное расположение прямых АВ и А1В1,

ВС и В1С1, А1С1 и AC.

2) Найдите площадь треугольника А1В1С1.

227*.Даны две скрещивающиеся прямые. Укажите множество всех точек пространства, через которые можно провести прямую, пересекающую каждую из двух данных прямых.

226	Параллельность прямых и плоскостей

Итог

Основное определение

Две плоскости называ-

ются параллельными,

если они не имеют общих точек.

α || β

Основные утверждения

Признак парал- Если две пересекаю- лельности двух щиеся прямые одной плоскостей плоскости соответственно параллельны двум прямым второй плоскости, то эти плос-

кости параллельны.

Теорема о пе- Если две параллель- ресечении двух ные плоскости пе- параллельных ресекаются третьей плоскостей плоскостью, то линии третьей пересечения плоскос-

тей параллельны.

a α,b α,a ×b,c β, d β, a || c, b || d α || β

α || β, a = γ∩α, b = γ∩β a || b

Теорема о су-	Через точку, располо-
ществовании и	женную	вне данной
единственнос-	плоскости, можно про-
ти плоскости,	вести	единственную
параллельной	плоскость, параллель-
данной	ную данной.

M α

β: α || β, М β

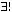
Готовимся к тематичес-

кому оцениванию по теме «Параллельность прямых и плоскостей»

Задания для самоконтроля

1.Четыре точки не принадлежат одной плоскости. Могут ли некоторые три из них лежать на одной прямой?

2.Могутлитриразличныеплоскостииметьровнодвеобщиеточки?

3.Могут ли две скрещивающиеся прямые быть одновременно параллельными третьей прямой?

4.Верно ли, что прямые а и b не параллельны, если не существует прямой с, параллельной а и b?

5.Могут ли равные отрезки иметь неравные проекции?

6.Может ли луч быть параллельной проекцией прямой?

7.Может ли квадрат быть изображением куба?

8.Верно ли, что через данную точку пространства можно провести только одну плоскость, параллельную данной прямой?

9.Всегда ли через данную точку можно провести прямую, параллельную двум данным плоскостям, не содержащим эту точку?

10.Можно ли через две скрещивающиеся прямые провести параллельные плоскости?

Ответы к заданиям для самоконтроля

1	2	3	4	5	6	7	8	9	10
Нет	Нет	Нет	Да	Да	Нет	Да	Нет	Да	Да

Образец контрольной работы

Два параллелограмма АBCD и АBC1D1 лежат в различных плоскостях.

1°) Определите взаимное расположение прямых CD и C1D1.

2°) Определите взаимное расположение прямой C1D1 и плоскости

АВС.

3°) Постройте линию пересечения плоскостей DD1С1 и ВСС1.

4°)ОпределитевзаимноерасположениеплоскостейАDD1 иВCC1.

5) Через точку М, делящую отрезок АВ в отношении 2:1, считая от точки А, проведите плоскость α, параллельную плоскости С1ВС. 6) Постройте точку пересечения прямой АС с плоскостью α и найдите отношение, в котором эта точка делит отрезок АС.

228		Параллельность прямых и плоскостей
Взаимное расположение прямых в пространстве
			Таблица 21
	Число общих точек
Не менее двух	Одна	Нет
лежат в одной	не лежат в од-
		плоскости	ной плоскости

a и b совпада-	a и b пересека-	a и b — парал-	a и b скрещи-
ют (a = b)	ются (а × b)	лельны (a \|\| b)	ваются (а · b)

Взаимноерасположениепрямыхиплоскостейвпространстве

			Таблица 22

	Число общих точек
Не менее двух	Одна	Отсуствуют

а лежит в α	а пересекает α	а і α — параллель-
(а α)	(а × α)	ны (а \|\| α)
Взаимное расположение плоскостей в пространстве
		Таблица 23
	Число общих точек
Не менее трех,	Не меньше одной, но	Отсуствуют
не лежащих на	нет общих точек, не ле-
одной прямой	жащих на одной прямой

α и β совпадают	α и β пересекаются	α и β — парал-
(α = β)	(α × β)	лельны (α \|\| β)

Тригонометрические

функции

С тригонометрическими функциями вы уже имели дело на уроках гео метрии. До сих пор их приложения, в основном, ограничивались решени ем треугольников, то есть речь шла о нахождении одних элементов тре угольника по другим. Из истории математики известно, что возникновение тригонометрии связано с измерением длин и углов. Однако, теперь сфера

ееприложений намного шире, чем в древности.

Слово «тригонометрия» происходит от греческих τριγωνον

(trigonon) – треугольник и µετρεω (metreo) — меряю, изме—

ряю. Буквально оно означает измерение треугольников.

Вэтой главе систематизируется материал, уже известный вам из кур са геометрии, продолжается изучение тригонометрических функций и их приложений для характеристики периодических процессов, в частности, вращательного движения, колебательных процессов и т. п.

Большинство применений тригонометрии касаются именно перио дических процессов, то есть процессов, повторяющихся через равные промежутки времени. Восход и закат Солнца, изменения времен года, вращения колеса — это простейшие примеры таких процессов. Меха нические и электромагнитные колебания являются также важными при мерами периодических процессов. Поэтому исследование периодических процессов — важное задание. И роль математики в его решении является определяющей.

готовимся к изучению темы «Тригонометрические функции»

Изучение темы «Тригонометрические функции» целесообразно начать с повторения определений и свойств тригонометрических функций углов треугольников и их применений для решения как прямоугольных, так и произвольных треугольников.

Синус, косинус, тангенс, котангенс углов прямоугольного

треугольника

Таблица 24

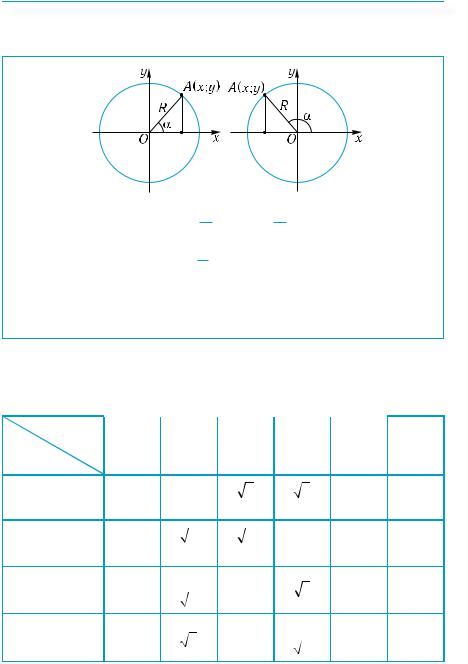
Синусом острого угла называют отношение противолежащего катета к гипотенузе:

sin α = ac .

Косинусом острого угла называют отношение прилежащего катета к гипотенузе:

cosα = bc .

Тангенсом острого угла называют отношение противолежащего катета к прилежащему:

tgα = ab .

Котангенсом острого угла называют отношение прилежащего катета к противолежащему:

ctgα = ab .

Готовимся к изучению темы «Тригонометрические функции»

231

Синус, косинус, тангенс, котангенс углов от 0° до 180°

Таблица 25

sin α = Ry ; cosα = Rx ;

tg α = xy ; ctg α = xy .

(х; у) — координаты точки А, расположенной на верхней полуокружности, α — угол, образованный радиусом ОА окружности с осью х.

Значения синуса, косинуса, тангенса, котангенса

некоторых углов

Таблица 26

Угол t

Функция	0°	30°	45°	60°	90°	180°

sin t	0	1		2		3		1	0
		2			2			2
cos t	1	3		2		1		0	–1
			2			2		2		не
tg t	0	1		1		3		0
					сущест-
3
									вует
ctg t	не				1		1		0	не
сущест-	3						сущест-
		3
	вует							вует

232	Тригонометрические функции

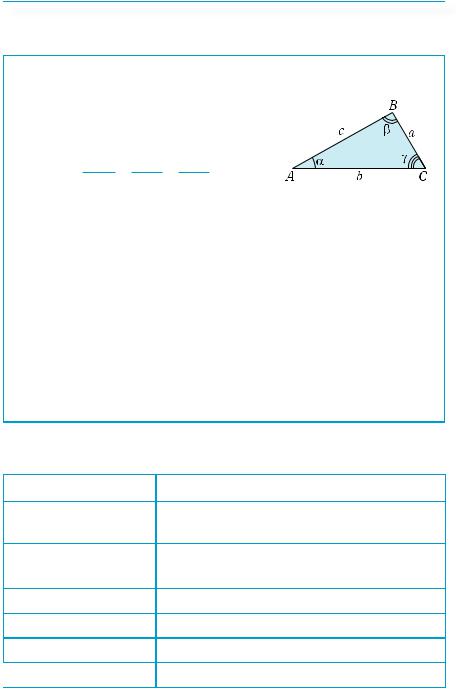
Решение произвольных треугольников

Таблица 27

Теорема синусов

Стороны треугольника пропорциональны синусам противоположных углов:

sina α = sinb β = sinc γ .

Теорема косинусов

Квадрат произвольной стороны треугольника равен суммеквадратовдвухдругихсторонбезудвоенногопроизведения этих сторон на косинус угла между ними:

c2 = a2 +b2 −2abcos γ , b2 = a2 + c2 −2accosβ , a2 = b2 + c2 −2bccosα.

Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними:

S = 12 absin γ = 12 acsinβ = 12 bcsin α .

Основные тригонометрические тождества

				Таблица 28
0° ≤ α ≤ 180°	sin2 α + cos2 α =1
0° ≤ α ≤ 180°, α ≠ 90°	2	1
1 + tg α = cos2 α

0° < α < 180°	1 + ctg2 α =		1
	sin2 α

0° ≤ α ≤ 90°

0° < α < 90°

0° ≤ α ≤ 180° 0° ≤ α ≤ 180°, α ≠ 90°

sin(90°− α) = cosα,	cos(90°− α) = sin α
tg(90°− α) = ctgα,	ctg(90°− α) = tg α
sin(180°− α) = cosα,	cos(180°− α) = −sin α

tg(180°− α) = −tg α

Тест для диагностики готовности к изучению темы «Тригонометрические функции»


1.	Дан треугольник АВС, С = 90°, ВС = 3 , АВ = 2. Чему рав-
	няется	В?				Б. 45°.						В. 60°.
	А. 30°.
	Г. Невозможно вычислить без вычислительных средств.
2.	Дан треугольник	АВС, С	= 90°,	ВС = 3,	В = 60°. Чему рав-
	няется	АВ?								3
	А. 3	3	.		Б. 6.		В.			.	Г.	3 .
3.					3

По данным сторонам прямоугольного треугольника найдите
	косинус меньшего его угла: а = 3, b = 4, c	= 5.	1,25.
	А. 0,8.			Б.	0,75.	В.	0,6.	Г.
4.	Какое из приведенных значений не может принимать коси-
	нус острого угла?
		7 −1	Б.	7	.	В.		7 2	Г.	7	.
	А.		.		8		.	8
		8								8

5.Сравните сумму синусов острых углов произвольного прямоугольного треугольника (обозначим ее через А) с единицей.

<1. Б. А = 1.

>1. Г. Сравнить невозможно. Расположите по возрастанию числа: а = sin 30°, b = cos 30°,

=tg 30°.

<b < c. Б. a < c < b. В. c < a < b. Г. b < a < c.

Сравните без вычислительных средств острые углы α и β,7.

если: cosα =	1	,cosβ =	2 .
А. α < β.	3		3
		Б. α = β.
В. α > β.			Г. Сравнить невозможно.

234

Тригонометрические функции

Для каких острых углов синус меньше косинуса?

А.

Для всех.

Б.

Для меньших 45°.

В.

Для больших 45°.

Г. Ни для каких.

Чему равен cos

α, если α — острый угол прямоугольного тре-

угольника и sin α =

А.

Б.

В.

12 .

Г.

10.

Длина тени дерева равна 15 м. Лучи Солнца образуют угол

30° с поверхностью Земли. Чему приближенно равна высота

дерева? Выберите наиболее точный результат.

26 м.

А.

8 м.

Б. 13 м.

В. 7м.

Г.

11.

Чему равно значение выражения

1 − x2

при х = – 0,8?

А.

0,6.

Б. –0,6.

В.

0,8.

Г. ≈ 1,34.

12.

Из формулы a2 +b2 = 4 выразите b < 0 через a.

А. b = 4 − a2 .

Б. b = a2 − 4 .

В.

b = − a2

− 4 .

Г.

b = − 4 − a2 .

13.

Точка А

расположена в ІІІ четверти на расстоянии 3 от оси х и

на расстоянии

10 от начала координат. Какие координаты

имеет точка А?

Б. (−1; 3).

В. (−1; −3).

Г. (−3; −1).

А.

(1; 3).

14.

Какая

из

следующих точек

не

принадлежит

окружности

x2 + y2

=1?

А.

−

;

Б. (0,5; 0,5).

В.

−

;

. Г.

(0,6; −0,8).

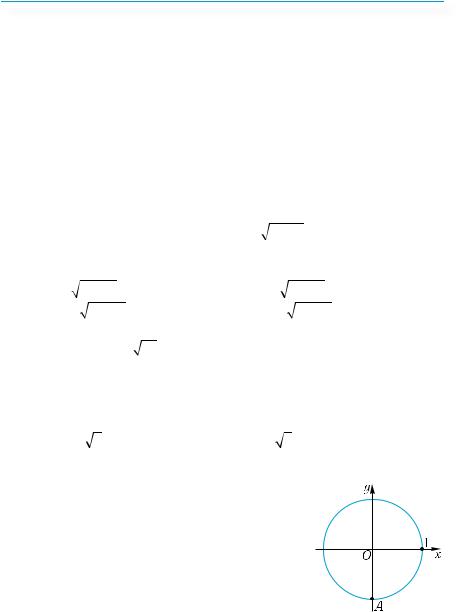
15.Укажите координаты точки А, лежащей на окружности радиуса 1 (см. рис.).

(−1; 0). Б. (1; 0).

(0; − 1). Г. (0; 1).А.В.

Источник

Содержание:

Параллельность в пространстве

В этом параграфе вы ознакомитесь с основными понятиями стереометрии, аксиомами стереометрии и следствиями из них. Расширите свои представления о многогранниках. Вы узнаете о взаимном расположении двух прямых, прямой и плоскости, двух плоскостей в пространстве. Ознакомитесь с правилами, по которым изображают пространственные фигуры на плоскости.

Основные понятия стереометрии. Аксиомы стереометрии

Изучая математику, вы со многими понятиями ознакомились с помощью определений. Так, из курса планиметрии вам хорошо знакомы определения четырехугольника, трапеции, окружности и др.

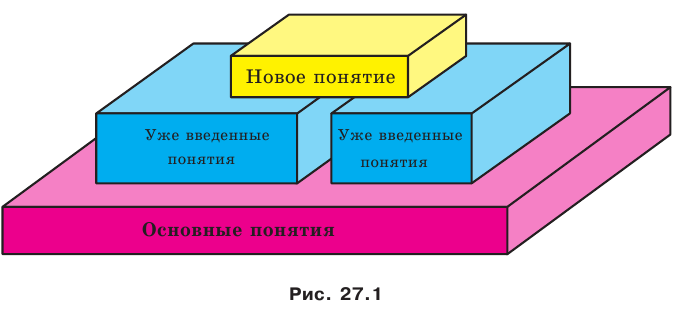
Определение любого понятия основано на других понятиях, содержание которых вам уже известно. Например, рассмотрим определение трапеции: «Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны». Видим, что определение трапеции основано на таких уже введенных понятиях, как четырехугольник, сторона четырехугольника, параллельные и непараллельные стороны и др. Итак, определения вводятся по принципу «новое основано на старом». Тогда ясно, что должны существовать первоначальные понятия, которым определений не дают. Их называют основными понятиями (рис. 27.1).

В изученном вами курсе планиметрии определения не давали таким фигурам, как точка и прямая. В стереометрии, кроме них, к основным понятиям отнесем еще одну фигуру — плоскость.

Наглядное представление о плоскости дают поверхность водоема в безветренную погоду, поверхность зеркала, поверхность полированного стола, мысленно продолженные во всех направлениях.

Используя понятие плоскости, можно считать, что в планиметрии мы рассматривали только одну плоскость, и все изучаемые фигуры принадлежали этой плоскости. В стереометрии же рассматривают бесконечно много плоскостей, расположенных в пространстве.

Как правило, плоскости обозначают строчными греческими буквами

Плоскость, так же как и прямая, состоит из точек, то есть плоскость — это множество точек.

Существует несколько случаев взаимного расположения точек, прямых и плоскостей в пространстве. Приведем примеры.

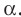
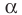
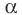
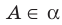
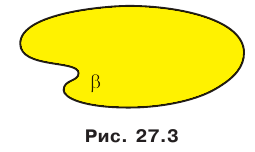
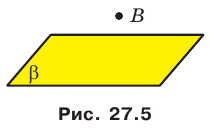
На рисунке 27.4 изображена точка А, принадлежащая плоскости . Также говорят, что точка А лежит в плоскости или плоскость проходит через точку А. Кратко это можно записать так: .

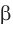
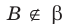
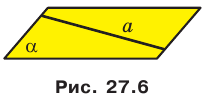
На рисунке 27.5 изображена точка В, не принадлежащая плоскости . Кратко это можно записать так: .

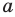
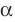
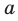
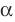
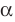
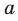
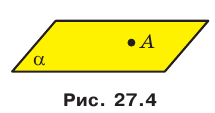
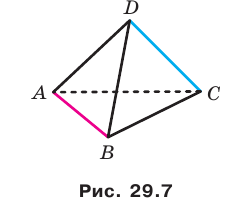
На рисунке 27.6 изображена прямая , принадлежащая плоскости . Также говорят, что прямая лежит в плоскости или плоскость проходит через прямую . Кратко это можно записать так:

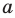
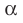
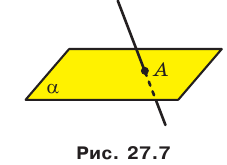
Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость. На рисунке 27.7 изображена прямая , пересекающая плоскость в точке А. Записывают:

В дальнейшем, говоря «две точки», «три точки», «две плоскости» и т.п., будем иметь в виду, что это разные точки, разные прямые и разные плоскости. Если две плоскости имеют общую точку, то говорят, что эти плоскости пересекаются.

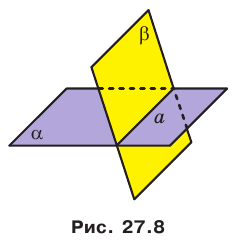
На рисунке 27.8 изображены плоскости 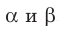, пересекающиеся по прямой . Записывают:

На начальном этапе изучения стереометрии невозможно доказывать теоремы, опираясь на другие утверждения, поскольку этих утверждений еще нет. Поэтому первые свойства, касающиеся точек, прямых и плоскостей в пространстве, принимают без доказательства и называют аксиомами. Отметим, что ряд аксиом стереометрии по формулировкам дословно совпадают со знакомыми вам аксиомами планиметрии.

Например:

какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей;
через любые две точки можно провести прямую, и притом только одну.

Мы не будем знакомиться со строгим аксиоматическим построением стереометрии. Рассмотрим лишь некоторые утверждения, выражающие основные свойства плоскостей пространства, основываясь на которых обычно строят курс стереометрии в школе.

Аксиома А1. В любой плоскости пространства выполняются все аксиомы планиметрии.

Если в любой плоскости пространства выполняются аксиомы планиметрии, то выполняются и следствия из этих аксиом, то есть теоремы планиметрии. Следовательно, в стереометрии можно пользоваться всеми известными нам свойствами плоских фигур.

Аксиома А2. Через любые три точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Рисунки 27.9-27.11 иллюстрируют эту аксиому.

Из этой аксиомы следует, что три точки пространства, не лежащие на одной прямой, определяют единственную плоскость, про ходящую через эти точки. Поэтому для обозначения плоскости можно указать любые три ее точки, не лежащие на одной прямой.

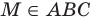
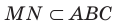
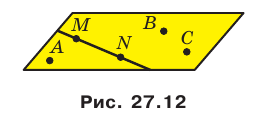
Например, на рисунке 27.12 изображена плоскость АВС. Запись означает, что точка М принадлежит плоскости АВС. Запись означает, что прямая MN принадлежит плоскости АВС (рис. 27.12).

Аксиома АЗ. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.

Например, на рисунке 27.13 точки А, В и С принадлежат плоскости АВС. Тогда можно записать: 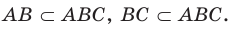Из этой аксиомы следует, что если прямая не принадлежит плоскости, то она имеет с данной плоскостью не более одной общей точки.

Утверждение, сформулированное в аксиоме АЗ, часто используют на практике, когда хотят проверить, является ли данная поверхность ровной (плоской). Для этого к поверхности в разных местах прикладывают ровную рейку и проверяют, есть ли зазор между рейкой и поверхностью (рис. 27.14).

Аксиома А4. Если две плоскости имеют общую точку, то они пересекаются по прямой.

Эту аксиому можно проиллюстрировать с помощью согнутого листа бумаги или с помощью вашего учебника (рис. 27.15).

Пример:

Докажите, что если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Решение:

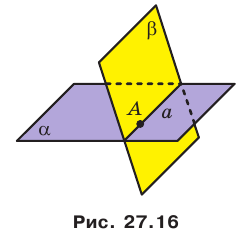
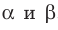
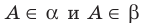
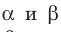
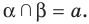
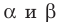
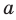
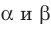
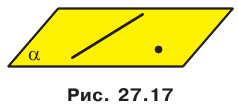
Пусть точка А является общей для двух плоскостей , то есть (рис. 27.16). По аксиоме А4 плоскости пересекаются по прямой. Пусть Тогда все общие точки плоскостей принадлежат прямой . Точка А является общей для плоскостей . Следовательно, Кроме аксиом, есть и другие свойства, описывающие взаимное расположение точек, прямых и плоскостей в пространстве. Опираясь на аксиомы, можно доказать, например, следующие утверждения (следствия из аксиом стереометрии).

Теорема 27.1. Через прямую и не принадлежащую ей точку проходит плоскость, и притом только одна (рис. 27.17).

Теорема 27.2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 27.18).

Из аксиомы А2 и теорем 27.1 и 27.2 следует, что плоскость однозначно определяется:

тремя точками, не лежащими на одной прямой;
прямой и точкой, не принадлежащей этой прямой;
двумя пересекающимися прямыми.

Таким образом, мы указали три способа задания плоскости.

Пространственные фигуры

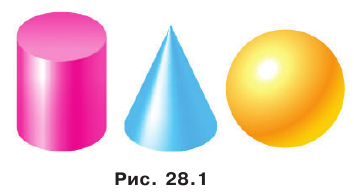
Начальные сведения о многогранниках. В стереометрии, кроме точек, прямых и плоскостей, рассматривают пространственные фигуры, то есть фигуры, не все точки которых лежат в одной плоскости. Некоторые из пространственных фигур вам уже знакомы. Так, на рисунке 28.1 изображены цилиндр, конус и шар. Подробно эти фигуры вы будете изучать в 11 классе.

На рисунке 28.2 изображена еще одна знакомая вам пространственная фигура — пирамида. Эта фигура является частным видом многогранника. Примеры многогранников показаны на рисунке 28.3.

Поверхность многогранника состоит из многоугольников. Их называют гранями многогранника. Стороны многоугольников называют ребрами многогранника, а вершины — вершинами многогранника (рис. 28.4).

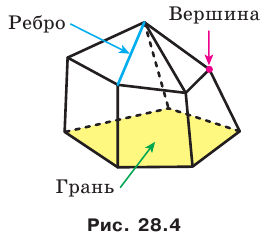
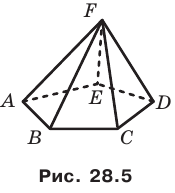
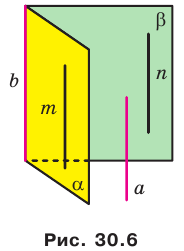
На рисунке 28.5 изображена пятиугольная пирамида FABCDE.

Поверхность этого многогранника состоит из пяти треугольников, которые называют боковыми гранями пирамиды, и одного пятиугольника, который называют основанием пирамиды. Вершину F, общую для всех боковых граней, называют вершиной пирамиды.

Ребра FA, FB, FC, FD и FE называют боковыми ребрами пирамиды, а ребра А В, ВС, CD, DE и ЕА — ребрами основания пирамиды.

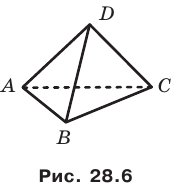
На рисунке 28.6 изображена треугольная пирамида DABC. Треугольную пирамиду называют также тетраэдром.

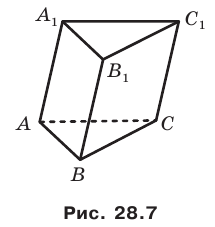
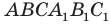
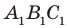
Еще одним частным видом многогранника является призма. На рисунке 28.7 изображена треугольная призма . Этот многогранник имеет пять граней, две из которых — равные треугольники АВС и Их называют основаниями призмы.

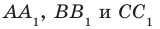
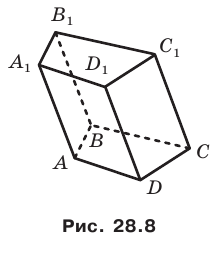
Остальные грани призмы — параллелограммы. Их называют боковыми гранями призмы. Ребра называют боковыми ребрами призмы.

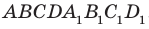
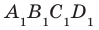
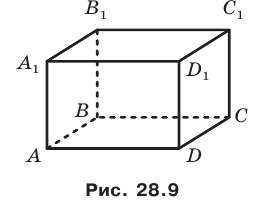
На рисунке 28.8 изображена четырехугольная призма . Ее поверхность состоит из двух равных четырехугольников ABCD и (основания призмы) и четырех параллелограммов (боковые грани призмы).

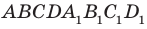
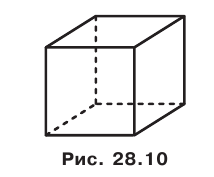
Вы знакомы также с частным видом четырехугольной призмы — прямоугольным параллелепипедом. На рисунке 28.9 изображен прямоугольный параллелепипед . Все грани прямоугольного параллелепипеда являются прямоугольниками.

В свою очередь, частным видом прямоугольного параллелепипеда является куб. Все грани куба — равные квадраты (рис. 28.10).

Четырехугольную призму, основанием которой является параллелограмм, называют параллелепипедом.

В курсе геометрии 11 класса вы более подробно ознакомитесь с многогранниками и их частными видами.

Пример:

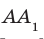
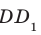
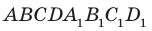
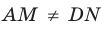
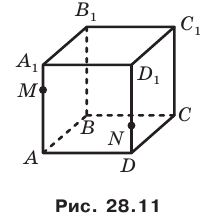
На ребрах и куба отметили соответственно точки М и N так, что (рис. 28.11). Постройте точку пересечения прямой MN с плоскостью АВС.

Решение:

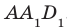
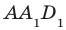
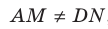
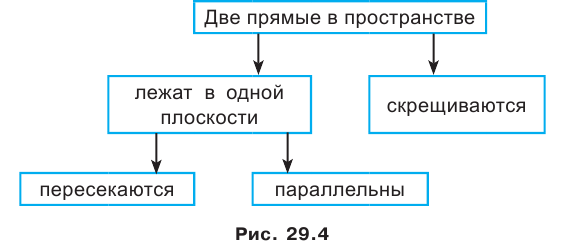
Точки М и N принадлежат плоскости . Тогда по аксиоме АЗ прямая MN принадлежит этой плоскости. Аналогично прямая AD также принадлежит плоскости . Из планиметрии известно, что прямые, лежащие в одной плоскости, или параллельны, или пересекаются. Поскольку , то прямые AD и MN пересекаются. Пусть X — точка их пересечения (рис. 28.12). Точки А и D принадлежат плоскости АВС. Тогда по аксиоме АЗ прямая AD принадлежит этой же плоскости. Точка X принадлежит прямой AD. Следовательно, точка X принадлежит плоскости АВС. Поскольку точка X также принадлежит прямой MN, то прямая MN пересекает плоскость АВС в точке X.

Взаимное расположение двух прямых в пространстве

Из курса планиметрии вы знаете, что две прямые называют пересекающимися, если они имеют только одну общую точку. Такое же определение пересекающихся прямых дают и в стереометрии. Вам также известно, что две прямые называют параллельными, если они не пересекаются. Можно ли это определение перенести в стереометрию?

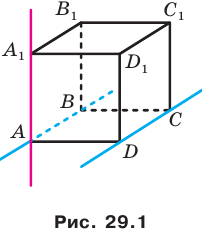
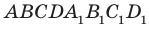
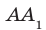
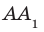
Обратимся к рисунку 29.1, на котором изображен куб . Каждая из прямых АВ и не имеет с прямой DC общих точек. При этом прямые АВ и DC лежат в одной плоскости — в плоскости АВС, а прямые и DC не лежат в одной плоскости, то есть не существует плоскости, которая проходила бы через эти прямые. Этот пример показывает, что в стереометрии для двух прямых, не имеющих общих точек, возможны два случая взаимного расположения: прямые лежат в одной плоскости и прямые не лежат в одной плоскости. Для каждого из этих случаев дадим соответствующее определение.

Определение. Две прямые в пространстве называют параллельным и, если они лежат в одной плоскости и не пересекаются. Если прямые 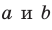параллельны, то записывают:

Определение. Две прямые в пространстве называют скрещивающимися, если они не лежат в одной плоскости. Например, на рисунке 29.1 прямые АВ и DC — параллельные, а прямые 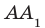и DC — скрещивающиеся.

Наглядное представление о параллельных прямых дают колонны здания, корабельный лес, бревна сруба (рис. 29.2).

Наглядное представление о скрещивающихся прямых дают провода линий электропередачи, различные элементы строительных конструкций (рис. 29.3). Итак, существуют три возможных случая взаимного расположения двух прямых в пространстве (рис. 29.4):

прямые пересекаются;
прямые параллельны;
прямые скрещиваются.

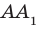
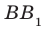
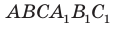
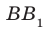
Два отрезка называют параллельными (скрещивающимися), если они лежат на параллельных (скрещивающихся) прямых. Например, ребра и треугольной призмы (рис. 29.5) являются параллельными, а ребра АС и — скрещивающимися.

Теорема 29.1. Через две параллельные прямые проходит плоскость, и притом только одна.

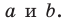
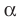
Доказательство. Пусть даны параллельные прямые Докажем, что существует единственная плоскость такая, что

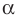
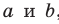
Существование плоскости , проходящей через прямые , следует из определения параллельных прямых.

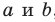
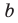
Если предположить, что существует еще одна плоскость, проходящая через прямые , то через прямую а и некоторую точку прямой будут проходить две различные плоскости, что противоречит теореме 27.1.

Существует три способа задания плоскости. Теорему 29.1 можно рассматривать как еще один способ задания плоскости — с помощью двух параллельных прямых.

Установить параллельность двух прямых, лежащих в одной плоскости, можно с помощью известных вам из курса планиметрии признаков параллельности двух прямых. А как установить, являются ли две прямые скрещивающимися? Ответить на этот вопрос позволяет следующая теорема.

Теорема 29.2 (признак скрещивающихся прямых). Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые — скрещивающиеся (рис. 29.6).

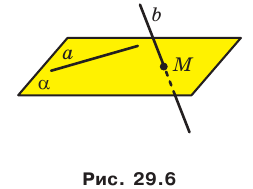
На рисунке 29.7 ребра АВ и DC тетраэдра DABC являются скрещивающимися. Действительно, прямая DC пересекает плоскость АВС в точке С, не принадлежащей прямой АВ. Следовательно, по признаку скрещивающихся прямых прямые АВ и DC являются скрещивающимися.

Параллельность прямой и плоскости

Вам уже известны два возможных случая взаимного расположения прямой и плоскости:

прямая принадлежит плоскости, то есть все точки прямой принадлежат плоскости;
прямая пересекает плоскость, то есть прямая имеет с плоскостью только одну общую точку.

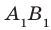
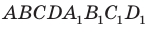
Понятно, что возможен и третий случай, когда прямая и плоскость не имеют общих точек. Например, прямая, содержащая ребро куба , не имеет общих точек с плоскостью АВС (рис. 30.1).

Определение. Прямую и плоскость называют параллельными, если они не имеют общих точек.

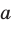
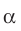
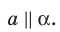
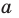
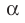
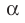
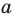
Если прямая и плоскость параллельны, то записывают: Также принято говорить, что прямая параллельна плоскости , а плоскость параллельна прямой .

Наглядное представление о прямой, параллельной плоскости, дают некоторые спортивные снаряды. Например, брусья параллельны плоскости пола (рис. 30.2). Другой пример — водосточная труба: она параллельна плоскости стены (рис. 30.3).

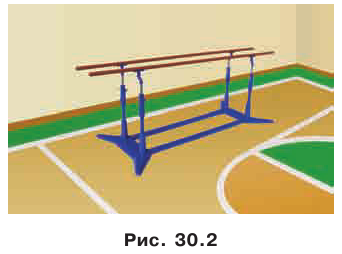
Выяснять, параллельны ли данные прямая и плоскость, с помощью определения затруднительно. Гораздо эффективнее пользоваться следующей теоремой.

Теорема 30.1 (признак параллельности прямой и плоскости). Если прямая, не принадлежащая данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.

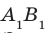
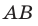
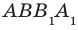
Например, на рисунке 30.1 прямые и содержат противолежащие стороны квадрата . Эти прямые параллельны.

Поскольку 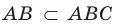, то по признаку параллельности прямой и плоскости

Отрезок называют параллельным плоскости, если он принадлежит прямой, параллельной этой плоскости. Например, ребро АВ куба параллельно плоскости 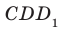(рис. 30.1).

Вы умеете устанавливать параллельность двух прямых с помощью теорем-признаков, известных из планиметрии. Рассмотрим теоремы, описывающие достаточные условия параллельности двух прямых в пространстве.

Теорема 30.2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения плоскостей параллельна данной прямой.

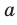
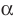
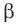
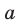
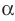
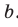
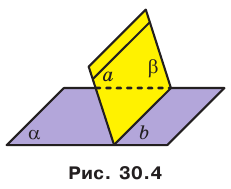
На рисунке 30.4 прямая параллельна плоскости . Плоскость проходит через прямую и пересекает плоскость по прямой . Тогда

Теорема 30.3. Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются по прямой, отличной от двух данных, то эта прямая параллельна каждой из двух данных прямых.

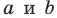
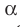
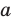
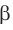
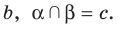
На рисунке 30.5 прямые параллельны, плоскость проходит через прямую , а плоскость — через прямую Тогда

Теорема 30.4. Две прямые, параллельные третьей прямой, параллельны между собой.

Пример:

Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна прямой их пересечения.

Решение:

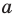
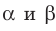
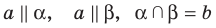
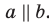
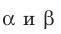
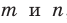
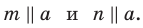
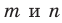
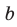
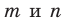
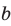
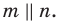
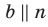
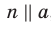
Пусть даны прямая и плоскости такие, что (рис. 30.6). Докажем, что В плоскостях найдутся соответственно такие прямые , что Если хотя бы одна из прямых совпадает с прямой , то утверждение задачи доказано. Если же каждая из прямых отлична от прямой , то по теореме 30.4 Воспользовавшись теоремой 30.3, приходим к выводу, что . Но , следовательно,

Заказать решение задач по высшей математике

Параллельность плоскостей

Рассмотрим варианты возможного взаимного расположения двух плоскостей. Вы знаете, что две плоскости могут иметь общие точки, то есть пересекаться. Понятно, что две плоскости могут и не иметь общих точек. Например, плоскости АВС и 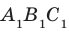, содержащие основания призмы, не имеют общих точек (рис. 31.1).

Определение. Две плоскости называют параллельны ми, если они не имеют общих точек.

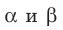
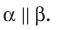
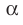
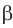
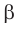
Если плоскости параллельны, то записывают: Также принято говорить, что плоскость параллельна плоскости или плоскость параллельна плоскости

Наглядное представление о параллельных плоскостях дают потолок и пол комнаты; поверхность воды, налитой в аквариум, и его дно (рис. 31.2).

Из определения параллельных плоскостей следует, что любая прямая, лежащая в одной из двух параллельных плоскостей, параллельна другой плоскости.

В тех случаях, когда надо выяснить, являются ли две плоскости параллельными, удобно пользоваться следующей теоремой.

Теорема 31.1 (признак параллельности двух плоскостей). Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.

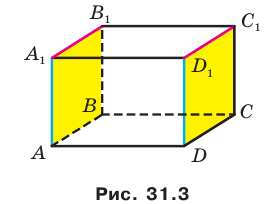
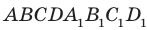
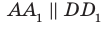
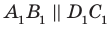
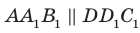
Например, на рисунке 31.3 изображен прямоугольный параллелепипед . Имеем: и . Тогда по признаку параллельности двух плоскостей .

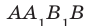
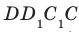
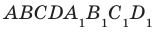
Будем говорить, что два многоугольника параллельны, если они лежат в параллельных плоскостях. Например, грани и прямоугольного параллелепипеда параллельны (рис. 31.3). Рассмотрим некоторые свойства параллельных плоскостей.

Теорема 31.2. Через точку в пространстве, не принадлежащую данной плоскости, проходит плоскость, параллельная данной плоскости, и притом только одна (рис. 31.4).

Теорема 31.3. Прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны (рис. 31.5).

Пример:

Докажите, что отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Решение:

Пусть даны параллельные плоскости и параллельные прямые АВ и такие, что (рис. 31.6). Докажем, что . Параллельные прямые АВ и задают некоторую плоскость причем

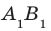
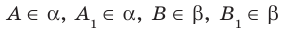
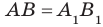
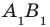
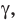
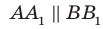
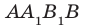
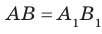
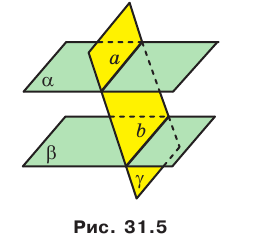
По теореме 31.3 получаем: . Следовательно, четырехугольник — параллелограмм. Отсюда .

Параллельное проектирование

Многие явления и процессы, наблюдаемые нами в повседневной жизни, служат примерами преобразований, при которых образом пространственной фигуры является плоская фигура. Увидеть одно из таких явлений можно в солнечную погоду, когда предмет отбрасывает тень на плоскую поверхность (рис. 32.1). Этот пример иллюстрирует преобразование фигуры, которое называют параллельным проектированием. С помощью этого преобразования на плоскости создают изображения пространственных фигур.

Многие рисунки настоящего учебника, на которых изображены пространственные фигуры, можно рассматривать как тени, отбрасываемые на плоскость страницы предметами, освещенными параллельными лучами. Ознакомимся подробнее с параллельным проектированием.

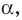
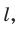
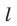
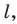
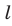
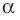
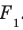
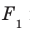
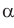
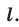
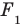
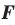
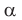
Пусть даны плоскость прямая пересекающая эту плоскость, и фигура F (рис. 32.2). Через каждую точку фигуры F проведем прямую, параллельную прямой (если точка фигуры F принадлежит прямой то будем рассматривать саму прямую ). Точки пересечения всех проведенных прямых с плоскостью образуют некоторую фигуру . Описанное преобразование фигуры F называют параллельным проектированием. Фигуру называют параллельной проекцией фигуры F на плоскость в направлении прямой Также фигуру называют изображением фигуры на плоскости в направлении прямой

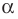
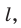
Выбирая выгодные положения плоскости и прямой можно получить наглядное изображение данной фигуры F. Это связано с тем, что параллельное проектирование обладает рядом замечательных свойств (см. теоремы 32.1-32.3). Благодаря этим свойствам изображение фигуры похоже на саму фигуру.

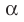
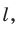
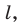
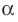
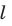
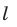
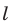
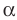
Пусть даны плоскость и прямая пересекающая эту плоскость. Если прямая параллельна прямой то ее проекцией на плоскость является точка (рис. 32.3). Проекцией прямой также является точка. Если отрезок параллелен прямой или лежит на прямой , то его проекцией на плоскость является точка (рис. 32.3).

В следующих теоремах будем рассматривать прямые и отрезки, не параллельные прямой и не лежащие на ней.

Теорема 32.1. Параллельной проекцией прямой является прямая; параллельной проекцией отрезка является отрезок (рис. 32.4).

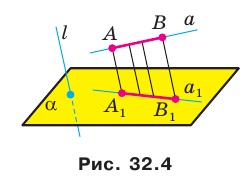
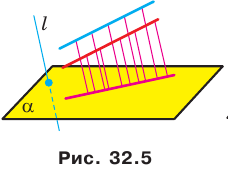
Теорема 32.2. Параллельной проекцией двух параллельных прямых являются или прямая (рис. 32.5), или две параллельные прямые (рис. 32.6). Параллельные проекции двух параллельных отрезков лежат на одной прямой или на параллельных прямых (рис. 32.6).

Теорема 32.3. Отношение параллельных проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению самих отрезков (рис. 32.7).

Рассмотрим изображения некоторых многоугольников на плоскости 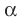в направлении прямой

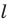
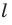
Если прямая параллельна плоскости многоугольника или принадлежит этой плоскости, то изображением многоугольника является отрезок. Теперь рассмотрим случай, когда прямая пересекает плоскость многоугольника.

Из свойств параллельного проектирования следует, что параллельной проекцией треугольника является треугольник (рис. 32.8).

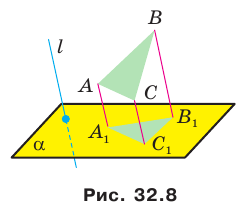
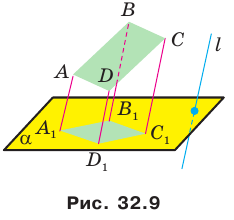
Поскольку при параллельном проектировании сохраняется параллельность отрезков, то изображением параллелограмма (в частности, прямоугольника, ромба, квадрата) является параллелограмм (рис. 32.9).

Также из свойств параллельного проектирования следует, что изображением трапеции является трапеция.

Параллельной проекцией окружности является фигура, которую называют эллипсом (рис. 32.10).

Изображения объектов с помощью параллельного проектирования широко используют в самых разных областях промышленности, например в автомобилестроении (рис. 32.11).

ГЛАВНОЕ В ПАРАГРАФЕ 4

Основные аксиомы стереометрии

А1. В любой плоскости пространства выполняются все аксиомы планиметрии.
А2. Через любые три точки пространства, не лежащие на одной прямой, проходит плоскость, и притом только одна.
АЗ. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
А4. Если две плоскости имеют общую точку, то они пересекаются по прямой.

Плоскость однозначно определяется:

тремя точками, не лежащими на одной прямой;
прямой и точкой, не принадлежащей этой прямой;
двумя пересекающимися прямыми;
двумя параллельными прямыми.

Взаимное расположение двух прямых в пространстве

Две прямые называют пересекающимися, если они имеют только одну общую точку.
Две прямые в пространстве называют параллельными, если они лежат в одной плоскости и не пересекаются.
Две прямые в пространстве называют скрещивающимися, если они не лежат в одной плоскости.

Свойство параллельных прямых

Через две параллельные прямые проходит плоскость, и притом только одна.

Признак скрещивающихся прямых

Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые — скрещивающиеся.

Параллельность в пространстве

Прямую и плоскость называют параллельными, если они не имеют общих точек. Две плоскости называют параллельными, если они не имеют общих точек.

Признак параллельности прямой и плоскости

Если прямая, не принадлежащая данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.

Условия параллельности двух прямых в пространстве

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения плоскостей параллельна данной прямой.
Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются по прямой, от личной от двух данных, то эта прямая параллельна каждой из двух данных прямых.
Две прямые, параллельные третьей прямой, параллельны между собой.

Признак параллельности двух плоскостей

Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.

Свойства параллельных плоскостей

Через точку в пространстве, не принадлежащую данной плоскости, проходит плоскость, параллельная данной плоскости, и притом только одна.

Прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны.

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Перпендикулярность в пространстве
Векторы и координаты в пространстве
Множества
Рациональные уравнения
Числовые последовательности
Предел числовой последовательности
Предел и непрерывность числовой функции одной переменной
Функции, их свойства и графики

Источник