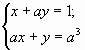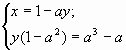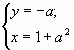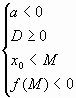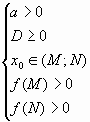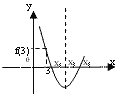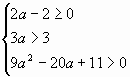Как найти параметр алгебра

Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2022 года это №17. И даже в вариантах ОГЭ они есть. Что же означает это слово — параметр?

Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».

Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.

Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?

Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.

Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».

Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.

1. Теперь пример из школьной математики.

Все мы помним, что такое квадратное уравнение. Это уравнение вида , где коэффициент а не равен нулю.

Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.

Дискриминант квадратного уравнения:

Если , квадратное уравнение имеет два корня: и

Если , квадратное уравнение имеет единственный корень

Если , квадратное уравнение не имеет действительных корней. Рассмотрим уравнение . Его дискриминант равен Если , то есть , это квадратное уравнение имеет два корня.

Если при , уравнение имеет единственный корень.

Если , то есть с > 1, корней нет.

В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.

Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.

И еще две простые задачи с параметром.

2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.

Квадратное уравнение имеет два различных корня, когда .

Найдем дискриминант уравнения

В нем

Т.к. , получим:

Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).

Найдем корни квадратного уравнения . Это и

Разложим левую часть неравенства на множители:

Значит,

Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и

Записываем ответ:

3. При каких значениях параметра k система уравнений не имеет решений?

Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:

Первое уравнение задает прямую с угловым коэффициентом . Второе уравнение — прямую с угловым коэффициентом -2.

Система уравнений не имеет решений, если эти прямые не пересекаются, то есть параллельны. Это значит, что и .

Действительно, в этом случае первое уравнение задает прямую , а второе — параллельную ей прямую

Ответ: 10

Читаем дальше:

Графический метод решения задач с параметрами.

На этой странице вы узнаете

• Игра в прятки: как значение одной переменной может помочь найти другую?
• Парадокс: как стоять на месте и бежать с любой скоростью одновременно? 
• Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? 

Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье. 

Что такое параметр 

Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов? 

Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно (frac{20}{5} = 4). А если было 10 градусов, то искомое число было бы равно (frac{20}{10} = 2). 

Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными. 

Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a”  называется параметр. 

Параметр — это условная буква, вместо которой можно подставить число. 

То есть параметр — это еще одна переменная, которая может принять несколько значений. 

Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.

Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 

Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.

Линейные уравнения с параметром

Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a. 

(x = frac{20}{a})

Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5 

Что, если a=0? Мы получаем уравнение (x = frac{20}{0}), у которого нет решения, поскольку на 0 делить нельзя. 

Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0. 

Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a (neq) 0 — x = 20a. 

Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев. 

1) b (neq) 0. 

Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b. 

Получаем уравнение ax = 15. Как найти начальную скорость Пети? (x = frac{15}{a}). 

Такое уравнение мы уже решали выше. Получаем два случая: 

• Если a = 0 — решений нет. 
• Если a (neq) 0, то изначальная скорость Пети была равна (x = frac{15}{a}). 

2) b = 0. 

Мы получаем уравнение ax = 0. Также разберем два случая значений параметра: 

• a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось? 

Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений. 

• a (neq) 0. Здесь получается, что равен 0 уже х: (x = frac{0}{a} = 0). 

Подведем итог. Как можно решить уравнение вида ax = b?

• Если a = 0, b = 0 — бесконечное множество решений. 
• Если a = 0, b (neq) 0 — решений нет. 
• Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 

Квадратные уравнения с параметром

Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции». 

Квадратное уравнение имеет вид ax² + bx + c = 0, а графиком функции y = ax² + bx + c будет парабола. 

Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.  

Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней: 

• При D > 0 уравнение имеет два корня. 
• При D = 0 уравнение имеет один корень. 
• При D < 0 уравнение не имеет корней. 

Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х. 

Рассмотрим три уравнения. 

1) x² — x — 2 = 0
Решим уравнение с помощью дискриминанта. 
D = 1² — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня. 

(x_1 = frac{1 + 3}{2} = 2)
(x_2 = frac{1 — 3}{2} = -1)

Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) . 

2) x² -4x + 4 = 0
Решим уравнение с помощью дискриминанта. 
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень. 

(x = frac{4}{2} = 2)

Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0). 

3) x² — 5x + 7 = 0
Решим уравнение с помощью дискриминанта. 
D = 25 — 4 * 1 * 7 = 25 — 28 = -3

Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет. 

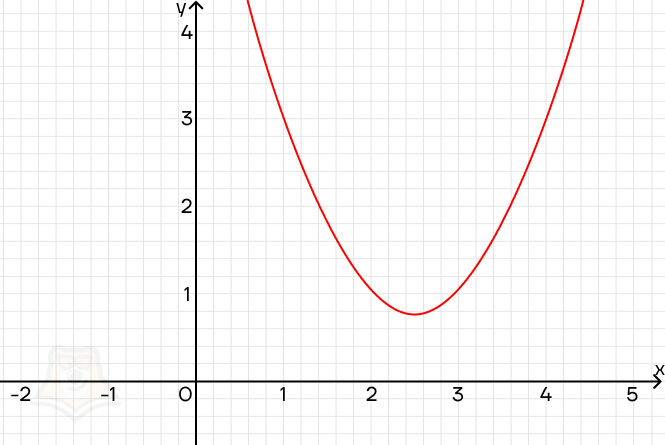
Где можно применить эти знания, решая параметры? 

Пример 1. Найдите все значения параметра a, при которых уравнение x² + (3a + 11)x + 18,25 + a = 0 имеет два различных решения. 

Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?

Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным. 

1. Для начала найдем сам дискриминант. 

D = (3a + 11)² — 4 * 1 * (a + 18,25) = 9a² + 66a + 121 — 4a — 73 = 9a² + 62a + 48

2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a² + 62a + 48 > 0

3. Решим его «Методом интервалов».

9a² + 62a + 48 = 0
D = 3844 — 1728 = 2116
(a_1 = frac{-62 + 46}{18} = -frac{16}{18} = -89)
(a_2 = frac{-62 — 46}{18} = -frac{108}{18} = -6)

4. Дискриминант будет положительным при (a in (-infty; -6) cup (-frac{8}{9}; +infty)). Это и будет ответ. 

Ответ: (a in (-infty; -6) cup (-frac{8}{9}; +infty)).

Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения. 

Пример 2. При каких значениях параметра a уравнение (2a + 1)x² — ax + 3a + 1 = 0 имеет два различных решения? 

Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0? 

Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи. 

1. Поскольку по условию должно быть 2 решения, мы получаем, что a (neq) -0,5. 

2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения. 

D = a² — 4 * (2a + 1) * (3a + 1) = a² — 24a² — 20a -4 = -23a² — 20a — 4

3. Составим неравенство и решим его:

-23a² — 20a — 4 > 0
23a² + 20a + 4 < 0
23a² + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
(a_1 = frac{-20 + 4 sqrt{2}}{46} = frac{2sqrt{2} — 10}{23})
(a_2 = frac{-20 — 4sqrt{2}}{46} = frac{-2sqrt{2} — 10}{23})

4. Разложим уравнение на множители: 

(23a^2 + 20a + 4 = 23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23}))

5. Получаем неравенство:

(23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23} < 0)

6.Тогда  (a in (frac{-2sqrt{2} — 10}{23}; frac{2sqrt{2} — 10}{23})). Вспомним, что a (neq) -0,5, следовательно, мы получаем ответ (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23})).

Ответ: (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23}))

Теорема Виета 

Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax² + bx + c = 0, то его корни можно найти с помощью следующей системы: 

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения. 

Пример 3. При каких значениях параметра a корни уравнения x² — 3ax — a(a — 1) = 0 удовлетворяют условию x₁ = 5x₂. 

Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0: 

D = 9a² — 4 * 1 * (-a² + a) = 9a² + 4a² — 4a = 13a² — 4a = a(13a — 4)

Получаем неравенство a(13a — 4) > 0, следовательно, (a in (-infty; 0) cup (frac{4}{13}; +infty)). 

2. По теореме Виета найдем корни уравнения: 

3. По условию x₁ = 5x₂, тогда 5x₂ + x2 = 6x₂ = 3a, откуда получаем:
(x_2 = frac{3a}{6} = frac{a}{2})
(x_1 = 5 * a_2 = frac{5a}{2})

4. Подставим во второе уравнение системы:
(frac{a}{2} * frac{5a}{2} = a — a^2)
(frac{5a^2}{4} = a — a^2 | * 4)
5a² = 4a — 4a²
(9a^2 — 4a = 0 rightarrow a(9a — 4) = 0 rightarrow a = 0, a = frac{4}{9})

5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня. 

a = 0 не подходит, поскольку ограничение (a in (-infty; 0) cup (frac{4}{13}; +infty)) не включает точку 0. 

(a = frac{4}{9}) подходит, поскольку (frac{4}{9} > frac{4}{13}). 

Ответ: (a = frac{4}{9})

Условия на корни квадратного трехчлена 

Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев. 

1. Корни квадратного трехчлена меньше, чем число N. 

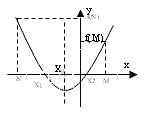
Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз. 

Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N. 

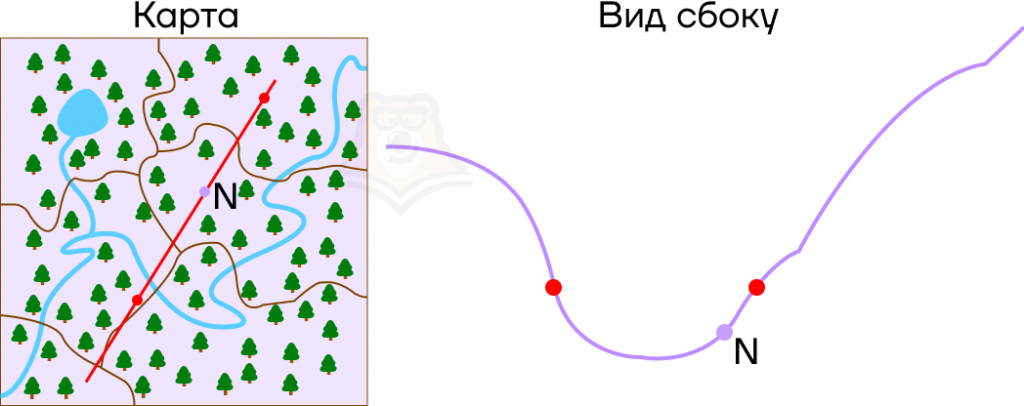
Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту. 

Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка. 

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа. 

Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы. 

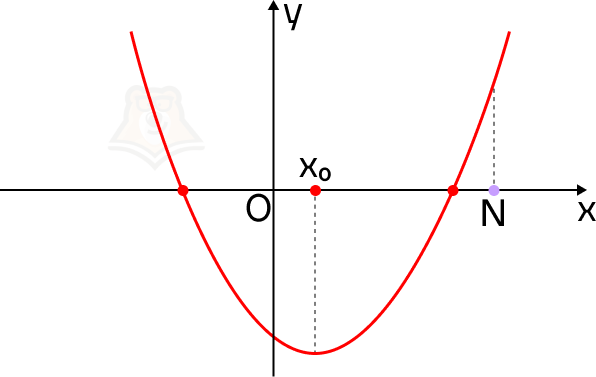
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N. 

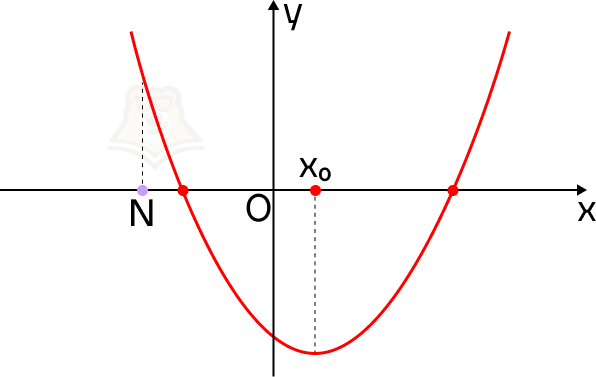
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов. 

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними. 

В этом случае смотровая площадка окажется между привалами. 

Аналогичным способом можно проследить изменение условий при любом положении точки N на графике. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг. 

Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы. 

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения. 

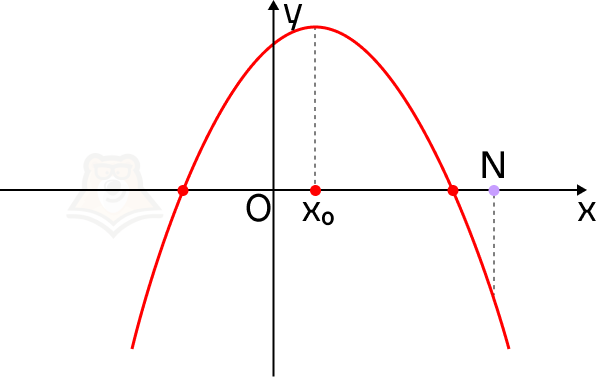
Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

2. Корни квадратного трехчлена больше, чем число N. 

Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы. 

Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы. 

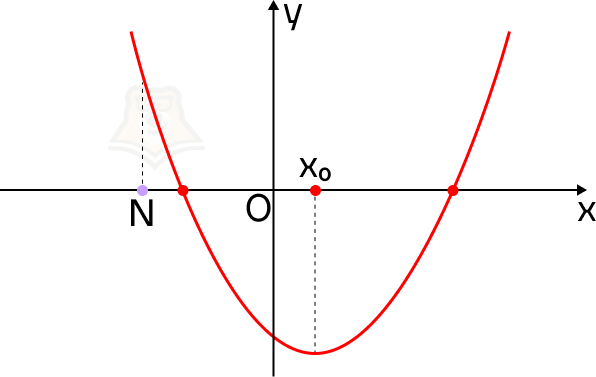
Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько. 

В итоге должна получиться система, с помощью которой можно решить задачу.

Фактчек

• Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 
• При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b (neq) 0 — решений нет. Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 
• При решении квадратного уравнения обязательно проверять коэффициент перед x². Если коэффициент будет равен 0, то уравнение станет линейным.
• При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней. 
• Решить квадратное уравнение можно и с помощью теоремы Виета. 
• Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций. 

Проверь себя

Задание 1. 
Что такое параметр?

1. Это буква a, вместо которой можно подставить число.
2. Это коэффициент перед x² в квадратном уравнении.
3. Это переменная х.
4. Это значение функции в определенной точке. 

Задание 2. 
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?

1. Решений нет.
2. Одно решение.
3. Бесконечное множество решений.
4. Невозможно определить количество решений. 

Задание 3. 
При каких значениях дискриминанта уравнение будет иметь корни?

1. D > 0
2. D = 0
3. D < 0
4. D (neq) 0

Задание 4. 
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?

1. Справа.
2. Слева.
3. Совпадать с точкой А.
4. Невозможно определить расположение вершины. 

Задание 5. 
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?

1. Значение функции в точке В будет меньше 0.
2. Значение функции в точке В будет равно 0.
3. Значение функции в точке В будет больше 0.
4. Невозможно определить значение функции. 

Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.

Основы работы с параметром

Параметр – это буквенный коэффициент в уравнении.

Параметр – это всегда число, а не переменная, но мы не знаем, чему конкретно равен параметр. Например,

(y = kx + b)

это уравнение прямой, в котором (x) – переменная, (y) – зависимая от неё функция, а (k) и (b) – коэффициенты. Это значит, что (k) и (b) – какие-то числа, параметры. Когда мы видим конкретное уравнение прямой, например,

(y = — 5x +

мы можем сказать, что в данном случае параметр (k = — 5), а параметр (b = . В зависимости от параметров функция может по-разному себя вести, но сам вид линейной функции не поменяется.

УРАВНЕНИЕ С ПАРАМЕТРОМ:

Существуют уравнения, где есть две неизвестных: (x) – корень уравнения и (a) (или любая другая буква) – параметр. Решение таких уравнений сводится не к поиску конкретных корней, а к анализу их количества. Для этого мы предполагаем, чему будут равны корни уравнения при определенных параметрах.

АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЙ С ПАРАМЕТРОМ

Рассмотрим примеры.

Пример №1:

Сколько корней имеет уравнение

(ax = 3a + 7)

1. Данное уравнение не имеет ограничений для (x), поэтому перейдем ко второму пункту.

2. Начнем рассуждать. В случае работы с параметром нужно предположить, как мы будем искать корень, если коэффициент при икс равен нулю и если не равен ему. В данном случае коэффициент при иксе и есть параметр. Допустим, (a = 0), тогда уравнение будет иметь вид:

(0 = 7)

Это невозможно, из чего делаем вывод, что при (a = 0) корней нет.

1. Теперь представим, что параметр не равен нулю, а равен любому другому числу (a neq 0), тогда выразим икс:

(x = frac{3a + 7}{a})

При условии, что (a neq 0), а равно обычному числу, (x) будет принимать одно единственное значение.

1. Так мы нашли, при каких параметрах уравнение будет иметь один корень, нужно проверить этот корень на ограничения. Этих ограничений из п.1 нет, значит мы полностью проанализировали уравнение и узнали, сколько корней оно будет иметь во всех возможных случаях изменения параметра:

({корней нет при a = 0 }{один корень frac{3a + 7}{a} при a neq 0 })

Ответ так и запишем.

Ответ: (корней нет при a = 0); (один корень frac{3a + 7}{a} при a neq 0).

При работе с линейными уравнениями нет ограничений для переменных и для параметра. Сейчас мы рассмотрим дробно-рациональное уравнение с параметром, где на каждом этапе нужно помнить об ограничениях в знаменателе.

Пример №2:

Сколько корней имеет уравнение

(frac{4}{x — 3} — frac{k}{2} = 2)

1. Для начала нужно выписать все ограничения для переменной. Знаменатель не может быть равен нулю, значит:

(x — 3 neq 0)

(x neq 3)

(frac{8}{2left( x — 3 right)} — frac{kleft( x — 3 right)}{2left( x — 3 right)} = frac{4left( x — 3 right)}{2(x — 3)})

(frac{8 — kx + k3}{2(x — 3)} = frac{4x — 12}{2(x — 3)})

Ограничение для переменной мы записали, поэтому смело можно убрать знаменатель и приравнять числители. Про ограничение не забывать!

(8 — kx + 3k = 4x — 12)

1. Вправо перенесем все с иксами, а влево перенесем все остальные числа:

(8 + 3k + 12 = 4x + kx)

(20 + 3k = xleft( 4 + k right))

1. Мы снова пришли к ситуации, когда (x) умножается на какое-то число ((4 + k)), значение которого мы не знаем, т. к. в нём есть параметр. Снова анализируем количество корней, если весь коэффициент перед (x) равен нулю, то есть:

(4 + k = 0)

(k = — 4)

тогда

(x = frac{20 + 3k}{0})

Чего не может быть, значит корней нет.

1. Рассмотрим случай, когда (4 + k neq 0):

(k neq — 4)

тогда

(x = frac{20 + 3k}{k})

Получается, что существует один единственный корень.

1. Мы не учли то, что единственным корнем может оказаться число 3, но в начале мы записали ограничение (x neq 3). Поэтому уравнение будет иметь один корень ( x = frac{20 + 3k}{k}) при (k neq — 4), если

(x = frac{20 + 3k}{k} neq 3)

Найдем такой параметр (k), при котором (x = 3). Нужно проверить, есть ли такой параметр, и если есть – исключить его:

(frac{20 + 3k}{k} = 3)

(20 + 3k = 3k)

(20 = 0)

Что невозможно, значит такого параметра не существует, и уравнение имеет ровно один корень без ограничений, кроме (k neq — 4). Запишем ответ.

Ответ: корней нет при (k = — 4); один корень (x = frac{20 + 3k}{k}) при (k neq — 4).

Уравнения с параметрами.

Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.

Что такое уравнение с параметром?

Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.

Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3

Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.

А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос — сколько можно делать одно и то же?

Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a — переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.

Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.

Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.

Таким образом, под термином «уравнение с параметром», фактически, скрывается целое семейство «почти одинаковых уравнений» , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр — это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.

Рассмотрим еще один пример.

Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.

С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6

Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?

Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению «почти одинаковых уравнений» могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.

Графические способы решения уравнений

Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.

Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.

Рассмотрим примеры.

1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1.

2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

3. Решить уравнение
log₂х = −0,5х + 4

Ответ: x = 2.

Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов — степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.

Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже «от руки» разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:

1. Предварительный вывод: х ≈ 4.
2. Проверка: log₂4 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
3. Окончательный вывод х = 4.

Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.

Решение уравнений с параметрами с помощью графиков.

Задача 1.

Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.

При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a

Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.

Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.

Аналогично, разбираемся с оставшимися двумя участками.

На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .

На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .

Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)

Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.

Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.

График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а — параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.

Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.

Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений:

Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета.

Таким образом, окончательный ответ: <2;4;6>.

Задача 2.

Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.

Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с «волной». Строим от руки эскиз графика.

Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.

Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения y_max и y_min через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.

Ответ:

Задача для самостоятельного решения

Задача 3.

При каком наибольшем отрицательном значении параметра а уравнение имеет один корень?

Ответ: -1,625

Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).

Переход на главную страницу сайта «Математичка».

Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

Что такое параметр? Простые задачи с параметрами

Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2022 года это №17. И даже в вариантах ОГЭ они есть. Что же означает это слово — параметр?

Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».

Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.

Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?

Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.

Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».

Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.

1. Теперь пример из школьной математики.

Все мы помним, что такое квадратное уравнение. Это уравнение вида , где коэффициент а не равен нулю.

Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.

Дискриминант квадратного уравнения:

Если , квадратное уравнение имеет два корня: и

Если , квадратное уравнение имеет единственный корень

Если , квадратное уравнение не имеет действительных корней. Рассмотрим уравнение . Его дискриминант равен Если , то есть , это квадратное уравнение имеет два корня.

Если при , уравнение имеет единственный корень.

Если , то есть с > 1, корней нет.

В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.

Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.

И еще две простые задачи с параметром.

2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.

Квадратное уравнение имеет два различных корня, когда .

Найдем дискриминант уравнения

Т.к. , получим:

Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).

Найдем корни квадратного уравнения . Это и

Разложим левую часть неравенства на множители:

Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и

3. При каких значениях параметра k система уравнений не имеет решений?

Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:

Первое уравнение задает прямую с угловым коэффициентом . Второе уравнение — прямую с угловым коэффициентом -2.

Система уравнений не имеет решений, если эти прямые не пересекаются, то есть параллельны. Это значит, что и .

Действительно, в этом случае первое уравнение задает прямую , а второе — параллельную ей прямую

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а = -1, то 0х = -2
Корней нет

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

Ответы:

1. При а1 х =;

1. При а3 х = ;

1. При а1, а-1, а0 х = ;

при а = 1 х – любое действительное число, кроме х = 1

1. При а2, а0 х = ;

1. При а-3, а-2, а0, 5 х =

1. При а + с0, с0 х = ;

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

a =

Если а -4/5 и а 1, то Д > 0,

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

В итоге

4(а – 1)(а – 6) > 0 — 2(а + 1) 0

а 6 а > — 1 а > 5/9

6

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.

Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log₃2 , или х 2 – хlog₃2 + 1 = 0.

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х₁ = -3, х₂ = а = >

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?

Ответ:

1. 0 25/2
2. при а = 1, а = -2,2
3. 0 0, х1/4 (3)

х = у

Если а = 0, то –

2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

Ответ: x + 9a 3 ) = x имеет ровно два корня.

Найдите, при каких значениях а уравнение log ₂ (4 x – a) = x имеет единственный корень.

При каких значениях а уравнение х – log ₃ (2а – 9 х ) = 0 не имеет корней.

Ответы:

при а 16.06.2009

источники:

Что такое параметр? Простые задачи с параметрами

http://urok.1sept.ru/articles/534897

Анализируя экзаменационные работы по
математике, приходишь к выводу, что за курс
математики в общеобразовательной школе
учащимися должны быть отработаны умения решения
задач с параметрами. Кроме непосредственной
подготовки учащихся к экзаменам по данному
разделу математики (решение задач с параметрами),
главная его задача — поднять на более высокий
уровень изучение математики в школе, следующий
за развитием умений и навыков решения
определенного набора стандартных задач. Ибо,
решение задач с параметрами требует наличия
определенного уровня математической культуры,
навыков обобщения и разделения задачи на
элементарные, аргументирования и обоснования
своих действий, рассуждения на отвлеченном
уровне, т.е. навыков проведения логических
операций.

Знакомить учащихся с заданиями с параметрами
следует, начиная с 7 класса, постепенно включая их
в список задач к общему курсу.

• В 7 классе представляется возможным вводить
  решение линейных уравнений с параметрами и
  простейших систем линейных уравнений с
  параметрами.
• В курсе 8 класса следует разобрать способы
  решения некоторых типов уравнений второй
  степени с параметрами.
• В 9 классе — рассмотреть расположение корней
  квадратного трехчлена в зависимости от
  параметра и решение связанных с этим вопросом
  системы заданий.

В курсе алгебры 7 класса в параграфе
«Линейное уравнение с одной переменной»
следует разобрать решение уравнения ах = в с
неизвестным х как уравнение параметрами а и в.
Здесь учащихся следует познакомить с понятием
«параметры» (те переменные а, в, с, :, которые при
решении уравнения считаются постоянными, или те
коэффициенты, которые заданы не конкретными
числами, а обозначены буквами).

На уроках обобщения, следующих за этим
параграфом возможно разобрать решение линейного
уравнения ах + в = с с неизвестным х и параметрами
а, в, с.

В течение учебного года можно предлагать для
решения задания следующего типа.

1. Решить уравнение с неизвестным х. (Решить
уравнение с параметрами — значит указать при
каких значениях параметров существуют решения и
каковы они.)

1) рх =10;	7) ах — 3 = 2х + 5;
2) ах +7=8;	3х + 4 = ах — 8;
3) вх — а = вх;	9) рх — 3 = 3х — р;
4) 3 — вх = 14;	10) к — 5х = -5 + кх;
5) ах + 3 = 3;	11) (а — 1)х + 2 = а + 1;
6) 2ах — 4 = 0;	12) ах + 2х + 3 = 1 — х;
	13) а2(х — 5)=25(х — а).

Знакомить учащихся с решением систем линейных
уравнений с параметрами следует начинать после
изучения параграфа «Системы линейных уравнений
с двумя переменными», котором разбирается
графический способ решения систем линейных
уравнений.

Предлагаются следующие задания.

Подобрать значения параметров а и в, чтобы:

а) система имела единственное решение;

б) система не имела решений

1) 2) 3) 4) 5)

Работая с последней системой, следует
подробнее разобрать ответы на поставленные
вопросы.

Решение. 1) если , то система примет вид

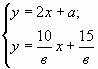
если т.е. система имеет
единственное решение;

если = и т.е. и система не имеет решения;

2) если система
примет вид и
имеет единственное решение.

Ответ: если система
имеет единственное решение;

если , , то система не имеет
решения.

Решите систему уравнений с параметрами к и р,
если :

1) 2)

Решение первой системы получается из знания
взаимного расположения графиков линейных
функций ( Ответ: (0;3)), решение второй системы
предполагает умение решать системы линейных
уравнений аналитическим методом.

Ответ: (1;3)

При всех значениях параметра а решить систему
уравнений

Решение.

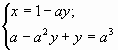
1) если , т.е.
, то данная
система равносильна

2) если а=1, то система имеет видх=1
— у

3) если а= — 1, то система равносильна уравнению
х=1+у.

Ответ: при
(1+а²; -а)

при а=1 (1-у; у)

при а=-1 (1+у; у)

Решите систему уравнений с двумя неизвестными
х и у:

1) Ответ:
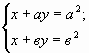
если bа, то
(-ab; b+a); если b=a, то (a²-ay; y).

2) Ответ:
если b?, то x=1
y=b;если b=?,то x=2-3y, y- любое .

3) Ответ:
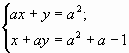
при , то х=а-1,
у=а;

при а=1, то х — любое число, у=1-х;

при а=-1, то х — любое число, у=1+х.

Задачи с параметрами для решения в 8 классе
предполагают знания по теме «Квадратные
уравнения», «Дробные рациональные уравнения»,
«Неравенства».

Задачи с параметрами, дополняющие список задач
из учебника к теме «Квадратные уравнения».

Найдите к и второй корень уравнения:

х² — 5х + к = 0, если х₁=5;

х² +кх — 15=0, если х₁=3.

Найдите все числа р и с такие, что корни
уравнения х² + рх + с =0, равны р и с.

При каких а уравнение (1+а)х²+3ах — 1=0 имеет
единственное решение?

Решите уравнение ах²=1.

Задания с параметрами, предлагаемые для
выполнения после изучения темы «Неравенства».

1. Найдите все значения параметра а, для которых
квадратное уравнение (а+1)х² + 2(а+1)х+а-2=0 а)
имеет два различных корня;

б) не имеет корней;

в) имеет два равных корня.

2. При всех а решите уравнение ах² — 2х + 4= 0.

3. Решите уравнение ах² + 2х + 1 = 0.

4. Найдите все значения параметра а, для которых
уравнение 4х² — 2х + а =0

а) имеет два различных корня;

б) не имеет корней.

5. Найдите все значения параметра а, для которых
уравнение имеет единственный корень

а) ах² — (2а+6)х + 3а + 3 = 0;

б) ах² + (4а+2)х + 3а + 3/2 = 0.

После изучения главы I «Рациональные дроби»
можно предлагать учащимся решать более сложные
системы линейных уравнений с параметрами.

1. При всех значениях параметров а и в решить
систему

1) 2) 3) 4) 5) 6)

Решение 1 системы.

если , , то ;

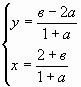
если 1+а=0, а = -1, то , чтобы система имела решение, необходимо,

чтобы в = -2, тогда , если ,
то решений нет.

Ответ: если ,
то (; )

если а = -1, в = -2, то (2+у; у)

если а = -1 , в-2,
то решений нет.

В 9 классе представляется
целесообразным после изучения главы I
«Квадратичная функция» вернуться к решению
уравнений второй степени с параметрами,
предлагая учащимся для решения задания
следующего типа.

1. Решите квадратные уравнения.

1) 2х² — (а — 1)х + а + 1 = 0;

2) ах² + (а + 1)х +а² +а = 0;

3) ах² + 2х(а + 1) + а +3 = 0;

4) (а — 2)х² + ах + 1 = 0;

5) х² — ах +2а + 4 = 0;

6) (а + 1)х² — х + (1 — а) = 0.

2. Найдите все значения а, при которых уравнение
имеет хотя бы один корень.

1) х² — 2(а — 1)х + 2а + 1 = 0;

2) (а — 2)х² — 2ах + 2а — 3 = 0.

3. Найдите все значения а, при которых сумма
квадратов корней уравнения х² — ах + а + 7 = 0
равна 10.

Решение. Так как D0, a²-4(a+7)?0, . Если а такое, что
найдутся корни х₁ и х₂, то х₁+х₂=а
и х₁х₂=а+7. х₁²+х₂²=(х₁+х₂)²
— 2х₁х₂=а² — 2(а+7).

Решим уравнение а² — 2а — 14=10, а=6, а = -4, т.к. 6
не принадлежит найденному множеству значений а,
то а = -4. Ответ: а = -4.

4. Найдите все значения в, при которых уравнение
имеет два различных корня.

1) (в — 1)х² + 2х + 1 = 0;

2) вх² — 2х — 2 = 0.

В конце учебного года в 9 классе на уроках
«Повторение:» нужно познакомить учащихся с
графическим методом решения уравнений 2-ой
степени с параметрами, научить распознавать
положение параболы на плоскости в зависимости от
коэффициентов.

Для этого необходимо напомнить:

прямая х= — в/(2а) — ось параболы, х₀= — в/(2а) —
первая координата вершины параболы;

Знак коэффициента а показывает направление
ветвей параболы;

Дискриминант D=b² — 4ac определяет,
пересекается ли парабола с осью Ох.

Указанные свойства парабол позволяют получить
следующие факты, касающиеся расположения корней
квадратного трехчлена на числовой оси.

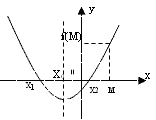
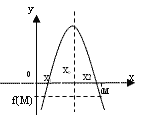
1. Корни квадратного трехчлена х₁ и х₂
(f(х) = ах²+вх+с) будут строго меньше числа М,
если выполняются следующие условия (очевидные,
благодаря рисунку).

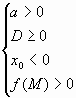
2. Если М I R, то х₁< М < х₂, в том и
только в том случае, когда а*f(М) < 0.

a<0, f(M) >0

a>0, f(M) <0.

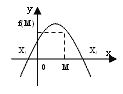
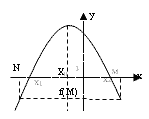
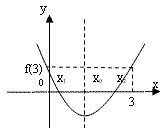
3. Оба корня х₁ и х₂ квадратного
трехчлена f(х)=ах²+вх+с принадлежат
интервалу(М;N), если и только если выполняются
условия:

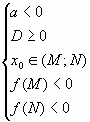
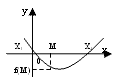
Задания, соответствующие другим случаям
расположения корней квадратного трехчлена (оба
корня больше некоторого числа М; если отрезок [М;
N] целиком лежит на интервале (х₁;х₂) и
другие) решаются, следуя аналогичным
требованиям, проиллюстрированным на рисунке,
который отвечает конкретному заданию.

1. При каких значениях а оба корня уравнения х²
— 6ах + 2 — 2а + 9а²= 0 больше трех?

.

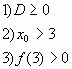
2. При каких значениях а оба корня уравнения х²
— ах +2 = 0 лежат на интервале (0;3)?

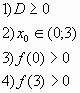
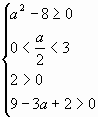
Ответ: .

3. При каких значениях а один корень уравнения
ах² +х +1 = 0 больше 2, а другой меньше 2?

Ответ: .

4. При каких значениях m оба корня уравнения (m+2)х²
— 2mх +3m = 0 положительны?

Ответ: -3 m < -2.

5. Найдите все значения а, при которых один из
корней многочлена (а²+а+1)х²+(а -1)х +а²
больше 3, а другой меньше 3.

f(3)*a<0?, т.е.(10a²+12a+6)
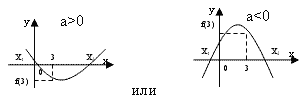
* (а²+а+1)<0.

Ответ: решений нет.

6. При каких значениях а один корень уравнения (а²+а+1)х²
+(2а — 3)х +(а — 5) = 0 больше 1, а другой меньше 1?

Ответ: .

7. При каких значениях а оба корня уравнения х²
+4ах + (1-2а+4а²) = 0 меньше -1?

Ответ: a>1.

8. Существуют ли такие а, что корни уравнения х²+2х+а=0
различны и лежат между числами -1 и 1?

Ответ: таких а не существует.

9. При каких значениях а оба корня уравнения (2 —
а)х² — 3ах +2а = 0 больше 1/2?

Ответ: .

10. При каких значениях а оба корня уравнения ах²
— (а+1)х +2 = 0 по модулю меньше 1?

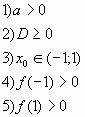
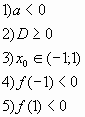
Ответ: .

11. Найдите все значения а, при которых уравнение
4х² — 2х + а = 0 имеет два корня, каждый из
которых принадлежит интервалу (-1;1).

Ответ: .

12. Найдите все значения а, при которых корни
уравнения х² — 2ах + а² — 1 = 0 заключены
между числами 2 и 4.

Литература.

1. Д.К. Фадеев и др. «Задачи по алгебре для 6-8
   классов», М., Просвещение, 1988
2. В.В. Ткачук «Математика — абитуриенту», МЦНМО,
   ТЕИС, 1996
3. С.А.Шестаков, Е.В.Юрченко «Уравнения с
   параметрами», СЛОГ, 1993
4. Г.Я. Ястребинецкий «Задачи с параметрами», М.,
   Просвещение, 1986
5. В.В. Вавилов и др. «Задачи по математике.
   Алгебра», М., Наука, 1987
6. Н.Я. Виленкин и др.» Алгебра 8″, М., Просвещение,
   1995
7. Л.И. Звавич др. «Задания для проведения
   письменного экзамена по математике в 9 классе»,
   М., Просвещение, 1994
8. В.В. Мочалов, В.В. Сильвестров «Уравнения и
   неравенства с параметрами», Чебоксары,
   Издательство Чувашского университета,2000
9. А.Х. Шахмейстер «Уравнения и неравенства с
   параметрами»,С.-Петербург, Москва, 2006