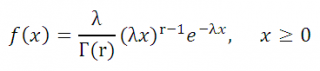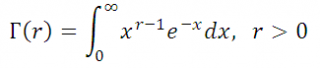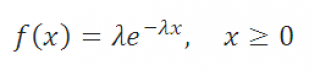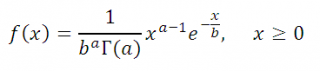|
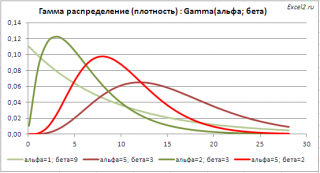
Probability density function |
||
|
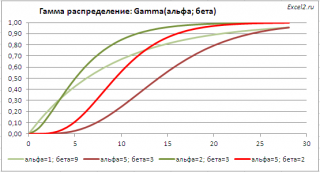
Cumulative distribution function |
||
| Parameters |
|
|
|---|---|---|
| Support |
 |
 |
 |
 |
|
| CDF |
 |
 |
| Mean |
 |
 |
| Median | No simple closed form | No simple closed form |
| Mode |
 , ,  |
 |
| Variance |
 |
 |
| Skewness |
 |
 |
| Ex. kurtosis |
 |
 |
| Entropy |
 |
 |
| MGF |
 |
 |
| CF |
 |
 |
| Fisher information |
 |
 |
| Method of Moments |
![{displaystyle k={frac {E[X]^{2}}{V[X]}}quad quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/79060985aa8683bbf0b380d57ca56522822342ca) ![{displaystyle theta ={frac {E[X]}{V[X]}}quad quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/89fae7d83e69c30943d7a57721fe6e5f06233f0c) |
![{displaystyle alpha ={frac {E[X]^{2}}{V[X]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87074b8ec525badd064920b64dcff7be1c51ceaa) ![{displaystyle beta ={frac {V[X]}{E[X]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd6471243541db87fec37f42819883877a319653) |
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter
and a scale parameter
.
- With a shape parameter
and an inverse scale parameter
, called a rate parameter.
In each of these forms, both parameters are positive real numbers.
The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 

Definitions[edit]
The parameterization with k and θ appears to be more common in econometrics and other applied fields, where the gamma distribution is frequently used to model waiting times. For instance, in life testing, the waiting time until death is a random variable that is frequently modeled with a gamma distribution. See Hogg and Craig[2] for an explicit motivation.
The parameterization with 

If k is a positive integer, then the distribution represents an Erlang distribution; i.e., the sum of k independent exponentially distributed random variables, each of which has a mean of θ.
Characterization using shape α and rate β[edit]
The gamma distribution can be parameterized in terms of a shape parameter α = k and an inverse scale parameter β = 1/θ, called a rate parameter. A random variable X that is gamma-distributed with shape α and rate β is denoted
The corresponding probability density function in the shape-rate parameterization is
where 
For all positive integers, 
The cumulative distribution function is the regularized gamma function:
where 
If α is a positive integer (i.e., the distribution is an Erlang distribution), the cumulative distribution function has the following series expansion:[4]
Characterization using shape k and scale θ[edit]
A random variable X that is gamma-distributed with shape k and scale θ is denoted by
Illustration of the gamma PDF for parameter values over k and x with θ set to 1, 2, 3, 4, 5 and 6. One can see each θ layer by itself here [2] as well as by k [3] and x. [4].
The probability density function using the shape-scale parametrization is
Here Γ(k) is the gamma function evaluated at k.
The cumulative distribution function is the regularized gamma function:
where 
It can also be expressed as follows, if k is a positive integer (i.e., the distribution is an Erlang distribution):[4]
Both parametrizations are common because either can be more convenient depending on the situation.
Properties[edit]
Mean and variance[edit]
The mean of gamma distribution is given by the product of its shape and scale parameters:
The variance is:
The square root of the inverse shape parameter gives the coefficient of variation:
Skewness[edit]
The skewness of the gamma distribution only depends on its shape parameter, k, and it is equal to 
Higher moments[edit]
The nth raw moment is given by:
Median approximations and bounds[edit]
Bounds and asymptotic approximations to the median of the gamma distribution. The cyan-colored region indicates the large gap between published lower and upper bounds.
Unlike the mode and the mean, which have readily calculable formulas based on the parameters, the median does not have a closed-form equation. The median for this distribution is the value 
A rigorous treatment of the problem of determining an asymptotic expansion and bounds for the median of the gamma distribution was handled first by Chen and Rubin, who proved that (for 
where 




K. P. Choi found the first five terms in a Laurent series asymptotic approximation of the median by comparing the median to Ramanujan’s 
Two gamma distribution median asymptotes which are conjectured to be bounds (upper solid red and lower dashed red), of the from 
Log–log plot of upper (solid) and lower (dashed) bounds to the median of a gamma distribution and the gaps between them. The green, yellow, and cyan regions represent the gap before the Lyon 2021 paper. The green and yellow narrow that gap with the lower bounds that Lyon proved. Lyon’s conjectured bounds further narrow the yellow. Mostly within the yellow, closed-form rational-function-interpolated bounds are plotted along with the numerically calculated median (dotted) value. Tighter interpolated bounds exist but are not plotted, as they would not be resolved at this scale.
Partial sums of these series are good approximations for high enough 

Berg and Pedersen also proved many properties of the median, showing that it is a convex function of 





A closer linear upper bound, for 

for
(with equality at
)
which can be extended to a bound for all 
An approximation to the median that is asymptotically accurate at high 

which goes negative for 
In 2021, Lyon proposed several closed-form approximations of the form 



is a lower bound, asymptotically tight as
is an upper bound, asymptotically tight as
Lyon also derived two other lower bounds that are not closed-form expressions, including this one based on solving the integral expression substituting 1 for 
(approaching equality as
)
and the tangent line at 

(with equality at
)
where Ei is the exponential integral.[10]
Additionally, he showed that interpolations between bounds could provide excellent approximations or tighter bounds to the median, including an approximation that is exact at 

where 



For the simplest interpolating function considered, a first-order rational function
the tightest lower bound has
and the tightest upper bound has
The interpolated bounds are plotted (mostly inside the yellow region) in the log–log plot shown. Even tighter bounds are available using different interpolating functions, but not usually with closed-form parameters like these.[10]
Summation[edit]
If Xi has a Gamma(ki, θ) distribution for i = 1, 2, …, N (i.e., all distributions have the same scale parameter θ), then
provided all Xi are independent.
For the cases where the Xi are independent but have different scale parameters, see Mathai [11] or Moschopoulos.[12]
The gamma distribution exhibits infinite divisibility.
Scaling[edit]
If
then, for any c > 0,
by moment generating functions,
or equivalently, if
(shape-rate parameterization)
Indeed, we know that if X is an exponential r.v. with rate λ, then cX is an exponential r.v. with rate λ/c; the same thing is valid with Gamma variates (and this can be checked using the moment-generating function, see, e.g.,these notes, 10.4-(ii)): multiplication by a positive constant c divides the rate (or, equivalently, multiplies the scale).
Exponential family[edit]
The gamma distribution is a two-parameter exponential family with natural parameters k − 1 and −1/θ (equivalently, α − 1 and −β), and natural statistics X and ln(X).
If the shape parameter k is held fixed, the resulting one-parameter family of distributions is a natural exponential family.
Logarithmic expectation and variance[edit]
One can show that
or equivalently,
where 
where 
This can be derived using the exponential family formula for the moment generating function of the sufficient statistic, because one of the sufficient statistics of the gamma distribution is ln(x).
Information entropy[edit]
The information entropy is
In the k, θ parameterization, the information entropy is given by
Kullback–Leibler divergence[edit]
Illustration of the Kullback–Leibler (KL) divergence for two gamma PDFs. Here β = β0 + 1 which are set to 1, 2, 3, 4, 5 and 6. The typical asymmetry for the KL divergence is clearly visible.
The Kullback–Leibler divergence (KL-divergence), of Gamma(αp, βp) («true» distribution) from Gamma(αq, βq) («approximating» distribution) is given by[13]
Written using the k, θ parameterization, the KL-divergence of Gamma(kp, θp) from Gamma(kq, θq) is given by
Laplace transform[edit]
The Laplace transform of the gamma PDF is
[edit]
General[edit]
- Let
be
independent and identically distributed random variables following an exponential distribution with rate parameter λ, then
~ Gamma(n, 1/λ) where n is the shape parameter and λ is the rate, and
where the rate changes nλ.
- If X ~ Gamma(1, λ) (in the shape–rate parametrization), then X has an exponential distribution with rate parameter λ. In the shape-scale parametrization, X ~ Gamma(1, λ) has an exponential distribution with rate parameter 1/λ.
- If X ~ Gamma(ν/2, 2) (in the shape–scale parametrization), then X is identical to χ2(ν), the chi-squared distribution with ν degrees of freedom. Conversely, if Q ~ χ2(ν) and c is a positive constant, then cQ ~ Gamma(ν/2, 2c).
- If θ=1/k, one obtains the Schulz-Zimm distribution, which is most prominently used to model polymer chain lengths.
- If k is an integer, the gamma distribution is an Erlang distribution and is the probability distribution of the waiting time until the kth «arrival» in a one-dimensional Poisson process with intensity 1/θ. If
-
- then
- If X has a Maxwell–Boltzmann distribution with parameter a, then
- If X ~ Gamma(k, θ), then
follows an exponential-gamma (abbreviated exp-gamma) distribution.[14] It is sometimes referred to as the log-gamma distribution.[15] Formulas for its mean and variance are in the section #Logarithmic expectation and variance.
- If X ~ Gamma(k, θ), then
follows a generalized gamma distribution with parameters p = 2, d = 2k, and
[citation needed].
- More generally, if X ~ Gamma(k,θ), then
for
follows a generalized gamma distribution with parameters p = 1/q, d = k/q, and
.
- If X ~ Gamma(k, θ) with shape k and scale θ, then 1/X ~ Inv-Gamma(k, θ−1) (see Inverse-gamma distribution for derivation).
- Parametrization 1: If
are independent, then
, or equivalently,
- Parametrization 2: If
are independent, then
, or equivalently,
- If X ~ Gamma(α, θ) and Y ~ Gamma(β, θ) are independently distributed, then X/(X + Y) has a beta distribution with parameters α and β, and X/(X + Y) is independent of X + Y, which is Gamma(α + β, θ)-distributed.
- If Xi ~ Gamma(αi, 1) are independently distributed, then the vector (X1/S, …, Xn/S), where S = X1 + … + Xn, follows a Dirichlet distribution with parameters α1, …, αn.
- For large k the gamma distribution converges to normal distribution with mean μ = kθ and variance σ2 = kθ2.
- The gamma distribution is the conjugate prior for the precision of the normal distribution with known mean.
- The matrix gamma distribution and the Wishart distribution are multivariate generalizations of the gamma distribution (samples are positive-definite matrices rather than positive real numbers).
- The gamma distribution is a special case of the generalized gamma distribution, the generalized integer gamma distribution, and the generalized inverse Gaussian distribution.
- Among the discrete distributions, the negative binomial distribution is sometimes considered the discrete analog of the gamma distribution.
- Tweedie distributions – the gamma distribution is a member of the family of Tweedie exponential dispersion models.
- Modified Half-normal distribution – the Gamma distribution is a member of the family of Modified half-normal distribution.[16] The corresponding density is
, where
denotes the Fox–Wright Psi function.
- For the shape-scale parameterization
, if the scale parameter
where
denotes the Inverse-gamma distribution, then the marginal distribution
where
denotes the Beta prime distribution.
Compound gamma[edit]
If the shape parameter of the gamma distribution is known, but the inverse-scale parameter is unknown, then a gamma distribution for the inverse scale forms a conjugate prior. The compound distribution, which results from integrating out the inverse scale, has a closed-form solution known as the compound gamma distribution.[17]
If, instead, the shape parameter is known but the mean is unknown, with the prior of the mean being given by another gamma distribution, then it results in K-distribution.
Weibull and Stable count[edit]
The gamma distribution 
Its shape parameter 
where 



Statistical inference[edit]
Parameter estimation[edit]
Maximum likelihood estimation[edit]
The likelihood function for N iid observations (x1, …, xN) is
from which we calculate the log-likelihood function
Finding the maximum with respect to θ by taking the derivative and setting it equal to zero yields the maximum likelihood estimator of the θ parameter, which equals the sample mean 
Substituting this into the log-likelihood function gives
We need at least two samples: 





where 

If we let
then k is approximately
which is within 1.5% of the correct value.[18] An explicit form for the Newton–Raphson update of this initial guess is:[19]
At the maximum-likelihood estimate 


Caveat for small shape parameter[edit]
For data, 


This probability will approach 1 for small 





In order to test an implementation of a maximum-likelihood estimator that takes logarithmic data as input, it is useful to be able to generate non-underflowing logarithms of random gamma variates, when 
scipy.stats.loggamma, this can be done as follows:[20] sample 



Closed-form estimators[edit]
Consistent closed-form estimators of k and θ exists that are derived from the likelihood of the generalized gamma distribution.[21]
The estimate for the shape k is
and the estimate for the scale θ is
Using the sample mean of x, the sample mean of ln(x), and the sample mean of the product x·ln(x) simplifies the expressions to:
If the rate parameterization is used, the estimate of 
These estimators are not strictly maximum likelihood estimators, but are instead referred to as mixed type log-moment estimators. They have however similar efficiency as the maximum likelihood estimators.
Although these estimators are consistent, they have a small bias. A bias-corrected variant of the estimator for the scale θ is
A bias correction for the shape parameter k is given as[22]
Bayesian minimum mean squared error[edit]
With known k and unknown θ, the posterior density function for theta (using the standard scale-invariant prior for θ) is
Denoting
Integration with respect to θ can be carried out using a change of variables, revealing that 1/θ is gamma-distributed with parameters α = Nk, β = y.
The moments can be computed by taking the ratio (m by m = 0)
which shows that the mean ± standard deviation estimate of the posterior distribution for θ is
Bayesian inference[edit]
Conjugate prior[edit]
In Bayesian inference, the gamma distribution is the conjugate prior to many likelihood distributions: the Poisson, exponential, normal (with known mean), Pareto, gamma with known shape σ, inverse gamma with known shape parameter, and Gompertz with known scale parameter.
The gamma distribution’s conjugate prior is:[23]
where Z is the normalizing constant with no closed-form solution.
The posterior distribution can be found by updating the parameters as follows:
where n is the number of observations, and xi is the ith observation.
Occurrence and applications[edit]
Consider a sequence of events, with the waiting time for each event being an exponential distribution with rate 


The gamma distribution has been used to model the size of insurance claims[28] and rainfalls.[29] This means that aggregate insurance claims and the amount of rainfall accumulated in a reservoir are modelled by a gamma process – much like the exponential distribution generates a Poisson process.
The gamma distribution is also used to model errors in multi-level Poisson regression models because a mixture of Poisson distributions with gamma-distributed rates has a known closed form distribution, called negative binomial.
In wireless communication, the gamma distribution is used to model the multi-path fading of signal power;[citation needed] see also Rayleigh distribution and Rician distribution.
In oncology, the age distribution of cancer incidence often follows the gamma distribution, wherein the shape and scale parameters predict, respectively, the number of driver events and the time interval between them.[30][31]
In neuroscience, the gamma distribution is often used to describe the distribution of inter-spike intervals.[32][33]
In bacterial gene expression, the copy number of a constitutively expressed protein often follows the gamma distribution, where the scale and shape parameter are, respectively, the mean number of bursts per cell cycle and the mean number of protein molecules produced by a single mRNA during its lifetime.[34]
In genomics, the gamma distribution was applied in peak calling step (i.e., in recognition of signal) in ChIP-chip[35] and ChIP-seq[36] data analysis.
In Bayesian statistics, the gamma distribution is widely used as a conjugate prior. It is the conjugate prior for the precision (i.e. inverse of the variance) of a normal distribution. It is also the conjugate prior for the exponential distribution.
Random variate generation[edit]
Given the scaling property above, it is enough to generate gamma variables with θ = 1, as we can later convert to any value of β with a simple division.
Suppose we wish to generate random variables from Gamma(n + δ, 1), where n is a non-negative integer and 0 < δ < 1. Using the fact that a Gamma(1, 1) distribution is the same as an Exp(1) distribution, and noting the method of generating exponential variables, we conclude that if U is uniformly distributed on (0, 1], then −ln(U) is distributed Gamma(1, 1) (i.e. inverse transform sampling). Now, using the «α-addition» property of gamma distribution, we expand this result:
where Uk are all uniformly distributed on (0, 1] and independent. All that is left now is to generate a variable distributed as Gamma(δ, 1) for 0 < δ < 1 and apply the «α-addition» property once more. This is the most difficult part.
Random generation of gamma variates is discussed in detail by Devroye,[37]: 401–428 noting that none are uniformly fast for all shape parameters. For small values of the shape parameter, the algorithms are often not valid.[37]: 406 For arbitrary values of the shape parameter, one can apply the Ahrens and Dieter[38] modified acceptance-rejection method Algorithm GD (shape k ≥ 1), or transformation method[39] when 0 < k < 1. Also see Cheng and Feast Algorithm GKM 3[40] or Marsaglia’s squeeze method.[41]
The following is a version of the Ahrens-Dieter acceptance–rejection method:[38]
- Generate U, V and W as iid uniform (0, 1] variates.
- If
then
and
. Otherwise,
and
.
- If
then go to step 1.
- ξ is distributed as Γ(δ, 1).
A summary of this is
where 
While the above approach is technically correct, Devroye notes that it is linear in the value of k and generally is not a good choice. Instead, he recommends using either rejection-based or table-based methods, depending on context.[37]: 401–428
For example, Marsaglia’s simple transformation-rejection method relying on one normal variate X and one uniform variate U:[20]
- Set
and
.
- Set
.
- If
and
return
, else go back to step 2.
With 

References[edit]
- ^ Park, Sung Y.; Bera, Anil K. (2009). «Maximum entropy autoregressive conditional heteroskedasticity model» (PDF). Journal of Econometrics. 150 (2): 219–230. CiteSeerX 10.1.1.511.9750. doi:10.1016/j.jeconom.2008.12.014. Archived from the original (PDF) on 2016-03-07. Retrieved 2011-06-02.
- ^ Hogg, R. V.; Craig, A. T. (1978). Introduction to Mathematical Statistics (4th ed.). New York: Macmillan. pp. Remark 3.3.1. ISBN 0023557109.
- ^ Scalable Recommendation with Poisson Factorization, Prem Gopalan, Jake M. Hofman, David Blei, arXiv.org 2014
- ^ a b Papoulis, Pillai, Probability, Random Variables, and Stochastic Processes, Fourth Edition
- ^ Jeesen Chen, Herman Rubin, Bounds for the difference between median and mean of gamma and Poisson distributions, Statistics & Probability Letters, Volume 4, Issue 6, October 1986, Pages 281–283, ISSN 0167-7152, [1].
- ^ Choi, K. P. «On the Medians of the Gamma Distributions and an Equation of Ramanujan», Proceedings of the American Mathematical Society, Vol. 121, No. 1 (May, 1994), pp. 245–251.
- ^ a b Berg, Christian & Pedersen, Henrik L. (March 2006). «The Chen–Rubin conjecture in a continuous setting» (PDF). Methods and Applications of Analysis. 13 (1): 63–88. doi:10.4310/MAA.2006.v13.n1.a4. S2CID 6704865. Retrieved 1 April 2020.
- ^ a b Berg, Christian and Pedersen, Henrik L. «Convexity of the median in the gamma distribution».
- ^ Gaunt, Robert E., and Milan Merkle (2021). «On bounds for the mode and median of the generalized hyperbolic and related distributions». Journal of Mathematical Analysis and Applications. 493 (1): 124508. arXiv:2002.01884. doi:10.1016/j.jmaa.2020.124508. S2CID 221103640.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b c Lyon, Richard F. (13 May 2021). «On closed-form tight bounds and approximations for the median of a gamma distribution». PLOS One. 16 (5): e0251626. arXiv:2011.04060. Bibcode:2021PLoSO..1651626L. doi:10.1371/journal.pone.0251626. PMC 8118309. PMID 33984053.
- ^ Mathai, A. M. (1982). «Storage capacity of a dam with gamma type inputs». Annals of the Institute of Statistical Mathematics. 34 (3): 591–597. doi:10.1007/BF02481056. ISSN 0020-3157. S2CID 122537756.
- ^ Moschopoulos, P. G. (1985). «The distribution of the sum of independent gamma random variables». Annals of the Institute of Statistical Mathematics. 37 (3): 541–544. doi:10.1007/BF02481123. S2CID 120066454.
- ^ W.D. Penny, [www.fil.ion.ucl.ac.uk/~wpenny/publications/densities.ps KL-Divergences of Normal, Gamma, Dirichlet, and Wishart densities][full citation needed]
- ^ «ExpGammaDistribution—Wolfram Language Documentation».
- ^ «scipy.stats.loggamma — SciPy v1.8.0 Manual». docs.scipy.org.
- ^ Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 June 2021). «The Modified-Half-Normal distribution: Properties and an efficient sampling scheme». Communications in Statistics — Theory and Methods. 52 (5): 1591–1613. doi:10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.
- ^ Dubey, Satya D. (December 1970). «Compound gamma, beta and F distributions». Metrika. 16: 27–31. doi:10.1007/BF02613934. S2CID 123366328.
- ^ Minka, Thomas P. (2002). «Estimating a Gamma distribution» (PDF).
- ^ Choi, S. C.; Wette, R. (1969). «Maximum Likelihood Estimation of the Parameters of the Gamma Distribution and Their Bias». Technometrics. 11 (4): 683–690. doi:10.1080/00401706.1969.10490731.
- ^ a b Marsaglia, G.; Tsang, W. W. (2000). «A simple method for generating gamma variables». ACM Transactions on Mathematical Software. 26 (3): 363–372. doi:10.1145/358407.358414. S2CID 2634158.
- ^ Ye, Zhi-Sheng; Chen, Nan (2017). «Closed-Form Estimators for the Gamma Distribution Derived from Likelihood Equations». The American Statistician. 71 (2): 177–181. doi:10.1080/00031305.2016.1209129. S2CID 124682698.
- ^ Louzada, Francisco; Ramos, Pedro L.; Ramos, Eduardo (2019). «A Note on Bias of Closed-Form Estimators for the Gamma Distribution Derived from Likelihood Equations». The American Statistician. 73 (2): 195–199. doi:10.1080/00031305.2018.1513376. S2CID 126086375.
- ^ Fink, D. 1995 A Compendium of Conjugate Priors. In progress report: Extension and enhancement of methods for setting data quality objectives. (DOE contract 95‑831).
- ^ Jessica., Scheiner, Samuel M., 1956- Gurevitch (2001). «13. Failure-time analysis». Design and analysis of ecological experiments. Oxford University Press. ISBN 0-19-513187-8. OCLC 43694448.
- ^ Golubev, A. (March 2016). «Applications and implications of the exponentially modified gamma distribution as a model for time variabilities related to cell proliferation and gene expression». Journal of Theoretical Biology. 393: 203–217. Bibcode:2016JThBi.393..203G. doi:10.1016/j.jtbi.2015.12.027. ISSN 0022-5193. PMID 26780652.
- ^ Poon, Art; Davis, Bradley H; Chao, Lin (2005-07-01). «The Coupon Collector and the Suppressor Mutation». Genetics. 170 (3): 1323–1332. doi:10.1534/genetics.104.037259. ISSN 1943-2631. PMC 1451182. PMID 15879511.
- ^ Vineyard, Michael; Amoako-Gyampah, Kwasi; Meredith, Jack R (July 1999). «Failure rate distributions for flexible manufacturing systems: An empirical study». European Journal of Operational Research. 116 (1): 139–155. doi:10.1016/s0377-2217(98)00096-4. ISSN 0377-2217.
- ^ p. 43, Philip J. Boland, Statistical and Probabilistic Methods in Actuarial Science, Chapman & Hall CRC 2007
- ^ Wilks, Daniel S. (1990). «Maximum Likelihood Estimation for the Gamma Distribution Using Data Containing Zeros». Journal of Climate. 3 (12): 1495–1501. Bibcode:1990JCli….3.1495W. doi:10.1175/1520-0442(1990)003<1495:MLEFTG>2.0.CO;2. ISSN 0894-8755. JSTOR 26196366.
- ^ Belikov, Aleksey V. (22 September 2017). «The number of key carcinogenic events can be predicted from cancer incidence». Scientific Reports. 7 (1): 12170. Bibcode:2017NatSR…712170B. doi:10.1038/s41598-017-12448-7. PMC 5610194. PMID 28939880.
- ^ Belikov, Aleksey V.; Vyatkin, Alexey; Leonov, Sergey V. (2021-08-06). «The Erlang distribution approximates the age distribution of incidence of childhood and young adulthood cancers». PeerJ. 9: e11976. doi:10.7717/peerj.11976. ISSN 2167-8359. PMC 8351573. PMID 34434669.
- ^ J. G. Robson and J. B. Troy, «Nature of the maintained discharge of Q, X, and Y retinal ganglion cells of the cat», J. Opt. Soc. Am. A 4, 2301–2307 (1987)
- ^ M.C.M. Wright, I.M. Winter, J.J. Forster, S. Bleeck «Response to best-frequency tone bursts in the ventral cochlear nucleus is governed by ordered inter-spike interval statistics», Hearing Research 317 (2014)
- ^ N. Friedman, L. Cai and X. S. Xie (2006) «Linking stochastic dynamics to population distribution: An analytical framework of gene expression», Phys. Rev. Lett. 97, 168302.
- ^ DJ Reiss, MT Facciotti and NS Baliga (2008) «Model-based deconvolution of genome-wide DNA binding», Bioinformatics, 24, 396–403
- ^ MA Mendoza-Parra, M Nowicka, W Van Gool, H Gronemeyer (2013) «Characterising ChIP-seq binding patterns by model-based peak shape deconvolution», BMC Genomics, 14:834
- ^ a b c Devroye, Luc (1986). Non-Uniform Random Variate Generation. New York: Springer-Verlag. ISBN 978-0-387-96305-1. See Chapter 9, Section 3.
- ^ Ahrens, J. H.; Dieter, U. (1974). «Computer methods for sampling from gamma, beta, Poisson and binomial distributions». Computing. 12 (3): 223–246. CiteSeerX 10.1.1.93.3828. doi:10.1007/BF02293108. S2CID 37484126.
- ^ Cheng, R. C. H.; Feast, G. M. (1979). «Some Simple Gamma Variate Generators». Journal of the Royal Statistical Society. Series C (Applied Statistics). 28 (3): 290–295. doi:10.2307/2347200. JSTOR 2347200.
- ^ Marsaglia, G. The squeeze method for generating gamma variates. Comput, Math. Appl. 3 (1977), 321–325.
External links[edit]
- «Gamma-distribution», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. «Gamma distribution». MathWorld.
- ModelAssist (2017) Uses of the gamma distribution in risk modeling, including applied examples in Excel.
- Engineering Statistics Handbook
| Плотность вероятности Плотности гамма-распределений |
|
| Функция распределения Функции гамма-распределений |
|
| Параметры |  — коэффициент масштаба — коэффициент масштаба
|
| Носитель | 
|
| Плотность вероятности | 
|
| Функция распределения | 
|
| Математическое ожидание | 
|
| Медиана | |
| Мода |  , когда , когда 
|
| Дисперсия | 
|
| Коэффициент асимметрии | 
|
| Коэффициент эксцесса | 
|
| Информационная энтропия |  
|
| Производящая функция моментов |  , когда , когда 
|
| Характеристическая функция | 
|
Га́мма распреде́ление в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр 
Определение
Пусть распределение случайной величины 
где функция
имеет вид
и обладает следующими свойствами:
константы 




Замечание. Иногда используют другую параметризацию семейства гамма-распределений. Или вводят
третий параметр — сдвига.
Моменты
Математическое ожидание и дисперсия случайной величины 
,
.
Свойства гамма-распределения
.
.
- Гамма-распределение бесконечно делимо.
Связь с другими распределениями
- Экспоненциальное распределение является частным случае гамма-распределения:
.
.
- Распределение хи-квадрат является частным случае гамма-распределения:
.
- Согласно центральной предельной теореме, при больших
гамма-распределение может быть приближено нормальным распределением:
при
.
.
Моделирование гамма-величин
Учитывая свойство масштабирования по параметру θ, указанное выше, достаточно смоделировать гамма-величину для θ = 1. Переход к другим значениям параметра осуществляется простым умножением.
Используя тот факт, что распределение 

Теперь, используя свойство k-суммирования, обобщим этот результат:
где Ui — независимые случайные величины, равномерно распределённые на интервале (0, 1].
Осталось смоделировать гамма-величину для 0 < k < 1 и ещё раз применить свойство k-суммирования. Это является самой сложной частью.
Ниже приведён алгоритм без доказательства. Он является примером выборки с отклонением.
- Положить m равным 1.
- Сгенерировать
и
— независимые случайные величины, равномерно распределённые на интервале (0, 1].
- Если
, где
, перейти к шагу 4, иначе к шагу 5.
- Положить
. Перейти к шагу 6.
- Положить
.
- Если
, то увеличить m на единицу и вернуться к шагу 2.
- Принять
за реализацию
.
Подытожим:
где
[k] является целой частью k, а ξ сгенерирована по алгоритму, приведённому выше при δ = {k} (дробная часть k);
Ui and Vl распределены как указано выше и попарно независимы.
|
править |
hu:Gamma-eloszlás
nl:Gamma-verdeling
sv:Gammafördelning
Рассмотрим Гамма распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL
ГАММА.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров распределения.
Гамма распределение
(англ.
Gamma
distribution
)
зависит от 2-х параметров:
r
(определяет форму распределения) и λ (определяет масштаб).
Плотность вероятности
этого распределения задается следующей формулой:
где Г(r) – гамма-функция:
если r – положительное целое, то Г(r)=(r-1)!
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Вышеуказанная форма записи
плотности распределения
наглядно показывает его связь с
Экспоненциальным распределением
. При r=1
Гамма распределение
сводится к
Экспоненциальному распределению
с параметром λ.
Если параметр λ – целое число, то
Гамма распределение
является суммой
r
независимых и одинаково распределенных по
экспоненциальному закону
с параметром λ случайных величин
x
. Таким образом, случайная величина
y
=
x
1
+
x
2
+…
x
r
имеет
гамма распределение
с параметрами
r
и λ.
Экспоненциальное распределение
, в свою очередь, тесно связано с дискретным
распределением Пуассона
. Если
Распределение Пуассона
описывает число случайных событий, произошедших за определенный интервал времени, то
Экспоненциальное распределение,
в этом случае,описывает длину временного интервала между двумя последовательными событиями.
Из этого следует, что, например, если время до наступления первого события описывается
экспоненциальным распределением
с параметром λ, то время до наступления второго события описывается
гамма распределением
с r = 2 и тем же параметром λ.
Гамма распределение в MS EXCEL
В MS EXCEL принята эквивалентная, но отличающаяся параметрами форма записи
плотности
гамма распределения
.
Параметр α (
альфа
) эквивалентен параметру
r
, а параметр
b
(
бета
) – параметру
1/λ
. Ниже будем придерживаться именно такой записи, т.к. это облегчит написание формул.
В MS EXCEL, начиная с версии 2010, для
Гамма распределения
имеется функция
ГАММА.РАСП()
, английское название — GAMMA.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина X, имеющая
гамма распределение
, примет значение меньше или равное x).
Примечание
: До MS EXCEL 2010 в EXCEL была функция
ГАММАРАСП()
, которая позволяет вычислить
интегральную функцию распределения
и
плотность вероятности
.
ГАММАРАСП()
оставлена в MS EXCEL 2010 для совместимости.
Графики функций
В
файле примера
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Гамма распределение
имеет обозначение Gamma
(альфа; бета).
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
Примечание
: Для удобства написания формул в
файле примера
для параметров распределения
альфа и бета
созданы соответствующие
Имена
.
Примечание
: Зависимость от 2-х параметров позволяет построить распределения разнообразных форм, что расширяет применение этого распределения.
Гамма распределение
, как и
Экспоненциальное распределение
часто используется для расчета времени ожидания между случайными событиями. Кроме того, возможно использование применение этого распределения для моделирования уровня осадков и при проектировании дорог.
Как было показано выше, если параметр
альфа
= 1, то функция
ГАММА.РАСП()
возвращает
экспоненциальное распределение
с параметром
1/бета
. Если параметр
бета
= 1, функция
ГАММА.РАСП()
возвращает стандартное
гамма распределение
.
Примечание
: Т.к.
ХИ2-распределение
является частным случаем
гамма распределения
, то формула
=ГАММА.РАСП(x;n/2;2;ИСТИНА
) для целого положительного n возвращает тот же результат, что и формула
=ХИ2.РАСП(x;n; ИСТИНА)
или
=1-ХИ2.РАСП.ПХ(x;n)
. А формула
=ГАММА.РАСП(x;n/2;2;ЛОЖЬ)
возвращает тот же результат, что и формула
=ХИ2.РАСП(x;n; ЛОЖЬ)
, т.е.
плотность вероятности
ХИ2-распределения.
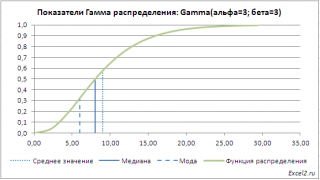
В
файле примера на листе Графики
приведен расчет
Среднего значения (математического ожидания)
гамма распределения
равного
альфа*бета
и
дисперсии (квадрата стандартного отклонения)
равного
альфа*бета
2
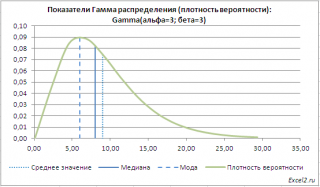
. Там же построены графики
функции распределения
и
плотности вероятности
с отмеченными значениями
среднего
,
медианы
и
моды
.
Генерация случайных чисел и оценка параметров
Для генерирования массива чисел, имеющих
гамма распределение
, можно использовать формулу
=ГАММА.ОБР(СЛЧИС(); альфа; бета)
Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Если случайные числа содержатся в диапазоне
B15:B214
, то оценку параметра
альфа
можно сделать с использованием формулы
=СРЗНАЧ(B15:B214)^2/ДИСП.В(B15:B214)
Для оценки параметра
бета
используйте формулу
=ДИСП.В(B15:B214)/СРЗНАЧ(B15:B214)
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
|
∞ |
1 |
∞ |
∞ |
−2k |
2 |
2 |
1 |
|||||||||||||||
|
= − 8 ∑(−1)k k 2 |
e− |
2k 2z2 |
= −2 ∑(−1)k e |
hZ |
= |
. |
Отсюда |
|||||||||||||||
|
− 2k 2 |
||||||||||||||||||||||
|
2 k =1 |
h |
k =1 |
2 |
|||||||||||||||||||
|
Z |
||||||||||||||||||||||
|
∞ |
−2k |
2 |
2 |
1 |
∞ |
−2k |
2 |
2 |
∞ |
−2k |
2 |
2 |
||||||||||
|
2 ∑(−1)k e |
hZ |
+1 |
= − |
+1, но 1+ 2 ∑(−1)k e |
hZ |
= ∑ |
(−1)k e |
hZ = |
||||||||||||||
|
k =1 |
2 |
k =1 |
−∞ |
|||||||||||||||||||
|
= K (hZ2 )= |
1 |
Тогда |
hZ2 = |
1 |
= 0.8276. Итак, |
медиана распределения |
||||||||||||||||
|
2 |
K −1 |
2 |
||||||||||||||||||||
равна hZ = 0.9097.
Гамма–распределение полезно при представлении распределения величин (вес, длина), которые не могут быть отрицательными или значения которых ограничены снизу известным числом. Как и семейство распределений Вейбулла, семейство гамма–распределений включает экспоненциальное распределение как частный случай.
Гамма–распределение определяется формулой
|
f X (x) = |
1 |
− |
x |
||||
|
xαe |
β , x > 0. |
(2.5.1) |
|||||
|
Γ(α +1)β α+1 |
|||||||
Распределение двухпараметрическое. Параметр масштаба β > 0 , часто используется другой параметр λ, λ = 1
|
f (x) = |
1 |
e− |
x |
1 |
||||
|
β |
= λe−λx , λ = |
. |
(2.5.2) |
|||||
|
Γ(1)β |
||||||||
|
β |
α в распределении должно быть больше –1.
|
F(x) = |
1 |
x |
− |
t |
|||
|
Функция распределения |
∫t αe |
βdt. |
(2.5.3) |
||||
|
Γ(α +1)β α+1 |
|||||||
|
0 |
Вид функции плотности вероятности и функции распределения сильно зависят от параметра α. На рис. 2.7 приведены графики функций плотностей (слева) и функций распределения (справа) для значений параметра α, равного нулю (для f 1 и F1), двум (для f 2 и F 2 ) и семи (для
f 3 и F3 ).
49
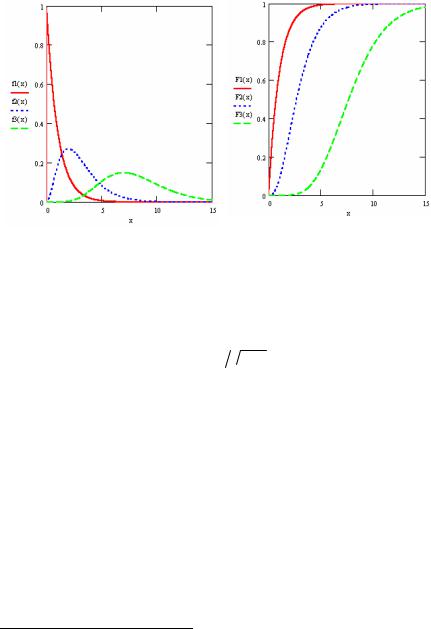
Рис. 2.7. Кривые плотности и распределения гамма-распределения
Числовые характеристики распределения:
1)математическое ожидание mX = β(α +1);
2)дисперсия DX = β2 (α +1);
3)мода d X = βα, α ≥ −1 ;
4)коэффициент асимметрии A = 2 
5)коэффициент эксцесса E = 6
При α +1 = n
α1 + α2 + 2.
2.6. Распределение Вейбулла (Вейбулла – Гнеденко )
Это распределение весьма широко применяется в последние два десятилетия. Особенно оно полезно в задачах долговечности и надежности. Его можно рассматривать как обобщение экспоненциального распределения, поскольку в нем три параметра, и оно сводится к экспоненциальному при подходящем выборе одного из них.
Борис Владимирович Гнеденко (1912-1995) — советский математик.
50
Плотность распределения вероятностей смещенного (трехпараметрического) распределения Вейбулла определяется как
|
c x − a c−1 |
x−a c |
||||||
|
f X (x) = |
− |
||||||
|
b |
|||||||
|
e |
, x ≥ a, b > 0, c > 0. |
(2.6.1) |
|||||
|
b |
|||||||
|
b |
Параметр масштаба b иногда называют характерным временем жизни. Обычно распределение делают двухпараметрическим, полагая a = 0. Тогда получают так называемое классическое распределение Вейбулла с плотностью вероятности
|
α−1 |
−λx |
α |
|||
|
, x > 0, |
(2.6.2) |
||||
|
f X (x) = αλ x |
e |
||||
|
0, |
x ≤ 0. |
||||
Здесь α, λ > 0 и α = с, λ =1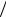
цию плотности экспоненциального распределения. Обычно проще работать с функцией распределения Вейбулла, которая имеет вид
|
F(x) = 1 − e−λxα . |
(2.6.3) |
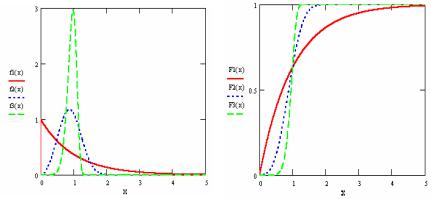
Графики функции распределения и функции плотности вероятности зависят от значения параметра формы α (или c в формуле (2.6.1)). Далее на рис. 2.8 приведены графики функций плотности вероятностей и функ-
Рис. 2.8. Кривые плотности и распределения закона Вейбулла
ций распределения для ряда значений параметра формы: f 1 и F1 для α = 1 , f 2 и F 2 для α = 3 , наконец, f 3 и F3 для α = 8 .
Числовые характеристики двухпараметрического распределения выражаются через гамму-функцию и равны:
51

|
c |
+1 |
− |
1 |
α +1 |
||||||||||||||||||||||||||||
|
α |
||||||||||||||||||||||||||||||||
|
1) |
математическое ожидание mX |
= bΓ |
= λ |
Γ |
; |
|||||||||||||||||||||||||||
|
c |
α |
|||||||||||||||||||||||||||||||
|
2) |
дисперсия |
|||||||||||||||||||||||||||||||
|
2 |
c + 2 |
2 |
c +1 |
− |
2 |
α + 2 |
2 |
α |
+1 |
|||||||||||||||||||||||
|
α |
||||||||||||||||||||||||||||||||
|
DX = b |
Γ |
− Γ |
= |
λ |
Γ |
− Γ |
; |
|||||||||||||||||||||||||
|
c |
c |
α |
α |
|||||||||||||||||||||||||||||
|
1 |
1 |
− |
1 |
1 |
1 |
|||||||||||||||||||||||||||
|
c |
α |
|||||||||||||||||||||||||||||||
|
α |
||||||||||||||||||||||||||||||||
|
3) |
мода d X |
= b 1 |
− |
, |
c ≥1, |
или d X = |
λ |
1 − |
, |
α ≥ 1, |
||||||||||||||||||||||
|
c |
||||||||||||||||||||||||||||||||
|
α |
||||||||||||||||||||||||||||||||
|
0, |
c < 1, |
0, |
α < 1; |
|||||||||||||||||||||||||||||
4)медиана hX = b(ln 2)1
5)коэффициент асимметрии
|
c + 3 |
c + |
2 |
c +1 |
+ |
c +1 |
||||||||||||||||||||||||||||
|
Γ |
c |
−3Γ |
c |
Γ |
c |
2Γ3 |
c |
||||||||||||||||||||||||||
|
A = |
; |
||||||||||||||||||||||||||||||||
|
c + 2 |
− Γ |
2 |
c |
+1 3 2 |
|||||||||||||||||||||||||||||
|
Γ |
c |
c |
|||||||||||||||||||||||||||||||
|
6) коэффициент эксцесса |
|||||||||||||||||||||||||||||||||
|
c + 4 |
c + |
3 c +1 |
c + 2 |
c +1 |
c +1 |
||||||||||||||||||||||||||||
|
Γ |
− 4Γ |
Γ |
+ |
6Γ |
Γ2 |
− 3Γ4 |
|||||||||||||||||||||||||||
|
c |
c |
c |
c |
c |
c |
||||||||||||||||||||||||||||
|
E = |
. |
||||||||||||||||||||||||||||||||
|
c + 2 |
2 |
c +1 2 |
|||||||||||||||||||||||||||||||
|
Γ |
− Γ |
||||||||||||||||||||||||||||||||
|
c |
c |
||||||||||||||||||||||||||||||||
Распределение Вейбулла часто используется в теории надежности для описания времени безотказной работы приборов.
2.7. Лабораторная работа № 2. Семейства вероятностных распределений в математических пакетах STATGRAPHICS и MAHTCAD
Пакет STATGRAPHICS Plus for Windows предоставляет возможность работать с 22 наиболее распространенными распределениями вероятностей: Бернулли, биномиальным, дискретным равномерным, геометрическим, отрицательным биномиальным, Пуассона, бета-распределением,
распределением χ2 -квадрат, Эрланга , экспоненциальным, распределени-
ем экстремального значения, F -распределением (распределением дисперсионного отношения), гамма–распределением, распределением Лапласа,
Агнер Краруп Эрланг (1878-1929) – датский математик.
52
Рис. 2.9. Контекстное меню
логистическим распределением, логнормальным, нормальным, распределением Парето , Стьюдента, треугольным, равномерным и распределением Вейбулла.
Для доступа к процедурам, работающими с распределениями, в головном меню пакета необходимо выбрать пункт Plot→Probability Distribution (Графики→Распределение вероятностей). Появится дополнительное меню, содержащее все 22 перечисленных распределения. По умолчанию выделено распределение № 17 – нормальное. Рассмотрим, например, геометрическое распределение. Для этого отметим его в меню распределений и щелкнем по кнопке ОК; появится заставка распределения вероятностей со своим дополнительным меню, содержащим четыре пункта: Input Dialog (Диалог ввода), Tabular Options (Табличные процедуры), Graphics Options (Графические процедуры) и Save Results (Сохранение результата).
Для ввода параметров исследуемого распределения необходимо щелкнуть правой кнопкой мыши в любом месте заставки распределения вероятностей. Появится дополнительное (контекстное) меню следующего вида (рис. 2.9). Назначение процедур этого меню таково.
1.Pane Options (Панель процедур) позволяет задать объем генерируемой выборки выбранного распределения, уровни квантилей и тому подобное в зависимости от контекста вычислений.
2.Analysis Options (Процедуры анализа)
позволяет задать параметры выбранного закона распределения. Это либо характеристики положения и рассеивания для непрерывных распре-
делений, либо вероятности событий для дискретных. Пакет позволяет моделировать и выводить на экран до пяти однотипных распределений.
3.Print распечатывает содержимое текущего проекта или его части.
4.Copy to Gallery копирует содержимое текущего проекта в специальный инструмент – StatGallery. Он позволяет расположить в одном окне или на одном листе до девяти различных фрагментов текста и графических иллюстраций. Это часто бывает необходимым для составления отчетной документации.
Для рассматриваемого геометрического распределения выберем пункт Analysis Options. Появится новая закладка следующего вида
(рис. 2.10).
Введем в поля ввода следую-
щие вероятности: 0.05, 0.25, 0.5, 0.75 и 0.95. После щелчка левой
Рис. 2.10. Меню для задания параметров геометрического распределения
Вильфридо Парето (1848-1923)-итальянский экономист и социолог.
53

Рис. 2.12. Меню задания квантилей или процентных точек
кнопкой мыши по кнопке ОК эти данные заносятся в поле заставки геометрического распределения.
Формы представления выбранного распределения можно задать с помощью двух пунктов меню заставки геометрического распределения ве-
роятностей Tabular Options и Graphics Options. Меню Tabular Options име-
ет следующий вид (рис. 2.11). Процедуры этого меню при задании пунктов выставлением галочки в соот-
|
ветствующем поле выполняет такие |
|
|
действия. |
|
|
Analysis Summary (Сводка ана- |
|
|
лиза) указывает номер распределе- |
|
|
ния и его параметры. |
|
|
Cumulative Distribution (Функ- |
|
|
ция распределения) вычисляет |
|
|
функцию распределения. Первона- |
|
|
чально таблица этой функции для |
|
|
Рис. 2.11. Панель табличных параметров |
всех пяти разновидностей рассмат- |
|
в анализе распределения вероятностей |
риваемого распределения строится |
следующим образом. Для одного значения переменной (по умолчанию x0 = 0 ) вычисляются вероятности левого (Lower Tail Area) и правого (Up-
per Tail Area) хвостов распределения, т.е. вероятности P(X < x0 ) и P(X > x0 ), и вероятность (для дискретных распределений) или значение функции плотности (для непрерывных) при x = x0 . Переменную x0 мож-
но изменить или задать до пяти ее различных значений, щелкнув правой кнопкой мыши в поле заставки Cumulative Distribution и выбрав пункт меню Pane Options.
Появится дополнительное подменю следующего вида (рис. 2.12). Введем в поля ввода этого меню такие значения: 0.1, 1.0, 5.0, 10.0 и 30.0.
Inverse CDF (Обратная функция распределения, значения процентилей) вычисляет для заданных на заставке геометрического распределения вероят-
ностей 0.05, 0.25, 0.5, 0.75 и 0.95 про-
цент наблюдений, лежащих левее указанного числа. Можно задать и иные значения. Для этого необходимо щелч-
ком правой кнопки мыши вызвать пункт меню Pane Options и в появившейся заставке задать набор из пяти нужных числовых значений.
Random Numbers (Случайные числа) порождает последовательность
54

Рис. 2.14. Дополнительное меню StatGallery
Рис. 2.13. Панель графических параметров в анализе распределения вероятностей
независимых одинаково распределенных случайных чисел, подчиняющихся выбранному распределению – одному из упомянутых двадцати двух.
В пункте Graphics Options (рис. 2.13) можно построить графики следующих функций.
Density/Mass Function – функция плотности вероятности для непрерывных распределений или графическое изображение ряда распределения для дискретных распределений. Графики функций выдаются с соответствующими заголовками и автоматически оцифровываются.
Если на график выводится несколько кривых, то они обозначаются различными типами линий – непрерывной, пунктирной, точечной и другими. Справа от графика указывается легенда – связь между типами линий и параметрами кривых, выводимых на график.
CDF (Cumulative Distribution
Function – функция распределения). Первые две формы представления распределений из этого меню являются наиболее употребительными. Последние три еще не использовались нами на практике.
Survivor Function (Функция выживаемости) равна единице минус функция распределения. Это хорошо видно при сравнении графиков обеих функций.
Log Survivor Function (Логарифм функции выживаемости). Имеется в виду натуральный логарифм этой функции.
Hazard Function (Функция риска). Функцией риска называется частное от деления плотности распределения на функцию выживаемости.
После нажатия кнопки ОК меню Graphical Options на правой половине экрана монитора выводятся графики всех заданных функций. Двойной щелчок левой кнопки мыши на любом графике или заставке разворачивает и сворачивает их на весь экран. Заполним теперь лист StatGallery и оформим отчет о проделанной лабораторной работе.
В любом месте открытого поля StatGallery щелкнем правой кнопкой мыши. Появится дополнительное меню (рис. 2.14). Это меню задает порядок и форму расположения текстовой и графической информации на листе отчета. Назначение процедур этого меню следующее:
1. Modify Arrangement (Задание классифи-
кации) вызывает подменю StatGallery Options, распределяющее рисунки и
55
Рис. 2.15. Меню StatGallery, распределяющее рисунки и текст на листе отчета
текст различным образом в поле StatGallery (рис. 2.15). С его помощью информацию на листе отчета можно расположить девятью способами.
2. Print – распечатывает содержимое StatGallery.
3. Erase Graph – сти-
рает часть информации из поля отчета. Вызываемое подменю имеет строение, аналогичное предыдущему подменю.
4. Move Graph – пере-
мещает части отчета по полю StatGallery. При этом можно заменить предыдущую информацию новой (Replace), или затереть ее наложением (Overlay).
5. Clear Gallery – очищает поле StatGallery.
Вызовем пункт меню StatGallery Options и зададим расположение шести элементов отчета способом «по три». В отчет включим заставки Probability Distributions (Top Left), Cumulative Distributions (Center Left), Inverse CDF (Bottom Left) и графики трех функций Probability (Top Center), Cumulative Probability (Center) и Log Survivor Probability (Bottom Center). В результате получим лист отчета (рис. 2.16). К сожалению, более трех элементов в строку и столбец поля StatGallery поместить нельзя.
Воспользуемся, наконец, пунктом дополнительного меню заставки распределения вероятностей Save Results и сохраним полученные результаты. Появится дополнительное подменю следующего вида (рис. 2.17). В полях Save везде поставим галочки, а в полях Target Variables (Плановые переменные) наберем имена случайных выборок Geom1,…, Geom5.
После нажатия клавиш File→Save Data File As и набора имени Geom сгенерированные выборки будут помещены в базу данных пакета STATGRAPHICS.
В пакете реализовано уникальное средство для сохранения результатов работы и создания собственных статистических проектов. Все, что пользователь считает ценным в своем варианте анализа (методы, параметры статистических процедур, графика, табличные схемы и так далее) можно сохранить в виде нового файла StatFolio. Затем этот файл по мере надобности можно изменять и дополнять, используя многократно. Сохраним и мы результаты нашей работы, выбрав File→Save StatFolio As→Geometric.
56
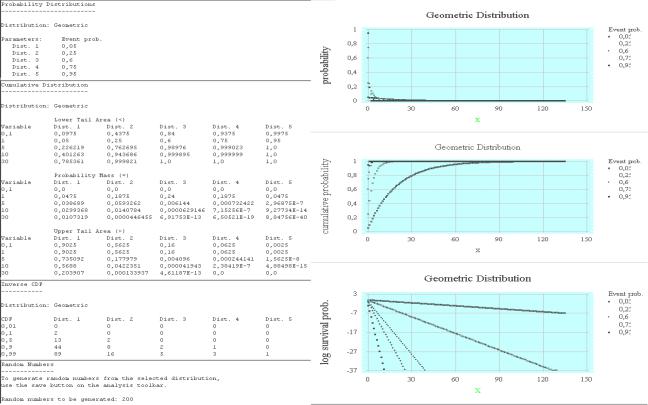
Рис. 2.16. Некоторые табличные и графические характеристики геометрического распределения
Рис. 2.17. Меню пункта Save Results
Задание № 1. По номеру вашей фамилии в журнале преподавателя выбрать распределение в пункте Probability Distributions (если номер больше 22, выбирать номер минус 15), задать пять однотипных распределений, варьируя параметры выбранного распределения, вычислить и вывести на экран дисплея все пункты меню Tabular Options и Graphical Options. Объем выборок задать равным 50. Полученные результаты записать на лист отчета в StatGallery и сохранить в личном статистическом проекте под оригинальным именем (имя: LAB2№группыФИО).
В пакете MATHCAD статистические функции условно разделяются на четыре раздела: статистики совокупностей, распределения вероятностей, гистограммы и случайные числа. Пакет MATHCAD имеет более широкую область применения, статистические функции составляют лишь одну из его более чем двадцати глав. В связи с этим статистические процедуры не сопровождаются непосредственно связанной с ними графикой. Результаты каждой процедуры требуют поэтому индивидуального графического отображения.
Приведем перечень и дадим описание основным встроенным статистическим функциям пакета MATHCAD.
1. Статистики совокупностей. MATHCAD содержит всего шесть функций для вычисления статистических оценок случайных совокупностей.
mean(A) — возвращает среднее значение элементов массива A размерности m × n по формуле
|
mean(A) = |
1 |
m−1n−1 |
||
|
∑ ∑ Ai, j ; |
(2.7.1) |
|||
|
mn i =0 j =0 |
median(A) — возвращает медиану. Медианой называется величина, больше и меньше которой в вариационном ряду расположено одинаковое число членов ряда. Если число элементов массива A четно, то медиана определяется как среднее арифметическое двух центральных элементов вариационного ряда;
56

var(A) — вычисляет дисперсию элементов массива A ; cvar(A,B) — возвращает ковариацию по формуле
|
cvar(A, B) = |
1 |
m−1n−1[A |
− mean(A)][B |
− mean(B)], |
(2.7.2) |
||
|
∑ ∑ |
i, j |
i, j |
|||||
|
mn i =0 j =0 |
|||||||
|
где черта указывает комплексно-сопряженную величину; |
|||||||
|
stdev(A) — вычисляет |
среднее |
квадратическое |
отклонение |
stdev(A)= var(A) ;
наконец, функция corr(A, B) находит коэффициент корреляции для двух массивов A и B .
2. Распределение вероятностей и случайные числа. В пакете MATHCAD можно работать лишь с шестнадцатью статистическими распределениями: биномиальным, геометрическим, отрицательным биномиальным,
Пуассона, бета-распределением, распределением χ2 -квадрат, экспонен-
циальным, F -распределением, гамма–распределением, логистическим, логнормальным, нормальным, распределением Стьюдента, равномерным, распределениями Вейбулла и Коши.
Функции плотности вероятности, функции распределения, обращения функций распределения и функции, моделирующие случайные числа, имеют похожие названия, отличающиеся лишь первой буквой в имени. Эти функции и их параметры приведены в табл. 1.
|
Т а б л и ц а 1 |
|||||
|
Номер по |
Обратные |
Функции, |
|||
|
порядку и |
Функции |
Функции |
функции рас- |
||
|
генерирующие |
|||||
|
название рас- |
плотности |
распределе- |
пределения |
случайные |
|
|
пределения |
вероятности |
ния |
(значения про- |
||
|
числа |
|||||
|
центилей) |
|||||
|
qbinom(α,n,p), |
rbinom (m,n,p), |
||||
|
1. Биноми- |
dbinom(k,n,p) |
pbinom(k,n,p) |
где m- число |
||
|
альное |
где P(X≤x)=α |
случайных |
|||
|
чисел |
|||||
|
2. Геометри- |
dgeom(k,p) |
pgeom(k,p) |
qgeom(α,p) |
rgeom(m,p) |
|
|
ческое |
|||||
|
3. Отрица- |
dnbinom |
pnbinom |
onbinom |
rnbinom |
|
|
тельное бино- |
(k,n,p) |
(k,n,p) |
(α,n,p) |
(m,n,p) |
|
|
миальное |
|||||
|
4. Пуассона |
dpois(k,λ) |
ppois(k,λ) |
qpois(α,λ) |
rpois(m,λ) |
|
|
5. Бета – рас- |
dbeta(x,n1,n2) |
pbeta(x,n1,n2) |
qbeta(α,n1,n2) |
rbeta(m,n1,n2) |
|
|
пределение |
|||||
|
6. χ2 -квадрат |
dchisq(x,n) |
pchisq(x,n) |
qchisq(α,n) |
rchisq(m,n) |
|
|
распределение |
|||||
|
57 |

|
Окончание табл. 1 |
||||||
|
Номер по |
Обратные |
Функции, |
||||
|
порядку и |
Функции |
Функции |
функции рас- |
|||
|
генерирующие |
||||||
|
название рас- |
плотности |
распределе- |
пределения |
случайные |
||
|
пределения |
вероятности |
ния |
(значения про- |
|||
|
числа |
||||||
|
центилей) |
||||||
|
7. Экспо- |
dexp(x,λ) |
pexp(x,λ) |
qexp(α,λ) |
rexp(m,λ) |
||
|
ненциальное |
||||||
|
8. F — рас- |
dF(x,n1,n2) |
pF(x,n1,n2) |
qF(α,n1,n2) |
rF(m,n1,n2) |
||
|
пределение |
||||||
|
9. Гамма – |
dgamma(x,n) |
pgamma(x,n) |
qgamma(α,n) |
rgamma(m,n) |
||
|
распределение |
||||||
|
10. Логисти- |
dlogis(x,l,n) |
plogis(x,l,n) |
qlogis(α,l,n) |
rlogis(m,l,n) |
||
|
ческое |
||||||
|
11. Логнор- |
dlnorm(x,μ,σ) |
plnorm(x,μ,σ) |
qlnorm(α,μ,σ) |
rlnorm(m,μ,σ) |
||
|
мальное |
||||||
|
pnorm(x,μ,σ), |
||||||
|
12. Нормаль- |
dnorm(x,μ,σ) |
qnorm(α,μ,σ) |
rnorm(m,μ,σ) |
|||
|
cnorm(x)= |
||||||
|
ное |
||||||
|
pnorm(x,0,1) |
||||||
|
13. Стьюдента |
dt(x,n) |
pt(x,n) |
qt(α,n) |
rt(m,n) |
||
|
14. Равномер- |
runif(m,a,b), |
|||||
|
dunif(x,a,b) |
punif(x,a,b) |
qunif(α,a,b) |
rnd(x)= |
|||
|
ное |
||||||
|
runif(1,0,x) |
||||||
|
pweibull(x,n) |
||||||
|
15. Вейбулла |
dweibull(x,n) |
qweibull(α,n) |
rweibull(m,n) |
|||
|
16. Коши |
dcauchy(x,l,n) |
pcauchy(x,l,n) |
qcauchy(α,l,n) |
rcauchy(m,l,n) |
||
Функции, вырабатывающие случайные числа, генерируют псевдослучайные последовательности (подробнее см. разд. 3). Эти последовательности зависят от некоторого целого числа, называемого стартовым значением. Для изменения стартового значения в пункте меню пакета MATHCAD Математика надо выбрать Генератор случайных чисел и ввести необходимое целое число.
3. Для вычисления частотного распределения и построения гистограмм в пакете MATHCAD имеется одна функция hist(int,A). Она возвращает вектор, представляющий частоты, с которыми величины, содержа-
щиеся в векторе A , попадают в интервалы, представляемые вектором int. Элементы массива int должны быть упорядочены по возрастанию. Возвращаемый результат – вектор, содержащий на один элемент меньше, чем int. Его элементы – частоты fi есть числа n(A) значений в массиве A ,
удовлетворяющих условию inti < n(A) < inti+1 .
В качестве примера в пакете MATHCAD рассмотрим моделирование распределения Коши. Это распределение имеет плотность вероятности
58
|
f (x) = |
λ |
, |
− ∞ < x < ∞, |
(2.7.3) |
|
π[λ2 + (x − μ)2 ] |
||||
|
где μ- параметр положения (медиана), |
λ > 0 — параметр рассеивания (сре- |
динное отклонение). Математического ожидания и моментов распределение не имеет.
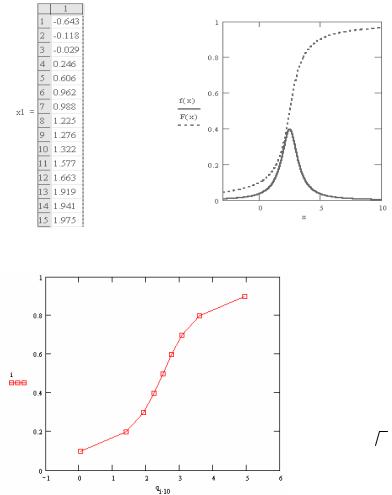
Наберем в пакете MATHCAD следующую программу:
|
ORIGIN :=1 μ := 2.5 |
λ := 0.8 |
|
x1 := rcauchy(50, μ, λ) |
x1 := sort(x1) |
|
f(x): = dcauchy(x, μ, λ) |
F(x) := pcauchy(x, μ, λ) |
i := 0.1,0.2…1 qi*10 := qcauchy(i, μ, λ)
m := mean(x1) m = 2.506
med := median(x1) med = 2.654
D := var(x1)
D = 1.723
σ := stdev(x1) σ = 1.313
xmin := min(x1) xmax := max(x1) xmin = −0.643 xmax = 6.159
E := 0.477 
E = 0.885
R := xmax — xmin
59
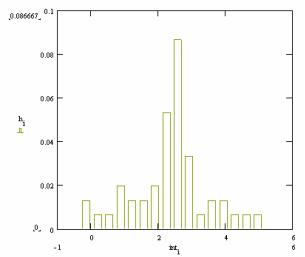
|
R = 6.802 |
m := 20 L := |
R |
|||||
|
m |
|||||||
|
i :=1…20 |
inti := xmin + |
L |
(2 i-1) |
||||
|
2 |
|||||||
|
h := hist(int ,x1) |
|||||||
|
hi |
|||||||
|
i :=1…20 |
h : = |
||||||
|
i |
50 |
||||||
Значение E , равное срединному отклонению, — это параметр рассеивания распределения Коши. В нашем случае он должен быть близок к заданному значению λ . Следует отметить, что функции mean и var по формуле
(2.7.1) и формуле,
аналогичной (2.7.2), формально находят числовые значения
смоделированной выборки, которые, однако, вовсе не являются математическим ожиданием и дисперсией распределения Коши.
Итак, на примере данного распределения выполнен примерно такой же объем работ и построены те же графики, которые в пакете STATGRAPHICS получаются автоматически заданием лишь соответствующего пункта меню.
Задание № 2. По номеру вашей фамилии в журнале преподавателя выбрать распределение из табл. 1 (если номер больше 16, выбирать номер минус 15), самостоятельно задать все необходимые параметры распределения; построить графики функции плотности вероятности, функции распределения, функции значений процентилей, смоделировать случайную выборку данного распределения длиной в 100 единиц, вычислить числовые характеристики выборки и построить ее гистограмму.
60
Гамма-распределение
Одной из непрерывных случайных величин и непрерывных распределений является гамма-распределение, поскольку мы знаем, что непрерывная случайная величина имеет дело с непрерывными значениями или интервалами, так же как и гамма-распределение с конкретной функцией плотности вероятности и функцией массы вероятности, в последовательном обсуждении, которое мы обсуждаем в подробно описать концепцию, свойства и результаты с примерами гамма-случайной величины и гамма-распределения.
Гамма-случайная величина или гамма-распределение | что такое гамма-распределение | определить гамма-распределение | функция плотности гамма-распределения | функция плотности вероятности гамма-распределения | доказательство гамма-распределения
Непрерывная случайная величина с функцией плотности вероятности
как известно, является гамма-случайной величиной или гамма-распределением, где α> 0, λ> 0 и гамма-функция
у нас есть очень частое свойство гамма-функции путем интегрирования по частям как
Если продолжить процесс, начиная с n, то
и, наконец, значение гаммы единицы будет
таким образом значение будет
cdf гамма-распределения | совокупное гамма-распределение | интеграция гамма-распределения
Компания кумулятивное распределение функция (cdf) гамма-случайной величины или просто функция распределения гамма-случайной величины такая же, как и у непрерывной случайной величины, при условии, что функция плотности вероятности отличается, т.е.
здесь функция плотности вероятности такая, как определено выше для гамма-распределения, кумулятивную функцию распределения мы также можем записать как
в обоих вышеперечисленных форматах значение pdf выглядит следующим образом
где α> 0, λ> 0 — действительные числа.
Формула гамма-распределения | формула гамма-распределения | уравнение гамма-распределения | вывод гамма-распределения
Чтобы найти вероятность для гамма-случайной величины, функция плотности вероятности, которую мы должны использовать для различных заданных α> 0, λ> 0, имеет вид
и используя приведенный выше PDF-файл, распределение для гамма-случайной величины мы можем получить следующим образом:
Таким образом, формула гамма-распределения требует значения pdf и пределов для гамма-случайной величины в соответствии с требованием.
Пример гамма-распределения
показать, что полная вероятность гамма-распределение является единицей с заданной функцией плотности вероятности, т.е.
при λ> 0, α> 0.
Решение:
используя формулу для гамма-распределения
так как функция плотности вероятности для гамма-распределения равна
который равен нулю для всех значений меньше нуля, поэтому вероятность теперь будет
используя определение гамма-функции
и подстановки получаем
таким образом
Среднее значение и дисперсия гамма-распределения | математическое ожидание и дисперсия гамма-распределения | математическое ожидание и дисперсия гамма-распределения | Среднее значение гамма-распределения | математическое ожидание гамма-распределения | ожидание гамма-распределения
В следующем обсуждении мы найдем среднее значение и дисперсию для гамма-распределения с помощью стандартных определений математического ожидания и дисперсии непрерывных случайных величин,
Ожидаемое значение или среднее значение непрерывной случайной величины X с функцией плотности вероятности
или гамма случайная величина X будет
средство доказательства гамма-распределения | ожидаемое значение доказательства гамма-распределения
Чтобы получить ожидаемое значение или среднее значение гамма-распределения, мы будем следовать определению и свойству гамма-функции,
сначала по определению математического ожидания непрерывной случайной величины и функции плотности вероятности гамма-случайной величины мы имеем
путем отмены общего множителя и использования определения гамма-функции
теперь, когда у нас есть свойство гамма-функции
ценность ожидания будет
таким образом, среднее или ожидаемое значение гамма-случайной величины или гамма-распределения, которое мы получаем, равно
дисперсия гамма-распределения | дисперсия гамма-распределения
Дисперсия гамма-случайной величины с заданной функцией плотности вероятности
или дисперсия гамма-распределения будет
доказательство дисперсии гамма-распределения
Как мы знаем, дисперсия — это разница ожидаемых значений как
для гамма-распределения у нас уже есть значение среднего
теперь сначала давайте вычислим значение E [X2], поэтому по определению математического ожидания для непрерывной случайной величины имеем
поскольку функция f (x) является функцией распределения вероятностей гамма-распределения как
поэтому интеграл будет только от нуля до бесконечности
поэтому по определению гамма-функции мы можем написать
Таким образом, используя свойство гамма-функции, мы получили значение как
Теперь поместим ценность этих ожиданий в
таким образом, значение дисперсии гамма-распределения или гамма-случайной величины равно
Параметры гамма-распределения | двухпараметрическое гамма-распределение | 2 переменных гамма-распределения
Гамма-распределение с параметрами λ> 0, α> 0 и функцией плотности вероятности
имеет среднее значение и дисперсию статистических параметров как
и
поскольку λ — положительное действительное число, для упрощения и упрощения обработки другой способ — установить λ = 1 / β, чтобы получить функцию плотности вероятности в виде
вкратце функцию распределения или кумулятивную функцию распределения для этой плотности мы можем выразить как
эта функция гамма-плотности дает среднее значение и дисперсию как
и
что очевидно из подстановки.
Обычно используются оба способа либо гамма-распределение с параметром α и λ, обозначаемым гамма (α, λ) или гамма-распределение с параметрами β и λ, обозначенными гамма (β, λ) с соответствующими средними статистическими параметрами и дисперсией в каждой форме.
Оба они не что иное, как одно и то же.
График гамма-распределения | график гамма-распределения | гистограмма гамма-распределения
Характер гамма-распределения мы можем легко визуализировать с помощью графика для некоторых конкретных значений параметров, здесь мы рисуем графики для функции плотности вероятности и функции кумулятивной плотности для некоторых значений параметров.
возьмем функцию плотности вероятности в виде
тогда кумулятивная функция распределения будет
Описание: графики для функции плотности вероятности и кумулятивной функции распределения путем фиксации значения альфа как 1 и изменения значения бета.
Описание: графики для функции плотности вероятности и кумулятивной функции распределения путем фиксации значения альфа как 2 и изменения значения бета.
Описание: графики для функции плотности вероятности и кумулятивной функции распределения путем фиксации значения альфа как 3 и изменения значения бета.
Описание: графики для функции плотности вероятности и кумулятивную функцию распределения, фиксируя значение бета как 1 и изменяя значение альфа
Описание: графики для функции плотности вероятности и кумулятивной функции распределения путем фиксации значения бета как 2 и изменения значения альфа.
Описание: графики для функции плотности вероятности и кумулятивной функции распределения путем фиксации значения бета как 3 и изменения значения альфа.
Как правило, разные кривые для изменения альфа
Таблица гамма-распределения | стандартная таблица распределения гаммы
Числовое значение гамма-функции
числовые значения неполной гамма-функции:
Численное значение гамма-распределения для построения эскиза графика функции плотности вероятности и кумулятивной функции распределения для некоторых начальных значений выглядит следующим образом
| 1x | f (x), α = 1, β = 1 | f (x), α = 2, β = 2 | f (x), α = 3, β = 3 | P (x), α = 1, β = 1 | P (x), α = 2, β = 2 | P (x), α = 3, β = 3 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0.1 | 0.904837418 | 0.02378073561 | 1.791140927E-4 | 0.09516258196 | 0.001209104274 | 6.020557215E-6 |
| 0.2 | 0.8187307531 | 0.0452418709 | 6.929681371E-4 | 0.1812692469 | 0.00467884016 | 4.697822176E-5 |
| 0.3 | 0.7408182207 | 0.06455309823 | 0.001508062363 | 0.2591817793 | 0.01018582711 | 1.546530703E-4 |
| 0.4 | 0.670320046 | 0.08187307531 | 0.00259310613 | 0.329679954 | 0.01752309631 | 3.575866931E-4 |
| 0.5 | 0.6065306597 | 0.09735009788 | 0.003918896875 | 0.3934693403 | 0.02649902116 | 6.812970042E-4 |
| 0.6 | 0.5488116361 | 0.1111227331 | 0.005458205021 | 0.4511883639 | 0.03693631311 | 0.001148481245 |
| 0.7 | 0.4965853038 | 0.1233204157 | 0.007185664583 | 0.5034146962 | 0.04867107888 | 0.001779207768 |
| 0.8 | 0.4493289641 | 0.1340640092 | 0.009077669195 | 0.5506710359 | 0.06155193555 | 0.002591097152 |
| 0.9 | 0.4065696597 | 0.1434663341 | 0.01111227331 | 0.5934303403 | 0.07543918015 | 0.003599493183 |
| 1 | 0.3678794412 | 0.1516326649 | 0.01326909834 | 0.6321205588 | 0.09020401043 | 0.004817624203 |
| 1.1 | 0.3328710837 | 0.1586611979 | 0.01552924352 | 0.6671289163 | 0.1057277939 | 0.006256755309 |
| 1.2 | 0.3011942119 | 0.1646434908 | 0.01787520123 | 0.6988057881 | 0.1219013822 | 0.007926331867 |
| 1.3 | 0.272531793 | 0.1696648775 | 0.0202907766 | 0.727468207 | 0.1386244683 | 0.00983411477 |
| 1.4 | 0.2465969639 | 0.1738048563 | 0.02276101124 | 0.7534030361 | 0.1558049836 | 0.01198630787 |
| 1.5 | 0.2231301601 | 0.1771374573 | 0.02527211082 | 0.7768698399 | 0.1733585327 | 0.01438767797 |
| 1.6 | 0.201896518 | 0.1797315857 | 0.02781137633 | 0.798103482 | 0.1912078646 | 0.01704166775 |
| 1.7 | 0.1826835241 | 0.1816513461 | 0.03036713894 | 0.8173164759 | 0.2092823759 | 0.01995050206 |
| 1.8 | 0.1652988882 | 0.1829563469 | 0.03292869817 | 0.8347011118 | 0.2275176465 | 0.02311528775 |
| 1.9 | 0.1495686192 | 0.1837019861 | 0.03548626327 | 0.8504313808 | 0.2458550043 | 0.02653610761 |
| 2 | 0.1353352832 | 0.1839397206 | 0.03803089771 | 0.8646647168 | 0.2642411177 | 0.03021210849 |
| 2.1 | 0.1224564283 | 0.1837173183 | 0.04055446648 | 0.8775435717 | 0.2826276143 | 0.03414158413 |
| 2.2 | 0.1108031584 | 0.183079096 | 0.04304958625 | 0.8891968416 | 0.3009707242 | 0.03832205271 |
| 2.3 | 0.1002588437 | 0.1820661424 | 0.04550957811 | 0.8997411563 | 0.3192309458 | 0.04275032971 |
| 2.4 | 0.09071795329 | 0.1807165272 | 0.04792842284 | 0.9092820467 | 0.3373727338 | 0.04742259607 |
| 2.5 | 0.08208499862 | 0.179065498 | 0.05030071858 | 0.9179150014 | 0.3553642071 | 0.052334462 |
| 2.6 | 0.07427357821 | 0.1771456655 | 0.05262164073 | 0.9257264218 | 0.373176876 | 0.05748102674 |
| 2.7 | 0.06720551274 | 0.1749871759 | 0.05488690407 | 0.9327944873 | 0.3907853875 | 0.0628569343 |
| 2.8 | 0.06081006263 | 0.1726178748 | 0.05709272688 | 0.9391899374 | 0.4081672865 | 0.06845642568 |
| 2.9 | 0.05502322006 | 0.1700634589 | 0.05923579709 | 0.9449767799 | 0.4253027942 | 0.07427338744 |
| 3 | 0.04978706837 | 0.1673476201 | 0.0613132402 | 0.9502129316 | 0.4421745996 | 0.08030139707 |
поиск альфа и бета для гамма-распределения | как рассчитать альфа и бета для гамма-распределения | оценка параметров гамма-распределения
Для гамма-распределения, находящего альфа и бета, мы возьмем среднее значение и дисперсию гамма-распределения.
и
теперь мы получим значение беты как
so
и
таким образом
только взяв некоторые дроби из гамма-распределения, мы получим значение альфа и бета.
проблемы гамма-распределения и их решения | пример задач гамма-распределения | руководство по гамма-распределению | вопрос о гамма-распределении
1. Рассмотрите время, необходимое для решения проблемы для клиента, — это гамма-распределение в часах со средним значением 1.5 и дисперсией 0.75, что было бы вероятность того, что проблема время решения превышает 2 часа, если время превышает 2 часа, какова вероятность того, что проблема будет решена не менее чем за 5 часов.
Решение: поскольку случайная величина имеет гамма-распределение со средним значением 1.5 и дисперсией 0.75, поэтому мы можем найти значения альфа и бета, и с помощью этих значений вероятность будет
P (X> 2) = 13e-4= 0.2381
и
P (X> 5 | X> 2) = (61/13) e-6= 0.011631
2. Если отрицательная обратная связь за неделю от пользователей смоделирована в гамма-распределении с параметрами альфа 2 и бета как 4 после 12 недель отрицательной обратной связи после реструктуризации качества, может ли реструктуризация улучшить производительность на основе этой информации?
Решение: Поскольку это моделируется в гамма-распределении с α = 2, β = 4
мы найдем среднее значение и стандартное отклонение как μ = E (x) = α * β = 4 * 2 = 8
поскольку значение X = 12 находится в пределах стандартного отклонения от среднего значения, поэтому мы не можем сказать, что это улучшение или не улучшение за счет реструктуризации качества, чтобы доказать, что улучшение, вызванное предоставленной информацией о реструктуризации, является недостаточным.
3. Пусть X будет гамма-распределение с параметрами α=1/2, λ=1/2, найти функцию плотности вероятности для функции Y=квадратный корень из X
Решения: вычислим кумулятивную функцию распределения для Y как
теперь дифференцируя это по y, получаем функцию плотности вероятности для Y как
и диапазон для y будет от 0 до бесконечности
Вывод:
Концепция гамма-распределения в вероятности и статистике является одним из важных повседневных применимых распределений экспоненциального семейства, до сих пор обсуждались все концепции базового и более высокого уровня, связанные с гамма-распределение, если вам требуется дополнительное чтение, просмотрите упомянутые книги. Вы также можете посетить математика страница для получения дополнительной темы
https://en.wikipedia.org/wiki/Gamma_distribution
Первый курс вероятности Шелдона Росс
Очерки вероятности и статистики Шаума
Введение в вероятность и статистику от ROHATGI и SALEH






![{displaystyle {begin{aligned}f(x;alpha ,beta )&={frac {x^{alpha -1}e^{-beta x}beta ^{alpha }}{Gamma (alpha )}}quad {text{ for }}x>0quad alpha ,beta >0,\[6pt]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebf760a328d5b468fea5f9f1d47cca54b558b6da)










![{displaystyle mathrm {E} [X^{n}]=theta ^{n}{frac {Gamma (k+n)}{Gamma (k)}}=theta ^{n}prod _{i=1}^{n}(k+i-1);{text{ for }}n=1,2,ldots .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67b2480d1a1107cd132f94b5280db23ddde59033)
























![{displaystyle operatorname {E} [ln(X)]=psi (alpha )-ln(beta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6da14ff7ed563c7e86154998ef6fd180e79c9bfa)
![{displaystyle operatorname {E} [ln(X)]=psi (k)+ln(theta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186737f3b184bf00519b3a4b1412a560e1216093)
![{displaystyle operatorname {var} [ln(X)]=psi ^{(1)}(alpha )=psi ^{(1)}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b193ce127d5d0de9a3430b7dc803c092262f7b5c)
![{displaystyle {begin{aligned}operatorname {H} (X)&=operatorname {E} [-ln(p(X))]\[4pt]&=operatorname {E} [-alpha ln(beta )+ln(Gamma (alpha ))-(alpha -1)ln(X)+beta X]\[4pt]&=alpha -ln(beta )+ln(Gamma (alpha ))+(1-alpha )psi (alpha ).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37a24251136eb110aea24081dcffb2ee9e9648d8)

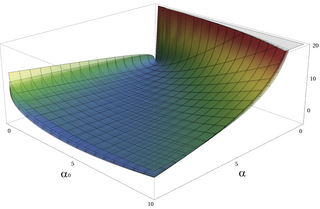




























![{displaystyle f(x;k)=displaystyle int _{0}^{infty }{frac {1}{u}},W_{k}left({frac {x}{u}}right)left[ku^{k-1},{mathfrak {N}}_{frac {1}{k}}left(u^{k}right)right],du,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7fdb1229d8546f9459b5bfdae27e98ee789a192)




















![{displaystyle operatorname {E} [x^{m}]={frac {Gamma (Nk-m)}{Gamma (Nk)}}y^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61ae01ae77aa6c640cbaa1bb2a8863454827916a)




















![{displaystyle mathbb {E} [X]=ktheta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/442edfcb678a45fa030d29a5fa4fced4af4614fe)
![{displaystyle mathrm {D} [X]=ktheta ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c5a194940da28ad8586ff8ee3e86e4ee14f6b33)

















![{displaystyle theta left(xi -sum _{i=1}^{[k]}{ln U_{i}}right)sim Gamma (k,theta ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8816ea8e64d96b972b73077057df79b9ec43fab)