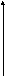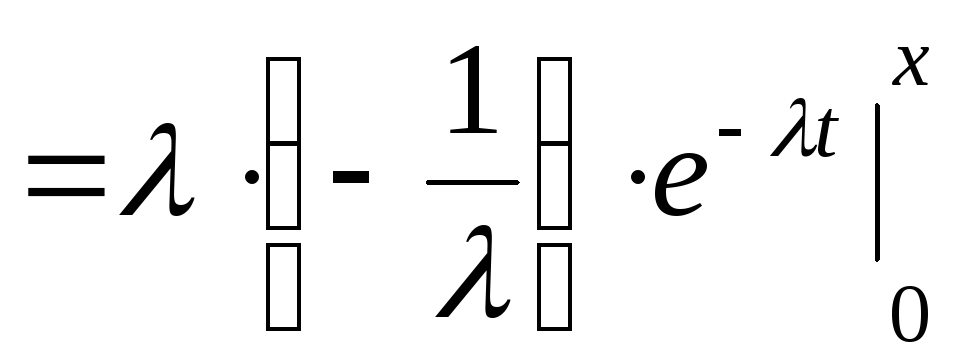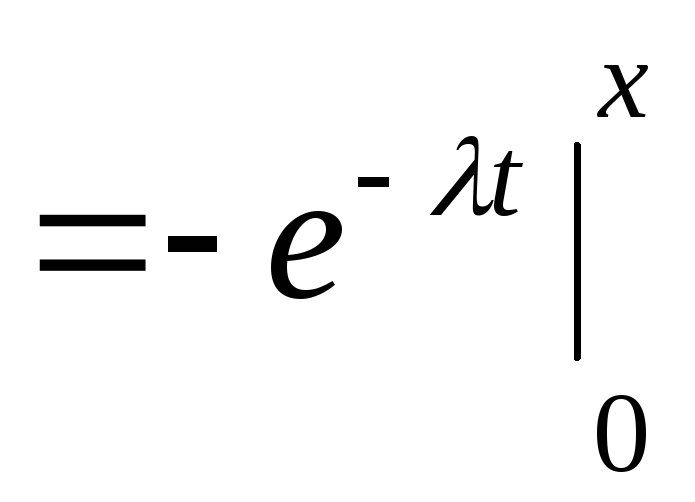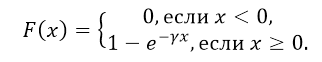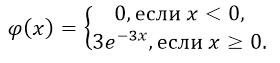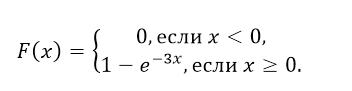Показательное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
, которое описывается плотностью:
где
–
постоянная положительная величина.
Показательное
распределение определяется одним параметром
. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется, проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.
Функция распределения
показательного закона:
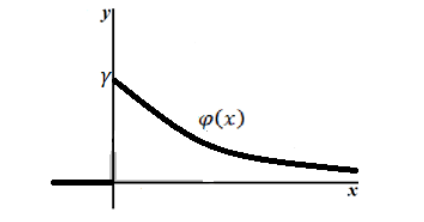
Графики плотности и
функции распределения показательного закона изображены на рисунке.
Вероятность попадания в
интервал
непрерывной
случайной величины
, распределенной по показательному закону:
Числовые характеристики показательного (экспоненциального) распределения
Математическое ожидание случайной величины, распределенной по показательному закону:
Дисперсия случайной величины, распределенной по показательному закону:
Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:
Коэффициенты асимметрии и эксцесса
для показательного распределения:
Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.
Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени
между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром
–
интенсивностью потока.
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Примеры решения задач
Пример 1
Случайная величина
задана функцией распределения
Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.
Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Математическое
ожидание случайной величины, распределенной по показательному закону:
Среднее
квадратическое отлонение:
Вероятность того, что
случайная величина примет значение от 0,2 до 1
Ответ
.
Пример 2
На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e-5t.
Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.
Решение
В нашем случае
параметр показательного распределения
Математическое
ожидание:
Дисперсия:
Среднее
квадратическое отклонение:
Ответ:
Пример 3
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду xmod, медиану xmed , если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
распределения случайной величины
, распределенной по
показательному закону:
Функция
распределения:
Построим
графики дифференциальной и интегральной функций распределения:
График дифференциальной функции распределения
График интегральной функции распределения
Математическое
ожидание показательно распределенной случайной величины
:
Дисперсия:
Среднее
квадратическое отклонение:
найдем, исходя из условия:
Пример 4
Случайная
величина
распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания
в интервал (0,5;1).
Решение
Дисперсия
случайной величины, распределенной по показательному закону:
Математическое
ожидание случайной величины, распределенной по показательному закону:
Вероятность
попадания в интервал
непрерывной случайной величины
, распределенной по
показательному закону:
В нашем
случае:
Ответ:
Задачи контрольных и самостоятельных работ
Задача 1
Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.
Задача 3
Вероятность
безотказной работы элемента распределена по экспоненциальному закону
f(t)=e-0.05t
Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.
Задача 4
Непрерывная
случайная величина X задана интегральной функцией распределения
Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].
Задача 5
Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.
Задача 6
Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x1,x2]
или [x3,x4]? Записать
функции f(x),F(x) и построить их графики.
λ=1/10, x1=3, x2=5, x3=4, x4=8
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.
Задача 8
Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t1=750 до t2=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.
Задача 9
Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe-λt (t≥0). Среднее время
восстановления канала — 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.
Задача 10
Дана плотность
распределения случайной величины X.
По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?
Задача 11
Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.
Задача 12
Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:
а) не более 5 минут.
б) более 5 минут.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Случайная величина ξ подчинена
показательному закону с параметром λ=5:
Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.
Задача 14
Случайная
величина ξ имеет плотность вероятностей (показательное распределение)
Найдите
вероятность P{ξ>Mξ}
Задача 15
Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.
Задача 16
Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.
Задача 17
Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t0. Найти вероятности
следующих событий:
Задача 18
Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σx=3.
Требуется:
1) найти
функцию плотности f(x).
2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].
Задача 19
Случайная
величина ξ задана функцией распределения
Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.
Задача 20
Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Экспоненциально распределенная случайная величина
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по показательному (или экспоненциальному) закону.
Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:
$$
f(x)=
left{
begin{array}{l}
0, x lt 0\
lambda e^{-lambda x}, xge 0 \
end{array}
right.
$$
Функция распределения величины $X$:
$$
F(x)=
left{
begin{array}{l}
0, x lt 0\
1- e^{-lambda x}, xge 0 \
end{array}
right.
$$
Здесь $lambda$ — единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/lambda$, $D(X)=1/lambda^2$.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.
Понравилось? Добавьте в закладки
Примеры решений
Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.
Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?
Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.
Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^{-2t}$ при $tge 0$ и $f(t)=0$ при $tlt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.
Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.
Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^{-3x}$ при $x gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 8. Непрерывная случайная величина $xi$ распределена по показательному закону с параметром $lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $xi$ и вероятность того, что $xi$ принимает значения, меньшие своего математического ожидания.
Задача 9. Случайная величина $xi$ распределена по показательному закону с параметром 2. Найти $M_{xi}$, $D_{xi}$ вероятность попадания $xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $xi$.
Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(lambda)$. Найдите вероятность события $|Х — МХ | lt 3sigma$ («правило $3sigma$» для показательного распределения).
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Определение.
Непрерывная
случайная величина
,
плотность распределения которой задается
формулой
называется
показательной
или
экспоненциальной
с параметром
.
График плотности
вероятности
равномерно
распределенной случайной величины
изображен на рисунке 1
Рис.
1.
В большом числе
случаев показательное распределение
описывает время безотказной работы
прибора, при этом число
интерпретируется как интенсивность
отказа. Это распределение находит также
широкое применение в демографии.
Свойства показательного распределения
Свойство 1.
Интегральная
функция распределения показательной
случайной величины записывается в виде

Доказательство.
Для того, что бы найти интегральную
функцию распределения показательной
случайной величины, воспользуемся
свойством 3 дифференциальной функции
распределения
.
Рассмотрим следующие
два случая:
-
Если
,
топри
.
Поэтому
.
-
Если
,
то из свойства аддитивности определенного
интеграла получаем
.
Из рассмотренных
случаев следует, что интегральная
функция
показательно распределенной случайной
величины записывается в виде
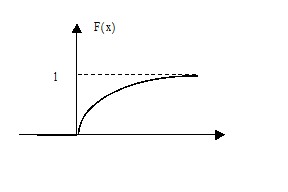
График интегральной
функции
показательно распределенной случайной
величины изображен на рисунке 2
|
1 |
Рис.
2.
Свойство 2.
Математическое
ожидание случайной показательной
случайной величины определяется по
формуле
.
Доказательство.
.
Свойство 3.
Дисперсия
случайной величины показательной
случайной величины определяется по
формуле
.
Доказательство.
Воспользовавшись формулой для вычисления
дисперсии непрерывной случайной величины
,
находим
Свойство 4.
Среднее квадратическое отклонение
случайной величины показательной
случайной величины вычисляется по
формуле
.
Доказательство.
Так как среднее квадратическое отклонение
,
то среднее
квадратическое отклонение для равномерно
распределенной случайной величины
находим
Пример.
5. Нормальный закон распределения.
Нормальный закон
распределения наиболее часто встречается
на практике, Главная особенность,
выделяющая его среди других законов,
состоит в том, что он является предельным
законом, к
которому приближаются другие законы
распределения при весьма часто
встречающихся типичных условиях.
Определение.
Непрерывная
случайная величина
имеет
нормальный
закон распределения или
закон
распределения Гаусса
с параметрами
и
,
если ее плотность распределения
вероятности имеет вид

Кривую нормального
закона распределения называют нормальной
или
гауссовой
кривой.
Выясним прежде
всего теоретико-вероятностный смысл
параметров нормального закона
распределения.
Теорема.
Если случайная величина
распределена по нормальному закону, то
1) математическое
ожидание случайной величины
равно параметру
этого закона, т.е.
,
2) средне
квадратическое отклонение случайной
величины
равно параметру
этого закона, т.е.
.
Доказательство.
Для того чтобы
определить вид нормальной кривой,
проведем исследование дифференциальной
функции распределения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Показательное распределение
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Отметим здесь основные понятия и формулы, связанные с показательным распределением непрерывной случайной величины $X$ не вдаваясь в подробности их вывода.
Определение 1
Показательным или экспоненциальным распределения непрерывной случайной величины $X$ называется распределение, плотность которого имеет вид:
Рисунок 1.
где $gamma $ — положительная константа.
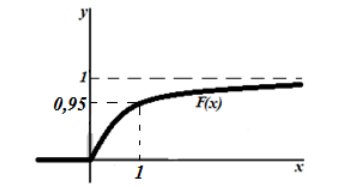
График плотности показательного распределения имеет вид (рис. 1):
Рисунок 2. График плотности показательного распределения.
Функция показательного распределения
Как нетрудно проверить, функция показательного распределения имеет вид:
Рисунок 3.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
где $gamma $ — положительная константа.
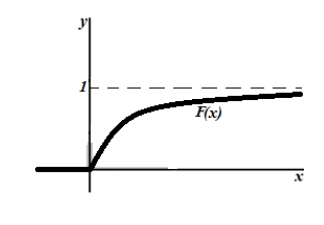
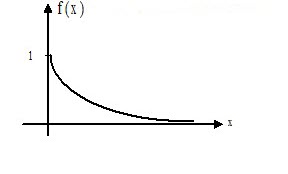
График функции показательного распределения имеет вид:
Рисунок 4. График функции показательного распределения.
Вероятность попадания случайной величины при показательном распределении
Вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ при показательном распределении вычисляется по следующей формуле:
Математическое ожидание: $Mleft(Xright)=frac{1}{gamma }.$
Дисперсия: $Dleft(Xright)=frac{1}{{gamma }^2}.$
Среднее квадратическое отклонение: $sigma left(Xright)=frac{1}{gamma }$.
Пример задачи на показательное распределение
Пример 1
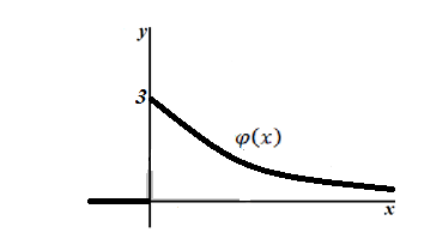
Случайная величина $X$ подчиняется экспоненциальному закону распределения. На участке области определения $left[0,infty )right.$ случайная величина $X$ имеет плотность вида $varphi left(xright)=alpha e^{-3x}$.
-
Найти плотность распределения и построить её график.
-
Найти функцию распределения и построить её график.
-
Найти вероятность того, что случайная величина попадет в интервал $(0,2;;0,4)$.
-
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение данного распределения.
Решение:
- Так как случайная величина подчиняется показательному закону распределения, то $alpha =3.$ Таким образом, плотность данного распределения будет иметь вид:
Рисунок 5.
Построим её график. Максимальное значения функция плотности распределения достигнет в точке $left(0,gamma right)=(0,3)$
Рисунок 6.
- Так как $gamma =3$, то по формуле функции показательного распределения, функция распределения в нашем случае будет иметь вид:
Рисунок 7.
При $x=1, Fleft(1right)=1-e^{-3}=1-0,05=0,95$, получаем график
Рисунок 8.
- Для нахождения искомой вероятности будем пользоваться следующей формулой:
[Pleft(alpha Получим:
[Pleft(0,2Для нахождения значений функции $y=e^{-x}$ существуют специальные таблицы, из них легко находим, что $e^{-0,6}=0,549, e^{-1,2}=0,302$. Значит:
[Pleft(0,2
[Mleft(Xright)=sigma left(Xright)=frac{1}{gamma }=frac{1}{3}.] [Dleft(Xright)=frac{1}{{gamma }^2}=frac{1}{9}.]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 20.02.2023
Показательное распределение
Показательным или экспоненциальным, называется распределение вероятностей непрерывной случайной величины $X$, которое описывается плотностью $ f( x )=left{ { { begin{array} { c } { 0, ,при,x<0 } \ { lambda e^ { -lambda x } ,при,xgeqslant 0, ,lambda -const } \ end{array} } }right. $
и имеет один параметр $lambda $. В этом его преимущество перед другими распределениями.
Найдем функцию распределения $F(x)$ $ begin{array} { l } F( x )=intlimits_ { -infty } ^x { f( x )dx } =intlimits_ { -infty } ^0 { 0dx } +intlimits_0^x { lambda e^ { -lambda x } dx } =left. { frac { lambda e^ { -lambda x } } { -lambda } }right|_0^x =-( { e^ { -lambda x } -e^0 } )=1-e^ { -lambda x } \ F( x )=left{ { { begin{array} { c } { 0,,xleqslant 0 } \ { 1-e^ { -lambda x } ,,xgeqslant 0 } \ end{array} } }right. \ end{array} $
Найдём вероятность попадания в интервал { a,b } случайной величины, распределенной по показательному закону, заданному функцией распределения $ F( x )=left{ { { begin{array} { c } { 0,,xleqslant 0 } \ { 1-e^ { -lambda x } ,,xgeqslant 0 } \ end{array} } }right. $
используя формулу
$P( { aleqslant x<b } )=F( b )-F( a )$ и учитывая, что $F( a )=1-e^ { -lambda a } , F( b )=1-e^ { -lambda b } $, получим $P( { aleqslant x<b } )=1-e^ { -lambda a } -1+e^ { -lambda b } =e^ { -lambda b } -e^ { -lambda a } $
для $e^ { -x } -$ существуют таблицы.
Или $P( { aleqslant x<b } )=e^ { -lambda b } -e^ { -lambda a } $
Числовые характеристики показательного распределения.
Пусть непрерывная, случайная величина $x$ распределена по показательному закону
$ f( x )=left{ { { begin{array} { c } { 0,,при,x<0 } \ { lambda e^ { -lambda x } ,,при,xgeqslant 0 } \ end{array} } }right. $
Найдём математическое ожидание
$M( x )=intlimits_0^infty { xf( x )dx } =lambda intlimits_0^infty { xe^ { -lambda x } dx } =$ $left.| begin{array} { c } { u=x } \ { dv=e^ { -lambda x } dx } \ end{array} begin{array} { c } { du=dx } \ { v=frac { e^ { -lambda x } } { -lambda } } \ end{array} right.| =lambda ( -left. { frac { xe^ { -lambda x } } { -lambda } }right|_0^infty +frac { 1 } { lambda } intlimits_0^infty { e^ { -lambda x } dx } )=$ $= mathop { lim } limits_ { Ato infty } left. { frac { x } { e^ { lambda x } } } right|_0^A -mathop { lim } limits_ { Ato infty } left. { frac { e^ { -lambda x } } { lambda } } right|_0^A = mathop { lim } limits_ { Ato infty } ( { frac { A } { e^ { lambda A } } -frac { 0 } { e^ { -0lambda } } } )-mathop { lim } limits_ { Ato infty } frac { 1 } { lambda } ( { frac { 1 } { e^ { lambda A } } -frac { 1 } { e^ { 0A } } } )=-frac { 1 } { lambda } mathop { lim } limits_ { Ato infty } ( { -frac { 1 } { e^ { 0A } } } )=frac { 1 } { lambda } $
Дисперсия
$D( x )=intlimits_0^infty { x^2f( x )dx-M^2( x ) } =lambda intlimits_0^infty { x^2e^ { -lambda x } dx } = left| по,частям,дважды right| -M^2( x )= frac { 2 } { lambda ^2 } -frac { 1 } { lambda ^2 } =frac { 1 } { lambda ^2 } \ sigma ( x )=sqrt { D( x ) } =frac { 1 } { lambda } $
Итак, параметры показательного распределения:
Математическое ожидание $M( x )=frac { 1 } { lambda } $.
Дисперсия $D(X)=frac { 1 } { lambda ^2 } $.
Среднее квадратическое отклонение $sigma (X)=frac { 1 } { lambda } $