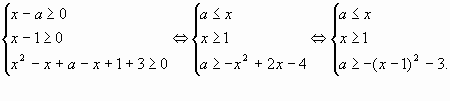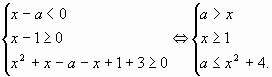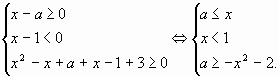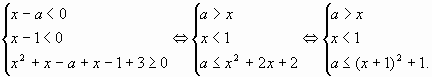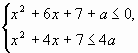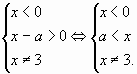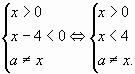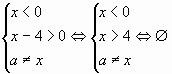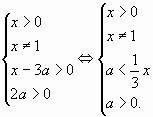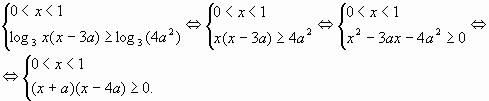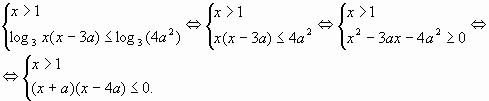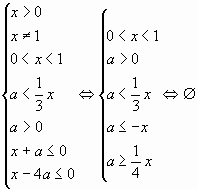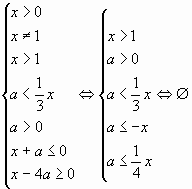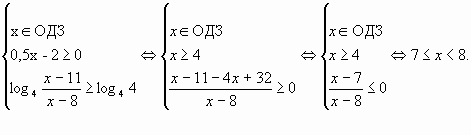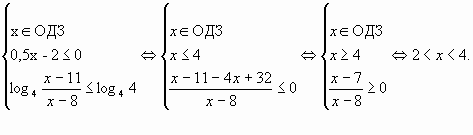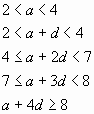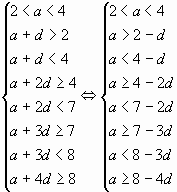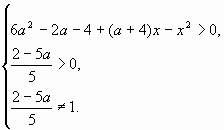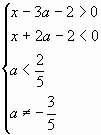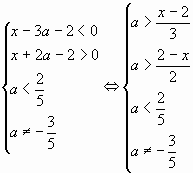Как найти параметр в математике

Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2022 года это №17. И даже в вариантах ОГЭ они есть. Что же означает это слово — параметр?

Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».

Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.

Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?

Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.

Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».

Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.

1. Теперь пример из школьной математики.

Все мы помним, что такое квадратное уравнение. Это уравнение вида , где коэффициент а не равен нулю.

Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.

Дискриминант квадратного уравнения:

Если , квадратное уравнение имеет два корня: и

Если , квадратное уравнение имеет единственный корень

Если , квадратное уравнение не имеет действительных корней. Рассмотрим уравнение . Его дискриминант равен Если , то есть , это квадратное уравнение имеет два корня.

Если при , уравнение имеет единственный корень.

Если , то есть с > 1, корней нет.

В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.

Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.

И еще две простые задачи с параметром.

2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.

Квадратное уравнение имеет два различных корня, когда .

Найдем дискриминант уравнения

В нем

Т.к. , получим:

Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).

Найдем корни квадратного уравнения . Это и

Разложим левую часть неравенства на множители:

Значит,

Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и

Записываем ответ:

3. При каких значениях параметра k система уравнений не имеет решений?

Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:

Первое уравнение задает прямую с угловым коэффициентом . Второе уравнение — прямую с угловым коэффициентом -2.

Система уравнений не имеет решений, если эти прямые не пересекаются, то есть параллельны. Это значит, что и .

Действительно, в этом случае первое уравнение задает прямую , а второе — параллельную ей прямую

Ответ: 10

Читаем дальше:

Графический метод решения задач с параметрами.

На этой странице вы узнаете

• Игра в прятки: как значение одной переменной может помочь найти другую?
• Парадокс: как стоять на месте и бежать с любой скоростью одновременно? 
• Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? 

Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье. 

Что такое параметр 

Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов? 

Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно (frac{20}{5} = 4). А если было 10 градусов, то искомое число было бы равно (frac{20}{10} = 2). 

Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными. 

Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a”  называется параметр. 

Параметр — это условная буква, вместо которой можно подставить число. 

То есть параметр — это еще одна переменная, которая может принять несколько значений. 

Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.

Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 

Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.

Линейные уравнения с параметром

Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a. 

(x = frac{20}{a})

Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5 

Что, если a=0? Мы получаем уравнение (x = frac{20}{0}), у которого нет решения, поскольку на 0 делить нельзя. 

Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0. 

Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a (neq) 0 — x = 20a. 

Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев. 

1) b (neq) 0. 

Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b. 

Получаем уравнение ax = 15. Как найти начальную скорость Пети? (x = frac{15}{a}). 

Такое уравнение мы уже решали выше. Получаем два случая: 

• Если a = 0 — решений нет. 
• Если a (neq) 0, то изначальная скорость Пети была равна (x = frac{15}{a}). 

2) b = 0. 

Мы получаем уравнение ax = 0. Также разберем два случая значений параметра: 

• a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось? 

Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений. 

• a (neq) 0. Здесь получается, что равен 0 уже х: (x = frac{0}{a} = 0). 

Подведем итог. Как можно решить уравнение вида ax = b?

• Если a = 0, b = 0 — бесконечное множество решений. 
• Если a = 0, b (neq) 0 — решений нет. 
• Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 

Квадратные уравнения с параметром

Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции». 

Квадратное уравнение имеет вид ax² + bx + c = 0, а графиком функции y = ax² + bx + c будет парабола. 

Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.  

Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней: 

• При D > 0 уравнение имеет два корня. 
• При D = 0 уравнение имеет один корень. 
• При D < 0 уравнение не имеет корней. 

Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х. 

Рассмотрим три уравнения. 

1) x² — x — 2 = 0
Решим уравнение с помощью дискриминанта. 
D = 1² — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня. 

(x_1 = frac{1 + 3}{2} = 2)
(x_2 = frac{1 — 3}{2} = -1)

Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) . 

2) x² -4x + 4 = 0
Решим уравнение с помощью дискриминанта. 
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень. 

(x = frac{4}{2} = 2)

Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0). 

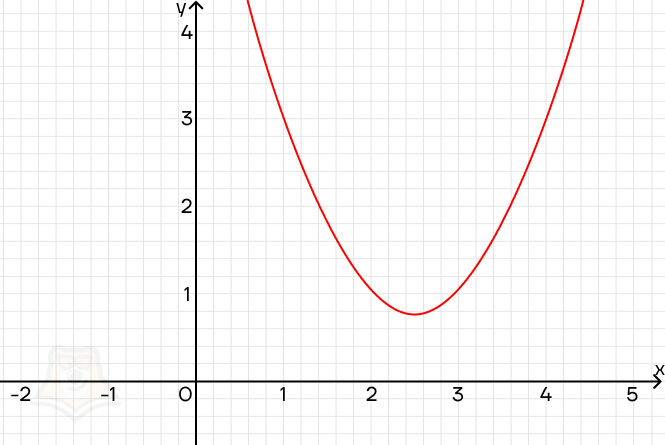
3) x² — 5x + 7 = 0
Решим уравнение с помощью дискриминанта. 
D = 25 — 4 * 1 * 7 = 25 — 28 = -3

Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет. 

Где можно применить эти знания, решая параметры? 

Пример 1. Найдите все значения параметра a, при которых уравнение x² + (3a + 11)x + 18,25 + a = 0 имеет два различных решения. 

Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?

Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным. 

1. Для начала найдем сам дискриминант. 

D = (3a + 11)² — 4 * 1 * (a + 18,25) = 9a² + 66a + 121 — 4a — 73 = 9a² + 62a + 48

2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a² + 62a + 48 > 0

3. Решим его «Методом интервалов».

9a² + 62a + 48 = 0
D = 3844 — 1728 = 2116
(a_1 = frac{-62 + 46}{18} = -frac{16}{18} = -89)
(a_2 = frac{-62 — 46}{18} = -frac{108}{18} = -6)

4. Дискриминант будет положительным при (a in (-infty; -6) cup (-frac{8}{9}; +infty)). Это и будет ответ. 

Ответ: (a in (-infty; -6) cup (-frac{8}{9}; +infty)).

Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения. 

Пример 2. При каких значениях параметра a уравнение (2a + 1)x² — ax + 3a + 1 = 0 имеет два различных решения? 

Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0? 

Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи. 

1. Поскольку по условию должно быть 2 решения, мы получаем, что a (neq) -0,5. 

2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения. 

D = a² — 4 * (2a + 1) * (3a + 1) = a² — 24a² — 20a -4 = -23a² — 20a — 4

3. Составим неравенство и решим его:

-23a² — 20a — 4 > 0
23a² + 20a + 4 < 0
23a² + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
(a_1 = frac{-20 + 4 sqrt{2}}{46} = frac{2sqrt{2} — 10}{23})
(a_2 = frac{-20 — 4sqrt{2}}{46} = frac{-2sqrt{2} — 10}{23})

4. Разложим уравнение на множители: 

(23a^2 + 20a + 4 = 23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23}))

5. Получаем неравенство:

(23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23} < 0)

6.Тогда  (a in (frac{-2sqrt{2} — 10}{23}; frac{2sqrt{2} — 10}{23})). Вспомним, что a (neq) -0,5, следовательно, мы получаем ответ (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23})).

Ответ: (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23}))

Теорема Виета 

Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax² + bx + c = 0, то его корни можно найти с помощью следующей системы: 

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения. 

Пример 3. При каких значениях параметра a корни уравнения x² — 3ax — a(a — 1) = 0 удовлетворяют условию x₁ = 5x₂. 

Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0: 

D = 9a² — 4 * 1 * (-a² + a) = 9a² + 4a² — 4a = 13a² — 4a = a(13a — 4)

Получаем неравенство a(13a — 4) > 0, следовательно, (a in (-infty; 0) cup (frac{4}{13}; +infty)). 

2. По теореме Виета найдем корни уравнения: 

3. По условию x₁ = 5x₂, тогда 5x₂ + x2 = 6x₂ = 3a, откуда получаем:
(x_2 = frac{3a}{6} = frac{a}{2})
(x_1 = 5 * a_2 = frac{5a}{2})

4. Подставим во второе уравнение системы:
(frac{a}{2} * frac{5a}{2} = a — a^2)
(frac{5a^2}{4} = a — a^2 | * 4)
5a² = 4a — 4a²
(9a^2 — 4a = 0 rightarrow a(9a — 4) = 0 rightarrow a = 0, a = frac{4}{9})

5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня. 

a = 0 не подходит, поскольку ограничение (a in (-infty; 0) cup (frac{4}{13}; +infty)) не включает точку 0. 

(a = frac{4}{9}) подходит, поскольку (frac{4}{9} > frac{4}{13}). 

Ответ: (a = frac{4}{9})

Условия на корни квадратного трехчлена 

Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев. 

1. Корни квадратного трехчлена меньше, чем число N. 

Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз. 

Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N. 

Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту. 

Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка. 

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа. 

Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы. 

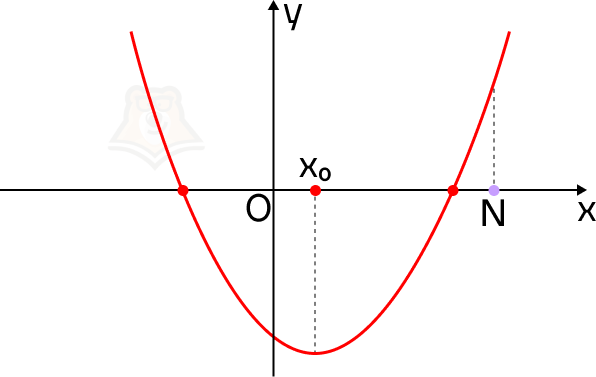
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N. 

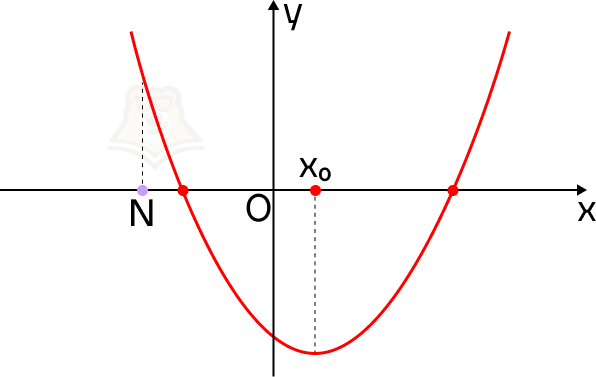
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов. 

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними. 

В этом случае смотровая площадка окажется между привалами. 

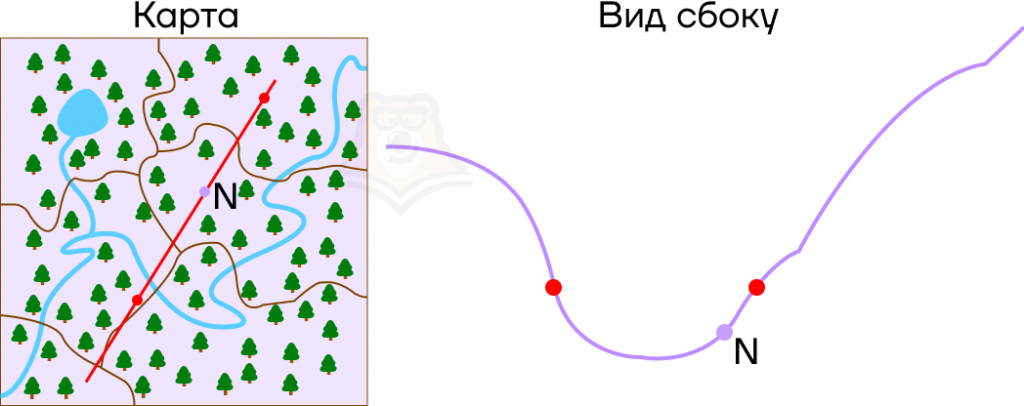
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг. 

Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы. 

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения. 

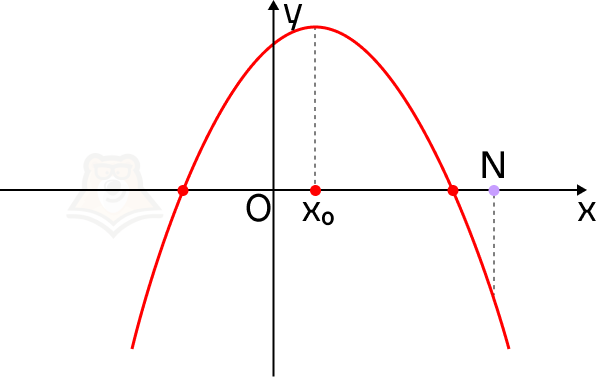
Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

2. Корни квадратного трехчлена больше, чем число N. 

Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы. 

Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы. 

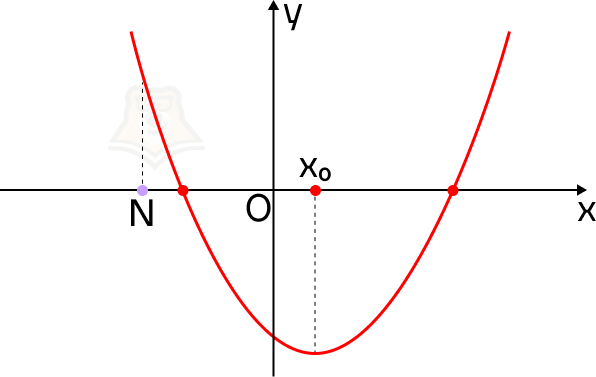
Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько. 

В итоге должна получиться система, с помощью которой можно решить задачу.

Фактчек

• Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 
• При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b (neq) 0 — решений нет. Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 
• При решении квадратного уравнения обязательно проверять коэффициент перед x². Если коэффициент будет равен 0, то уравнение станет линейным.
• При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней. 
• Решить квадратное уравнение можно и с помощью теоремы Виета. 
• Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций. 

Проверь себя

Задание 1. 
Что такое параметр?

1. Это буква a, вместо которой можно подставить число.
2. Это коэффициент перед x² в квадратном уравнении.
3. Это переменная х.
4. Это значение функции в определенной точке. 

Задание 2. 
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?

1. Решений нет.
2. Одно решение.
3. Бесконечное множество решений.
4. Невозможно определить количество решений. 

Задание 3. 
При каких значениях дискриминанта уравнение будет иметь корни?

1. D > 0
2. D = 0
3. D < 0
4. D (neq) 0

Задание 4. 
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?

1. Справа.
2. Слева.
3. Совпадать с точкой А.
4. Невозможно определить расположение вершины. 

Задание 5. 
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?

1. Значение функции в точке В будет меньше 0.
2. Значение функции в точке В будет равно 0.
3. Значение функции в точке В будет больше 0.
4. Невозможно определить значение функции. 

Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.

Основы работы с параметром

Параметр – это буквенный коэффициент в уравнении.

Параметр – это всегда число, а не переменная, но мы не знаем, чему конкретно равен параметр. Например,

(y = kx + b)

это уравнение прямой, в котором (x) – переменная, (y) – зависимая от неё функция, а (k) и (b) – коэффициенты. Это значит, что (k) и (b) – какие-то числа, параметры. Когда мы видим конкретное уравнение прямой, например,

(y = — 5x +

мы можем сказать, что в данном случае параметр (k = — 5), а параметр (b = . В зависимости от параметров функция может по-разному себя вести, но сам вид линейной функции не поменяется.

УРАВНЕНИЕ С ПАРАМЕТРОМ:

Существуют уравнения, где есть две неизвестных: (x) – корень уравнения и (a) (или любая другая буква) – параметр. Решение таких уравнений сводится не к поиску конкретных корней, а к анализу их количества. Для этого мы предполагаем, чему будут равны корни уравнения при определенных параметрах.

АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЙ С ПАРАМЕТРОМ

Рассмотрим примеры.

Пример №1:

Сколько корней имеет уравнение

(ax = 3a + 7)

1. Данное уравнение не имеет ограничений для (x), поэтому перейдем ко второму пункту.

2. Начнем рассуждать. В случае работы с параметром нужно предположить, как мы будем искать корень, если коэффициент при икс равен нулю и если не равен ему. В данном случае коэффициент при иксе и есть параметр. Допустим, (a = 0), тогда уравнение будет иметь вид:

(0 = 7)

Это невозможно, из чего делаем вывод, что при (a = 0) корней нет.

1. Теперь представим, что параметр не равен нулю, а равен любому другому числу (a neq 0), тогда выразим икс:

(x = frac{3a + 7}{a})

При условии, что (a neq 0), а равно обычному числу, (x) будет принимать одно единственное значение.

1. Так мы нашли, при каких параметрах уравнение будет иметь один корень, нужно проверить этот корень на ограничения. Этих ограничений из п.1 нет, значит мы полностью проанализировали уравнение и узнали, сколько корней оно будет иметь во всех возможных случаях изменения параметра:

({корней нет при a = 0 }{один корень frac{3a + 7}{a} при a neq 0 })

Ответ так и запишем.

Ответ: (корней нет при a = 0); (один корень frac{3a + 7}{a} при a neq 0).

При работе с линейными уравнениями нет ограничений для переменных и для параметра. Сейчас мы рассмотрим дробно-рациональное уравнение с параметром, где на каждом этапе нужно помнить об ограничениях в знаменателе.

Пример №2:

Сколько корней имеет уравнение

(frac{4}{x — 3} — frac{k}{2} = 2)

1. Для начала нужно выписать все ограничения для переменной. Знаменатель не может быть равен нулю, значит:

(x — 3 neq 0)

(x neq 3)

(frac{8}{2left( x — 3 right)} — frac{kleft( x — 3 right)}{2left( x — 3 right)} = frac{4left( x — 3 right)}{2(x — 3)})

(frac{8 — kx + k3}{2(x — 3)} = frac{4x — 12}{2(x — 3)})

Ограничение для переменной мы записали, поэтому смело можно убрать знаменатель и приравнять числители. Про ограничение не забывать!

(8 — kx + 3k = 4x — 12)

1. Вправо перенесем все с иксами, а влево перенесем все остальные числа:

(8 + 3k + 12 = 4x + kx)

(20 + 3k = xleft( 4 + k right))

1. Мы снова пришли к ситуации, когда (x) умножается на какое-то число ((4 + k)), значение которого мы не знаем, т. к. в нём есть параметр. Снова анализируем количество корней, если весь коэффициент перед (x) равен нулю, то есть:

(4 + k = 0)

(k = — 4)

тогда

(x = frac{20 + 3k}{0})

Чего не может быть, значит корней нет.

1. Рассмотрим случай, когда (4 + k neq 0):

(k neq — 4)

тогда

(x = frac{20 + 3k}{k})

Получается, что существует один единственный корень.

1. Мы не учли то, что единственным корнем может оказаться число 3, но в начале мы записали ограничение (x neq 3). Поэтому уравнение будет иметь один корень ( x = frac{20 + 3k}{k}) при (k neq — 4), если

(x = frac{20 + 3k}{k} neq 3)

Найдем такой параметр (k), при котором (x = 3). Нужно проверить, есть ли такой параметр, и если есть – исключить его:

(frac{20 + 3k}{k} = 3)

(20 + 3k = 3k)

(20 = 0)

Что невозможно, значит такого параметра не существует, и уравнение имеет ровно один корень без ограничений, кроме (k neq — 4). Запишем ответ.

Ответ: корней нет при (k = — 4); один корень (x = frac{20 + 3k}{k}) при (k neq — 4).

Сразу оговорюсь — для того, чтобы научиться решать задачи с параметром, не выйдет просто прочитать краткую инструкцию с указаниями, что вам делать. Нужно потратить некоторое время, чтобы научиться решать такие задачи. Здесь необходимо развитое аналитическое мышление (задачи бывают совершенно разные и нужно уметь анализировать разные функции), отличное умение решать все типы уравнений и неравенств (если вы не можете решить любое задание С1 или С3, то для вас будет очень сложно решить и С6), знание, как ведут себя различные функции и умение строить их графики. Как видите, все не так уж просто, но и 4 первичных балла дают не просто так. Тем не менее, решить С6 более чем реально, нужно набраться терпения. На самом деле, не так уж и много материала, да и раз вы задумались о С6, скорее всего, большинство необходимых знаний у вас есть, в основном придется потратить время на отработку практических навыков и разбор различных методов решения. Материал разбит на несколько частей, и я рекомендую внимательно их изучить, разбирая представленные примеры.

Решение уравнения или неравенства с параметром обычно предполагает несколько случаев, и ни один из них нельзя потерять.
Для того, чтобы решить задачу с параметром, необходимо для начала преобразовать заданное выражение к более простому виду, если это, конечно, возможно. При этом необходимо понимать, какие преобразования являются равносильными, а какие нет. В противном случае могут появиться посторонние корни, которые будет нужно проверить (это не всегда просто, поэтому рекомендую стараться использовать равносильные преобразования).

Рекомендации к выполнению задания 18 ЕГЭ:

1. Надо избавиться от логарифмов, модулей, показательных степеней и т.д.
2. Еще раз внимательно прочитать задание. Понять, что от вас требуется.
3. Попытаться проанализировать получившееся после преобразований выражение на наличие каких-либо специальных свойств функции (периодичность, возрастание/убывание, четность/нечетность и т.д.)
4. Часто решить задачу с параметром можно и удобно при помощи графиков. Иногда удобно выполнять построения на обычной координатной плоскости (Х, У), а иногда удобно построить графики в плоскости (Х, а), где а – параметр. Данный способ решения возможен, если вы видите знакомые функции (параболы, прямые, гиперболы, окружности и т.д.). Разумеется, бывает несколько способов решения поставленной задачи, но графический, как правило, наименее громоздок и прост для понимания. Ведь графики показывают поведение функций, и весь необходимый анализ появится у вас перед глазами.
5. Важно помнить, что методы решения уравнения или неравенства зависят от степени многочлена. Для этого необходимо рассматривать те значения параметра, при которых (если это возможно) обращается в нуль коэффициент при старшей степени. Пример: (a*x^2-3*x+1=0), при (a=0) выражение принимает вид (-3*x+1=0), т.е. превращается в линейную функцию, а способы решения квадратного и линейного уравнений различны.

В последние годы на вступительных экзаменах, на
итоговом тестировании в форме ЕГЭ предлагаются
задачи с параметрами. Эти задачи позволяют
диагностировать уровень математического и,
главное, логического мышления абитуриентов,
способность осуществлять исследовательскую
деятельность, а также просто знание основных
разделов школьного курса математики.

Взгляд на параметр как на равноправную
переменную находит своё отражение в графических
методах. В самом деле, поскольку параметр “равен
в правах” с переменной, то ему, естественно,
можно “выделить” и свою координатную ось. Таким
образом, возникает координатная плоскость . Отказ
от традиционного выбора букв и для обозначения
осей, определяет один из эффективнейших методов
решения задач с параметрами – “метод
областей”. Наряду с другими методами,
применяемыми при решении задач с параметрами, я
знакомлю своих учеников и с графическими
приёмами, обращая внимание на то, как распознать
“такие” задачи и как выглядит процесс решения
задачи.

Самые общие признаки, которые помогут узнавать
задачи, подходящие под рассматриваемый метод:

Задача 1. “При каких значениях параметра неравенство
выполняется при всех ?”

Решение. 1). Раскроем модули с учётом знака
подмодульного выражения:

2). Запишем все системы получившихся
неравенств:

а)

б)
в)

г)

3). Покажем множество точек, удовлетворяющих
каждой системе неравенств (рис.1а).

4). Объединяя все области, показанные на
рисунке штриховкой, можно заметить, что
неравенству не удовлетворяют точки ,
лежащие внутри парабол.

На рисунке видно, что при любом значении
параметра
можно найти область, где лежат точки, координаты
которых удовлетворяют исходному неравенству.
Неравенство выполняется при всех , если . Ответ:
при .

Рассмотренный пример представляет собой
“открытую задачу” — можно рассмотреть решение
целого класса задач, не изменяя рассмотренное в
примере выражение, в которых технические
трудности построения графиков уже преодолены.

Задача. При каких значениях параметра уравнение не
имеет решений? Ответ: при .

Задача. При каких значениях параметра уравнение имеет
два решения? Запишите оба найденных решения.

Ответ: , тогда , ;

,
тогда ;

,
тогда ; , тогда , .

Задача. При каких значениях параметра уравнение имеет
один корень? Найдите этот корень. Ответ: при при .

Задача. Решите неравенство .

(“Работают” точки, лежащие внутри парабол).

Ответ: , ;

, ; ,
решений нет;

, ; , .

Задача 2.Найдите все значения параметра а,
при каждом из которых система неравенств
образует на числовой прямой отрезок длины 1.

Решение. Перепишем исходную систему в таком
виде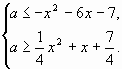

Все решения этой системы (пары вида )
образуют некоторую область, ограниченную
параболами и (рис 1).

Очевидно, решением системы неравенств будет
отрезок длины 1 при и при . Ответ: ; .

Задача 3.Найдите все значения параметра , при которых
множество решений неравенства
содержит число , а так же содержит два отрезка длиной , не
имеющие общих точек.

Решение. По смыслу неравенства ;
перепишем неравенство, умножив обе его части на (),
получаем неравенство:

, ,

, ,

(1)

Неравенство (1) равносильно совокупности двух
систем:

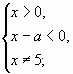
1) 2)

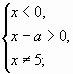
Покажем области, которые соответствуют этим
системам (рис. 2).

Очевидно, интервал не может содержать отрезка
длины . Значит, два непересекающихся отрезка
длины содержатся в интервале Это
возможно при , т.е. при . Ответ: .

Задача 4.Найдите все значения параметра , при каждом из
которых множество решений неравенства
содержит отрезок длиной 4 и при этом содержится в
некотором отрезке длиной 7.

Решение. Проведём равносильные
преобразования, учитывая, что и .

, ,

, ,

;
последнее неравенство равносильно совокупности
двух систем:

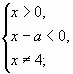
1) 2)

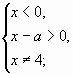
Покажем области, которые соответствуют этим
системам (рис. 3).

1) При множество решений – это интервал длиной,
меньшей 4. При множество решений – это объединение
двух интервалов .Содержать отрезок длиной 4 может
только интервал . Но тогда , и объединение уже не
содержится ни в каком отрезке длиной 7. Значит,
такие не удовлетворяют условию.

2) множество решений – это интервал . Он
содержит отрезок длиной 4, только если его длина
больше 4, т.е. при . Он содержится в отрезке длиной
7, только если его длина не больше 7, т. е. при , тогда . Ответ:
.

Задача 5. Найдите все значения параметра , при
которых множество решений неравенства
содержит число 4, а также содержит два
непересекающихся отрезка длиной 4 каждый.

Решение. По условия . Домножим обе части
неравенства на (). Получим равносильное неравенство, в
котором сгруппируем все члены в левой части и
преобразуем её в произведение:

, ,

, .

Из последнего неравенства следует:

1) 2)

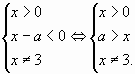
Покажем области, которые соответствуют этим
системам (рис. 4).

а) При получаем интервал , не
содержащий числа 4. При получаем интервал , также
не содержащий числа 4.

б) При получаем объединение двух
интервалов. Непересекающиеся отрезки длиной 4
могут располагаться только в интервале . Это
возможно только в том случае, если длина
интервала больше 8, т. е. если . При
таких выполнено и другое условие: . Ответ:
.

Задача 6. Найдите все значения параметра , при которых
множество решений неравенства
содержит какой-нибудь отрезок длиной 2, но не
содержит никакого отрезка длиной 3.

Решение. По смыслу задания ,
умножим обе части неравенства на ,
сгруппируем все члены в левой части неравенства
и преобразуем её в произведение:

, ,

, . Из
последнего неравенства следует:

1)
2)

Покажем область, которая соответствует первой
системе (рис. 5).

Очевидно, что условие задачи выполняется, если . Ответ:
.

Задача 7. Найдите все значения параметра , при
которых множество решений неравенства 1+
содержится в некотором отрезке длиной 1 и при
этом содержит какой-нибудь отрезок длиной 0,5.

Решение. 1). Укажем ОДЗ переменной и параметра:

2). Перепишем неравенство в виде

, ,

, ,

(1).
Неравенство (1) равносильно совокупности двух
систем:

1)

2)

С учётом ОДЗ решения систем выглядят так:

1)

а) 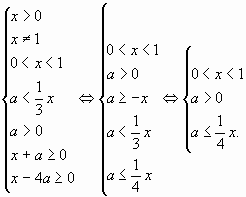б)

Покажем область, соответствующую системе а) (рис. 6).

2)

а) 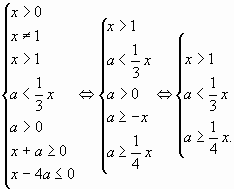б)

Покажем область, соответствующую системе а) (рис.
7). Ответ: .

Задача 8. Шесть чисел образуют возрастающую
арифметическую прогрессию. Первый, второй и
четвертый члены этой прогрессии являются
решениями неравенства , а остальные

не являются решениями этого
неравенства. Найдите множество всех возможных
значений первого члена таких прогрессий.

Решение. I. Найдём все решения неравенства

а). ОДЗ: 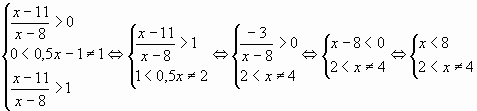, т.е.

(учли в решении, что функция возрастает на ).

б). На ОДЗ неравенство равносильно неравенству , т.е. , что
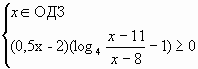
даёт:

1).

2).

Очевидно, решением неравенства служит
множество значений .

II. Проиллюстрируем вторую часть задачи о
членах возрастающей арифметической прогрессии
рисунком (рис. 8, где —
первый член, — второй и т.д.). Заметим, что:

или имеем систему линейных неравенств:

решим её графическим способом. Строим прямые и , а
также прямые

, , , , , , .

Все решения этой системы образуют область,
показанную штриховкой на рисунке (рис.9).

Ответ: возможные значения первого члена .

Задача 9. Найдите все значения при которых в
области определения функции
столько же целых чисел, сколько их в области
определения функции

Решение. I. Покажем, что в области определения
второй функции имеется ровно три целых числа.
Целые значения
из области определения функции
удовлетворяют условию , тогда это числа: -1; 0; 1.

Функция чётная;

Заметим, если , то .

II. Функция определена, если

Найдём корни квадратного трёхчлена

тогда .

Перепишем систему неравенств в виде

(*)

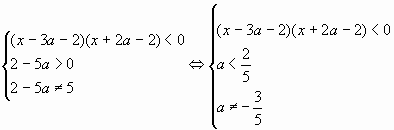
Последняя система равносильна совокупности
двух систем:

а) 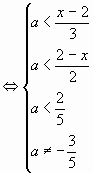б)

На плоскости покажем графическое решение системы (*)
(см. рис.10).

Вероятно, что 3 целых числа в области
определения функции следует искать среди чисел 0,
1, 2, 3 и, может быть, числа 4. Проведём
дополнительные прямые , , , , и посмотрим, при каких
выполняется условие задачи.

Очевидно, что в области определения функции ровно 3
целых числа при всех

Ответ:

Разобранные задачи достаточно убедительно
демонстрируют эффективность предложенного
метода. Однако, к сожалению, сфера применения
этого метода ограничена трудностями, с которыми
можно столкнуться при построении графического
образа.

Задачи для самостоятельного решения

Задача 1. Найдите все значения параметра а,
при каждом из которых система неравенств
образует на числовой прямой отрезок длины 1.

Ответ: ; .

Задача 2. Найдите все значения параметра а,
при каждом из которых система неравенств 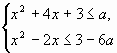имеет
единственное решение.

Ответ:

Задача 3. Найдите все значения параметра , при которых в
множестве решений неравенства можно
расположить два отрезка длиной 1 и длиной 4,
которые не имеют общих точек.

Ответ: .

Задача 4. Найдите все значения параметра , при
которых множество решений неравенства
содержится в некотором отрезке длиной 4 и при
этом содержит какой-нибудь отрезок длиной 2.

Ответ: .

Задача 5. Семь чисел образуют убывающую
арифметическую прогрессию с разностью .
Первый, второй и шестой члены этой прогрессии
являются решениями неравенства , а
остальные не являются решениями этого
неравенства. Найдите множество всех возможных
значений разности этой прогрессии.

Ответ: .