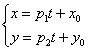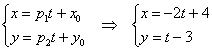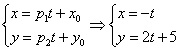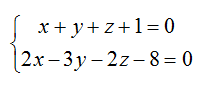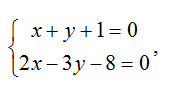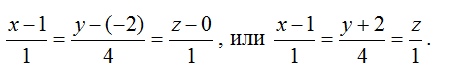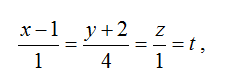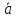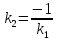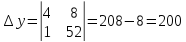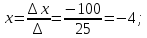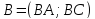Как найти параметрические уравнения для прямой - Исправление недочетов и поиск решений вместе с Examum.ru

Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x + B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

k = tg φ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки M(x₁, y₁) и N(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂, то уравнение прямой можно найти, используя следующую формулу

x — x₁	=	y — y₁
x₂ — x₁	y₂ — y₁

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x₀y = m t + y₀

где N(x₀, y₀) — координаты точки лежащей на прямой, a = {l, m} — координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки N(x₀, y₀) лежащей на прямой и направляющего вектора a = {l; m} (l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Пример 1. Найти уравнение прямой проходящей через две точки M(1, 7) и N(2, 3).

Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки

x — 12 — 1 = y — 73 — 7

Упростив это уравнение получим каноническое уравнение прямой

x — 11 = y — 7-4

Выразим y через x и получим уравнение прямой с угловым коэффициентом

y — 7 = -4(x — 1)

y = -4x + 11

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 7} = {1; -4}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = -4t + 7

Пример 2. Найти уравнение прямой проходящей через две точки M(1, 3) и N(2, 3).

Решение. Так как M_y — N_y = 0, то невозможно записать уравнение прямой проходящей через две точки.

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 3} = {1; 0}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = 3

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Если прямая проходит через две точки M(x₁, y₁, z₁) и N(x₂, y₂, z₂), такие что x₁ ≠ x₂, y₁ ≠ y₂ и z₁ ≠ z₂, то уравнение прямой можно найти используя следующую формулу

x — x₁	=	y — y₁	=	z — z₁
x₂ — x₁	y₂ — y₁	z₂ — z₁

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x₀
y = m t + y₀
z = n t + z₀

где (x₀, y₀, z₀) — координаты точки лежащей на прямой, {l; m; n} — координаты направляющего вектора прямой.

Каноническое уравнение прямой в пространстве

Если известны координаты точки M(x₀, y₀, z₀) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x — x₀	=	y — y₀	=	z — z₀
l	m	n

Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

	A₁x + B₁y + C₁z + D₁ = 0
A₂x + B₂y + C₂z + D₂ = 0

при условии, что не имеет место равенство

A₁	=	B₁	=	C₁	.
A₂	B₂	C₂

Источник

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

каноническое уравнение,
параметрическое уравнение,
общее уравнение прямой,
уравнение прямой с угловым коэффициентом,
уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Каноническое уравнение прямой на плоскости

{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}

x_a и y_a — координаты первой точки A,

x_b и y_b — координаты второй точки B

Параметрическое уравнение прямой на плоскости

{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}

x_a, y_a — координаты точки, лежащей на прямой,

{l;m} — координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Каноническое уравнение прямой в пространстве

{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}

x_a, y_a и z_a — координаты первой точки A,

x_b, y_b и z_b — координаты второй точки B

Параметрическое уравнение прямой в пространстве

{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }

x_a, y_a и z_a — координаты точки, лежащей на прямой,

{l;m;n} — координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Пример нахождения уравнения прямой, проходящей через две точки

Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).

Каноническое уравнение прямой

Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}

Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}

Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}

Уравнение прямой с угловым коэффициентом

Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}

Параметрическое уравнение прямой

Параметрическое уравнение прямой имеет вид:

{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }

где {x_a, y_b} — координаты точки, лежащей на прямой, {{l;m}} — координаты направляющего вектора прямой, t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.

Найдем координаты направляющего вектора:

overline{AB} = {x_b — x_a; y_b — y_a} = {3-1; 8-2} = {2; 6}

Получаем параметрическое уравнение:

begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}

Используем калькулятор для проверки полученного ответа.

Источник

2.4. Параметрические уравнениЯ прямой

Если известна некоторая точка , принадлежащая прямой, и направляющий вектор этой прямой, то параметрические уравнения данной прямой задаются системой:

В чём смысл? Параметр принимает все значения от «минус» до «плюс» бесконечности и каждому значению параметра соответствует конкретная точка прямой

Задача 71

Составить параметрические уравнения прямой по точке и направляющему вектору .

Решение закончилось, не успев начаться:

Как найти точки прямой? Возьмём какое-нибудь значение параметра, например, . Тогда соответствующая точка:

Обратная задача: как проверить, будет ли точка принадлежать данной прямой? Подставим её координаты параметрические уравнения:

Из обоих уравнений следует, что , значит, система совместна (имеет решение) и точка действительно принадлежит данной прямой.

Рассмотрим более содержательные примеры:

Задача 72

Составить параметрические уравнения прямой

Решение: по условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку. Найдём направляющий вектор:

Теперь нужно найти какую-нибудь точку, принадлежащую прямой, здесь проще всего обнулить «иксовую» координату , тогда:

Составим параметрические уравнения прямой:

Ответ:

И небольшое творческие задание для самостоятельного решения.

Задача 73

Составить параметрические уравнения прямой, если известна принадлежащая ей точка и вектор нормали

Решение и ответ в конце книги.

Укрепляем заложенный геометрический фундамент простейшими задачами с прямой:

2.5.1. Взаимное расположение двух прямых

2.3. Уравнение прямой в отрезках

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей

Решение

1) Найдем координаты фиксированной точки. Из исходной системы уравнений

исключим z.

Положим z=0, тогда:

откуда находим: x=1, y= -2.

Таким образом, нашли координаты фиксированной точки M0(1,-2,0).

2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:

3) Запишем канонические уравнения:

4) Обозначив,

получаем параметрические уравнения:

x=t+1, y=4t-2, z=4

Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

Уравнения прямой (различные виды). Параметрические уравнения прямой.

Направляющим
вектором прямой
называется любой вектор параллельный
данной прямой.

Пусть
на прямой дана точка

с координатами (,)
и дан направляющий вектор прямой= (,).

Пусть
точка М
(x,
y)
– произвольная точка прямой, тогда
вектор
коллинеарен вектору.

По
признаку коллинеарности эти векторы
пропорциональны.

Обозначим
коэффициент пропорциональности tи
назовем параметром.

Тогда
получим
=t·
.

Запишем
это равенство в координатной форме:

()
=t
(,).

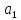
Следовательно,

(1)

– параметрические
уравнения прямой на плоскости.

По
аналогии, в пространстве получим:

Уравнение прямой проходящей через две данные точки.

Из
параметрических уравнений прямой
выразим параметрt.

Получим:

– уравнение
прямой проходящей через данную точку
с данным направляющим вектором
(каноническое уравнение).

В
пространстве уравнение (2) примет вид:

Пусть
на прямой даны две точки
(,)
и(,).

Тогда

=
= (‒;‒).

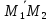
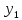
Подставим
его координаты в формулу (2).

Получим:

– уравнение
прямой, проходящей через две данные
точки.

В
пространстве это уравнение примет вид:

Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.

Угловым
коэффициентом
прямой называется тангенс угла наклона
прямой, образованный ею с положительным
направлением оси OX.

k=
α,
a≠
90⁰

Пусть
на прямой даны две точки М₁(х_1,y₁),
M₂(х_2,y₂).

Найдем
угловой коэффициент этой прямой. Из
∆М₁M₂С
получим

т.е.

– формула
углового коэффициента прямой по
координатам.

Заменим
точку М₂(x,
y)
на произвольную точку M(x,
y)
и подставим ее координаты в формулу
(1).

Получим:

Из
формулы (2) следует

y
‒ y₁=
k
× (x
‒ x₁)

– уравнение
прямой проходящей через данную точку
с данным угловым коэффициентом.

Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).

Нормальным
вектором прямой(нормалью)
называется любой вектор перпендикулярный
данной прямой.

Обозначается
= (a,
b).

Пусть
на прямой дана точка М₁
(x_1,y₁)
и дан нормальный вектор прямой
= (a,
b).

Пусть
М
(x_,y)
произвольная точка прямой.

Тогда
вектор
перпендикулярен вектору.
Следовательно, их скалярное произведение×= 0.

Запишем
это равенство в координатной форме.

Так
как
=(а;
b)
и
= (x
–x₁;
y
–y₁),
то равенство
×= 0, согласно формуле,
×

= x₁×
x₂+
y₁×
y₂,
в координатной форме примет вид:

a·
( x–x₁)
+ b·
(y–y₁)
= 0

– уравнение
прямой, проходящей через данную точку
с данным нормальным вектором.

Общее уравнение прямой.

Раскроем
скобки в уравнении a·(x‒x₁)+
b·(y‒y₁)=0.

Следовательно,
ax
‒ ax₁+
by ‒ by₁=
0 или
ax + by +(‒ ax₁‒
by₁)
= 0.

Обозначим
‒ ax₁—
by₁=с,

тогда
получим общее уравнение прямой:

ax
+ by
+ с = 0

–
общее
уравнение прямой.

Выразим
из общего уравнения прямойyчерез
x:

Следовательно,

‒ формула
углового коэффициента по координатам
нормального вектора.

Формула угла между прямыми.

Угол
между прямыми:
;
равен углу между их нормальными векторами,
т. е.

()
=().

Воспользовавшись
формулой скалярного произведения
векторов, получим:

Тогда

Если
прямые заданные уравнениями:

;
,

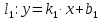
тогда

Следовательно,

По
формулам (1) или (2) находят угол между
прямыми.

Условия параллельности и перпендикулярности прямых.

Если
,
то
= 0. Следовательно,

= 0 и
=0.

Получим:

‒ условие
параллельности прямых.

Если
,
то 
=
и
‒ не существует, то есть
= 0. Следовательно,

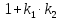
‒ условие
перпендикулярности прямых.

Пример:

Даны
уравнения сторон треугольника

Найти:

1)
Длину │CD│
и уравнение высоты CD.

2)
Систему неравенств определяющих
треугольник.

3)
B.

Решение:

Найдем
координаты вершин треугольника.

A
(– 4;

B
(5; – 4)

C
(10; 6)

1)
Найдем уравнение высоты CD.

CD
AB

;

│·
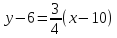
4

–уравнение
высоты CD.

D
(2; 0)

Найдем
длину │CD│.

2)
Найдем систему неравенств определяющих
треугольник.

или
– уравнениеAB.

–уравнение
BC.

или
– уравнениеAC.

–система
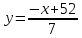
неравенств определяющих ∆ABC.

3)
Найдем
B.

или

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник