Как найти параметрическое уравнение прямой пирамиды



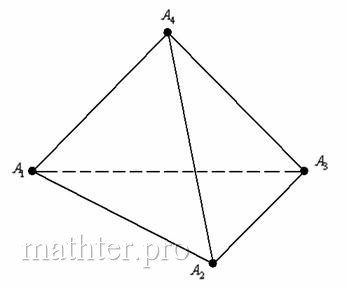
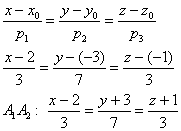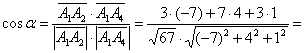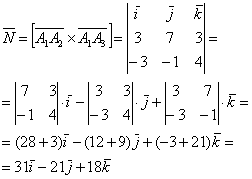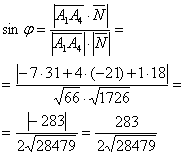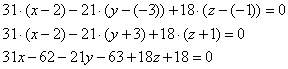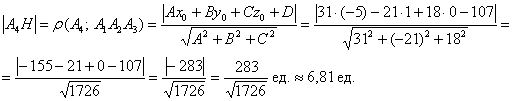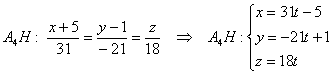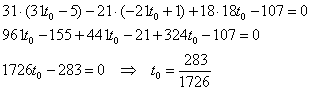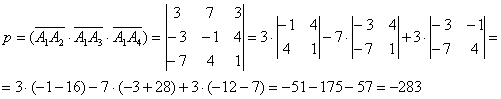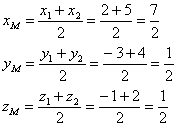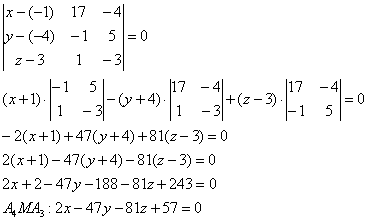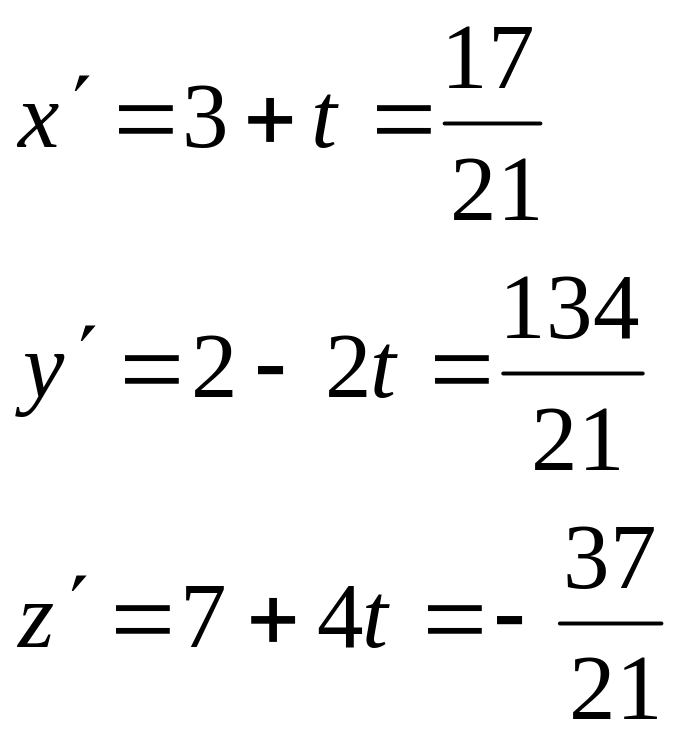5.7. Задача с треугольной пирамидой

Концептуально эта задача напоминает задачу с треугольником на плоскости. Только вот треугольников у нас теперь

четыре, и образуют они треугольную пирамиду или тетраэдр:

У треугольной пирамиды есть:

– четыре вершины;

– шесть рёбер (сторон);

– четыре грани.

Чем богаты, тем и рады.

Не буду перечислять геометрические свойства данной фигуры, известные из школьной программы, поскольку аналитическую геометрию интересует совсем

другое, а именно: уравнения рёбер, плоскостей, всевозможные длины, углы и некоторые другие вещи, которые вы увидите прямо сейчас. Типовая задача

формулируется так:

Задача 166

Треугольная пирамида задана координатами своих вершин, пусть это будут вершины . Требуется: … если повезёт, то только 3-4 пункта из перечисленных:

1) найти длину ребра ;

2) составить уравнения стороны ;

3) найти угол между рёбрами ;

4) найти площадь грани ;

5) найти угол между ребром  и плоскостью ;

6) составить уравнение грани ;

7) составить уравнения высоты , опущенной из вершины  на грань ;

вычислить длину высоты ;

9) найти основание высоты ;

10) вычислить объем пирамиды;

11) составить уравнения медианы  грани ;

12) составить уравнение плоскости, проходящей через прямую  и вершину ;

13) найти угол между плоскостями  и

14) выполнить чертёж пирамиды  в прямоугольной системе координат.

15) перекреститься левой пяткой.

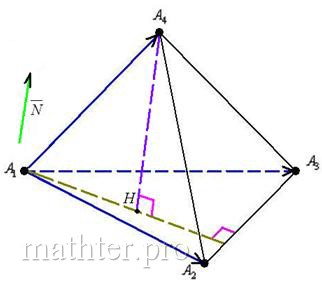
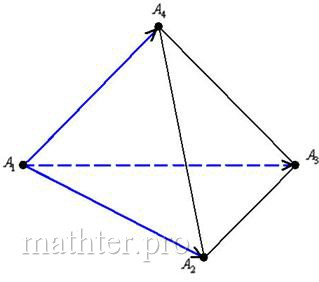
Во-первых, разберёмся с обозначениями вершин. Самый распространённый вариант, когда они обозначены буквами :

Если бегло просмотреть пункты условия, то легко заметить, что

там часто встречается грань . Чаще всего требуется составить уравнение этой

«особенной» грани, а также найти её площадь. В качестве «особенной» вершины выступает точка , обычно из неё строится перпендикуляр к плоскости .

А всё это я сказал к тому, что в вашей задаче могут быть совершенно другие обозначения вершин. Например, . Здесь «особой» гранью, скорее всего, будет , а «особенной» точкой – вершина .

В этой связи очень важно выполнить схематический рисунок пирамиды, чтобы не запутаться в дальнейшем алгоритме решение. Да, более подготовленные

читатели могут представлять тетраэдр мысленно, но для «чайников» чертёж просто обязателен.

Итак, на предварительном этапе разбираемся с обозначениями вершин, анализируем условие, находим «особенную» плоскость и точку и

выполняем бесхитростный набросок на черновике.

С чего начать решение? Начать лучше всего с того, что загнать координаты вершин в Геометрический

калькулятор (см. приложения), который автоматически рассчитает наиболее популярные пункты. Ибо приятно заранее знать

правильные ответы

Но расписать-то всё нужно подробно. И поэтому оформление решения удобно начать с нахождения векторов. Почти всегда векторы

откладываются от первой вершины, в данном случае – от точки :
Решим эту элементарную задачу:
     

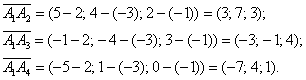
Чтобы комфортнее воспринимать информацию, координаты четырёх точек и трёх полученных вектора рекомендую переписать на отдельный листочек.

Это же сделайте, когда  будете решать свою задачу – чтобы каждый раз не выискивать нужный вектор, нужную точку. Их удобно держать перед

глазами.

Понеслось:

1) Найдём длину ребра . Длина данного ребра равна длине вектора :

Я обычно округляю результаты до двух знаков после запятой, но в условии задачи может быть дополнительное указание проводить округления,

например, до 1 или 3 десятичных знаков.

Полагаю, в случае надобности никого не затруднит аналогичным образом найти длину ребра   или . Как вариант, можно использовать

формулу расстояния между двумя точками: . Но зачем? У нас уже найдены

векторы.

2) Найдём уравнения ребра . Строго говоря, здесь следует

сказать «уравнения прямой, которая содержит ребро», но этим почти всегда пренебрегают. «По умолчанию» обычно подразумевается, что студент запишет канонические уравнения прямой.

Уравнения ребра  составим по точке  (можно взять ) и направляющему

вектору :

Для проверки подставляем координаты точек  в полученное уравнение. Обе

должны «подойти».

3) Найдём угол между сторонами :

Перед вами обычный угол пространственного треугольника,

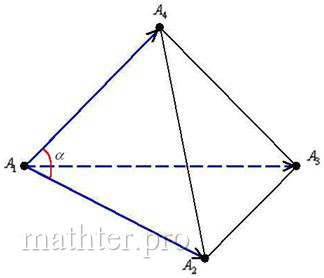
который рассчитывается как угол между векторами: . И снова при делах задро тривиальная формула:

 – заметьте, что в ходе вычислений можно (и нужно) использовать ранее полученные результаты, в данном случае нам

уже известно, что  (см. пункт 1).

С помощью обратной функции находим сам угол:

4) Найдём площадь грани :

Площадь треугольника вычислим с помощью векторного произведения векторов, используя формулу:


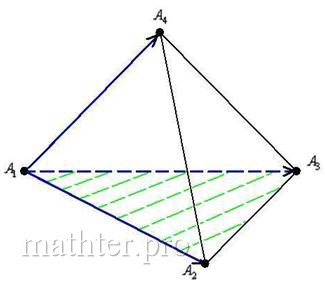
Найдём векторное произведение:


и вычислим его длину:

 …и вынести из-под корня ничего нельзя, поэтому он войдёт в ответ в

неизменном виде.

Таким образом, площадь грани :

Если получаются страшноватые числа, не обращайте внимания, обычная картина. Главное, не допустить ошибку в вычислениях.

5) Найдём угол  между ребром  и плоскостью , прошу прощения за неточность

последующих чертежей, я рисую от руки:

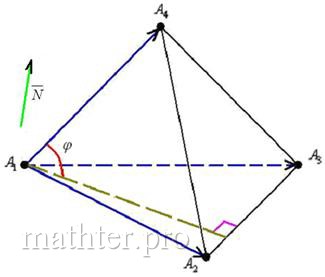
Это стандартная задача, рассмотренная в Задаче 162 (пункт

«д»). Используем формулу:

и с помощью арксинуса рассчитываем сам угол:

6) Составим уравнение грани . А точнее, «уравнение  плоскости,

которая содержит грань». Первая мысль – использовать точки , но есть более выгодное решение. У нас уже найден

вектор нормали  плоскости . Поэтому уравнение грани  составим по точке  (можно взять  либо ) и вектору нормали :

Таким образом:

Для проверки можно подставить координаты точек  в полученное уравнение, все три точки

должны «подойти».

7) Как составить уравнения высоты пирамиды? Звучит грозно, решается просто.

Уравнения высоты , опущенной из вершины  на грань , составим по точке  и направляющему

вектору :

 – по умолчанию записываем канонические уравнения.

Вектор нормали в рассматриваемой задаче работает «на всю катушку», и как только вам предложили найти площадь грани, составить уравнение грани или

уравнения высоты – сразу «пробивайте» векторное произведение.

Длину высоты  найдём как расстояние от точки  до плоскости :

Результат громоздкий, поэтому позволим себе вольность не избавляться от иррациональности в знаменателе.

Теперь пунктик потруднее:

9) Найдём основание высоты – точку . Тема пересечения

прямой и плоскости подробно муссировалась в той же в Задаче 162 (пункт «б»). Повторим.

Перепишем уравнения высоты в параметрической форме:

Неизвестным координатам точки  соответствует вполне конкретное значение

параметра :
, или: .

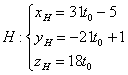
Основание высоты, понятно, лежит в плоскости. Подставим параметрические координаты точки  в уравнение :

Кому-то покажется жестью, но на самом деле шифер  Который шуршит.

Полученное значение параметра подставим в координаты нашей точки:
 

Сурово, но идеально точно. Я проверил.

10)  Объём треугольной пирамиды в ангеме традиционно рассчитывается с помощью

смешанного произведения векторов:

Таким образом,

И тут уместно выполнить проверку, вычислив объем тетраэдра по школьной формуле , где  – площадь грани,  – длина высоты, опущенной к этой грани. Уместно ПОТОМУ, что мы знаем и площадь грани , и длину высоты :
, чему мы очень рады.

11) Составим уравнения медианы  грани . Ничего сложного, обычная медиана обычного пространственного треугольника:
По сравнению с треугольником на

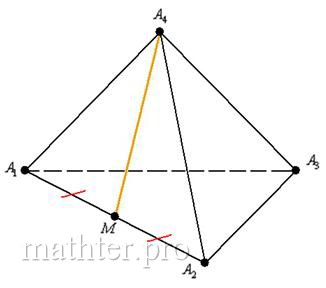
плоскости, добавится лишь дополнительная координата. Нам известны вершины , и по формулам координат середины отрезка находим адрес точки :

Уравнения медианы можно составить по двум точкам, но сначала (см. по ссылке, почему) лучше найти

направляющий вектор: . В качестве направляющего можно взять любой

коллинеарный вектор, и сейчас подходящий момент избавиться от дробей:

Уравнения медианы составим по точке  и направляющему вектору :

Заметьте, что уравнения с эстетической точки зрения лучше составить по точке , так как координаты точки «эм» – дробные. Проверка обыденна, нужно подставить координаты точек  в полученные уравнения.

12) Составим уравнение плоскости, проходящей через прямую  и вершину :

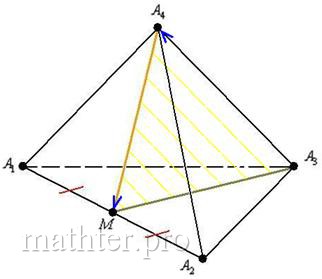
Увы, мы не знаем «вкусный» вектор нормали, и поэтому уравнение

плоскости  придётся добывать по точке и двум

неколлинеарным векторам.

В качестве точки обязательно выбираем «одинокую» точку, которая не принадлежит прямой, в данном случае – это вершина . Один из нужных  векторов уже известен: , но, конечно же, удобнее выбрать друга-мажора . Ему в пару подходит вектор , но лучше .
Ибо координаты этого вектора будут целыми:

Уравнение плоскости составим по точке  и двум неколлинеарным векторам :

Непременно проверяем, что координаты точек  удовлетворяют

полученному уравнению.

13) Найдём угол между плоскостями  и .

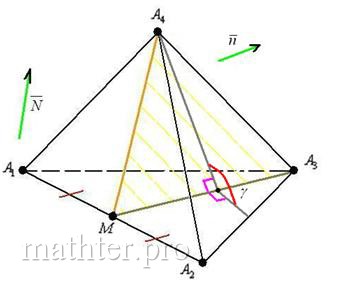
Это типовая задача.

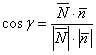
Обозначим искомый угол через  и используем формулу: , где  – вектор

нормали плоскости . Напоминаю, что вектор  и его длина  уже известны.

Осталось из уравнения  снять вектор нормали:  и аккуратно провести вычисления:

Возиться с такими корнями смысла нет, поэтому сразу находим угол:

От тупизны подальше за ответ таки лучше принять смежного соседа:

14) Выполним точный чертёж пирамиды  прямоугольной системе координат. Да, конечно, существуют программы и онлайн сервисы для построения чертежей, но не

факт, что они под рукой, и не факт, что такой чертёж будет качественным. Поэтому я расскажу вам о ручном способе построения – в тетради с помощью

карандаша и линейки.

С чего начать?

Во-первых, нужно правильно изобразить декартову систему координат на клетчатой бумаге. Во-вторых, необходимо уметь строить точки в трёхмерном пространстве, о чём мы уже вспомнили, когда разбирали канонические уравнения прямой. И сейчас тема получает продолжение.

Построим точку .  Для этого отмеряем 2 единицы в положительном направлении

оси  и 3 единицы в отрицательном направлении оси . В плоскости  прочерчиваем тонкие

пунктирные дорожки, которые параллельны соответствующим  координатным осям. Пересечение этих дорожек отмечено ромбиком (слева

внизу):

Теперь, в соответствии с отрицательной «зетовой» координатой, отмеряем 1 единицу вниз и тоже проводим пунктирную дорожку. Здесь и будет находиться

наша точка , она расположена в нижнем полупространстве.

Для точки  отмеряем 5 единиц «на себя» и 4 единицы вправо, строим параллельные

осям пунктирные дорожки и находим их точку пересечения. В соответствии с «зетовой» координатой, чертим пунктиром «подставку для точки» – 2 единицы

вверх. Данная точка расположена в верхнем полупространстве.

Аналогично строятся две другие точки. Заметьте, что вершина  лежит в самой

плоскости .

Теперь нужно разобраться в удалённости точек, а в этом как раз и помогут пунктирные линии. Немного включаем пространственное воображение и

внимательно смотрим на ось . Очевидно, что самая близкая к нам вершина – , а самая удалённая – .

Строим рёбра. Если есть сомнения, то сначала тонко-тонко прочерчиваем все 6 сторон и начинаем разбираться, какие рёбра видимы, а какие нет. Лучше начать от самой близкой точки . Очевидно, что все

три «исходящих» ребра в поле нашего зрения:

Должен предостеречь, что так бывает далеко не всегда, одно ребро, например, может быть от нас скрыто. Не теряйте визуального восприятия

пространства!

Какие ещё стороны в зоне видимости? ВиднЫ рёбра , а вот сторона  спряталась за пирамидой. Обратите внимание, что она лежит в нижнем

полупространстве и проходит под осями :

Готово.

Следует отметить, что чертеж-«конфетка» получается далеко не всегда. Бывает, что фортуна разворачивается задом. Так, грань пирамиды может полностью

или частично закрывать всё остальное (слева).
       

Но самое скверное, когда перекрываются рёбра (справа). Тут сразу три ребра выстроились на одной прямой (правая верхняя прямая). В

подобной ситуации можно жирно прочертить накладывающиеся стороны разными цветами и ниже чертежа записать дополнительные комментарии о расположении

пирамиды. А можно поступить творчески – поменять оси местами (например,  и ).

Существуют и более мелкие неприятности, например, одна из сторон пирамиды может наложить на координатную ось (а то и вовсе расположиться за ней).
Увы, перечисленные случаи – не редкость на практике.

В конце решения следует выполнить Пункт 15, после чего желательно записать ответ, где по пунктам перечислить

полученные результаты.

6.1. Поверхности второго порядка

5.6.7. Добро пожаловать в «реальные боевые условия»!

| Оглавление |



Автор: Aлeксaндр Eмeлин

1.Определяем уравнение плоскости, проходящей через грань А1А2А3
$$begin{vmatrix}x-x_1 & y-y_1 & z-z_1\
x_2-x_1 & y_2-y_1 & z_2-z_1\
x_3-x_1 & y_3-y_1 & z_3-z_1end{vmatrix} = 0 ;$$

$$begin{vmatrix}x-8 & y-6 & z-4\
10-8 & 5-6 & 5-4\
5-8 & 6-6 & 8-4end{vmatrix} =
begin{vmatrix}x-8 & y-6 & z-4\
2 & -1 & 1\
-3 & 0 & 4end{vmatrix} = $$
$$=(x-8)(-1times4-1times0)-(y-6)(2times4-1(-3))+(z-4)(2times0-(-1)(-3))=$$
$$= -4(x-8)-11(y-6)-3(z-4) = -4x+32-11y+66-3z+12=$$ $$=-4x-11y-3z+110 = 0$$

Уравнение плоскости: $%-4x-11y-3z+110=0$%
или, если умножить на -1: $%4x+11y+3z-110=0$%

2.Получаем уравнение прямой, перпендикулярной плоскости А1А2А3 и проходящей через точку A4 (т.е. высоту пирамиды)

Из уравнения плоскости $%4x+11y+3z-110=0$% берем коэффициенты при x,y,z и получаем нормальный вектор: {4,11,3}.
Параметрическое уравнение прямой с заданным направляющим вектором {A,B,C} и проходящей через данную точку (x0,y0,z0):

$$left{begin{array}{l}x=x_0+At\y=y_0+Bt\z=z_0+Ctend{array}right.$$

Подставляем нормальный вектор плоскости и точку A4:

$$left{begin{array}{l}x=8+4t\y=10+11t\z=7+3tend{array}right.$$

Получили параметрическое уравнение высоты пирамиды.
Если нужно каноническое уравнение, в каждом уравнении выражаем параметр t, а потом приравниваем:

$$left{begin{array}{l}t=frac{x-8}4\t=frac{y-10}{11}\t=frac{z-7}3end{array}right.$$

$$frac{x-8}4 = frac{y-10}{11} = frac{z-7}3$$

Уравнение высоты: $%frac{x-8}4 = frac{y-10}{11} = frac{z-7}3$%

Решение:

Найдем уравнение плоскости А1А2А3:	x	y	z–2	= 0
3	0	3
-2	1	-5

-3x + 9y +3z – 6 = 0

Итак,
А₁А₂А₃:
x
– 3y
– z
+ 2 = 0.

Нормальный
вектор этой плоскости n{1,
-3, -1} будет направляющим для искомой
прямой. Значит, ее каноническое уравнение
имеет вид:

x – 4	=	y – 1	=	z – 2
1	-3	-1

Задача
10.
Составьте уравнения плоскостей, отстоящих
от плоскости 2x–3y+z–5
=0 на 3.

РЕШЕНИЕ:

1) Точка
М(0, 0, 5) принадлежит этой плоскости.
Действительно, 2∙0–3∙0+5–5=0. Найдем
уравнение прямой L,
проходящей через точку М перпендикулярно
данной плоскости:

L:	x=2t
y=-3t
z=5+t

2)
Плоскость, отстоящая от данной на 3 –
это плоскость, проходящая через точку
А(x₀,
y₀,
z₀)
параллельно данной (нормальный вектор
равен {2, -3, 1}), где x₀,
y₀,
z₀
являются
решениями системы:

x
₀
=
2t₀,

y₀
=
-3t₀,

z₀
=
5+t₀,

(4t₀+9t₀+5+t₀-5)²=9∙14

;

3)
Плоскость Р₁,
проходящая через точку

и имеющая нормальный вектор {2, -3, 1}, будет
одной из искомых.

Плоскость
Р₂
проходящая через точку

и
имеющая нормальный вектор {2, -3, 1}, также
будет искомой.

Ответ:
P₁:

;
P₂:

Задача
11.
В пирамиде с вершинами А₁(1;-2;1),
А₂(3;-2;1),
А₃(-2;1;0),
А₄(2;2;5)
найдите:

1. уравнение
   грани А₁А₂А₃;

2. уравнение
   плоскости, проходящей через высоту
   пирамиды, опущенную из вершины А₄
   на грань А₁А₂А₃
   ,
   и
   вершину А₁
   пирамиды;

3. уравнение
   прямой, проходящей через вершину А₂
   параллельно ребру А₁А₄;

4. точку,
   симметричную вершине А₄,
   относительно
   грани А₁А₂А_3.

РЕШЕНИЕ:

1)

А1А2А3:	x–4	y	z	= 0
-6	1	2
4	2	0

–4x + 16 + 8y – 16z = 0

x – 2y + 4z – 4 =
0

2)
Найдем уравнение высоты A₄H
пирамиды, опущенной из вершины А₄
на грань А₁А₂А₃.
Направляющим для нее будет вектор {1,
-2, 4}.

A4H:	x=3+t
y=2–2t
z=7+4t

Точка
М(2, 4, 3) принадлежит этой прямой. Тогда
плоскость проходит через точки А₄(3;2;7),
М(2, 4, 3) и А₁(4,
0, 0) и ее уравнение будет иметь вид:

x–4	y	z	= 0
3	2	7
2	4	3

-22(x–4)
+
5y
+
8z = 0

22x – 5y – 8z – 88
= 0

3)
Найдем уравнение прямой А₁А₄:

.
Ее направляющий вектор {-1, 2, 7} будет
направляющим и для искомой прямой. Имеем
ее каноническое уравнение:

4)
Искомая точка

принадлежит прямой A₄H
и

Н=
–A₄H.

21t+23=–23

Т.е

имеет координаты

Ответ:
x
– 2y
+ 4z
– 4 = 0; 22x
– 5y
– 8z
– 88 = 0;

;

Задача
12. Найти точки пересечения
поверхности и прямой:

1+z2 =	x2	+	y2
16	9

y
+3 = 0,

x
+y
-4z
+3 = 0.

РЕШЕНИЕ:

1) Найдем параметрическое задание прямой:

q=[n1,n2] =	i	j	k	= -4i+j—k
0	1	0
1	1	-4

П
усть
z₁=2,
то y
= -3

x
+ y
= 5

y
= -3

x
= 8

Точка
А(8, -3, 2) принадлежит прямой. Тогда прямую
можно задать следующим образом:

x
= 8 — 4t

y
= –3 + t

z
= 2 — t

2) Пусть
М(x₀,
y₀,
z₀)
– точка пересечения прямой и плоскости,
тогда:

x₀
=
4(2-t₀),

y₀
=
-3+t₀,

z₀
=
2-t₀,

t₀=6,5
или t₀=
–4,5

Имеем:
M₁(8,
-3, 2) и М₂(-18,
3,5, -4,5).

Ответ:
M₁(8,
-3, 2) и М₂(-18,
3,5, -4,5).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

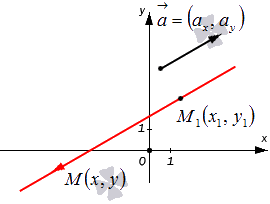
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.

Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x — x 1 , y — y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) являются коллинеарными.

Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:

M 1 M → = λ · a → , где λ – некоторое действительное число.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

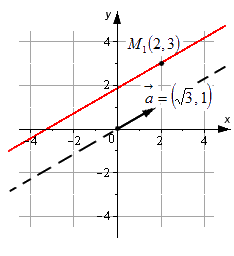
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .

Решение

На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Ответ: x = 2 + 3 · λ y = 3 + λ

Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .

К примеру, нам заданы направляющий вектор прямой a → = ( 2 , — 1 ) , а также точки М 1 ( 1 , — 2 ) и М 2 ( 3 , — 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = — 2 — λ или x = 3 + 2 · λ y = — 3 — λ .

Следует обратить внимание и на такой факт: если a → = ( a x , a y ) — направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = — 2 — 5 · λ . Тогда a → = ( 2 , — 5 ) — направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · — 5 ) = 2 μ , — 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор — 2 · a → = ( — 4 , 10 ) , ему соответствует значение μ = — 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 — 4 · λ y = — 2 + 10 · λ .

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x — x 1 a x = y — y 1 a y .

Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

При этом не должно смущать, если a x или a y будут равны нулю.

Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = — 2 — 4 · λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = — 2 — 4 · λ

Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y ⇔ ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ A x + B y + C = 0

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = — 1 + 2 · λ y = — 3 · λ

Решение

Для начала осуществим переход к каноническому уравнению:

x = — 1 + 2 · λ y = — 3 · λ ⇔ λ = x + 1 2 λ = y — 3 ⇔ x + 1 2 = y — 3

Полученная пропорция идентична равенству — 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: — 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x — x 1 a x = y — y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :

x — x 1 a x = y — y 1 a y = λ ⇔ λ = x — x 1 a x λ = y — y 1 a y

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x — 2 5 = y — 2 2

Решение

Приравняем части известного уравнения к параметру λ : x — 2 5 = y — 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x — 2 5 = y — 2 2 = λ ⇔ λ = x — 2 5 λ = y — 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x — 3 y — 3 = 0 .

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

4 x — 3 y — 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = — 1 3 + 4 · λ

Ответ: x = 3 · λ y = — 1 3 + 4 · λ

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .

Решение

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5

Ответ: 1 1 2 , 5

Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .

Решение

Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:

4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .

Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:

— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4

Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

1. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Пример 8

Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ

Ответ: x = 1 2 + x · λ y = 2 3 — λ .

Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ

Ответ: x = 3 · λ y = — 7 — 2 · λ

1. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Пример 10

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .

Как найти параметрическое уравнение прямой пирамиды

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Пример 1:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти:

1) координаты и модули векторов А₁ А₂и А₁ А₄;  

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) площадь грани А₁ А₂ А₃;         

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂ А₃;

7) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3.

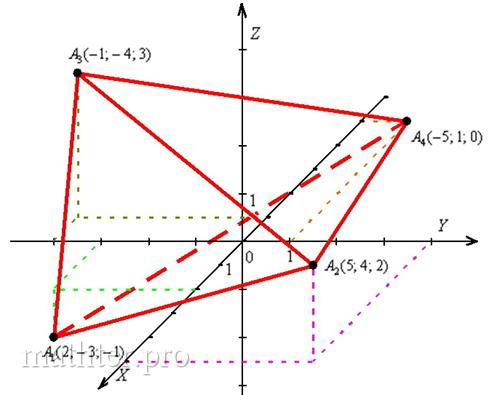
Сделать чертеж.

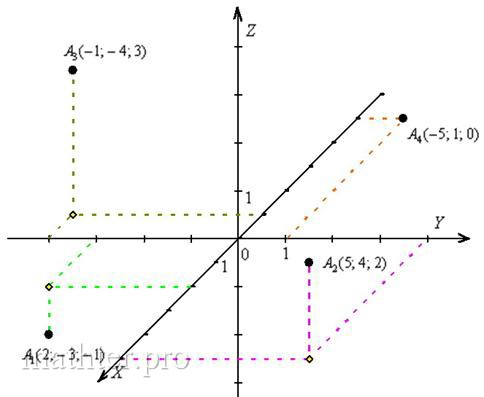
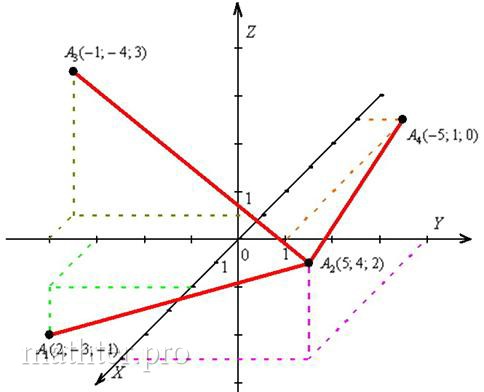
А₁ (0; 4; -4), А₂ (5; 1; -1), А₃ (-1; -1; 3), А₄ (0; -3; 7).

Решение от преподавателя:

Пример 2:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

1. А₁ (7; 7; 3), А₂ (6; 5; 8), А₃ (3; 5; 8), А₄ (8; 4; 1).

Решение от преподавателя:

Пример 3:

Решение от преподавателя:

 Уравнение плоскости. 
Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

(x-3)(1*2-0*3) — (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y — 3z-38 = 0 

Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.267) = 15.486^o 

Уравнение высоты пирамиды через вершину A₄(0,2,2) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 

Уравнение плоскости через вершину A₄(0,2,2) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением: 
A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
2(x-0)+13(y-2)-3(z-2) = 0 
или 
2x+13y-3z-20 = 0

Пример 4:

Решение от преподавателя:

Даны координаты пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 

1. Уравнение плоскости. 
   Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

(x-0)(3*2-8*3) — (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x — 15y + 33z-18 = 0 
Упростим выражение: -6x — 5y + 11z-6 = 0 

2) Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.193) = 11.128^o 

3) Уравнение высоты пирамиды через вершину A₄(0,5,4) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 

4) Уравнение плоскости через вершину A₄(0,5,4) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости

5)  Координаты вектора  A₁A₄(0;4;3) 

Уравнение прямой, проходящей через точку А₁(0,1,1) параллельно вектору А₁А₂(0,4,3) имеет вид:

Пример 5:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Пример 6:

Решение от преподавателя:

1) Даны координаты  вершин пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 
Координаты векторов. 
Координаты векторов:       A₁A₂(3;3;3)        A₁A₄(0;4;3) 

 Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   ,    где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
Найдем угол между ребрами A₁A₂(3;3;3) и A₁A₃(0;4;3): 

А₁ = arccos(0,808)

Найдем площадь грани с учётом геометрического смысла векторного произведения: 
S =
Найдем векторное произведение

=i(3*2-8*3) — j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i — 15j + 33k 

3) Объем пирамиды. 
Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

Координатывекторов:A₁A₂(3;3;3)    A₁A₃(-3;8;2) A₁A₄(0;4;3) :      

Пример 7:

Решение от преподавателя:

1. Угол между ребрами. 
   Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   
   где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   γ = arccos(0) = 90.003⁰ 
2. Площадь грани 
   Площадь грани можно найти по формуле: 
   
   где 
   
   Найдем площадь грани A₁A₂A₃ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   
   Площадь грани A₁A₂A₃ 
3. Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

где определитель матрицы равен: 
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18 

Пример 8:

Даны координаты вершин пирамиды А₁А₂А₃А₄ . Найти:

1) длину ребра А₁А₂;

2) угол между рёбрами А₁А₂  и А₁А₄ ;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

Сделать чертёж.

А₁(3; 5; 4),        А₂(8; 7; 4),            А₃(5; 10; 4),          А₄(4; 7; 8).

Решение от преподавателя:

1) Длина ребра A₁A₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребрами А₁А₄ и гранью А₁А₂А₃;

Найдем уравнение стороны А₁А₄:

Вектор нормали:  к плоскости А₁А₂А₃.

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

Итак: z=4 – уравнение плоскости А₁А₂А₃.

уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

A₄O – высота:

Уравнение A₄O:

Т.к. , то

В результате получаем уравнение высоты:

Пример 9:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя: