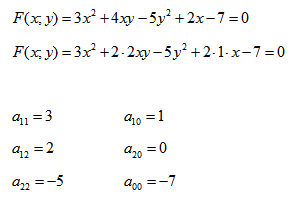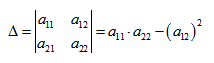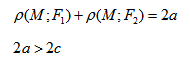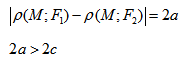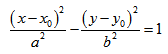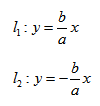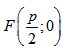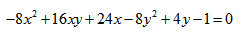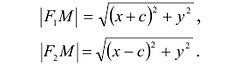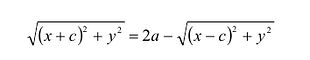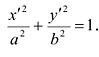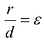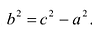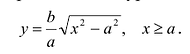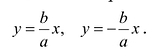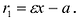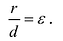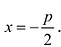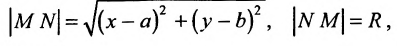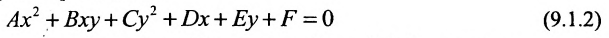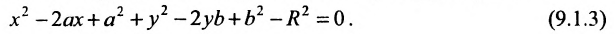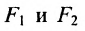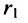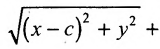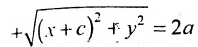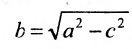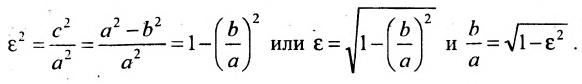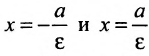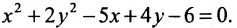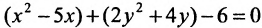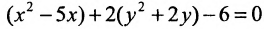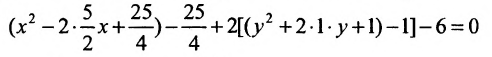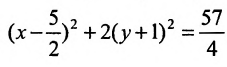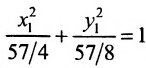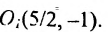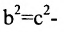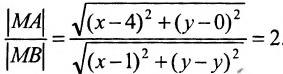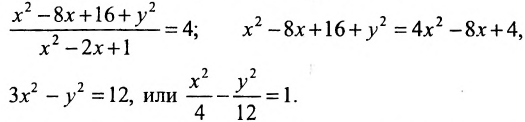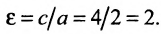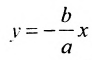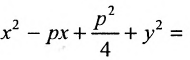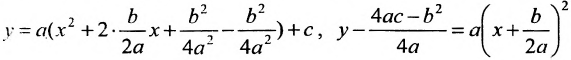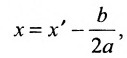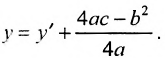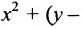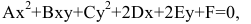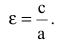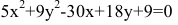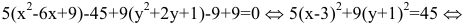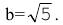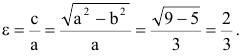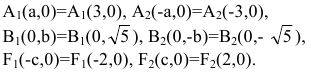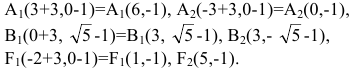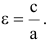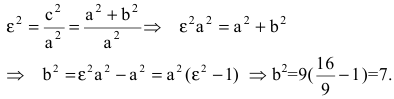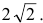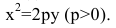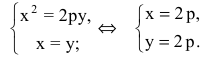Как найти параметры кривой второго порядка

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:  Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули. или можно встретить следующую форму записи: К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.

Покажем на примере определение значений коэффициентов.

Рассмотрим кривую второго порядка: 

Вычислим определитель из коэффициентов:

Если Δ = 0, кривая второго порядка параболического типа,

если Δ > 0, кривая второго порядка эллиптического типа,

если Δ < 0, кривая второго порядка гиперболического типа.

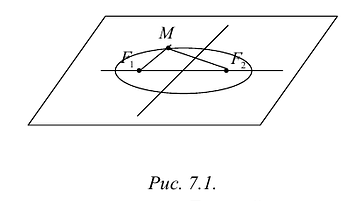
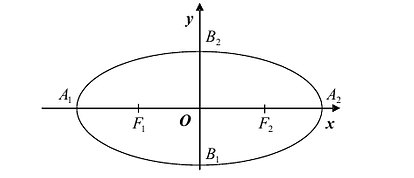
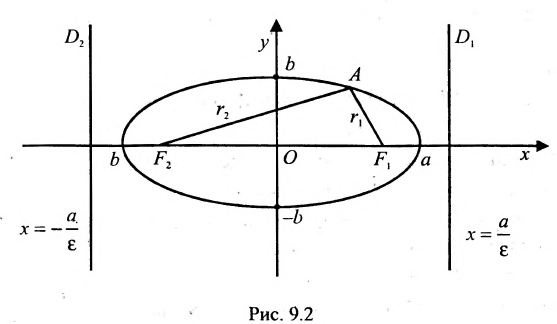
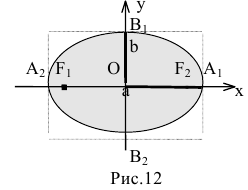
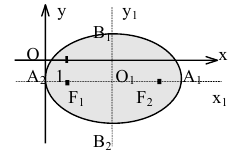
Эллипс — множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F₁ и F₂ есть величина постоянная, большая расстояния между этими точками.

F₁ и F₂ — фокусы.  

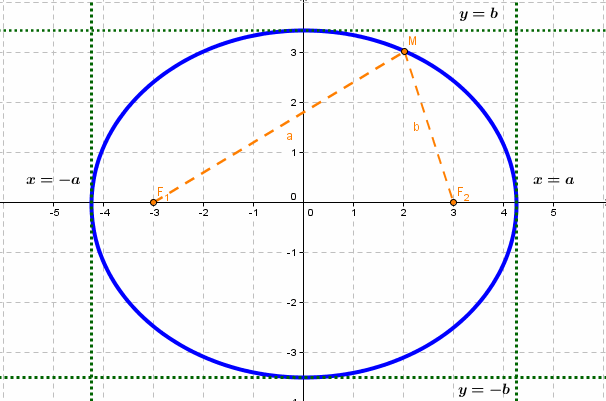с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус.

Каноническое уравнение эллипса с центром симметрии в начале координат:

2а — большая ось эллипса, 2b — малая ось эллипса.

а — большая полуось эллипса, b — малая полуось эллипса.

Если a = b, то имеем окружность с радиусов R = a = b:

Если центр эллипса находится не в начале координат, а в некоторой точке C(x₀;y₀),  оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:

 

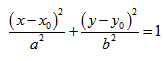
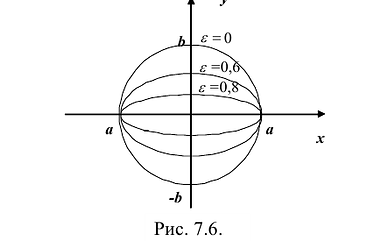
Эксцентриситет — число, равное отношению  фокального расстояния к большей полуоси:

 

Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.

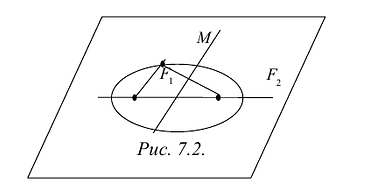
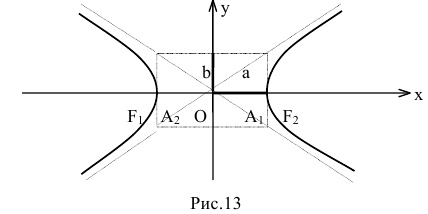
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F₁ и F₂ есть величина постоянная, меньшая расстояния между этими точками.

F₁ и F₂ — фокусы.

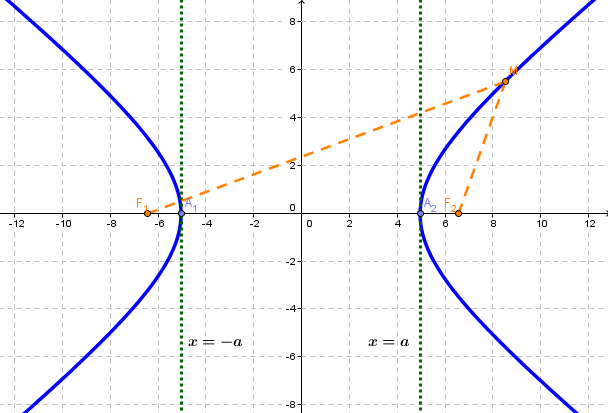с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус. А1(-а;0),  А2(а;0) — вершины.

Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.

Каноническое уравнение гиперболы с центром симметрии в начале координат:

 

x — действительная ось, y — мнимая ось.

а — действительная полуось,   b —  мнимая полуось.

Если центр гиперболы находится в некоторой точке C(x₀;y₀),  оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:

Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.

Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.

Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.

f₁ —  правая директриса,   f₂ —  левая директриса.

Уравнения директрис:

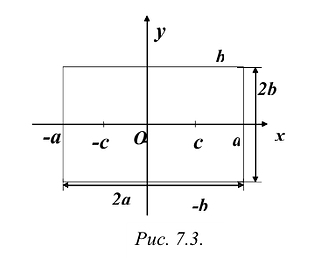
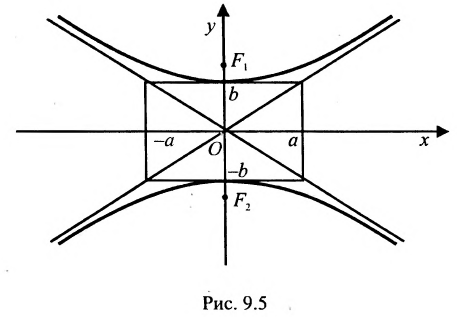
Порядок построения гиперболы:

1. Строим прямоугольник со сторонами 2a и 2b.

2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.

3. Строим гиперболу с вершинами в точках А₁(-а;0),  А₂(а;0).

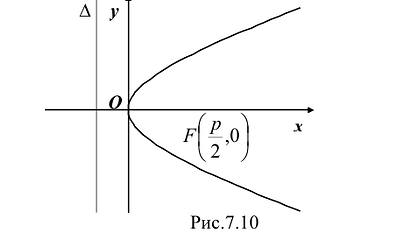
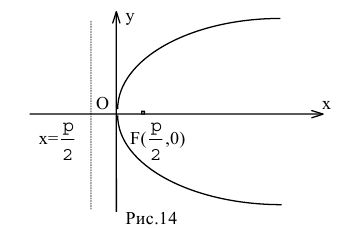
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.

F — фокус параболы, f — директриса параболы. 

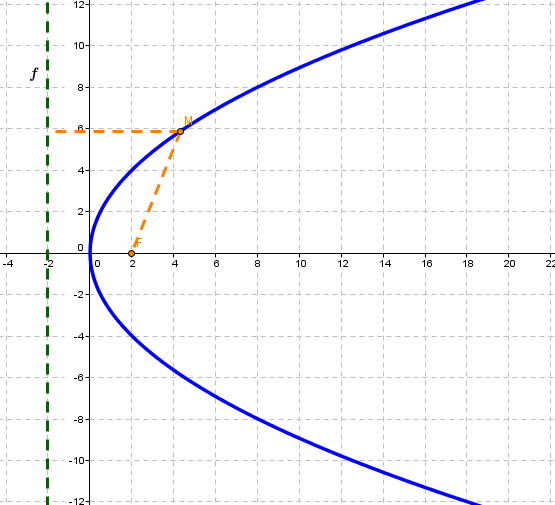р — фокальное расстояние  Фокус параболы: Директриса параболы:

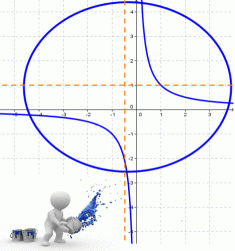
Пример по теме кривые второго порядка №1

Привести к каноническому виду и построить график кривой второго порядка. 

 

Пример по теме кривые второго порядка №2

По виду уравнения определить тип кривой и нарисовать ее в декартовой системе координат:

 

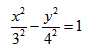
Пример по теме кривые второго порядка №3

Построить кривую второго порядка:

 

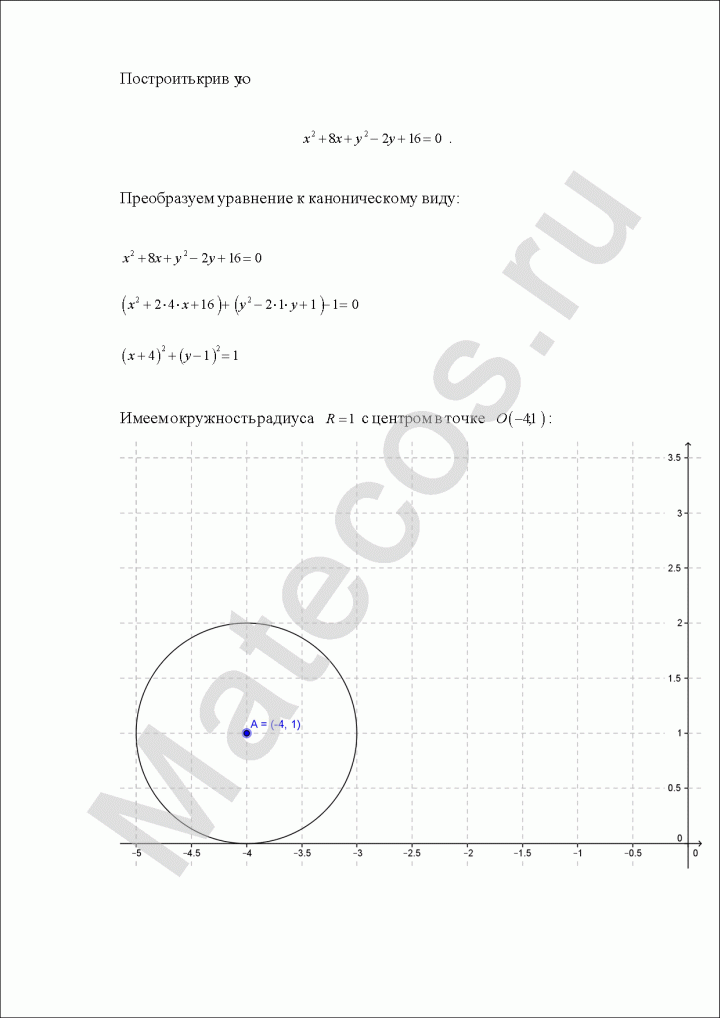
Пример по теме кривые второго порядка №4

Построить кривую второго порядка:

 

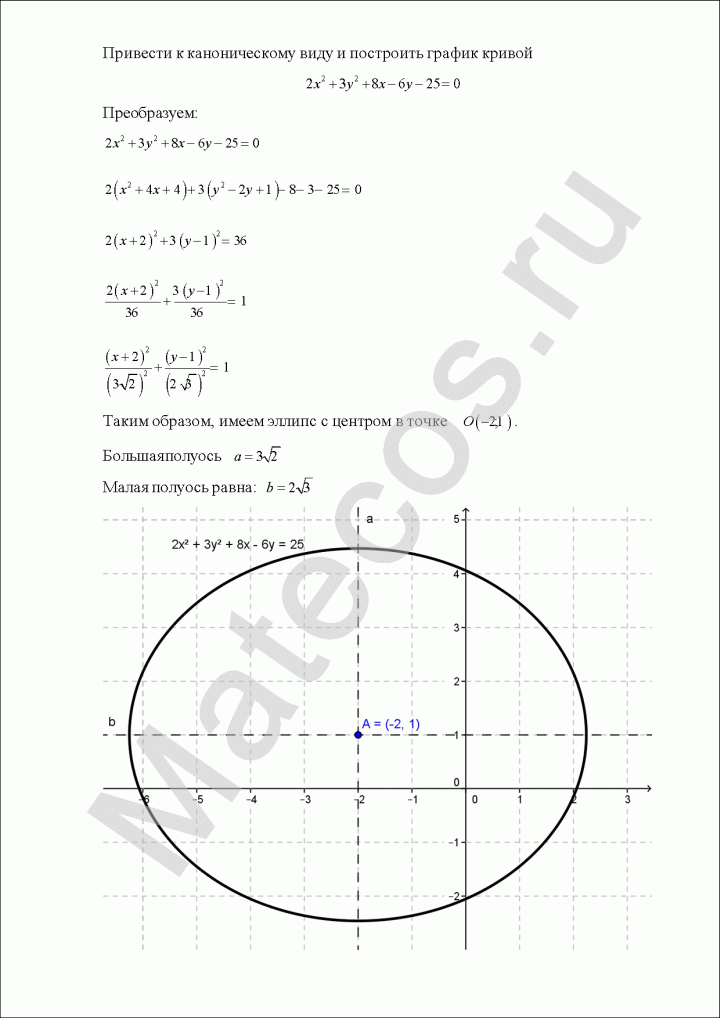
Пример по теме кривые второго порядка №5

Провести заданное уравнение линии второго порядка к каноническому виду и построить ее:

Пример по теме кривые второго порядка №6

Определить центр и радиус окружности:

 

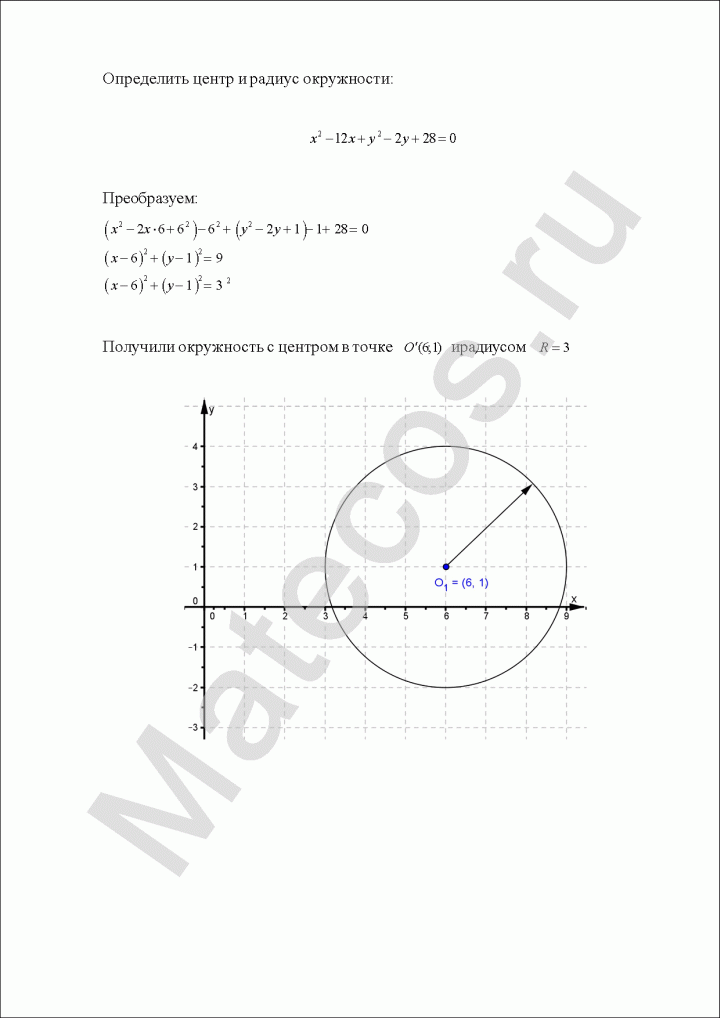
Пример по теме кривые второго порядка №7

Определить центр и полуоси эллипса:

 

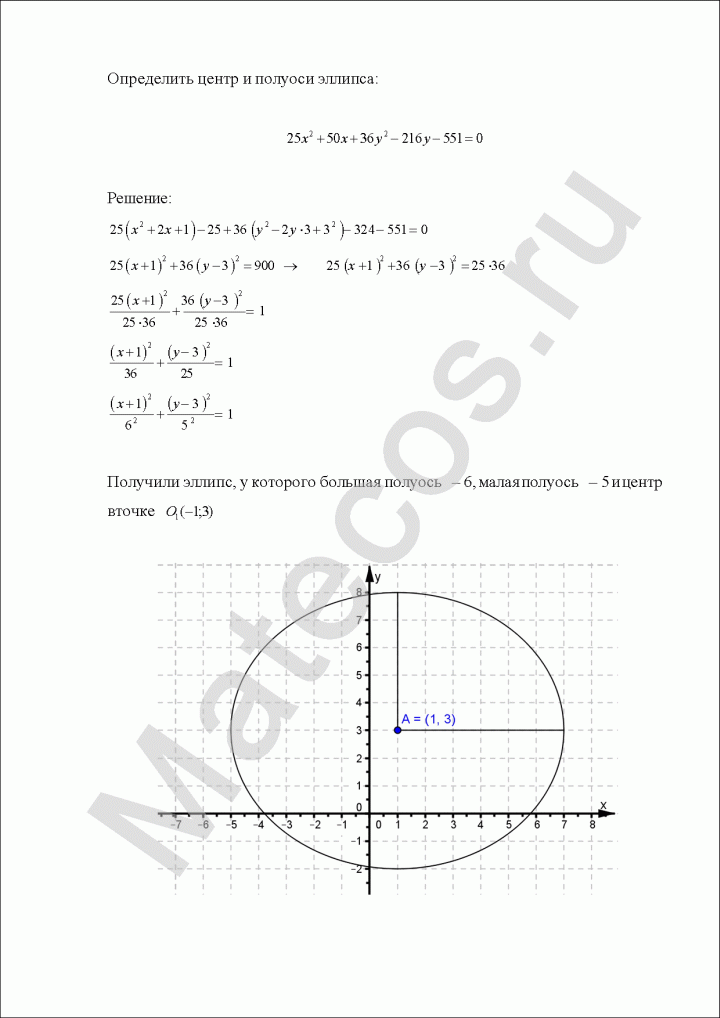
Пример по теме кривые второго порядка №8

Определить центр, полуоси и асимптоты гиперболы:

 

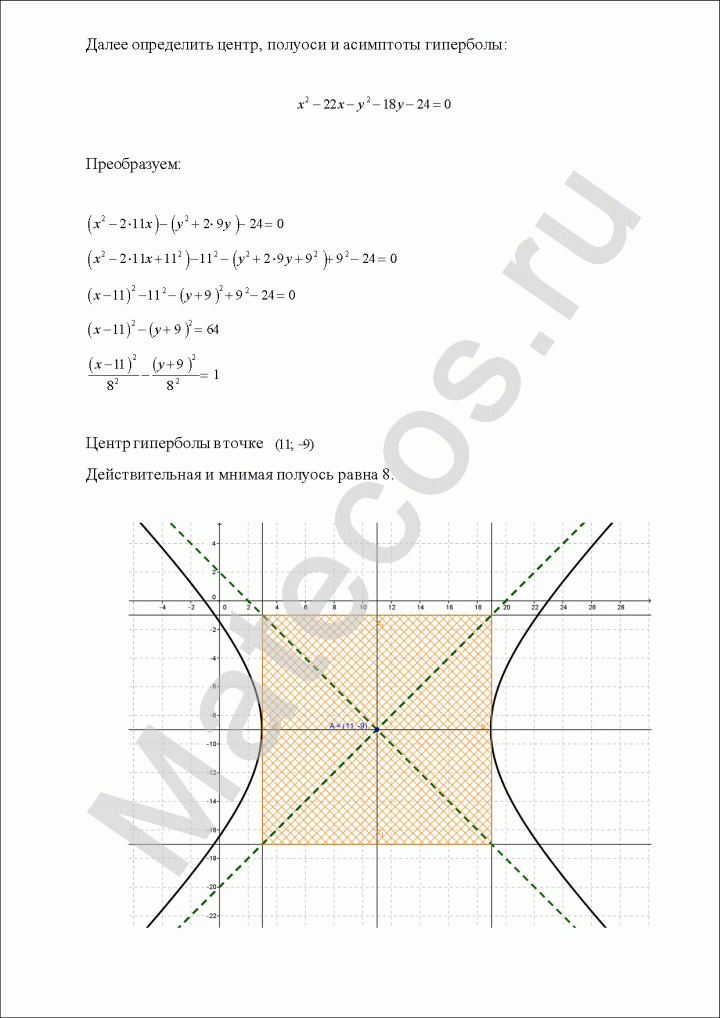
Пример по теме кривые второго порядка №9

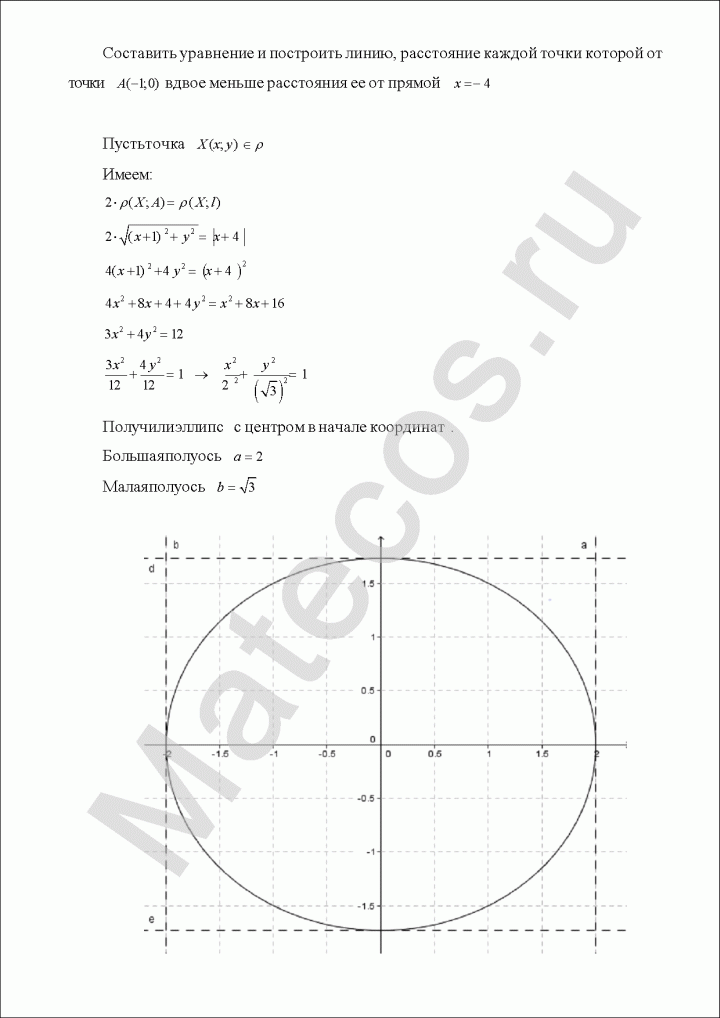
Составить уравнение и построить линию, расстояние каждой точки которой от точки A(-1;0) вдвое меньше расстояния ее от прямой x=-4

Пример по теме кривые второго порядка №10

Определить тип кривой второго порядка:

Пример по теме кривые второго порядка №11

Дана кривая:

Докажите, что эта кривая – эллипс.

Найдите координаты центра симметрии.

Найдите его большую и малую полуоси.

Запишите уравнение фокальной оси.

Постройте данную кривую.

Пример по теме кривые второго порядка №12

Дана кривая:

Доказать, что данная кривая – парабола.

Найти координаты вершины параболы.

Найдите значение ее параметра.

Запишите уравнение оси симметрии параболы.

Постройте данную параболу.

Пример по теме кривые второго порядка №13

Дана кривая:

Докажите, что кривая – гипербола.

Найдите координаты центра симметрии гиперболы.

Найдите действительную и мнимую полуоси гиперболы.

Запишите уравнение фокальной оси гиперболы.

Найдите данную гиперболу.

Пример по теме кривые второго порядка №14

Все графике в этой статье были построены в Geogebra.Подробно о построении графиков функции быстрым и удобным способом читать тут:

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

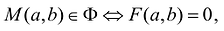
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с<а. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.

Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами и с суммой расстояний от произвольной точки эллипса до фокусов, равной 2 а (Рис. 7.1).

Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы положительное направление оси — от , начало координат выберем в середине отрезка . Тогда координаты точек будут соответственно (-с,0) и (с,0).

Пусть М(х,у) — произвольная точка эллипса, тогда:

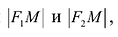
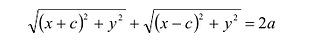
Подставляя сюда значения имеем:

(7.1)

Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим

его:

Возведя обе части уравнения в квадрат и приведя подобные члены, получим:

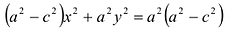
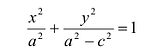
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем или

(7.2)

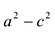
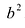
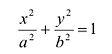
Положительную величину обозначим через. Тогда уравнение (7.2) примет вид:

(7.3)

Оно называется каноническим уравнение эллипса.

Координаты точек эллипса ограничены неравенствами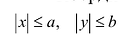. Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами 2а и 2b •

Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки 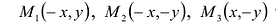также ему принадлежат. А это означает, что эллипс — линия симметричная относительно координатных осей Ох и Оу.

Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:

(7.4)

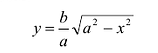
При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.

Рис. 7.4

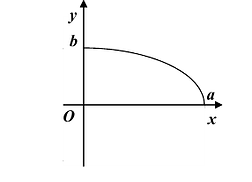
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).

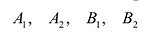
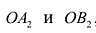
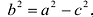
Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии — точка О — центром эллипса. Точки пересечения эллипса с осями координат называются вершинами эллипса. Отрезки , а также их длины а и Ь называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси Ох (как в нашем случае), из равенства следует, что a>b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

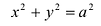
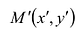
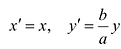
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

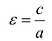
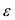
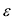
Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

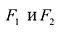
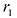
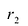
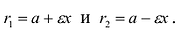
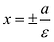
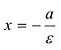
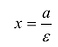
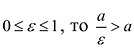
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Гипербола

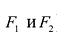
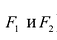
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

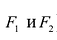
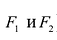
Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а <с.

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 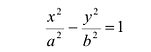(7.6) где ху — координаты произвольной точки гиперболы,

Уравнение (7.6) называется каноническим уравнением гиперболы.

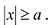
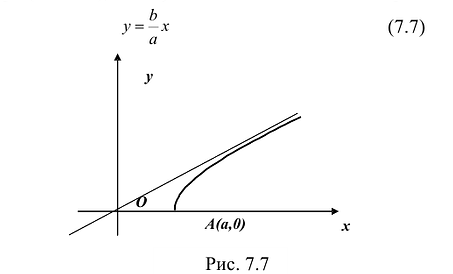
Из уравнения (7.6) видно, что . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми х = -а и х = а.

Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:

График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:

Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты

Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).

Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 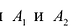, пересечения гиперболы с осью Ох называются вершинами гиперболы. Величины а и Ь называются полуосями гиперболы. Если а=Ь, то гипербола называется равносторонней.

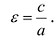
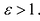
Эксцентриситетом гиперболы называется число. Для любой гиперболы . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси Ох. На рисунке 7.9 изображены гиперболы с различными значениями £.

Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами. Их длины и задаются формулами:

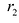
Для правой — ветви ,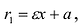

Для левой — ветви

Прямые 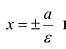называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением

Парабола

Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой 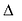(директрисы).

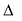
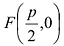
Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом F и точкой D пересечения оси Ох с директрисой . Если обозначить через р расстояние фокуса от директрисы, то и уравнение директрисы будет иметь вид

В выбранной системе координат уравнение параболы имеет вид:

(7.8)

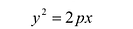
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти .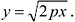

При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10).

Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.

Исследование на плоскости уравнения второй степени

Рассмотрим уравнение:

(7.9)

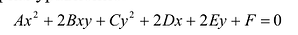
где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) — уравнение второй степени относительно х и у.

Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол

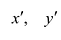
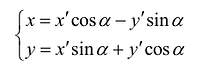
Старые координаты х, у выражаются через новые координаты по формулам:

(7.10)

Подставив выражения для х и у в уравнение (8), получим: 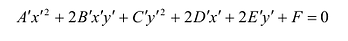(7.11)

Это уравнение в системе координат задает ту же линию, что и уравнение (7. 9) в системе Оху.

Если в уравнении (7.9) , то за счет выбора угла а в (7.10) можно добиться того, что В’ = 0. Для этого угол а надо взять таким, чтобы . Поэтому будем считать В’= 0, тогда уравнение (7.11) примет вид:

(7.12)

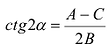
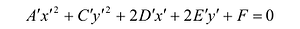
Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:

(7.13)

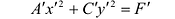
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:

Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.

Кривые второго порядка в высшей математике

Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.

Окружность

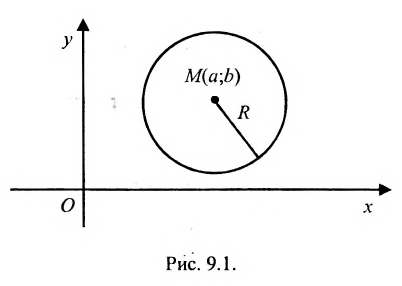
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки — центра окружности.

Если точка 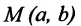— центр (рис.9.1), N(x,y) — произвольная точка окружности и R — её радиус, то согласно определения можно записать

или

Найдём условия, при которых общее уравнение второй степени с двумя переменными

определяет окружность. Раскрыв скобки в (9.1.1), получим

Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,

, при выполнении которых общее уравнение (9.1.2) определяет окружность.

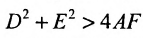
Эллипс

Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.

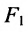
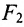
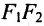
Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами и. Пусть начало координат лежит на середине отрезка . Выведем уравнение эллипса.

Если точка А — произвольная точка эллипса с координатами (х, у), то

(9.2.1)

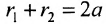
где 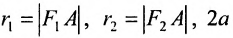— постоянная сумма. Так как

расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 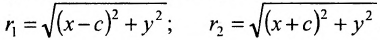. Подстави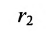в значения

и в (9.2.1), получаем уравнение

Обе части этого уравнения возведем в квад-Упростив и обозначив

получим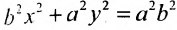. Разделим обе части уравнения на правую часть

Уравнение (9.2.2) называется каноническим уравнением эллипса, где а — большая полуось, b — малая полуось.

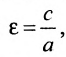
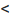
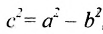
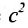
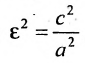
Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет , т.е. отношение расстояния между фокусами этого эллипса к длине его большей полуоси. Так как са, то эксцентриситет каждого эллипса меньше единицы. Поскольку

, то подставив значение в равенство, получим

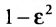
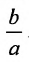
Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше , тем меньше, следовательно, отношение . Это значит, что эллипс вытянут вдоль оси Ох. В случае Ь=а и получаем окружность.

Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 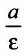от него, называются директрисами эллипса. Уравнения директрис

Пример:

Исследовать, какая линия определяется уравнением

Решение:

Сгруппируем члены, содержащие одну и туже переменную, получим

Из второй скобки вынесем коэффициент при 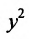, после чего предыдущее уравнение примет вид

В каждой из скобок выделим полный квадрат

или

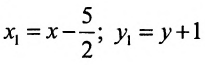
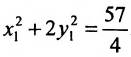
Произведём замену: . Исследуемое уравнение принимает вид: .

Разделив обе части этого уравнения на 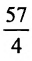, получим канонический вид данного уравнения:

Заданное уравнение определяет эллипс с полуосями 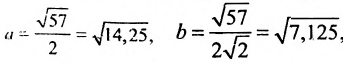, центр которого находится в точке

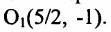
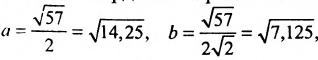
Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку . В новой системе координат строим основной прямоугольник со сторонами , стороны которого параллельны новым осям координат, а центр находится в точке . Вписываем в него эллипс.

Гипербола

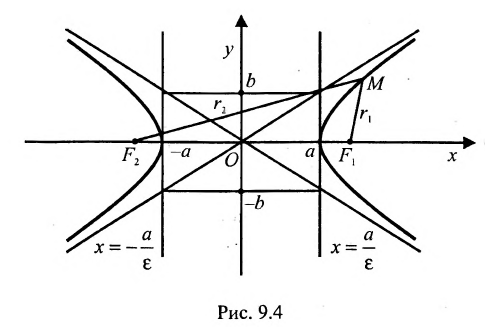
Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению).

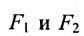
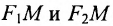
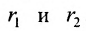
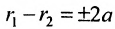
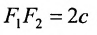
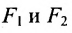
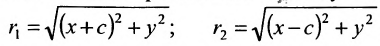
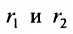
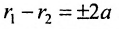
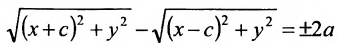
Пусть М- произвольная точка гиперболы с фокусами (рис. 9.4). Отрезки называются фокальными радиусами точки М и обозначаются По определению гиперболы . Так как и т.к. расположены симметрично относительно начала координат, то, применяя формулу для вычисления расстояния между двумя точками, находим . Заменяя в равенстве найденными выражениями, получаем:

.

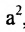
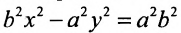
Возведя в квадрат обе части этого уравнения и обозначая , получим: или, разделив все члены уравнения на правую часть, приводим его к виду:

Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.

Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 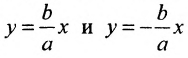. Поэтому, если требуется построить гиперболу с полуосями а и b, то следует, прежде всего, построить ее основной прямоугольник, затем асимптоты.

Уравнение вида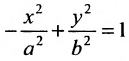 определяет гиперболу, вершины которой расположены на оси Оу (Рис. 9.5).

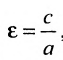
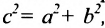
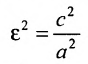
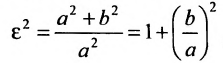
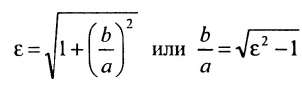
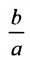
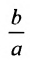
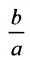
Форму гиперболы характеризует её эксцентриситет , т.е. отношение расстояния между фокусами этой гиперболы к расстоянию между её вершинами. Поскольку , то подставив в формулу получимоткуда. Следовательно, эксцентриситет oредсляется отношением , а отношение — эксцентриситетом. Следовательно, эксцентриситет характеризует форму гиперболы. Чем меньше эксцентриситет, тем меньше отношение , а это значит, что основной прямоугольник вытянут в направлении оси, соединяющей вершины.

Прямые, заданные уравнениями 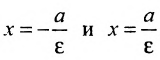называются директрисами гиперболы.

Пример:

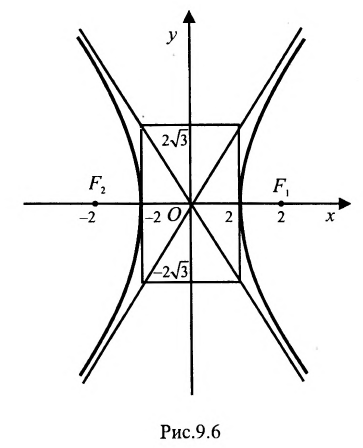
Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.

Решение:

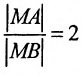
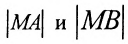
В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) — произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи .Подставив значения расстояний, которые находим по формуле расстояния между двумя точками, получим:

Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:

Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая .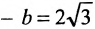

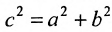
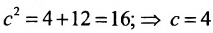
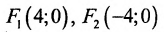
Определим фокусы гиперболы. Для гиперболы выполняется равенство . Следовательно, .А — фокусы гиперболы. Как видно, заданная точка

А(4, 0) является правым фокусом гиперболы.

Эксцентриситет полученной гиперболы равен

Подставив значения а и b в уравнения асимптот 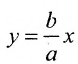и

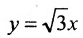
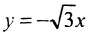
у =—получим уравнения асимптот гиперболы:и .

Для построения гиперболы строим основной прямоугольник с полуосями 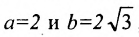, затеем асимптоты и а далее строим и саму гиперболу (рис.9.6).

• Заказать решение задач по высшей математике

Парабола

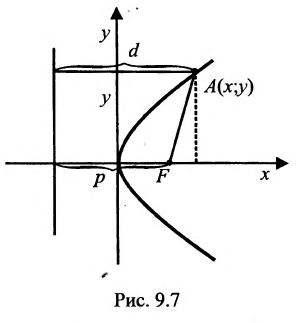
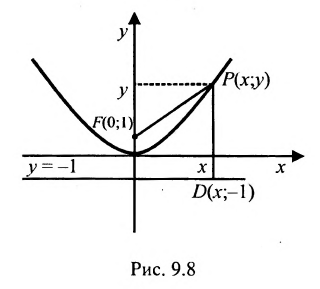
Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).

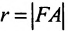
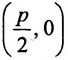
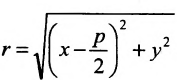
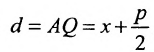
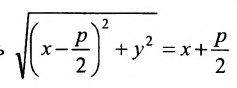
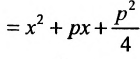
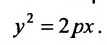
Обозначим фокус параболы — F, расстояние от фокуса до директрисы — р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 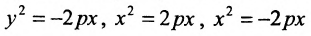также определяют параболы.

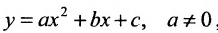
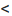
Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

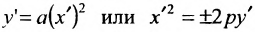
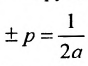
В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

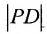
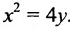
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.

Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и

Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.

Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.

Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

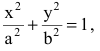
Число а называют большей полуосью эллипса, число 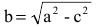— мень-

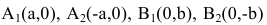
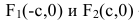
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид 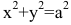и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы 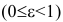и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

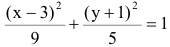
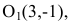
Найдем эксцентриситет эллипса:

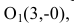
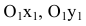
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты 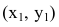вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением гиперболы.

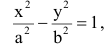
Число а называют действительной полуосью гиперболы, число

— мнимой полуосью гиперболы, 2а и 2b — соответственно действительной и мнимой осями гиперболы. Точки называют вершинами гиперболы, — ее фокусами (рис. 13).

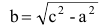
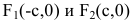
Координатные оси являются осями симметрии гиперболы, а начало координат — ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.

Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 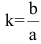), которые называются асимптотами гиперболы.

Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси:

Эксцентриситет гиперболы изменяется от единицы до бесконечности 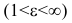и характеризует форму гиперболы. Чем меньше эксцентриситет гиперболы, тем ее ветви более сжаты к оси Ох.

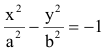
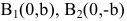
Замечание. Каноническое уравнение определяет сопряженную гиперболу с действительной полуосью b, вершинами в точках и фокусами на оси Оу.

Пример:

Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.

Решение:

Каноническое уравнение гиперболы имеет вид

По условию задачи нам известно: а=3, Найдем мнимую полуось.

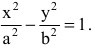
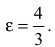
Следовательно, уравнение искомой гиперболы:

Задача решена.

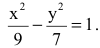
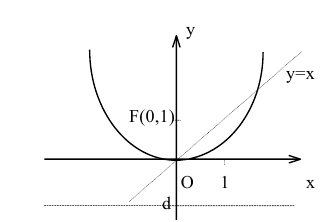
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 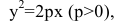которое называется каноническим уравнением параболы.

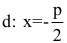
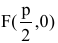
Точка O(0,0) называется вершиной параболы, число р — параметром параболы, — директрисой пир,болы, а — ее фокусом. Прямая у=0 является осью симметрии параболы, ветви которой направлены вправо. Центра симметрии у параболы нет (рис. 14).

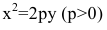
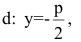
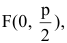
Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид (уравнение параболы с вертикальной осью, уравнением директрисы фокусом ветви направлены вверх).

Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:

Пример:

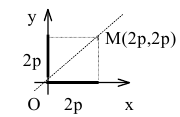
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной

Решение:

Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:

Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений

Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной 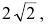который является гипотенузой равнобедренного прямоугольного треугольника с катетами 2р.

По теореме Пифагора

Тогда искомое уравнение параболы

Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).

Задача решена.

Примеры решений: кривые второго порядка

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.

См. также: Решения по аналитической геометрии на плоскости,
Решения задач с квадратичными формами

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

$$9x^2-4y^2-90x-8y+185=0.$$

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

$$6x^2+2sqrt{5}xy+2y^2=21.$$

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

$$3x^2-6y^2-12x-108y-492=0.$$

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

$$9x^2+25y^2-18x-100y-116=0.$$

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

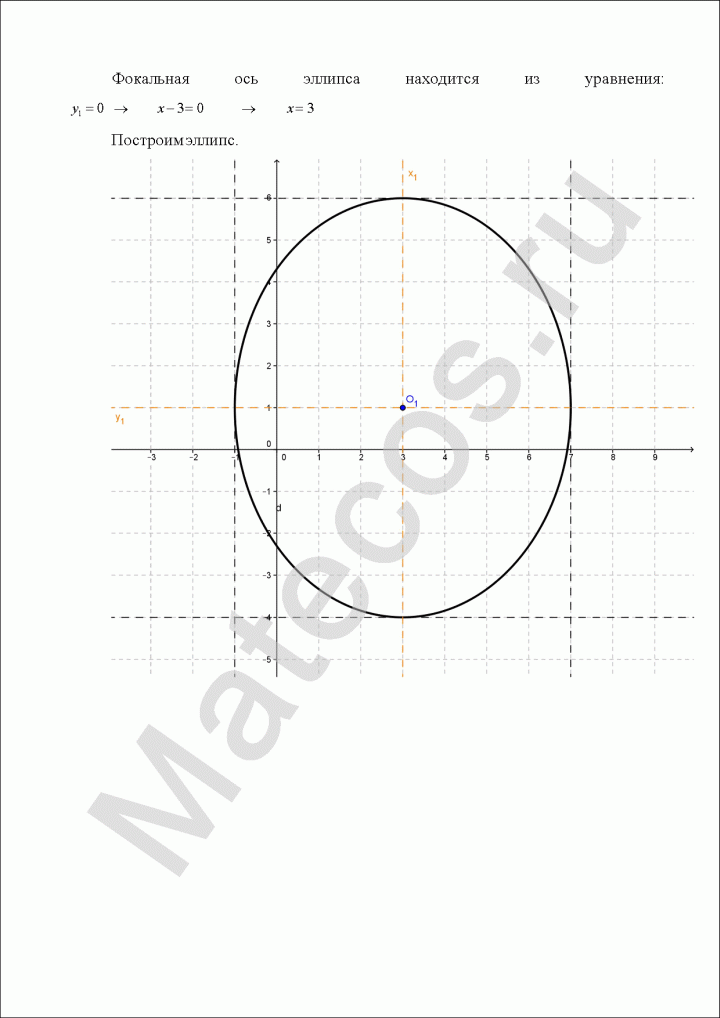
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt{2/5}$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.

Содержание:

1. Кривые второго порядка и их нахождение и решение
2. Окружность
3. Эллипс
4. Гипербола
5. Парабола
6. Общее уравнение второго порядка с двумя переменными
7. Кривые второго порядка
8. Окружность и его уравнения
9. Эллипс и его уравнения
10. Гипербола и ее уравнение
11. Асимптоты гиперболы
12. Парабола и ее уравнение
13. Линии второго порядка. Общее уравнение линии второго порядка
14. Окружность и ее уравнение
15. Каноническое уравнение эллипса. Эксцентриситет
16. Каноническое уравнение гиперболы. Асимптоты. Эксцентриситет
17. Каноническое уравнение параболы
18. Кривые линии второго порядка
19. Круг 
20. Эллипс 
21. Гипербола 
22. Парабола
23. Общее уравнение кривой второго порядка: типы кривых
24. Канонические уравнения окружности и эллипса
25. Каноническое уравнение гиперболы. Асимптоты гиперболы
26. Парабола. Каноническое уравнение
27. Возведение общего уравнения кривой второго порядка к каноническому виду
28. Квадратичные формы. Применение к превращению уравнений кривой 2-го порядка

Кривые второго порядка и их нахождение и решение

Кривые, которые получаются при пересечении круговой конической поверхности плоскостью называются конечными поверхностями или кониками. К ним относятся такие кривые как окружность, эллипс, гипербола, парабола.

Действительно:

— Если плоскость пересекает коническую поверхность перпендикулярно оси вращения, то в пересечении образуется окружность, если плоскость проходит через вершину конуса, то в пересечении образуется точка, то есть вырожденная окружность (рис. 1).

— Если плоскость пересекает только одну часть конической поверхности и не параллельна ни одной образующей, тогда в пересечении будет эллипс (рис. 2).

— Если плоскость пересекает одну часть конической поверхности и параллельна одной образующей, тогда в пересечении будет парабола (рис. 3а), если плоскость проходит через вершину и одну из образующих, тогда в пересечении будет прямая, то есть вырожденная парабола (рис. 3б).

— Если плоскость пересекает две части конической поверхности и параллельна оси конической поверхности, то в пересечении будет гипербола (рис. 4а), если секущая плоскость проходит через вершину конуса и пересекает две его части, то в пересечении будет пара прямых, которые пересекаются, то есть вырожденная гипербола (рис. 4б).

Рассмотрим каждую из этих кривых.

Окружность

Окружностью называется множество точек плоскости, равноудалённых от данной точки, которая называется центром. Если точка С — цент окружности, R — её радиус, М — произвольная точка окружности, то по определению окружности

Данное равенство является уравнением окружности радиуса R с центром в точке С.

Пусть на плоскости задана прямоугольная декартовая система координат (рис. 5) и точка  центр окружности радиуса R. Пусть М(х, у) — произвольная точка этой окружности. Поскольку , то уравнение окружности можно записать 

Данное уравнение называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке 

Например, уравнение 

является уравнением окружности радиуса R=5, с центром в точке (1; -3).

Если центр окружности совпадает с началом координат, то уравнение окружности принимает вид:

Данное уравнение называют каноническим уравнением окружности.

Пример 1. Составить уравнение окружности радиуса R=9 с центром в точке C(3; -6).

Решение: 

Подставив значения координат точки С и значение радиуса в уравнение окружности, получаем , или

Пример 2. Доказать, что уравнение  является уравнением окружности. Найти её центр и радиус.

Решение: 

Преобразуем левую часть заданного уравнения

Это уравнение является уравнением окружности с центром в точке (-2; 1), радиус окружности равен 3.

Эллипс

Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же самой плоскости постоянна и больше чем расстояние между этими точками.

Такие точки называются фокусами эллипса, а расстояние между ними фокальным расстоянием. Покажем, как, исходя из определения эллипса, можно разбить эллиптическую клумбу. Забьём в землю два колышка (рис. 6) потом нитку свяжем в кольцо и натянем это кольцо на оба колышка. Натянув нитку третьим колышком, чертим эллипс. Изменив расстояние между колышками и длину нитки, получаем эллипсы разных размеров и форм.

Обозначим фокусы эллипса буквами  Путь фокальное расстояние . Если М — произвольная точка эллипса (рис. 7), то по определению эллипса сумма  является величиной постоянной. Обозначив её через , получаем

Заметим, что по определению эллипса  то есть  Предыдущее равенство является уравнением эллипса. Если точка  совпадает с точкой  то уравнение эллипса приобретает вид

Это уравнение является уравнением окружности радиуса  с центром в точке . Таким образом, окружность является отдельным случаем эллипса.

Выберем систему координат так, чтобы ось абсцисс проходила через фокусы эллипса, ось ординат через середину отрезка  и перпендикулярна ему.

Тогда фокусами будут точки  любая точка эллипса, тогда

подставляя найденные значения  в уравнении эллипса, получаем

Сведём данное уравнение до простейшего вида. Для этого перенесём второе слагаемое в правую часть и возведём обе части в квадрат

после упрощений получаем

Возведя обе части в квадрат получаем

по определению эллипса  поэтому  положительное число. Обозначим его через , то есть . Тогда уравнение приобретает вид

Разделив обе части равенства на  получим

Это уравнение называется каноническим уравнением эллипса.

Если  то есть  то уравнение эллипса приобретает вид

что вычисляет уравнение окружности.

Пример 1. Составить каноническое уравнение эллипса, который проходит через точку М(5;0), если фокальное расстояние равно 6.

Решение:

Поскольку фокальное расстояние равняется 6, то с=3. Запишем уравнение эллипса

По условию задачи точка М(5; 0) принадлежит эллипсу, следовательно

отсюда  Найдём 

Следовательно, искомым уравнением эллипса является уравнение 

Пример 2. Доказать, что уравнение  является уравнением эллипса, найти координаты фокусов и фокальное расстояние.

Решение:

Разделив обе части уравнений на 3600, получаем

это является уравнением эллипса.

Из уравнение  следует, что  Поскольку  отсюда с=8. Фокусы эллипса находятся в точках  и . Фокальное расстояние

Исследуем эллипс по его уравнению.

1. Эллипс не проходит через начало системы координат, так как координаты точки О(0; 0) не удовлетворяют уравнение.

2. Эллипс пересекает каждую из осе координат в двух точках.

Чтобы вычислить координаты точек пересечения эллипса с осью Ох, необходимо решить уравнение , и  у=0, получим 

Следовательно, точками пересечения эллипса с осью Ох будут 

Аналогично находим точки пересечения с осью Оу: 

Точки А, В, С, D называют вершинами эллипса.

Отрезок АВ называется большой осью эллипса, отрезок ВD  — малой осью. Фокусы эллипса   и  лежат на большой оси. Длина большой оси равняется , малой оси . Числа  и  называются полуосями эллипса.

3. Эллипс имеет две взаимно перпендикулярные оси симметрии, а также центр симметрии.

Это легко показать, так как неизвестные в уравнение входят только во второй степени. Центр симметрии эллипса называется центром эллипса.

4. Эллипс можно получить равномерным сжиманием окружности.

Рассмотрим окружность радиуса  с центром в начале координат. Пусть  произвольная точка окружности (рис. 9).

Тогда . Точки  на окружности поставим поставим в соответствие точку  такую, чтобы  и . Точки  найдём благодаря сдвигу точки , при котором абсцисса не меняется, а ордината уменьшается в отношении. Координаты точки  удовлетворяют уравнение эллипса

Следовательно,  находится на эллипсе.

Таким образом, эллипс можно достать с окружности равномерным сжатием до оси Ох, при котором, ордината точек уменьшается в том самом соотношении . Отсюда вытекает, что форма эллипса зависит от значения . Чем меньше это соотношение, тем более сжатым будет эллипс, и, наоборот, чем больше соотношение , тем эллипс будет более округлым. Если значение  наибольшее, то есть =1, то эллипс превращается в окружность. Для характеристики формы эллипса целесообразно пользоваться не соотношением , а соотношением . Соотношение полу-фокусного расстояния с к большой полуоси  называется эксцентриситетом эллипса. Его обозначают буквой е.

Поскольку , то эксцентриситет эллипса удовлетворяет неравенство . Отсюда 

Пример. Дано два эллипса . Сравнить их форму.

Решение:

Перепишем уравнение эллипсов в виде . Для первого эллипса  соответственно  Для второго эллипса , соответственно . В данном случаи , соответственно второй эллипс сжатый до большой оси больше чем первый.

Гипербола

Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний к двум данным точкам плоскости постоянный и меньший чем расстояние между этими точками.

Такие точки называются фокусами гиперболы, а расстояние между ними — фокальным расстоянием.

Обозначим фокусы гиперболы буквами  Пусть фокальное расстояние 

Если М — произвольная точка гиперболы (рис. 10), то по определению гиперболы модуль разности  постоянный. Обозначив его как , получаем

Отметим, что по определениям гиперболы , то есть 

Данное равенство является уравнением гиперболы. Выберем систему координат так, чтобы ось абсцисс проходила через фокус гиперболы; ось ординат проходила через середину отрезка  перпендикулярно ему. Тогда фокусами гиперболы будут точки и 

Пусть  любая точка гиперболы, тогда

 и

Подставляя значения  и  в уравнение получим

Это уравнение является гиперболой в выбранной системе координат. Его можно привести к более простому виду.

Пусть , тогда уравнение можно записать без знака модуля:

Возведём обе части уравнения в квадрат

По определению гиперболы  поэтому  положительное число. Обозначим его , то есть положим , тогда уравнение приобретает вид

Разделив почленно на , получим уравнение

Если , тогда уравнение записывают без знака модуля

и также, как при , сводится к конечному виду.

Уравнение  называется каноническим уравнением гиперболы.

Пример 1. Записать каноническое уравнение гиперболы, которая проходит через точку , если фокальное расстояние гиперболы равняется 10.

Решение. Поскольку  то с=5. Запишем каноническое решение уравнения гиперболы

По условию точка принадлежит гиперболе, следовательно:

Из второго уравнения получим соотношение для вычисления

Решим систему:

найдём  Искомым уравнением является уравнение 

Пример 2. Доказать, что уравнение

является уравнением гиперболы. Найти координаты фокусов.

Решение: Разделив обе части уравнения на 580, получим

Это является уравнением гиперболы, для которой . Из соотношения  находим  Следовательно, фокусы гиперболы находятся в точках 

Исследуем гиперболу по её уравнениям.

Рассмотрим гиперболу, заданную в некоторой прямоугольной декартовой системе координат своим каноническим уравнением

Приведём такие свойства гиперболы:

1. Гипербола не имеет общих точек с осью Оу, а ось Ох пересекает в двух точках.

Чтобы вычислить координаты точек пересечения гиперболы с осью Оу, необходимо решить совместно их уравнения

Подставляя х=0 в уравнение гиперболы, получим , а это означает, что система не имеет решения. Следовательно, гипербола не пересекает ось ординат.

Чтобы вычислить координаты точек пересечения с осью Ох, необходимо решить совместно их уравнения

Точка пересечения гиперболы с осью Ох должна иметь ординату у=0 и, кроме того, должна принадлежать гиперболе. Подставив у=0 в уравнение гиперболы, получим

Следовательно, точками пересечения гиперболы с осью Ох будут точки  и ; они называются вершинами гиперболы.

Отрезок АВ называется действительной осью гиперболы. Длина отрезка АВ, очевидно, равна . Число  называют действительной полуосью гиперболы, число b — мнимой полуосью.

2. Гипербола имеет две взаимно перпендикулярные оси симметрии.

В уравнение переменные х и у входят только во второй степени. Таким образом, если координаты точки N(x; y) удовлетворяют уравнение, то это же уравнение будут удовлетворять и координаты точек  и 

Легко увидеть, что точка  симметрична точке N относительно оси ординат, точка N₂ симметрична точке N относительно оси абсцисс. Таким образом, гипербола имеет две оси симметрии, они взаимно перпендикулярны.

3. Гипербола имеет центр симметрии.

Если координаты точки N(x; y) удовлетворяют уравнение гиперболы, то это же уравнение удовлетворяют и координаты  Точка К, очевидно, симметрична точке N относительно начала координат. Таким образом, гипербола имеет центр симметрии.

Центр симметрии гиперболы называется центром гиперболы.

4. Гипербола пересекается с прямой  в двух точках. Если  то общих точек у гиперболы и прямой нет.

Чтобы вычислить координаты точек пересечения гиперболы и прямой у=kх, необходимо решить систему уравнений

При , то есть при  полученное уравнение, а потому и система решений не имеют. Следовательно, прямые, которые проходят через начало координат с угловым коэффициентом,  модуль которого больше или равен  не пересекают гиперболу. Прямые, уравнения которых имеют вид , называются асимптотами гиперболы.

При  то есть при  система имеет два решения:

Таким образом, каждая прямая, которая проходит через начало координат с угловым коэффициентом, модуль которой меньше чем  пересекает гиперболу в двух точках. При k=0 из формул получаем  то есть прямая у=0 пересекает гиперболу в её вершинах.

Поскольку гипербола симметрична относительно осей координат, то достаточно выучить её формулу в первом квадранте координатной плоскости. По формулам

имеем, что из возрастания k от  (при этом прямая у=kх поворачивается против часовой стрелки) и абсциссы, и ординаты точек пересечения прямой с гиперболой возрастают. Прямая у=kх пересекает гиперболу в более отдалённых от начала координат точках. Следовательно, гипербола имеет вид, изображённый на рис. 11. Она составляется из двух не связанных между собой частей, которые называются её ветками.

Как уже видели (рис. 11), ветка гиперболы размещена выше от асимптоты  и ниже от асимптоты . Поэтому соотношения  полуосей гиперболы определяют её формулу. Чем меньше это соотношение, тем сильнее гипербола сжата до оси Ох.

Как и в случаи эллипса, для характеристики формулы гиперболы целесообразно пользоваться не соотношением , а соотношением .

Соотношение полуфокусного расстояния с к действительной полуоси  называется эксцентриситетом гиперболы. Эксцентриситет обозначают буквой е. Следовательно,

Поскольку для гиперболы , то эксцентриситет гиперболы удовлетворяет неравенству .

Выразим эксцентриситет гиперболы через соотношение  её полуосей:

то есть: 

Согласно формуле, меньшим значением соотношения  соответствуют меньшие значения эксцентриситету. Таким образом, чем меньше эксцентриситет гиперболы, тем сильнее сжата она к оси абсцисс.

Гипербола называется равносторонней (или равнобокой), если длины её полуосей равны между собой. Поскольку для равносторонней гиперболы  то её уравнение имеет вид:

Асимптотами равносторонней гиперболы являются прямые у=х и у= -х. Следовательно, асимптоты равносторонней гиперболы взаимно перпендикулярны.

Эксцентриситет равносторонней гиперболы:

Пример 3. Даны фокусы гиперболы  и  и её асимптоту 4х+3у=0. Найти уравнение гиперболы.

Решение. 

Записав уравнение асимптоты в виде , найдём соотношение полуосей гиперболы 

Из условия задачи вытекает, что с=10. Поэтому  Задача сводится к решению уравнений

Подставив  во второе уравнение системы, получим

откуда  Теперь находим  Следовательно, гипербола имеет уравнение 

Парабола

Параболой называется множество точек на плоскости, для каждой из которых расстояние до данной точки равно расстоянию до данной прямой, которая не проходит через данную точку.

Такая точка называется фокусом параболы, а прямая — директрисой (направляющей). Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается как р.

Выберем систему координат таким образом, чтобы ось Ох была проведена через фокус F перпендикулярно к директрисе. Точка пересечения оси абсцисс с директрисой обозначим D (рис. 12), за начало координат О возьмём середину отрезка DF, за положительное направление оси Ох — направление луча OF/

В этой системе координат фокус F имеет координаты , а уравнением директрисы является уравнение

 

Пусть М(х; у) — любая искомая точка искомого множества. Опустим из точки М перпендикуляр на директрису, и пусть N — основа этого перпендикуляра. Тогда |MN| является расстоянием от точки М до директрисы и, следовательно, 

Это уравнение является уравнением параболы в выбранной системе координат. Его можно упростить. В следствии того, что обе части уравнения неотъемлемые, то уравнение

равносильно предыдущему уравнению. В результате преобразований получим уравнение

Оно называется каноническим уравнением параболы.

Приведём такие свойства параболы:

1. Парабола имеет ось симметрии.

Переменная у входит в уравнение только во второй степени. Поэтому, если координаты точки М₁(х; у) удовлетворяют уравнение параболы, то и его координаты N₂ (х; -у) будут удовлетворять его. Точка N₁ симметрична точке N₂ относительно оси Ох. Следовательно, ось Ох является симметрией параболы. Ось симметрии параболы называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Вершина параболы находится в начале координат.

2. Парабола расположена в полуплоскости 

Правда, поскольку параметр р положительный, то уравнения могут удовлетворять только точки с неотрицательными абсциссами, то есть точки полуплоскости 

3. Парабола является объединением графиков функций

Чтобы убедиться в этом, достаточно решить уравнение относительно переменной у.

Пример 1. Световой луч у=-2 падает на зеркало, осевым сечением которого является парабола у²=24х (рис. 14). Найти уравнение прямой, которой принадлежит отражённый луч.

Решение.

Если падающий луч параллельный главной оптической оси параболического зеркала, то отражённый луч проходит через его фокус. В этом случаи ось параболического зеркала совпадает с осью Ох. Прямая у=-2 параллельна оси абсцисс, и поэтому отражённый луч пройдёт через фокус параболы у²=24х. Поскольку 2р=24, то есть , то фокусом параболы является точка F(6; 0).

Чтобы найти точки падения светового луча, необходимо решить систему уравнений

Решив эту систему, найдём точку падения луча .

Отражённый луч принадлежит прямой, которая проходит через точки  и .

Запишем уравнение этой прямой

Отсюда получим 

Если фокус параболы расположенный левее оси Оу (рис. 15), то есть имеет координаты , то уравнение параболы будет:

Если фокус параболы лежит на оси Оу (рис. 16), то есть имеет координаты , то уравнение параболы будет:

Если фокус параболы лежит правее оси Оу (рис. 17), то есть имеет координаты , то уравнение параболы будет:

Общее уравнение второго порядка с двумя переменными

Общее уравнение второго порядка с двумя переменными имеет вид

Рассмотренные ранее канонические уравнения прямых являются частными случаями данного уравнения.

1.  уравнение будет иметь вид

и, соответственно, будет уравнением окружности.

2.  уравнение будет иметь вид

и, соответственно, будет уравнением эллипса.

3.  уравнение будет иметь вид

и, соответственно, будет уравнением гиперболы.

4.  уравнение будет иметь вид

и, соответственно, будет уравнением параболы.

Кривые второго порядка

Кривыми второго порядка называются линии, уравнения которых являются уравнениями второй степени относительно бегущих координат. Общий вид уравнения кривой второго порядка

Ax² + Bxy + Cy² + Dx + Ey + F = 0.                                                                           (2.109)

К кривым второго порядка относятся круг, эллипс, гипербола и парабола.

Окружность и его уравнения

Определение 1. Окружностью называется множество точек плоскости, равноудаленных от заданной точки, называется центром окружности.

Рис. 50.

Пусть центр окружности находится в произвольной точке С (a, b) (рис. 50). Выходя из определения 1, расстояние произвольной точки M (x, y) плоскости к центру C (a, b) — величина постоянная и равна r. По формуле (2.3) имеем . Возведя обе части этого равенства в квадрат, получим уравнение, которое называется нормальным уравнением окружности:
(x – a) ² + (y – b) ² = r ².                                                                                           (2.110)
Выясним условия, при которых общее уравнение второй степени с двумя переменными (2.109) является уравнением окружности. В этом уравнении А, В и С не равны нулю одновременно, т .е. A² + B² + C² ≠ 0. Когда в уравнении (2.110) раскрываем скобки, то получим
x² + y² – 2ax – 2by + (a² + b² – r²) = 0.                                                                 (2.111)

Чтобы уравнения (2.109) и (2.111) представляли одну и ту же линию, нужно, чтобы коэффициент B = 0, а все остальные пропорциональны, в частности
 ,  отсюда A = C ≠ 0. Теперь уравнение (2.109) имеет вид:

Ax² + Ay² + Dx + Ey + F = 0.                                                                                     (2.112)

Уравнение (2.112) называется общим уравнением окружности.

Обе части уравнения (2.112) поделим на A ≠ 0 и дополним члены, содержащие x и y, до полных квадратов. Получим
                                      (2.113)

Сравнивая (2.113) с уравнением окружности (2.110), можно сделать вывод, что уравнение (2.109) является уравнением окружности при следующих трех условиях:
1) A = C,                  2) B = 0,                      3) D² + E² – 4AE > 0.

При выполнении этих условий для окружности (2.113) центр находится в точке   а  радиус 

Пример 1. Привести общее уравнение окружности x² + y² – 6x + 4y – 3 = 0 к нормальному виду.

Решение. Сгруппируем члены с x и y и дополним их до полного квадрата, тогда получим
(x² – 6 x + 9) – 9 + (y² + 4 y + 4) – 4 – 3 = 0,   или   (x – 3) ² + (y + 2) ² = 16.  Координаты центра окружности a = 3, b = 2, а радиус окружности r = 4.

Пример 2 (экономического характера). Два предприятия, расстояние между которыми 80 км, производят некоторую продукцию, причем фабрично-заводская цена продукции на обоих предприятиях одинакова и равна p. Пусть транспортные расходы на перевозку единицы продукции от компании A до потребителя составляет 10 руб./км, а от компании B составляет 6 руб./км. Как будет размещен рынок сбыта, если расходы потребителей должны быть одинаковыми?

Рис. 51.

Решение. Оси координат проведем через середину отрезка AB. Предположим, что потребитель находится в точке M (x, y); введем обозначения AM = s₁, BM = s₂ (рис. 51). Расходы потребителя на покупку единицы изделия у компании A составляют
p + s₁⋅ 10, а у предприятия B — p + s₂⋅ 6. Расходы потребителей одинаковые, если p + s₁⋅ 10 = p + s₂⋅ 6, или  10 s₁ = 6 s₂,   5 s₁ = 3 s₂.
Из рис. 51 видно, что   или  
Аналогично     или   . 

Для потребителя расходы на покупку продукции одинаковые, если . Возведем обе части в квадрат и сгруппируем. Получим x² + y² + 170 x + 1600 = 0  и, выделив полный квадрат относительно x, имеем

(x + 85)² + y² = 5625.  Это нормальное уравнение окружности, центр которой находится на оси абсцисс с абсциссой «–85», а радиус окружности r = 75.

Для потребителей, которые находятся на этой окружности, расходы на покупку изделия одинаковы. Для потребителей, которые находятся за окружностью, расходы на покупку продукции меньше на предприятии B, а для потребителей, которые находятся внутри окружности — на предприятии A. Значит, рынок будет распределен следующим образом:

а) потребители, которые находятся внутри окружности, будут приобретать данные изделия на предприятии А;

б) для потребителей, находящихся на окружности, все равно, на каком предприятии будут производиться закупки;

в) потребители, которые находятся снаружи окружности, будут закупать изделия на предприятии В.

Эллипс и его уравнения

Определение 2. Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.

Исходя из определения 2, выведем уравнение эллипса. Пусть заданы две точки, которые называются фокусами,  F₁ и F₂, расстояние между которыми обозначим через 2с (фокальное расстояние) (рис.52). Через фокусы проведем прямую, которую возьмем за ось абсцисс, а за ось ординат возьмем прямую, перпендикулярную оси OX, проходящую через середину отрезка F₁F₂ (точка О).

Поскольку расстояние между фокусами приняли за 2с, то координаты фокусов будут соответственно  F₁ (c, 0) и F₂ (–c, 0). 

Рис. 52.

Пусть M (x, y) произвольная точка эллипса. Отрезки F₁M и F₂M, соединяющие точку эллипса с его фокусами, называют локальными радиус-векторами этой точки и обозначают r₁ и r₂ . Тогда  r₁ + r₂  является величиной постоянной по определению, обозначим ее через 2а:
r₁ + r₂ =  2а                                                                                            (2.114)
(2а > 2с, потому что в треугольнике F₁MF₂  сумма двух сторон больше третьей). Покажем, какому уравнению удовлетворяют координаты точки M (x, y).
Найдем  r₁ и  r₂:
,                                                                        (2.115)
.                                                                        (2.116)

Возведя обе части (2.115) и (2.116) в квадрат и отнимая, получим
.                                                                                      (2.117)
Расписав разность квадратов в (2.117) и учитывая (2.114), получим
.                                                                                    (2.118)
Рассмотрим систему из уравнений (2.114) и (2.118):
                                                                                (2.119)
Из этой системы находим
                                                                                    (2.120)
.                                                                                      (2.121)
Подставим (2.121) в (2.116), получим
,   или
.                                                         (2.122)
Обозначим a² – c² = b²                                                                     (2.123)
и тогда (2.122) перепишем после простых преобразований в виде
.                                                                                    (2.124)

Уравнение (2.124) является каноническим уравнением эллипса. Это уравнение второй степени, значит, эллипс — кривая второго порядка. Уравнение (2.124) содержит x и y в четных степенях, значит, кривая, определяемая этим уравнением, симметрична относительно осей Оx и Оy. Оси симметрии эллипса называют его осями. Точку О называют центром эллипса. Из уравнения (2.124) найдем y:
                                                    (2.125)
Так как у, который находится в первом квадранте, является положительным, то
.                                                                                    (2.126)
Из равенства (2.126) видно, если x = 0, то y = b и при возрастании x от нуля до a, y убывает от b к нулю.

В первом квадранте часть эллипса — это дуга  A₁B₁. Если провести зеркальное отражение этой дуги относительно осей координат, то мы получим весь эллипс (рис. 52).

Если в уравнении (2.124) y = 0, то x = ± a, a если x = 0, то y = ± b. Значит вершинами эллипса есть точки A₁ (a, 0), A₂ (–a, 0),  B₁ (0, b),  B₂ (0, –b).  Отрезок A₂ A₁ = 2a, а отрезок B₂ B₁ = 2b. Эти
отрезки соответственно называются большой и малой осями эллипса. Соответственно, a и b — большая и малая полуоси эллипса.

Определение 3. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси.

Обозначим эксцентриситет через ε, то тогда
.                                                                                 (2.127)
Если a = b (ε = 0), то эллипс превращается в окружность. Подставим (2.127) в (2.120) и (2.121), тогда получим
r₁ = a – εx,                                                                                            (2.128)
r₂ = a + εx.                                                                                             (2.129)

Эти формулы используются при решении задач.

Пример 3. Составить каноническое уравнение эллипса, зная, что большая ось 2a = 10, а эксцентриситет ε = 0,8.

Решение. Из уравнения (2.127) найдем c. Зная, что a = 5, c = a ⋅ ε = 5 ⋅ 0,8 = 4. А теперь найдем b из равенства (2.123):

b² = a² – c² = 5² – 4² = 25 – 16 = 9,  b = 3.
Подставляя a = 5, b = 3  в уравнение (2.124), получим  .

Гипербола и ее уравнение

Определение 4. Гиперболой называется множество точек плоскости, абсолютное значение разницы расстояний которых от двух заданных точек, называемых фокусами, есть величина постоянная.

Основываясь на определении 4, выведем каноническое уравнение гиперболы. Пусть заданы две точки F₁ и F₂ , являющиеся фокусами гиперболы. Обозначим расстояние между ними через 2c, а абсолютную величину разности расстояний точки гиперболы от точек F₁ и F₂ обозначим через 2a (a > 0). За ось абсцисс возьмем прямую, проходящую через фокусы, а за ось ординат возьмем прямую, перпендикулярную оси абсцисс и проходящую через середину отрезка F₂F₁ (рис. 58), то есть через точку О. Поскольку  F₂F₁ = 2с, то координатами фокусов будут соответственно F₁ (c; 0) и F₂(–c; 0), а фокальные радиусы соответственно r₁ = F₁M,  r₂ = F₂M,   ,  где M (x, y) — произвольная точка гиперболы.

Рис. 58.

Пользуясь формулой расстояния между двумя точками и определением 4, имеем уравнение гиперболы:
                               (2.130)
Запишем это уравнение в таком виде:   

  или

 .                                  (2.131)

Возведя в квадрат обе части этого уравнения, получим:

или после упрощения .  Опять возведя обе части полученного уравнения в квадрат, получим после упрощений
x² (c² – a²) – a² y² = a² (c² – a²).                                                                   (2.132)

Разделив обе части уравнения (2.132) на a² (c² – a²), получим:
.                                                                                       (2.133)

Покажем, что c² – a² > 0 (c > a). Поскольку в любом треугольнике разность двух сторон меньше трех, то
  или  2a < 2c, или a < c . Тогда c² – a²  величина положительная, и ее обозначим через b². То есть
c² – a² = b².                                                                                                     (2.134)

Подставляя (2.134) в (2.133), получим каноническое уравнение гиперболы
.                                                                                               (2.135)

Уравнение (2.135) является уравнением второй степени, значит гипербола является кривой второго порядка. Исследуем форму гиперболы по ее уравнению (2.135). Поскольку уравнение содержит x и y только в четных степенях, то гипербола симметрична относительно обеих осей координат.
Найдя y и x из уравнения (2.135), получим
                                                                         (2.136)
                                                                         (2.137)

Из уравнения (2.136) можно сделать следующие выводы:

а) значения у мнимые, если | х | < a , значит гипербола не пересекает оси Оу и не имеет точек, находящихся в полосе, ограниченной прямыми х = ± a;

б) когда x = ± a, y = 0, значит гипербола пересекает ось абсцисс в двух точках A₁ (a, 0) и  A₂ (–a, 0), которые называются вершинами гиперболы;

в) для каждого | x | > a, ордината y имеет два значения, которые отличаются только знаком, отсюда следует, что гипербола симметрична относительно оси Оx.

Уравнение (2.137) показывает, что гипербола симметрична и относительно оси Оy.

При неограниченном росте абсциссы x ордината также неограниченно растет. Поскольку гипербола находится вне полосы, ограниченной прямыми x = ± a, то гипербола состоит из двух отдельных веток (рис. 59).

Отрезок A₂ A₁ называется действительной осью гиперболы, а точки A₁ (a, 0) и A₂ (–a, 0) —вершинами гиперболы. Отрезок  B₁B₂, соединяющий точки В₁ (0, b) и В₂ (0, –b), называется мнимой осью гиперболы. Точки F₁ (c, 0) и F₂ (–c, 0) называются фокусами гиперболы.

Рис. 59.

Гипербола, которая определяется уравнением    , имеет действительную ось B₂B₁ = 2b,  а воображаемая ось A₂A₁ = 2a (показана на рис. 59 пунктиром) называется сопряженной по отношению к гиперболе
 .

Если действительная и мнимая оси равны, то гипербола называется равносторонней, а ее уравнение будет x² — y² = a².

Степень сжатия гиперболы характеризуется ее эксцентриситетом.

Определение 5. Эксцентриситетом гиперболы называется отношение расстояния между фокусами 2с к длине ее действительной оси 2a, то есть
.                                                                                                      (2.138)
Так как для гиперболы с > a, то ε > 1.

Примечание. Для гиперболы легко показать как связаны  r₁ и  r₂ с ε, а именно

  (х > 0),
    (х > 0),                                                              (2.139)
     (х < 0),
    (x <0).                                                             (2.140)

Формулы (2.139) и (2.140) получаются аналогично как и для эллипса.

Предоставим читателю самостоятельно убедиться в справедливости формул (2.139) и (2.140).

Асимптоты гиперболы

Определение 6. Прямая l называется асимптотой кривой (k), если расстояние d = MN от точки M кривой до точки N прямой l стремится к нулю при неограниченном удаленные точки M от начала координат вдоль кривой (k) в том или ином направлении (рис. 60).

Рис. 60.

Покажем, что прямая     (2.141) является асимптотой гиперболы (2.135). Для этого рассмотрим прямую MN, параллельной оси Oy (рис. 59). Абсцисса точки M и точки N одна и та же, то есть x, а ордината точки M является y, а точки N ∈ Y.

Найдем разницу между ординатами (Y-y)  точек N и M, которые имеют одну и ту же абсциссу .

Теперь умножим и разделим правую часть этого равенства на  и после упрощений получим .
Отсюда видно, что при неограниченном увеличении абсциссы x разница (Y-y) неограниченно уменьшается. Таким образом, точка гиперболы ограниченно удаляясь по ветке гиперболы, неограниченно приближается к асимптоте , но никогда ее не достигает. Значит, гипербола (2.135) имеет две асимптоты    и , которые совпадают с диагональю прямоугольника и проходят через начало координат.

Пример 4. Составить уравнение гиперболы, если известно, что она проходит через точку M₁ (10; 5) и имеет асимптоты   и  .
Решение. Из условия задачи получаем, что   и координатs точки M₁ удовлетворяют уравнению гиперболы, то есть   Таким образом, получили систему двух уравнений с двумя неизвестными:

Из первого уравнения находим    и подставляем во второе уравнение   или   
Отсюда   Далее находим  
Итак, искомое уравнение гиперболы будет  

Парабола и ее уравнение

Определение 7. Параболой называется множество точек плоскости, одинаково удаленных от заданной точки, называемой фокусом, и от заданной прямой, называемой директрисой.

Исходя из определения 7, выведем уравнение параболы. Пусть прямая AB является директрисой параболы, а точка F является ее фокусом (рис. 61).

Рис. 61.

Проведем через точку F прямую, перпендикулярную директрисе AB, и возьмем эту прямую за ось абсцисс, а за ось ординат возьмем прямую, перпендикулярную оси абсцисс и проходящую через точку O, середину отрезка CF. Длину отрезка CF обозначим через p (p > 0). Координаты фокуса будут , а уравнение директрисы AB  есть  .
Пусть точка M (x, y) является произвольной точкой параболы. Опустим из точки M перпендикуляр на директрису AB в точке D и соединим точку M с фокусом F. Тогда
по определению 7 имеем, что DM = MF. Точка D имеет координаты   По формуле расстояния между двумя точками находим
.

Это и будет уравнение параболы относительно выбранной системы координат. Возведя обе части данного уравнения в квадрат и упростив, получим
y² = 2 px.                                                                                                   (2.142)

Уравнение (2.142) и является каноническим уравнением параболы. Как видно из уравнения (2.142), парабола является линией второго порядка, и все ее точки размещены справа от оси Оy. Парабола проходит через начало координат. Решив уравнение (2.142) относительно y, получим
.                                                                                       (2.143)

Так как p > 0, то y будет действительной величиной только тогда, когда x положительные, а когда p < 0, то парабола определена для x ≤ 0.

Из (2.143) видно, что каждому значению x соответствует два знания y, которые равны по абсолютной величине, но противоположны по знаку.

Значит ось Оx является осью симметрии для параболы. Точку O (0,0) называют вершиной параболы.

Если x неограниченно растет, то и y неограниченно растет. Величина р называется параметром параболы и при увеличении р парабола расширяется, то есть ее точки будут удаляться от оси Ох.

Если уравнение параболы имеет вид y² = –2px, то вершина параболы находится в начале координат, осью симметрии является ось абсцисс, но парабола размещена слева от оси Oy (рис. 62), а директриса такой параболы будет размещена справа от оси ординат, а фокус будет слева от начала координат.
Если директриса параболы параллельна оси абсцисс, а фокус находится на оси ординат, то уравнение параболы имеет вид:         x² = ± 2py.                                   (2.144)

             
Рис. 62.                                                                  Рис. 63.

Парабола (2.144) изображена на рис. 63. Эта парабола симметрична относительно оси Oy и размещена над осью абсцисс, если в уравнении взять знак (+), и под осью абсцисс, если взять знак (-).

Если в уравнении (2.144) обозначить , то получим уравнение параболы y = ax², которую изучают в средней школе.

Пример 5. Фермы, поддерживающие железнодорожный мост длиной 112 м, имеют вид параболы, которая задается уравнением y = ax². Найти уравнение соответствующей параболы, если наибольшая высота мостовой арки составляет 44 м.

Решение. Возьмем за начало координат вершину фермы. Тогда симметричные точки в основании фермы будут иметь координаты (-56; -44) и (56; -44). Подставляя любую пару координат в уравнение y = ax², получим — 44 = a ⋅ 3136. Отсюда
.
Таким образом, мостовая ферма имеет вид параболы .

Линии второго порядка. Общее уравнение линии второго порядка

Напомним, что линия второго порядка — это множество точек, координаты которых удовлетворяют уравнениям вида

, (1)

где коэффициенты a,b,c,d,e,f— действительные числа, причем хотя бы одно из чисел a,b,c отлично от нуля, то есть . В частности, к линиям второго порядка относятся окружность, эллипс, гипербола и парабола. Заметим, что множеством точек (;) с действительными координатами, удовлетворяющими уравнению (1), может быть не только одна из названых линий. Уравнение (1) может определять на плоскости также две прямые (), одну прямую (-2 =0), точку ( =0) или не определять ни одной точки ( + 1 = 0).

Линии второго порядка называют также коническими сечениями, так как их можно получить пересечением кругового конуса с плоскостью. Окружность образуется как линия пересечения плоскости, перпендикулярной к оси конуса и не проходящей через его вершину (рис. 1, а); эллипс — линия пересечения плоскости, пересекающей все образующие конуса, не перпендикулярная к оси конуса и не проходящая через его вершину (рис. 1, б); если пересечь двуполостной конус плоскостью, параллельной двум образующим, то получим гиперболу (рис. 1, в), а одной образующей — параболу (рис. 1, г).

Кривые второго порядка — важная составляющая окружающего мира.

1. Планеты Солнечной системы движутся по эллипсам, имеющим общий фокус, в котором расположено Солнце.

2. Если в фокусе параболы разместить источник света, то лучи, отразившись от параболы, пойдут параллельно ее оси. На этом свойстве основывается конструкция прожектора.

3. Движение материальной точки под действием центрального поля силы тяготения осуществляется по одной из линий второго порядка.

Окружность и ее уравнение

Окружностью называют множество точек плоскости (рис. 2), находящихся на одинаковом расстоянии (радиус окружности) от заданной точки плоскости (центра окружности). Уравнение окружности имеет вид

. (2)

Если в уравнении (2) раскрыть скобки, то получим общее уравнение окружности

, (3)

где А = -2а , В = -2b, С = . Поэтому окружность — линия второго порядка.

Рис. 2. Окружность

Уравнение окружности имеет следующие свойства.

1°. Коэффициенты и равны между собой.

2°. В уравнении отсутствует член с произведением .

Если центр окружности расположен в начале координат, то а =b = 0 и уравнение (2) имеет вид

. (4)

Уравнение (4) называется каноническим уравнением окружности.

Пример №7

Найти центр и радиус окружности .

Решение:

Сгруппируем произведения с переменной и переменной и дополним полученные выражения до полных квадратов:

Поэтому, точка (-2; 3) — центр окружности, a = 6 — его радиус.

Каноническое уравнение эллипса. Эксцентриситет

Возьмем на плоскости две точки и , и разместим прямоугольную систему координат так, чтобы ось проходила через них, а начало координат делило отрезок пополам. Эллипсом называют множество всех точек плоскости, сумма расстояний которых от данных точек и этой плоскости, называемых фокусами, есть величина постоянная и больше расстояния между фокусами (рис. 3, а). Расстояние между фокусами называют фокальным и обозначают через . Сумму расстояний от произвольной точки эллипса до фокусов обозначим через . Тогда фокусы имеют координаты (-с; 0 и (c; 0), и по определению эллипса , то есть а > с.

Каноническим уравнением эллипса называется равенство

(5)

где

. (6)

Отметим некоторые свойства эллипса.

1°. Эллипс симметричен относительно осей и , а также относительно точки (0; 0), которую называют центром эллипса.

2°. Эллипс пересекает оси координат в точках (а; 0), (-а; 0), (0; b), (0; —b). Эти точки называются вершинами эллипса (рис. 3, б). Величины и называются, соответственно, большой и малой осями эллипса, а числа а и b — большой и малой полуосями эллипса.

3°. Если а = b , то уравнение (5) принимает вид , то есть получается уравнение окружности. Поэтому окружность является частным случаем эллипса. При а = b имеем с = 0, то есть окружность — это эллипс, у которого фокусы совпадают с его центром.

Мера отклонения эллипса от окружности характеризуется величиной , которая называется эксцентриситетом эллипса и равняется отношению половины его фокального расстояния к длине большой полуоси:

(7)

причем , поскольку . Из формул (6) и (7) получим

.

Итак, если = 0 , то b = а , то есть эллипс превращается в окружность; если приближается к единице, то отношение осей b/а уменьшается, то есть эллипс все больше растягивается вдоль оси .

4°. Пусть — произвольная точка эллипса с фокусами и (рис. 3, б). Расстояния и , называются фокальными радиусами точки . Очевидно, что . Прямые называются директрисами эллипса. Отношение фокальных радиусов произвольной точки эллипса к расстояниям от этой точки до соответствующих директрис есть величина постоянная и равна эксцентриситету эллипса, то есть

. (8)

Пример №8

Составить каноническое уравнение эллипса, фокусы которого расположены на оси симметрично начала координат, если расстояние между фокусами равно 14, а эксцентриситет равен 7/9 .

Решение:

Поскольку 2с = 14, то с = 7. Из формул (7) и (6) получим а = 9 и = 32. Поэтому искомое уравнение имеет вид

Каноническое уравнение гиперболы. Асимптоты. Эксцентриситет

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Обозначим через и фокусы гиперболы, расстояние между ними — через 2с, а модуль разности расстояний от произвольной точки гиперболы до фокусов — через 2а. По определению а<с. Возьмем на плоскости прямоугольную систему координат так, чтобы ось проходила через фокусы, а начало координат делило бы отрезок пополам (рис. 4). Точка плоскости принадлежит гиперболе тогда и только тогда, когда . Каноническое уравнение гиперболы имеет вид

(9) где

(10)

. Рис. 4. Гипербола и ее свойства Рассмотрим некоторые свойства гиперболы.

1°. Гипербола симметрична относительно осей , и начала координат.

2°. Удаляясь в бесконечность, переменная точка гиперболы неограниченно приближается к одной из прямых

-. (11)

Такие прямые называются асимптотами гиперболы.

Оси симметрии называются осями гиперболы, а точка пересечения осей — ее центром. Ось пересекает гиперболу в двух точках (а; 0) и (-а; 0), которые называются вершинами гиперболы. Действительной осью называют отрезок , соединяющий вершины гиперболы, и его длину . Отрезок , который соединяет точки (0; b) и (0; —b), и его длина, называется мнимой осью. Величины а и b, соответственно, называются действительной и мнимой полуосями гиперболы. Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы.

При построении гиперболы (9) удобно сначала построить ее основной прямоугольник (рис. 4), провести прямые, проходящие через противоположные вершины этого прямоугольника, — асимптоты гиперболы и определить вершины и гиперболы. Уравнение

12)

также определяет гиперболу, которая называется сопряженной гиперболе (9). Гипербола (12) показана на рис. 4 штриховой линией. Вершины этой гиперболы находятся в точках (0; b) и (0; —b), а ее асимптоты совпадают с асимптотами гиперболы (9).

3°. Эксцентриситет гиперболы определяется как отношение половины фокального расстояния к длине ее действительной полуоси:

. (13)

Поскольку с > а, то > 1. Кроме того, из формул (10) и (13) следует, что

Поэтому эксцентриситет гиперболы характеризует ее форму: чем больше эксцентриситет, тем больше отношение , то есть тем больше основной прямоугольник растягивается в направлении оси , а гипербола отклоняется oт оси ; чем ближе эксцентриситет к единице, тем больше основной прямоугольник растягивается в направлении оси и гипербола приближается к этой оси.

4°. Прямые ., где а — действительная полуось гиперболы, а — ее эксцентриситет, называют директрисами гиперболы. Директрисы гиперболы имеют такое же свойство (8), как и директрисы эллипса.

Пример №9

Составить каноническое уравнение гиперболы, фокусы которой расположены на оси симметрично начала координат, действительная ось равна 6, а эксцентриситет .

Решение:

Поскольку 2а = 6, то а= 3. Из формул (10) и (13) находим, что b = 4. Искомое уравнение имеет вид

Каноническое уравнение параболы

Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой, и не проходит через фокус.

Пусть заданы фокус и директриса, причем расстояние между ними равно р. Возьмем прямоугольную систему координат так, чтобы ось проходила через фокус, перпендикулярно к директрисе, а ось делила расстояние между фокусом и директрисой пополам. Тогда фокус имеет координаты , а — уравнение директрисы. Пусть — произвольная точка плоскости, а отрезки МВ и MF расстояния от нее до директрисы и фокуса. Точка М тогда принадлежит параболе, когда MВ = MF (рис. 5).

Рис. 5. Парабола и ее свойства

Каноническое уравнение параболы имеет вид

. (14)

Ось симметрии параболы называется ее осью; точка пересечения оси с параболой — вершиной параболы; число, равное расстоянию от фокуса до директрисы, — параметром параболы. Осью параболы, заданной уравнением (14), является ось , вершиной — точка (0; 0) и параметром — число р .

Замечание. Используя свойство 4° эллипса и гиперболы и определение параболы, можно дать такое общее определение кривой второго порядка (кроме окружности): множество точек, для которых отношение расстояния до фокуса и до соответствующей директрисы есть величина постоянная. Это эллипс при 0 < < 1, парабола при = 1 или гипербола при > 1.

Пример №10

В параболу вписан равносторонний треугольник так, что одна из вершин совпадает с вершиной параболы. Найти сторону треугольника и сделать рисунок.

Решение:

Пусть точка А() — одна из вершин треугольника. Тогда другими его вершинами будут точки и (0; 0). Поскольку треугольник равносторонний, то АВ = АО= ВО, откуда . Решая это уравнение вместе с уравнением , находим . Поэтому сторона треугольника равна .

Рис. 6 Иллюстрация к примеру 4.

Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:

Другие темы которые вам помогут понять высшую математику:

Кривые линии второго порядка

Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.

Круг 

Кругом называется геометрическое место точек плоскости, которые равноудалены от одной и той же точки этой плоскости (рис. 2.13). 

Уравнение круга с центром  и радиусом  имеет вид:  (2.16). В случае, когда центр круга находится в начале координат, уравнение имеет вид: 

Круг — уравнение второго порядка. Общее уравнение кривой второго порядка:  являет собой круг, если коэффициенты при квадратах координат равны между собой   и если отделенный член с произведением координат  то есть 

Эллипс 

Эллипсом называется геометрическое место точек, сумма расстояний которых к двум фиксированным точкам, что называются фокусами, является постоянными и равны  (рис. 2.14). Каноническое уравнение эллипса имеет вид: 

Координаты фокусов эллипса  и  Расстояние между фокусами равно  Точки пересечения эллипса с осями координат   и  — называются вершинами эллипса. 

Отрезки  — называются осями эллипса. 

Эксцентриситет эллипса 

Расстояние  и  точки  эллипса к эго фокусам называются фокальными радиусами этой точки и обозначаются по формулам: 

 

Две прямые, которые параллельны к малой оси эллипса и находятся от нее на расстоянии  называются директрисами эллипса. Их уравнение: 

  или 

Уравнение эллипса с осями, что параллельные координатными осям, имеет вид: 

где  — координаты центра эллипса. 

Гипербола 

Гиперболой называют геометрическое место точек, для каждой их которых абсолютное значение разницы расстояний от двух заданный точек, что называется фокусами, является величина постоянная и равна  (рис. 2.15). Каноничное уравнение гиперболы имеет вид: 

Координаты фокусов гиперболы  и  Расстояние между фокусами равно 

Точки пересечения гиперболы с осью абсцисс   называются действительными вершинами. Расстояние  называется действительной осью гиперболы. 

Точки  называются мнимыми вершинами, а отрезок  — мнимой осью гиперболы. 

Эксцентриситет гиперболы 

Расстояние  и  точки  гиперболы к его фокусам называются фокальными радиусами этой точки и обозначаются формулами: 

по условию, что точка  лежит на правой ветке гиперболы. 

Две прямые, которые параллельны мнимой оси гиперболы и находятся от нее на расстоянии  называются директрисами гиперболы. Их уравнение:  

Прямые, которые обозначаются уравнением: 

называются асимптотами гиперболы.

Две гиперболы, что заданы уравнениями: 

называются спряженными. Они имеют общие асимптоты. 

Если оси гиперболы равны, то есть  то гипербола называется равнобедренной или равносторонней. Ее уравнение имеет вид: 

Ее асимптотами служат биссектрисы координатных углов. 

Если за оси координат принять асимптоты равносторонней гиперболы, то ее уравнение получит вид:  где 

Парабола

Параболой называется геометрическое место точек равноудаленных от заданной точки — фокуса и заданной прямой — директрисы (рис. 2.16).

Каноничное уравнение параболы имеет вид: 

где  — расстояние от фокуса к директрисе. Вершина параболы находится в начале координат, осью симметрии является ось абсцисс. 

Координаты фокуса   Уравнение директрисы    имеет вид: 

Фокальный радиус  параболы равен 

Эксцентриситет параболы считается равным единице, то есть 

Если осью симметрии параболы служит ось ординат (рис. 2.17), то уравнение параболы имеет вид: 

Уравнение директрисы в этом случае: 

Уравнение параболы с осью симметрии =, которая параллельна одной из координатных осей, имеет вид: 

или 

где  — координаты вершин параболы. 

Примеры решения задач:

Задача 2.51.

Сложить уравнение круга с центром в точке  и радиусам, что равны 6. 

Решение. В уравнении (2.16)  получим   Сразу получим: 

Задача 2.52 

Обозначить центр и радиус угла, которое задано уравнением:

Решение. Как в заданном уравнении коэффициент при  и  равны между собой и отделенный член с произведением координат, то заданное уравнение является уравнением круга. Его необходимо привести к виду (2.16). Выпишем члены, которые содержат только  и член, которые содержат только 

Выделим полный квадрат: 

Левая часть заданного уравнения запишем так: 

откуда: 

Уравнивая полученное уравнение с уравнением (2.16) приходим к выводу, что это уравнение обозначает круг, центр которого имеет координаты 

Задача 2.53 

Сложить уравнение круга, что проходит через точки  и  если центр его лежит на прямой 

Решение. Каноническое уравнение круга: 

Так как круг проходит через точки  и  то координаты этих точек должны удовлетворять уравнению круга. Отсюда имеет два уравнения: 

если центр круга находится на прямой  то координаты центра должны удовлетворять уравнению прямой. Получим третье уравнение: 

решим систему уравнений: 

отнимем от первого уравнения второе.

Получим систему: 

Получим: 

подставим полученное значение  в уравнении  получим значение параметра 

Таким образом, координаты центра круга: 

Чтобы обозначить  воспользуется уравнением: 

Следует, уравнение круга: 

Задача 2.54

Сложим уравнение круга, что проходит через три заданные точки:   и 

Решение. Искомое уравнение имеет вид  Так как круг проходит через заданные точки, то координаты каждой из этих точек удовлетворяют уравнению круга. 

Подставим по очереди в искомое уравнение координаты заданных точек, получим три уравнения для определения  и 

От первого уравнения отнимем второе, а потом от первого уравнения отнимем третье. Получим систему двух уравнений с двумя неизвестными: 

Откуда. 

Для нахождения  воспользуемся точкой  и уравнением: 

искомое уравнение круга имеет вид: 

Задача 2.55 

Найти длину осей, координаты фокусов и эксцентриситет эллипса 

Решение. Приведем эти уравнения к каноничному виду (2.17): 

Разделив обе части заданного уравнения на 144, получим: 

отсюда получим, что  Следует,   Зная   и  из соотношения  находим 

Координаты фокусов будут:  и  

эксцентриситет эллипса 

Задача 2.56 

Большая ось эллипса равно 8, а расстояние между директрисами равно 16. Найти уравнение эллипса. Чему равен его эксцентриситет? 

Решение. Для нахождения уравнения эллипса необходимо найти его полуоси   и   По условию 

Полуось  находим из соотношения  а  можно найти, используя расстояние между директрисами 

Таким образом, 

Получим уравнение эллипса: 

Эксцентриситет эллипса будет 

Задача 2.57 

Сложить уравнение гиперболы, фокусы которого находятся на оси абсцисс, симметрично началу координат, если задана точка  гиперболы и уравнения асимптот 

Решение. Для нахождения уравнения гиперболы   необходимо найти ее полуось   и   Воспользуется условием: точка  находятся на гиперболе, а это означает, что координаты точки  должны удовлетворять уравнению гиперболы: 

Уравнение асимптот  а у нас получится  следует, 

Получили систему уравнений: 

Подставим полученные значения параметров в каноничное уравнение гиперболы: 

Таким образом, получим искомое уравнение гиперболы: 

Задача 2.58 

Найти каноническое уравнение гиперболы, если угол между ее асимптотами равно  и расстояние между фокусами равны  

Решение. Каноничное уравнение гиперболы имеет вид: 

Уравнение асимптот  где  а  — угол наклона асимптоты к оси 

Так как угол между асимптотами равен , то 

Отсюда, 

По условию задачи  то  Из соотношения  получим второе уравнение: 

Решим систему уравнений: 

Получим уравнение: 

Задача 2.59

Вычислить длину стороны правильного треугольника, который вписан в параболу  

Решение. Треугольник  размещенный симметрично относительно оси параболы. Одна из его вершин совпадает с вершиной параболы, а противоположная сторона — перпендикуляр к оси параболы (рис. 2.18).

По условию задачи  равносторонний. Угол  то  Пусть координаты точки Из  получим  то есть 

Следует, точка  имеет координаты 

Эта точка лежит на параболе, ее координаты удовлетворяют уравнению параболы. Отсюда: 

тогда, 

Длина сторон треугольника 

Общее уравнение кривой второго порядка: типы кривых

Кривой второго порядка называется линия, которая описывается уравнением

где  переменные — текущие координаты точек линии;

заданные действительные числа — коэффициенты при переменных и свободный член ; при этом числа одновременно не могут равняться нулю: 

Уравнение (8.1) называют общим уравнением линии 2-го порядка. При определенных условиях относительно значений коэффициентов при переменных и свободного члена оно описывает одну из четырех, знакомых со школы, кривых: круг, эллипс, гиперболу, параболу.

Однако может случиться, что не существует точек с действительными координатами, которые бы удовлетворяли уравнения (8.1). В этом случае кривую 2-го порядка называют мнимой кривой. Например, уравнение , определяет воображаемое круг.

Кроме того, имеют место случаи вырождения кривых 2-го порядка в прямые или точку. К примеру:

уравнению удовлетворяют лишь координаты точки 

уравнения параллельных или совпадающих прямых;

уравнения прямых, пересекающихся 

Известно, что в зависимости от знака величины уравнения (8.1) описывает один из трех типов линий второго порядка:
1) эллиптический, если уравнение (8.1) описывает эллипс (окружность при и ), кажущуюся кривую или кривую, вырождается в точку;
2) гиперболический, если уравнение (8.1) описывает гиперболу или пару прямых, пересекающихся;
3) параболический, если уравнение (8.1) описывает параболу, пару параллельных прямых или воображаемую кривую.

Канонические уравнения окружности и эллипса

Круг — это множество точек плоскости, расстояние от которых до одной фиксированной точки, называется центром, является величиной постоянной. Расстояние от центра круга до любой точки называют радиусом круга.

Каноническое уравнение окружности (7.2) было получено в примере к главе 7:

Если в уравнении (8.2) раскрыть скобки, получим общее уравнение кривой 2-го порядка при  и , то есть уравнение

которое называется общим уравнением круга.

Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух фиксированных точек (фокусов) является величиной постоянной. Пусть точка является произвольной точкой эллипса (рис. 8.1), фокусы эллипса расположены на оси и находятся в точках , а сумма расстояний точек эллипса к фокусам
равна .

Рис. 8.1

Тогда согласно определению эллипса имеет место соотношение: . Используя формулу расстояния между двумя точками, имеем:

или 

Далее избавляемся от иррациональности поднесением к квадрату обеих частей (8.4) и упрощаем:

или

Уравнение (8.5) называют каноническим уравнением эллипса.
Поскольку (сумма двух сторон треугольника больше третьей стороны), поэтому обозначение — через является корректным.

Анализируя уравнение (8.5), делаем выводы:
1) точки эллипса не выходят за пределы прямоугольника, который описывается неровностями: (рис. 8.2), что вытекает из развязанного относительно переменной уравнения (8.5):

Рис. 8.2

2) эллипс является симметричным относительно осей координат, поскольку уравнение содержит только квадраты текущих координат и , поэтому координатные оси являются осями симметрии эллипса; ось симметрии, на которой лежат фокусы, называется фокальной осью; точку пересечения осей симметрии называют центром симметрии, или центром эллипса;
3) кривая пересекает координатные оси в точках — вершинах эллипса — с абсциссами и с ординатами (рис. 8.2): , отрезки и , соединяющих противоположные вершины эллипса, а также их длины и , называют соответственно большой и малой осями эллипса; длины и — большой и малой полуосями.

Форма эллипса относительно оси определяется отношением расстояния между фокусами к большой оси , которое называется эксцентриситетом эллипса :

С помощью соотношения эксцентриситет  легко подать через полуоси и :

Каноническое уравнение окружности (см. (7.3)) является частным случаем канонического уравнения эллипса (8.5) при условии, что . Но если , то . То есть, эксцентриситет окружности равен нулю.

Если эксцентриситет эллипса стремится к нулю (), то по своей форме эллипс приближается к кругу; если же приближается к единице (), то полуось эллипса  стремится к нулю, а эллипс — к вырождению в отрезок.

Известно, что планеты и кометы движутся по орбитам, имеющих форму эллипса. Орбиты планет близки к кругам, а орбиты комет — до вытянутых эллипсов (эксцентриситет орбиты Земли и кометы Галлея равны соответственно 0,02 и 0,97).

Прямые , параллельные малой оси эллипса, называются директрисами эллипса.

Расстояния от произвольной точки эллипса до его фокусов называют локальными радиусами эллипса (рис. 8.1):

Фокальные радиусы связаны соотношением (по определению эллипса), а их связь с эксцентриситетом описывается равенствами 

Замечания. Каноническое уравнение эллипса можно получить, выбирая фокусы на оси , тогда будет большой полуось .

Найдем уравнение эллипса , который проходит через точку , а его эксцентриситет равен 0,8. Для этого необходимо определить параметры его уравнения.

Поскольку точка , то ее координаты удовлетворяют уравнениюе эллипса. Согласно условию зада

чи , откуда . Таким образом, для нахождения параметров эллипса имеем систему уравнений:

Следовательно, уравнение эллипса имеет вид:

Каноническое уравнение гиперболы. Асимптоты гиперболы

Гиперболой называется множество точек плоскости, модуль разности расстояний которых до двух фиксированных точек, называемых фокусами, есть величиной постоянной, отличной от нуля.

Выберем оси координат таким образом, чтобы фокусы гиперболы и были расположены на оси , а модуль разности расстояний от точек гиперболы до фокусов обозначим 

Воспользуемся рисунком 8.1, на котором теперь — произвольная точка гиперболы. Согласно определению . Отсюда, применив формулу расстояния между двумя точками, получаем:

или

Выполняем преобразования, аналогичные тем, которые осуществлялись при выводе уравнения эллипса:

или

Уравнение (8.9) называется каноническим уравнением гиперболы.

Поскольку (разница двух сторон треугольника всегда меньше третьей стороны), поэтому разница  — есть положительным числом, которое обозначили через .
Анализ полученного уравнения позволяет прийти к выводам:
1) точки гиперболы выходят (кроме двух) за пределы вертикальной полосы, которая описывается неравенством: (рис. 8.3). Это следует из развязанного относительно переменной уравнения (8.9):

2) гипербола симметрична относительно осей координат, поскольку ее уравнение содержит только квадраты переменных и , поэтому координатные оси являются осями симметрии гиперболы; ось симметрии, на которой лежат фокусы, называется фокальной, или действительной осью; вторая — мнимой осью симметрии; точка пересечения осей симметрии является центром симметрии гиперболы, или центром гиперболы;
3) кривая пересекает ось в точках — вершинах гиперболы — с абсциссами (рис. 8.3); с осью кривая общих точек не имеет; ось называется действительной, а вот  — мнимой осями гиперболы. Отрезок , соединяющий вершины гиперболы, принадлежит действительной оси ; отрезок принадлежит воображаемой оси гиперболы .

Рис. 8.3

Прямоугольник со сторонами и и центром симметрии в начале координат называют основным прямоугольником гиперболы.

Асимптотой гиперболы называется прямая, расстояние до которой от точек гиперболы стремится к нулю при неограниченном росте абсциссы .

Асимптоты гиперболы описываются уравнениями прямых:

на которых лежат диагонали основного прямоугольника гиперболы.

Пусть точка гиперболы, где . Найдем расстояние от этой точки до асимптоты с уравнением по формуле (7.26):

Поделим и умножим правую часть (8.11) на выражение, сопряженный к выражению под знаком модуля, то есть на выражение , тогда получим:

При неограниченном росте знаменатель дроби неограниченно увеличивается, а самый дробь уменьшается и приближается к нулю.
Аналогично можно показать, что прямая также является асимптотой гиперболы.

Согласно определению асимптот гиперболы ее геометрическое изображение начинают с построения основного прямоугольника и его диагоналей.

Части графика кривой при и называют ветвями гиперболы.

Как и для эллипса, форму гиперболы характеризует отношение фокусного расстояния к действительной оси , как и для эллипса, такое отношение называется эксцентриситетом:

Прямые , параллельные мнимой оси гиперболы, называются директрисами гиперболы.

Расстояния от произвольной точки гиперболы до ее фокусов называют фокальными радиусами гиперболы:

Фокальные радиусы связаны соотношением (по определению гиперболы), а их связь с эксцентриситетом описывается равенствами , , где знак соответствует правой (левой) ветви гиперболы.

Примечание:
1) каноническое уравнение гиперболы в случае расположения ее фокусов на оси  имеет вид:

тогда действительной осью гиперболы является , а мнимой — .
Кривые, описываемые уравнениями (8.9) и (8.14), называются взаимно сопряженными гиперболами;

2) если в уравнениях (8.9) и (8.14) , то получим:

 или 

Кривые, описываемые уравнениями (8.15), называются равносторонними гиперболами.

Пусть задано общее уравнение гиперболы: .

Найдем ее параметры и определим координаты вершин.

Запишем уравнение гиперболы в канонической форме:
Отсюда имеем: и , тогда полуоси гиперболы, а вершины гиперболы имеют координаты:

Парабола. Каноническое уравнение

Параболой называется множество точек плоскости, равноудаленных от фиксированной точки (фокуса) и фиксированной прямой (директрисы).

Выберем на плоскости систему координат (рис. 8.4). Обозначим расстояние от фокуса параболы до директрисы через . Найдем уравнение параболы с фокусом в точке , и директрисой, параллельной оси , с уравнением

Рис. 8.4

Пусть произвольная точка параболы. Тогда согласно определению параболы . По формуле расстояния между двумя точками имеем:

или

Уравнение (8.16) называется каноническим уравнением параболы.
Число — расстояние от фокуса до директрисы — называют параметром параболы.

Анализ уравнения (8.16) позволяет прийти к выводам:
1) парабола симметрична относительно оси , потому переменная входит в
уравнения в второй степени; ось симметрии () называют осью параболы (рис. 8.5 а) переменная не может быть отрицательной ; точка , принадлежащей кривой и является точкой пересечения параболы с ее осью, называется вершиной параболы;
2) при росте по модулю от до  переменная y неограниченно растет по закону . Если , то получаем уравнение параболы , которое известно еще из школьного курса математики.

Парабола с фокусом в точке и директрисой  (Рис. 8.5 в) описывается уравнением:

Рис. 8.5

Задачи на составление канонических уравнений параболы сводятся к отысканию только одной величины — параметра 

Составим каноническое уравнение параболы, проходящей через точку , а ее осью является ось .

Поскольку точка лежит в четвертом квадранте и осью симметрии параболы является ось , то соответствующее уравнение имеет вид: . Подставляем координаты заданной точки в уравнение и находим значение p, при котором оно удовлетворяется:

 или 

Уравнение и определяют ветви параболы. Кривые круга, эллипс и гипербола называются центральными кривыми второго порядка, а парабола — нецентральной; ее эксцентриситетом считается отношение фокального радиуса   произвольной точки параболы до расстояния (рис. 8.4) от этой точки до директрисы, то есть . 

Задача вывода уравнений кривых 2-го порядка усложняется, если центр центральных кривых лежит не в начале координат и (или) оси симметрии не является координатными осями; а для нецентральных кривых — если фокус не лежит на координатной оси и (или) директриса не ортогональная одной из осей координат.

Для установления положение на плоскости кривых 2-го порядка, которые описываются общим уравнением, путем параллельного переноса и (или) поворота исходной системы координат переходят к такой системе координат, в которой общее уравнение приобретает каноническому виду.

Возведение общего уравнения кривой второго порядка к каноническому виду

Выберем на плоскости две системы координат, тогда координаты той же точки в этих системах будут разными.

Задача преобразования координат заключается в том, чтобы найти связь между координатами точек в двух системах координат, одну из которых назовем выходной, вторую — новой. Любую новую систему координат (рис. 8.6) можно получить из исходной системы параллельным переносом, то есть перемещением начала координат в точку с сохранением направления осей (что дает систему координат ), а затем поворотом системы на определенный угол вокруг точки .

Рис. 8.6

Параллельный перенос. Выберем на плоскости произвольную точку . Пусть — исходная, — новая система координат (рис. 8.7) с началом в точке . Тогда пара определяет координаты точки в исходной системе координат, а — координаты этой же точки в новой системе координат.

Рис. 8.7

Введем в рассмотрение радиусы-векторы 

Вектор является разницей векторов  и  что позволяет определить связь между координатами точки в системах координат: 

Соотношения (8.17) называются формулами параллельного переноса.

Поворот осей координат. Установим связь между координатами произвольной точки плоскости в системах с общим началом и различным направлением осей координат. Пусть — исходная, а — новая системы координат (рис. 8.8), тогда пара ( определяет координаты точки в исходной системе координат, а — координаты этой же точки в новой системе координат.

Рис. 8.8

Обозначим через угол поворота исходной системы вокруг точки . Найдем направляющие косинусы новых осей и в исходной системе, или, что то же самое, координаты единичных векторов и новой системы координат в системе :

Найдем проекции вектора на новые оси координат как скалярные произведения этого вектора на направляющие векторы и  соответственно:

Соотношение (8.18) называют формулами поворота осей координат.

Если осуществляется параллельный перенос и поворот осей координат, то исходные координаты , можно определить через новые следующим образом:

Найдем уравнение равносторонней гиперболы в системе координат, которая полученная из исходной системы поворотом вокруг начала координат на угол .

По формуле (8.18) выражаем текущие координаты точек исходной системы через текущие координаты новой системы:

Подставляем выражения для и в исходное уравнение и получаем уравнение гиперболы в новых координатах, асимптотами которой является оси новой системы :

Рассмотрим применение формул параллельного переноса и поворота осей координат до сведения общего уравнения кривой 2-го порядка к каноническому виду.

1. Сведение к каноническому виду общего уравнения, не содержит произведения переменных

Преобразование уравнения (8.20) в уравнение каноническому виду осуществляется с помощью параллельного переноса системы координат, которому предшествует выделение полных квадратов по обоим переменным.

Пусть задано общее уравнение кривой: Определим тип этой кривой и ее параметры. Решение задачи предполагает следующие этапы:
а) устанавливаем тип заданной кривой   уравнение описывает кривую гиперболического типа;

б) группируем в левой части уравнения члены с переменными , и выделяем полные квадраты двучлена с этими переменными:

в) вводим новые координаты: и записываем каноническое уравнение в новой системе с началом в точке

Итак, заданная кривая 2-го порядка является гиперболой с полуосями: и центром в точке

2. Возведение общего уравнения кривой к каноническому виду.

Преобразование этого уравнения в уравнение каноническому виду осуществляется в два этапа:
1-й этап. С помощью поворота осей координат сводим общее уравнение к уравнению (8.20), которое не содержит произведения переменных. Соответствующий угол поворота осей определяется соотношением (выводить его не будем):

откуда по формулам тригонометрии имеем:

где знак выбирается в зависимости от того, в какой четверти находится угол .

По формуле (8.18) выражаем текущие координаты точек исходной системы через текущие координаты новой системы:

что дает возможность получить уравнения относительно переменных и , которое не содержит их произведения.

2-й этап. С помощью параллельного переноса осей координат превращаем уравнение, которое было получено на первом этапе, на уравнение канонического виду.

Замечания. Преобразование общего уравнения кривой 2-го порядка можно начинать с параллельного переноса осей с целью избавиться членов, содержащих переменные в первой степени. В этом случае получают квадратичную форму, которую приводят к каноническому виду известными методами, например, методами Лагранжа, Якоби, Сильвестра. Кроме того применяют аппарат приведения матрицы коэффициентов квадратичной формы к диагональному виду с помощью собственных чисел и собственных векторов этой матрицы. Данные методы являются достаточно громоздкими и выходят за рамки данного учебника.

Приведем еще один пример применения параллельного переноса осей.

Проведем исследование кривой 2-го порядка, заданной общим уравнением:

Это уравнение можно представить в виде дробно линейной функции:

Поделим числитель на знаменатель дроби (8.24), то есть выделяем целую часть дроби, а именно:

Обозначим:

Уравнение (8.25) в новой системе координат приобретает следующий вид:

Следовательно, графиком дробно-линейной функции является гипербола с асимптотами, параллельными осям координат, и центром симметрии в точке 

Квадратичные формы. Применение к превращению уравнений кривой 2-го порядка

Пусть переменные величины. Квадратичной формой называется однородный многочлен второй степени относительно переменных

 

где  коэффициенты при переменных (числовые параметры).

Квадратичная форма , в которой a , называется симметричной:

Квадратичная форма , которая содержит только квадраты переменных, называется канонической (или говорят: имеет канонический вид):

Матрица  составленная из числовых параметров  называется матрицей квадратичной формы, a матрица-столбец  вектором переменных.

Теорема 8.1 (о матричной записи квадратичной формы). Любую квадратичную форму можно представить в матричном виде как произведение двух линейных преобразований, первое из которых тождественно , а матрицей второго есть матрица квадратичной формы: 

Доказательство. С помощью тождественных алгебраических преобразований получаем:

Теорема обобщается на квадратичные формы относительно любого конечного числа переменных:

При переменные обозначают буквами без индексов: .

Теорема 8.2 (о сведении симметричной квадратичной формы к каноническому виду). Если вектор переменных является линейной комбинацией векторов ортонормированного базиса , составленного из собственных векторов матрицы , то симметричная квадратичная форма приобретает каноническому виду:

где  — коэффициенты разложения вектора по базису  собственные числа матрицы симметричной квадратичной формы.

Доказательство. Подставим в матричный запись квадратичной формы вместо его выражение через базис из собственных векторов и матрицы , и раскроем скобки в соответствии со свойствами линейного оператора:

После перехода к ортонормированному базису с учетом свойств: , получаем (8.29).

Если по теореме 8.2 сводить к каноническому виду уравнение кривых второго порядка, то в зависимости от того, каким будет определитель матрицы квадратичной формы  сравнению с нулем, возможны следующие случаи:

кривая эллиптического типа;

кривая гиперболического типа; 

кривая параболического типа.

Покажем справедливость третьего соотношения:

Пусть, тогда 

Найдем собственные числа:

В новом (ортонормированном) базисе уравнением кривой будет квадрат только одной переменной, а значит соответствующая линия является кривой параболического типа.

Аналогично доводятся другие случаи, когда каноническая форма (8.29) содержит слагаемые соответствии с одинаковыми или разными знаками.
Для использования квадратичных форм с целью упрощения уравнений кривых второго порядка коэффициенты при переменных обозначают строчными буквами с индексами:

Сведем к канонической форме общее уравнение кривой

где 

В данном уравнении  для свободного члена предлагается рассмотреть три значения.

а) . Осуществим параллельный перенос так, чтобы в новой системе координат уравнение не имело переменных в первой степени. Для этого переходим к новым координатам:

решаем систему двух линейных уравнений:

определяя таким образом начало новой координатной системы :

В системе кривая описывается уравнением

 

которое в левой части содержит квадратичную форму относительно переменных 

Находим собственные числа матрицы этой квадратичной формы:

Поскольку , то кривая эллиптического типа.

Определяем собственные векторы, принадлежащие каждому собственному числу:

Векторы и составляют ортогональный базис новой системы координат .
Переходим от полученного базиса к ортонормированному:

в котором каноническая форма заданного уравнения имеет вид:

 и описывает воображаемый эллипс.

В системе исходное уравнение принимает вид:

Следовательно, имеем случай вырождения кривой в точку.

 Каноническая форма заданного уравнения в новой системе такова: 

то есть кривой является эллипс с параметрами 

Замечания. Для кривых параболического типа упрощения уравнения начинают, как правило, с поворота осей координат.

В заключение отметим, что существуют величины, составленные из коэффициентов уравнения (и свободного члена), которые не изменяются при переходе от одной прямоугольной декартовой системы координат к другой такой же системы. Эти величины называются инвариантами кривой второго порядка. К ним относятся:
1) сумма коэффициентов при квадратах координат:
2) определитель, образованный из коэффициентов при старших членах:

3) определитель, составленный из параметров уравнения:

По значениям инвариантов, возведенными в табл. 8.1, устанавливают не только тип кривой, но и возможные случаи ее вырождения.

Инварианты кривой второго порядка и распознавания за ними типа кривой           Таблица 8.1

Установим, вырожденная ли линия второго порядка, заданная уравнением:

Вычисляем инварианты кривой и анализируем результаты:

Согласно табл. 8.1 кривая гиперболического типа, распадается на две прямые, пересекающиеся: