Равномерное распределение
Перейдем теперь
к часто используемым на практике
распределениям непрерывной случайной
величины.
Непрерывная с.в.
Х
называется равномерно
распределенной
на отрезке [a,b],
если плотность ее вероятности постоянна
на этом отрезке, а вне его равна 0 (т.е.
случайная величина Х
сосредоточена на отрезке [a,b],
на котором имеет постоянную плотность).
По данному определению плотность
равномерно распределенной на отрезке
[a,b]
случайной величины Х
имеет вид:
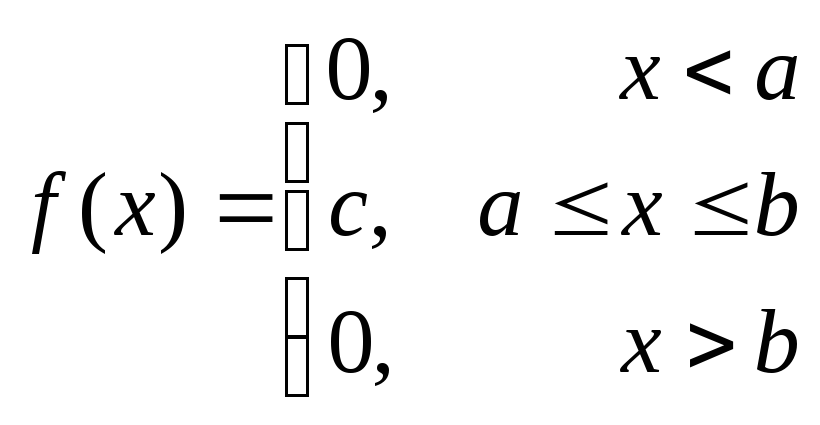
где с
есть некоторое число. Впрочем, его легко
найти, используя свойство плотности
вероятности для с.в., сосредоточенных
на отрезке
[a,b]:
.
Отсюда следует, что,
откуда.
Поэтомуплотность
равномерно распределенной на отрезке
[a,b]
случайной величины Х
имеет вид:

Судить о равномерности
распределения н.с.в. Х
можно из следующего соображения.
Непрерывная случайная величина имеет
равномерное распределение на отрезке
[a,b],
если она принимает значения только из
этого отрезка, и любое число из этого
отрезка не имеет преимущества перед
другими числами этого отрезка в смысле
возможности быть значением этой случайной
величины.
К случайным
величинам, имеющим равномерное
распределение относятся такие величины,
как время ожидания транспорта на
остановке (при постоянном интервале
движения длительность ожидания равномерно
распределена на этом интервале), ошибка
округления числа до целого (равномерно
распределена на [−0.5,
0.5]) и другие.
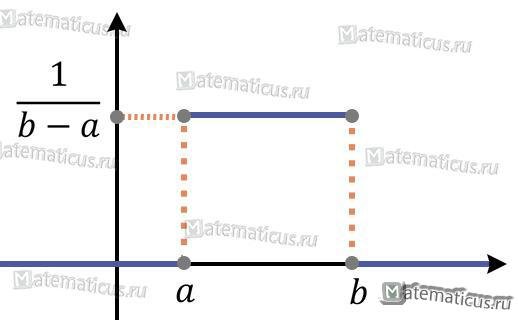
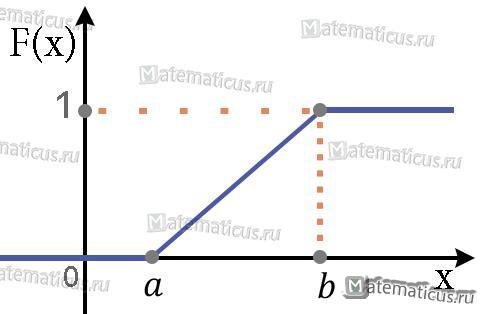
Вид функции
распределения F(x)
равномерно распределенной отрезке
[a,b]
случайной величины Х
ищется по известной плотности вероятности
f(x)
c
помощью формулы их связи
.
В результате соответствующих вычислений
получаем следующую формулу для функции
распределенияF(x)
равномерно распределенной отрезке
[a,b]
случайной величины Х
:

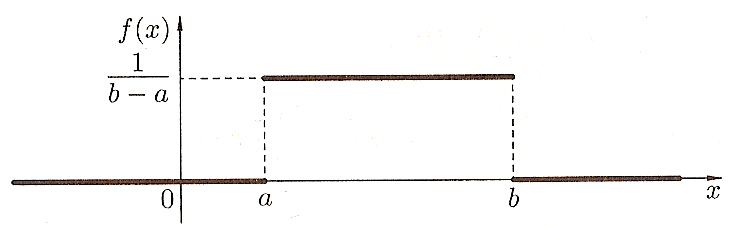
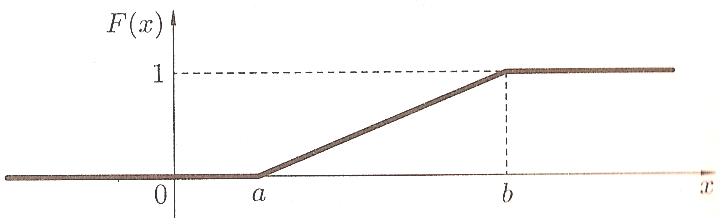
На рисунках
приведены графики плотности вероятности
f(x)
и функции распределения f(x)
равномерно
распределенной отрезке [a,b]
случайной величины Х
:
Математическое
ожидание, дисперсия, среднее квадратическое
отклонение, мода и медиана равномерно
распределенной отрезке [a,b]
случайной величины Х
вычисляются по плотности вероятности
f(x)
обычным образом (и достаточно просто
из-за простого вида f(x)).
В результате получаются следующие
формулы:
,
а модой d(X)
является любое число отрезка [a,b].
Найдем вероятность
попадания равномерно распределенной
отрезке [a,b]
случайной величины Х
в интервал
,
полностью лежащий внутри [a,b].
Учитывая известный вид функции
распределения, получаем:
.
Таким образом,
вероятность попадания равномерно
распределенной отрезке [a,b]
случайной величины Х
в интервал
,
полностью лежащий внутри [a,b],
не зависит от положения этого интервала,
а зависит только от его длины и прямо
пропорциональна этой длине.
Пример.
Интервал движения автобуса составляет
10 минут. Какова вероятность того, что
пассажир, подошедший к остановке, прождет
автобус менее 3 минут? Каково среднее
время ожидания автобуса?
Нормальное распределение
Это распределение
наиболее часто встречается на практике
и играет исключительную роль в теории
вероятностей и математической статистике
и их приложениях, поскольку такое
распределение имеют очень многие
случайные величины в естествознании,
экономике, психологии, социологии,
военных науках и так далее. Данное
распределение является предельным
законом, к которому приближаются (при
определенных естественных условиях)
многие другие законы распределения. С
помощью нормального закона распределения
описываются также явления, подверженные
действию многих независимых случайных
факторов любой природы и любого закона
их распределения. Перейдем к определениям.
Непрерывная
случайная величина называется
распределенной по нормальному
закону (или закону Гаусса),
если ее плотность вероятности имеет
вид:

где числа а
и σ
(σ>0)
являются параметрами этого распределения.
Как уже было
сказано, закон Гаусса распределения
случайных величин имеет многочисленные
приложения. По этому закону распределены
ошибки измерений приборами, отклонение
от центра мишени при стрельбе, размеры
изготовленных деталей, вес и рост людей,
годовое количество осадков, количество
новорожденных и многое другое.
Приведенная
формула плотности вероятности нормально
распределенной случайной величины
содержит, как было сказано, два параметра
а
и σ
, а потому задает семейство функций,
меняющихся в зависимости от значений
этих параметров. Если применить обычные
методы математического анализа
исследования функций и построения
графиков к плотности вероятности
нормального распределения, то можно
сделать следующие выводы.
-
Плотность
вероятности f(x)>0
для всех значений х,
а потому график функции расположен над
осью х. -
Ось х
является асимптотой графика при х
→ ± ∞,
поскольку
.
Поэтому на бесконечности график
«прижимается» к осих. -
Функция f(х)
имеет единственную точку максимума
х=а,
а максимальное значение
.
-
График функции
симметричен относительно вертикальной
прямой с уравнением х=а. -
С помощью второй
производной можно убедиться, что точки
графика
являются точками
его перегиба.
Исходя из полученной
информации, строим график плотности
вероятности f(x)
нормального распределения (он называется
кривой Гаусса − рисунок).
Выясним, как влияет
изменение параметров а
и σ
на форму кривой Гаусса. Очевидно (это
видно из формулы для плотности нормального
распределения), что изменение параметра
а
не меняет форму кривой, а приводит лишь
к ее сдвигу вправо или влево вдоль оси
х.
Зависимость от σ
сложнее. Из проведенного выше исследования
видно, как зависит величина максимуму
и координаты точек перегиба от параметра
σ
. К тому же надо учесть, что при любых
параметрах а
и σ
площадь под кривой Гаусса остается
равной 1 (это общее свойство плотности
вероятности). Из сказанного следует,
что с ростом параметра σ
кривая становится более пологой и
вытягивается вдоль оси х.
На рисунке изображены кривые Гаусса
при различных значениях параметра σ
( σ1<
σ< σ2
) и одном и
том же значении параметра а.
Выясним вероятностный
смысл параметров а
и σ
нормального распределения. Уже из
симметричности кривой Гаусса относительно
вертикальной прямой, проходящей через
число а
на оси х
понятно, что среднее значение (т.е.
математическое ожидание М(Х))
нормально распределенной случайной
величины равно а.
Из этих же соображений мода и медиана
тоже должны быть равны числу а. Точные
расчеты по соответствующим формулам
это подтверждают. Если же мы выписанное
выше выражение для f(x)
подставим в формулу для дисперсии
,
то после (достаточно непростого)
вычисления интеграла получим в ответе
числоσ2.
Таким образом, для случайной величины
Х,
распределенной по нормальному закону,
получились следующие основные ее
числовые характеристики:
.
Поэтому вероятностный
смысл параметров нормального распределения
а
и σ
следующий. Если с.в. Х
распределена нормально с параметрами
а
и σ,
то ее среднее значение равно а,
а среднее квадратическое отклонение
равно σ.
Найдем теперь
функцию распределения F(x)
для случайной величины Х,
распределенной по нормальному закону,
используя выписанное выше выражение
для плотности вероятности f(x)
и формулу
.
При подстановкеf(x)
получается «неберущийся» интеграл.
Все, что удается сделать для упрощения
выражения для F(x),
это представление этой функции в виде:
,
где Ф(х)
− так называемая функция
Лапласа,
которая имеет вид

Интеграл, через
который выражается функция Лапласа,
тоже является неберущимися (но при
каждом х
этот интеграл может быть вычислен
приближенно с любой наперед заданной
точностью). Однако вычислять его и не
потребуется, так как в конце любого
учебника по теории вероятностей есть
таблица для определения значений функции
Ф(х)
при заданном значении х.
В дальнейшем нам понадобится свойство
нечетности функции Лапласа: Ф(−х)=
−Ф(х)
для всех
чисел х.
Найдем теперь
вероятность того, что нормально
распределенная с.в. Х
примет значение из заданного числового
интервала (α,
β). Из общих
свойств функции распределения Р(α<X<
β)=F(β)
−
F(α).
Подставляя α
и
β в выписанное
выше выражение для F(x),
получим
.
Как сказано выше,
если с.в. Х
распределена нормально с параметрами
а
и σ,
то ее среднее значение равно а,
а среднее квадратическое отклонение
равно σ.
Поэтому среднее
отклонение значений этой с.в. при
испытании от числа а
равно σ. Но
это среднее отклонение. Поэтому возможны
и бо´льшие отклонения. Узнаем, насколько
возможны те или иные отклонения от
среднего значения. Найдем вероятность
того, что значение распределенной по
нормальному закону случайной величины
Х
отклониться от ее среднего значения
М(Х)=а
менее, чем на некоторое число δ, т.е.
Р(|X−a|<δ
) :
.
Таким образом,
.
Подставляя в это
равенство δ=3σ,
получим вероятность того, что значение
с.в. Х
(при одном испытании) отклонится от
среднего значения менее чем на утроенное
значение σ
(при среднем отклонении, как мы помним,
равном σ):
(значениеФ(3)
взято из таблицы значений функции
Лапласа). Это почти 1
! Тогда
вероятность противоположного события
(что значение отклонится не менее, чем
на 3σ)
равна 1−0.997=0.003,
что очень близко к 0.
Поэтому это событие «почти невозможно»
−
случается крайне редко (в среднем 3
раза из 1000).
Это рассуждение является обоснованием
широко известного «правила трех сигм».
Правило трех
сигм. Нормально
распределенная случайная величина при
единичном испытании
практически не отклоняется от своего
среднего далее, чем на 3σ.
Еще раз подчеркнем,
что речь идет об одном испытании . Если
испытаний случайной величины много, то
вполне возможно, что какое-либо ее
значение и удалится от среднего далее,
чем 3σ.
Это подтверждает следующий
Пример.
Какова вероятность, что при 100 испытаниях
нормально распределенной случайной
величины Х
хотя бы одно ее значение отклонится от
среднего более, чем на утроенное среднее
квадратическое отклонение? А при 1000
испытаниях?
Решение. Пусть
событие А
означает, что при испытании случайной
величины Х
ее значение отклонилось от среднего
более, чем на 3σ.
Как только
что было выяснено, вероятность этого
события
р=Р(А)=0.003 . Проведено
100 таких испытаний. Надо узнать вероятность
того, что событие А
произошло хотя
бы раз, т.е.
произошло от 1
до 100
раз. Это типичная задача схемы Бернулли
с параметрами n=100
(число независимых испытаний), р=0.003
(вероятность события А
в одном испытании), q=1−p=0.997.
Требуется найти Р100(1≤k≤100).
В данном случае, конечно, проще найти
сначала вероятность противоположного
события Р100(0)
− вероятность того, что событие А
не произошло ни разу ( т.е. произошло 0
раз) . Учитывая связь вероятностей самого
события и ему противоположного, получим:
.
Не так уж мало.
Вполне может произойти (происходит в
среднем в каждой четвертой такой серии
испытаний). При 1000
испытаний по такой же схеме можно
получить, что вероятность хотя бы одного
отклонения далее, чем на 3σ,
равно:
. Так что можно с большой уверенностью
дождаться хотя бы одного такого
отклонения.
Пример.
Рост
мужчин определенной возрастной группы
распределен нормально с математическим
ожиданием a,
и среднеквадратическим отклонением σ.
Какую долю костюмов k-го
роста следует предусмотреть в общем
объеме производства для данной возрастной
группы, если k-ый
рост определяется следующими пределами:
1
рост:
158 −
164см
2 рост:
164 − 170см
3 рост:
170 − 176см
4 рост:
176 − 182см
Решение.
Решим задачу при следующих значениях
параметров: а=178,
σ=6, k=3.
Пусть
с.в. Х
−
рост случайно выбранного мужчины (она
распределена по условию нормально с
заданными параметрами). Найдем вероятность
того, что наугад выбранному мужчине
понадобится 3-й
рост. Пользуясь нечетностью функции
Лапласа Ф(х)
и таблицей ее значений:
P(170<X<176)
=Ф((176−178)/6) − Ф((170−178)/6) = Ф(−0.3333)
−Ф(−1.3333)=
Ф(1.3333) −Ф(0.3333)=0.4082−0.1293=0.2789.
Поэтому в общем объеме производства
надо предусмотреть 0.2789*100%=27.89%
костюмов 3-го
роста.
Равномерное случайное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Равномерным называют распределение вероятностей непрерывной случайной величины
, если на интервале
, которому принадлежат все возможные
значения
, плотность сохраняет постоянное значение.
Функция распределения
равномерного закона:
Числовые характеристики равномерного распределения
Математическое ожидание равномерно распределенной случайной величины:
Дисперсия
равномерного случайного
распределения:
Среднее квадратическое отклонение случайной величины, распределенной равномерно:
Для равномерного распределения коэффициент асимметрии:
Коэффициент эксцесса
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Кроме равномерного, основные законы распределения непрерывных случайных величин:
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Экспоненциальный (показательный) закон распределения случайной величины
Примеры решения задач
Пример 1
Все
значения равномерно распределенной случайной величины X лежат на отрезке [2;8].
Найти вероятность попадания случайной величины X в промежуток (1;5).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность вероятности
равномерного распределения на интервале
:
Искомая вероятность:
Ответ:
.
Пример 2
Случайная
величина X равномерно распределена на интервале (2;7). Составить f(x), F(x),
построить графики. Найти M(X), D(X).
Решение
Плотность
вероятности случайной величины, распределенной равномерно на интервале
В нашем
случае
Получаем:
Функцию
распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
Построим
графики:
График плотности распределения
График функции распределения
Математическое
ожидание величины, распределенной равномерно:
Дисперсия:
Среднее
квадратическое отклонение:
Пример 3
Минутная
стрелка электрических часов перемещается скачком в конце каждой минуты. Найти
вероятность того, что в данное мгновение часы покажут время, которое отличается
от истинного не более чем на 20 с.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
равномерного распределения:
Вероятность
того, что в данное мгновение часы покажут время, которое отличается от
истинного не более чем на 20 с:
Ответ:
Пример 4
Пассажир
метро в случайный момент времени приходит на платформу. Известно, что среднее
квадратическое отклонение времени ожидания поезда равно 0,8 мин. Найти интервал
времени следования поездов в метро.
Решение
Дисперсия
равномерного распределения:
при
начале интервала
:
Искомый
интервал времени:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Случайные
величины X2, X3, X4 имеют равномерное,
показательное и нормальное распределения соответственно. Найти вероятности
P(3<Xi<6), если у этих случайных величин
математические ожидания и средние квадратические отклонения равны 3.
Задача 2
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите M(X), D(X),σ, xmod, xmed, если известно, что
случайная величина X имеет равномерное распределение с параметрами a=2 и b=4.
Задача 3
Найти: M(X) НСВ X,
распределенной равномерно в интервале (1;9); функцию распределения F(x) и
функцию плотности вероятности f(x); вероятность попадания
НСВ X в интервал (2;7).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Непрерывная случайная величина X равномерно распределена на сегменте [1; 8.5].
Найти:
1) дифференциальную и интегральную
функцию распределения, а также построить их графики.
2) математическое ожидание и
дисперсию;
2) вероятность того, что X примет какое-нибудь значение из интервала (1;20).
Задача 5
Интервал движения парома 3 часа.
Найти: а) числовые характеристики времени ожидания для случайного пассажира; б)
вероятность времени ожидания менее 40 минут.
Задача 6
Равномерно распределенная случайная
величина
задана
плотностью распределения f(x)=0.125 в интервале (1;9) и f(x)=0 вне его.
Найти M(X), D(X), σ(X).
Задача 7
Случайная
величина X равномерно распределена на отрезке [5;11]. Найдите
математическое ожидание X, дисперсию X,
медиану, P(7<X<15), x0.2.
Задача 8
Случайная
величина
равномерно распределена на отрезке [-1;9].
Запишите функцию плотности распределения, изобразите ее график. Найдите
вероятность того, что X примет значение в
интервале (-3;2). Найдите математическое ожидание X и медиану. Укажите
найденные значения на графике f(x).
Задача 9
Вычислить
вероятность того, что при 10 испытаниях значение X три раза попадет в
интервал [-1;1], если случайная величина X распределена по
равномерному закону на интервале [0;4].
Задача 10
Трамваи
данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной
остановке в некоторый момент времени. Какова вероятность появления пассажира не
ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2
мин до отхода следующего трамвая?
Задача 11
Найти
функцию распределения, плотность, математическое ожидание и дисперсию случайной
величины, распределенной равномерно на отрезке [2,4].
Задача 12
Цена
деления шкалы прибора равна 0,4. Показания прибора округляют до ближайшего
деления. Найти вероятность того, что при отсчете будет сделана ошибка
округления, большая 0,05.
Задача 13
СВ X
распределена равномерно в промежутке [1∕3,5∕4]. Найти функцию плотности
распределения f(x), функцию распределения F(x),
математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X). Построить
графики функций f(x) и F(x). Найти вероятность того, что x∈[1,5∕4].
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Шкала
рычажных весов, установленных в лаборатории, имеет цену делений 1 г. При
измерении массы химических компонентов смеси отсчет делается с точностью до
целого деления с округлением в ближайшую сторону. Какова вероятность, что
абсолютная ошибка определения массы будет заключена между значениями σ и 2σ.
Задача 15
Автобусы
некоторого маршрута идут строго по расписанию с интервалом 5 мин. Найти
вероятность того, что пассажир, подошедший к остановке будет ждать очередного
автобуса меньше трех минут.
Задача 16
Все
значения равномерно распределенной случайной величины Х принадлежат отрезку
[2,8]. Найти вероятность попадания случайной величины X в отрезок [3,5].
Задача 17
Случайная величина X имеет равномерное распределение на отрезке [1,6].
Найти дисперсию D(X) и вероятность попадания случайной величины X в интервал (2,4).
Задача 18
По маршруту
независимо друг от друга ходит два автобуса: №20 –через 10 и №15 –через 7
минут. Студент приходит на остановку в случайный момент. Какова вероятность
того, что ему придется ждать автобус менее трех минут.
Задача 19
Автобусы идут с интервалом 5 минут.
Считая, что случайная величина X – время
ожидания автобуса на остановке, распределена равномерно на указанном интервале,
найти среднее время ожидания и дисперсию времени ожидания.
Задача 20
Шкала
секундомера имеет цену деления 0,2 с. Какова вероятность сделать по этому
секундомеру отсчет времени с ошибкой менее 0,05 с, если отсчет делается наудачу
с округлением в ближайшую сторону, до целого деления?
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Закон равномерного движения
Случайную величину равномерно распределённой на интервале (a, b) и её плотность вероятности равна некоторой постоянной величине на этом интервале и нулю вне него.
a, b — параметры распределения.
Таким образом, случайная непрерывная величина X имеет равномерное распределение, если она принимает значения хi (где i=1…n, n — независимые испытания) с одинаковыми вероятностями,
$pleft( {{x_i}} right) = frac{1}{n}$
Случайная величина X на промежутке от а до b имеет равномерное распределение, если плотность распределение равна
на заданном промежутке, а вне его р(х)=0
График плотности вероятности
или плотность распределения можно записать в виде:
Функция распределения в этом случае имеет вид:
График функции распределения
Математическое ожидание случайной непрерывной величины X вычисляется следующим образом:
Математическое ожидание получается из выражения:
[Mleft( X right) = intlimits_a^b {xfleft( x right)dx = frac{1}{{left( {b — a} right)}}intlimits_a^b {xdx = left. {frac{{{x^2}}}{{2left( {b — a} right)}}} right|} _a^b = frac{{{b^2} — {a^2}}}{{2left( {b — a} right)}} = frac{{left( {b + a} right)}}{2}} ]
Дисперсия случайной непрерывной величины X вычисляется следующим образом:
Дисперсия выводится из выражения:
$Dleft( X right) = intlimits_a^b {{x^2}fleft( x right)dx — {{left[ {Mleft( X right)} right]}^2} = frac{1}{{left( {b — a} right)}}} {intlimits_a^b {{x^2}dx — left[ {frac{{a + b}}{2}} right]} ^2} = $
$=left. {frac{{{x^3}}}{{3left( {b — a} right)}}} right|_a^b — {left[ {frac{{a + b}}{2}} right]^2} = frac{{{a^2} + ab + {b^2}}}{3} — {left[ {frac{{a + b}}{2}} right]^2}= frac{{{{left( {b — a} right)}^2}}}{{12}}$
Среднее квадратическое отклонение (СКО) равно:
[sigma left( X right) = sqrt {Dleft( X right)} = sqrt {frac{{{{left( {b — a} right)}^2}}}{{12}}} = frac{{left( {b — a} right)sqrt 3 }}{6}]
Медиана равна:
$frac{{a + b}}{2}$
Мода:
Любое число из отрезка [a, b]
Пример 1
Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 10 с.
Решение
В условии задачи, случайная непрерывная величина X — это показание часов, которая соответствует равномерному закону распределения СВ в диапазоне от 0 секунд до 60 секунд.
Вычислим плотность распределения данной СВ:
$pleft( x right) = frac{1}{{60 — 0}} = frac{1}{60}$
Это событие может произойти либо в интервале (0; 10), либо в интервале (50; 60), то есть стрелка может переместиться как вправо, так и влево на на 10 с и данные два события независимые. По теореме сложения, получаем
Р(0<X<10)+Р(50<X<60)
Подставляя значения в формулу, имеем
Пример 2
Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете
будет сделана ошибка:
а) меньшая 0,04;
б) большая 0,05
Решение
а) Найдем вероятность того, что при отсчете будет сделана ошибка меньшая 0,04 через интеграл:
б) Аналогично, большая 0,05
Пример 3
Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин.
Решение
Плотность распределения равномерной случайной величины равна:
$pleft( x right) = frac{1}{{5 — 0}} = frac{1}{5}$
Вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин равна:
Пример 4
Ребро куба х измерено приближенно, причем а≤х≤b. Рассматривая ребро куба как случайную величину X, распределенную равномерно в интервале (а;b), найти математическое ожидание и дисперсию объема куба.
Решение
Плотность распределения случайной величины равна:
В виду того, что X3 , тогда математическое ожидание:
Найдём дисперсию:
From Wikipedia, the free encyclopedia


|
Probability density function
|
|
|
Cumulative distribution function |
|
| Notation |
![{displaystyle {mathcal {U}}_{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/906b38f0905adef68e3c8c7ca6de15858f7742ce) |
|---|---|
| Parameters |
 |
| Support |
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) |
![{displaystyle {begin{cases}{frac {1}{b-a}}&{text{for }}xin [a,b]\0&{text{otherwise}}end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/648692e002b720347c6c981aeec2a8cca7f4182f) |
|
| CDF |
![{displaystyle {begin{cases}0&{text{for }}x<a\{frac {x-a}{b-a}}&{text{for }}xin [a,b]\1&{text{for }}x>bend{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2948c023c98e2478806980eb7f5a03810347a568) |
| Mean |
 |
| Median |
 |
| Mode |
 |
| Variance |
 |
| MAD |
 |
| Skewness |
 |
| Ex. kurtosis |
 |
| Entropy |
 |
| MGF |
 |
| CF |
 |
In probability theory and statistics, the continuous uniform distributions or rectangular distributions are a family of symmetric probability distributions. Such a distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds.[1] The bounds are defined by the parameters, 

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




Definitions[edit]
Probability density function[edit]
The probability density function of the continuous uniform distribution is:
The values of 



![{displaystyle [c,d],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9d224646c92ef76fbe024ed2eb56cb2964cab95)





Any probability density function integrates to 


In terms of mean 

Cumulative distribution function[edit]
The cumulative distribution function of the continuous uniform distribution is:
Its inverse is:
In terms of mean 

its inverse is:
Example 1. Using the continuous uniform distribution function[edit]
For a random variable 

In a graphical representation of the continuous uniform distribution function ![{displaystyle [f(x){text{ vs }}x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d57d12780dd2f37ecebcef1541f0fdccf1d5358e)


Example 2. Using the continuous uniform distribution function (conditional)[edit]
For a random variable 

The example above is a conditional probability case for the continuous uniform distribution: given that 






Generating functions[edit]
Moment-generating function[edit]
The moment-generating function of the continuous uniform distribution is:[6]
[7]
from which we may calculate the raw moments 
For a random variable following the continuous uniform distribution, the expected value is 

For the special case 
the moment-generating function reduces to the simple form:
Cumulant-generating function[edit]
For 

![{displaystyle [-{tfrac {1}{2}},{tfrac {1}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cb7c3f1928e147f684b9cba323e45f0840c4ef4)



Standard uniform distribution[edit]
The continuous uniform distribution with parameters 


One interesting property of the standard uniform distribution is that if 






Relationship to other functions[edit]
As long as the same conventions are followed at the transition points, the probability density function of the continuous uniform distribution may also be expressed in terms of the Heaviside step function as:
or in terms of the rectangle function as:
There is no ambiguity at the transition point of the sign function. Using the half-maximum convention at the transition points, the continuous uniform distribution may be expressed in terms of the sign function as:
Properties[edit]
Moments[edit]
The mean (first raw moment) of the continuous uniform distribution is:
The second raw moment of this distribution is:
In general, the 
The variance (second central moment) of this distribution is:
Order statistics[edit]
Let 






The expected value is:
This fact is useful when making Q–Q plots.
The variance is:
See also: Order statistic § Probability distributions of order statistics
Uniformity[edit]
The probability that a continuously uniformly distributed random variable falls within any interval of fixed length is independent of the location of the interval itself (but it is dependent on the interval size 
Indeed, if 
![{displaystyle [x,x+ell ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884130fbd3c593f4108f325e7ce5f5724e808872)
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

which is independent of 
Generalization to Borel sets[edit]
This distribution can be generalized to more complicated sets than intervals. Let 






[edit]
- If X has a standard uniform distribution, then by the inverse transform sampling method, Y = − λ−1 ln(X) has an exponential distribution with (rate) parameter λ.
- If X has a standard uniform distribution, then Y = Xn has a beta distribution with parameters (1/n,1). As such,
- The standard uniform distribution is a special case of the beta distribution, with parameters (1,1).
- The Irwin–Hall distribution is the sum of n i.i.d. U(0,1) distributions.
- The sum of two independent, equally distributed, uniform distributions yields a symmetric triangular distribution.
- The distance between two i.i.d. uniform random variables also has a triangular distribution, although not symmetric.
Statistical inference[edit]
Estimation of parameters[edit]
Estimation of maximum[edit]
Minimum-variance unbiased estimator[edit]
Given a uniform distribution on ![{displaystyle [0,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba22e25e8f8604f012c599a7d4962562c4bb3f02)

where 

Maximum likelihood estimator[edit]
The maximum likelihood estimator is:
where 

Method of moment estimator[edit]
The method of moments estimator is:
where 
Estimation of midpoint[edit]
The midpoint of the distribution, 
Confidence interval[edit]
For the maximum[edit]
Let 
![{displaystyle U_{[0,L]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e995684064674d2d06963db2a581277bfa0c0e6)



where
is the indicator function of
The confidence interval given before is mathematically incorrect, as
cannot be solved for 

for
for any unknown but valid
one then chooses the smallest 

Occurrence and applications[edit]
The probabilities for uniform distribution function are simple to calculate due to the simplicity of the function form.[2] Therefore, there are various applications that this distribution can be used for as shown below: hypothesis testing situations, random sampling cases, finance, etc. Furthermore, generally, experiments of physical origin follow a uniform distribution (e.g. emission of radioactive particles).[1] However, it is important to note that in any application, there is the unchanging assumption that the probability of falling in an interval of fixed length is constant.[2]
Economics example for uniform distribution[edit]
In the field of economics, usually demand and replenishment may not follow the expected normal distribution. As a result, other distribution models are used to better predict probabilities and trends such as Bernoulli process.[10] But according to Wanke (2008), in the particular case of investigating lead-time for inventory management at the beginning of the life cycle when a completely new product is being analyzed, the uniform distribution proves to be more useful.[10] In this situation, other distribution may not be viable since there is no existing data on the new product or that the demand history is unavailable so there isn’t really an appropriate or known distribution.[10] The uniform distribution would be ideal in this situation since the random variable of lead-time (related to demand) is unknown for the new product but the results are likely to range between a plausible range of two values.[10] The lead-time would thus represent the random variable. From the uniform distribution model, other factors related to lead-time were able to be calculated such as cycle service level and shortage per cycle. It was also noted that the uniform distribution was also used due to the simplicity of the calculations.[10]
Sampling from an arbitrary distribution[edit]
The uniform distribution is useful for sampling from arbitrary distributions. A general method is the inverse transform sampling method, which uses the cumulative distribution function (CDF) of the target random variable. This method is very useful in theoretical work. Since simulations using this method require inverting the CDF of the target variable, alternative methods have been devised for the cases where the CDF is not known in closed form. One such method is rejection sampling.
The normal distribution is an important example where the inverse transform method is not efficient. However, there is an exact method, the Box–Muller transformation, which uses the inverse transform to convert two independent uniform random variables into two independent normally distributed random variables.
Quantization error[edit]
In analog-to-digital conversion, a quantization error occurs. This error is either due to rounding or truncation. When the original signal is much larger than one least significant bit (LSB), the quantization error is not significantly correlated with the signal, and has an approximately uniform distribution. The RMS error therefore follows from the variance of this distribution.
Random variate generation[edit]
There are many applications in which it is useful to run simulation experiments. Many programming languages come with implementations to generate pseudo-random numbers which are effectively distributed according to the standard uniform distribution.
On the other hand, the uniformly distributed numbers are often used as the basis for non-uniform random variate generation.
If 



History[edit]
While the historical origins in the conception of uniform distribution are inconclusive, it is speculated that the term «uniform» arose from the concept of equiprobability in dice games (note that the dice games would have discrete and not continuous uniform sample space). Equiprobability was mentioned in Gerolamo Cardano’s Liber de Ludo Aleae, a manual written in 16th century and detailed on advanced probability calculus in relation to dice.[11]
See also[edit]
- Discrete uniform distribution
- Beta distribution
- Box–Muller transform
- Probability plot
- Q–Q plot
- Rectangular function
- Irwin–Hall distribution — In the degenerate case where n=1, the Irwin-Hall distribution generates a uniform distribution between 0 and 1.
- Bates distribution — Similar to the Irwin-Hall distribution, but rescaled for n. Like the Irwin-Hall distribution, in the degenerate case where n=1, the Bates distribution generates a uniform distribution between 0 and 1.
References[edit]
- ^ a b c Dekking, Michel (2005). A modern introduction to probability and statistics : understanding why and how. London, UK: Springer. pp. 60–61. ISBN 978-1-85233-896-1.
- ^ a b c Walpole, Ronald; et al. (2012). Probability & Statistics for Engineers and Scientists. Boston, USA: Prentice Hall. pp. 171–172. ISBN 978-0-321-62911-1.
- ^ Park, Sung Y.; Bera, Anil K. (2009). «Maximum entropy autoregressive conditional heteroskedasticity model». Journal of Econometrics. 150 (2): 219–230. CiteSeerX 10.1.1.511.9750. doi:10.1016/j.jeconom.2008.12.014.
- ^ a b c «Uniform Distribution (Continuous)». MathWorks. 2019. Retrieved November 22, 2019.
- ^ a b c Illowsky, Barbara; et al. (2013). Introductory Statistics. Rice University, Houston, Texas, USA: OpenStax College. pp. 296–304. ISBN 978-1-938168-20-8.
- ^ Casella & Berger 2001, p. 626
- ^ https://www.stat.washington.edu/~nehemyl/files/UW_MATH-STAT395_moment-functions.pdf[bare URL PDF]
- ^ https://galton.uchicago.edu/~wichura/Stat304/Handouts/L18.cumulants.pdf[bare URL PDF]
- ^ Nechval KN, Nechval NA, Vasermanis EK, Makeev VY (2002) Constructing shortest-length confidence intervals. Transport and Telecommunication 3 (1) 95-103
- ^ a b c d e Wanke, Peter (2008). «The uniform distribution as a first practical approach to new product inventory management». International Journal of Production Economics. 114 (2): 811–819. doi:10.1016/j.ijpe.2008.04.004 – via Research Gate.
- ^ Bellhouse, David (May 2005). «Decoding Cardano’s Liber de Ludo». Historia Mathematica. 32: 180–202. doi:10.1016/j.hm.2004.04.001.
Further reading[edit]
- Casella, George; Roger L. Berger (2001), Statistical Inference (2nd ed.), ISBN 978-0-534-24312-8, LCCN 2001025794
External links[edit]
- Online calculator of Uniform distribution (continuous)
| Плотность вероятности Плотность непрерывного равномерного распределения |
|
| Функция распределения Функция распределения непрерывного равномерного распределения |
|
| Параметры |  , ,  — коэффициент сдвига, — коэффициент сдвига,  — коэффициент масштаба — коэффициент масштаба
|
| Носитель | 
|
| Плотность вероятности | 
|
| Функция распределения | 
|
| Математическое ожидание | 
|
| Медиана | 
|
| Мода | любое число из отрезка ![{displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
|
| Дисперсия | 
|
| Коэффициент асимметрии | 
|
| Коэффициент эксцесса | 
|
| Информационная энтропия | 
|
| Производящая функция моментов | 
|
| Характеристическая функция | 
|
Непреры́вное равноме́рное распределе́ние — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Определение
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке ![{displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


Пишут: ![{displaystyle Xsim U[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d509fb56e608a786132dbf75361145b770d13b)




Функция распределения
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка ![{displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
.
Производящая функция моментов
Простым интегрированием получаем:
,
откуда находим все интересующие моменты непрерывного равномерного распределения:
,
,
.
Вообще,
.
Стандартное равномерное распределение
Если 

![{displaystyle Xsim U[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3610abb42eb437d4b299a01c755ba35989970ea)
- Если случайная величина
, и
, где
, то
.
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
См. также
- Дискретное равномерное распределение;
- Метод обратного преобразования.
|
править |
bn:সম-বিন্যাস (অবিচ্ছিন্ন)
da:Ligefordeling
eo:Kontinua uniforma distribuo
he:התפלגות אחידה
nl:Uniforme verdeling (continu)
no:Uniform sannsynlighetsmodell
pl:Rozkład jednostajny
su:Sebaran seragam#Kasus_kontinyu
sv:Likformig sannolikhetsfördelning



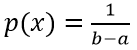
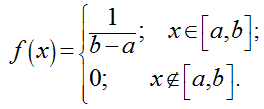
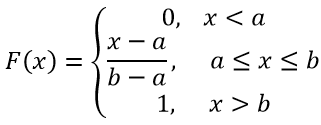
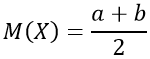
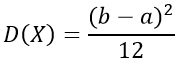
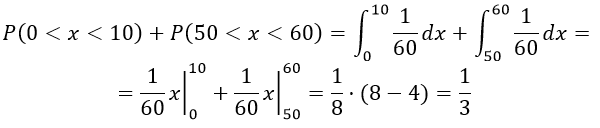
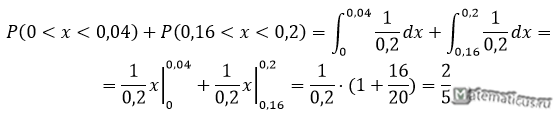
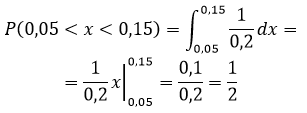
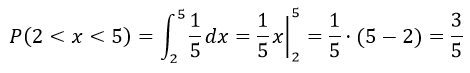
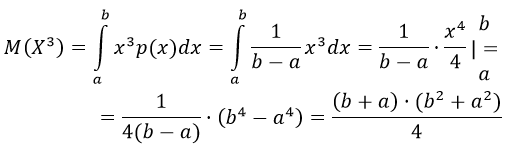



![{displaystyle f(x)={begin{cases}{frac {1}{b-a}}&{text{for }}aleq xleq b,\[8pt]0&{text{for }}x<a {text{ or }} x>b.end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1592bd4a48c6e3defe80032e220d1b4c0ef1e0f5)

![{displaystyle F(x)={begin{cases}0&{text{for }}x<a,\[8pt]{frac {x-a}{b-a}}&{text{for }}aleq xleq b,\[8pt]1&{text{for }}x>b.end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32f8fa14b36ce1147021a210b875bcc4b91d24a3)









![{displaystyle f(x)={begin{cases}{frac {1}{2b}}&{text{for }}-bleq xleq b,\[8pt]0&{text{otherwise}};end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/528f4cb42767408146084a01d1836f80926a6458)










![{displaystyle P{big (}Xin [x,x+ell ]{big )}=int _{x}^{x+ell }{frac {dy}{b-a}}={frac {ell }{b-a}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bf0fab14e4d142e28c428c6f7575ba448bd73d0)



![{displaystyle f(t)=n{frac {1}{L}}left({frac {t}{L}}right)^{n-1}!=n{frac {t^{n-1}}{L^{n}}}1!!1_{[0,L]}(t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb994d51861c2c29398652df1cf3c2b79caf0a)
![{displaystyle 1!!1_{[0,L]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79cff43b95a58c16bc9a5d97be265cabd4a635bb)
![{displaystyle [0,L].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/865dd4a189168d3c11e65b12bbb7880568652e1f)
![{displaystyle Pr {big (}[{hat {theta }},{hat {theta }}+varepsilon ]ni theta {big )}geq 1-alpha }](https://wikimedia.org/api/rest_v1/media/math/render/svg/551b3f94638b0326d17c9d4dca7536f6ceeb3826)
![{displaystyle Pr {big (}[{hat {theta }},{hat {theta }}(1+varepsilon )]ni theta {big )}geq 1-alpha }](https://wikimedia.org/api/rest_v1/media/math/render/svg/76d99f8778c0be6fce3a7ac95c58b20b2f1a9c0d)


![{displaystyle f_{X}(x)=left{{begin{matrix}{1 over b-a},&xin [a,b]\0,&xnot in [a,b]end{matrix}}right..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4039fd993e626203670e60134ceb7e7929a5df3)



![{displaystyle mathbb {E} left[Xright]={frac {a+b}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3529daac6c04d15e40b6dc193b3b14d67f01ad)
![{displaystyle mathbb {E} left[X^{2}right]={frac {a^{2}+ab+b^{2}}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94a9118d445bc34cfb654224f1e06635edfdda79)

![{displaystyle mathbb {E} left[X^{n}right]={frac {1}{n+1}}sum limits _{k=1}^{n}{a^{k}b^{n-k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b0dff464b7d6318a2255f0fe3722f8e90fb08ea)


![{displaystyle Ysim U[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5417fbdca4f361c01d679c458e937f8ae6a17675)