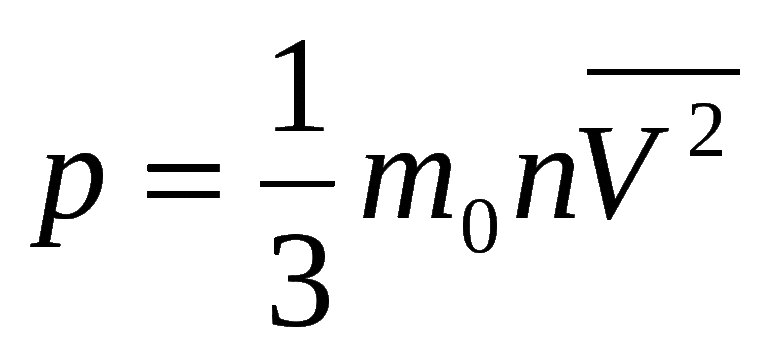Как найти парциальное давление смеси газов - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

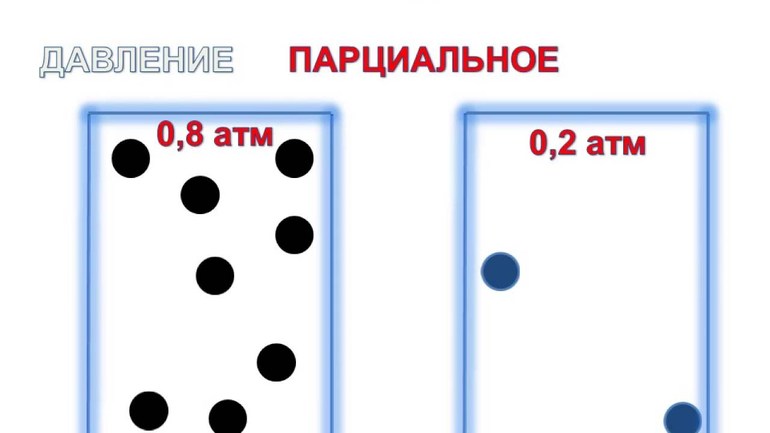
В химии «парциальным давлением» называют давление, которое оказывает отдельно взятый компонент из газовой смеси внешней среды, например, на колбу, баллон или границу атмосферы. Вы можете подсчитать давление каждого газа, если знаете его количество, какой объем он занимает и какова его температура. Затем вы можете сложить парциальные давления и найти общее парциальное давление смеси газов, или найдите вначале общее давление, а затем — парциальное.

1
Примите каждый газ как «идеальный». В химии «идеальный газ» — тот, который взаимодействует с другими веществами, не вступая с ними в соединение. Отдельные молекулы могут сталкиваться друг с другом и отталкиваться, как шары для бильярда, не деформируясь при этом.^[1]
- Давление идеального газа возрастает, если его поместить в меньший объем, и уменьшается, если газ находится в большем объеме. Это отношение называется законом Бойля-Мариотта, по имени ученых Роберта Бойля и Эдма Мариотта. Математическая запись закона: k = P x V или, упрощенно, k = PV, где k представляет константу соотношения, P — давление, а V — объем.^[2]
- Давление может быть указано в нескольких различных единицах. Одна из них, Паскаль (Па), определяется как сила в 1 ньютон, приложенная к площади в 1 квадратный метр. Другой вариант представления давления — в атмосферах (атм). Эта единица определяется как давление земной атмосферы на уровне моря. Давление в 1 атмосферу равно 101,325 Па.^[3]
- Температура идеального газа возрастает при увеличении его объема и снижается при уменьшении объема. Это отношение называют законом Чарльза, по имени Жака Чарльза. Математическая запись закона: k = V / T, где k — константа соотношения между объемом и температурой, V вновь представляет объем газа, а T — его температуру.^[4]^[5]
- Температура газов в этих уравнениях приведена в градусах Кельвина, ее можно найти, прибавив 273 к числу градусов Цельсия в температуре газа.
- Эти два отношения можно объединить в одно уравнение: k = PV / T, которое также можно записать как PV = kT.
2
Определите количество газов. У газов есть и масса, и объем. Объем обычно измеряют в литрах (л), но есть два варианта подсчета массы.
- Обычно массу измеряют в граммах или, если она достаточно велика, в килограммах.
- Поскольку газы обычно весят очень мало, их масса также вычисляется в отдельной единице измерения, называемой молекулярной массой, или молярной массой. Молярная масса определяется как сумма атомарных весов всех атомов в газообразном веществе, каждый атом сравнивается с массой карбона (12)^[6]
- Поскольку атомы и молекулы слишком малы, чтобы работать с ними непосредственно, количество газа определяется в молях. Количество молей в данном газе можно найти, разделив массу на молярную массу, значение отмечается буквой n.
- Мы можем заменить постоянную k константу в уравнении газа числом n, количеством молей (mol), и ввести новую константу R. Тогда уравнение будет записано в виде nR = PV/T или PV = nRT.^[7]
- Значение R зависит от единиц, в которых измеряются давление газа, объемы и температура. Для объема в литрах, температуры в Кельвинах и давления в атмосферах, значение равно 0,0821 л атм/K мол. Это можно записать в виде 0,0821 л атм K^-1 мол ^-1, чтобы избежать использования разделительной черты при указании единиц измерения.^[8]
3
Понимание закона Дальтона о парциальном давлении. Закон, открытый химиком и физиком Джоном Дальтоном, который первым предположил, что химические элементы состоят из отдельных атомов,^[9] гласит: общее давление смеси газов равняется сумме давлений каждого газа в смеси.
- Закон Дальтона можно записать в таком виде: P_общее = P₁ + P₂ + P₃ … с таким количеством слагаемых после знака равенства, каково количество газов в смеси.
- Уравнение закона Дальтона можно расширить при работе с газами, чье индивидуальное давление неизвестно, но для которых известны температура и объем. Парциальное давление газа — такое же, как и для равного объема газа, полностью занимающего отведенный объем.
- Для каждого парциального давления мы можем переписать уравнение идеального газа. Вместо PV = nRT мы может оставить только P в левой части перед знаком равенства. Чтобы сделать это, обе части уравнения нужно разделить на V: PV/V = nRT/V. Две V слева сокращаются, остается P = nRT/V.
- Затем для каждого P справа мы можем выполнить замену, вписав уравнение парциального давления: P_общее =(nRT/V) ₁ + (nRT/V) ₂ + (nRT/V) ₃ …
Реклама

1
Определите уравнение парциального давления для газов, с которыми вы работаете. Для вычислительных целей возьмем пример: в колбе объемом 2 литра содержится 2 газа, нитроген (N₂), оксиген (O₂) и карбон диоксид, углекислый газ (CO₂). Каждого газа — по 10 г, температура каждого газа в колбе равна 37 градусам Цельсия. Нужно найти парциальное давление каждого газа и общее давление смеси газов на емкость.
- Наше уравнение парциального давления будет выглядеть следующим образом: P_total = P_{нитроген} + P_{оксиген} + P_{карбон диоксид}.
- Поскольку мы пытаемся найти давление, которое оказывает каждый из газов, знаем объем и температуру и можем найти количество молей каждого газа, основываясь на массе вещества, мы можем переписать уравнение в следующей форме: P_общее =(nRT/V) _{нитроген} + (nRT/V) _{оксиген} + (nRT/V) _{карбон диоксид}
2

Переведите температуру в градусы Кельвина. Температура по Цельсию равна 37 градусам, потому мы добавим 273 к 37 и получим 310 градусов K.
3
Найдите количество молей каждого газа в образце. Число молей газа равно массе газа, деленной на его молярную массу,^[10] которая, как уже говорилось, равна сумме весов всех атомов в составе.
- Для нашего первого газа, нитрогена (N₂), каждый атом обладает атомарной массой 14. Поскольку нитроген содержит два атома (состоит из двухатомных молекул), мы должны умножить 14 на 2, чтобы найти молярную массу нитрогена, она равна 28. Затем мы делим массу в граммах, 10 г, на 28, чтобы получить количество молей, которое приблизительно равно 0,4 моль.
- У второго газа, оксигена (O₂), масса каждого атома равна 16. Оксиген также двухатомный газ, потому мы умножаем 16 на 2 и получаем молярную массу, равную 32. Разделив 10 г на 32, мы получим примерно 0,3 моль оксигена в составе образца смеси газов.
- Третий газ, карбон диоксид (CO₂), состоит из 3 атомов: одного атома карбона с атомарной массой 12 и двух атомов оксигена, каждый с атомарной массой 16. Мы складываем все три веса: 12 + 16 + 16 = 44 составляет молярную массу. Разделив 10 г на 44, мы получим примерно 0,2 моля карбон диоксида.
4
Подставьте значения для молей, объема и температуры. Наше уравнение будет выглядеть так: P_общее =(0,4 * R * 310/2) _{нитроген} + (0,3 *R * 310/2) _{оксиген} + (0,2 * R *310/2) _{карбон диоксид}.
- Для простоты мы оставили текущие значения единиц измерения. Эти единицы уйдут после математических вычислений, и останутся только те, которые участвуют в определении давления.
5

Подставьте значение константы R. Мы будем указывать парциальное и общее давление в атмосферах, потому используем значение R, равное 0,0821 л атм/K моль. Подстановка этого значения в уравнение дает нам P_общее =(0,4 * 0,0821 * 310/2) _{нитроген} + (0,3 *0,0821 * 310/2) _{оксиген} + (0,2 * 0,0821 * 310/2) _{карбон диоксид}.
6
Подсчитайте парциальное давление каждого газа. Сейчас все значения на месте, пора перейти к математическим вычислениям.
- Чтобы найти парциальное давление нитрогена, умножим 0,4 моль на нашу константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,4 * 0,0821 * 310/2 = 5,09 атм, приблизительно.
- Для получения парциального давления оксигена умножим 0,3 моль на константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,3 *0,0821 * 310/2 = 3,82 атм, приблизительно.
- Чтобы найти парциальное давление карбон диоксида, умножаем 0,2 моль на константу 0,0821 и температуру 310 градусов K, затем делим на 2 литра: 0,2 * 0,0821 * 310/2 = 2,54 атм, приблизительно.
- Теперь сложим полученные значения давлений и найдем общее давление: P_общее = 5,09 + 3,82 + 2,54, или 11,45 атм, приблизительно.
Реклама

1
Определите парциальное давление, как и раньше. Вновь, возьмем в пример колбу на 2 литра с тремя газами: нитрогеном (N₂), оксигеном (O₂) и карбон диоксидом (CO₂). У нас по 10 г каждого газа, температура каждого газа в колбе равна 37 °C.
- Температура по Кельвину будет такой же, 310 градусов, как и раньше, у нас будет примерно 0,4 моль нитрогена, 0,3 моль оксигена и 0,2 моль карбон диоксида.
- Мы также будем указывать давление в атмосферах, потому будем использовать значение 0,0821 л атм/K моль для константы R.
- Таким образом, наше уравнение парциального давления на текущий момент выглядит так же, как раньше: P_общее =(0,4 * 0,0821 * 310/2) _{нитроген} + (0,3 *0,0821 * 310/2) _{оксиген} + (0,2 * 0,0821 * 310/2) _{карбон диоксид}.
2
Сложите количество молей каждого газа в образце, чтобы найти общее количество молей в смеси газов. Поскольку объем и температура одинаковы для всех газов, не говоря о том, что каждая молярная масса умножается на одну и ту же константу, мы можем использовать распределительное свойство умножения и переписать уравнение в следующем виде: P_общее = (0,4 + 0,3 + 0,2) * 0,0821 * 310/2.
- Складываем 0,4 + 0,3 + 0,2 = 0,9 моль смеси газов. Это упростит наше выражение до P_общее = 0,9 * 0,0821 * 310/2.
3

Найдите общее давление смеси газов. Умножаем 0,9 * 0,0821 * 310/2 = 11,45 моль, приблизительно.
4
Найдите пропорцию каждого газа в смеси. Для этого разделите количество молей каждого газа на общее количество молей в смеси.
- У нас 0,4 моль нитрогена, потому 0,4/0,9 = 0,44 (44 процента) в образце, приблизительно.
- У нас 0,3 моль оксигена, потому 0,3/0,9 = 0,33 (33 процента) в образце, приблизительно.
- У нас 0,2 моль карбон диоксида, потому 0,2/0,9 = 0,22 (22 процента) в образце, приблизительно.
- Хотя в вычислениях выше сумма приблизительных значений в процентах дает всего 0,99, точные значения являются периодическими, так что сумма на самом деле будет равна повторяющимся девяткам после запятой. По определению это то же самое, что 1 или 100 процентов.
5
Умножим пропорциональное количество каждого газа на общее давление, чтобы найти парциальное давление.
- Умножаем 0,44 * 11,45 = 5,04 атм, приблизительно.
- Умножаем 0,33 * 11,45 = 3,78 атм, приблизительно.
- Умножаем 0,22 * 11,45 = 2,52 атм, приблизительно.
Реклама

Советы

Вы заметите небольшую разницу в значениях при вычислении сначала парциального давления, а затем общего, и при подсчете вначале общего, а затем парциального давления. Помните, что приведенные значения даны приблизительно, поскольку они округлены до 1 или 2 знаков после запятой для простоты подсчетов и понимания. Если вы выполняете вычисления самостоятельно без округления, вы заметите или меньшую разницу между значениями или не заметите ее вовсе.

Предупреждения

Знание парциального давления газов может стать вопросом жизни и смерти для дайверов. Слишком низкое парциальное давление кислорода может привести к бессознательному состоянию или смерти, но слишком высокое парциальное давление азота или кислорода также может привести к отравлению.^[11]^[12]

Вам потребуются

Калькулятор
Справочник атомарных весов / молярных масс

Об этой статье

Эту страницу просматривали 82 723 раза.

Была ли эта статья полезной?

Источник

Смесям идеальных газов характерно свойство аддитивности двух показателей: парциального давления и объёма. Другими словами, любому включённому в смесь инертному газу характерно такое поведение, какое было бы, если б он в единственном числе заполнял предлагаемый объём. Для лучшего понимания разумно разобраться, что выражают указанные величины.

Определения

Давление – действующая на единицу поверхности сила, прямопропорциональная числу и скоростью сталкивающихся с этой поверхностью молекул, зависящей от температуры.

Парциальное давление – давление, оказываемое компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя этот объём и текущую температуру.

Объём – ограниченное чертой трёхмерное пространство, вмещающее вещество и отображающее его форму.

Парциальный объём – объём, занимаемый компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя первоначальное давление и температуру.

Идеальный газ – научная модель для познания газов, не учитывающая силу молекулярного взаимодействия.

Смесь идеальных газов – это совокупность газов, каждый из которого, находясь в смеси, при сохранении заданных условий, не вступает в химическую реакцию с остальными компонентами.

Говоря об идеальных газах и их смеси, следует понимать, что изменение условий, например температуры или давления, всё же может спровоцировать химическую реакцию. Важным параметром такой смеси является молярная (весовая) концентрация газового компонента. Данная величина измеряется в мг/м³ и показывает количество конкретного компонента в единице объёма газовой смеси.

Парциальное давление

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальное давление, создаваемое i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем p_i.

Формула

Формула парционального давления:

[p i=frac{m_{i}}{mu_{i}} frac{R T}{V}=mu_{i} frac{R T}{V}]

Где V– объём смеси, R = 8,31
Дж/моль*K– универсальная газовая постоянная, а T –
температура.

Следует отметить, что равность средней кинетической энергии находящихся в смеси молекул определяет равенство температур всех компонентов термодинамически уравновешенной газовой смеси. Найти общее давление смеси идеальных газов представляется возможным через закон Дальтона, отражаемый аддитивность парциальных давлений, а именно [p=sum p_{i}].

Пользуясь данным законом, найдём давление смеси идеальных газов через следующую формулировку: [p=sum_{i}^{N}=1 rightarrow p_{i}=frac{R T}{V} sum_{i}^{N}=1^{v_{i}}], где N – количество вошедших в смесь газов, v_i– количественный показатель молей i-го газа. Отсюда парциальное давление можно выразить формулой [p_{i}=x_{i} p], где x_i – молярная концентрация i-го газа.

Понятие парциального объёма

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальный объём, занимаемый i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем V_i. Аддитивность парциального объёма определяет закон Амага, выраженный формулой [V=sum_{i}^{N}=1 V_{i}].

Формула

Пользуясь данным законом, можно вывести формулу нахождения парциального объёма через следующую формулировку:
[v_{i}=frac{p^{V_{i}}}{R T}]; [p=frac{R T}{V} frac{p}{R T} sum_{i}^{N}=mathbf{1}^{V}_{i}] , отсюда
следует, что — [boldsymbol{V=sum_{i}^{N}=1^{V_{i}}}, text{ а } boldsymbol{V_{i}=x_{i} V}].

Зная, что характеризующие состояние смеси инертных газов показатели подчиняются уравнению Менделеева-Клапейрона, выведем формулу:

[p V=frac{m}{mu_{s m}} R T] данное уравнение свои параметры относит ко всей газовой смеси.

[pV=mR_{s m} T] такой вариант уравнения содержит показатель R_sm, обозначающий удельную газовую составляющую смеси.

Уравнение Менделеева-Клапейрона показывает возможность изменения трёх характеризующих состояние идеального газа параметров.

Нет времени решать самому?

Наши эксперты помогут!

Примеры вычисления парциального давления и объёма

Задача №1

Условие: в сосуде объёмом 2 м³, при постоянной температуре 290 К находится 0,20*10^-3 кг гелия и 1*10^-3 кг водорода. Необходимо вычислить давление смеси и парциальное давление гелия.

Решение.

Сначала вычислим количество молей каждого компонента, используя следующую формулу:

[mathrm{v}{mathrm{i}}=frac{mathrm{m}{mathrm{i}}}{mu_{mathrm{i}}}]

Для расчёта количество молей водорода в смеси нам понадобится его молярная масса, которую возьмём из таблицы Менделеева:

[mu_{mathrm{H}_{2}}=2 * 10^{-3} frac{mathrm{кг}}{text { моль }}]

Теперь можно найти количество молей водорода в смеси:

[mathrm{v}_{mathrm{H}_{2}}=frac{mathrm{m}_{mathrm{H}_{2}}}{mu_{mathrm{H}_{2}}}=frac{1 * 10^{-3}}{2 * 10^{-3}}=0,5 text { (моль) }]

Зная молярную массу гелия из таблицы Менделеева, рассчитаем количество молей гелия в смеси:

[mathrm{v}_{mathrm{He}}=frac{mathrm{m}_{mathrm{He}}}{mu_{mathrm{He}}}=frac{4 * 10^{-3}}{20 * 10^{-3}}=0,2 text { (моль) }]

Теперь можно найти парциальное давление каждого из компонентов с помощью уравнения Менделеева-Клапейрона:

[mathrm{p}_{mathrm{i}} mathrm{V}=mathrm{v}_{mathrm{i}} mathrm{RT}]

Сначала нужно рассчитать давление водорода:

[mathrm{p}_{mathrm{H}_{2}} mathrm{~V}=mathrm{v}_{mathrm{H}_{2}} mathrm{RT} rightarrow mathrm{p}_{mathrm{H}_{2}}=frac{mathrm{v}_{mathrm{H}_{2}} mathrm{RT}}{mathrm{V}}=frac{0,5 * 8,31 * 290}{1}=1205 text { (Па) }]

Рассчитаем парциальное давление гелия:

[mathrm{p}_{mathrm{He}}=frac{mathrm{v}_{mathrm{He}} mathrm{RT}}{mathrm{V}}=frac{0,2 * 8,31 * 290}{1}=482 text { (Па) }]

Теперь найдём полное давление газовой смеси, сложив значения компонентов:

[mathrm{p}=mathrm{p}_{mathrm{H}_{2+}} mathrm{p}_{mathrm{H}}=1205+482=1687 text { Па }]

Ответ: парциальное давление гелия равно 482 Па, а общее давление 1205 Па.

Задача №2

Условие: идеальная газовая смесь состоит из 0,5 кг углекислого газа и 0,25 кг кислорода, какой объём они займут, если давление равно 1 атм, а температура смеси равна 300 К?

Решение.

Найдём суммарную массу газовой смеси:

[mathrm{m}=mathrm{m}_{mathrm{O}_{2}}+mathrm{m}_{mathrm{CO}_{2}}=0,5+0,25=0,75 text { (кг) }]

Вычислим массовые компоненты смеси:

[g_{mathrm{O}_{2}}=frac{0,25}{0,75}=0,33] [mathrm{g}_{mathrm{CO}_{2}}=frac{0,5}{0,75}=0,67]

Тогда газовая постоянная смеси равняется:

[mathrm{R}_{mathrm{sm}}=mathrm{R} sum_{mathrm{i}=1}^{mathrm{N}} frac{mathrm{g}_{mathrm{i}}}{mu_{mathrm{i}}}=8,31left(frac{0,33}{32 * 10^{-3}}+frac{0,67}{46 * 10^{-3}}right)=200left(frac{text { Дж }}{text { кгК }}right)]

Пользуясь уравнением Менделеева-Клапейрона, и, зная, что 1 атм равна 10⁵Па,вычислим объём смеси:

[mathrm{V}_{mathrm{sm}}=frac{mathrm{m}_{mathrm{sm}} mathrm{R}_{mathrm{sm}} mathrm{T}_{mathrm{sm}}}{mathrm{P}_{mathrm{sm}}}=frac{0,75 * 200 * 300}{10^{5}}=0,45left(mathrm{м}^{3}right)]

Ответ: при заданных условиях смесь займёт 0,45 м^3.

Навык определения парциальных давлений и объёма актуален в машиностроении, энергетике и других промышленностях, связанных с использованием тепловых двигателей, приводимых в действие парами высокой температуры.

Источник

Download Article

Determining the pressure of each gas in a mixture

Download Article

Understanding Gas Properties

Calculating Partial, Then Total Pressures

Calculating Total, then Partial Pressures

Expert Q&A

Tips

Things You’ll Need

In chemistry, “partial pressure” refers to the pressure that each gas in a gas mixture exerts against its surroundings, such as a sample flask, a diver’s air tank, or the boundary of an atmosphere. You can calculate the pressure of each gas in a mixture if you know how much of it there is, what volume it takes up, and its temperature. You can then add these partial pressures together to find the total pressure of the gas mixture, or, you can find the total pressure first and then find the partial pressures.

1
Treat each gas as an “ideal” gas. An ideal gas, in chemistry, is one that interacts with other gases without being attracted to their molecules. Individual molecules may strike one another and bounce off like billiard balls without being deformed in any way.^[1]
- The pressures of ideal gases increase as they are squeezed into smaller spaces and decrease as they expand into larger areas. This relationship is called Boyle’s Law, after Robert Boyle. It is written mathematically as k = P x V or, more simply, k = PV, where k represents the constant relationship, P represents pressure and V represents volume.^[2]
- Pressures may be given using one of several possible units. One is the pascal (Pa), defined as a force of one newton applied over a square meter. Another is the atmosphere (atm), defined as the pressure of Earth’s atmosphere at sea level. A pressure of 1 atm is equal to 101,325 Pa.^[3]
- The temperatures of ideal gases increase as their volumes increase and decrease as their volumes decrease. This relationship is called Charle’s Law after Jacques Charles. It is written mathematically as k = V / T, where k represents the constant relationship between the volume and temperature, V again represents the volume, and T represents temperature. ^[4]^[5]
- Temperatures for gases in this equation are given in degrees Kelvin, which are found by adding 273 to the number of degrees Celsius in the gas’ temperature.
- These two relationships can be combined into a single equation: k = PV / T, which can also be written as PV = kT.
2
Define the quantities the gases are measured in. Gases have both mass and volume. Volume is usually measured in liters (l), but there are two kinds of mass.
- Conventional mass is measured in grams or, if there is a sufficiently large mass, kilograms.
- Because of how lightweight gases usually are, they are also measured with another form of mass called molecular mass or molar mass. Molar mass is defined as the sum of the atomic weights of each atom in the compound the gas is composed of, with each atom compared against the standard value of 12 for carbon’s molar mass.^[6]
- Because atoms and molecules are too small to work with, quantities of gases are defined in moles. The number of moles present in a given gas can be found by dividing the mass by the molar mass and can be represented by the letter n.
- We can replace the arbitrary k constant in the gas equation with the product of n, the number of moles (mol), and a new constant R. The equation can now be written nR = PV/T or PV = nRT.^[7]
- The value of R depends on the units used to measure the gases’ pressures, volumes, and temperatures. For volume in liters, temperature in degrees Kelvin, and pressure in atmospheres, its value is 0.0821 L atm/K mol. This may also be written 0.0821 L atm K^-1 mol ^-1 to avoid using the division slash with units of measure.^[8]
Advertisement
3
Understand Dalton’s Law of Partial Pressures. Developed by chemist and physicist John Dalton, who first advanced the concept of chemical elements being made up of atoms,^[9] Dalton’s Law states that the total pressure of a gas mixture is the sum of the pressures of each of the gases in the mixture.
- Dalton’s Law can be written in equation form as P_total = P₁ + P₂ + P₃ … with as many addends after the equal sign as there are gases in the mixture.
- The Dalton’s Law equation can be expanded on when working with gases whose individual partial pressures are unknown, but for which we do know their volumes and temperatures. A gas’ partial pressure is the same pressure as if the same quantity of that gas were the only gas in the container.
- For each of the partial pressures, we can rewrite the ideal gas equation so that instead of the form PV = nRT, we can have only P on the left side of the equal sign. To do this, we divide both sides by V: PV/V = nRT/V. The two V’s on the left side cancel out, leaving P = nRT/V.
- We can then substitute for each subscripted P on the right side of the partial pressures equation: P_total =(nRT/V) ₁ + (nRT/V) ₂ + (nRT/V) ₃ …

1
Define the partial pressure equation for the gases you’re working with. For the purposes of this calculation, we’ll assume a 2-liter flask holds 3 gases: nitrogen (N₂), oxygen (O₂), and carbon dioxide (CO₂). There are 10g of each gas, and the temperature of each gas in the flask is 37 degrees C (98.6 degrees F). We need to find the partial pressure for each gas, and the total pressure the gas mixture exerts in the container.
- Our partial pressure equation becomes P_total = P_nitrogen + P_oxygen + P_{carbon dioxide}.
- Since we’re trying to find the pressure each gas exerts, we know the volume and temperature, and we can find how many moles of each gas is present based on the mass, we can rewrite this equation as : P_total =(nRT/V) _nitrogen + (nRT/V) _oxygen + (nRT/V) _{carbon dioxide}
2

Convert the temperature to degrees Kelvin. The Celsius temperature is 37 degrees, so we add 273 to 37 to get 310 degrees K.
3
Find the number of moles of each gas present in the sample. The number of moles of a gas is the mass of that gas divided by its molar mass,^[10] which we said was the sum of the atomic weights of each atom in the compound.
- For our first gas, nitrogen (N₂), each atom has an atomic weight of 14. Because the nitrogen is diatomic (forms two-atom molecules), we have to multiply 14 by 2 to find that the nitrogen in our sample has a molar mass of 28. We then divide the mass in grams, 10 g, by 28, to get the number of moles, which we’ll approximate as 0.4 mol of nitrogen when rounding to the nearest tenth.
- For our second gas, oxygen (O₂), each atom has an atomic weight of 16. Oxygen is also diatomic, so we multiply 16 by 2 to find the oxygen in our sample has a molar mass of 32. Dividing 10 g by 32 gives us approximately 0.3 mol of oxygen in our sample.
- Our third gas, carbon dioxide (CO₂), has 3 atoms: one of carbon, with an atomic weight of 12; and two of oxygen, each with an atomic weight of 16. We add the three weights: 12 + 16 + 16 = 44 as the molar mass. Dividing 10 g by 44 gives us approximately 0.2 mol of carbon dioxide.
4
Plug in the values for the moles, volume, and temperature. Our equation now looks like this: P_total =(0.4 * R * 310/2) _nitrogen + (0.3 *R * 310/2) _oxygen + (0.2 * R *310/2) _{carbon dioxide}.
- For simplicity’s sake, we’ve left out the units of measure accompanying the values. These units will cancel out after we do the math, leaving only the unit of measure we’re using to report the pressures in.
5

Plug in the value for the constant R. We’ll report the partial and total pressures in atmospheres, so we’ll use the value for R of 0.0821 L atm/K mol. Plugging this value into the equation now gives us P_total =(0.4 * 0.0821 * 310/2) _nitrogen + (0.3 *0.0821 * 310/2) _oxygen + (0.2 * 0.0821 * 310/2) _{carbon dioxide}.
6
Calculate the partial pressures for each gas. Now that we have the values in place, it’s time to do the math.
- For the partial pressure of nitrogen, we multiply 0.4 mol by our constant of 0.0821 and our temperature of 310 degrees K, then divide by 2 liters: 0.4 * 0.0821 * 310/2 = 5.09 atm, approximately.
- For the partial pressure of oxygen, we multiply 0.3 mol by our constant of 0.0821 and our temperature of 310 degrees K, then divide by 2 liters: 0.3 *0.0821 * 310/2 = 3.82 atm, approximately.
- For the partial pressure of carbon dioxide, we multiply 0.2 mol by our constant of 0.0821 and our temperature of 310 degrees K, then divide by 2 liters: 0.2 * 0.0821 * 310/2 = 2.54 atm, approximately.
- We now add these pressures to find the total pressure: P_total = 5.09 + 3.82 + 2.54, or 11.45 atm, approximately.

1
Define the partial pressure equation as before. Again, we’ll assume a 2-liter flask holding 3 gases: nitrogen (N₂), oxygen (O₂), and carbon dioxide (CO₂). There are 10g of each gas, and the temperature of each gas in the flask is 37 degrees C (98.6 degrees F).
- The Kelvin temperature will still be 310 degrees, and, as before, we have approximately 0.4 mol of nitrogen, 0.3 mol of oxygen, and 0.2 mol of carbon dioxide.
- Likewise, we’ll still report the pressures in atmospheres, so we’ll use the value of 0.0821 L atm/K mol for the R constant.
- Thus, our partial pressures equation still looks the same at this point: P_total =(0.4 * 0.0821 * 310/2) _nitrogen + (0.3 *0.0821 * 310/2) _oxygen + (0.2 * 0.0821 * 310/2) _{carbon dioxide}.
2
Add the number of moles of each gas in the sample to find the total number of moles in the gas mixture. Because the volume and temperature are the same for each sample in the gas, not to mention each molar value is multiplied by the same constant, we can use the distributive property of mathematics to rewrite the equation as P_total = (0.4 + 0.3 + 0.2) * 0.0821 * 310/2.
- Adding 0.4 + 0.3 + 0.2 = 0.9 mol of gas mixture. This further simplifies the equation to P_total = 0.9 * 0.0821 * 310/2.
3

Find the total pressure of the gas mixture. Multiplying 0.9 * 0.0821 * 310/2 = 11.45 mol, approximately.
4
Find the proportion each gas makes of the total mixture. To do this, divide the number of moles of each gas into the total number of moles.
- There are 0.4 mol of nitrogen, so 0.4/0.9 = 0.44 (44 percent) of the sample, approximately.
- There are 0.3 mol of nitrogen, so 0.3/0.9 = 0.33 (33 percent) of the sample, approximately.
- There are 0.2 mol of carbon dioxide, so 0.2/0.9 = 0.22 (22 percent) of the sample, approximately.
- While the above approximate percentages add to only 0.99, the actual decimals are repeating, so the sum would actual be a repeating series of 9s after the decimal. By definition, this is the same as 1, or 100 percent.
5
Multiply the proportional amount of each gas by the total pressure to find the partial pressure.
- Multiplying 0.44 * 11.45 = 5.04 atm, approximately.
- Multiplying 0.33 * 11.45 = 3.78 atm, approximately.
- Multiplying 0.22 * 11.45 = 2.52 atm, approximately.

Add New Question

Question

How do I calculate the pressure before the solution was made?

Bess Ruff is a Geography PhD student at Florida State University. She received her MA in Environmental Science and Management from the University of California, Santa Barbara in 2016. She has conducted survey work for marine spatial planning projects in the Caribbean and provided research support as a graduate fellow for the Sustainable Fisheries Group.

Environmental Scientist

Expert Answer

Support wikiHow by
unlocking this expert answer.

If you know the volume of a gas and the relationship the volume of that gas has with pressure then you can calculate initial pressure (i.e. the pressure before the solution was made) using the equation for Boyle’s Law included in the article.
Question

What is a partial pressure of oxygen in a container that contains 2.0 mol of oxygen, 3.0 mol of nitrogen, and 1.0 mol of carbon dioxide when the total pressure is 900 Torr?

Use the law of partial pressures (P_total = P_O + P_N + P_CO2) along with the ideal gas law, PV = nRT.
Question

How many molecules are there in a 3.46 gram sample of hydrogen chloride?

Hydrogen chloride is composed of one atom of hydrogen and one atom of chlorine. You can find the molar mass of HCl by adding the molar masses of hydrogen and chlorine, this will give you how many moles of HCl there are per gram. Use this to convert from grams to moles.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

You’ll notice a slight difference in the values from finding the partial pressures first, then the total pressure and from finding the total pressure first, then the partial pressures. Remember that the values given were stated as approximate values, due to rounding to either 1 or 2 decimal places to make the values easier to understand. If you work out the calculations yourself with a calculator without rounding, you’ll notice either a smaller discrepancy between the two methods or none at all.

Knowledge of partial pressures of gases can become a matter of life or death for divers. Too low a partial pressure of oxygen can lead to unconsciousness and death, while too high a partial pressure of either nitrogen or oxygen can also be toxic.^[11]

Things You’ll Need

Calculator
Reference book of atomic weights/molar masses

References

About This Article

Article SummaryX

To calculate partial pressure, start by applying the equation k = PV to treat the gas as an ideal gas according to Boyle’s law. Then, convert the equation into Kelvin, if it isn’t already, by adding 273 to the temperature in Celsius. After you’ve done that, begin finding the partial pressure of each gas by using the formula P = nRT/V. If there is more than 1 gas, you should use Dalton’s law of partial pressures by plugging in the partial pressure of each gas into the equation Ptotal = P1 + P2 + P3. To learn how to find partial pressure by finding the total pressure first, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 396,648 times.

Reader Success Stories

«I like how it’s easy to understand with all the diagrams implemented.»

Did this article help you?

Источник

Трактовка закона

Учёный Дальтон в 1801 году сформировал закон парциальных давлений: Па смеси из идеальных газов равняется сумме рi её компонентов. Уравнение имеет следующий вид: Рсм=n (сумма pi), где n — число долей смеси.

Для определения парциального давления в химии используется отдельный компонент из атмосферного воздуха. При расчете учитывается значение каждого отдельного вещества, их число, температуры с объёмами. При необходимости можно найти общий показатель, сложив давление каждого компонента в отдельности.

Каждый газ в сосуде должен обозначаться как «идеальный». При нормальных условиях они взаимодействуют с углекислым газом, водородом, водой, азотом, водяным паром, кислородом, компонентами крови и прочими компонентами из таблицы Менделеева. При этом не образуются соединения. Отдельные молекулы способны сталкиваться между собой, отталкиваясь, но не деформируясь.

Физические и химические задачи решаются с помощью формулы парциального давления (закон открыли учёные Бойль и Мариотт): (k = P x V). Кроме полного варианта, уравнение записывается сокращённо k = PV, где:

k равно постоянной величине;
Р — давление;
V — объем.

Второстепенные значения

Давление может измеряться в разных величинах: процент, паскаль (Па). Смысл последнего: сила в 1 ньютон приложена к площади в 1 кв. м. Если результат такой зависимости записывается в атмосферах, тогда для его нахождения потребуется учесть, что одна атмосфера равняется 101,325 Па.

Температура идеального газа повышается, если увеличивается объём, а снижается, если уменьшается последний показатель. Такое соотношение может называться законом Чарльза, который имеет следующий математический вид: k = V / T. Значение температуры в уравнении измеряется в градусах Кельвина. Оно зависит от градусов Цельсия. Чтобы его найти, прибавляется 273.

Уравнение используется в химии для определения мольной доли (концентрация, которая выражается через отношение количества молей 1 компонента к суммарному числу молей пары веществ, входящих в смесь). Кроме объёма, для газа характерна молярная масса (вес одной доли компонента) и объём. Существуют легкие способы её подсчёта:

Стандартная. Измеряется в граммах и килограммах.
Молекулярная. Так как газы весят мало, их вес вычисляется в специальной единице измерения — молярная масса. Для её определения суммируется вес составных атомов. Каждый компонент сравнивается с массой карбона, равной 12.

Уравнения Дальтона и Бойля

Физик и химик Дальтон считается первым учёным, предположившим структуру атомных элементов, их свойства. Общее давление вычисляется следующим образом: Р= P1 + P2 + P3. Пример: в колбе содержится по 10 г оксигена и нитрогена. Их общее Р будет равно 20 (10+10). Для вычисления pi используется температура, равная 37 градусам Цельсия.

Чтобы перевести её в градусы Кельвина, значение по Цельсию, равное 37, добавляется к 273. Результат — 310. Для вычисления количества молей газов используется масса, поделённая на молярную. Если уравнение касается нитрогена, вес каждого компонента соответствует цифре 14.

Так как вещество содержит в себе 2 атома, то 14х2, что равно 28. Масса в граммах делится на полученный результат. Таким способом вычисляется количество молей, приблизительно равное 0,4 моль. Чтобы найти аналогичное значение у оксигена, применяется масса 16. Вещество относится к двухатомным газам, поэтому 16х2 равняется 32. По результатам получается, что 0,3 моль оксигена содержится в составе газовой смеси.

Если в задаче указывается общее давление и pi в атмосферах, тогда используется в качестве константы R (0.0821 л атм/K моль). При подстановке данных в уравнение можно узнать Pобщее. Чтобы вычислить ПД нитрогена, 0,4 моль умножается на константу и температуру. Результат делится на 2 литра, что приблизительно равно 5.09 атм. Аналогичные шаги выполняются для вычисления ПД оксигена. Конечный результат равен 3.82 атм.

Свойства веществ

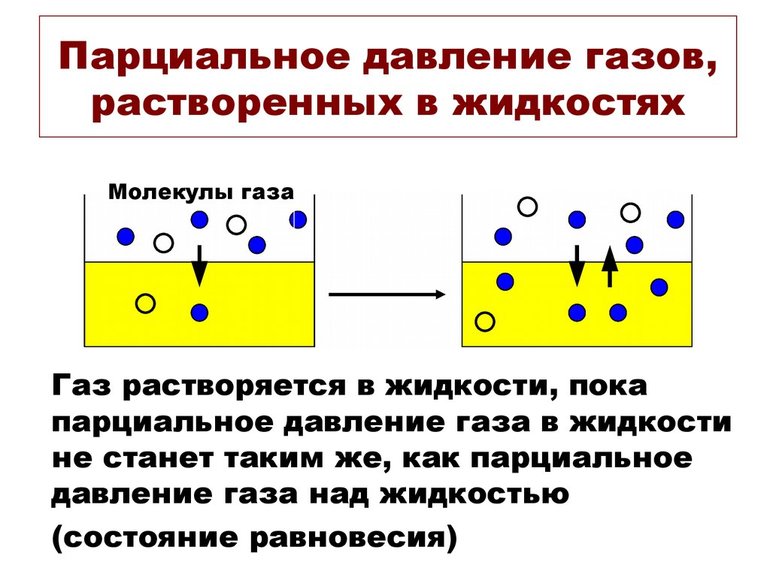
Значение pi газа, растворённого в жидкости, равняется pi того вещества, который образовался бы в фазе газообразования в случае равновесия с жидкостью при аналогичной температуре. Парциальное давление (ПД) измеряется в качестве термодинамической активности молекул вещества.

Газы постоянно вытекают из сферы с высоким ПД в область с низким давлением. Чем больше такая разница, тем быстрее поток. Газам свойственно растворяться, диффундировать, реагировать на ПД. В некоторых случаях показатель не зависит от концентрации газовой смеси.

При решении задач в области химии и физики учитываются свойства газов: сжимаемость и способность расширяться. Они не имеют своей формы, поэтому расширяются до заполнения сосуда, принимая его форму. По аналогичной причине они не имеют объёма. Газ давит на стенки ёмкости по всем направлениям одинаково. Характерное свойство компонентов — способность смешиваться между собой в разных соотношениях.

Так как объём зависит от температуры и давления, поэтому в норме должно быть 0 °C и 760 мм рт. ст. При этом нет места влаги. Если объём считается нормальным, его обозначают стоящей впереди буквой. Подобная зависимость отображается в термодинамике с помощью графика. Если доказана зависимость объема от давления, при этом температура постоянная, используются изотермы (линии, которые изображают на диаграмме процесс с неизменной температурой).

Точки и функции

В законе Бойля чётко указана зависимость объёма от давления при одинаковой температуре. Если данные нанести на график в функцию давления, через точки можно будет провести кривую. Точный эксперимент и незначительный разброс точек позволяют описать объёмное поведение системы с небольшой погрешностью.

Несколько подобных кривых для разных температур во всём диапазоне изученных условий позволяет описать объёмное поведение газа. Одновременно отображаются кривые постоянного давления, которые описывают изменения основных показателей. Чтобы получить окончательные результаты, кривые требуют незначительного сглаживания. Подобные графики сделать самостоятельно менее сложно.

Объём газа при неизменной температуре сильно изменяется с колебаниями давления. Но графически представить такую зависимость в широком диапазоне изменения давлений трудно. Если охвачена широкая область изменения, используются крупные масштабы.

Для упрощения процесса построения на график наносится зависимость произведения Р от давления при одной температуре, что существенно уменьшает область выявления функции. Наибольший эффект получается от применения 1−2 специальных функций объёма, которые называются коэффициентом сжимаемости и остаточным объёмом.

Каждое понятие характеризуется объёмным поведением газа с учётом его отклонений от нормального состояния вещества и созданных идеальных условий. Чтобы упростить поставленную задачу, график отображается на специальной бумаге либо при помощи компьютерных программ. Во втором случае достаточно ввести данные. Сервис самостоятельно строит прямые, кривые и прочие элементы графика.

Простые зависимости лучше отображать в стандартных программах Word. Графические сложные задачи в химии и физике решаются с помощью «Agrafer» — известная компьютерная программа, которая используется не только студентами, но и школьниками.

Источник

Газовая
смесь находится в состоянии равновесия,
если концентрации компонентов и её
параметры состояния во всём объёме
имеют одинаковые значения. При этом
температура всех газов, входящих в
смесь, одинакова и равна температуре
смеси Т_см.

В
равновесном состоянии молекулы каждого
газа рассеяны равномерно по всему объёму
смеси, то есть имеют свою определённую
концентрацию и, следовательно, своё
давление р_i,
Па, которое называется парциальным.
Оно определяется следующим образом.

Парциальное
давление равно давлению данного
компонента при условии, что он один
занимает весь объём, предназначенный
для смеси при температуре смеси Т_см.

По
закону английского химика и физика
Дальтона, сформулированному в 1801 году,
давление смеси идеальных газов р_см
равно сумме парциальных давлений её
компонентов р_i:

, (2)

где
n
– число компонентов.

Выражение
(2) также называется законом
парциальных давлений.

3.3. Приведённый объём компонента газовой смеси. Закон Амага

По
определению приведённым объёмом i-го
компонента газовой смеси V_i,
м³,
называется объём, который один этот
компонент мог бы занимать при условии,
что его давление и температура будут
равны давлению и температуре всей
газовой смеси.

Закон
французского физика Амага, сформулированный
примерно в 1870 году, гласит: сумма
приведённых объёмов всех компонентов
смеси равна объёму смеси V_см:

,
м³. (3)

3.4. Химический состав газовой смеси

Химический
состав газовой смеси может задаваться
тремя
различными
способами.

Рассмотрим
газовую смесь, состоящую из n
компонентов. Смесь занимает объём V_см,
м³,
имеет массу М_см,
кг, давление р_см,
Па и температуру Т_см,
К. Также число молей смеси равно N_см,
моль. При этом масса одного i-го
компонента m_i,
кг, а число молей этого компонента ν_i,
моль.

Очевидно, что:

, (4)

. (5)

Используя для
рассматриваемой смеси закон Дальтона
(2) и Амага (3) можно записать:

, (6)

, (7)

где
р_i
– парциальное давление i-го
компонента, Па; V_i
– приведённый объём i-го
компонента, м³.

Однозначно
химический состав газовой смеси может
быть задан либо массовыми, либо мольными,
либо объёмными долями её компонентов:

, (8)

, (9)

, (10)

где
g_i,
k_i
и r_i
– массовая, мольная и объёмная доли
i-го
компонента смеси соответственно
(безразмерные величины).

Очевидно, что:

,
,. (11)

Часто
на практике химический состав смеси
задаётся не долями i-го
компонента, а его процентами.

Например,
в теплотехнике приближённо принимается,
что сухой воздух состоит из 79 объёмных
процентов азота и 21 объёмного процента
кислорода.

Процент
i-го
компонента в смеси вычисляется путём
умножения его доли на 100.

Для примера с сухим
воздухом будем иметь:

. (12)

где

и
–
объёмные доли азота и кислорода в сухом
воздухе; N₂
и О₂
– обозначение объёмных процентов азота
и кислорода соответственно, % (об.).

Примечание:

1)
Мольные доли идеальной смеси численно
равны объёмным долям: k_i
= r_i.
Докажем это.

Пользуясь
определением объёмной доли (10)
и законом Амага (3) можем записать:

, (13)

где
V_i
– приведённый объём i-го
компонента, м³;
ν_i
– число молей i-го
компонента, моль;
–
объём одного моля i-го
компонента при давлении смеси р_см
и температуре
смеси Т_см,
м³/моль.

Из
закона Авогадро (см. п. 2.3 данного
приложения) следует, что при одинаковых
температуре и давлении один моль любого
газа (компонента смеси) занимает один
и тот же объём. В частности, при Т_см
и р_см
это будет
некоторый объём V¹,
м³.

Сказанное
позволяет записать равенство:

. (14)

Подставляя
(14)
в (13)
получаем требуемое:

. (15)

2)
Объёмные доли компонентов газовой смеси
можно рассчитать, зная их парциальные
давления. Покажем это.

Рассмотрим
i-ый
компонент идеальной газовой смеси в
двух различных состояниях: когда он
находится при своём парциальном давлении
р_i;
когда он занимает свой приведённый
объём V_i.

Уравнение
состояния идеального газа справедливо
для любых его состояний, в частности, и
для двух, названных выше.

В соответствии
с этим, и учитывая определение удельного
объёма, можем записать:

, (16)

,(17)

где
R_i
– газовая постоянная i-го
компонента смеси, Дж/(кг·К).

После
деления обоих частей (16)
и (17)
друг на друга получаем требуемое:

. (18)

Из
(18)
видно, что парциальные давления
компонентов смеси можно рассчитать по
её химическому составу, при известном
общем давлении смеси р_см:

. (19)

Соседние файлы в папке фотп2014

Источник