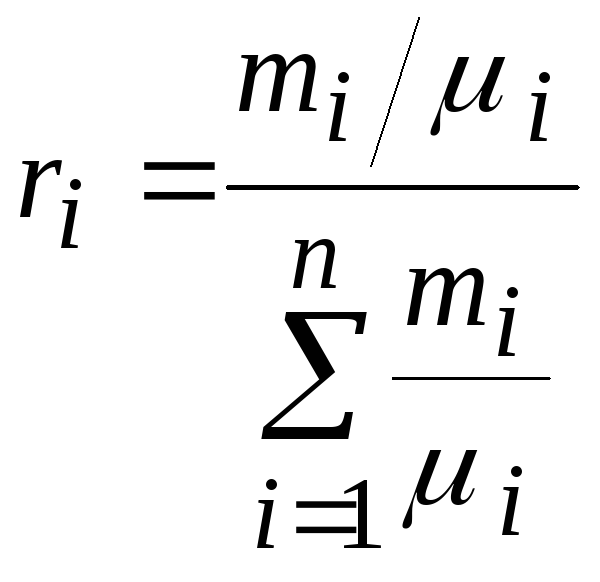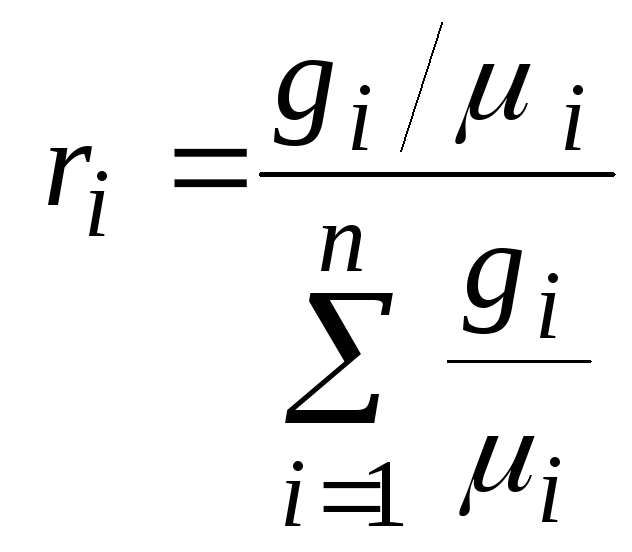Как найти парциальный объем газа - Исправление недочетов и поиск решений вместе с Examum.ru

Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.

Определение 1

Смесь идеальных газов – это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.

При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие. Важный параметр любой такой смеси – так называемая весовая концентрация gi i-ного газа-компонента.

Здесь:

N – количество газов, из которых состоит смесь;
xi i-го газа – молярная концентрация указанного газа в составе смеси;
νi – количество молей i-го газа, присутствующего в смеси.

Понятие парциального давления

Парциальное давление – это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:

Определение 2

Парциальным называется давление pi, которое могло бы создаваться i-ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.

Формула парциального давления будет выглядеть так:

pi=miμiRTV=μiRTV

Объем смеси здесь обозначен буквой V, ее температура – T.

Следует подчеркнуть, что поскольку средние кинетические энергии молекул смеси равны, то существует и равенство температур всех компонентов газовой смеси, находящейся в состоянии термодинамического равновесия.

Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона в следующей формулировке:

p=∑i=1Npi=RTV∑i=1Nνi

Исходя из него, мы можем выразить парциальное давление так:

pi=xip.

Понятие парциального объема

У газовой смеси также есть такая характеристика, как парциальный объем.

Определение 3

Парциальный объем Vi i-газа в газовой смеси – это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.

Если речь идет о смеси идеальных газов, то к ней применим закон Амага:

V=∑i=1NVi

В самом деле, при выражении νi из формулы выше у нас получится следующее:

νi=pViRT; p=RTVpRT∑i=1NVi→V=∑i=1NVi

Для расчета парциального объема газа используется следующая формула:

Vi=xiV.

Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона. Формула будет выглядеть так:

pV=mμsmRT.

Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:

pV=mRsmT.

Здесь параметры Rsm=Rμsm=R∑i=1Nqiμi означают удельную газовую постоянную смеси.

Пример 1

Условие: имеется сосуд объемом 1 м3, в котором находится 0,10·10-3 кг гелия и 0,5·10-3 кг водорода. Постоянная температура равна 290 К. Вычислите давление смеси и парциальное давление гелия в нем.

Решение

Начнем с вычисления количества молей каждого компонента смеси. Для этого можно использовать формулу:

νi=miμi

Зная, что молярная масса водорода, согласно таблице Менделеева, составляет μH2=2·10-3 кгмоль, мы можем найти количество его молей в смеси по формуле:

νH2=mH2μH2

Считаем, что получится:

νH2=0,5·10-32·10-3=0,25 (моль).

Точно такие же расчеты проводим и для гелия, зная, что μHe=4·10-3 кгмоль:

Теперь с помощью уравнения Менделеева-Клайперона можно найти парциальное давление каждого компонента:

piV=νiRT.

Сначала рассчитаем давление водорода:

pH2V=νH2RT→pH2=νH2RTV

Парциальное давление будет равно:

pH2=0,25·8,31·2901=602,5 (Па).

Теперь то же самое подсчитываем для гелия:

pHe=0,025·8,31·2901=60,25 (Па).

Чтобы найти общее давление смеси газов, сложим сумму давлений ее составляющих:

p=pH2+pHe

Подставляем полученные ранее значения и находим нужный результат:

p=602,5+60,25=662,75 (Па).

Ответ: общее давление смеси составляет 662,75 Па, а парциальное давление гелия в смеси равно 60,25 Па.

Пример 2

Условие: дана смесь газов, состоящая из 1 кг углекислого газа и 0,5 кг O2. Если считать их идеальными, какой объем они будут занимать при давлении в 1 атм? Температура смеси равна 300К.

Решение

Начнем с вычисления общей массы газовой смеси.

m=mO2+mCO2

Значит, m=1+0,5=1,5.

Переходим к вычислению массовых компонентов смеси:

gO2=0,51,5=0,33;gCO2=11,5=0,67.

Тогда газовая постоянная смеси будет равна:

Rsm=R∑i=1Ngiμi

Rsm=8,310,3332·10-3+0,6746·10-3=200 ДжкгК.

Объем смеси вычисляем с помощью уравнения Менделеева-Клайперона:

Vsm=msmRsmTsmpsm

Вспомнив, что по условию давление равно 1 атм, что равно105 Па, вычислим объем:

Vsm=1,5·200·300105=0,9 м3.

Ответ: при указанных условиях смесь займет объем, равный 0,9 м3.

Источник

Смесям идеальных газов характерно свойство аддитивности двух показателей: парциального давления и объёма. Другими словами, любому включённому в смесь инертному газу характерно такое поведение, какое было бы, если б он в единственном числе заполнял предлагаемый объём. Для лучшего понимания разумно разобраться, что выражают указанные величины.

Определения

Давление – действующая на единицу поверхности сила, прямопропорциональная числу и скоростью сталкивающихся с этой поверхностью молекул, зависящей от температуры.

Парциальное давление – давление, оказываемое компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя этот объём и текущую температуру.

Объём – ограниченное чертой трёхмерное пространство, вмещающее вещество и отображающее его форму.

Парциальный объём – объём, занимаемый компонентом газовой смеси, при условии удаления других компонентов из занимаемого объёма, сохраняя первоначальное давление и температуру.

Идеальный газ – научная модель для познания газов, не учитывающая силу молекулярного взаимодействия.

Смесь идеальных газов – это совокупность газов, каждый из которого, находясь в смеси, при сохранении заданных условий, не вступает в химическую реакцию с остальными компонентами.

Говоря об идеальных газах и их смеси, следует понимать, что изменение условий, например температуры или давления, всё же может спровоцировать химическую реакцию. Важным параметром такой смеси является молярная (весовая) концентрация газового компонента. Данная величина измеряется в мг/м³ и показывает количество конкретного компонента в единице объёма газовой смеси.

Парциальное давление

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальное давление, создаваемое i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем p_i.

Формула

Формула парционального давления:

[p i=frac{m_{i}}{mu_{i}} frac{R T}{V}=mu_{i} frac{R T}{V}]

Где V– объём смеси, R = 8,31
Дж/моль*K– универсальная газовая постоянная, а T –
температура.

Следует отметить, что равность средней кинетической энергии находящихся в смеси молекул определяет равенство температур всех компонентов термодинамически уравновешенной газовой смеси. Найти общее давление смеси идеальных газов представляется возможным через закон Дальтона, отражаемый аддитивность парциальных давлений, а именно [p=sum p_{i}].

Пользуясь данным законом, найдём давление смеси идеальных газов через следующую формулировку: [p=sum_{i}^{N}=1 rightarrow p_{i}=frac{R T}{V} sum_{i}^{N}=1^{v_{i}}], где N – количество вошедших в смесь газов, v_i– количественный показатель молей i-го газа. Отсюда парциальное давление можно выразить формулой [p_{i}=x_{i} p], где x_i – молярная концентрация i-го газа.

Понятие парциального объёма

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальный объём, занимаемый i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем V_i. Аддитивность парциального объёма определяет закон Амага, выраженный формулой [V=sum_{i}^{N}=1 V_{i}].

Формула

Пользуясь данным законом, можно вывести формулу нахождения парциального объёма через следующую формулировку:
[v_{i}=frac{p^{V_{i}}}{R T}]; [p=frac{R T}{V} frac{p}{R T} sum_{i}^{N}=mathbf{1}^{V}_{i}] , отсюда
следует, что — [boldsymbol{V=sum_{i}^{N}=1^{V_{i}}}, text{ а } boldsymbol{V_{i}=x_{i} V}].

Зная, что характеризующие состояние смеси инертных газов показатели подчиняются уравнению Менделеева-Клапейрона, выведем формулу:

[p V=frac{m}{mu_{s m}} R T] данное уравнение свои параметры относит ко всей газовой смеси.

[pV=mR_{s m} T] такой вариант уравнения содержит показатель R_sm, обозначающий удельную газовую составляющую смеси.

Уравнение Менделеева-Клапейрона показывает возможность изменения трёх характеризующих состояние идеального газа параметров.

Нет времени решать самому?

Наши эксперты помогут!

Примеры вычисления парциального давления и объёма

Задача №1

Условие: в сосуде объёмом 2 м³, при постоянной температуре 290 К находится 0,20*10^-3 кг гелия и 1*10^-3 кг водорода. Необходимо вычислить давление смеси и парциальное давление гелия.

Решение.

Сначала вычислим количество молей каждого компонента, используя следующую формулу:

[mathrm{v}{mathrm{i}}=frac{mathrm{m}{mathrm{i}}}{mu_{mathrm{i}}}]

Для расчёта количество молей водорода в смеси нам понадобится его молярная масса, которую возьмём из таблицы Менделеева:

[mu_{mathrm{H}_{2}}=2 * 10^{-3} frac{mathrm{кг}}{text { моль }}]

Теперь можно найти количество молей водорода в смеси:

[mathrm{v}_{mathrm{H}_{2}}=frac{mathrm{m}_{mathrm{H}_{2}}}{mu_{mathrm{H}_{2}}}=frac{1 * 10^{-3}}{2 * 10^{-3}}=0,5 text { (моль) }]

Зная молярную массу гелия из таблицы Менделеева, рассчитаем количество молей гелия в смеси:

[mathrm{v}_{mathrm{He}}=frac{mathrm{m}_{mathrm{He}}}{mu_{mathrm{He}}}=frac{4 * 10^{-3}}{20 * 10^{-3}}=0,2 text { (моль) }]

Теперь можно найти парциальное давление каждого из компонентов с помощью уравнения Менделеева-Клапейрона:

[mathrm{p}_{mathrm{i}} mathrm{V}=mathrm{v}_{mathrm{i}} mathrm{RT}]

Сначала нужно рассчитать давление водорода:

[mathrm{p}_{mathrm{H}_{2}} mathrm{~V}=mathrm{v}_{mathrm{H}_{2}} mathrm{RT} rightarrow mathrm{p}_{mathrm{H}_{2}}=frac{mathrm{v}_{mathrm{H}_{2}} mathrm{RT}}{mathrm{V}}=frac{0,5 * 8,31 * 290}{1}=1205 text { (Па) }]

Рассчитаем парциальное давление гелия:

[mathrm{p}_{mathrm{He}}=frac{mathrm{v}_{mathrm{He}} mathrm{RT}}{mathrm{V}}=frac{0,2 * 8,31 * 290}{1}=482 text { (Па) }]

Теперь найдём полное давление газовой смеси, сложив значения компонентов:

[mathrm{p}=mathrm{p}_{mathrm{H}_{2+}} mathrm{p}_{mathrm{H}}=1205+482=1687 text { Па }]

Ответ: парциальное давление гелия равно 482 Па, а общее давление 1205 Па.

Задача №2

Условие: идеальная газовая смесь состоит из 0,5 кг углекислого газа и 0,25 кг кислорода, какой объём они займут, если давление равно 1 атм, а температура смеси равна 300 К?

Решение.

Найдём суммарную массу газовой смеси:

[mathrm{m}=mathrm{m}_{mathrm{O}_{2}}+mathrm{m}_{mathrm{CO}_{2}}=0,5+0,25=0,75 text { (кг) }]

Вычислим массовые компоненты смеси:

[g_{mathrm{O}_{2}}=frac{0,25}{0,75}=0,33] [mathrm{g}_{mathrm{CO}_{2}}=frac{0,5}{0,75}=0,67]

Тогда газовая постоянная смеси равняется:

[mathrm{R}_{mathrm{sm}}=mathrm{R} sum_{mathrm{i}=1}^{mathrm{N}} frac{mathrm{g}_{mathrm{i}}}{mu_{mathrm{i}}}=8,31left(frac{0,33}{32 * 10^{-3}}+frac{0,67}{46 * 10^{-3}}right)=200left(frac{text { Дж }}{text { кгК }}right)]

Пользуясь уравнением Менделеева-Клапейрона, и, зная, что 1 атм равна 10⁵Па,вычислим объём смеси:

[mathrm{V}_{mathrm{sm}}=frac{mathrm{m}_{mathrm{sm}} mathrm{R}_{mathrm{sm}} mathrm{T}_{mathrm{sm}}}{mathrm{P}_{mathrm{sm}}}=frac{0,75 * 200 * 300}{10^{5}}=0,45left(mathrm{м}^{3}right)]

Ответ: при заданных условиях смесь займёт 0,45 м^3.

Навык определения парциальных давлений и объёма актуален в машиностроении, энергетике и других промышленностях, связанных с использованием тепловых двигателей, приводимых в действие парами высокой температуры.

Источник

Для сравнения
количества газов в смеси по объему,
необходимо их объемы при температуре
смеси привести к
одинаковому
давлению.

Если этим
одинаковым давлением
является давление смеси
,
то приведенные
к этому
давлению объемы
компонентов называются парциальными.

Парциальный
(приведенный) объем

— это объем, который занимал бы i-тый
компонент, если бы он один находился
при температуре
и давлении смеси .

Для понимания
физического смысла парциального объема
рассмотрим смесь двух идеальных газов.
Как отмечалось ранее, молекулы обоих
газов равномерно распределены по всему
объему ,
занимаемому смесью при давлении
и температуре .

Представим себе,
что каким-то
образом удалось разделить
молекулы этих двух газов так, что в общем
объеме
первый газ занимает объем ,
а второй —
при одинаковой температуре .
Для того, чтобы эта гипотетическая
система находилась в
равновесии
и газы не
смешивались
за счет разности давлений, давление в
объемах
и
должно быть одинаковым
и равным общему давлению смеси ,
т. е.

Или в общем случае

Типичной
студенческой ошибкой
является подстановка в это уравнение
вместо
давления смеси

величины парциального давления .

1.4.4. Задание состава смеси идеальных газов объемными долями.

Во многих практических
задачах состав смеси газов задается
объемными долями:

где:
— парциальный объем i-го
газа в составе смеси газов, занимающей
объем .

Установим связь
между объемными и мольными долями газов
смеси.

Т. к. универсальная
газовая постоянная
Дж / (кмоль · К)

связана с удельными
газовыми постоянными ,
Дж / (кг · К), соотношением

то из определения
парциального объема идеального газа в
составе смеси получим:

или
,

где: -число
киломолей i-го
газа.

Просуммировав
значения
для всех газов, входящих в смесь, получим

где:
и

Разделив выражения
для
на выражение для
получим

Т. о. для смеси
идеальных
газов мольная
и объемная доли i-го
газа
равны между
собой по величине

1.4.5. Формулы пересчета для различных способов задания состава газовых смесей

Получим формулу
пересчета мольных долей на массовые и
наоборот.

Т. к. и ,
то
.

Разделив числитель
и знаменатель полученного выражения
на массу смеси
получим

или окончательно:

Т. к. и ,

то .

Разделив числитель
и знаменатель этого выражения на
получим ,

или окончательно

1.4.6. Кажущаяся молекулярная масса смеси газов

Для упрощения
расчетов смесь идеальных газов условно
полагают однородным
газом с той
же суммарной массой
и с тем же
суммарным числом молекул,
равным

где
— число молекул в единице объема смеси
газов;

— число Авогадро
(число молекул в одном киломоле вещества):

, 1 / кмоль

Молекулярная масса
такого однородного газа обозначается

и называется кажущейся молекулярной
массой смеси:

Разделив числитель
и знаменатель этого выражения на ,
получим ,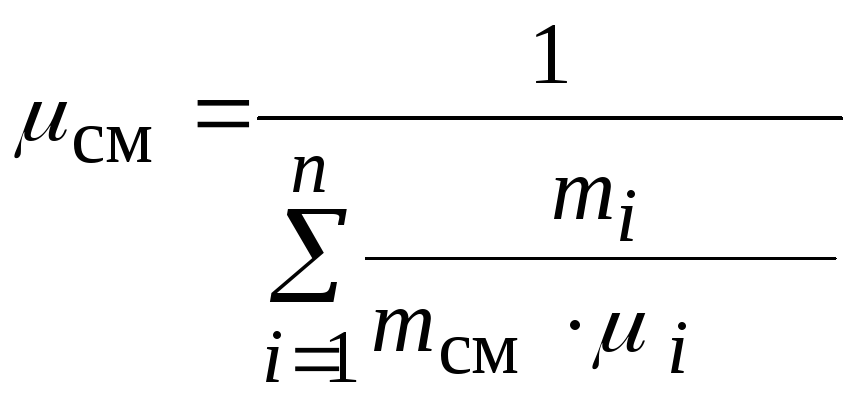

или окончательно

Через мольные доли
величина
выражается проще:

или окончательно

Источник

Андрей Геннадьевич Блохин

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Так как парциальное давление и парциальный объем — понятия, относящиеся к смесям газов, определим сначала, что такое смесь идеальных газов. Итак, смесью газов, называется совокупность нескольких разных газов, невступающих в химическую реакцию при заданных условиях. При других условиях (например, повышении давления) те же газы могут химически реагировать. Смеси характеризуются такой физической величиной, как весовая концентрация $g_i$ i — го газа, являющегося компонентом смеси, при этом:

где N — общее количество разных газов в смеси,

и молярной концентрацией $x_i i-го$ газа в смеси, при этом:

где ${nu }_i$- количество молей $i-го$ газа в смеси.

Что такое парциальное давление

Характеристикой состояния компоненты смеси идеальных газов является парциальное давление.

Определение

Парциальное давление $(p_{i })$ $i-го$ газа в смеси называется давление, которое создавал бы этот газ, если кроме него все остальные газы отсутствовали, но объем и температура остались неизменными.

[p_{i }=frac{m_i}{{mu }_i}frac{RT}{V}=н_ifrac{RT}{V} left(3right),]

где $V- $объем смеси, $T$- температура смеси. Здесь необходимо отметить, что вследствие равенства средних кинетических энергий молекул смесей можно говорить о равенстве температур всех компонент смесей в состоянии термодинамического равновесия.

Давление смеси идеальных газов p определяется по закону Дальтона:

[p=sumlimits^N_{i=1}{p_i}=frac{RT}{V}sumlimits^N_{i=1}{{nu }_i} left(4right).]

Следовательно, парциальное давление, можно выразить как:

[p_i=x_ip left(5right).]

Что такое парциальный объем

Другим важным параметром состояния смеси газов является парциальный объем.

Определение

Парциальным объемом $V_i$ $i-го$ газа в смеси называют тот объем, который имел бы газ, если бы из смеси убрали все остальные газы, при неизменной температуре и объеме:

[V_i=н_ifrac{RT}{p}left(6right).]

«Парциальное давление и объём» 👇

Для смеси идеальных газов выполняется закон Амага:

[V=sumlimits^N_{i=1}{V_i}left(7right).]

Действительно, если из (6) выразить ${nu }_i$ и подставить в (4), получим:

[{nu }_i=frac{pV_i}{RT};; p=frac{RT}{V}frac{p}{RT}sumlimits^N_{i=1}{V_i}to V=sumlimits^N_{i=1}{V_i}]

Парциальный объем можно рассчитать по формуле:

[V_i=x_iV left(8right).]

Параметры состояния смеси идеальных газов подчиняются уравнению Менделеева — Клайперона в следующем виде:

[pV=frac{m}{{mu }_{sm}}RT left(9right),]

где все параметры в уравнении (9) относятся к смеси в целом.

Или уравнение (9) иногда удобнее записывать в таком виде:

[pV=mR_{sm}T left(10right),]

где $R_{sm}=frac{R}{{mu }_{sm}}=Rsumlimits^N_{i=1}{frac{g_i}{{mu }_i}}$ — удельная газовая постоянная смеси.

Пример 1

Задание: При 290 K в сосуде объемом 1$м^3$ содержится 0,5${cdot 10}^{-3}$ кг водорода и 0,10${cdot 10}^{-3}$ кг гелия. Найдите парциальное давление гелия и давление смеси.

Решение:

Найдем количество молей для каждой компоненты смеси, используя формулу:

[{nu }_i=frac{m_i}{{mu }_i} left(1.1right),]

тогда количество молей водорода в смеси, если с помощью таблицы Менделеева находим, что молярная масс водорода ${mu }_{H_2}=2cdot {10}^{-3}frac{кг}{моль}$:

[{nu }_{H_2}=frac{m_{H_2}}{{mu }_{H_2}}]

Проведем расчет:

[{nu }_{H_2}=frac{0,5{cdot 10}^{-3}}{2cdot {10}^{-3}}=0,25 (моль)]

Аналогично рассчитаем ${nu }_{He} ({mu }_{He}=4cdot {10}^{-3}frac{кг}{моль}):$

[{nu }_{He}=frac{0,10{cdot 10}^{-3}}{4cdot {10}^{-3}}=0,025 left(мольright).]

Используем уравнение Менделеева — Клайперона найдем парциальные давления каждой компоненты смеси:

[p_iV={nu }_iRT left(1.2right).]

Тогда давление водорода:

[p_{H_2}V={nu }_{H_2}RTto p_{H_2}=frac{{nu }_{H_2}RT}{V}left(1.3right)]

Рассчитаем парциальное давление водорода:

[p_{H_2}=frac{0,25cdot 8,31cdot 290}{1}=602,5 (Па)]

Аналогично найдем парциальное давление гелия:

[p_{He}=frac{0,025cdot 8,31cdot 290}{1}=60,25 (Па)]

Давление смеси найдем как сумму давлений составляющих ее компонент:

[p=p_{H_2}+p_{He} left(1.4right).]

Следовательно, давление смеси равно:

$p=602,5+60,25=662,75$ (Па)

Ответ: Парциальное давление гелия равно $60,25$ Па, давление смеси $662,75$ Па.

Пример 2

Задание: В состав смеси газов входят 0,5 кг $O_2$ и 1 кг $CO_2$. Определить объем, который займет смесь газов при давлении в одну атмосферу, если газы считать идеальными. Температуру смеси принять равной 300 К.

Решение:

Найдем массу смеси газов:

[m=m_{O_2}+m_{CO_2}left(2.1right).]

Следовательно,

[m=1+0,5=1,5 left(кгright).]

Найдем массовые компоненты смеси $g_i$:

[g_{O_2}=frac{0,5}{1,5}=0,33]

[g_{CO_2}=frac{1}{1,5}=0,67]

Рассчитаем газовую постоянную смеси:

[R_{sm}=Rsumlimits^N_{i=1}{frac{g_i}{{mu }_i}} (2.2)]

[R_{sm}=8,31left(frac{0,33}{32cdot {10}^{-3}}+frac{0,67}{46cdot {10}^{-3}}right)=200 left(frac{Дж}{кгК}right)]

Выражение для объема смеси, полученное из уравнение Менделеева — Клайперона:

[V_{sm}=frac{m_{sm}R_{sm}T_{sm} }{p_{sm}}left(2.3right)]

Проведем вычисления объема, учитывая, что p=1атм.=$ {10}^5Па$:

[V_{sm}=frac{1,5cdot 200cdot 300}{{10}^5}=0,9 м^3]

Ответ: Смесь занимает объем 0,9 $м^3.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Загрузить PDF

В химии «парциальным давлением» называют давление, которое оказывает отдельно взятый компонент из газовой смеси внешней среды, например, на колбу, баллон или границу атмосферы. Вы можете подсчитать давление каждого газа, если знаете его количество, какой объем он занимает и какова его температура. Затем вы можете сложить парциальные давления и найти общее парциальное давление смеси газов, или найдите вначале общее давление, а затем — парциальное.

1
Примите каждый газ как «идеальный». В химии «идеальный газ» — тот, который взаимодействует с другими веществами, не вступая с ними в соединение. Отдельные молекулы могут сталкиваться друг с другом и отталкиваться, как шары для бильярда, не деформируясь при этом.^[1]
- Давление идеального газа возрастает, если его поместить в меньший объем, и уменьшается, если газ находится в большем объеме. Это отношение называется законом Бойля-Мариотта, по имени ученых Роберта Бойля и Эдма Мариотта. Математическая запись закона: k = P x V или, упрощенно, k = PV, где k представляет константу соотношения, P — давление, а V — объем.^[2]
- Давление может быть указано в нескольких различных единицах. Одна из них, Паскаль (Па), определяется как сила в 1 ньютон, приложенная к площади в 1 квадратный метр. Другой вариант представления давления — в атмосферах (атм). Эта единица определяется как давление земной атмосферы на уровне моря. Давление в 1 атмосферу равно 101,325 Па.^[3]
- Температура идеального газа возрастает при увеличении его объема и снижается при уменьшении объема. Это отношение называют законом Чарльза, по имени Жака Чарльза. Математическая запись закона: k = V / T, где k — константа соотношения между объемом и температурой, V вновь представляет объем газа, а T — его температуру.^[4]^[5]
- Температура газов в этих уравнениях приведена в градусах Кельвина, ее можно найти, прибавив 273 к числу градусов Цельсия в температуре газа.
- Эти два отношения можно объединить в одно уравнение: k = PV / T, которое также можно записать как PV = kT.
2
Определите количество газов. У газов есть и масса, и объем. Объем обычно измеряют в литрах (л), но есть два варианта подсчета массы.
- Обычно массу измеряют в граммах или, если она достаточно велика, в килограммах.
- Поскольку газы обычно весят очень мало, их масса также вычисляется в отдельной единице измерения, называемой молекулярной массой, или молярной массой. Молярная масса определяется как сумма атомарных весов всех атомов в газообразном веществе, каждый атом сравнивается с массой карбона (12)^[6]
- Поскольку атомы и молекулы слишком малы, чтобы работать с ними непосредственно, количество газа определяется в молях. Количество молей в данном газе можно найти, разделив массу на молярную массу, значение отмечается буквой n.
- Мы можем заменить постоянную k константу в уравнении газа числом n, количеством молей (mol), и ввести новую константу R. Тогда уравнение будет записано в виде nR = PV/T или PV = nRT.^[7]
- Значение R зависит от единиц, в которых измеряются давление газа, объемы и температура. Для объема в литрах, температуры в Кельвинах и давления в атмосферах, значение равно 0,0821 л атм/K мол. Это можно записать в виде 0,0821 л атм K^-1 мол ^-1, чтобы избежать использования разделительной черты при указании единиц измерения.^[8]
3
Понимание закона Дальтона о парциальном давлении. Закон, открытый химиком и физиком Джоном Дальтоном, который первым предположил, что химические элементы состоят из отдельных атомов,^[9] гласит: общее давление смеси газов равняется сумме давлений каждого газа в смеси.
- Закон Дальтона можно записать в таком виде: P_общее = P₁ + P₂ + P₃ … с таким количеством слагаемых после знака равенства, каково количество газов в смеси.
- Уравнение закона Дальтона можно расширить при работе с газами, чье индивидуальное давление неизвестно, но для которых известны температура и объем. Парциальное давление газа — такое же, как и для равного объема газа, полностью занимающего отведенный объем.
- Для каждого парциального давления мы можем переписать уравнение идеального газа. Вместо PV = nRT мы может оставить только P в левой части перед знаком равенства. Чтобы сделать это, обе части уравнения нужно разделить на V: PV/V = nRT/V. Две V слева сокращаются, остается P = nRT/V.
- Затем для каждого P справа мы можем выполнить замену, вписав уравнение парциального давления: P_общее =(nRT/V) ₁ + (nRT/V) ₂ + (nRT/V) ₃ …
Реклама

1
Определите уравнение парциального давления для газов, с которыми вы работаете. Для вычислительных целей возьмем пример: в колбе объемом 2 литра содержится 2 газа, нитроген (N₂), оксиген (O₂) и карбон диоксид, углекислый газ (CO₂). Каждого газа — по 10 г, температура каждого газа в колбе равна 37 градусам Цельсия. Нужно найти парциальное давление каждого газа и общее давление смеси газов на емкость.
- Наше уравнение парциального давления будет выглядеть следующим образом: P_total = P_{нитроген} + P_{оксиген} + P_{карбон диоксид}.
- Поскольку мы пытаемся найти давление, которое оказывает каждый из газов, знаем объем и температуру и можем найти количество молей каждого газа, основываясь на массе вещества, мы можем переписать уравнение в следующей форме: P_общее =(nRT/V) _{нитроген} + (nRT/V) _{оксиген} + (nRT/V) _{карбон диоксид}
2

Переведите температуру в градусы Кельвина. Температура по Цельсию равна 37 градусам, потому мы добавим 273 к 37 и получим 310 градусов K.
3
Найдите количество молей каждого газа в образце. Число молей газа равно массе газа, деленной на его молярную массу,^[10] которая, как уже говорилось, равна сумме весов всех атомов в составе.
- Для нашего первого газа, нитрогена (N₂), каждый атом обладает атомарной массой 14. Поскольку нитроген содержит два атома (состоит из двухатомных молекул), мы должны умножить 14 на 2, чтобы найти молярную массу нитрогена, она равна 28. Затем мы делим массу в граммах, 10 г, на 28, чтобы получить количество молей, которое приблизительно равно 0,4 моль.
- У второго газа, оксигена (O₂), масса каждого атома равна 16. Оксиген также двухатомный газ, потому мы умножаем 16 на 2 и получаем молярную массу, равную 32. Разделив 10 г на 32, мы получим примерно 0,3 моль оксигена в составе образца смеси газов.
- Третий газ, карбон диоксид (CO₂), состоит из 3 атомов: одного атома карбона с атомарной массой 12 и двух атомов оксигена, каждый с атомарной массой 16. Мы складываем все три веса: 12 + 16 + 16 = 44 составляет молярную массу. Разделив 10 г на 44, мы получим примерно 0,2 моля карбон диоксида.
4
Подставьте значения для молей, объема и температуры. Наше уравнение будет выглядеть так: P_общее =(0,4 * R * 310/2) _{нитроген} + (0,3 *R * 310/2) _{оксиген} + (0,2 * R *310/2) _{карбон диоксид}.
- Для простоты мы оставили текущие значения единиц измерения. Эти единицы уйдут после математических вычислений, и останутся только те, которые участвуют в определении давления.
5

Подставьте значение константы R. Мы будем указывать парциальное и общее давление в атмосферах, потому используем значение R, равное 0,0821 л атм/K моль. Подстановка этого значения в уравнение дает нам P_общее =(0,4 * 0,0821 * 310/2) _{нитроген} + (0,3 *0,0821 * 310/2) _{оксиген} + (0,2 * 0,0821 * 310/2) _{карбон диоксид}.
6
Подсчитайте парциальное давление каждого газа. Сейчас все значения на месте, пора перейти к математическим вычислениям.
- Чтобы найти парциальное давление нитрогена, умножим 0,4 моль на нашу константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,4 * 0,0821 * 310/2 = 5,09 атм, приблизительно.
- Для получения парциального давления оксигена умножим 0,3 моль на константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,3 *0,0821 * 310/2 = 3,82 атм, приблизительно.
- Чтобы найти парциальное давление карбон диоксида, умножаем 0,2 моль на константу 0,0821 и температуру 310 градусов K, затем делим на 2 литра: 0,2 * 0,0821 * 310/2 = 2,54 атм, приблизительно.
- Теперь сложим полученные значения давлений и найдем общее давление: P_общее = 5,09 + 3,82 + 2,54, или 11,45 атм, приблизительно.
Реклама

1
Определите парциальное давление, как и раньше. Вновь, возьмем в пример колбу на 2 литра с тремя газами: нитрогеном (N₂), оксигеном (O₂) и карбон диоксидом (CO₂). У нас по 10 г каждого газа, температура каждого газа в колбе равна 37 °C.
- Температура по Кельвину будет такой же, 310 градусов, как и раньше, у нас будет примерно 0,4 моль нитрогена, 0,3 моль оксигена и 0,2 моль карбон диоксида.
- Мы также будем указывать давление в атмосферах, потому будем использовать значение 0,0821 л атм/K моль для константы R.
- Таким образом, наше уравнение парциального давления на текущий момент выглядит так же, как раньше: P_общее =(0,4 * 0,0821 * 310/2) _{нитроген} + (0,3 *0,0821 * 310/2) _{оксиген} + (0,2 * 0,0821 * 310/2) _{карбон диоксид}.
2
Сложите количество молей каждого газа в образце, чтобы найти общее количество молей в смеси газов. Поскольку объем и температура одинаковы для всех газов, не говоря о том, что каждая молярная масса умножается на одну и ту же константу, мы можем использовать распределительное свойство умножения и переписать уравнение в следующем виде: P_общее = (0,4 + 0,3 + 0,2) * 0,0821 * 310/2.
- Складываем 0,4 + 0,3 + 0,2 = 0,9 моль смеси газов. Это упростит наше выражение до P_общее = 0,9 * 0,0821 * 310/2.
3

Найдите общее давление смеси газов. Умножаем 0,9 * 0,0821 * 310/2 = 11,45 моль, приблизительно.
4
Найдите пропорцию каждого газа в смеси. Для этого разделите количество молей каждого газа на общее количество молей в смеси.
- У нас 0,4 моль нитрогена, потому 0,4/0,9 = 0,44 (44 процента) в образце, приблизительно.
- У нас 0,3 моль оксигена, потому 0,3/0,9 = 0,33 (33 процента) в образце, приблизительно.
- У нас 0,2 моль карбон диоксида, потому 0,2/0,9 = 0,22 (22 процента) в образце, приблизительно.
- Хотя в вычислениях выше сумма приблизительных значений в процентах дает всего 0,99, точные значения являются периодическими, так что сумма на самом деле будет равна повторяющимся девяткам после запятой. По определению это то же самое, что 1 или 100 процентов.
5
Умножим пропорциональное количество каждого газа на общее давление, чтобы найти парциальное давление.
- Умножаем 0,44 * 11,45 = 5,04 атм, приблизительно.
- Умножаем 0,33 * 11,45 = 3,78 атм, приблизительно.
- Умножаем 0,22 * 11,45 = 2,52 атм, приблизительно.
Реклама

Советы

Вы заметите небольшую разницу в значениях при вычислении сначала парциального давления, а затем общего, и при подсчете вначале общего, а затем парциального давления. Помните, что приведенные значения даны приблизительно, поскольку они округлены до 1 или 2 знаков после запятой для простоты подсчетов и понимания. Если вы выполняете вычисления самостоятельно без округления, вы заметите или меньшую разницу между значениями или не заметите ее вовсе.

Предупреждения

Знание парциального давления газов может стать вопросом жизни и смерти для дайверов. Слишком низкое парциальное давление кислорода может привести к бессознательному состоянию или смерти, но слишком высокое парциальное давление азота или кислорода также может привести к отравлению.^[11]^[12]

Вам потребуются

Калькулятор
Справочник атомарных весов / молярных масс

Об этой статье

Эту страницу просматривали 82 723 раза.

Была ли эта статья полезной?

Источник